End Face Attitude Detection of Special Steel Bars Based on Improved DBSCAN
Abstract
:1. Introduction
- A circle detection algorithm based on improved DBSCAN is proposed, which overcomes the problem that the current circle detection algorithm does not detect circles accurately in complex scenes.
- A method is proposed to represent the circumferential position of the current steel bar using the end face attitude angle, which provides a theoretical foundation for automatic surface defect location.
- An end face attitude detection system is proposed to solve the problem that surface defects of special steel bars cannot be located during automatic grinding.
2. Related Work and Related Definition
2.1. Related Work
2.2. Related Definitions
2.2.1. Definition for Circle Parameters of Connected Regions
2.2.2. Definition of Circle Parameter Density
- (1)
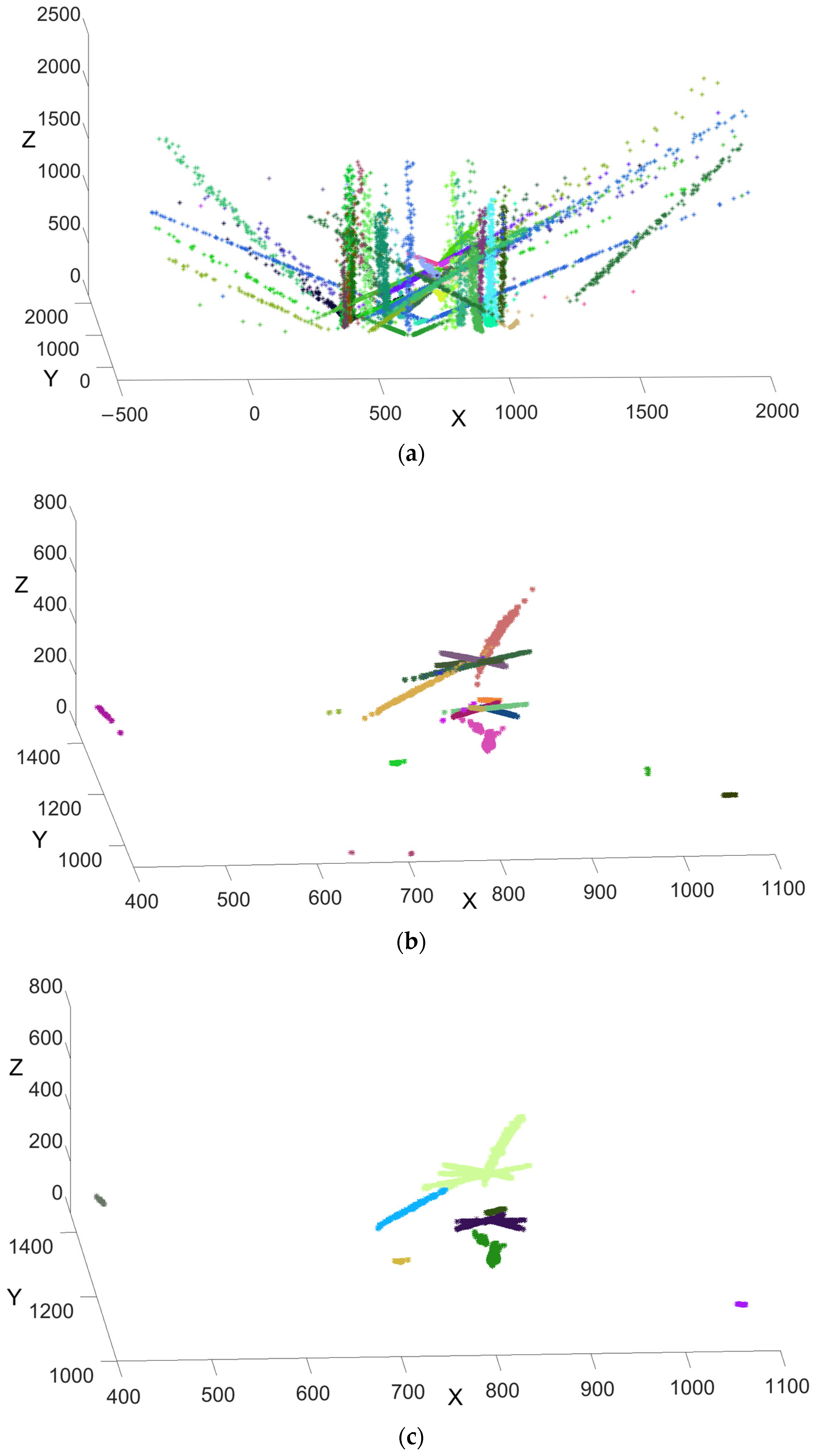
- Establish a coordinate system: As we know, are three-dimensional data , and a three-dimensional coordinate system can be established. Then, the circle parameter data are mapped to the three-dimensional coordinate .
- (2)
- Division of a cube block: In order to characterize the circle parameter data distribution, the maximum value , , and the minimum value , , in the three directions of X, Y and Z are taken, respectively, and the planes are drawn with Equations (5)–(7). Then the cube with a side length of is established.
- (3)
- Definition of circle parameter density: For any , it must fall in a certain cube , which is denoted as . If the number of in block is denoted as , the density of block can be defined as follows:
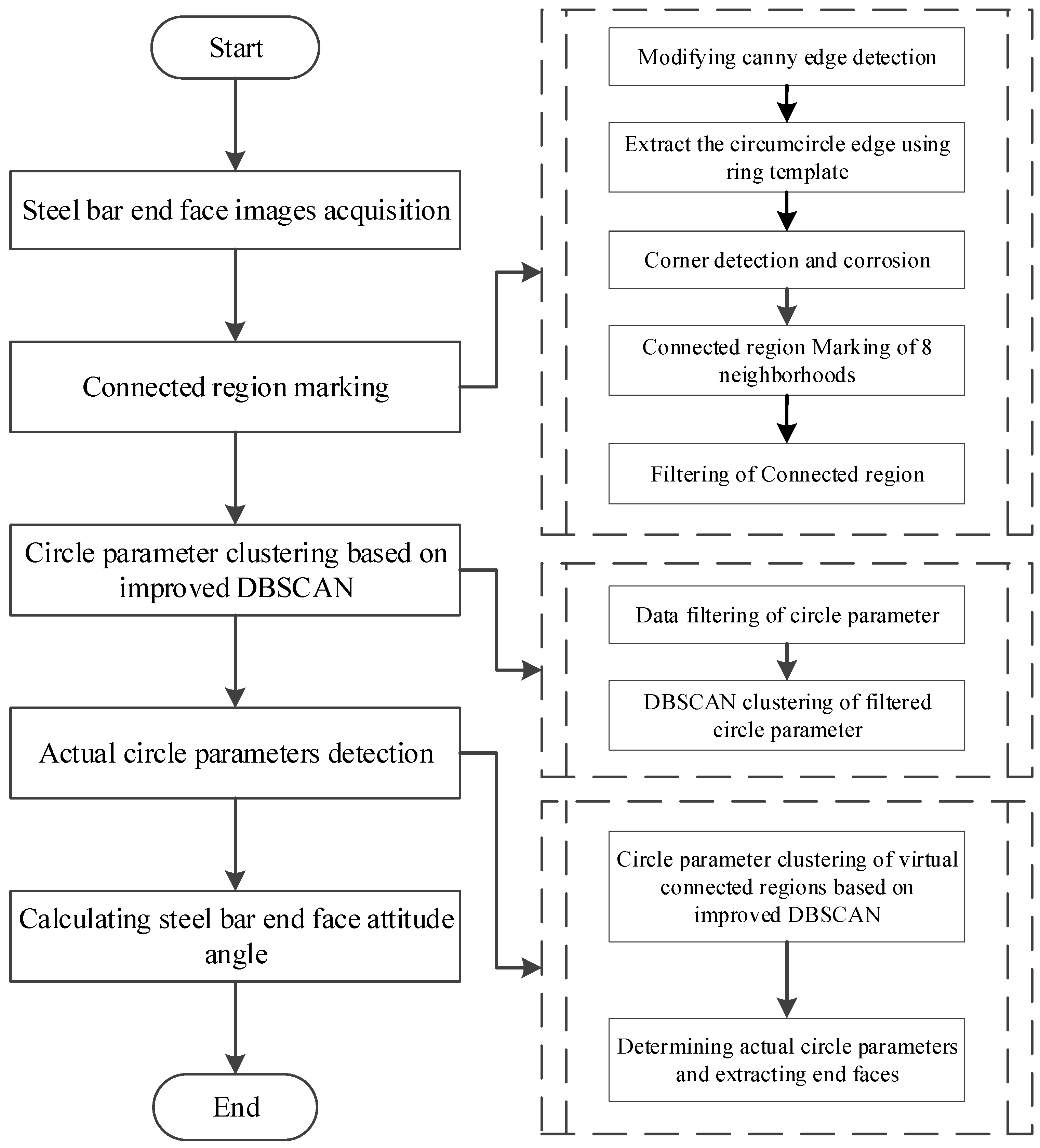
3. Proposed End Face Attitude Detection Algorithm for Special Steel Bars
3.1. Connected Regions Marking
3.1.1. Modifying Canny Edge Detection
3.1.2. Marking the Connected Regions
3.2. Circle Parameter Clustering Based on Improved DBSCAN
- (1)
- In order to reduce the large amount of useless data involved in clustering, and the circle parameter filtering is completed according to the following steps:
- (a)
- The coordinates of the circle center are set as the X and Y axes, respectively, and the coordinates of the radius are set as the Z axis. At this time, all the circle parameters are mapped to a three-dimensional coordinate .
- (b)
- According to Equation (8), the number of data is counted in the j-th cube, whose side length is , and the density values of cubes are acquired.
- (c)
- We set the cube density threshold to be ; when density value of a cube is , delete all data points in the cube, otherwise reserve them. The data filtering of the circle parameter data is completed. The result of the filtering can be seen in Figure 5b, and the same color in Figure 5b indicates that the filtered circle parameter data belong to the same connected region. After filtering, most of the invalid circle parameters are filtered out.
- (2)
- The core object, clustering number, unvisited sample set, and cluster division are initialized to , , , and , respectively.
- (3)
- For , all core objects are found as follows:
- (a)
- The sample number of the neighborhood subsample set of is calculated using distance measurements.
- (b)
- If the number of samples in the subsample set satisfies , the sample is added to the core object sample set .
- (4)
- If the core object is , the algorithm is ended, otherwise go to step (5).
- (5)
- In the core object set , a core object is selected randomly; the current cluster core object set, clustering number, the current cluster sample set. and the unvisited sample set are updated to , , , and , respectively.
- (6)
- If the current cluster core object queue , the current cluster is generated, and the cluster division and the new core object set are updated to and , respectively, then go to step (4).
- (7)
- A core object is fetched from the current cluster core object queue , the sample number of the neighborhood subsample set is found according to the distance neighborhood; let , and the current cluster sample set, the unvisited sample set, and the current cluster core object queue are updated to , , and , then go to step (6).
3.3. Actual Circle Parameter Detection
3.3.1. Generation of Virtual Connected Regions
3.3.2. Circle Parameter Clustering Results of Virtual Connected Regions
3.3.3. Determination of Circle Parameters
3.3.4. Verification of Circle Parameters
3.4. Acquisition of the Special Steel Bar End Face Attitude
3.4.1. Calculation steps of the Special Steel Bar End Face Attitude
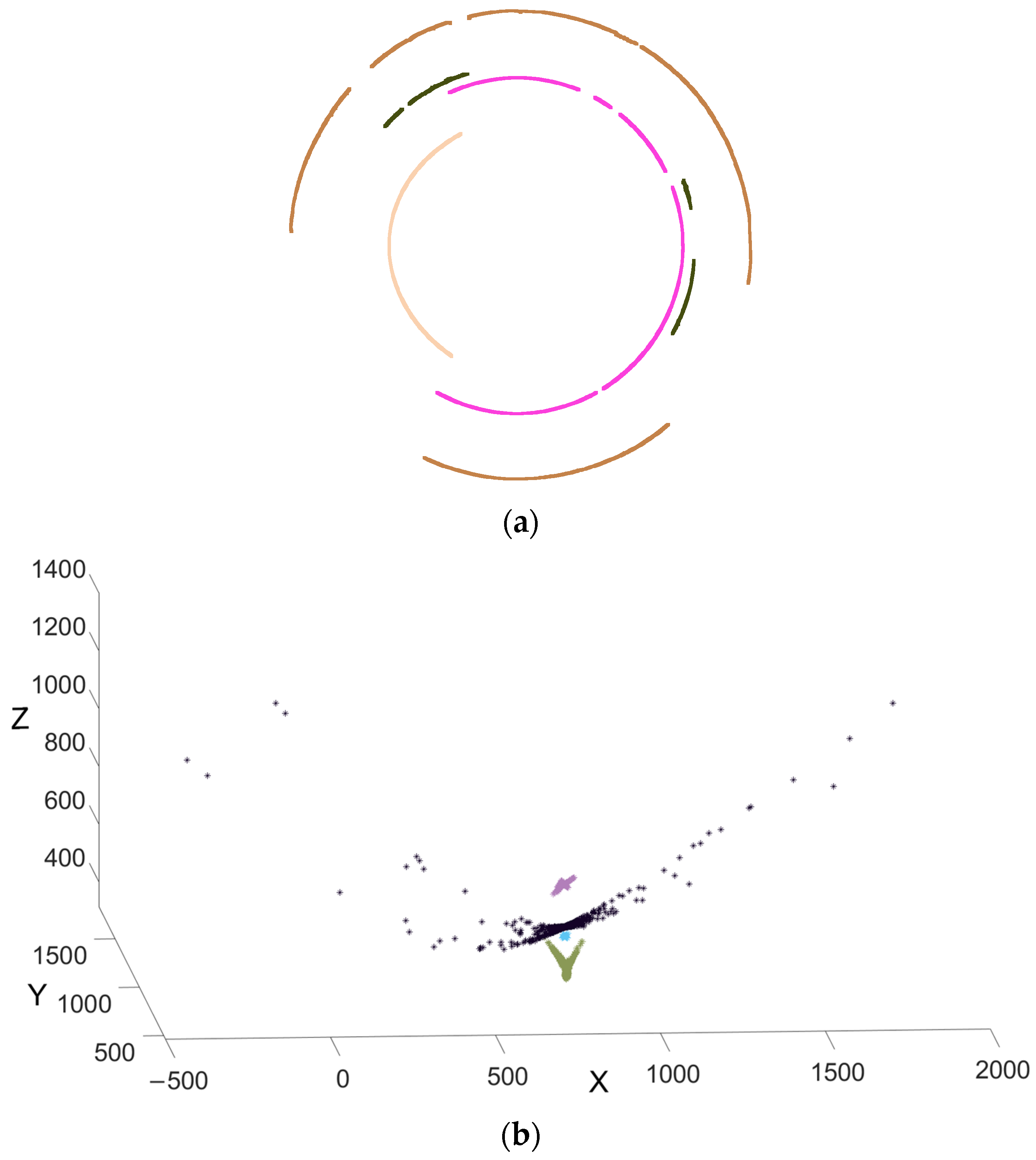
- (1)
- The circumcircle of the steel bar’s end face is detected according to our method, and the circle center and radius of the circumcircle are obtained. The results are shown in Figure 7b.
- (2)
- No matter how the steel bar is rotated, the circumcircle center of its end face remains the same. Therefore, the circumcircle center is taken as the coordinate origin . The horizontal and rightward direction passing through the origin is taken as the positive direction of the X-axis. The vertical upward direction passing through the origin is taken as the positive direction of the Y-axis, resulting in a Cartesian coordinate system .
- (3)
- The two-dimensional code on the steel bar’s end face is detected and identified, and the steel bar product information as well as the four endpoint positions of the two-dimensional code can be obtained.
- (4)
- The QR code end point is selected that is farthest from the center of the bar, and the angle between the vector and the positive direction of the X-axis is calculated, so the current attitude angle of the steel bar end face is obtained. The results are shown in Figure 7c, and the attitude angle is 25.393 degrees.
3.4.2. Fast Calculation Method of the Special Steel Bar End Face Attitude
4. Result Analysis of Steel Bar End Face Attitudes
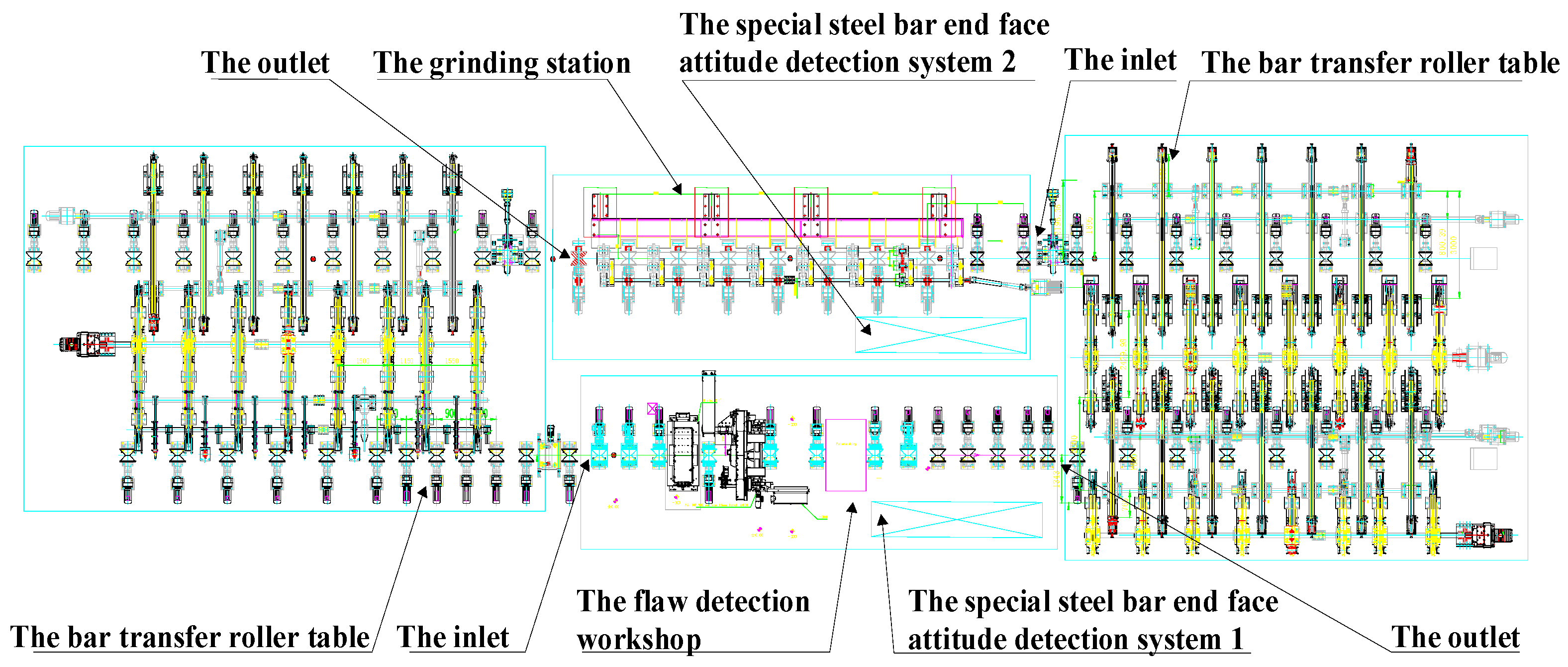
4.1. Constructing of Experimental Devices
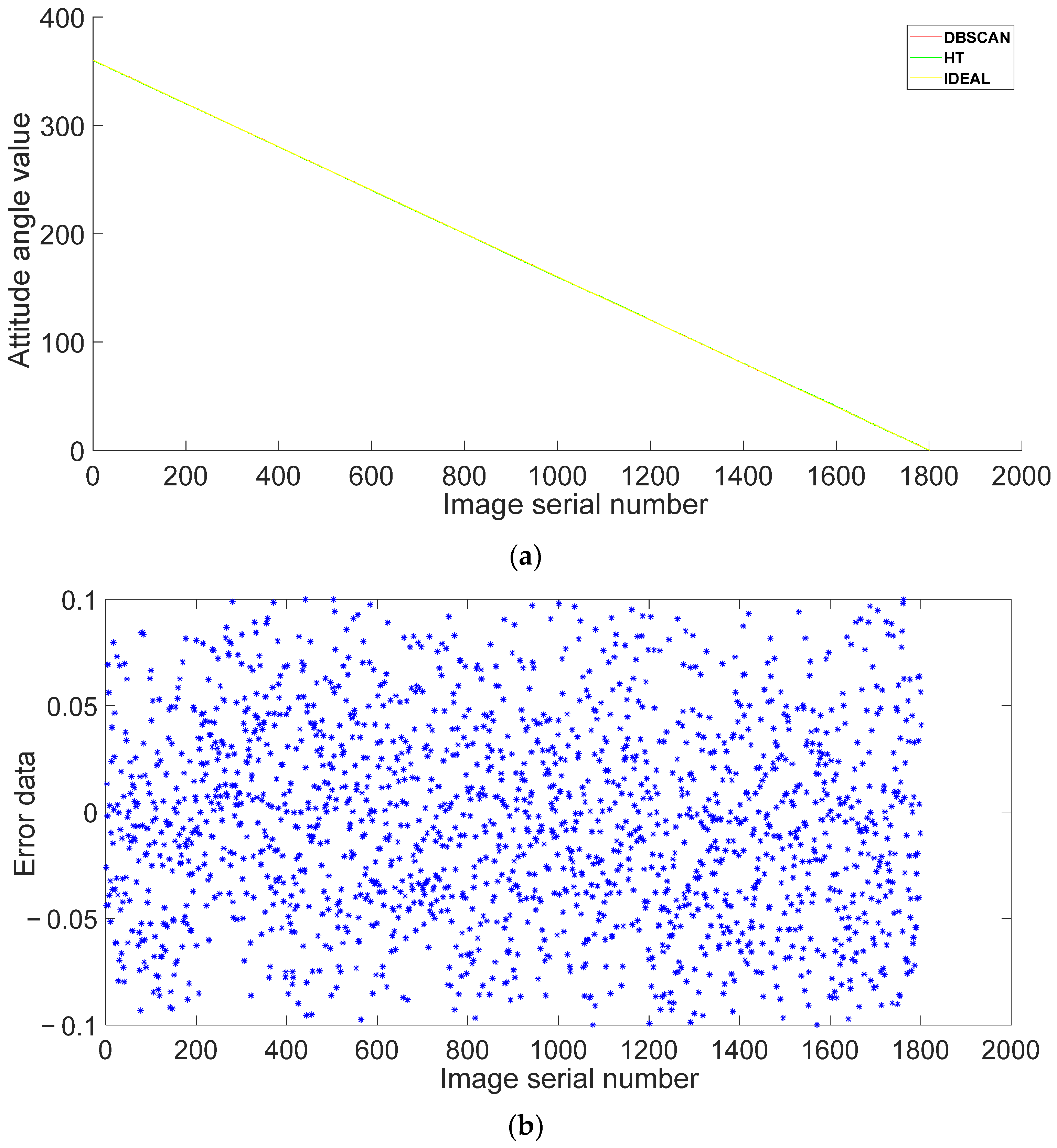
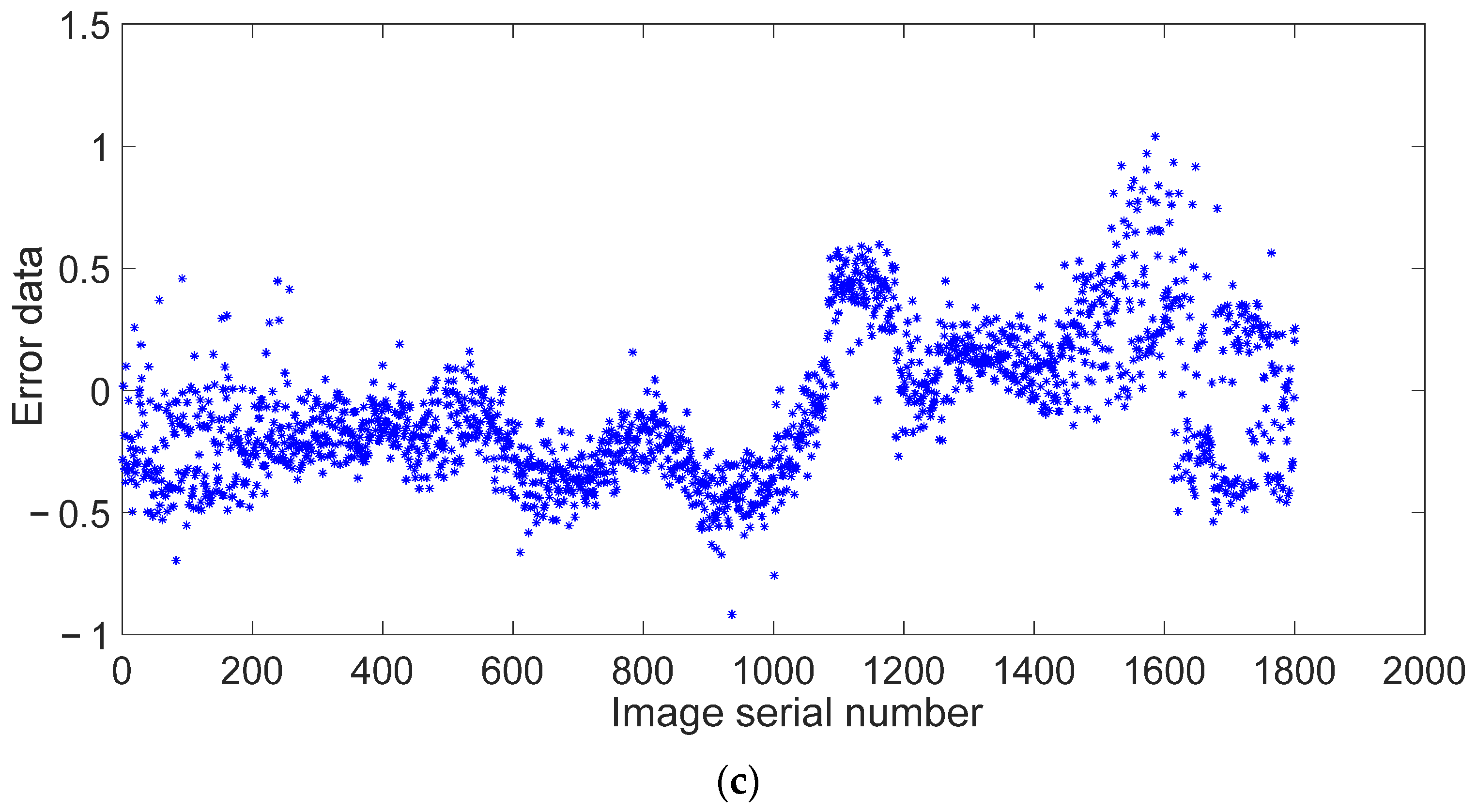
4.2. Analysis of Steel Bar End Face Attitude Detection Results
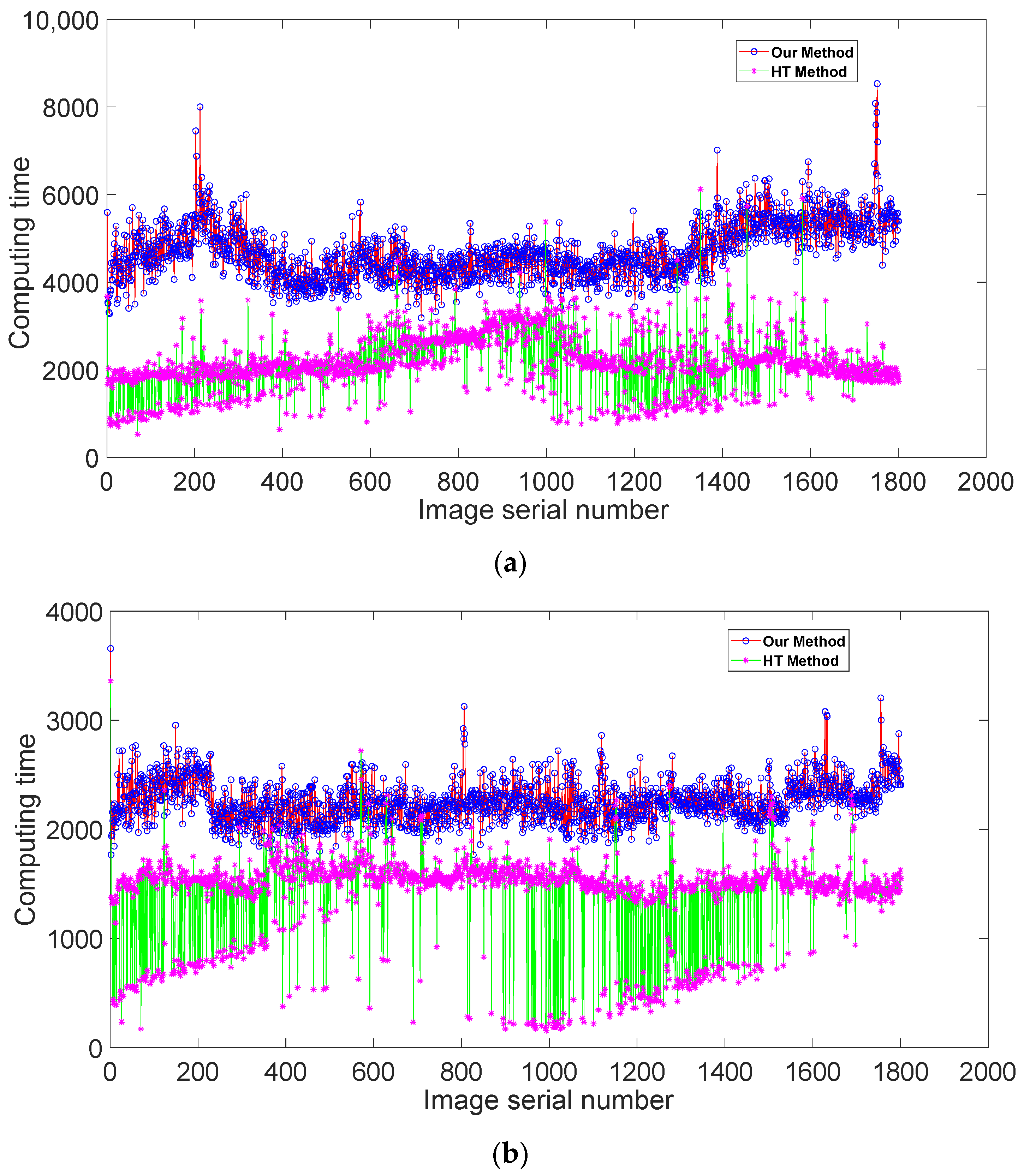
4.3. Estimation of Algorithm Execution Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, S.; Tian, M.; Xiao, P.; Pei, C.; Chen, Z.; Takagi, T. A hybrid nondestructive testing method of pulsed eddy current testing and electromagnetic acoustic transducer techniques for simultaneous surface and volumetric defects inspection. NDT E Int. 2017, 86, 153–163. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, L.; Xie, F. A method of steel ball surface quality inspection based on flexible arrayed eddy current sensor. Measurement 2019, 144, 192–202. [Google Scholar] [CrossRef]
- Ma, Q.; Gao, B.; Tian, G.; Yang, C.; Xie, L.; Chen, K. High sensitivity flexible double square winding eddy current array for surface micro-defects inspection. Sens. Actuators A Phys. 2020, 309, 111844. [Google Scholar] [CrossRef]
- Wu, D.; Liu, Z.; Wang, X.; Su, L. Mechanism analysis of influence of surface-breaking orientation on magnetic leakage field distribution. Acta Phys. Sin. 2017, 4, 262–272. [Google Scholar]
- Kikuchi, H.; Tschuncky, R.; Szielasko, K. Challenges for detection of small defects of submillimeter size in steel using magnetic flux leakage method with higher sensitive magnetic field sensors. Sens. Actuators A Phys. 2019, 300, 111642. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Xiao, J.; Yang, Z.; Wu, B.; He, C. A comparative study between magnetic field distortion and magnetic flux leakage techniques for surface defect shape reconstruction in steel plates. Sens. Actuators A Phys. 2019, 288, 10–20. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, H.; Chen, S.; Tian, G. Visual quantitative detection of rail surface crack based on laser ultrasonic technology. Optik 2021, 237, 166732. [Google Scholar] [CrossRef]
- Kou, X.; Pei, C.; Chen, Z. Fully noncontact inspection of closed surface crack with nonlinear laser ultrasonic testing method. Ultrasonics 2021, 114, 106426. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, X.; Qin, X.; Hua, L.; Liu, G.; Guan, S. Laser ultrasonic inspection of defects in wire arc additive manufactured samples with different surface profiles. Measurement 2022, 188, 110597. [Google Scholar] [CrossRef]
- Ramzan, B.; Malik, M.S.; Martarelli, M.; Ali, H.T.; Yusuf, M.; Ahmad, S.M. Pixel frequency based railroad surface flaw detection using active infrared thermography for Structural Health Monitoring. Case Stud. Therm. Eng. 2021, 27, 101234. [Google Scholar] [CrossRef]
- Puthiyaveettil, N.; Thomas, K.R.; Myrach, P.; Ziegler, M.; Rajagopal, P.; Balasubramaniam, K. Defect detection in steel bars up to 600 °C using laser line thermography. Infrared Phys. Technol. 2020, 111, 103565. [Google Scholar] [CrossRef]
- Lei, L.; Ferrarini, G.; Bortolin, A.; Cadelano, G.; Bison, P.; Maldague, X. Thermography is cool: Defect detection using liquid nitrogen as a stimulus. NDT E Int. 2019, 102, 137–143. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, Y. Research progress of surface defect detection method based on machine vision. Chin. J. Sci. Instrum. 2022, 43, 198–219. [Google Scholar]
- He, W.; Jiang, Z.; Ming, W.; Zhang, G.; Yuan, J.; Yin, L. A critical review for machining positioning based on computer vision. Measurement 2021, 184, 109973. [Google Scholar] [CrossRef]
- Koch, C.; Georgieva, K.; Kasireddy, V.; Akinci, B.; Fieguth, P. A review on computer vision based defect detection and condition assessment of concrete and asphalt civil infrastructure. Adv. Eng. Inform. 2015, 29, 196–210. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, H.; Shi, P. Chip Appearance Inspection Method for High-Precision SMT Equipment. Machines 2021, 9, 34. [Google Scholar] [CrossRef]
- Hefetz, I.; Pasternak, Z.; Liptz, Y.; Bet-Yosef, M. Preliminary investigation of the ability of fingerprint examiners in detection of sib-sib relationships based upon finger and palm prints similarities. Forensic Sci. Int. 2022, 337, 111381. [Google Scholar] [CrossRef] [PubMed]
- Song, L. Study on the Control System of the Special Steel Bar End Face Code Spraying Robot. Master’s Thesis, Hebei University of Science and Technology, Shijiazhuang, China, 2021. [Google Scholar]
- Feng, H. Research on the Key Technologies of Cartesian Coordinate Inkjet Robot System. Master’s Thesis, Hebei University of Science and Technology, Shijiazhuang, China, 2021. [Google Scholar]
- Guo, W. Study on Key Technologies of Marking and Recognition for End Faces of Special Steel Bars. Master’s Thesis, Hebei University of Science and Technology, Shijiazhuang, China, 2021. [Google Scholar]
- Peltokorpi, J.; Isojärvi, L.; Häkkinen, K.; Niemi, E. QR code-based material flow monitoring in a subcontractor manufacturer network. Procedia Manuf. 2021, 55, 110–115. [Google Scholar] [CrossRef]
- Li, L.; Qiu, J.; Lu, J.; Chang, C. An aesthetic QR code solution based on error correction mechanism. J. Syst. Softw. 2016, 116, 85–94. [Google Scholar] [CrossRef]
- Cai, J.; Huang, P.; Chen, L.; Zhang, B. An efficient circle detector not relying on edge detection. Adv. Space Res. 2016, 57, 2359–2375. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.W. A two-step circle detection algorithm from the intersecting chords. Pattern Recognit. Lett. 2001, 22, 787–798. [Google Scholar] [CrossRef]
- Soltany, M.; Zadeh, S.T.; Pourreza, H.R. Fast and accurate pupil positioning algorithm using circular hough transform and gray projection. Int. Conf. Comput. Commun. Manag. 2011, 5, 556–561. [Google Scholar]
- Mirzaei, M.; Rafsanjani, H.K. An automatic algorithm for determination of the nanoparticles from TEM images using circular hough transform. Micron 2017, 96, 86–95. [Google Scholar] [CrossRef]
- Berkaya, S.K.; Gunduz, H.; Ozsen, O.; Akinlar, C.; Gunal, S. On circular traffic sign detection and recognition. Expert Syst. Appl. 2016, 48, 67–75. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, L.; Zhang, X. Bundled round bars counting based on iteratively trained SVM. In Proceedings of the International Conference on Intelligent Computing Theories and Application, ICIC 2019, Nanchang, China, 3–6 August 2019; pp. 156–165. [Google Scholar]
- Hough, P.V. Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- Chen, T.; Chung, K.L. An efficient randomized algorithm for detecting circles. Comput. Vis. Image Underst. 2001, 83, 172–191. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Rui, Y.; Zhou, Z.; Cai, X.; Dong, L. A novel robust method for acoustic emission source location using DBSCAN principle. Measurement 2022, 191, 110812. [Google Scholar] [CrossRef]
- Zhang, S. The Applied Research on Image Processing Methods of Bar Automatic Counting. Master’s Thesis, Northeastern University, Shenyang, China, 2009. [Google Scholar]
- Zhu, L. Research on Counting Method of Bundled Bars Based on Machine Learning. Master’s Thesis, Shenyang Ligong University, Shenyang, China, 2020. [Google Scholar]
- Xie, W.; Yu, J.; Zhang, X.; Miao, C.; Zhang, F.; Liu, Z. Robot spraying system for special steel bar end. Hebei Metall. 2020, 11, 70–75. [Google Scholar]
- Zhang, F.; Guo, W.; Huang, Y.; Wang, C.; Huang, F. Study on character recognition algorithm for end face of bundled special steel bars. J. Hebei Univ. Sci. Technol. 2021, 42, 470–480. [Google Scholar]
- Yao, Z.; Yi, W. Curvature aided Hough transform for circle detection. Expert Syst. Appl. 2016, 51, 26–33. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, Z.; Ye, Y.; Jiang, J. Fast circle detection algorithm based on sampling from difference area. Optik 2018, 158, 424–433. [Google Scholar] [CrossRef]
- Chung, K.L.; Huang, Y.; Shen, S.; Andrey, S.K.; Dmitry, V.Y.; Ekaterina, V.S. Efficient sampling strategy and refinement strategy for randomized circle detection. Pattern Recognit. 2012, 45, 252–263. [Google Scholar] [CrossRef]
- Zhao, M.; Jia, X.; Yan, D. An occlusion-resistant circle detector using inscribed triangles. Pattern Recognit. 2021, 109, 107588. [Google Scholar] [CrossRef]
- González, M.R.; Martínez, M.E.; León, M.C.; Cervantes, H.; Brizuela, C.A. Multiple circle detection in images: A simple evolutionary algorithm approach and a new benchmark of images. Pattern Anal. Appl. 2021, 24, 1583–1603. [Google Scholar] [CrossRef]
- Lu, Y.; Duanmu, L.; Zhai, Z.; Wang, Z. Application and improvement of Canny edge-detection algorithm for exterior wall hollowing detection using infrared thermal images. Energy Build. 2022, 274, 112421. [Google Scholar] [CrossRef]





| (a) Research Status of Steel Bar End Face | ||||||
| Zhang [33] | Zhu [34] | Feng [19] | Xie [35] | Zhang [36] | ||
| Purposes | Statistics of the number of steel bars | Statistics of the number of steel bars | Providing positioning data | Providing positioning data | Identifying bars’ end face characters. | |
| Methods | Morphological methods | Iterative training method | Hough transform | Hough transform | Hough transform | |
| Common features | The end face detection mostly uses the HT method, and there is no research on the attitude angle of the end face. | |||||
| (b) Research Status of Circle Detection | ||||||
| HT | CACD | DRSCD | RCD | ITCD | EACD | |
| Shortcomings | Time-consuming, sensitive to noise and occlusions | Need for proper edge detection information | Sensitive to noise, complex scenes, and occlusions | Requires multiple valid points and is sensitive to occlusions | Sensitive to multiple occlusions in large circles | Needs to be improved for real images |
| Main problems | These methods have poor detection results in complex scenes, occlusions, and the presence of minimax circles. | |||||
| ≤0.01 | ≤0.03 | ≤0.05 | ≤0.07 | ≤0.09 | ≤0.10 | ≤0.20 | ≤0.50 | ≤0.80 | ≤1.10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Our Method (%) | 16.89 | 43.17 | 67.78 | 84.94 | 97.17 | 100 | 100 | 100 | 100 | 100 |
| HT method (%) | 2.50 | 5.22 | 9.67 | 13.44 | 17.11 | 18.89 | 41.28 | 94.28 | 99.22 | 100 |
| Without Template | With Template | |||
|---|---|---|---|---|
| HT Method | Our Method | HT Method | Our Method | |
| Maximum (s) | 6.125 | 8.532 | 3.359 | 3.656 |
| Minimum (s) | 0.531 | 3.187 | 0.156 | 1.765 |
| Average (s) | 2.158 | 4.695 | 1.402 | 2.254 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, J.; Wang, T.; Shi, W.; Xiong, X.; Huang, Q. End Face Attitude Detection of Special Steel Bars Based on Improved DBSCAN. Appl. Sci. 2023, 13, 12640. https://doi.org/10.3390/app132312640
Li Z, Zhang J, Wang T, Shi W, Xiong X, Huang Q. End Face Attitude Detection of Special Steel Bars Based on Improved DBSCAN. Applied Sciences. 2023; 13(23):12640. https://doi.org/10.3390/app132312640
Chicago/Turabian StyleLi, Ziliang, Jinzhu Zhang, Tao Wang, Wei Shi, Xiaoyan Xiong, and Qingxue Huang. 2023. "End Face Attitude Detection of Special Steel Bars Based on Improved DBSCAN" Applied Sciences 13, no. 23: 12640. https://doi.org/10.3390/app132312640
APA StyleLi, Z., Zhang, J., Wang, T., Shi, W., Xiong, X., & Huang, Q. (2023). End Face Attitude Detection of Special Steel Bars Based on Improved DBSCAN. Applied Sciences, 13(23), 12640. https://doi.org/10.3390/app132312640







