Two-Phase Non-Singular Terminal Sliding Mode Control of Nonlinear Systems

Abstract

This paper presents a two-phase non-singular terminal sliding mode control scheme for a class of nonlinear systems in the presence of external disturbances. A two-phase terminal sliding mode surface is constructed and utilized, such that our control scheme achieves fast finite-duration convergence in regions both close to and far away from the control objective, by which the transition state is set and a less conservative bound of the settling time is obtained and superior to the existing results. Meanwhile, the singularity is avoided by the utilization of the saturation function, with the simplicity of structure and implementation. Extensions to multi-input multi-output systems are carried out further. The numerical simulation of the single inverted pendulum and the industrial manipulator are conducted to verify the effectiveness of the proposed control strategy.

1. Introduction

Sliding mode control (SMC) has been widely studied due to the simplicity of its structure and computation, and strong robustness to external disturbances and the uncertainties of systems. It has been applied in many industrial systems such as robots, converter systems, motor positioners and so on [1,2,3,4]. SMC is essentially a two-fold nonlinear control method, which consists of (i) the selection of a sliding-mode surface, which determines the expected performance of systems when the system stays in its neighborhood, and (ii) the design of the control strategy, which steers the system to reach and reside on the sliding-mode surface strictly.

The conventional SMC schemes usually adopt the linear sliding-mode surface (LSM), which is inherently a nonlinear control scheme. It suffers from a chattering phenomenon and fails to satisfy the finite time convergence of the system dynamics. To suppress the chattering phenomenon, plenty of methods have been proposed, including but not limited to higher-order sliding modes (HOSM) [5,6,7,8] and super-twisting algorithms (STA) [9,10,11], and disturbance observers [12], and extended state observers [13]. To guarantee the finite time convergence, the terminal sliding mode (TSM) control approach has been developed [14,15,16,17], which applies the nonlinear sliding-mode surface to offer a fast and finite time convergences property and steady tracking performance. However, the singularity issue exists in the TSM control scheme, which is undesirable and may deteriorate the performance to a large extent in practical applications. Substantial research has been undertaken to overcome the singularity problem [18,19,20,21,22,23,24,25,26,27]. An indirect approach can be found in [18,19,20,21,22,23]. Refs [18,20] propose a modified TSM controller for second-order systems, where the power of the sliding surface is different from the common one. In [21], the terminal sliding mode is defined by inserting the arctangent function, suppressing the singularity. Ref. [22] proposes a new sliding variables to achieve the non-singularity. These indirect approaches aim at preventing the occurrence of singularity from the beginning, whereas the direct approach restricts the singularity by the limitation techniques straight [24,25]. The authors of [24,25] utilize the saturation and sinusoidal function, respectively, to restrain the singular term. Furthermore, a derivative and integral TSM control is presented in [28,29]. The sliding mode control can also be combined with other control schemes, such as adaptive control [30,31].

It is noted that the study of the settling time of system dynamics are not involved in the aforementioned literature, which excites more attention recently. The fixed-time stability (FTS), which investigates the estimation of the upper bound of the settling time, is first presented in [32], where the intrinsic feature of the fixed-time convergence is revealed and the application to the design of the SMC controller is also discussed. The most attractive feature of the FTS is that the estimation of the bound of the settling time has nothing to do with the initial condition, which is given as a constant and determined by the system parameters only. There are some studies on the FTS [25,33,34,35]. The authors of [25,33] offer a fast convergence solution for the design of TSM schemes. In [35], a state-dependent exponential coefficient is used in the sliding surface design. On the basis of the FTS, there is a doubt as to whether the bound of the settling time independent of the initial state is optimal or not and whether the selection of the segmentation of the system state is optimal and unique or not. Given this consideration, it is our great passion to improve the convergence property by finding the possibility of a less conservative bound of the settling time through other alternative system states. Based on the above discussion, the merit of the finite-duration attractor (FD) [36] fits in exactly with our wishes; it drives the system to the origin with a selectable transitional system state, leading to the convergence time of systems within a finite width, so that the influence of the initial state is customized by the designer rather than being ignored. Futhermore, the bound of the width is closer to the real one. Hence, how to construct a new attracting law with better convergence performance and more accurate settling time bound where the role of the transitional state and the initial state is a flexible choice inspires our interests.

In this paper, a two-phase terminal sliding mode surface is proposed to design a non-singular terminal sliding mode controller, such that systems undertaken achieve the fast finite-duration convergence in including regions both close to and far away from the control objective, where the merit of FDA is utilized and the constraints on the impact of the initial state and the setting of the transitional state are weakened. Furthermore, the less conservative bound of the settling time is examined with the optional role of the initial state and without the fixed transitional state. The non-singularity is also guaranteed by the utilization of the saturation function, with simplicity of structure and implementation. The numerical simulation of a single inverted pendulum is carried out to verify the effectiveness of the present scheme.

2. Preliminaries

Finite time systems usually can be categorized into these types:

(i) the power rate type, described by $\dot{x}=-k{x}^{\alpha },x\left(0\right)=x_0$, where $0<\alpha <1$ is a fraction where both numerator and denominator are positive odd integers; the settling time function is obtained as $t_s=\frac{x_0^{1-\alpha }}{k(1-\alpha )}$, in which the independent variable is the initial state $x_0$;

(ii) the power rate exponential type, given by $\dot{x}=-px-k{x}^{\alpha },x\left(0\right)=x_0$, where $p>0$, and $0<\alpha <1$ is a fraction where both numerator and denominator are positive odd integers; the settling time function is derived as $t_s=\frac{1}{p(1-\alpha )}ln(1+\frac{p}{k}{x}_0^{1-\alpha })$, similarly depending on the initial state $x_0$;

(iii) the double power rate type, depicted as $\dot{x}=-k_1{x}^{\alpha }-k_2{x}^{\beta },x\left(0\right)=x_0$, where $0<\alpha <1$ and $\beta >1$ are fractions where both numerator and denominator are positive odd integers; the settling time function is $t_s=\frac{x_0^{1-\alpha }}{k_1(1-\alpha )}F(a;b;c;-\frac{k_2}{k_1}{x}_0^{\beta -\alpha })$, where $a=1,$ $b=\frac{1-\alpha }{\beta -\alpha },c=b+a,F(·,·;·;·)$ is the Gauss hypergeometric function, and initial state $x_0$ is also an independent variable.

It is observed that the convergence rate of the finite time systems is different, where the settling time, from an arbitrary initial state $x_0$ to the equilibrium point $x\left(t\right)=0$, seemingly varies with the initial state $x_0$. In particular, for the double power rate one (iii), the accurate expression of the settling time is characterized by the hypergeometric function, for which is difficult to obtain the solution.

An agreement is reached substantially that the convergence rate of the finite time system needs to be fast and the arriving time needs to be short. Recently, a fixed-time stability was put forward in [32], by which the influence of the initial state on the settling time is eliminated. It provides an upper bound of settling time which is independent of the initial state. Later, Ref. [36] devised a finite-duration attractor, which offers an alternative choice of settling time so that the impact of the initial state can be customized by the designer. Specifically, the upper bound of equation (iii) given by [32,36] is presented as following

$$\begin{array}{c}\hfill {\overline{t}}_{s,d}=\frac{1}{k_1(1-\alpha )}+\frac{1}{k_2(\beta -1)}\end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\overline{t}}_{s,e}& =& \frac{x_t^{1-\alpha }}{k_1(1-\alpha )}+\frac{(x_t^{1-\beta }-x_0^{1-\beta })}{k_2(\beta -1)}\hfill \end{array}$$

(2)

where $x_t$ is the transition state chosen by the designer.

Remark 1.

Obviously, the upper bound in (2) equals to (1) when $x_t=1$ and the initial state $x_0$ is naturally ignored. A tight bound is provided by [36] for the double power rate one (iii), which presents a general expression of the settling time, with an appropriate selection of the transition state.

Remark 2.

Facilitated by the main thought of [36], we aim to construct a new type of terminal sliding mode surface by which the convergence rate improves and the singularity is avoided and presents an effective analysis method where a tight bound of the settling time is offered.

3. Problem Formulation

In order to narrow down the settling time of the finite time systems, the traditional double power rate attracting laws need to be attenuated such that regions both close to and far away from the equilibrium point are equipped with a fast convergence rate. The key to the modification of the finite time systems lies in the requirement for the essential convergence process, where the idea of a finite-duration attractor is borrowed and proper improvement is made accordingly.

In this paper, a new two-phase finite time system is constructed as follows:

$$\begin{array}{ccc}\hfill \dot{x}& =& \left\{\begin{array}{cc}-k_1{x}^{\alpha }-k_2{x}^{2-\alpha },\hfill & \left|x\right|\ge x_t\hfill \\ -k_{1}x-k_1{x}^{\alpha },\hfill & \left|x\right|<x_t\hfill \end{array}\right.\hfill \end{array}$$

(3)

where $k_1>0$ and $0<\alpha <1$ are fractions, in which both numerator and denominator are positive odd integers, respectively. $x_t$ is the transition state, satisfying $\left|x_t\right|\le \left|x_0\right|$, where $x_0\triangleq x\left(0\right)$ is the initial state and different selections of $x_t$ and $x_0$ obtain a different upper bound of the settling time.

Lemma 1.

Consider nonlinear system (3); its origin is finite-duration stable and its settling time is bounded and varies with the transition state and the initial state.

Proof of Lemma 1.

(i) $\left|x\right|\ge x_t$

Let $z=x^{1-\alpha }$, and the derivative of x can be rewritten as

$$\begin{array}{c}\hfill \dot{z}+k_1(1-\alpha )(1+{(\sqrt{\frac{k_2}{k_1}}z)}^2)=0\end{array}$$

(4)

Integrating both sides of (4) yields

$$\begin{array}{c}\hfill \arctan (\sqrt{\frac{k_2}{k_1}}z\left(t\right))=\arctan (\sqrt{\frac{k_2}{k_1}}z\left(0\right))-\sqrt{k_1{k}_2}(1-\alpha )t\end{array}$$

(5)

Then, the settling time from $x_0$ to $x_t$ is obtained as

$$\begin{array}{c}\hfill t_{s,1}=\frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_0^{1-\alpha })-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-\alpha })}{\sqrt{k_1{k}_2}(1-\alpha )}\end{array}$$

(6)

(ii) $\left|x\right|\le x_t$

Using the intermediate variable $z=x^{1-\alpha }$, the system can be expressed as

$$\begin{array}{c}\hfill \dot{z}+k_1(1-\alpha )(1+z)=0\end{array}$$

(7)

Solving the differential Equation (7),

$$\begin{array}{c}\hfill z\left(t\right)=e^{-k_1(1-\alpha )t}(1+z\left(0\right))-1\end{array}$$

(8)

and setting $z\left(t\right)=0$ gives the settling time from $x_t$ to 0

$$\begin{array}{ccc}\hfill t_{s,2}& =& \frac{1}{k_1(1-\alpha )}ln(1+x_t^{1-\alpha })\hfill \end{array}$$

(9)

Finally, the settling time of system (3) is written as

$$\begin{array}{ccc}\hfill t_s& =& \frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_0^{1-\alpha })-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-\alpha })}{\sqrt{k_1{k}_2}(1-\alpha )}+\hfill \\ & & \frac{1}{k_1(1-\alpha )}ln(1+x_t^{1-\alpha })\hfill \\ & \le & \frac{\pi }{2\sqrt{k_1{k}_2}(1-\alpha )}+\frac{x_t^{1-\alpha }}{k_1(1-\alpha )}\hfill \end{array}$$

(10)

It is observed from Equation (10) that the settling time is dependent on both the transition state $x_t$ and the initial state $x_0$ visibly, where it covers a duration within $[0,t_s]$ and the width of the duration $[0,t_s]$ is finite for all $x_t$ and $x_0$.

The proof is completed. □

Remark 3.

Note that the duration $[0,t_s]$ can be determined by each given $x_t$ and $x_0$, and its width depends on $x_t$ and $x_0$. However, the duration $[0,t_s]$ is finite for all $x_0$ since the upper bound of $t_s$ is independent of $x_0$, and the choice of the transition state has little impact on the duration width but has much benefit for the convergence process. Furthermore, the settling time is tailored by the designer, where the impact of the initial state is totally oriented by the requirements of the control objective, rather than ignored without consideration. Hence, the analysis of the finite duration of systems is of great value.

In this paper, we apply the two-phase finite time system (3) to the sliding mode control design in order to bring benefits to the convergence rate and enhance the control performance. A class of nonlinear systems is considered and described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=x_2\left(t\right)\hfill \\ {\dot{x}}_2\left(t\right)=f\left(x\right)+g\left(x\right)u+d(x,t)\hfill \end{array}\right.\end{array}$$

(11)

where $x={[x_1,x_2]}^T\in R^2$ is the state vector, $f\left(x\right)$ and $g\left(x\right)\ne 0$ are smooth nonlinear functions, $u\in R$ is the control input, and $d(x,t)$ represents the external disturbances satisfying $\left|d\right(x,t\left)\right|\le \delta$, where $\delta >0$.

The main control objective is to design a non-singular terminal sliding mode (NTSM) control input $u\left(t\right)$ by utilizing the finite-duration attractor, such that the state $x\left(t\right)$ converges to the origin during finite time and a tight upper bound of convergence time can be obtained as well.

4. The NTSM Controller Design

In this section, the NTSM controller with a finite-duration convergence attractor is presented, in which part-A provides the motivation of the non-singular controller design, and part-B puts forward the NTSM controller, where the performance analysis is carried out and the result is summarized in Theorem 1.

4.1. TSM with FD

For system (11), a TSM surface based on the finite-duration attractor (3) is developed as

$$\begin{array}{c}\hfill s=\left\{\begin{array}{cc}{x}_2+k_1{x}_1^{{\alpha }_1}+k_2{x}_1^{2-{\alpha }_1},\hfill & \left|x_1\right|\ge x_t\hfill \\ x_2+k_1{x}_1+k_1{x}_1^{{\alpha }_1},\hfill & \left|x_1\right|<x_t\hfill \end{array}\right.\end{array}$$

(12)

where $0<{\alpha }_1<1$ are fractions where both numerator and denominator are positive odd integers, and $k_1,k_2>0$, and $x_t$ is the transition state given by the designer. Focusing our attention on the TSM surface (12), it is easily found that the exponential in (12) has an essential difference from the existing TSM surface such as in [33], and it allows better convergence performance both at a short distance (i.e., reaching phase, $|x_1<x_t|$) and far away (i.e., traveling phase, $|x_1\ge x_t|$) from the origin.

The TSM controller is presented as

$$\begin{array}{ccc}\hfill u& =& -\frac{1}{g}(f+\gamma \mathrm{sign}\left(s\right)+k_1{\alpha }_1{x}_1^{{\alpha }_1-1}{x}_2+\hfill \\ & & ((\frac{k_1}{2}+\frac{k_2}{2})+(\frac{k_2}{2}-\frac{k_1}{2})\mathrm{sign}\left(\right|x_1|-x_t\left)\right)\times \hfill \\ & & (\frac{3-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|x_1|-x_t\left)\right)\times \hfill \\ & & x_1^{\frac{1-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|x_1|-x_t)}{x}_2+o_1{s}^{{\alpha }_2}\hfill \\ & & +((\frac{o_1}{2}+\frac{o_2}{2})+(\frac{o_2}{2}-\frac{o_1}{2})\mathrm{sign}\left(\right|s|-s_t\left)\right)\times \hfill \\ & & s^{\frac{3-{\alpha }_2}{2}+(\frac{1-{\alpha }_2}{2})\mathrm{sign}(|s|-s_t)})\hfill \end{array}$$

(13)

where $0<{\alpha }_2<1,o_1,o_2>0$, $\gamma \ge \delta$, and $s_t\triangleq s\left(x_t\right)$ is the sliding surface with the transition state, which can be chosen according to $x_t$.

The analysis is developed in the following.

Taking the derivative of s yields

$$\begin{array}{ccc}\hfill \dot{s}& =& \left\{\begin{array}{cc}-o_1{s}^{{\alpha }_2}-o_2{s}^{2-{\alpha }_2}-\gamma \mathrm{sign}\left(s\right)+d\hfill & \left|s\right|\ge s_t\hfill \\ -o_{1}s-o_1{s}^{{\alpha }_2}-\gamma \mathrm{sign}\left(s\right)+d\hfill & \left|s\right|<s_t\hfill \end{array}\right.\hfill \end{array}$$

(14)

By choosing the Lyapunov function $V=s^2$,

$$\begin{array}{ccc}\hfill \dot{V}& =& \left\{\begin{array}{cc}-2o_1{V}^{\frac{3-{\alpha }_2}{2}}-2o_2{V}^{\frac{{\alpha }_2+1}{2}}\hfill & V\ge V_t\hfill \\ -2o_{1}V-2o_1{V}^{\frac{{\alpha }_2+1}{2}}\hfill & V<V_t\hfill \end{array}\right.\hfill \end{array}$$

(15)

where $V_t\triangleq V\left(s_t\right)$ is the Lyapunov function with $s_t$. In the light of (10), the convergence time of $V\to 0$ can be expressed as

$$\begin{array}{ccc}\hfill t_{s,1}& =& \frac{\arctan (\sqrt{\frac{o_2}{o_1}}V{\left(0\right)}^{\frac{1-{\alpha }_2}{2}})-\arctan (\sqrt{\frac{o_2}{o_1}}{V}_t^{\frac{1-{\alpha }_2}{2}})}{\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\hfill \\ & & \frac{1}{o_1(1-{\alpha }_2)}ln(1+V_t^{\frac{1-{\alpha }_2}{2}})\hfill \\ & \le & \frac{\pi }{2\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\frac{V_t^{\frac{1-{\alpha }_2}{2}}}{o_1(1-{\alpha }_2)}\hfill \end{array}$$

(16)

It is seen that the settling time relies on the initial state, and the width of $[0,t_{s,1}]$ is a finite duration independent of $V_0$ for every $V\left(t\right)$.

As the sliding mode surface is reached, it is obtained that

$$\begin{array}{c}\hfill x_2={\dot{x}}_1=\left\{\begin{array}{cc}-k_1{x}_1^{{\alpha }_1}-k_2{x}_1^{2-{\alpha }_1},\hfill & \left|x_1\right|\ge x_t\hfill \\ -k_1{x}_1-k_1{x}_1^{{\alpha }_1},\hfill & \left|x_1\right|<x_t\hfill \end{array}\right.\end{array}$$

(17)

and the settling time from $x_1$ to 0 is formulated as

$$\begin{array}{ccc}\hfill t_{s,2}& =& \frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_1{\left(0\right)}^{1-{\alpha }_1})-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-{\alpha }_1})}{\sqrt{k_1{k}_2}(1-{\alpha }_1)}+\hfill \\ & & \frac{1}{k_1(1-{\alpha }_1)}ln(1+x_t^{1-{\alpha }_1})\hfill \\ & \le & \frac{\pi }{2\sqrt{k_1{k}_2}(1-{\alpha }_1)}+\frac{x_t^{1-{\alpha }_1}}{k_1(1-{\alpha }_1)}\hfill \end{array}$$

(18)

Integrating (16) and (18), the upper bound of settling time during the whole process is obtained as T,

$$\begin{array}{ccc}\hfill t_s& =& t_{s,1}+t_{s,2}\hfill \\ & =& \frac{\arctan (\sqrt{\frac{o_2}{o_1}}V{\left(0\right)}^{\frac{1-{\alpha }_2}{2}})-\arctan (\sqrt{\frac{o_2}{o_1}}{V}_t^{\frac{1-{\alpha }_2}{2}})}{\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\hfill \\ & & \frac{ln(1+V_t^{\frac{1-{\alpha }_2}{2}})}{o_1(1-{\alpha }_2)}+\frac{ln(1+x_t^{1-{\alpha }_1})}{k_1(1-{\alpha }_1)}+\hfill \\ & & \frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_1{\left(0\right)}^{1-{\alpha }_1})-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-{\alpha }_1})}{\sqrt{k_1{k}_2}(1-{\alpha }_1)}\hfill \\ & \le & \frac{\pi +2\sqrt{o_2}{V}_t^{\frac{1-{\alpha }_2}{2}}}{2\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\frac{\pi +2\sqrt{k_2}{x}_t^{1-{\alpha }_1}}{2\sqrt{k_1{k}_2}(1-{\alpha }_1)}\hfill \end{array}$$

(19)

However, it should be noted that controller (13) contains the singularity term $x_1^{{\alpha }_1-1}{x}_2$, which will incline to infinity if $x_1=0$ and $x_2\ne 0$ for the exponential $0<{\alpha }_1<1$. Therefore, the control input (13) cannot be guaranteed to be bounded in two phases (traveling and reaching phase) of the TSM, and applying a controller (13) has the risk of making the driving system unstable. Therefore, the singularity phenomenon needs to be handled.

4.2. NTSM with FD

Considering the aforementioned analysis of the TSM surface, the amendment should be carried out to upgrade the controller. On the basis of the two-phase sliding mode surface (12), the non-singular terminal sliding mode controller is proposed:

$$\begin{array}{ccc}\hfill u& =& -\frac{1}{g}(f+\gamma \mathrm{sign}\left(s\right)+k_1{\alpha }_1\mathrm{sat}(x_1^{{\alpha }_1-1}{x}_2,\xi )+\hfill \\ & & ((\frac{k_1}{2}+\frac{k_2}{2})+(\frac{k_2}{2}-\frac{k_1}{2})\mathrm{sign}\left(\right|x_1|-x_t\left)\right)\times \hfill \\ & & (\frac{3-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|x_1|-x_t\left)\right)\times \hfill \\ & & x_1^{\frac{1-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|x_1|-x_t)}{x}_2+o_1{s}^{{\alpha }_2}\hfill \\ & & +((\frac{o_1}{2}+\frac{o_2}{2})+(\frac{o_2}{2}-\frac{o_1}{2})\mathrm{sign}\left(\right|s|-s_t\left)\right)\times \hfill \\ & & s^{\frac{3-{\alpha }_2}{2}+(\frac{1-{\alpha }_2}{2})\mathrm{sign}(|s|-s_t)})\hfill \end{array}$$

(20)

where $0<{\alpha }_1,{\alpha }_2<1,o_1,o_2,k_1,k_2>0$, $\gamma \ge \delta$, and $\mathrm{sat}(a,b)=min\left\{\right|a|,b\}\mathrm{sign}\left(a\right)$ is the saturation function to restrain the singularity term, and $\xi$ is the given bound of $|x_1^{{\alpha }_1-1}{x}_2|$ to limit the infinity term.

The conclusions about NTSM controller (20) is drawn in the following theorem.

Theorem 1.

Considering the second-order nonlinear system (11), both NTSM surface (12) and NTSM controller (20) are proposed to guarantee the bounded control input and fast convergence, including in regions both close to and far away from the control objective. Moreover, the upper bound of the settling time during the whole process is given in (23).

Proof. 

Case 1: $|x_1^{{\alpha }_1-1}{x}_2|<\xi$.

In this area, the analysis of the terminal sliding mode surface and the settling time is consistent with before (section A), as the singularity does not appear. The convergence time from $x\left(0\right)$ to the origin 0 is identical to equation (19), written as

$$\begin{array}{ccc}\hfill t_{s,n1}& =& \frac{\arctan (\sqrt{\frac{o_2}{o_1}}V{\left(0\right)}^{\frac{1-{\alpha }_2}{2}})-\arctan (\sqrt{\frac{o_2}{o_1}}{V}_t^{\frac{1-{\alpha }_2}{2}})}{\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\hfill \\ & & \frac{ln(1+V_t^{\frac{1-{\alpha }_2}{2}})}{o_1(1-{\alpha }_2)}+\frac{ln(1+x_t^{1-{\alpha }_1})}{k_1(1-{\alpha }_1)}+\hfill \\ & & \frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_1{\left(0\right)}^{1-{\alpha }_1})-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-{\alpha }_1})}{\sqrt{k_1{k}_2}(1-{\alpha }_1)}\hfill \end{array}$$

(21)

Case 2: $|x_1^{{\alpha }_1-1}{x}_2|>\xi$.

The singularity phenomenon happens in this situation, and we define $|x_1^{{\alpha }_1-1}{x}_2|>\xi$ as the singularity area. It is obtained from (11) that

$$\begin{array}{ccc}\hfill x_1\left(t\right)& =& x_1\left(0\right)+{\int }_0^t{\dot{x}}_2\left(\tau \right)d\tau \hfill \end{array}$$

(22)

which indicates that $x_1\left(t\right)$ will increase monotonically in the presence of $x_1\left(0\right)>0$, and $x_1\left(t\right)$ will decrease monotonically if $x_2\left(t\right)<0$. Therefore, the system state will pass the singularity area in finite time, and the crossing time is denoted as $t\left(\zeta \right)$, and it has no impact on the finite convergence analysis. In the sequel, the settling time of system (11) is presented as

$$\begin{array}{ccc}\hfill t_{s,n}& =& \frac{\arctan (\sqrt{\frac{o_2}{o_1}}V{\left(0\right)}^{\frac{1-{\alpha }_2}{2}})-\arctan (\sqrt{\frac{o_2}{o_1}}{V}_t^{\frac{1-{\alpha }_2}{2}})}{\sqrt{o_1{o}_2}(1-{\alpha }_2)}+\hfill \\ & & \frac{ln(1+V_t^{\frac{1-{\alpha }_2}{2}})}{o_1(1-{\alpha }_2)}+\frac{ln(1+x_t^{1-{\alpha }_1})}{k_1(1-{\alpha }_1)}+t\left(\zeta \right)+\hfill \\ & & \frac{\arctan (\sqrt{\frac{k_2}{k_1}}{x}_1{\left(0\right)}^{1-{\alpha }_1})-\arctan (\sqrt{\frac{k_2}{k_1}}{x}_t^{1-{\alpha }_1})}{\sqrt{k_1{k}_2}(1-{\alpha }_1)}\hfill \end{array}$$

(23)

□

Remark 4.

Due to the lack of a specific description of the boundary of the singularity area, $t\left(\zeta \right)$ can not be given exactly, but the crossing time $t\left(\zeta \right)$ has no impact on the finite-duration convergence process. Moreover, it is seen that (23) is dependent on the initial state $x_1\left(0\right)$, and the width of settling time is finite for every given $x_1\left(0\right)$. The rule of choosing the bound of singularity term $x_1^{{\alpha }_1-1}{x}_2$ is to guarantee s away from the singularity area, i.e., $max\left\{\right|x_1^{{\alpha }_1-1}(k_1{x}_1^{{\alpha }_1}+k_1{x}_1^{2-{\alpha }_1})|,|x_1^{{\alpha }_1-1}(k_1{x}_1+k_1{x}_1^{{\alpha }_1})\left|\right\}\le \xi$.

4.3. Extensions to MIMO Systems

Consider a class of multi-input multi-output (MIMO) nonlinear systems,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{X}}_1=F_1(X_1,X_2)\hfill \\ {\dot{X}}_2=F_2(X_1,X_2)+B(X_1,X_2)U+D(X_1,X_2)\hfill \end{array}\right.\end{array}$$

(24)

where $X_1=[x_{11},x_{12},\dots ,x_{1,n}]\in {\mathrm{R}}^n$, $X_2=[x_{21},x_{22},\dots ,x_{2,n}]\in {\mathrm{R}}^n$ are the states, $F_1(·),F_2(·)$ are nonlinear vector functions, and $B(·)$ is a non-singular matrix, and $U\in {\mathrm{R}}^n$ is the control input, and $D(·)$ stands for the external disturbances. There are many practical systems that can be expressed by referring to (24). Therefore, the presented scheme can be applied to these plants.

Following assumptions are made:

Assumption A1.

The disturbance $D(·)$ is bounded and satisfies $\parallel D(X_1,X_2)\parallel =\overline{d}(X_1,X_2)$.

Assumption A2.

$\frac{\partial F_1}{\partial X_2}B(X_1,X_2)$ is a non-singular matrix.

The two-phase NTSM is constructed for system (24),

$$\begin{array}{c}\hfill \Xi =\left\{\begin{array}{cc}{\dot{X}}_1+{\Lambda }_1{X}_1^{{\Phi }_1}+{\Lambda }_2{X}_1^{2-{\Phi }_1},\hfill & \parallel X_1\parallel \ge X_t\hfill \\ {\dot{X}}_1+{\Lambda }_1{X}_1+{\Lambda }_1{X}_1^{{\Phi }_1},\hfill & \parallel X_1\parallel <X_t\hfill \end{array}\right.\end{array}$$

(25)

where $\Xi$ represents the n-dimensional sliding mode manifold, and the matrices are defined as ${\Lambda }_1=\mathrm{diag}({\lambda }_{11},{\lambda }_{12},\dots ,{\lambda }_{1n}),{\Lambda }_2=\mathrm{diag}({\lambda }_{21},{\lambda }_{22},\dots ,{\lambda }_{2n}),{\Phi }_1=\mathrm{diag}({\varphi }_{11},{\varphi }_{12},\dots ,{\varphi }_{1n})$, in which ${\lambda }_{1i}>0,{\lambda }_{2i}>0,i=1,\dots ,n$ and $0<{\varphi }_{1i}<1,i=1,\dots ,n$ are fractions in which the numerator and denominator are positive odd integers. $X_t$ is the transition state matrix given by the designer. The derivative of $X_1^{{\Phi }_1}$ is denoted as $\frac{d}{dt}(X_1^{{\Phi }_1})={\Phi }_1\mathrm{diag}\left(\right|X_1{|}^{{\Phi }_1-I_n}){\dot{X}}_1$, where $I_n$ is the n-dimensional unit matrix.

In the presence of Assumptions 1–3 and the two-phase manifold (25), the NTSM control input is developed as

$$\begin{array}{ccc}\hfill U& =& -{(\frac{\partial F_1}{\partial X_2}B)}^{-1}(\frac{\partial F_1}{X_1}{F}_1+\frac{\partial F_1}{\partial X_2}{F}_2+\parallel \frac{\partial F_1}{\partial X_2}\parallel \overline{d}+\hfill \\ & & M\frac{\Xi }{\parallel \Xi \parallel }+{\Lambda }_1{\Phi }_1\mathrm{sat}(X_1^{{\Phi }_1-I_n}{\dot{X}}_1,h)+\hfill \\ & & ((\frac{{\Lambda }_1}{2}+\frac{{\Lambda }_2}{2})+(\frac{{\Lambda }_2}{2}-\frac{{\Lambda }_1}{2})\mathrm{sign}\left(\right|X_1|-X_t\left)\right)\times \hfill \\ & & (\frac{3I_n-{\Phi }_1}{2}+\frac{I_n-{\Phi }_1}{2}\mathrm{sign}\left(\right|X_1|-X_t\left)\right)\times \hfill \\ & & X_1^{\frac{I_n-{\Phi }_1}{2}+\frac{I_n-{\Phi }_1}{2}\mathrm{sign}(\parallel X_1\parallel -X_t)}{\dot{X}}_1+\hfill \\ & & {\Gamma }_1{\Xi }^{{\Phi }_2}+((\frac{{\Gamma }_1}{2}+\frac{{\Gamma }_2}{2})+(\frac{{\Gamma }_2}{2}-\frac{{\Gamma }_1}{2})\times \hfill \\ & & \mathrm{sign}(\parallel \Xi \parallel -{\Xi }_t\left)\right){\Xi }^{\frac{3I_n-{\Phi }_2}{2}+\frac{I_n-{\Phi }_2}{2}\mathrm{sign}(\parallel \Xi \parallel -{\Xi }_t)}\hfill \end{array}$$

(26)

where ${\Gamma }_1=\mathrm{diag}({\gamma }_{11},{\gamma }_{12},\dots ,{\gamma }_{1n}),{\Gamma }_2=\mathrm{diag}({\gamma }_{21},{\gamma }_{22},\dots ,{\gamma }_{2n}),{\Phi }_2=\mathrm{diag}({\varphi }_{21},{\varphi }_{22},\dots ,$ ${\varphi }_{2n})$, in which ${\lambda }_{2i}>0,i=1,\dots ,n$ and $0<{\varphi }_{2i}<1,i=1,\dots ,n$ are fractions in which numerator and denominator are positive odd integers, and h is the bound of $\parallel \mathrm{diag}\left(\right|X_1{|}^{{\Phi }_1-I_n}){\dot{X}}_1\parallel$.

The analysis is conducted in line with the proof of Theorem 1, and is given as follows. For $\parallel \mathrm{diag}\left(\right|X_1{|}^{{\Phi }_1-I_n}){\dot{X}}_1\parallel <h$, the Lyapunov candidate function is chosen as $\tilde{V}={\Xi }^T\Xi$. Along with the manifold (25) and the control input (26), the derivative of $\tilde{V}$ can be expressed as

$$\begin{array}{ccc}\hfill \dot{\tilde{V}}& =& \left\{\begin{array}{cc}-2{\Gamma }_1{\tilde{V}}^{3I_n-{\Phi }_2}-2{\Gamma }_2{\tilde{V}}^{{\Psi }_2+I_n},\hfill & \parallel \tilde{V}\parallel \ge {\tilde{V}}_t\hfill \\ -{\Gamma }_1\tilde{V}-2{\Gamma }_1{\tilde{V}}^{{\Phi }_2+I_n},\hfill & \parallel \tilde{V}\parallel <{\tilde{V}}_t\hfill \end{array}\right.\hfill \end{array}$$

where ${\tilde{V}}_t=\tilde{V}\left({\Xi }_t\right)$. For $\parallel \mathrm{diag}\left(\right|X_1{|}^{{\Phi }_1-I_n}){\dot{X}}_1\parallel >h$, the singularity is restrained by the saturation function. According to Assumption 1, $X_1\left(t\right)=X_1\left(0\right)+{\int }_0^t{X}_2\left(\tau \right)d\tau$ can be obtained. The finite-duration convergence is ensured by carrying out the same analysis as the proof of Theorem 1.

The presented NTSM control scheme enables a class of MIMO nonlinear systems to be governed, where bounded control input and finite convergence are achieved by adopting the two-phase manifold (25).

5. Numerical Simulations

In this simulation study, the single inverted pendulum (SIP) system is considered. The dynamic equation of the SIP is formulated in the following.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\dot{x}}_1=x_2\hfill & \\ {\dot{x}}_2=\frac{\overline{g}sin\left(x_1\right)-ml{x}_2^{2}cos\left(x_1\right)sin\left(x_1\right)/(m_c+m)}{l(4/3-m{cos}^2\left(x_1\right)/(m_c+m))}\hfill & \\ +\frac{cos\left(x_1\right)/(m_c+m)}{l(4/3-m{cos}^2\left(x_1\right)/(m_c+m))}u+d\hfill & \end{array}\right.\end{array}$$

(27)

where $f=\frac{\overline{g}sin\left(x_1\right)-ml{x}_2^{2}cos\left(x_1\right)sin\left(x_1\right)/(m_c+m)}{l(4/3-m{cos}^2\left(x_1\right)/(m_c+m))}$, $g=\frac{cos\left(x_1\right)/(m_c+m)}{l(4/3-m{cos}^2\left(x_1\right)/(m_c+m))}$ and $x_1$ and $x_2$ denote the angle and speed, d represents the disturbance, and $\overline{g}=9.8$ is the gravitational acceleration, $m_c=1\mathrm{kg}$ is the mass of the cart, and $m=0.1\mathrm{kg}$ is the mass of the pendulum, and $l=0.5\mathrm{m}$ is the length to pendulum center of mass.

Part i. The effectiveness of the presented control scheme

We define $e_1\left(t\right)=x_1\left(t\right)-x_d\left(t\right)$ and $e_2\left(t\right)=x_2\left(t\right)-{\dot{x}}_d\left(t\right)$. The control objective is to design a two-phase non-singular TSM controller such that the pendulum system tracks the given reference trajectory $x_d\left(t\right)$ within finite time. On the basis of (20), the controller for the pendulum is constructed as

$$\begin{array}{ccc}\hfill u& =& -\frac{1}{g}(f+\gamma \mathrm{sign}\left(s\right)-{\ddot{x}}_d+k_1{\alpha }_1\mathrm{sat}(e_1^{{\alpha }_1-1}{e}_2,\zeta )+\hfill \\ & & ((\frac{k_1}{2}+\frac{k_2}{2})+(\frac{k_2}{2}-\frac{k_1}{2})\mathrm{sign}\left(\right|e_1|-e_{1t}\left)\right)\times \hfill \\ & & (\frac{3-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|e_1|-e_{1t}\left)\right)\times \hfill \\ & & e_1^{\frac{1-{\alpha }_1}{2}+\frac{1-{\alpha }_1}{2}\mathrm{sign}\left(\right|e_1|-e_{1t})}{e}_2+\hfill \\ & & o_1{s}^{{\alpha }_2}+((\frac{o_1}{2}+\frac{o_2}{2})+(\frac{o_2}{2}-\frac{o_1}{2})\mathrm{sign}\left(\right|s|-s_t\left)\right)\times \hfill \\ & & s^{\frac{3-{\alpha }_2}{2}+\frac{1-{\alpha }_2}{2}\mathrm{sign}\left(\right|s|-s_t)})\hfill \end{array}$$

(28)

where the sliding mode surface s is chosen as

$$\begin{array}{c}\hfill s=\left\{\begin{array}{cc}{e}_2+k_1{e}_1^{{\alpha }_1}+k_2{e}_1^{2-{\alpha }_1},\hfill & \left|e_1\right|\ge e_{1t}\hfill \\ e_2+k_1{e}_1+k_1{e}_1^{{\alpha }_1},\hfill & \left|e_1\right|<e_{1t}\hfill \end{array}\right.\end{array}$$

(29)

and the design parameters are: ${\alpha }_1=13/15,{\alpha }_2=5/9,k_1=2,k_2=1,o_1=2,o_2=1$ and $\gamma =2,\xi =2,e_{1t}=1.1,s_t=1.1$. The desired trajectory is given as $x_d=sin\left(0.5\pi t\right)$, and the disturbance is set as $d=sin\left(10x_1\right)+cos\left(x_2\right)$. The initial state is chosen as $x_1\left(0\right)=1.2,$ $x_2\left(0\right)=0.1$.

The simulation results are shown in Figure 1, Figure 2, Figure 3 and Figure 4. Figure 1 depicts the control input, where the chattering phenomenon exists due to the sign function $\mathrm{sign}(·)$. Figure 2 shows the sliding mode s, where the sliding mode surface converges to zero as t increases indicating the effectiveness of the control scheme. The system state $x_1$ and the reference signal $x_d$ are described in Figure 3 showing the tracking performance.

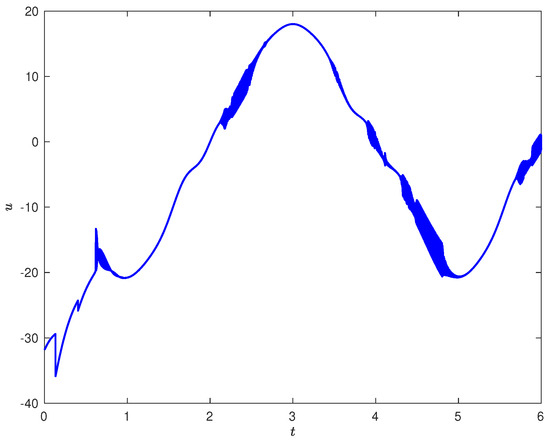
Figure 1. The Control input u.

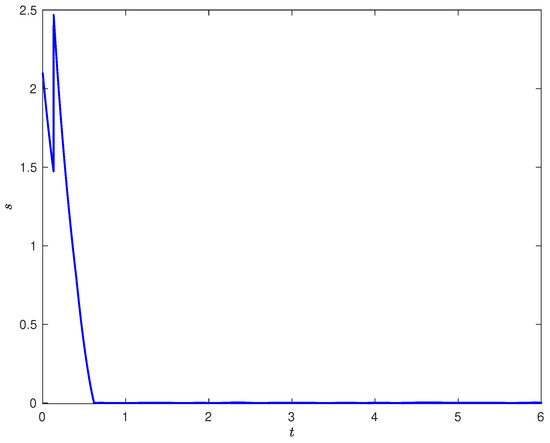
Figure 2. The Sliding surface s.

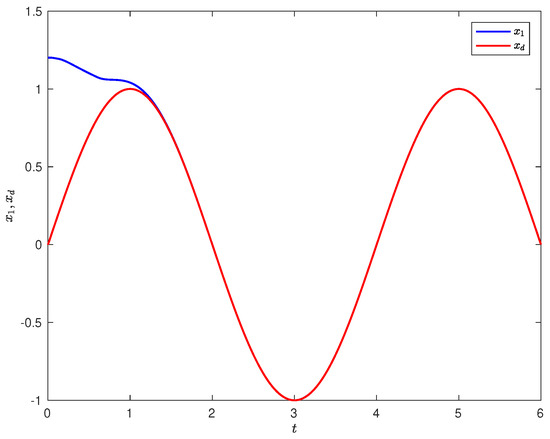
Figure 3. The Tracking performance $x_1$ and $x_d$.

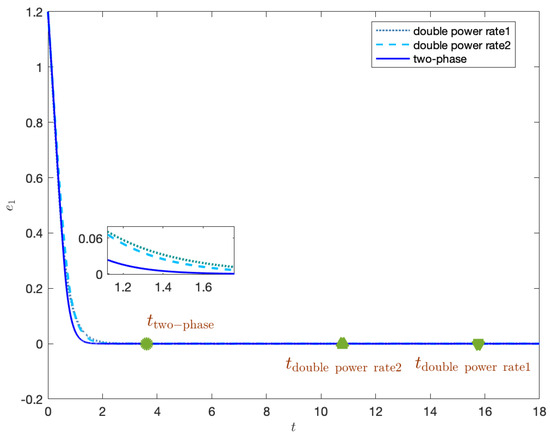
Figure 4. The Comparison of tracking error $e_1$.

Part ii. The comparison with the existing results

The analysis of the settling time for the sliding mode control scheme is the main characteristic for scholars. In this part, we are going to consider the difference between the existing results and those obtained from the analysis of the settling time. The sliding mode with double power rate is chosen as the comparator, where the results in [25,33] are both considered, described, respectively, as

$$\begin{array}{ccc}\hfill s_{\mathrm{double}\mathrm{power}\mathrm{rate}1}& =& e_2+o_1{e}_1^{{\beta }_1}+o_2{e}_2^{{\alpha }_1}\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill s_{\mathrm{double}\mathrm{power}\mathrm{rate}2}& =& e_2+o_1{e}_1^{\frac{1}{2}+\frac{{\beta }_1}{2}+(\frac{{\beta }_1}{2}-\frac{1}{2})\mathrm{sign}\left(\right|e_1|-1)}+o_2{e}_1^{{\alpha }_1}\hfill \end{array}$$

(31)

Applying these two sliding mode surfaces to the SIP problems, we design the non-singular TSM controllers with these two double power rate sliding mode surfaces as

$$\begin{array}{ccc}\hfill u_{\mathrm{double}\mathrm{power}\mathrm{rate}1}& =& -\frac{1}{g}(f+\gamma \mathrm{sign}\left(s\right)-{\ddot{x}}_d+o_1{\beta }_1{e}_1^{{\beta }_1-1}+o_2{\alpha }_1\mathrm{sat}(e_1^{{\alpha }_1-1}{e}_2)+\hfill \\ & & {\kappa }_1{s}^{{\beta }_2}+{\kappa }_2{s}^{{\alpha }_2})\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill u_{\mathrm{double}\mathrm{power}\mathrm{rate}2}& =& -\frac{1}{g}[f+\gamma \mathrm{sign}\left(s\right)-{\ddot{x}}_d+o_1(\frac{1}{2}+\frac{{\beta }_1}{2}+\hfill \\ & & (\frac{{\beta }_1}{2}-\frac{1}{2})\mathrm{sign}\left(\right|e_1|-1))e_1^{\frac{1}{2}+\frac{{\beta }_1}{2}+(\frac{{\beta }_1}{2}-\frac{1}{2})\mathrm{sign}\left(\right|e_1|-1)-1}{e}_2+\hfill \\ & & \mathrm{sat}(o_2{\alpha }_1{e}_1^{{\alpha }_1-1}{e}_2,\xi )+{\kappa }_1{s}^{\frac{1}{2}+\frac{{\beta }_2}{2}+(\frac{{\beta }_2}{2}-\frac{1}{2})\mathrm{sign}\left(\right|s|-1)}+{\kappa }_2{s}^{{\alpha }_2}]\hfill \end{array}$$

(33)

The two-phase one is referred to in the design in Part i.

According to the analysis in [25,33], the bound of settling time of the two sliding mode surfaces with double power rate are further derived as

$$\begin{array}{ccc}\hfill t_{\mathrm{double}\mathrm{power}\mathrm{rate}1}& =& \frac{1}{o_1({\beta }_1-1)}+\frac{1}{o_2(1-{\alpha }_1)}\hfill \\ & & +\frac{1}{{\kappa }_1({\beta }_2-1)}+\frac{1}{{\kappa }_2(1-{\alpha }_2)}\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill t_{\mathrm{double}\mathrm{power}\mathrm{rate}2}& =& \frac{1}{o_1({\beta }_1-1)}+\frac{ln(1+\frac{o_1}{o_2})}{o_1(1-{\alpha }_1)}-\hfill \\ & & \frac{V{\left(0\right)}^{-\frac{{\beta }_1-1}{1-{\alpha }_1}}}{({\beta }_1-1)o_1}+\frac{1}{{\kappa }_1({\beta }_2-1)}+\hfill \\ & & \frac{ln(1+\frac{{\kappa }_1}{{\kappa }_2})}{{\kappa }_1(1-{\alpha }_2)}\times -\frac{x{\left(0\right)}^{-\frac{{\beta }_1-1}{1-{\alpha }_1}}}{({\beta }_2-1){\kappa }_1}\hfill \end{array}$$

(35)

The comparison result is depicted in Figure 4, which shows that the convergence of system states using the two-phase TSM controller has a few more advantages than the other two control schemes. More importantly, the bound of the settling time given by (19), (34) and (35) also indicates, respectively, where the two-phase sliding mode surface with finite-duration stability is plainly less conservative than the other two sliding mode surfaces, since the two-phase sliding mode surface is selected.

Part iii. The application on the industrial manipulators

The dynamics of the n-link manipulator is $M\left(q\right)\ddot{q}+C(q,\dot{q})\dot{q}+G\left(q\right)=\tau$, where $q,\dot{q},\ddot{q}\in {\mathrm{R}}^n$ are the vectors of angular position, velocity and acceleration, respectively, and $M\left(q\right)=M_0\left(q\right)+\delta M\left(q\right),C(q,\dot{q})=C_0(q,\dot{q})+\delta C(q,\dot{q}),G\left(q\right)=G\left(q\right)+\delta G\left(q\right)$. The simulation example of the two-link rigid industrial manipulator is referred to in [18], written as

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{a}_{11}\left(q_2\right)& a_{12}\left(q_2\right)\\ a_{21}\left(q_2\right)& a_{22}\end{array}\right]\left[\begin{array}{c}{\ddot{q}}_1\\ {\ddot{q}}_2\end{array}\right]+\left[\begin{array}{c}-b_{12}\left(q_2\right){\dot{q}}_1^2-2b_{12}\left(q_2\right){\dot{q}}_1{\dot{q}}_2\\ b_{12}\left(q_2\right){\dot{q}}_2^2\end{array}\right]+\left[\begin{array}{c}{c}_1(q_1,q_2)g\\ c_2(q_1,q_2)g\end{array}\right]=\left[\begin{array}{c}{\tau }_1\\ {\tau }_2\end{array}\right]\end{array}$$

where $a_{11}\left(q_2\right)=(m_1+m_2)r_1^2+m_2{r}_2^2+2m_2{r}_1{r}_{2}cos\left(q_2\right)+J_1$, $a_{12}\left(q_2\right)=m_2{r}_2^2+m_2{r}_1{r}_{2}cos\left(q_2\right)$, $a_{22}=m_2{r}_2^2+J_2$, $b_{12}\left(q_2\right)=m_2{r}_1{r}_{2}sin\left(q_2\right)$, $c_1(q_1,q_2)=(m_1+m_2)r_{1}cos\left(q_2\right)+m_2{r}_{2}cos(q_1+q_2)$, $c_2(q_1,q_2)=m_2{r}_{2}cos(q_1+q_2)$.

The parameters are chosen as $r_1=1\mathrm{m},r_2=0.8\mathrm{m},J_1=5\mathrm{kg}\mathrm{m},J_1=5\mathrm{kg}\mathrm{m},m_1=0.5\mathrm{kg},m_2=1.5\mathrm{kg}$. The initial state is given as $q_1\left(0\right)=1,q_2\left(0\right)=1.5,{\dot{q}}_1\left(0\right)=0,{\dot{q}}_2\left(0\right)=0$, and the nominal values are selected as ${\widehat{m}}_1=0.4\mathrm{kg},{\widehat{m}}_2=1.2\mathrm{kg}$. The reference trajectory is given as $q_{d1}=1.25-(7/5)e^{-t}+(7/20)e^{-4t},q_{d2}=1.25+e^{-t}-(1/4)e^{-4t}$.

The two-phase sliding mode surface is designed as

$$\begin{array}{c}\hfill s=\left\{\begin{array}{cc}\dot{\tilde{q}}+k_1{\tilde{q}}^{{\alpha }_1}+k_2{\tilde{q}}^{2-{\alpha }_1},\hfill & \left|\tilde{q}\right|\ge q_{1t}\hfill \\ \dot{\tilde{q}}+k_1\tilde{q}+k_1{\tilde{q}}^{{\alpha }_1},\hfill & \left|\tilde{q}\right|<q_{1t}\hfill \end{array}\right.\end{array}$$

(36)

where $\tilde{q}=q-q_d$. Then, the NTSMC is given as

$$\begin{array}{ccc}\hfill u& =& C_q\dot{q}+G_q+M_q\ddot{q}-M_q{k}_1{\alpha }_1\dot{\tilde{q}}|{\tilde{q}}^{{\alpha }_1-1}|-M_q{k}_2(2-{\alpha }_1)\dot{\tilde{q}}{\left|\tilde{q}\right|}^{1-{\alpha }_1}-\hfill \\ & & -M_q(o_1\mathrm{sat}(s^{{\alpha }_2-1},h)+o_2\left(s^{1-{\alpha }_2}\right))\hfill \end{array}$$

(37)

where the parameters of the controller are chosen as $q_{1t}=\left[\begin{array}{c}0.8\\ 0.8\end{array}\right]$$k_1=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$, $k_2=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$, ${\alpha }_1=7/9$, ${\alpha }_2=5/9$, $o_1=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$, $o_2=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$, $h=0.05$. The simulation results are depicted in Figure 5 and Figure 6. Figure 5 shows the convergence process of the sliding mode surface, indicating the effectiveness of the presented control scheme. The tracking error is characterized in Figure 6, where satisfying performance is achieved.

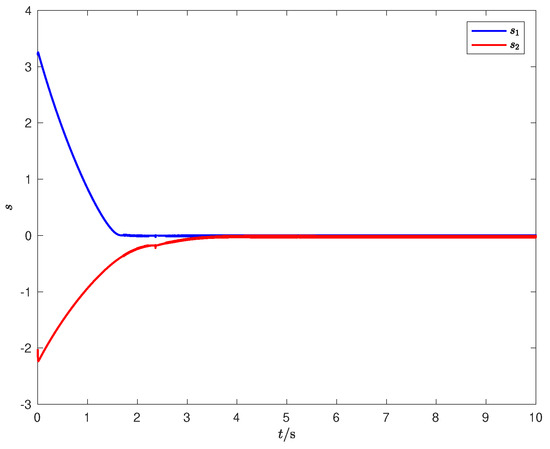
Figure 5. The sliding mode surface s of the manipulators.

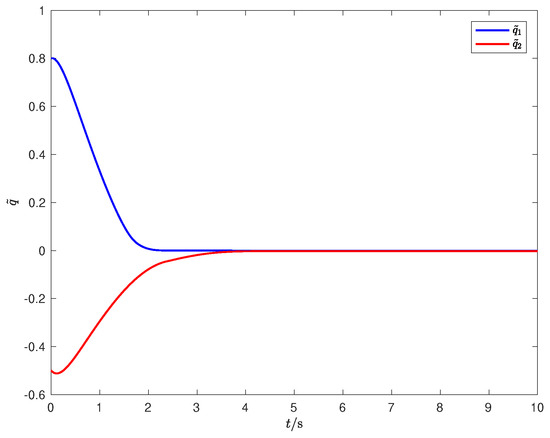
Figure 6. The tracking error of the manipulators.

6. Conclusions

This paper has studied a fast two-phase non-singular TSM control problem for a class of nonlinear systems with external disturbances. The fast finite-duration convergence can be achieved and the closed-loop settling time is obtained, and the singularity phenomenon is overcome for the adoption of the saturation function by employing the proposed control scheme. The application of the single inverted pendulum and the industrial manipulator is conducted and the simulation results suggest the effectiveness and superiority of the proposed control scheme.