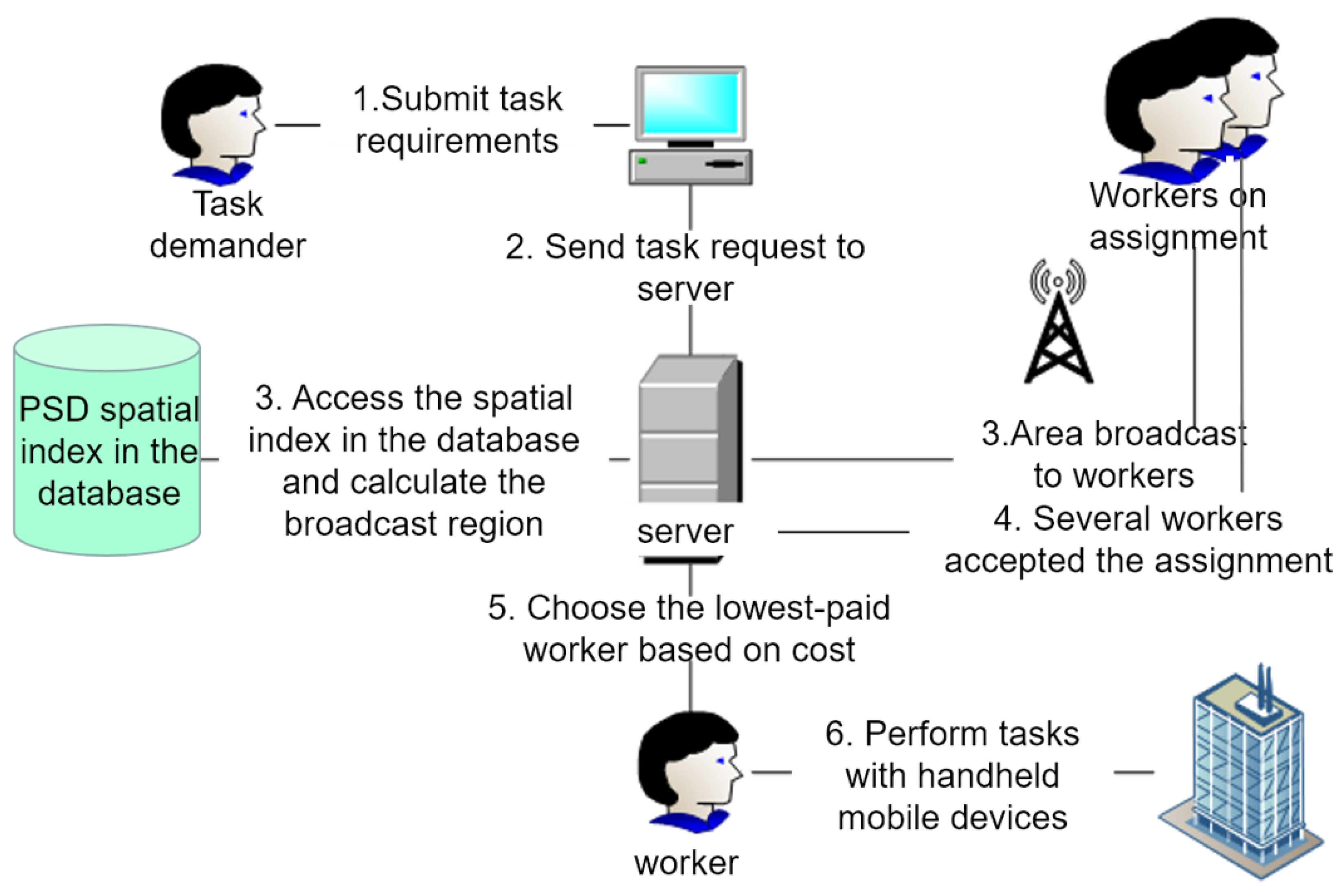
1. Introduction
The emergence of mobile crowdsensing technology [
1,
2,
3] comes from the integration of sensors and embedded devices. Handheld devices can acquire useful information in the real world by collecting, uploading and sharing data [
4,
5]. In various scenarios like social recommendations (e.g., food or hotel recommendations) and real-time monitoring of the surrounding environment (e.g., noise level monitoring) [
6,
7], an application uses a mobile device’s perception capabilities to enhance data credibility, thereby minimizing the expenses of installing sensor equipment. However, its implementation may inadvertently expose sensitive information about mobile users, including social connections and location data [
8,
9]. The platform’s task allocation relies on the user’s location, causing the data collected by the user’s device to potentially reveal their trajectory or other details. For instance, Google Maps utilizes “anonymous” location data from drivers to create real-time maps, yet it inadvertently discloses the driver’s route and location. An attacker with prior knowledge will use the known information to mine the user’s privacy to threaten the user’s personal safety. Therefore, when designing perceptual service applications, the first consideration is to protect the privacy and security of collectors. Only by designing a reasonable and effective data protection mechanism can users accept more tasks.
Users may disclose their own sensitive information when participating in crowdsensing: a malicious cloud platform may use user information to make profits, which will cause immeasurable losses to users and thus dampen the enthusiasm of mobile users for participating in crowdsensing. Therefore, how to solve the privacy protection problem in crowdsensing is crucial; privacy protection has gradually been paid great attention by scholars, and a variety of privacy protection methods have been proposed [
10,
11,
12,
13,
14]. In 2003, Beresford first proposed the concept of location privacy protection [
15]. Privacy protection is primarily focused on concealing users’ identity and location information for safeguarding their confidentiality [
16,
17]. Currently, common privacy protection methods include anonymity-based methods, reputation-based methods and differential privacy-based methods.
There are several mobile crowd awareness schemes using anonymity technology to protect privacy data at home and abroad [
18,
19,
20,
21], such as k-anonymity technology [
22]. The main idea of the k-anonymity technique proposed by Samarati and Sweeney is as follows: Assuming that the attacker is faced with massive data and there are a certain number of quasi-identifiers (such as age, gender, salary, etc.) in the massive data of which records cannot be identified, the attacker can use prior knowledge to narrow the data to a certain range of equivalence classes that satisfy their prior knowledge but cannot lock the attack target from the equivalence class [
22,
23]. This technology uses equivalence classes to protect personal privacy, and parameter k can measure the maximum information disclosure risk that users can bear [
24]. Nevertheless, anonymization is insufficient for privacy preservation, since mobile users may be traced via travel routes and social relations. Meanwhile, despite the efficacy of k-anonymity technology in data protection, its reliance on the attacker’s background knowledge poses a significant vulnerability. If faced with a new attacker possessing unknown prior knowledge, the attacker can potentially differentiate various records within the published equivalent dataset beyond the predicted scope, leading to deanonymization [
25]. So, the security of the k-anonymous model depends on the knowledge possessed by the attacker. And since it is impossible to prove that the algorithm can evaluate the mathematical process of privacy levels, it is not a very perfect privacy protection strategy.
Reputation-based approaches are popular in mobile crowdsensing for allocating tasks to mobile users, but they have their inherent weaknesses. Reputation-based mechanisms [
19,
26,
27,
28] can assign tasks to mobile users. However, the mechanism reliant on reputation is vulnerable due to its dependency on a trusted third party (TTP) for managing reputation, which makes it vulnerable to reputation-linking attacks, in which anonymous mobile users can be reidentified based on their reputations. The SPOON framework, proposed by Ni et al., addresses this weakness by utilizing proxy re-encryption and BBS signature technology to safeguard sensitive information of mobile users and customers. Named SPOON [
6], this framework enables registered customers and mobile users to anonymously demonstrate their ability and trustworthiness for participating in service perception tasks, ensuring the security of the tasks and reports. However, the effectiveness of this technology still relies on the guarantee provided by a trusted third party. If this third party breaches trust, the data remain vulnerable and unprotected.
The emergence of differential privacy technology effectively addresses the aforementioned issues. Differential privacy was originally used in the field of statistical databases (database). Dwork [
24,
25,
29] first applied differential privacy technology to the statistical database field with the aim of safeguarding individuals’ privacy information when publishing statistical data. Differential privacy is advantageous as it does not rely on an attacker’s prior knowledge and can be mathematically proven using a quantitative evaluation method. This technology has gained significant attention from privacy protection researchers and has been implemented in various areas, including privacy-protected data publishing and mining.
While designing privacy protection strategies to ensure the security of data, we should complete the task perception related to data collection as much as possible. To address this problem, this paper proposes a personalized data privacy protection algorithm based on an adaptive dynamic adjustment grid and the lowest paid task allocation strategy. Considering the privacy protection requirements of users at different levels, we have designed various levels of differentiated privacy protection mechanisms by incorporating the privacy budget allocation strategy. In addition, we consider a reward mechanism in task assignment to balance the effectiveness and security of user-uploaded location data. Experiments demonstrate that the strategy proposed in this paper not only safeguards the data but also empowers users to freely select the level of privacy protection.
In summary, this paper makes the following contributions:
Privacy protection in perception: We investigate the privacy protection problem in perception-oriented application services. Our aim is to design privacy protection strategies ensuring data security, with the capability to comprehensively fulfill the task of data collection perception.
Personalized data privacy protection: We propose a personalized data privacy protection algorithm based on an adaptive dynamic adjustment grid and the lowest paid task allocation strategy. Considering the varying levels of user privacy protection needs, we design different-level privacy protection mechanisms by incorporating the privacy budget allocation strategy. We also consider a reward mechanism in task allocation to balance the effectiveness and security of user-uploaded location data.
Extensive evaluation: We conduct thorough evaluations on various real-world datasets. The results demonstrate that our proposed strategy not only safeguards the data but also allows users to freely choose their preferred level of privacy protection.
The remainder of this paper is organized as follows. After reviewing the related works in
Section 2, we introduce the model framework in
Section 3. Then, the personalized privacy protection is proposed in
Section 4, followed by the evaluations in
Section 5 and discussion in
Section 6. Finally, we conclude this paper in
Section 7.
2. Related Work
2.1. Differential Privacy
A differential attack occurs when the attacker leverages existing knowledge to compare it with the query information, attempting to deduce the most probable guess. For instance, if a school releases the results of a course with 100 students, revealing that only six students failed, an attacker possessing the score information of 99 students can attempt to guess whether the remaining student passed or failed. Differential privacy protection technology introduces noise to the original data to ensure a similar data distribution. Consequently, when an attacker adds or removes data, the disparity in data distribution becomes indistinguishable, preventing the identification of specific users within the published data. The basic concepts and definitions of differential privacy are as follows:
(
-differential privacy) In the algorithm, a series of queries
Q are performed on any two adjacent datasets
D and
, and
is the probability of the set of all possible outputs of
Q.
is any subset of
. If the algorithm satisfies:
then this algorithm satisfies
-differential privacy, where datasets
D and
are adjacent datasets. That is, even if any tuple is changed, the probability difference of the output results is very small. The attacker cannot guess the dataset and can play a role in protecting user data [
30].
(Global sensitivity) When conducting a series of random queries
Q on any two adjacent datasets
D and
, the global sensitivity of the query function is the maximum Manhattan distance of the output. The global sensitivity can obtain the variation range of a query function on a pair of adjacent datasets. And the formula is as follows:
(Local sensitivity) When conducting a series of random queries
Q on any two adjacent datasets
D and
, the formula of local sensitivity is as follows:
The local sensitivity is determined via the query function and the distribution of the query dataset, whereas the global sensitivity is solely related to the query function and is independent of the query dataset. Utilizing local sensitivity poses a certain risk of data leakage. Therefore, in the algorithm proposed in this paper, we will adopt global sensitivity. As mentioned earlier, differential privacy can be achieved by introducing noise to the query results, yet excessive noise can impede data availability. Since sensitivity signifies a change in query results due to the deleting of any record in the dataset, it is commonly employed as a parameter to measure the amount of noise in differential privacy.
2.2. Noise-Adding Mechanism in Differential Privacy
Because differential privacy only allows access to the database through counting and summation, random noise needs to be added to each query result to protect data privacy. Only in this way can the attacker be prevented from guessing the existence of the target in the database and obtaining specific information from the set of query results. Next, we will introduce the common noise mechanism in differential privacy.
(Laplace mechanism) If we send a series of query requests to database
D: Query =
, the database will produce a real answer
q(
D). Differential privacy protection adds noise to the numerical results to obtain a series of results with the same probability distribution [
31,
32]. The Laplace mechanism solves this problem well and needs to provide a parameter
. It is calculated as follows:
The Laplace distribution has a mean of 0 and a variance of
, and it satisfies
-differential privacy. The noise added to the query set result
during the query is
. Therefore, the returned result is:
Clearly, the smaller the privacy budget, the greater the noise when adding to the original data, thereby enhancing the level of protection, but inevitably compromising the data’s availability. To cater to the personalized privacy protection requirements of users, this paper categorizes protection levels by assigning different privacy budgets.
2.3. Private Space Decomposition
In database management, there exists a specialized storage structure known as an index, which enables the rapid retrieval of required data. For instance, in a student information database, the index allows for the swift retrieval of specific student information. Common index storage is generally implemented using B-tree or B+tree, facilitating the quick location of specified data through dichotomy. However, these conventional indexes are designed solely for one-dimensional data. When dealing with data represented on two-dimensional coordinates, spatial indexes are employed in database management. Data storage commonly utilizes quadtree [
33], R-tree, k-d tree and the geohash algorithm to convert two-dimensional data into one-dimensional data, enabling the use of B-tree indexes for efficient spatial data point searches.
Building upon the definition of query function in differential privacy, Graham Cormode et al. proposed the concept of “private space decomposition (PSD)” in Reference [
34]. PSD is a concept applied in the field of data management. It refers to dividing the data space into smaller subspaces with the introduction of differential privacy protection measures in spatial data structures to achieve the goal of data privacy protection. Under the premise of privacy protection, introducing noise at different levels of the data space can safeguard data privacy while maintaining data structure effectiveness and retrievability. Private space decomposition technology is used in applications involving personal and private data to balance the requirements of data availability and privacy protection.
When using PSD for privacy protection in spatial indexing, it is common to utilize the spatial index tree structure and divide the geographical area into subintervals, which serve as the next-level nodes of the tree structure. Leaf nodes contain two-dimensional coordinates, while the parent node stores the summarized data information of child nodes adhering to differential privacy, essentially representing the index information. To ensure the objective of data privacy protection, noise is introduced to the spatial nodes during index establishment, ultimately leading to query results aligned with the distribution of differential privacy.
In addition to the tree hierarchy, the index for spatial data also has a plane structure, such as a grid structure. Wahbeh Qardaji et al. [
30] proposed the concept of a multilevel grid index and compared it with the traditional tree index. Their findings indicate that the multilevel grid offers better performance in terms of differential privacy protection than the traditional hierarchy. They further introduced the unified grid granularity method [
30]. Building upon the idea of unifying the grid granularity partition, Reference [
35] presented an adaptive grid (AG) method characterized by robustness and simplicity. This method calculates the size of the second grid based on the results of the first grid query. In comparison to the PSD, the AG method also demonstrates robustness and simplicity. While the dynamic grid utilizes some data in the second calculation of grid granularity, its impact on privacy protection is not significant. This paper inherits the adaptive grid (AG) method and makes improvements based on personalized user needs. When adding noise to the grid by using the Laplace mechanism, the personalized user needs are considered.
4. Personalized Privacy Protection
In this section, we introduce the three parts of our personalized privacy protection framework in detail. We first design the personalized private space decomposition framework. Based on that, we further design the task broadcast strategy. Finally, the task allocation algorithm based on worker compensation is presented.
4.1. Personalized Private Space Decomposition Framework Design
4.1.1. PSD
When constructing a worker index in the database, we operate under the following assumptions: Firstly, the workers’ residential places represent their current locations. Secondly, the platform possesses latitude and longitude coordinate data of workers. The third assumption is that the workers’ residential places are distributed within a known area. In the simulation experiment, the residential location can serve as a substitute for real-time location data, facilitating comparisons with the spatial index privacy protection algorithm of other data structures. This section introduces the spatial index frame design for the spatial location of workers. The dynamic division of the spatial grid employs the dynamic spatial meshing strategy outlined in
Section 3.1.
It is worth noting that the data privacy budget of each grid is the same when the above algorithm dynamically divides the spatial grid, so it cannot meet personalized needs. This paper makes some improvements on this basis.
4.1.2. Personalized Privacy Budget Allocation
When establishing the dynamic meshing results, using the conclusions in Reference [
30], we will reduce the total budget
. It is divided into two parts. The first part
is the privacy budget required to add noise to the node when establishing the first-level grid node. The second part
will be used to calculate the noisy count of the second-level grid nodes. And the calculation formula of
is as follows:
is the percentage of the total budget divided when dividing the first-level grid (
). According to the literature [
30], the parameter
is not critical for privacy protection results. When the range of
is from 0.2 to 0.6, the noisy data are roughly similar to the original data. Therefore, in order to achieve a personalized level of privacy protection, we will set
to a random number from 0.3 to 0.6.
4.1.3. Spatial Grid Division Strategy
When constructing a spatial index, it is necessary to organize each index into a grid containing a limited number of user nodes or a grid covering a small area, with each leaf node forming part of the subsequent tree structure. Drawing from index categories in the database, various forms of tree structure decomposition exist during spatial division:
No data decomposition required. The tree structure after division is precisely defined, and the division’s outcome relies solely on the definition of the tree structure. For instance, the quadtree is established by recursively dividing each node’s region into four subregions of equal area [
36].
Data decomposition required. This decomposition relies on the internal data of the node. For example, Hilbert R-tree: R-tree is a spatial decomposition formed by nested rectangles that may overlap.
Hybrid tree. The definition of a hybrid tree is that the establishment of some level nodes needs data support and the division of the remaining level nodes does not need data support. The construction process of a hybrid tree needs to be designed in combination with a specific framework.
When providing differential privacy protection for nodes in space, some researchers have adopted the above tree structure [
34,
37]. It is common to use recursive partitioning to establish quadtree and k-d tree. Although effective in maintaining differential privacy protection, applying one-dimensional hierarchical methods to two-dimensional datasets often results in deeper trees. When dealing with massive data, the construction of spatial indexes can extend to more than ten levels, with grid divisions often operating at a scale level.
Dynamic spatial meshing strategy AG: Reference [
35] proposed an adaptive grid (AG) method. This method aims to divide areas with concentrated worker data into more subareas and areas with sparse worker data into fewer subareas. In other words, AG addresses the drawback of the unified grid (UG) by calculating the sizes of second-level grid cells at different levels based on the data of the upper-level node.
The PSD algorithm in AG is introduced as follows: Firstly, we establish the root node of the mesh. Subsequently, we partition the root node into a grid of fixed size
. To introduce variability into the number of users in each grid cell, we add noise to the number of users in each grid cell by using Formula (
5). The author of Reference [
30] proposed the calculation formula for determining the granularity of the first-level grid node in AG, which is presented in Equation (
7):
where
N represents the number of data points on the workers’ location grid. The authors of Reference [
38] presented a substantial number of data. According to the experimental results, it was demonstrated that setting
c = 10 yields improved division results.
Subsequently, AG retrieves the count of workers in the first-level grids. With the number of these grids being
, we calculate the size of the second-level grid according to the number of query results. Each coarse-grained region is then adaptively subdivided into
finer-grained areas. The calculation formula of
is as follows:
To increase the granularity
and reduce the overhead, the author of Reference [
35] incorporated an additional parameter
into the heuristic algorithm, setting it to
. During the initialization phase, the particle size is set to
, and noise is added to the number of fine-grained grid cells using Formula (
5). Subsequently, the perturbed count of the corresponding fine-grained mesh is published alongside the structure of AG. Based on Formula (
1), the counting query algorithm of the AG model satisfies the requirements of
-differential privacy.
Personalized dynamic spatial meshing strategy PAG: For personalization, we set the privacy budget percentage
to a random value. Refer to Algorithm 1 for the specific algorithm.
Table 1 presents a description of the special symbols utilized in Algorithm 1, while
Figure 3 serves as an aid for comprehending the flowchart of Algorithm 1.
| Algorithm 1 PAG |
- Input:
Grid of workers’ location (WL) - Output:
Grid of workers’ location (WL) - 1:
calculate - 2:
Initialize the root node, initialize the queue and queue the root node - 3:
if queue is empty: - 4:
output the PAG tree - 5:
else: - 6:
pop queue leader node curr - 7:
If = 0: - 8:
divide WL into , , …, - 9:
establish first-layer nodes of PAG tree - 10:
put first-layer nodes into queue - 11:
randomly generated budget percentage - 12:
calculate and remaining privacy budget - 13:
execute step 3 - 14:
else: - 15:
If = 1: - 16:
divide into , , …, - 17:
establish second-layer nodes of PAG tree - 18:
add second-layer nodes to Laplace random noise count - 19:
put second-layer nodes into queue - 20:
execute step 3 - 21:
else: - 22:
If = 2: - 23:
calculate - 24:
divide into , , …, - 25:
establish third-layer nodes of PAG tree - 26:
add third-layer nodes to Laplace random noise count - 27:
put third-layer nodes into queue - 28:
execute step 3 - 29:
else: - 30:
divide into , , …, - 31:
establish fourth-layer nodes of PAG tree - 32:
add fourth-layer nodes to Laplace random noise count - 33:
put fourth-layer nodes into queue - 34:
execute step 3
|
According to References [
34,
35], we understand that the Laplace mechanism can introduce noise to the spatial index of the dataset, ensuring that the output of the counting query function satisfies the requirements of
-differential privacy.
4.2. Task Broadcast Strategy Design
Compared to tasks assigned directly by the platform, workers are more willing to accept the broadcast task, so the platform needs to find a reasonable broadcast area. In essence, the task broadcasting strategy must access the spatial indexes of workers and calculate a designated broadcast grid area centered around the task location. The decisive condition of this area is that the task can be accepted by the staff in the platform when the probability of completion can be achieved. As users generally prefer tasks closer to their current location for convenience [
38,
39], their acceptance rates vary depending on task proximity. The acceptance rate is a function that decreases with forward distance. In this paper, the linear decline function is selected. This chapter adopts the broadcast area algorithm described in Reference [
35]. This paper finds the secondary grid node where the task is located and continuously adds the neighbor nodes with workers. When there is a certain probability that the task can be completed, it ends the expansion of the broadcast area.
According to the literature [
39], approximately 10% of the platform’s workforce is responsible for more than 80% of the tasks; these individuals are referred to as super workers. Moreover, within the group of super workers, around 90% of them travel less than 40 miles a day. This attribute has been labeled as task locality in the literature [
37]. Additionally, prior research [
40] addressed the issue of content locality among users of platforms such as Flickr and Wikipedia, proposing the spatial content generation model (SCPM). The model calculates the average contribution distance (
MCD) of each worker as follows:
where
represents the distance between worker
and task
. As described in the literature [
35], the formula for calculating the maximum travel distance (
MTD) that workers are willing to accept for a task is as follows:
When the distance between the worker and the task exceeds the
MTD, the worker will not choose the task. Here, MAR denotes the maximum probability of a worker accepting the task. Additionally,
AR represents the probability that the staff will accept and complete the task.
AR is calculated as follows:
Here, dist represents the distance between the worker and the task. We establish a threshold, EU. If the probability of completing the broadcast area surpasses this threshold, it implies that at least one worker can accept the task. Assuming uniform AR among workers within a single secondary grid, the distance between workers and tasks is the average distance between tasks and the four corners of the secondary grid.
represents the noise count of workers within grid
c.
represents the task acceptance rate of workers in grid
c. The utility of grid
c is calculated as follows:
Next, two calculation schemes of broadcast area will be introduced.
Broadcast area calculation without considering the secondary grid division: Begin with the grid containing task
t as the initial broadcast area. If the current broadcast area’s utility is lower than
EU, the nearest neighbor to the task within the maximum travel range will be added to the broadcast area. The specific flow of the algorithm is outlined in Algorithm 2, while
Table 2 provides the interpretation of the symbols used in Algorithm 2.
| Algorithm 2 GDY |
- Input:
Task t, utility threshold EU, maximum travel area MTD - Output:
Broadcast area GR - 1:
Initialization GR is null, u = 0 - 2:
Initialize the maximum heap Q, where q is the second-level grid covering t - 3:
Pop { } from stack Q - 4:
If = null then output broadcast area GR, where GR is greater than MTD. Otherwise - 5:
If then - 6:
If then output broadcast area GR. Otherwise look for neighbors of C not in GR ∩ MTD - 7:
Add neighbors to Q and execute step 3
|
Broadcast area calculation considering two-level grid continuous division: In order to reduce the cost as much as possible, Algorithm 2 can divide the final secondary grid and find the adjacent subregions that can reach the threshold. The following are the improvement steps of Algorithm 2 and special symbol notes.
4.3. Task Allocation Algorithm Based on Worker Compensation
When facing the task allocation mechanism based on a dynamic grid, there are different task allocation methods according to different considerations of the decision-making mechanism. For example, the task is assigned to the workers who accept the task first (time first), the task is assigned to the workers closest to the task (location first), and the task proposed in this paper is assigned to the workers with the lowest salary (salary first). In order to improve the speed of task acceptance, the first accept first assign model is used to assign the task to the staff with the earliest response time among all response staff. In order to reduce the travel distance of the staff, the nearest first assignment model is used to assign the task to the staff member closest to the task among all the responding staff. This paper chooses to assign tasks to the workers with the lowest salary in the unit cost, that is, the lowest reward-first allocation algorithm.
When designing the remuneration, the worker
privacy budget and the distance between
and task
t are taken into account. Reward
[
i,0] is a linear combination of privacy budget and distance. The calculation formula is shown in Equation (
13):
For personal reasons (such as completing a task), even if some workers have a high probability, they may not complete the task. Therefore, it is necessary to simulate whether workers complete the task by using a random function. The greedy algorithm is used to find the current lowest paid worker, and Formula (
11) is used to calculate the probability
AR that the worker accepts the task, and the random function is called to simulate the probability that the worker actually accepts the task. If the random number is greater than
AR, the task is accepted and the assignment ends. Otherwise, continue to find the next worker until there is a worker to accept or no workers.
5. Experiments and Analyses
The personalized differential privacy protection strategy proposed in this paper adds complexity to task assignment. Introducing random Laplace mechanism noise can affect the efficiency and accuracy of task assignment to workers within the task assignment model. Hence, we aim to assess the effectiveness of the personalized privacy policy (PAG) proposed in this paper in safeguarding data against discrepancies between noisy and real data.
5.1. Experimental Settings
In our experiments, we utilized two widely used real-world datasets, Gowalla and Yelp, as the core foundations. Gowalla, a social network dataset, provides genuine location check-in data from users of the Gowalla mobile application, recording their activities at various global locations, including timestamps and user profiles. Within our model, we consider the users in Gowalla as workers, each check-in point being a previously accepted and executed task.
On the other hand, Yelp offers an extensive compilation of business- and user-related information sourced from the Yelp website. It encompasses intricate business data such as geographical coordinates, operating hours and user ratings, alongside user-generated reviews. With data points comprising 15,583 restaurants, 70,817 users and 335,022 reviews, we regarded restaurant locations as tasks and user reviews as accepted tasks.
Our experiments were conducted on a computer equipped with an Intel i7 CPU and an NVIDIA 3090 GPU. Each experiment was repeated multiple times to derive the average value as the final result.
5.2. Performance Evaluation Criteria
In the context of the task allocation mechanism, we emphasize the following indicators:
: Represents the average of the average difference between the actual query count and the noisy query count results. A smaller difference indicates better algorithm performance.
: Denoting the number of broadcast hops in the platform’s task dissemination region. A smaller number of hops suggests faster task completion.
ANW: Indicating the average number of workers required for each task broadcast. A smaller workforce implies higher quality worker selection.
TASR: Representing the acceptance rate by staff once the task is released on the platform. A higher ratio signifies more efficient worker selection.
WTD: Signifying the average distance that staff members need to travel in order to complete their assigned tasks. A smaller distance suggests better suitability of the selected workers for the tasks.
5.3. Experimental Results
In this paper, the simulation experiment will utilize datasets from the literature [
35]. The specific results of the simulation experiment evaluation are as follows:
5.3.1. Evaluation of Privacy Protection Performance of Personalized PSD Spatial Index
Based on the findings presented in Reference [
35], the grid structure demonstrates superior performance compared to other spatial index data structures in terms of differential privacy protection. Consequently, we solely consider one spatial index data structure for comparison. Specifically, our experiments are conducted on four spatial indexes: k-d tree, UG unified grid, AG adaptive grid and PAG personalized adaptive grid. Each of these algorithms is utilized to identify different spatial indexes. Furthermore, the spatial indexes with added noise are repeatedly counted within a specific range, allowing us to calculate the disparity between the actual data count and the noise-infused count for the same query. A smaller variance between the actual count and the noise count signifies a stronger data protection effect.
Given that our partition percentage is a randomly generated number during the actual internal division of the PAG grid, it becomes apparent that most workers allocate a significant portion of their privacy budget to the division of the first-level grid, with a comparatively smaller share allocated to the second-level grid nodes. Consequently, we set the privacy budget for k-d, UG and AG at 0.4, with a percentage of 0.5, and the privacy budget in PAG at 0.6. To ensure the accuracy and effectiveness of the experimental data, we conducted separate queries across various spatial indexes under different total privacy budgets. The average results from multiple seeds were calculated, followed by the computation of the average discrepancy between the query results of different spatial indexes under different total privacy budgets and the real data.
Figure 4 illustrates the experimental test data for different total privacy budgets in a line graph, while
Table 3 presents the average experimental values for different privacy budgets, with averageErr representing the average of the average difference between the actual query count and the noisy query count results.
5.3.2. Impact of Personalized Grid Structure on System Performance
We conducted a comparison of the communication cost between the PAG structure and the AG structure in task broadcasting. Using a set of 100 task coordinates, along with the AG spatial index and the PAG spatial index, we generated the broadcast areas
and
according to Algorithm 3, while
Table 4 provides the interpretation of the symbols used in Algorithm 3. Subsequently, we initiated broadcasting within the designated broadcast areas. Following this, we calculated the average number of notified workers (
ANW) and the number of propagation hops (
) for the task broadcast. The specific results are presented in
Table 5 and
Table 6.
| Algorithm 3 Subunit division algorithm of the secondary grid in broadcast area PCSH |
- Input:
Task location t, the last cell , the probability of task acceptance in the current grid - Output:
(subunit of ) - 1:
Calculate dist (the distance between and t) and (the worker’s probability) - 2:
(probability required) - 3:
(number of workers required) - 4:
Calculation of area percentile: - 5:
If covers t, then calculate the subunit C’ of C-based percentile and output; otherwise, perform step 6 - 6:
Find the subunit of adjacent to the current region and output it.
|
5.3.3. Impact of Minimum Reward Task Allocation Model on System Performance
Based on the simulation results of task broadcasting in
Section 4, we can further analyze the impact of the minimum reward task allocation model on the platform system’s performance. The primary indicators in this section are the success rate
TASR, representing the acceptance rate by staff once the task is released on the platform, and the distance
WTD that staff members need to travel in order to complete their assigned task. The specific experimental results are presented in
Table 7 and
Table 8.
7. Conclusions
During the process of mobile data collection, the protection of data collectors’ location data has become an increasingly critical concern. To prevent exposing real staff location information to potential attackers, certain documents, such as [
41,
42,
43,
44], have employed differential privacy technology to obfuscate location information on the local client before uploading the perturbed data to the platform. Building upon this prior work, this paper presents implementation algorithms for different privacy protection levels within specific grid cells in the second-level grid. Finally, the task allocation strategy of minimum reward allocation is proposed. We compare the algorithm proposed in this paper with the algorithm proposed by the author of Reference [
35] through experimental simulation. The purpose of the comparison is to analyze the effectiveness and practicability of the personalized privacy protection algorithm proposed in this paper in data protection. By analyzing the results, we can conclude that the task allocation model proposed in this paper has a positive impact on improving performance indicators such as the task completion rate in the task allocation process.
While the algorithm proposed in this paper yields favorable results in terms of data privacy protection and task allocation, it is not without its limitations. One prominent issue is that the algorithm sacrifices a portion of the communication cost for lower remuneration and a flexible privacy protection level. Our forthcoming area of improvement is to find a more suitable algorithm that minimizes the number of propagation hops during communication, consequently reducing the cost associated with it.