Method for Controlling Full-Frequency Band Environment Vibration by Coordinating Metro Vibration Sources and Propagation Paths
Abstract
:1. Introduction
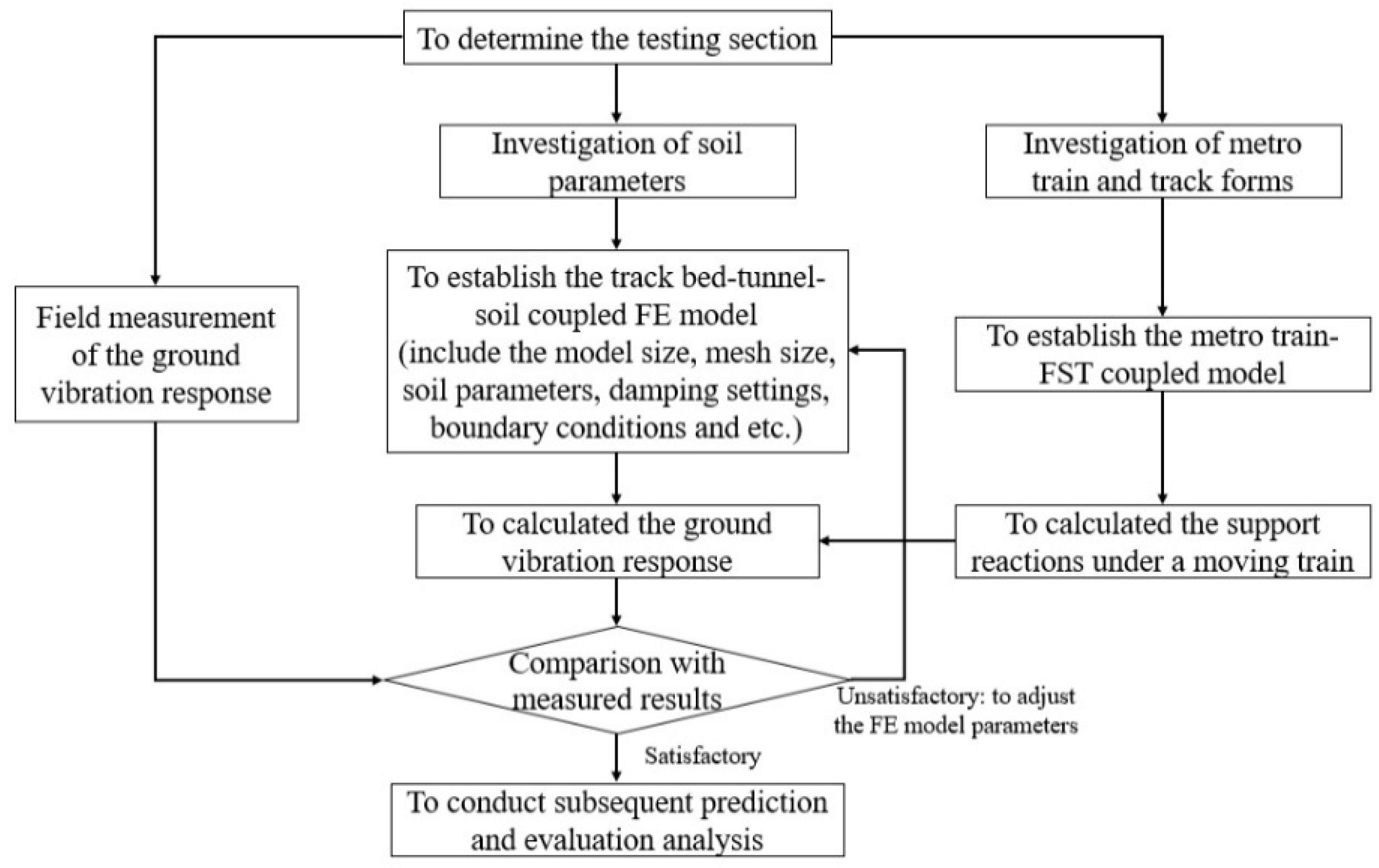
2. Establishment of Prediction Model
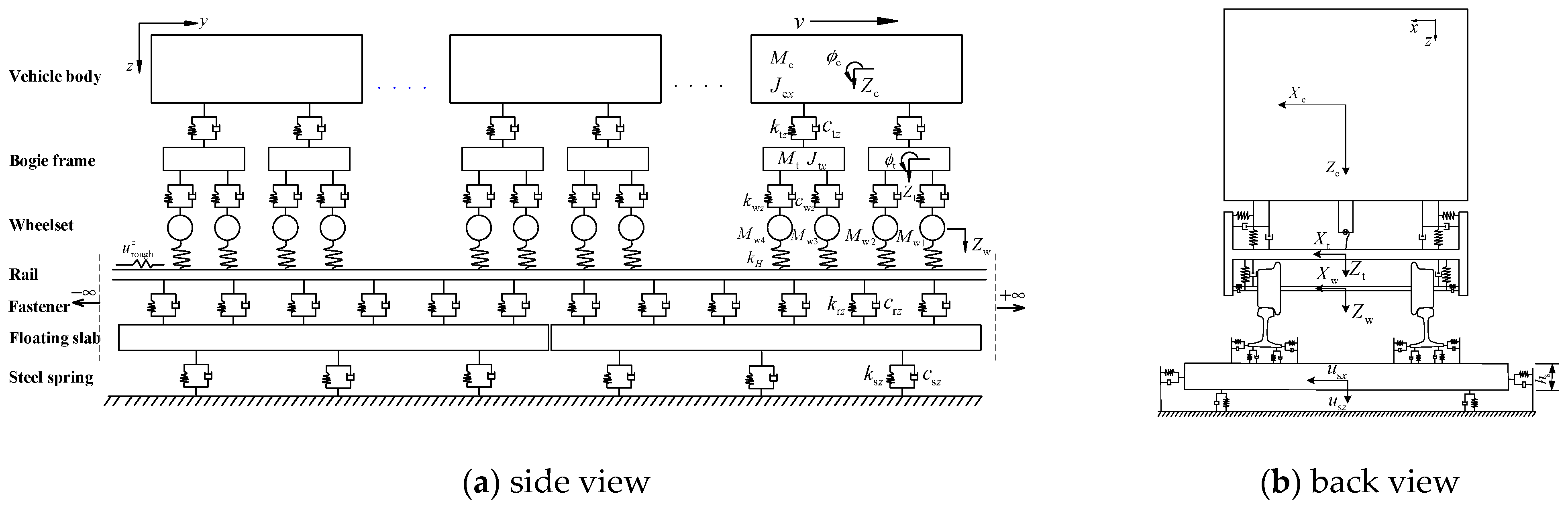
2.1. Metro Train–FST Coupled Model and Train Load Calculations
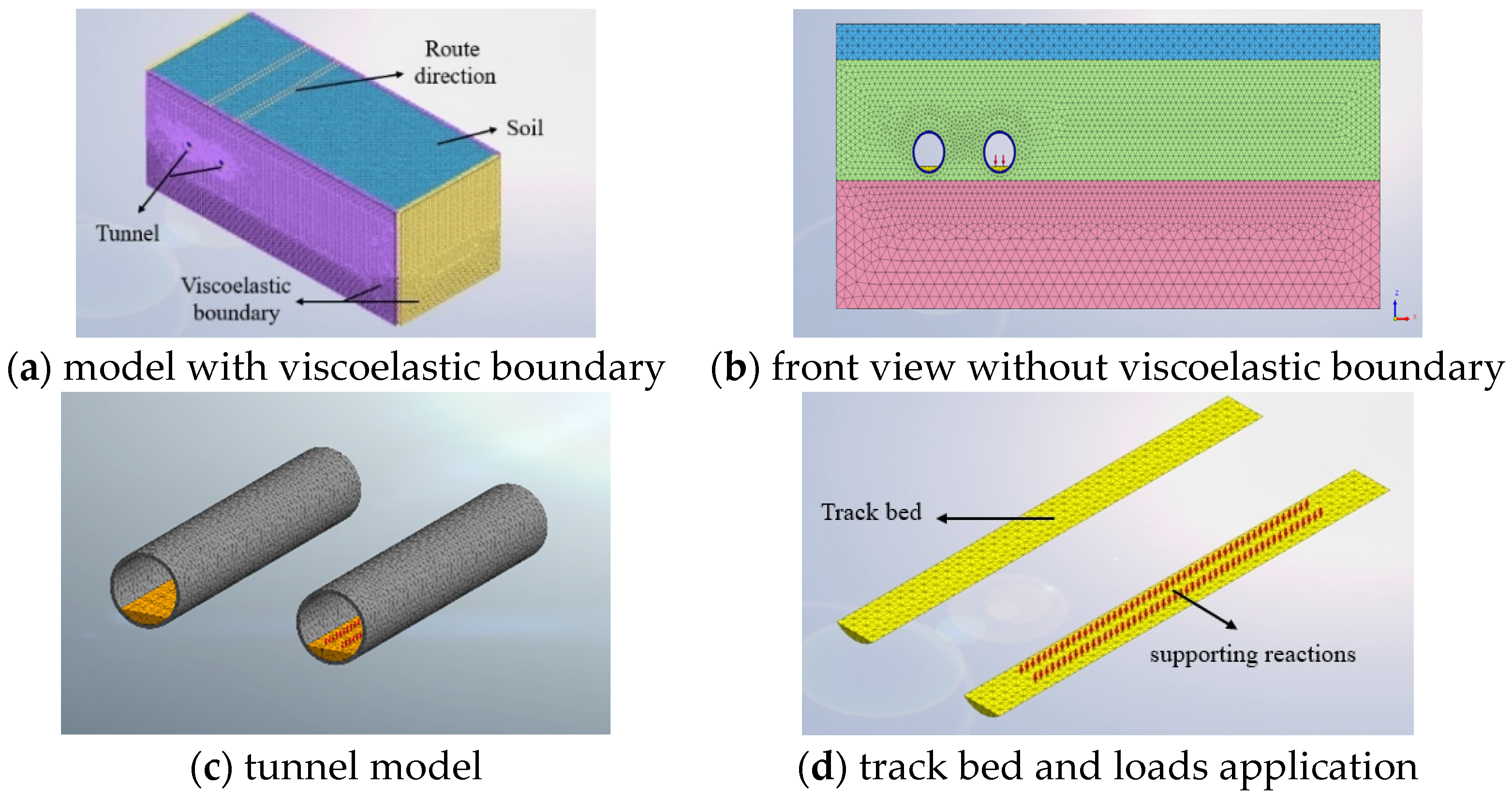
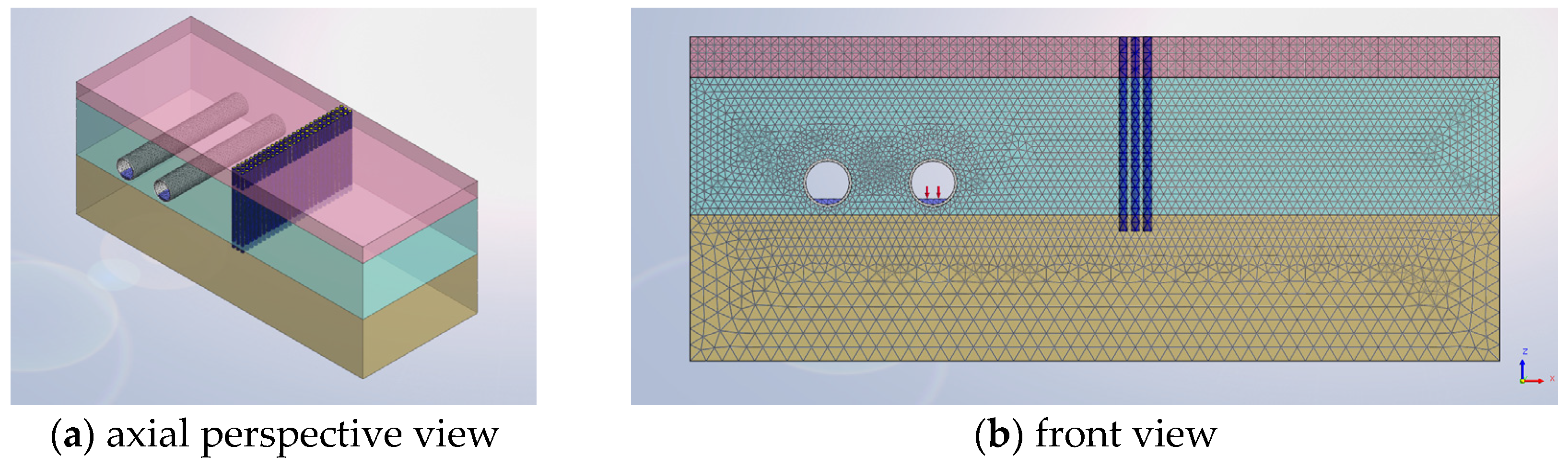
2.2. Track Bed–Tunnel–Soil Coupled FE Model
3. Field Measurements and Model Verification
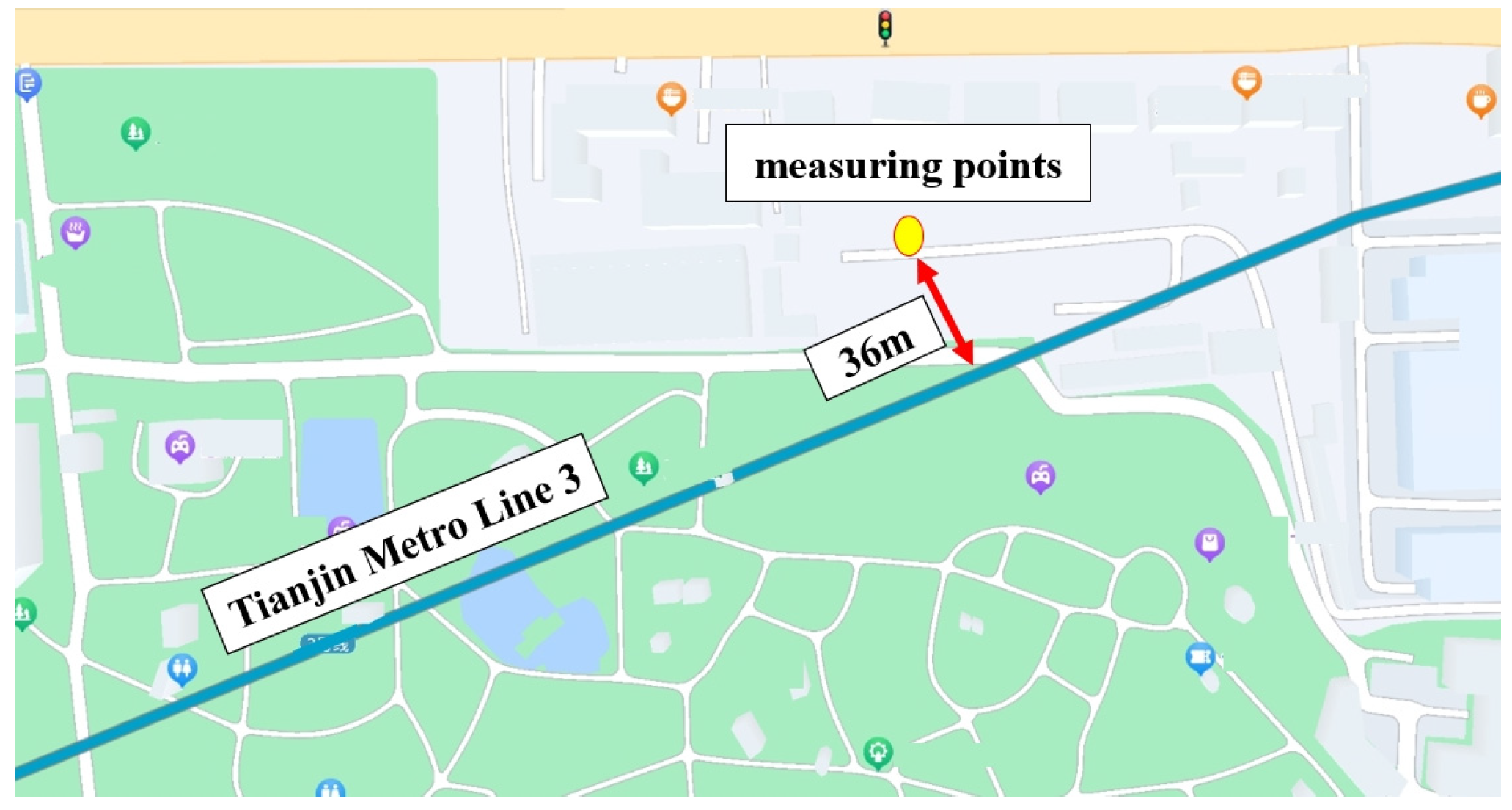
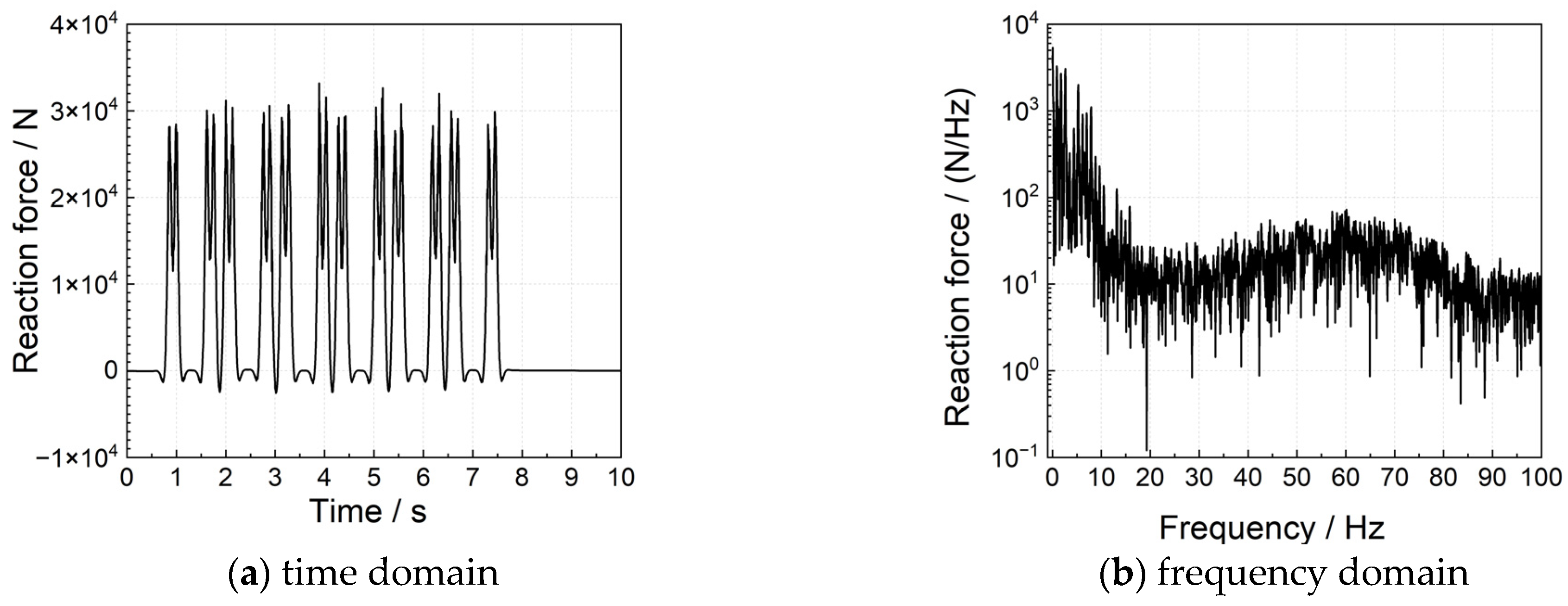
3.1. Outline of Measurements
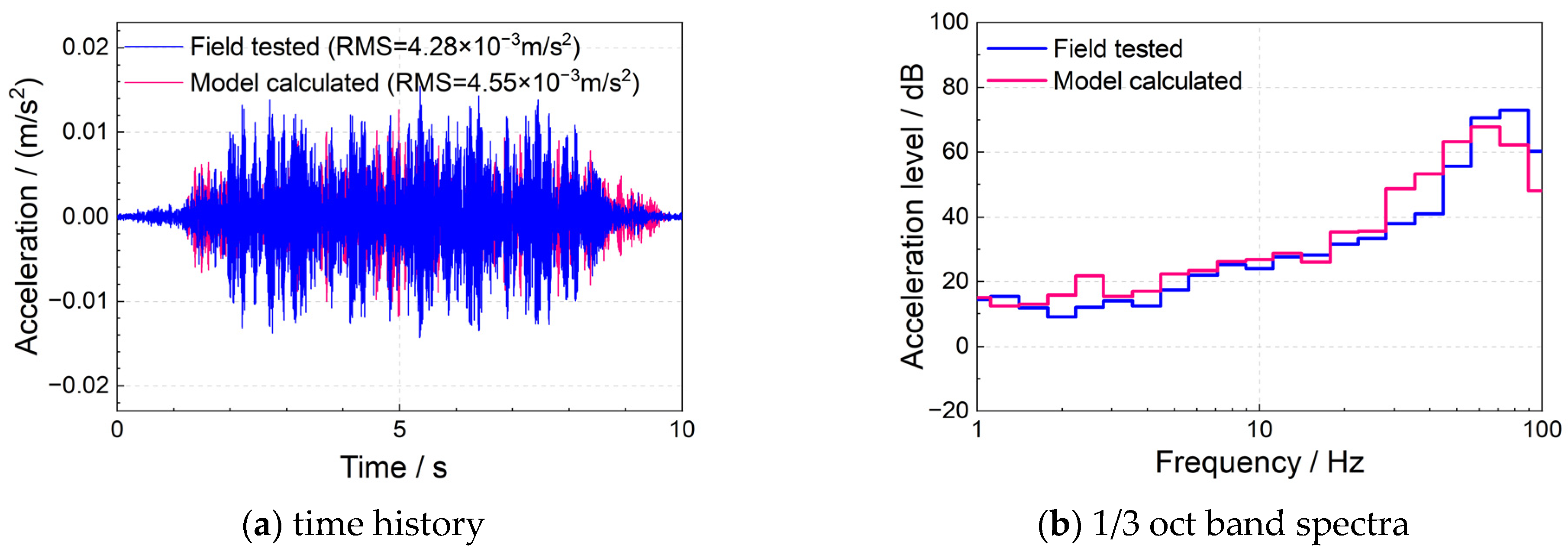
3.2. Model Verification
4. Case Study and Analysis of Vibration Control Effect
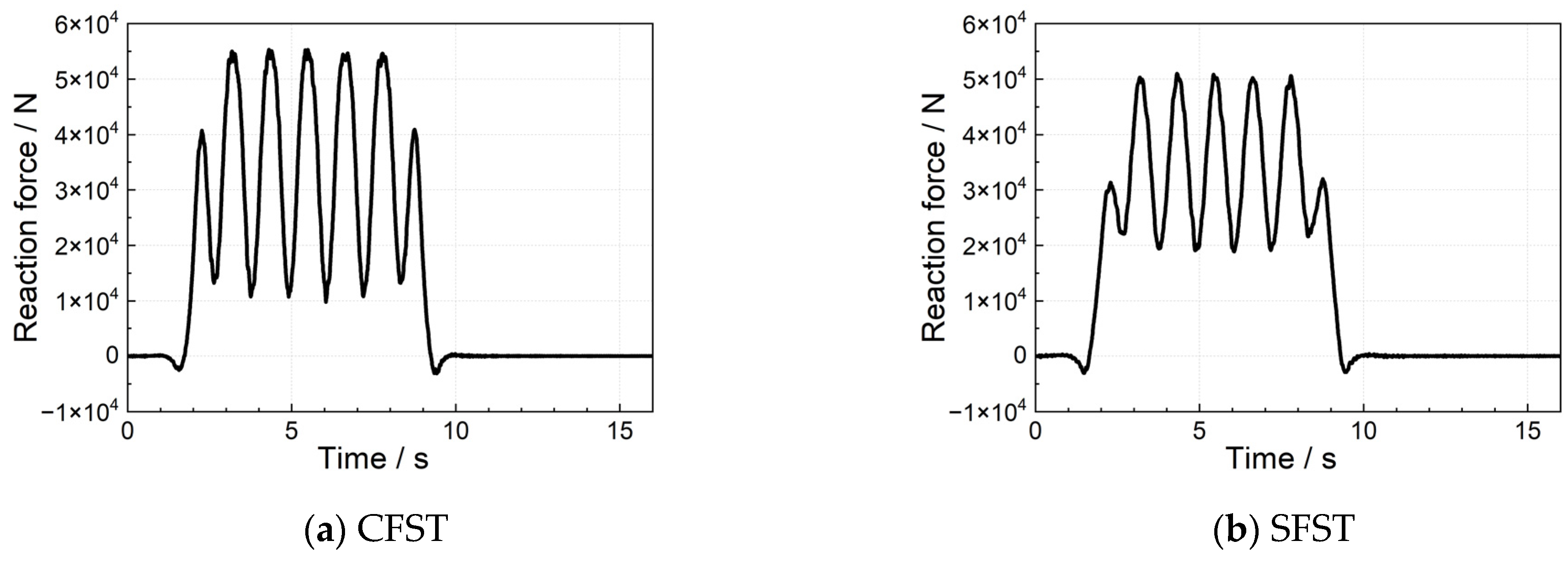
4.1. Design of FST
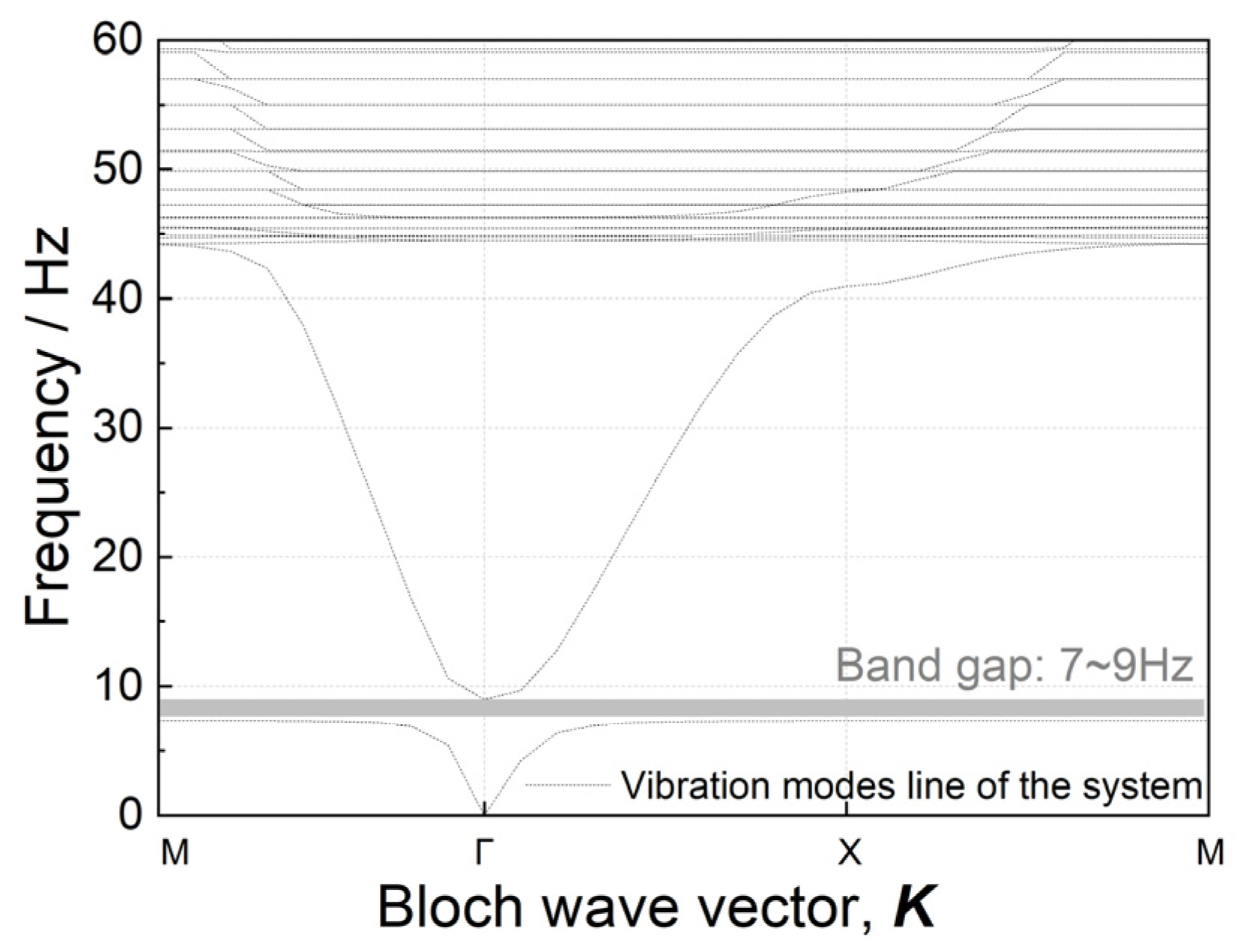
4.2. Design of Periodic Row Piles
4.3. Analysis of Ground Vibration-Reduction Effect
5. Conclusions
- (1)
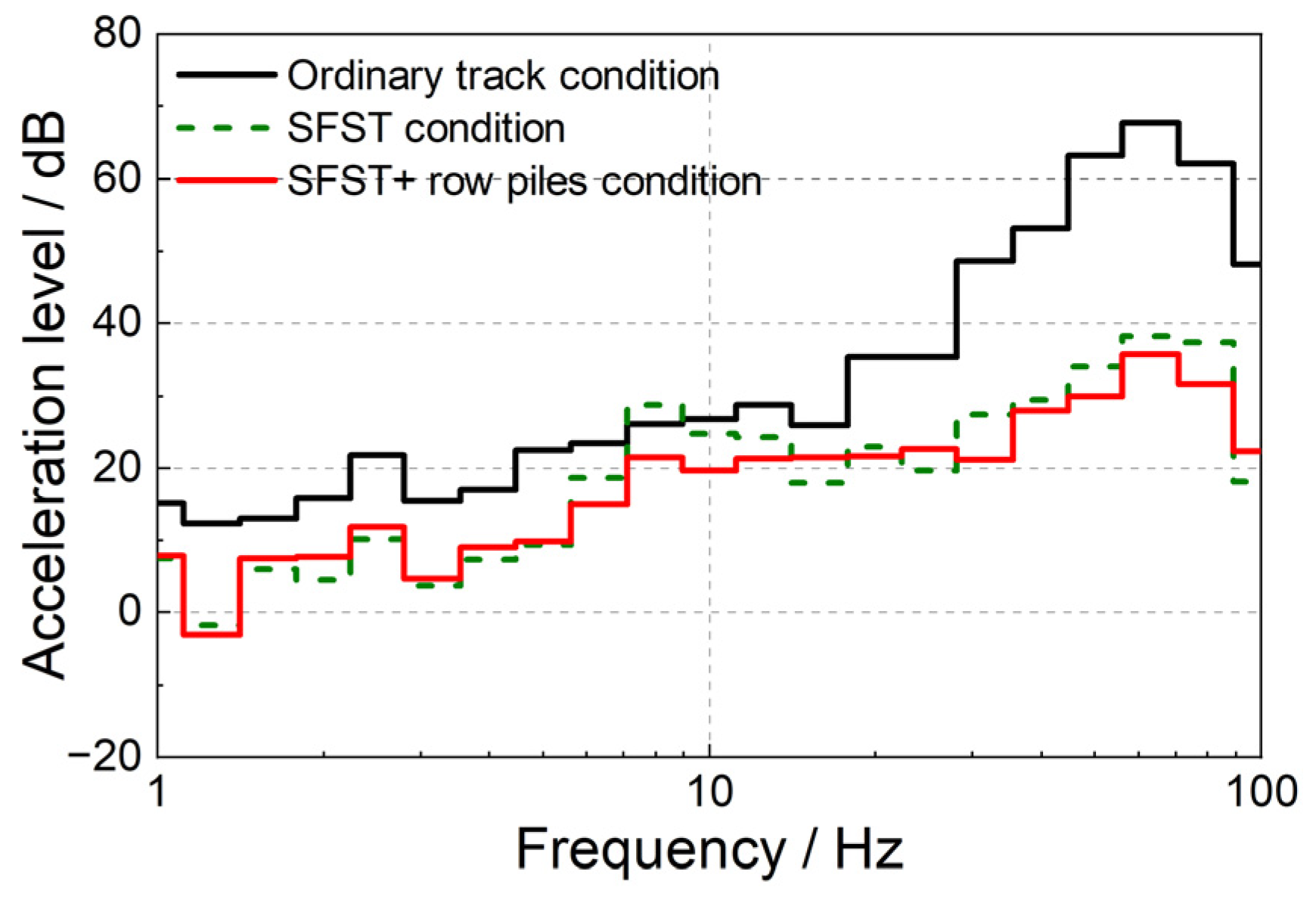
- CFSTs can reduce the frequency vibration level by up to 40 dB, but vibration amplification occurs at 10 Hz, with an amplification of approximately 8 dB. After thickness adjustment, damping and FST stiffness reduction, the natural frequency of the FST shifts to a low frequency of 8 Hz, and the ground vibration decreases by approximately 5–8 dB in the frequency band near the natural frequency of the FST, but the vibration amplification does not be change.
- (2)
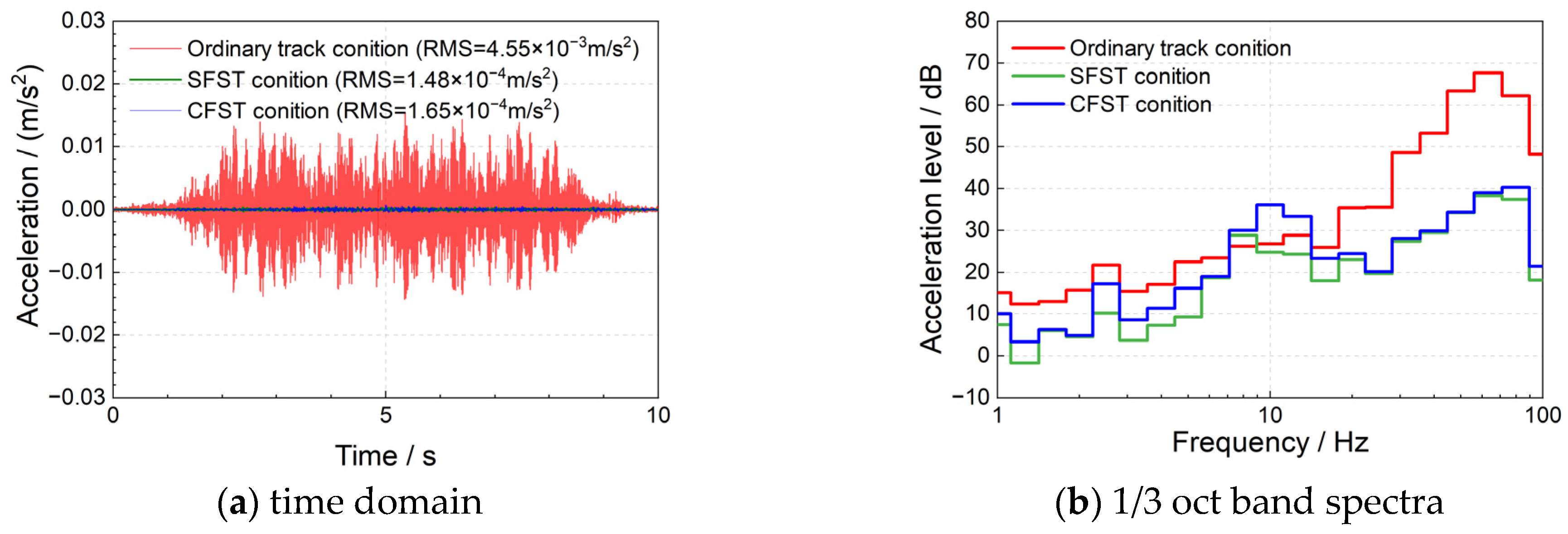
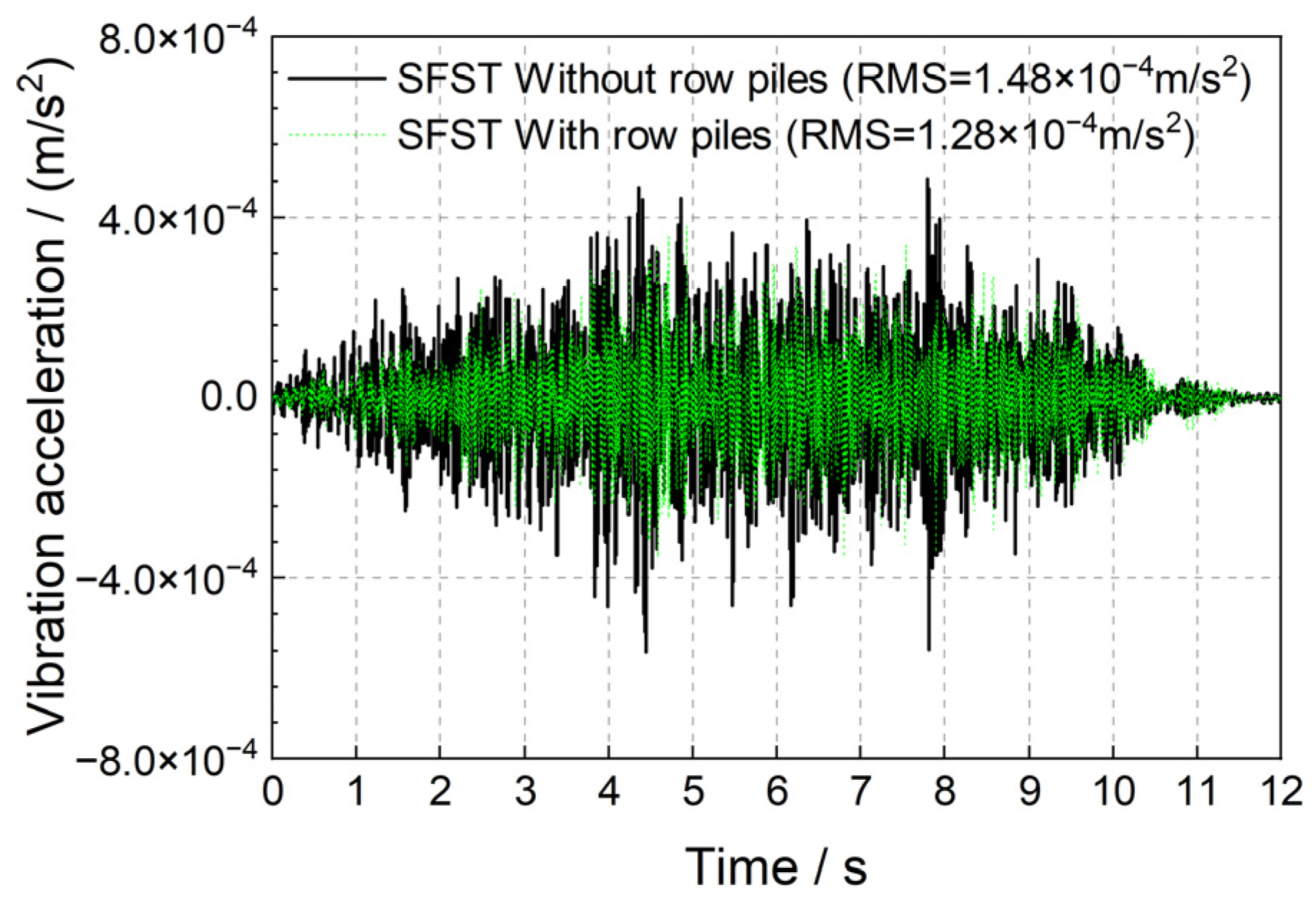
- The use of FST can significantly decrease the ground vibration acceleration, and the RMS value of vibration acceleration can be reduced by one order of magnitude. Adding row piles in FST lines can further reduce the RMS value of the ground vibration response by approximately 0.2 × 10−4 m/s2.
- (3)
- The designed local resonance periodic row piles, whose bandgap range is adjusted to 7–9 Hz, can effectively reduce ground vibration at the natural frequency of the FST, with a decrease of 3–5 dB, which is lower than the ground vibration level under ordinary track conditions.
- (4)
- Replacing local resonance-type row piles with hollow pipe piles significantly decreases the ground vibration below 7 Hz, which can be reduced by 4–10 dB compared with the conditions for local resonance row piles. This also decreases the ground vibration amplification at the natural vibration frequency of the FST, and the vibration level is lower than that of the ordinary track condition at this frequency.
- (5)
- The proposed comprehensive vibration control method that considers frequency matching and combines vibration reduction from the vibration source and propagation path solves the ground vibration amplification problem at the natural frequency of the FST in metro lines. Compared with ordinary tracks, the frequency vibration can be decreased by 4–12 dB in the frequency band below 20 Hz and by 10–35 dB in the frequency band above 20 Hz, realising ground vibration control in the full-frequency band. This study provides a new and effective method for vibration control in scenarios such as when using precision instruments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, X.; Qu, W. Experimental and Numerical Studies of Metro Train-Induced Vibrations on Adjacent Masonry Buildings. Int. J. Struct. Stab. Dyn. 2015, 16, 1550067. [Google Scholar] [CrossRef]
- Sadeghi, J.; Haghighi, E.; Esmaeili, M. Performance of under foundation shock mat in reduction of railway-induced vibrations. Struct. Eng. Mech. 2021, 78, 425–437. [Google Scholar] [CrossRef]
- Ma, M.; Li, M.; Qu, X.; Zhang, H. Effect of passing metro trains on uncertainty of vibration source intensity: Monitoring tests. Measurement 2022, 193, 110992. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, S.; Zhai, W.; Kouroussis, G.; Wang, Y.; Wang, K.; Lan, K.; Xu, F. Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel. Sci. Total Environ. 2019, 668, 485–499. [Google Scholar] [CrossRef] [PubMed]
- Marco, Z.; Giuseppe, C.P.; Giuseppe, T.; Marco, S. On the Influence of Shallow Underground Structures in the Evaluation of the Seismic Signals. Ing. Sismica 2021, 38, 23–35. [Google Scholar]
- Ma, M.; Liu, W.; Qian, C.; Deng, G.; Li, Y. Study of the train-induced vibration impact on a historic Bell Tower above two spatial overlapping metro lines. Soil Dyn. Earthq. Eng. 2016, 81, 58–74. [Google Scholar] [CrossRef]
- Sadeghi, J.; Esmaeili, M. Safe distance of cultural and historical buildings from subway lines. Soil Dyn. Earthq. Eng. 2017, 96, 89–103. [Google Scholar] [CrossRef]
- Gupta, S.; Degrande, G.; Lombaert, G.; Liu, W. Prediction of vibrations induced by underground railway traffic in Beijing. J. Sound Vib. 2008, 310, 608–630. [Google Scholar] [CrossRef]
- Ding, D.; Gupta, S.; Liu, W.; Lombaert, G.; Degrande, G. Prediction of vibrations induced by trains on line 8 of Beijing metro. J. Zhejiang Univ.-Sci. A 2010, 11, 280–293. [Google Scholar] [CrossRef]
- Ma, M.; Jiang, B.; Liu, W.; Liu, K. Control of Metro Train-Induced Vibrations in a Laboratory Using Periodic Piles. Sustainability 2020, 12, 5871. [Google Scholar] [CrossRef]
- Liang, R.; Ding, D.; Liu, W.; Sun, F.; Cheng, Y. Experimental study of the source and transmission characteristics of train-induced vibration in the over-track building in a metro depot. J. Vib. Control 2022, 29, 1738–1751. [Google Scholar] [CrossRef]
- Huang, S.; Chen, Y.; Zou, C.; Jian, S. Train-induced environmental vibrations by considering different building foundations along curved track. Transp. Geotech. 2022, 35, 100785. [Google Scholar] [CrossRef]
- Colaço, A.; Castanheira-Pinto, A.; Costa, P.A.; Ruiz, J.F. Combination of experimental measurements and numerical modelling for prediction of ground-borne vibrations induced by railway traffic. Constr. Build. Mater. 2022, 343, 127928. [Google Scholar] [CrossRef]
- Farahani, M.; Sadeghi, J.; Jahromi, S.; Sahebi, M.M. Modal based method to predict subway train-induced vibration in buildings. Structures 2023, 47, 557–572. [Google Scholar] [CrossRef]
- Sadeghi, J.; Vasheghani, M.; Khajehdezfuly, A. Propagation of structure-borne noise in building adjacent to subway lines. Constr. Build. Mater. 2023, 401, 132765. [Google Scholar] [CrossRef]
- Faizan, A.A.; Kırtel, O.; Çelebi, E.; Zülfikar, A.C.; Göktepe, F. Experimental validation of a simplified numerical model to predict train-induced ground vibrations. Comput. Geotech. 2022, 141, 104547. [Google Scholar] [CrossRef]
- Auersch, L. Different Types of Continuous Track Irregularities as Sources of Train-Induced Ground Vibration and the Importance of the Random Variation of the Track Support. Appl. Sci. 2022, 12, 1463. [Google Scholar] [CrossRef]
- Tao, Z.Y.; Zou, C.; Yang, G.R.; Wang, Y.M. A semi-analytical method for predicting train-induced vibrations considering train-track-soil and soil-pile-building dynamic interactions. Soil Dyn. Earthq. Eng. 2023, 167, 107822. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Zou, C.; Wu, J.; Shen, Z.; Chen, Y. Building coupling loss measurement and prediction due to train-induced vertical vibrations. Soil Dyn. Earthq. Eng. 2023, 164, 107644. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Shi, Z. Floating slab track with Inerter Enhanced Dynamic Vibration Absorbers. Veh. Syst. Dyn. 2023, 61, 589–615. [Google Scholar] [CrossRef]
- Ngo, T.; Indraratna, B. Mitigating ballast degradation with under-sleeper rubber pads: Experimental and numerical perspectives. Comput. Geotech. 2020, 122, 103540. [Google Scholar] [CrossRef]
- Zeng, Y.; Pan, P.; Zhang, D.; Yang, J. Experimental study of isolation in the backfill zone of the foundation pit (IBF) method to reduce ground-borne vibration in buildings. Eng. Struct. 2020, 202, 109740. [Google Scholar] [CrossRef]
- Sun, X.; Ma, M.; Jiang, B.; Cao, R. Ground vibration from freight railway: Environmental impact and potential mitigation measure at propagation path. Environ. Sci. Pollut. Res. 2022, 29, 44364–44377. [Google Scholar] [CrossRef] [PubMed]
- Sheng, T.; Bian, X.; Xiao, C.; Chen, Y.; Liu, G.; Li, Y. Experimental study on a geosynthetics isolator for the base vibration isolation of buildings neighboring metro transportation. Geotext. Geomembr. 2021, 49, 1066–1078. [Google Scholar] [CrossRef]
- Hemsworth, B. Reducing groundborne vibrations: State-of-the art study. J. Sound Vib. 2000, 231, 703–709. [Google Scholar] [CrossRef]
- Wei, K.; Liu, Z.; Liang, Y.; Wang, P. An investigation into the effect of temperature-dependent stiffness of rail pads on vehicle-track coupled vibrations. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 444–454. [Google Scholar] [CrossRef]
- Dere, Y. Effectiveness of the floating slab track system constructed at Konya light rail. Measurement 2016, 89, 48–54. [Google Scholar] [CrossRef]
- Vogiatzis, K.; Kouroussis, G. Prediction and efficient control of vibration mitigation using floating slabs: Practical application at Athens metro lines 2 and 3. Int. J. Rail Transp. 2015, 3, 215–232. [Google Scholar] [CrossRef]
- Xia, H.; Chen, J.; Xia, C.; Inoue, H.; Zenda, Y.; Qi, L. An experimental study of train-induced structural and environmental vibrations of a rail transit elevated bridge with ladder tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2010, 224, 115–124. [Google Scholar] [CrossRef]
- Alabbasi, S.; Hussein, M.; Abdeljaber, O.; Avci, O. A numerical and experimental investigation of a special type of floating-slab tracks. Eng. Struct. 2020, 215, 110734. [Google Scholar] [CrossRef]
- Kuo, C.; Huang, C.; Chen, Y. Vibration characteristics of floating slab track. J. Sound Vib. 2008, 317, 1017–1034. [Google Scholar] [CrossRef]
- Hui, C.; Ng, C. The effects of floating slab bending resonances on the vibration isolation of rail viaduct. Appl. Acoust. 2009, 70, 830–844. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, J.; Yan, H.; Zhang, L.; Cai, C. Low-frequency vibration control of floating slab tracks using dynamic vibration absorbers. Veh. Syst. Dyn. 2015, 53, 1296–1314. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, J.; Cai, C.; Pan, Z.; Zhai, W. Application of dynamic vibration absorbers in designing a vibration isolation track at low-frequency domain. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 546–557. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, J.; Cai, C.; Wang, K.; Zhai, W.; Yang, J.; Yan, H. Development of a Vibration Attenuation Track at Low Frequencies for Urban Rail Transit. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 713–726. [Google Scholar] [CrossRef]
- Jin, H.; Liu, W. Experimental study on vibration reduction characteristics of ladder track with different arrangement of sleeper pads. J. Mod. Transp. 2015, 48, 73–78. [Google Scholar] [CrossRef]
- Zhao, Z.; Wei, K.; Cheng, F.; Li, H.; Wang, P. A theoretical vibration-reduction effect analysis of the floating slab track supported by nonlinear variable stiffness isolators and semi-active magneto-rheological dampers. Struct. Control Health Monit. 2021, 28, e2829. [Google Scholar] [CrossRef]
- Zhao, C.; Zheng, J.; Sang, T.; Wang, L.; Yi, Q.; Wang, P. Computational analysis of phononic crystal vibration isolators via FEM coupled with the acoustic black hole effect to attenuate railway-induced vibration. Constr. Build. Mater. 2021, 283, 122802. [Google Scholar] [CrossRef]
- Sheng, X.; Zhao, C.; Yi, Q.; Wang, P.; Xing, M. Engineered metabarrier as shield from longitudinal waves: Band gap properties and optimization mechanisms. J. Zhejiang Univ.-Sci. A 2018, 19, 663–675. [Google Scholar] [CrossRef]
- Sheng, X.; Zeng, H.; Shi, C.; Du, Y. A study on low-frequency vibration-mitigation performance of a phononic Crystal floating slab track. J. Vib. Shock 2022, 41, 36–42. (In Chinese) [Google Scholar] [CrossRef]
- Huang, J.; Shi, Z. Attenuation zones of periodic pile barriers and its application in vibration reduction for plane waves. J. Sound Vib. 2013, 332, 4423–4439. [Google Scholar] [CrossRef]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1970. [Google Scholar]
- Shi, Z.; Huang, J. Feasibility of reducing three-dimensional wave energy by introducing periodic foundations. Soil Dyn. Earthq. Eng. 2013, 50, 204–212. [Google Scholar] [CrossRef]
- Wang, X.; Wan, S.; Nian, Y.; Zhou, P.; Zhu, Y. Periodic in-filled pipes embedded in semi-infinite space as seismic metamaterials for filtering ultra-low-frequency surface waves. Constr. Build. Mater. 2021, 313, 125498. [Google Scholar] [CrossRef]
- Ma, M.; Markine, V.; Liu, W.; Yuan, Y.; Zhang, F. Metro train-induced vibrations on historic buildings in Chengdu, China. J. Zhejiang Univ.-Sci. A 2011, 12, 782–793. [Google Scholar] [CrossRef]
- Gordon, C.G. Generic Vibration Criteria for Vibration-Sensitive Equipment. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, International Society for Optics and Photonics, Denver, CO, USA, 28 September 1999. [Google Scholar] [CrossRef]
- Mojtaba, V.; Javad, S.; Amin, K. Legal consequences of train-induced structure borne noise and vibration in residential buildings. Noise Mapp. 2022, 9, 170–188. [Google Scholar] [CrossRef]
- Standing Committee of the National People’s Congress. Law of the People’s Republic of China on the Prevention and Control of Noise Pollution; Standing Committee of the National People’s Congress: Beijing, China, 2022. [Google Scholar]
- Zou, C.; Moore, J.A.; Sanayei, M.; Tao, Z.; Wang, Y. Impedance Model of Train-Induced Vibration Transmission Across a Transfer Structure into an Over Track Building in a Metro Depot. J. Struct. Eng. 2022, 148, 04022187. [Google Scholar] [CrossRef]
- Xu, L.; Ma, M. Analytical solution of ground-borne vibration due to spatially periodic harmonic moving load on a tunnel embedded in layered soil. J. Zhejiang Univ.-Sci. A 2023, 24, 637–652. [Google Scholar] [CrossRef]
- Du, L.L. Study on the Theoretical Model of Coupled Vehicle & Track and Characteristics of Vibration Sources in a Curved Track; Beijing Jiaotong University: Beijing, China, 2018. [Google Scholar]
- Belotserkovskiy, P.M. Forced oscillations of infinite periodic structures: Applications to railway track dynamics. Veh. Syst. Dyn. 1998, 29 (Suppl. 1), 85–103. [Google Scholar] [CrossRef]
- Liu, W.; Du, L.; Liu, W.; Thompson, D.J. Dynamic response of a curved railway track subjected to harmonic loads based on the periodic structure theory. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1932–1950. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, K.; Cai, C. Fundamentals of vehicle–track coupled dynamics. Veh. Syst. Dyn. 2009, 47, 1349–1376. [Google Scholar] [CrossRef]
- Tan, X.; Liu, W. Dynamic response analysis model of a 3D floating slab track with discrete supports infrequency domain. J. Vib. Shock 2021, 40, 183–189. (In Chinese) [Google Scholar] [CrossRef]
- Liu, W.; Li, C.; Ma, L.; Du, L. A frequency-domain formulation for predicting ground-borne vibration induced by underground train on curved track. J. Sound Vib. 2023, 549, 117578. [Google Scholar] [CrossRef]
- Anis, Z.; Hedrick, J.K. Characterization of Rail Track Irregularities. In Final Report; Contract No. DOT-TSC-1206; U. S. DOT: Boston, MA, USA, 1977. [Google Scholar]
- Zhu, Z.; Wang, L.; Gong, W.; Yu, Z. Comparative analysis of several types of vertical wheel/rail relationship and construction of an improved iteration model for train-track-bridge system. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 1585–1593. [Google Scholar] [CrossRef]
- Wu, T.; Thompson, D. Theoretical Investigation of Wheel/Rail Non-Linear Interaction due to Roughness Excitation. Veh. Syst. Dyn. 2000, 34, 261–282. [Google Scholar] [CrossRef]
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Du, Y. 3D Consistent Viscous-spring Artificial Boundary and Viscous-spring Boundary Element. Eng. Mech. 2007, 24, 31–37. (In Chinese) [Google Scholar]
- Kouroussis, G.; Verlinden, O.; Conti, C. Finite-Dynamic Model for Infinite Media: Corrected Solution of Viscous Boundary Efficiency. J. Eng. Mech. 2011, 137, 509–511. [Google Scholar] [CrossRef]
- Jiang, B. Study on Periodic Piles for the Isolation of Train-Induced Environmental Vibration Based on Band Gap Theory; Beijing Jiaotong University: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Li, Z.; Ma, M.; Liu, K.; Jiang, B. Performance of rubber-concrete composite periodic barriers applied in attenuating ground vibrations induced by metro trains. Eng. Struct. 2023, 285, 116027. [Google Scholar] [CrossRef]





| No. | Soil Type | Thickness/m | Shear Wave Velocity/(m·s−1) | Density /(kg·m−3) | Poisson’s Ratio | Young’s Modulus/MPa | Shear Modulus/MPa |
|---|---|---|---|---|---|---|---|
| 1 | Plain fill | 3.0 | 130 | 1930 | 0.35 | 88.0 | 32.6 |
| 2 | Silty clay | 20.0 | 290 | 1880 | 0.45 | 458.0 | 157.9 |
| 3 | Silt | 20.0 | 360 | 2100 | 0.36 | 680.0 | 250.0 |
| Stratum Number | Spring Stiffness Coefficient | Spring Damping Coefficient | |||
|---|---|---|---|---|---|
| kx (kN/m3) | ky (kN/m3) | kz (kN/m3) | cp (kN·s/m) | cs (kN·s/m) | |
| 1 | 18,162 | 14,005 | -- | 527 | 253 |
| 2 | 54,543 | 42,059 | -- | 1825 | 550 |
| 3 | 84,736 | 49,619 | 50,790 | 1564 | 732 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| mass of car body Mc | 4.3 × 104 kg | stiffness of secondary suspension kt | 5.8 × 105 N/m |
| mass of bogie Mt | 3.6 × 103 kg | damping of secondary suspension ct | 1.6 × 105 Ns/m |
| mass of wheelset Mw | 1.7 × 103 kg | stiffness of primary suspension kw | 1.4 × 106 N/m |
| wheel–rail contact constant G | 5.147 × 10−8 m/N2/3 | damping of primary suspension cw | 5 × 104 Ns/m |
| moment of inertia of car body around x-axis | 1.7 × 106 kgm2 | moment of inertia of wheelset around z-axis | 706 kgm2 |
| moment of inertia of car body around y-axis | 2.205 × 105 kgm2 | moment of inertia of bogie around x-axis | 9.62 × 103 kgm2 |
| moment of inertia of car body around z-axis | 1.28 × 106 kgm2 | moment of inertia of bogie around y-axis | 1206 kgm2 |
| moment of inertia of bogie around z-axis | 2809 kgm2 | half-length between two bogies b | 6.3 m |
| static wheel–rail force P0 | 7 × 104 N | half-length between two wheelsets a | 1.1 m |
| length of carriage l | 19 m | fastening stiffness kr | 65 MN/m |
| mass of rail m | 60.64 kg/m | fastening damping cr | 30 kN/m |
| bending stiffness of rail EI | 6.625 MN·m2 | fastening spacing L | 0.6 m |
| loss factor of rail η | 0.01 | mass of slab ms | 2500 kg/m |
| steel spring spacing d | 1.2 m | elastic modulus of slab Es | 3.1 × 1010 N/m2 |
| loss factor of slab ηs | 0.05 |
| Parameter | CFST | SFST |
|---|---|---|
| slab thickness/m | 0.4 | 0.54 |
| slab length/m | 25 | 25 |
| slab width/m | 3 | 3 |
| vibration isolator stiffness/(MN/m) | 6.9 | 5.5 |
| vibration isolator damping/(MNs/m) | 0.03 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Jiang, B.; Qi, C.; Ma, M.; Liu, J.; Hu, W.; Wang, S. Method for Controlling Full-Frequency Band Environment Vibration by Coordinating Metro Vibration Sources and Propagation Paths. Appl. Sci. 2023, 13, 12979. https://doi.org/10.3390/app132412979
Tan X, Jiang B, Qi C, Ma M, Liu J, Hu W, Wang S. Method for Controlling Full-Frequency Band Environment Vibration by Coordinating Metro Vibration Sources and Propagation Paths. Applied Sciences. 2023; 13(24):12979. https://doi.org/10.3390/app132412979
Chicago/Turabian StyleTan, Xinyu, Bolong Jiang, Chunyu Qi, Meng Ma, Jizhao Liu, Wenlin Hu, and Shaolin Wang. 2023. "Method for Controlling Full-Frequency Band Environment Vibration by Coordinating Metro Vibration Sources and Propagation Paths" Applied Sciences 13, no. 24: 12979. https://doi.org/10.3390/app132412979
APA StyleTan, X., Jiang, B., Qi, C., Ma, M., Liu, J., Hu, W., & Wang, S. (2023). Method for Controlling Full-Frequency Band Environment Vibration by Coordinating Metro Vibration Sources and Propagation Paths. Applied Sciences, 13(24), 12979. https://doi.org/10.3390/app132412979






