A High-Precision Planar NURBS Interpolation System Based on Segmentation Method for Industrial Robot
Abstract
:1. Introduction
2. Segment NURBS into Bezier Curves Based on Closed-Loop Chord Error Constraint
2.1. Definition of NURBS Curve and Knot Insertion
2.2. Curve Segment Based on Closed-Loop Chord Error
| Algorithm 1: Segmentation of NURBS curve with chord error δc. | |
| Input: | Input NURBS curve parameters, Chord error δ |
| Output: | Bezier curves that satisfy the δc |
| 1: | knot insertion → Bezier curve Bi; |
| 2: | for i = 1 to Bezier curve number do |
| 3: | calculate the parameter u with zero curvature in the type-S curve Bi. |
| 4: | calculate the δmax in the type-C curve Bi. |
| 5: | If δmax > δc then |
| 6: | Bisection method → segment curve Bi → 1 Bi, 2Bi; |
| 7: | do algorithm 1 for 1Bi; |
| 8: | do algorithm 1 for 2Bi; |
| 9: | else |
| 10: | return 1Bi, 2Bi; |
| 11: | end |
| 12: | end |
3. S-Shaped Feed Rate Profile Generation and Dynamic Speed Adjustment
3.1. S-Shaped Feed Rate Profile
3.2. Dynamic Speed Control Planning
4. Bidirectional Feed Rate Scanning of S-Shaped Profile
| Algorithm 2: Bidirectional Scanning. | |
| Input: | is the end feed rate of the (i − 1)th segment (the start feed rate of the i-th segment); is the lookahead sublist of segment length; is the lookahead sublist of feed rates; Vmax is the maximum feed rate; At,max/Jt,max are the maximum tangential acceleration/jerk; is the maximum chord error; is the curvature at key points along the curve segment; An,max/Jn,max are the maximum normal acceleration/jerk; Ts is the sampling period. |
| Output: | Vend,i |
| Step 1: | 1.1. If N = 1, stop the lookahead calculation and let Vend,i = 0; Otherwise, go to 1.2. |
| 1.2. Let k = N − 1, = 0; | |
| Step 2: | 2.1. [0], Vend,i−1, [0], Jt,max, At,max, Ts are utilized in the backward scanning, recursively backtracking from the last segment of the lookahead window to the second segment, to calculate the end feed rate based on the current segment velocity and constraints; |
| 2.2. The minimum feed rate under the given geometric constraints, as well as the kinematic constraints in both the task space and joint space, is assigned as the end feed rate of the current segment. It is given that | |
| Step 3: | Let k = k − 1, if k = 0, go to step 4; Otherwise, go to step 2; |
| Step 4: | Let k = 0, = 0; |
| Step 5: | 5.1. , Vend,i−1, , Jt,max, At,max, Ts are utilized in the forward scanning, recursively from the first segment of the lookahead window to the (N − 1)th segment, to calculate the end feed rate ; |
| 5.2. Determine the feed rate at the end of the segment by | |
| Step 6: | Let k = k + 1, and if k = N − 1, stop and derive the result; Otherwise, go to step 4. |
5. NURBS Interpolation
6. Experiment and Results
6.1. NURBS Interpolator for Butterfly Curve
6.2. Experiment of Robot Path for a Fan NURBS Curve
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbasnejad, G.; Yoon, J.; Lee, H. Optimum kinematic design of a planar cable-driven parallel robot with wrench-closure gait trajectory. Mech. Mach. Theory 2016, 99, 1–18. [Google Scholar] [CrossRef]
- De Souza, A.F.; Coelho, R.T. Experimental investigation of feed rate limitations on highspeed milling aimed at industrial applications. Int. J. Adv. Manuf. Technol. 2007, 32, 1104–1114. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Books, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Elber, G.; Cohen, E. Tool path generation for freeform surface models. In Proceedings of the Second ACM Symposium on Solid Modeling and Applications, Montreal, QC, Canada, 19–21 May 1993; pp. 419–428. [Google Scholar]
- Lasemi, A.; Xue, D.; Gu, P. Recent development in CNC machining of freeform surfaces: A state-of-the-art review. Comput. Aided Des. 2010, 42, 641–654. [Google Scholar] [CrossRef]
- Sarkar, S.; Dey, P.P. A new iso-parametric machining algorithm for free-form surface. Proc. IMechE Part E J. Eng. Manuf. 2014, 228, 197–209. [Google Scholar] [CrossRef]
- Lee, R.S.; She, C.H. Tool path generation and error control method for multi-axis NC machining of spatial cam. Int. J. Mach. Tools Manuf. 1998, 38, 277–290. [Google Scholar] [CrossRef]
- Hua, L.; Huang, N.; Yi, B.; Zhao, Y.; Zhu, L. Global toolpath smoothing for CNC machining based on B-spline approximation with tool tip position adjustment. Int. J. Adv. Manuf. Technol. 2023, 125, 3651–3665. [Google Scholar] [CrossRef]
- Bi, Q.; Huang, J.; Lu, Y.; Zhu, L.; Ding, H. A general, fast and robust B-spline fitting scheme for micro-line tool path under chord error constraint. Sci. China Technol. Sci. 2019, 62, 321–332. [Google Scholar] [CrossRef]
- Huang, N.; Hua, L.; Huang, X.; Zhang, Y.; Zhu, L.; Biermann, D. B-spline-based corner smoothing method to decrease the maximum curvature of the transition curve. J. Manuf. Sci. Eng. 2022, 144, 054503. [Google Scholar] [CrossRef]
- Ward, R.A.; Sencer, B.; Jones, B.; Ozturk, E. Five-axis trajectory generation considering synchronization and nonlinear interpolation errors. J. Manuf. Sci. Eng. 2022, 144, 081002. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, W.; Ding, Y. A local toolpath smoothing method for a five-axis hybrid machining robot. Sci. China Technol. Sci. 2023, 66, 721–742. [Google Scholar] [CrossRef]
- Lin, M.T.; Tsai, M.S.; Yau, H.T. Development of a dynamics-based NURBS interpolator with real-time look-ahead algorithm. Int. J. Mach. Tools Manuf. 2007, 47, 2246–2262. [Google Scholar] [CrossRef]
- Du, X.; Huang, J.; Zhu, L.M. A complete S-shape feed rate scheduling approach for NURBS interpolator. J. Comput. Des. Eng. 2015, 2, 206–217. [Google Scholar] [CrossRef]
- Huang, J.; Du, X.; Zhu, L.M. Parallel acceleration/deceleration feedrate scheduling for computer numerical control machine tools based on bi-directional scanning technique. Proc. IMechE Part B J. Eng. Manuf. 2019, 233, 937–947. [Google Scholar] [CrossRef]
- Xinhua, L.; Junquan, P.; Lei, S.; Zhongbin, W. A novel approach for NURBS interpolation through the integration of acc-jerk-continuous-based control method and look-ahead algorithm. Int. J. Adv. Manuf. Technol. 2017, 88, 961–969. [Google Scholar] [CrossRef]
- Bollinger, J.G.; Duffie, N.A. Computer Control of Machines and Processes; Addison-Wesley Longman Publishing Co. Inc.: Reading, MA, USA, 1988. [Google Scholar]
- Ishizaki, K.; Shamoto, E. A new real-time trajectory generation method modifying trajectory based on trajectory error and angular speed for high accuracy and short machining time. Precis. Eng. 2022, 76, 173–189. [Google Scholar] [CrossRef]
- He, S.; Yan, C.; Deng, Y.; Lee, C.H.; Zhou, X. A tolerance constrained G2 continuous path smoothing and interpolation method for industrial SCARA robots. Robot Comput. Integr. Manuf. 2020, 63, 101907. [Google Scholar] [CrossRef]
- Barnett, E.; Gosselin, C. A Bisection Algorithm for Time-Optimal Trajectory Planning along Fully Specified Paths. IEEE Trans. Robot. 2020, 37, 131–145. [Google Scholar] [CrossRef]
- Mora, P.R. On the Time-Optimal Trajectory Planning along Predetermined Geometric Paths and Optimal Control Synthesis for Trajectory Tracking of Robot Manipulators; University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Lee, A.C.; Lin, M.T.; Pan, Y.R.; Lin, W.Y. The feedrate scheduling of NURBS interpolator for CNC machine tools. Comput. Aided Des. 2011, 43, 612–628. [Google Scholar] [CrossRef]
- Lai, J.Y.; Lin, K.Y.; Tseng, S.J.; Ueng, W.D. On the development of a parametric interpolator with confined chord error, feedrate, acceleration and jerk. Int. J. Adv. Manuf. Technol. 2008, 37, 104–121. [Google Scholar] [CrossRef]
- Nam, S.H.; Yang, M.Y. study on a generalized parametric interpolator with real-time jerk-limited acceleration. Comput. Aided Des. 2004, 36, 27–36. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Ng, T.C.; Chen, I.M. On algorithms for planning s-curve motion profiles. Int. J. Adv. Robot. Syst. 2008, 5, 11. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, X.; Yang, Z. A generic method to generate AS-curve profile in commercial motion controller. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Shpitalni, M.; Koren, Y.; Lo, C.C. Realtime curve interpolators. Comput. Aided Des. 1994, 26, 832–838. [Google Scholar] [CrossRef]
- Yeh, S.S.; Hsu, P.L. Adaptive-feedrate interpolation for parametric curves with a confined chord error. Comput. Aided Des. 2002, 34, 229–237. [Google Scholar] [CrossRef]
- Tikhon, M.; Ko, T.J.; Lee, S.H.; Kim, H.S. NURBS interpolator for constant material removal rate in open NC machine tools. Int. J. Mach. Tools Manuf. 2004, 44, 237–245. [Google Scholar] [CrossRef]
- Erwinski, K.; Paprocki, M.; Karasek, G. Comparison of NURBS trajectory interpolation algorithms for high-speed motion control systems. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 527–533. [Google Scholar]
- Huang, J.; Zhu, L.M. Feedrate scheduling for interpolation of parametric tool path using the sine series representation of jerk profile. Proc. IMechE Part B J. Eng. Manuf. 2017, 231, 2359–2371. [Google Scholar] [CrossRef]
- Fang, L.; Liu, G.; Li, Q.; Zhang, H. A high-precision non-uniform rational B-spline interpolator based on S-shaped feedrate scheduling. Int. J. Adv. Manuf. Technol. 2022, 121, 2585–2595. [Google Scholar] [CrossRef]
- Boehm, W. Inserting new knots into B-spline curves. Comput. Aided Des. 1980, 12, 199–201. [Google Scholar] [CrossRef]
- Lei, W.T.; Sung, M.P.; Lin, L.Y.; Huang, J.J. Fast real-time NURBS path interpolation for CNC machine tools. Int. J. Mach. Tools Manuf. 2007, 47, 1530–1541. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, L.M.; Ding, H. A real-time look-ahead interpolation methodology with curvature-continuous B-spline transition scheme for CNC machining of short line segment. Int. J. Mach. Tools Manuf. 2013, 65, 88–98. [Google Scholar] [CrossRef]
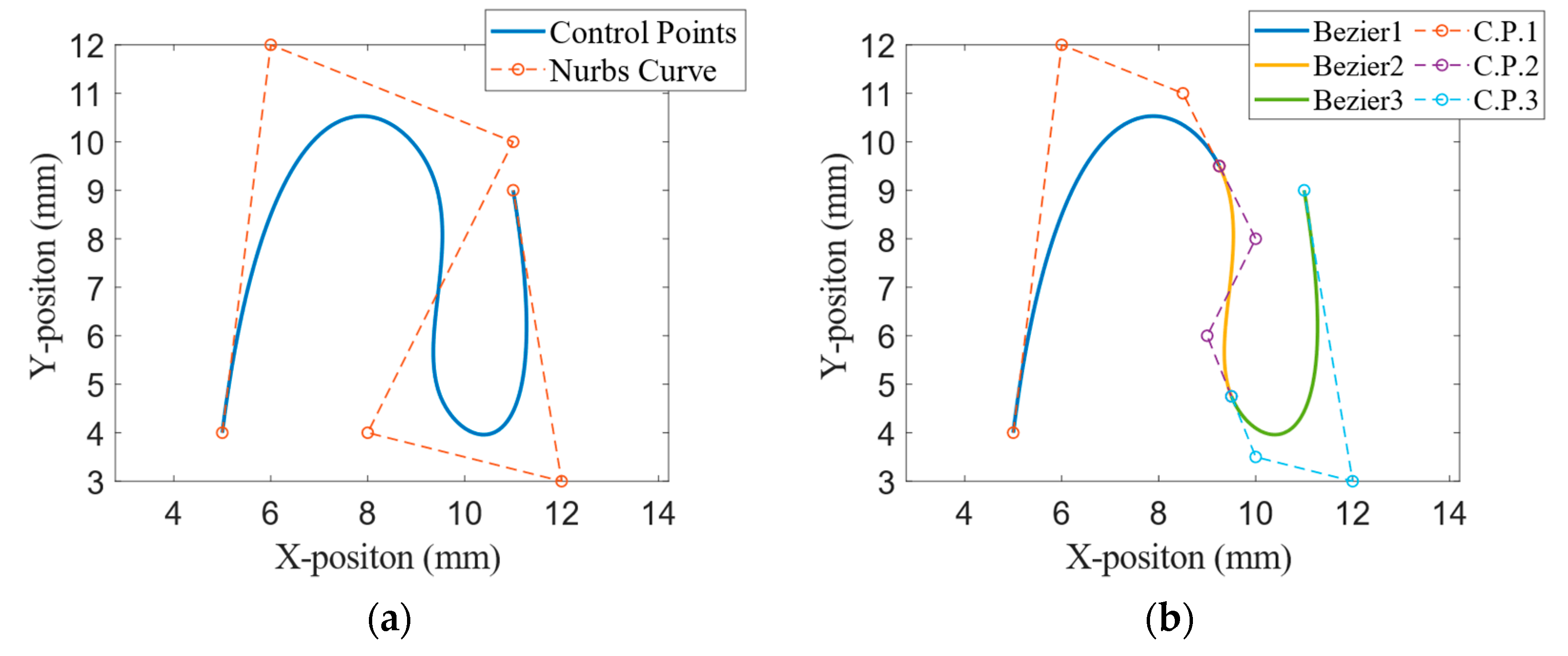













| Curve Types | Control Points | Node Vectors |
|---|---|---|
| NURBS | ||
| Bezier 1 | ||
| Bezier 2 | ||
| Bezier 3 |
| Parameters | X.D. [14] | L.H. [8] | L.F. [32] | Ours |
|---|---|---|---|---|
| Number of iterations | 0 | 9 | 0 | 5 |
| Iterations’ computational time (s) | 0 | 8 | 0 | 0.7 |
| Max chord error (mm) | 1.8 | 0.03 | 2 | 0.001 |
| End value of u | 0.997 | 0.997 | 0.999 | 1 |
| Truncation error (mm) | 0.001 | 0.001 | 0 | 0 |
| Bidirectional scanning (s) | 0.01 | 0.1 | 0.01 | 0.3 |
| Once s-shaped feed rate profile (s) | 0.00006 | 0.00006 | 0.00006 | 0.00007 |
| Interpolation time (s) | 9 | 10 | 13 | 10 |
| Total duration time (s) | 10 | 19 | 14 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xu, Y.; Cao, J.; Liu, J.; Zhao, Y. A High-Precision Planar NURBS Interpolation System Based on Segmentation Method for Industrial Robot. Appl. Sci. 2023, 13, 13210. https://doi.org/10.3390/app132413210
Liu X, Xu Y, Cao J, Liu J, Zhao Y. A High-Precision Planar NURBS Interpolation System Based on Segmentation Method for Industrial Robot. Applied Sciences. 2023; 13(24):13210. https://doi.org/10.3390/app132413210
Chicago/Turabian StyleLiu, Xun, Yan Xu, Jiabin Cao, Jinyu Liu, and Yanzheng Zhao. 2023. "A High-Precision Planar NURBS Interpolation System Based on Segmentation Method for Industrial Robot" Applied Sciences 13, no. 24: 13210. https://doi.org/10.3390/app132413210






