Prediction of Tunnel Blasting Vibration Velocity Considering the Influence of Free Surface
Abstract
:1. Introduction
2. Effect of Free Surface on Rock Blasting Mechanism
3. Effect of Free Surface on Tunnel Blast Vibration
3.1. Introduction to the Test
3.2. Analysis of Test Data
4. Blast Velocity Formula Considering the Effect of Free Surface
4.1. The Proposed Correction Formula for Blast Vibration Velocity
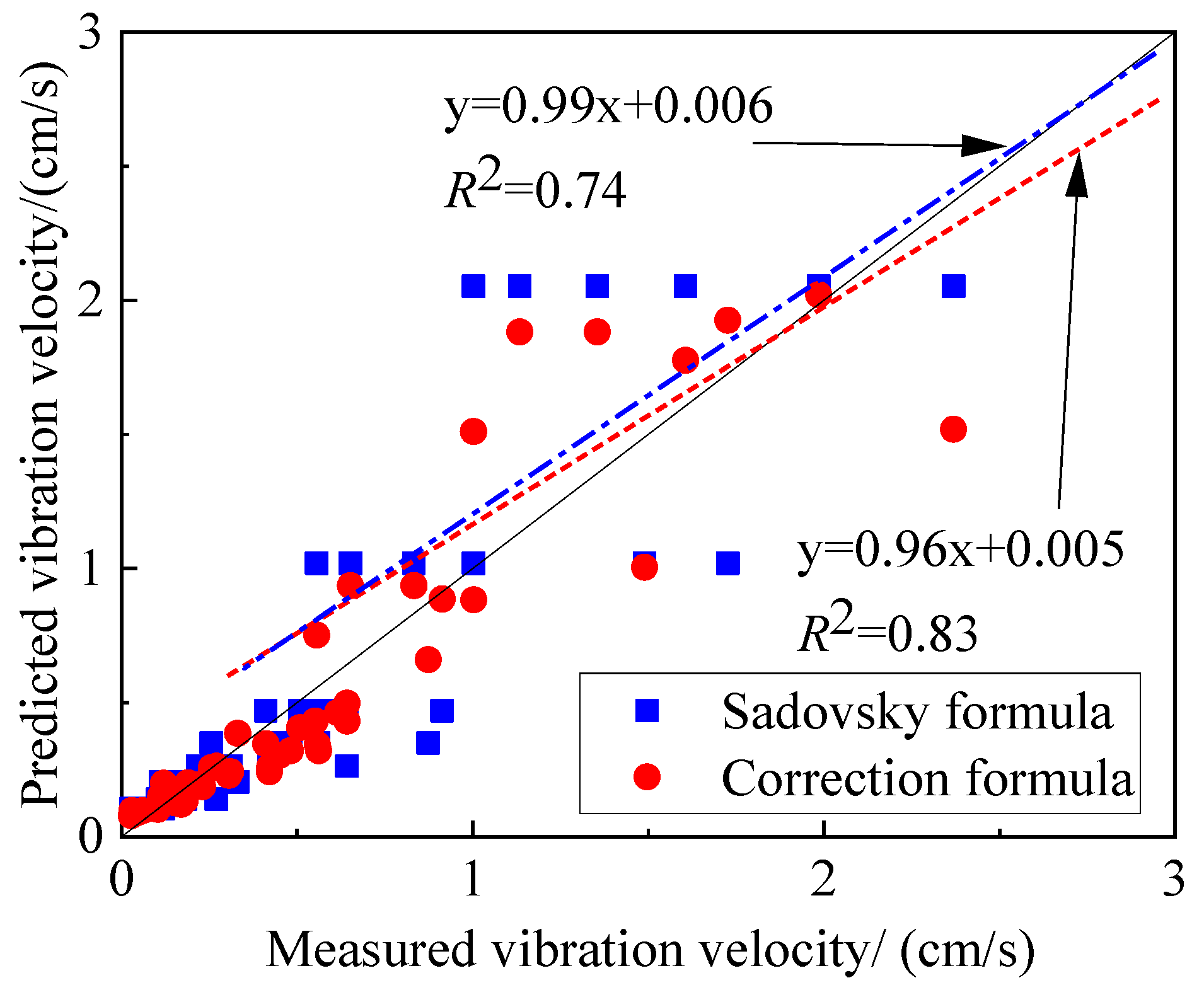
4.2. Verification of Blast Vibration Velocity Correction Formula
5. Engineering Applications
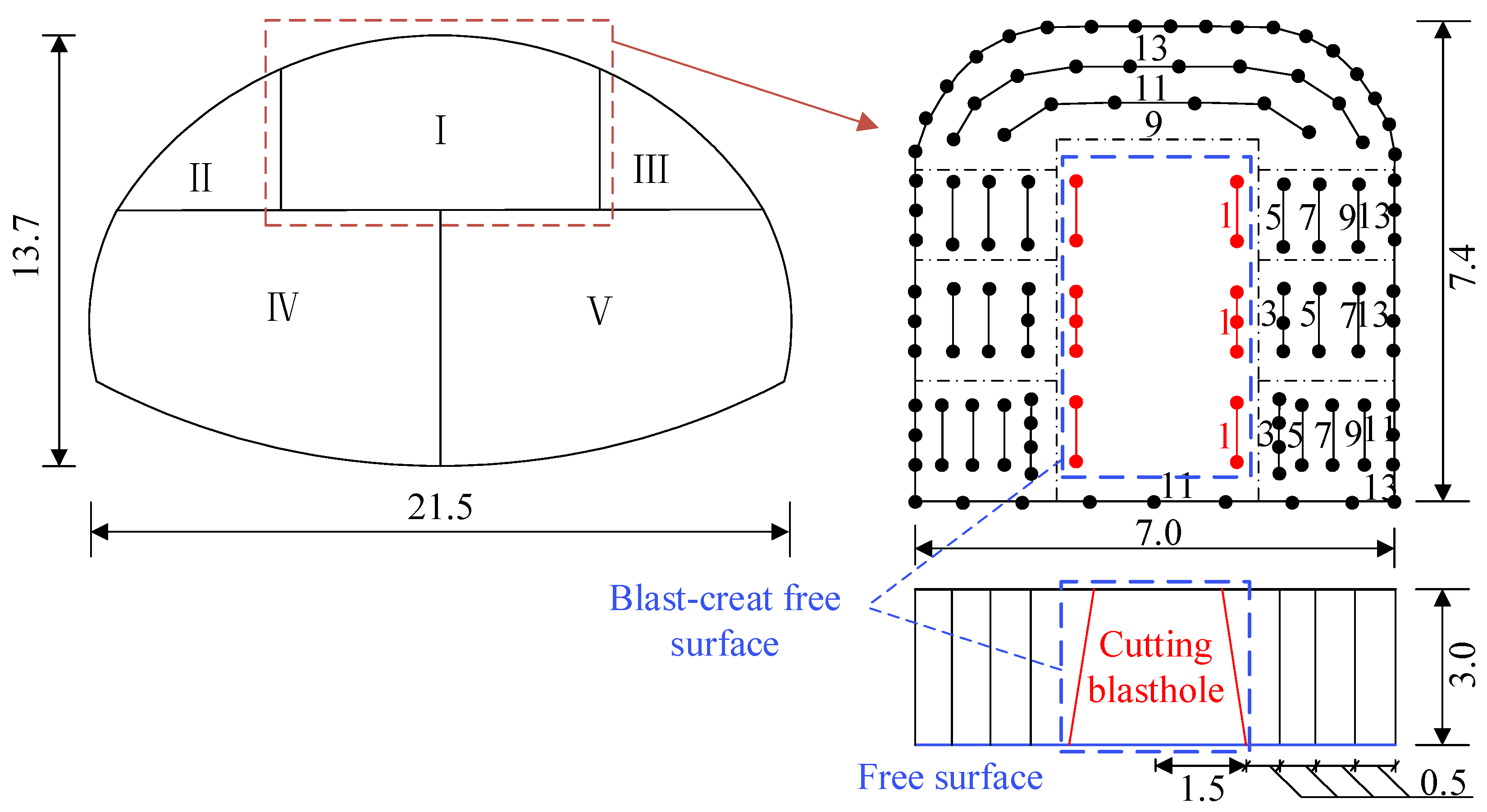
5.1. Project Overview
5.2. Formula Fitting
5.3. Control of Blasting Parameters
6. Conclusions
- (1)
- There is a strong relationship between the number of free faces and the minimum burden, with more free faces resulting in a lower vibration velocity and a smaller minimum burden resulting in a lower vibration velocity.
- (2)
- By introducing the number of free surfaces and burden distance to the Sadovsky formula for correction, the correction formula regression coefficient is R2 = 0.83 and R2 = 0.74 for the Sadovsky formula. The correction formula significantly enhances the ability to predict blast vibration, allowing for a greater application while more correctly reflecting the decay pattern of the blast vibration brought on by the free surface.
- (3)
- Through the analysis and fitting of the measured peak value of vibration velocity, the ratio of the parameter α of the proportional distance factor to the parameter η reflecting the free surface factor is 0.73/0.21. The contribution of the free surface factor to the attenuation of vibration velocity accounts for 21% of the total factors, which cannot be ignored.
- (4)
- The correction formula considering the number of free surfaces and burden distance can improve the accuracy of vibration velocity prediction. The prediction accuracy of the cutting blasthole is improved from 56.48% to 18.15% of the relative tolerance of the Sadovsky formula, and the average tolerance is improved from 24.79% to 13.32%. The correction formula can better predict the variation in vibration velocity at the site and provide a reliable basis for the design parameters of blasting at the site.
- (5)
- When the safe vibration velocity is known, the correction formula can be used to back-calculate the maximum charge for each series. This can be used to optimize the blasting design parameters for each series in the field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, P.K.; Roy, M.P. Damage to surface structures due to blast vibration. Int. J. Rock Mech. Min. Sci. 2010, 47, 949–961. [Google Scholar] [CrossRef]
- Zhao, H.b.; Long, Y.; Li, X.; Lu, L. Experimental and numerical investigation of the effect of blast-induced vibration from adjacent tunnel on existing tunnel. KSCE J. Civ. Eng. 2016, 20, 431–439. [Google Scholar] [CrossRef]
- Feher, J.; Cambal, J.; Cvoliga, M.; Kacmar, L.; Sulovec, V.; Suver, M.; Beca, J. Impacts of noise and technical seismicity from blasting works during tunnel construction on the surrounding environment. Acta Montan. Slovaca 2019, 24, 151–161. [Google Scholar]
- Noren-Cosgriff, K.M.; Ramstad, N.; Neby, A.; Madshus, C. Building damage due to vibration from rock blasting. Soil Dyn. Earthq. Eng. 2020, 138, 106331. [Google Scholar] [CrossRef]
- Wang, Y.L.; Tan, Z.S.; Chi, Y.L. Research on blasting control technology for blast in shallow tunnel crossing existing buildings. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2011; Volume 90, pp. 1768–1771. [Google Scholar]
- Jiang, N.; Zhou, C. Blasting vibration safety criterion for a tunnel liner structure. Tunn. Undergr. Space Technol. 2012, 32, 52–57. [Google Scholar] [CrossRef]
- Sanchidrian, J.A.; Segarra, P.; Lopez, L.M. Energy components in rock blasting. Int. J. Rock Mech. Min. Sci. 2007, 44, 130–147. [Google Scholar] [CrossRef]
- Wu, H.; Gong, M.; Zhao, Q.; Wu, X.; Liu, X. Vibration energy comparison helps identify formation time of new free surface in urban tunnel blasting. Appl. Sci. 2022, 12, 10061. [Google Scholar] [CrossRef]
- Joo, G.W.; Oh, T.M.; Cho, G.C. Free Surface Effects for Ground Vibration and Effective Burden by using Abrasive Waterjet System. In From Fundamentals to Applications in Geotechnics; IOS Press: Amsterdam, The Netherlands, 2015; pp. 2677–2684. [Google Scholar]
- Zou, B.; Xu, Z.; Wang, J.; Luo, Z.; Hu, L. Numerical investigation on influential factors for quality of smooth blasting in rock tunnels. Adv. Civ. Eng. 2020, 2020, 9854313. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, Z.; Zhang, X.; Yang, X.; Wang, J.; Zhou, L. Vibration response characteristics of adjacent tunnels under different blasting schemes. Shock. Vib. 2021, 2021, 5121296. [Google Scholar] [CrossRef]
- Yu, W.; Gao, W.; Yang, N. Study on Drilling and Blasting Construction of a Small-Spacing Tunnel and Vibration Characteristics of Intermediate Rock Strata. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 052094. [Google Scholar] [CrossRef]
- Lu, W.; Leng, Z.; Hu, H.; Chen, M.; Wang, G. Experimental and numerical investigation of the effect of blast-generated free surfaces on blasting vibration. Eur. J. Environ. Civ. Eng. 2018, 22, 1374–1398. [Google Scholar] [CrossRef]
- Uysal, O.; Arpaz, E.; Berber, M. Studies on the effect of burden width on blast-induced vibration in open-pit mines. Environ. Geol. 2007, 53, 643–650. [Google Scholar] [CrossRef]
- Ji, X.; Gao, S.; Zhao, H.; Liu, G. Research on the influence of the number of tunnel blasting free faces on ground vibration based on ANSYS/LSDYNA. In Proceedings of the Sixth International Conference on Electromechanical Control Technology and Transportation (ICECTT 2021), Chongqing, China, 6 February 2022. [Google Scholar]
- Qiu, X.; Shi, X.; Gou, Y.; Zhou, J.; Chen, H.; Huo, X. Short-delay blasting with single free surface: Results of experimental tests. Tunn. Undergr. Space Technol. 2018, 74, 119–130. [Google Scholar] [CrossRef]
- Shi, J.-J.; Guo, S.-C.; Zhang, W. Expansion of blast vibration attenuation equations for deeply buried small clearance tunnels based on dimensional analysis. Front. Earth Sci. 2022, 10, 791. [Google Scholar] [CrossRef]
- Jia, B.; Zhou, L.; Cui, J.; Chen, H. Attenuation model of tunnel blast vibration velocity based on the influence of free surface. Sci. Rep. 2021, 11, 21077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, T.; Du, Y.; Zhu, Q.; Zhang, X. Theoretical and numerical investigation of deep-hole cut blasting based on cavity cutting and fragment throwing. Tunn. Undergr. Space Technol. 2021, 111, 103854. [Google Scholar] [CrossRef]
- Zhang, X.T.; Zou, P.; Zhou, H.M.; Wang, H.L. Study and application on cutting technology of underground drifting blasting. In Advanced Materials Research; Trans Tech Publications Ltd.: Bach, Switzerland, 2012; Volume 549, pp. 1002–1006. [Google Scholar]
- Sim, Y.; Cho, G.-C.; Song, K.-I. Prediction of fragmentation zone induced by blasting in rock. Rock Mech. Rock Eng. 2017, 50, 2177–2192. [Google Scholar] [CrossRef]
- Li, Q.; Gao, Z.-H.; Yu, Q.; Huang, C.; Wang, K.; Xu, W.-L. Effect of explosive stress waves on the crack propagation in the defective medium using strain gauge method. KSCE J. Civ. Eng. 2022, 26, 2780–2788. [Google Scholar] [CrossRef]
- Guan, X.; Guo, C.; Mou, B.; Shi, L. Tunnel millisecond-delay controlled blasting based on the delay time calculation method and digital electronic detonators to reduce structure vibration effects. PLoS ONE 2019, 14, e0212745. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Lu, W.; Yang, S. Components and attenuation of seismic waves induced by horizontal smooth blasting. Explos. Shock Waves 2019, 39, 170–182. (In Chinese) [Google Scholar]


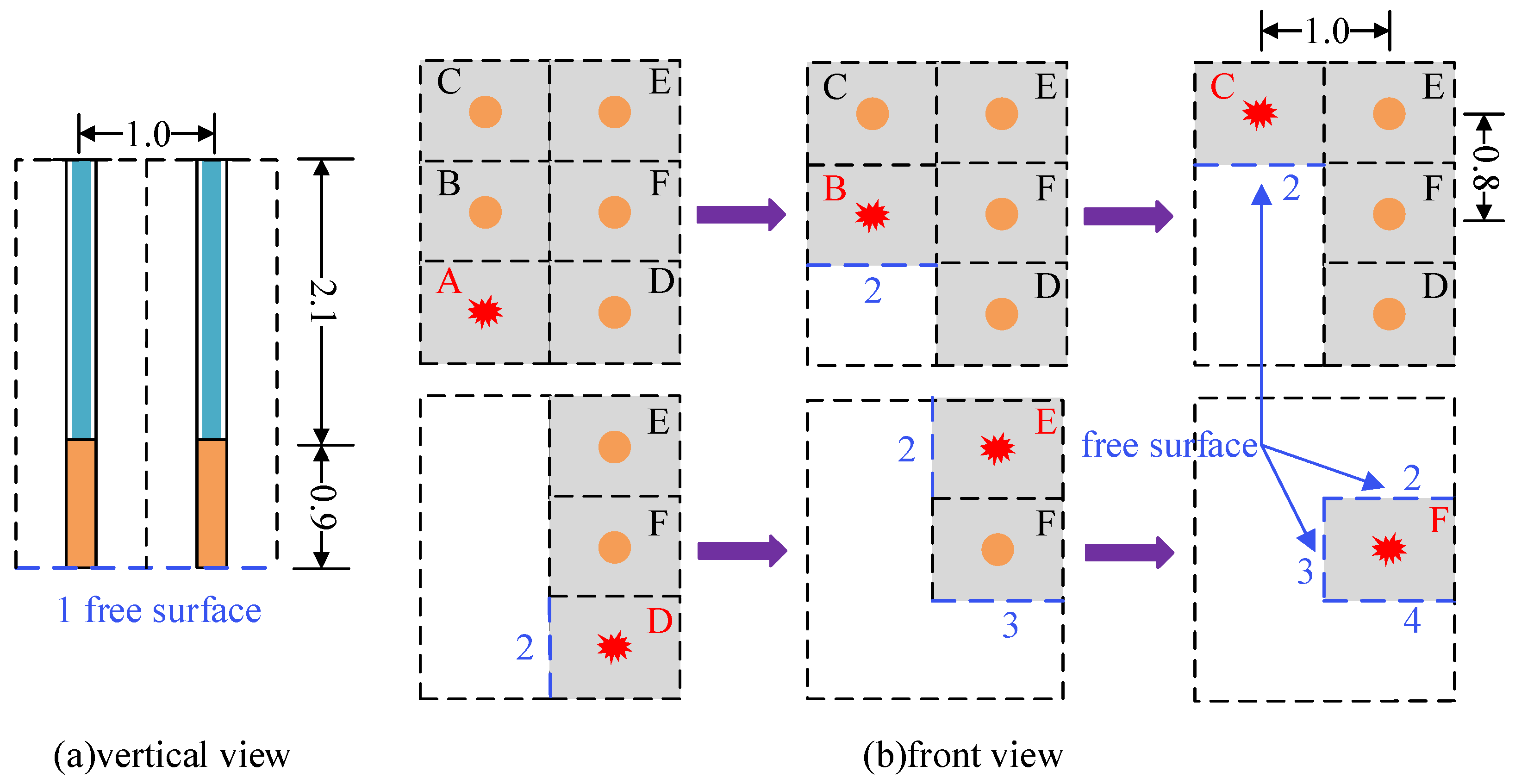

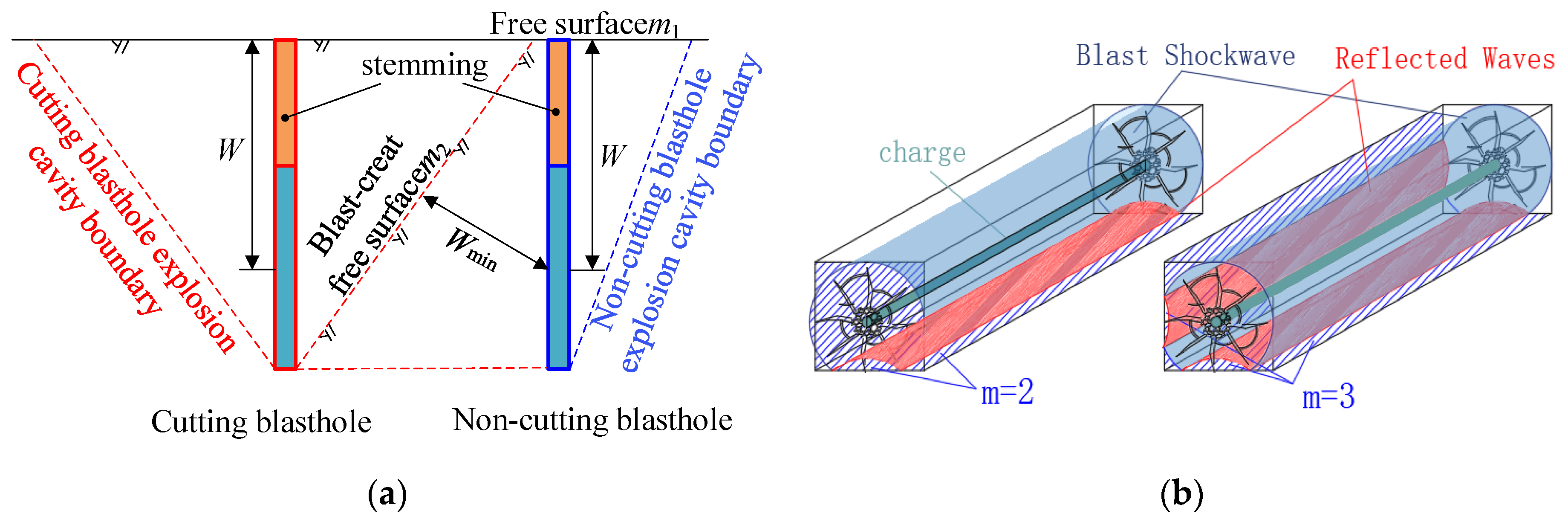

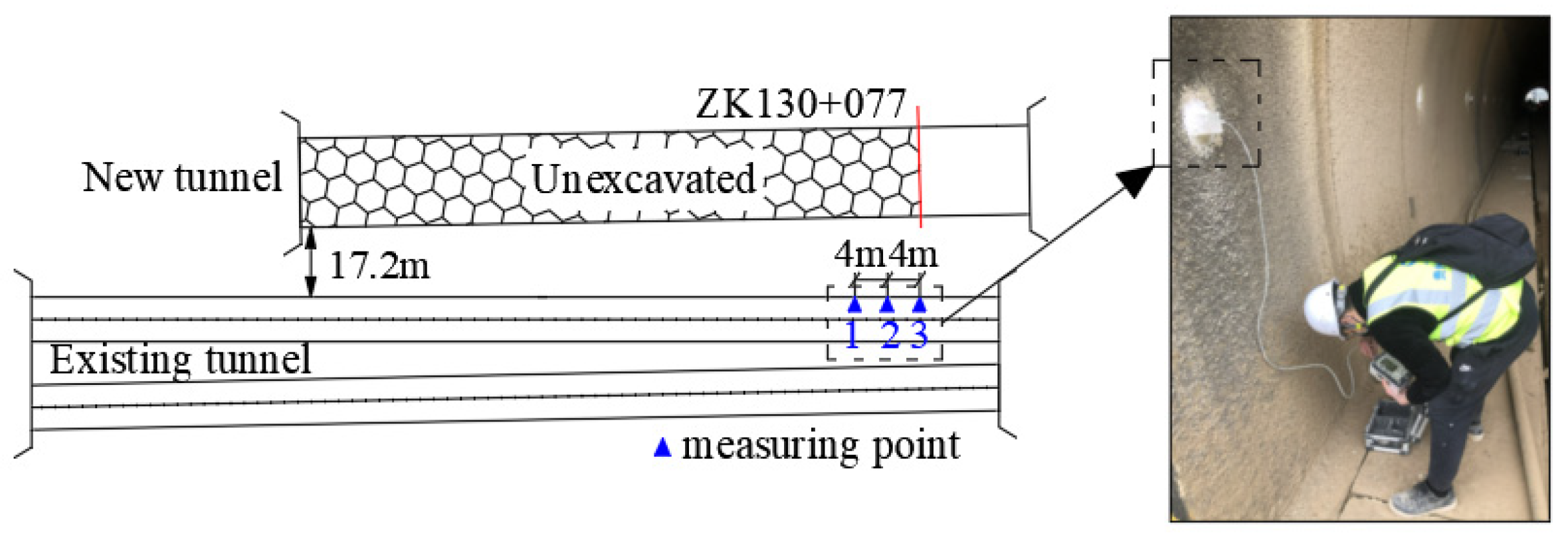
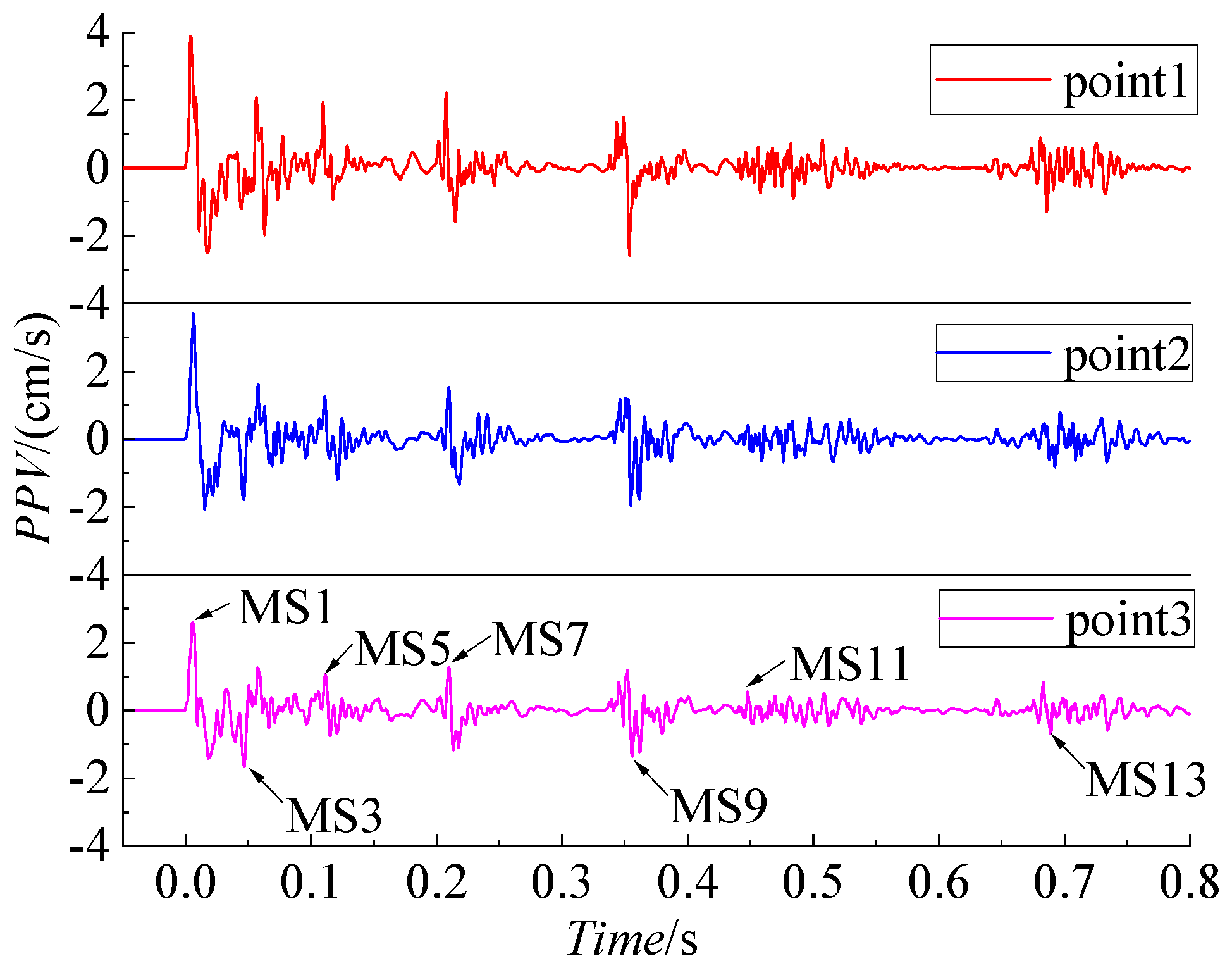
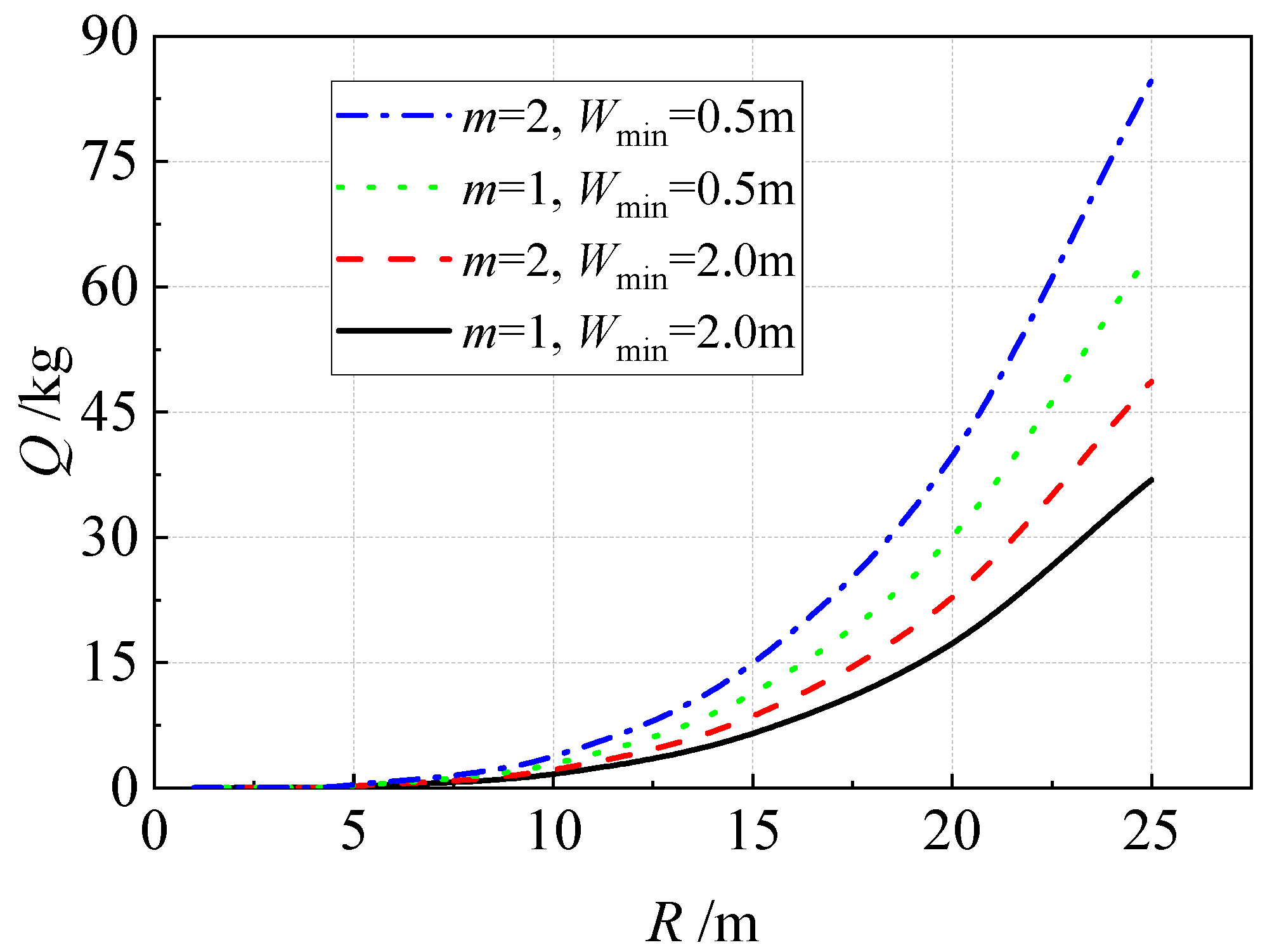
| Blasthole | Function | Q/kg | m | W/cm | Wmin/cm |
|---|---|---|---|---|---|
| A | Cutting blasthole | 2.1 | 1 | 1.95 | 1.95 |
| B | Non-cutting blasthole | 2.1 | 2 | 1.95, 0.4 | 0.4 |
| C | Non-cutting blasthole | 2.1 | 2 | 1.95, 0.4 | 0.4 |
| D | Non-cutting blasthole | 2.1 | 2 | 1.95, 0.5 | 0.5 |
| E | Non-cutting blasthole | 2.1 | 3 | 1.95, 0.5, 1.2 | 0.5 |
| F | Non-cutting blasthole | 2.1 | 4 | 1.95, 0.5, 0.4, 0.4 | 0.4 |
| Points Number | Vibration Velocity of Measuring Point/(cm/s) | Distance/m | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| 1 | 2.37 | 1.36 | 1.13 | 1.99 | 1.61 | 1.00 | 11.20 |
| 2 | 1.73 | 0.83 | 0.65 | 1.49 | 1.00 | 0.56 | 20.30 |
| 3 | 0.91 | 0.64 | 0.55 | 0.62 | 0.51 | 0.41 | 39.30 |
| 4 | 0.87 | 0.56 | 0.48 | 0.56 | 0.45 | 0.26 | 50.50 |
| 5 | 0.64 | 0.42 | 0.31 | 0.42 | 0.31 | 0.22 | 64.20 |
| 6 | 0.33 | 0.23 | 0.18 | 0.19 | 0.15 | 0.11 | 79.80 |
| 7 | 0.27 | 0.17 | 0.15 | 0.18 | 0.17 | 0.10 | 110.80 |
| 8 | 0.12 | 0.06 | 0.03 | 0.10 | 0.05 | 0.03 | 140.00 |
| Type | Blasthole Type | Detonator Series | Blasthole Number/Pieces | Charge Weight per Hole/kg | Total Charge /kg |
|---|---|---|---|---|---|
| The middle guide tunnel | Cutting blasthole | 1 | 10 | 2.4 | 33.6 |
| Breaking blasthole | 3 | 14 | 3.0~3.3 | 42.6 | |
| 5 | 12 | 2.4~3.3 | 34.2 | ||
| 7 | 12 | 2.1~3.3 | 37.0 | ||
| 9 | 14 | 0.9~2.7 | 28.5 | ||
| 11 | 17 | 0.9~1.8 | 18.6 | ||
| Contour blasthole | 11 | 6 | 0.9~1.5 | 8.1 | |
| 13 | 32 | 0.6~1.2 | 24.6 | ||
| Total | 121 | 216.1 |
| Points Number | Detonator Series | Q /kg | m | Wmin /cm | R /m | PPV /(cm/s) | Sadovsky Formula /(cm/s) | Tolerance | Correction Formula /(cm/s) | Tolerance |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | MS1 | 33.6 | 1 | 2.0 | 26.7 | 3.90 | 1.44 | 44.89% | 3.08 | 18.15% |
| MS3 | 42.6 | 2 | 0.5 | 26.7 | 2.09 | 1.94 | 53.78% | 1.63 | 29.43% | |
| MS5 | 34.2 | 2 | 0.5 | 26.7 | 1.96 | 1.47 | 37.46% | 1.29 | 20.14% | |
| MS7 | 25.8 | 2 | 0.5 | 26.7 | 2.23 | 1.62 | 25.85% | 1.40 | 8.52% | |
| MS9 | 28.5 | 2 | 0.5 | 26.7 | 1.50 | 1.17 | 1.69% | 1.06 | 11.34% | |
| MS11 | 26.7 | 2 | 0.5 | 26.7 | 0.73 | 0.55 | 0.16% | 0.55 | 0.14% | |
| MS13 | 24.6 | 2 | 0.5 | 26.7 | 0.90 | 0.97 | 17.18% | 0.90 | 8.38% | |
| 2 | MS1 | 33.6 | 1 | 2.0 | 26.9 | 3.72 | 1.65 | 55.63% | 3.53 | 5.19% |
| MS3 | 42.6 | 2 | 0.5 | 26.9 | 1.63 | 2.22 | 36.39% | 1.87 | 14.43% | |
| MS5 | 34.2 | 2 | 0.5 | 26.9 | 1.26 | 1.69 | 33.93% | 1.47 | 16.69% | |
| MS7 | 25.8 | 2 | 0.5 | 26.9 | 1.53 | 1.86 | 21.74% | 1.60 | 4.65% | |
| MS9 | 28.5 | 2 | 0.5 | 26.9 | 1.21 | 1.34 | 10.93% | 1.21 | 0.27% | |
| MS11 | 26.7 | 2 | 0.5 | 26.9 | 0.62 | 0.63 | 1.61% | 0.63 | 1.32% | |
| MS13 | 24.6 | 2 | 0.5 | 26.9 | 0.79 | 1.12 | 41.26% | 1.03 | 30.24% | |
| 3 | MS1 | 33.6 | 1 | 2.0 | 27.9 | 2.61 | 1.70 | 56.48% | 3.63 | 7.05% |
| MS3 | 42.6 | 2 | 0.5 | 27.9 | 1.26 | 2.29 | 9.40% | 1.92 | 8.27% | |
| MS5 | 34.2 | 2 | 0.5 | 27.9 | 1.07 | 1.74 | 11.45% | 1.51 | 22.90% | |
| MS7 | 25.8 | 2 | 0.5 | 27.9 | 1.29 | 1.92 | 14.09% | 1.65 | 26.20% | |
| MS9 | 28.5 | 2 | 0.5 | 27.9 | 1.19 | 1.38 | 7.96% | 1.24 | 17.31% | |
| MS11 | 26.7 | 2 | 0.5 | 27.9 | 0.55 | 0.65 | 11.24% | 0.65 | 11.55% | |
| MS13 | 24.6 | 2 | 0.5 | 27.9 | 0.83 | 1.15 | 27.52% | 1.06 | 17.51% | |
| Average tolerance | 24.79% | 13.32% | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Zhang, X.; Zhou, X.; Duan, Y.; Chen, J. Prediction of Tunnel Blasting Vibration Velocity Considering the Influence of Free Surface. Appl. Sci. 2023, 13, 1373. https://doi.org/10.3390/app13031373
Zeng X, Zhang X, Zhou X, Duan Y, Chen J. Prediction of Tunnel Blasting Vibration Velocity Considering the Influence of Free Surface. Applied Sciences. 2023; 13(3):1373. https://doi.org/10.3390/app13031373
Chicago/Turabian StyleZeng, Xiaohui, Xuemin Zhang, Xianshun Zhou, Ya Duan, and Jin Chen. 2023. "Prediction of Tunnel Blasting Vibration Velocity Considering the Influence of Free Surface" Applied Sciences 13, no. 3: 1373. https://doi.org/10.3390/app13031373





