Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers
Abstract
:1. Introduction
2. Numerical and Experimental Methods
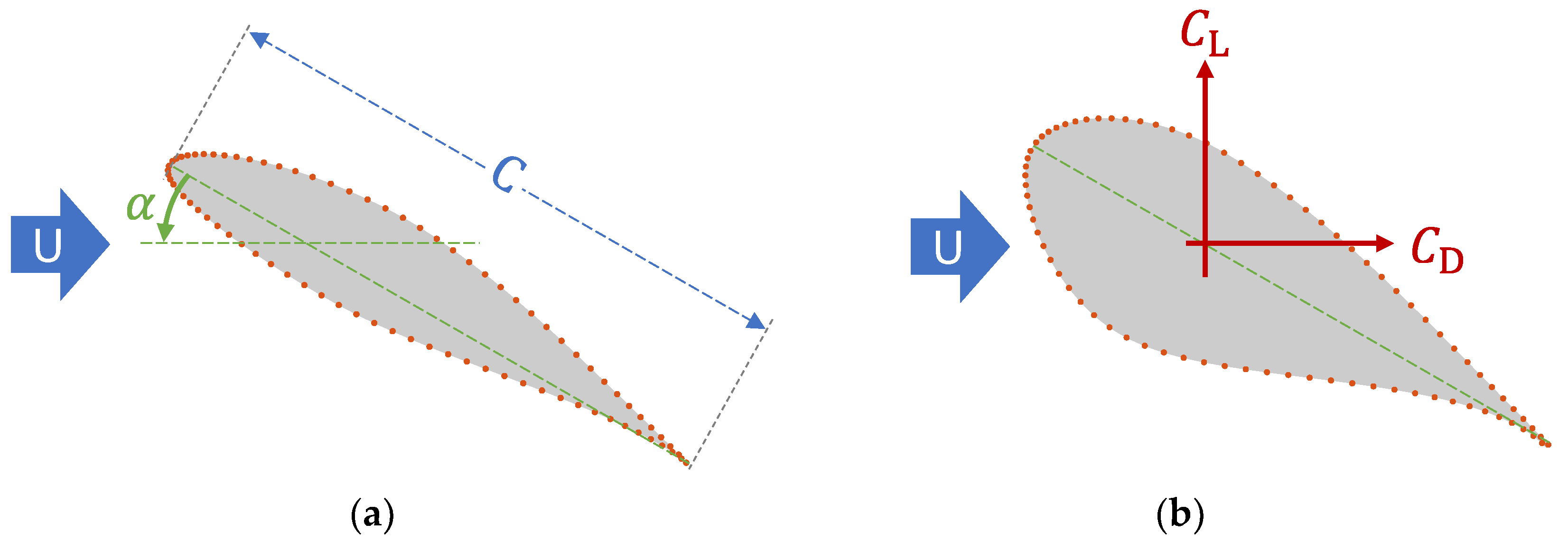
2.1. General Formulation of the Problem
2.2. Vortex Particle Simulation (VPM)
2.3. Application of XFOIL
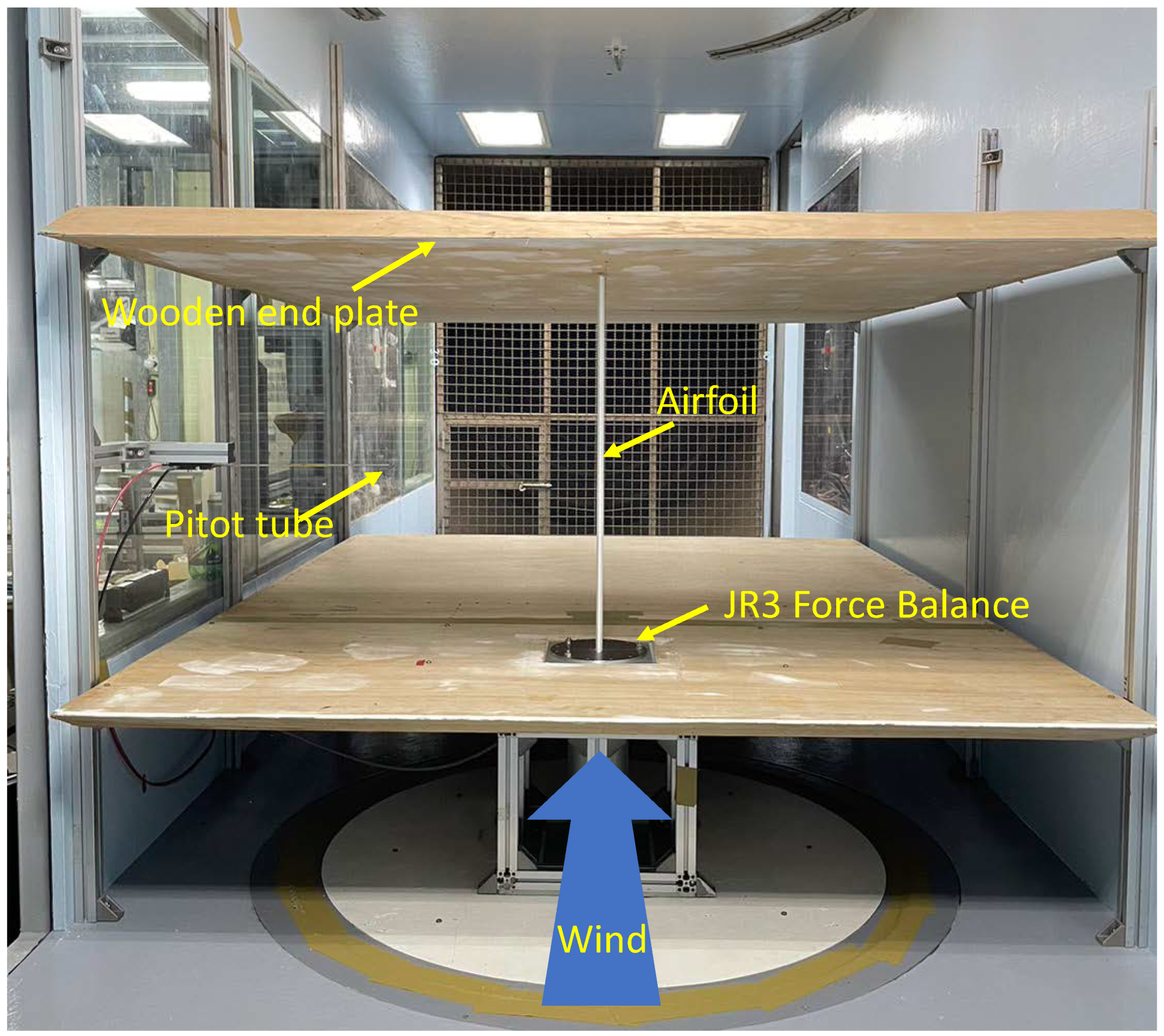
2.4. Wind Tunnel Experiments
3. Results and Discussion
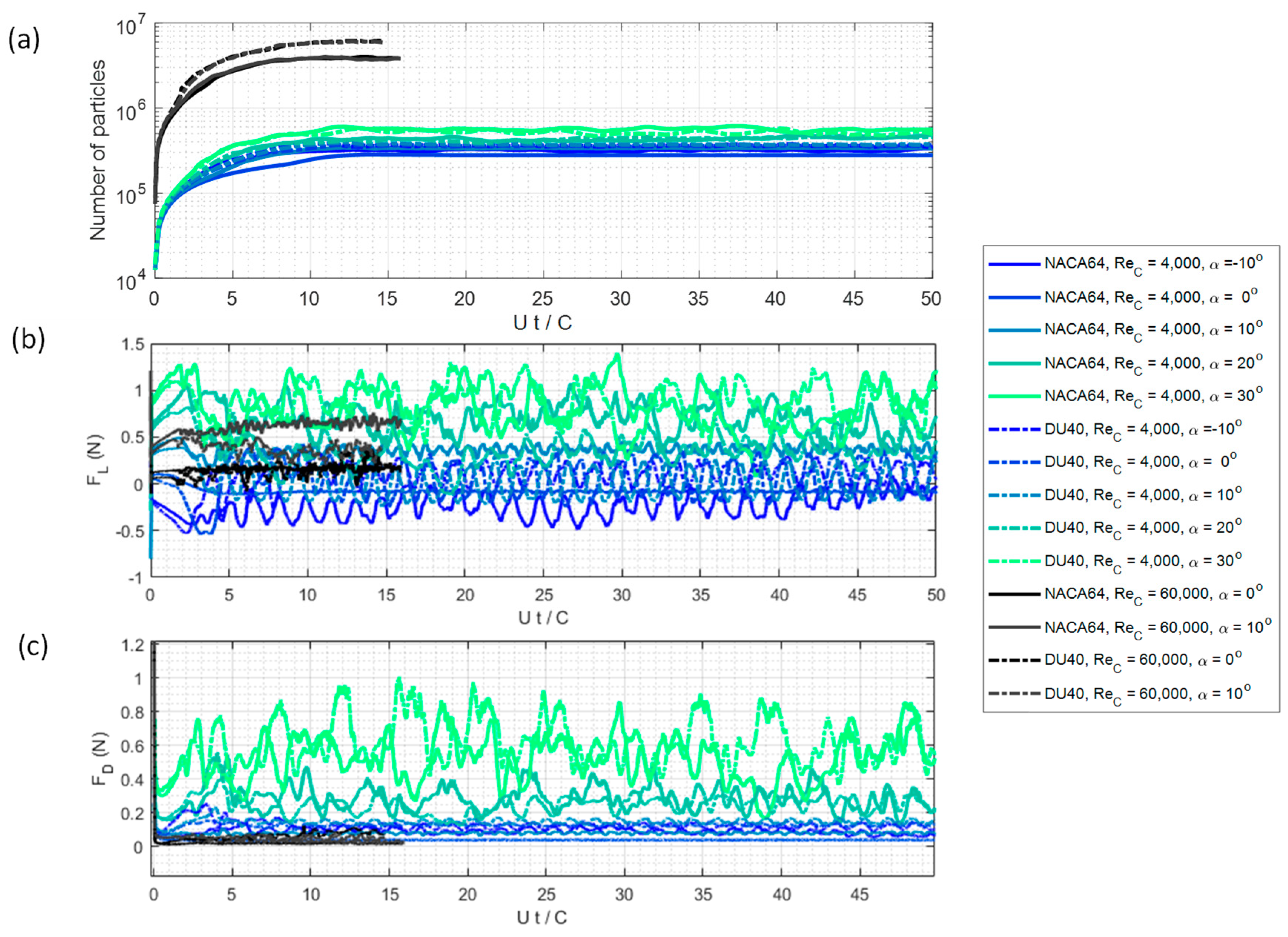
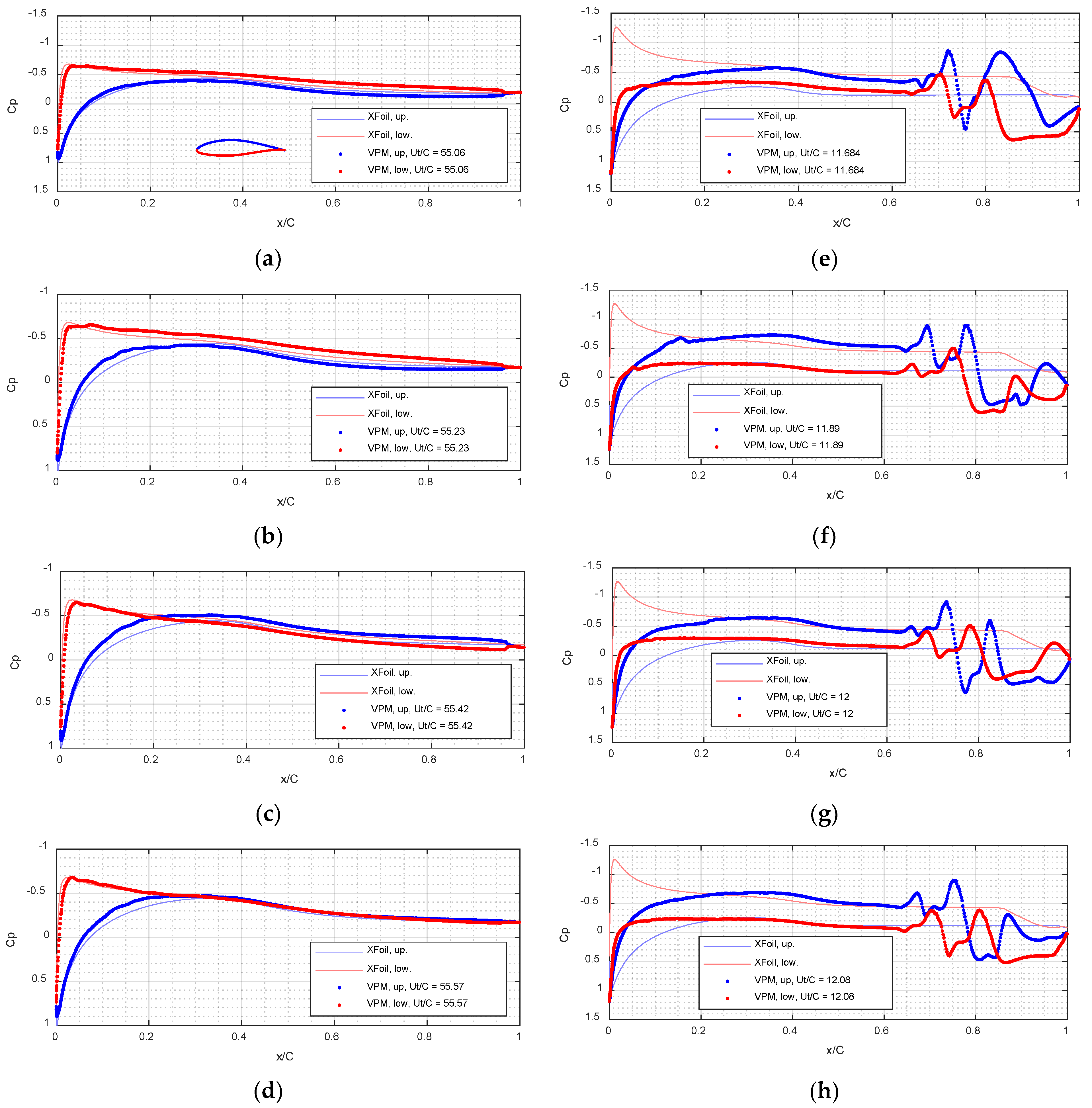
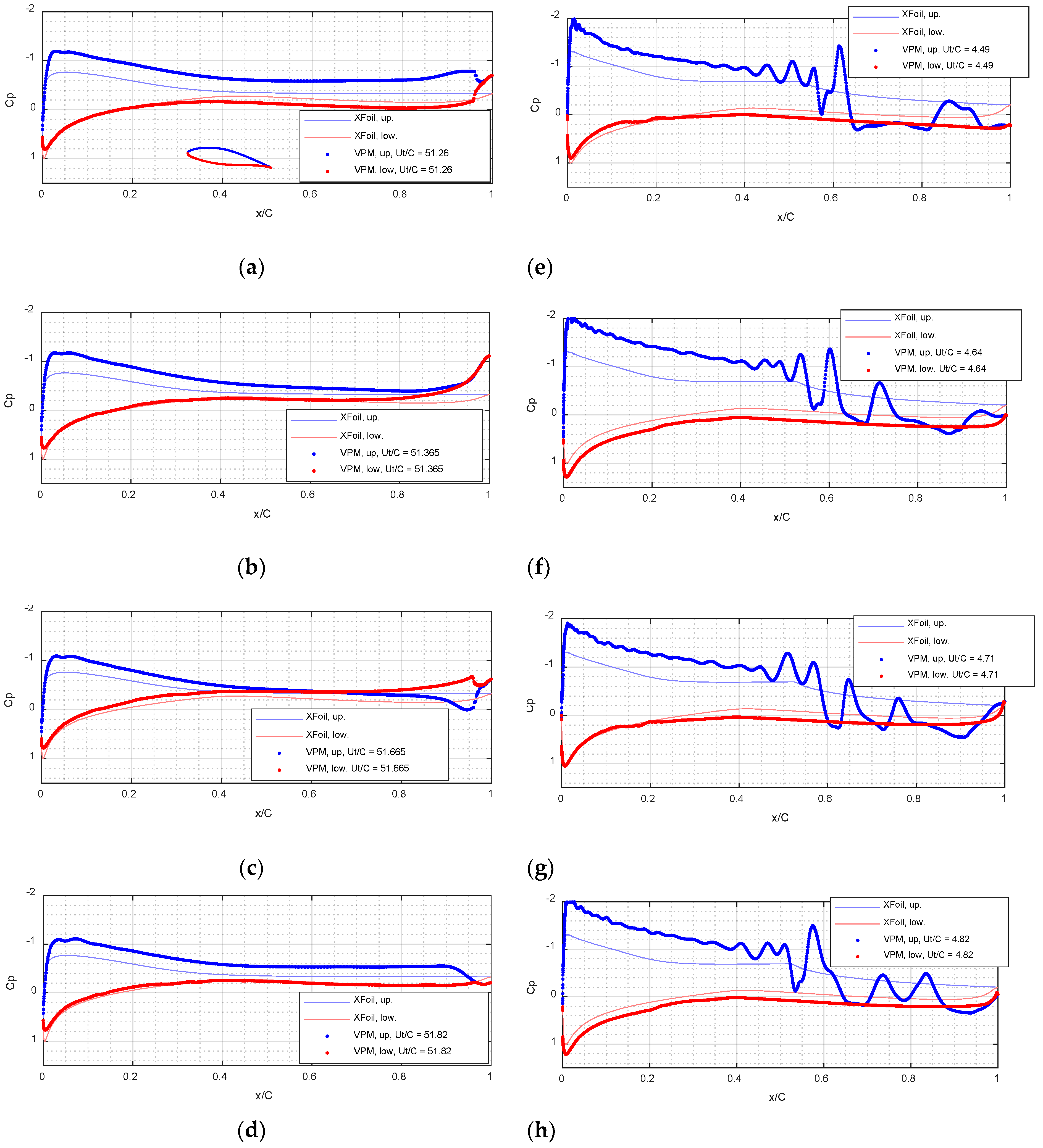
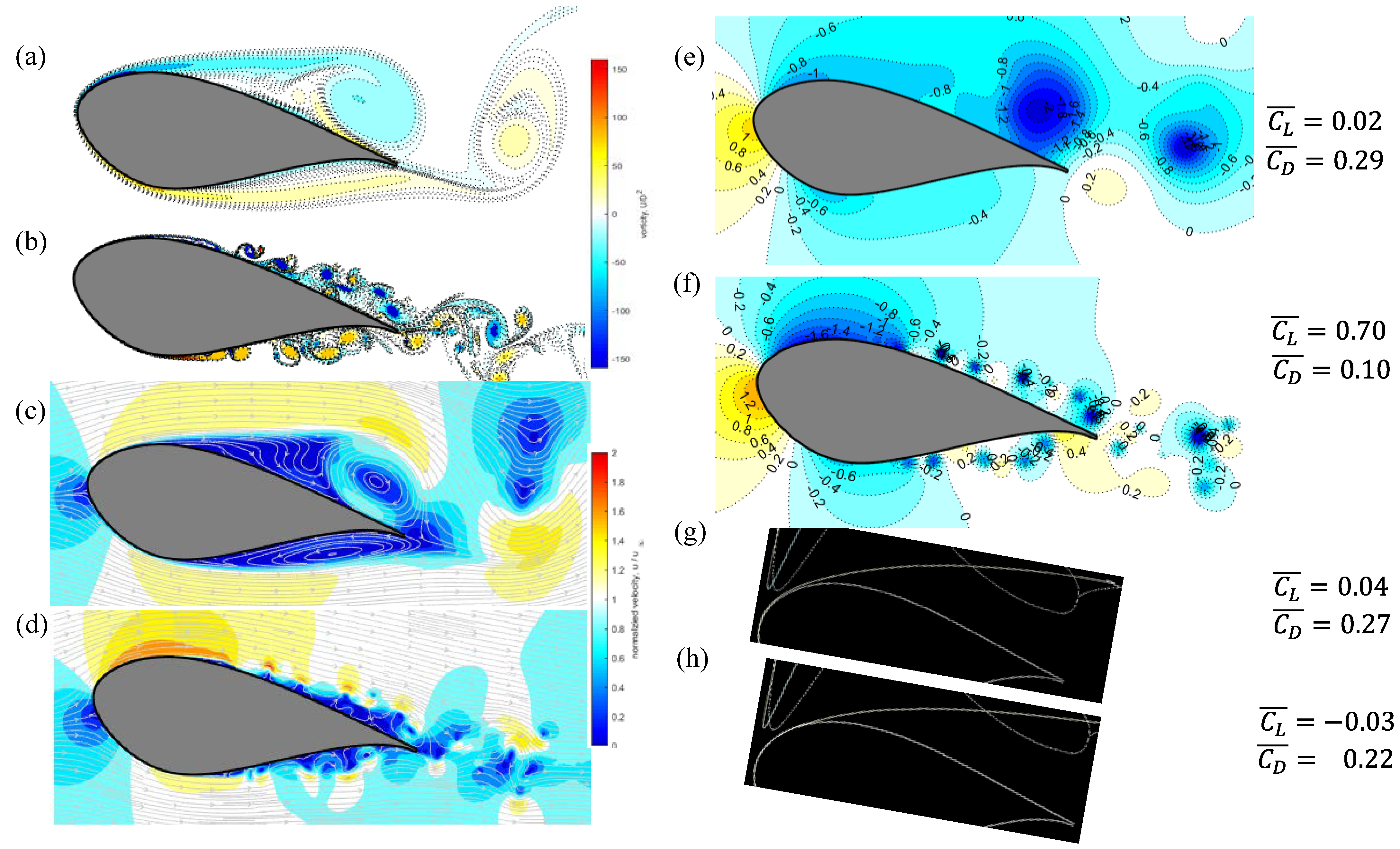
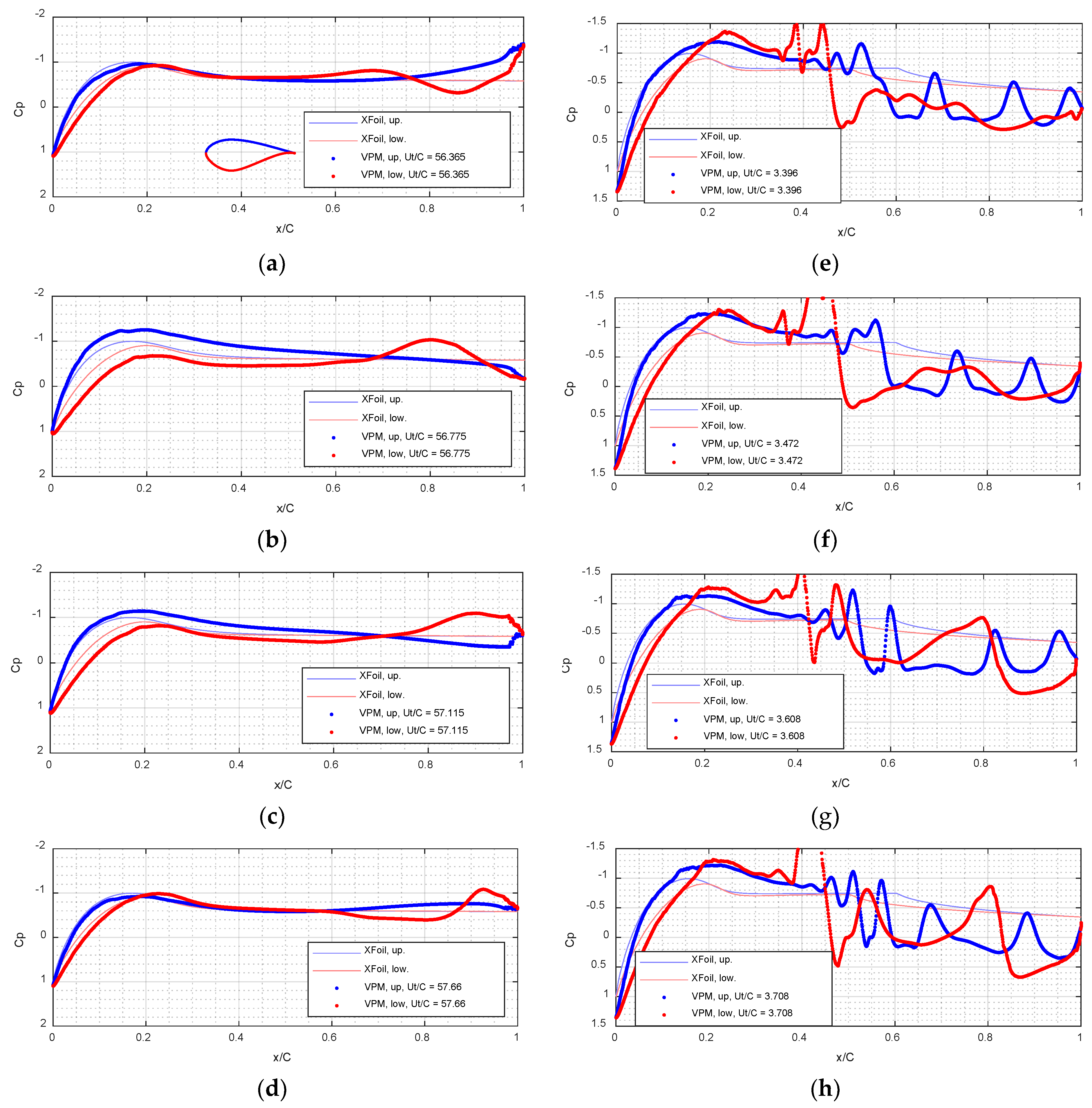
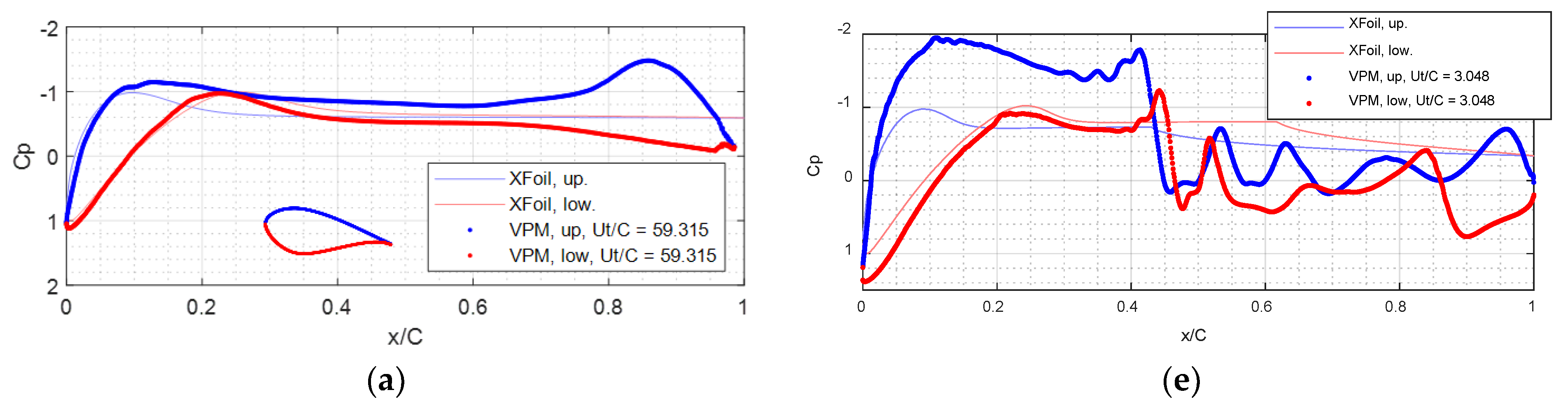
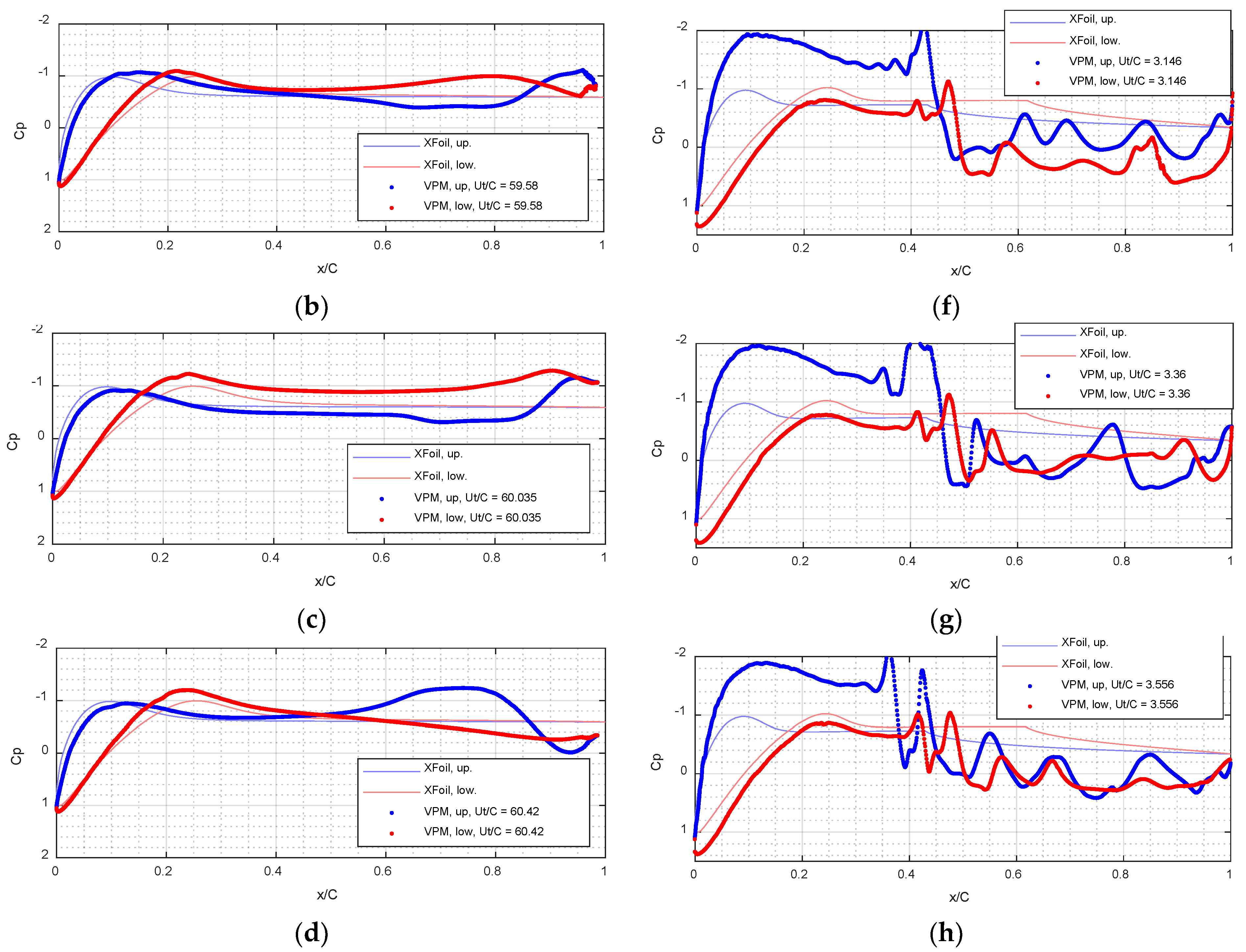
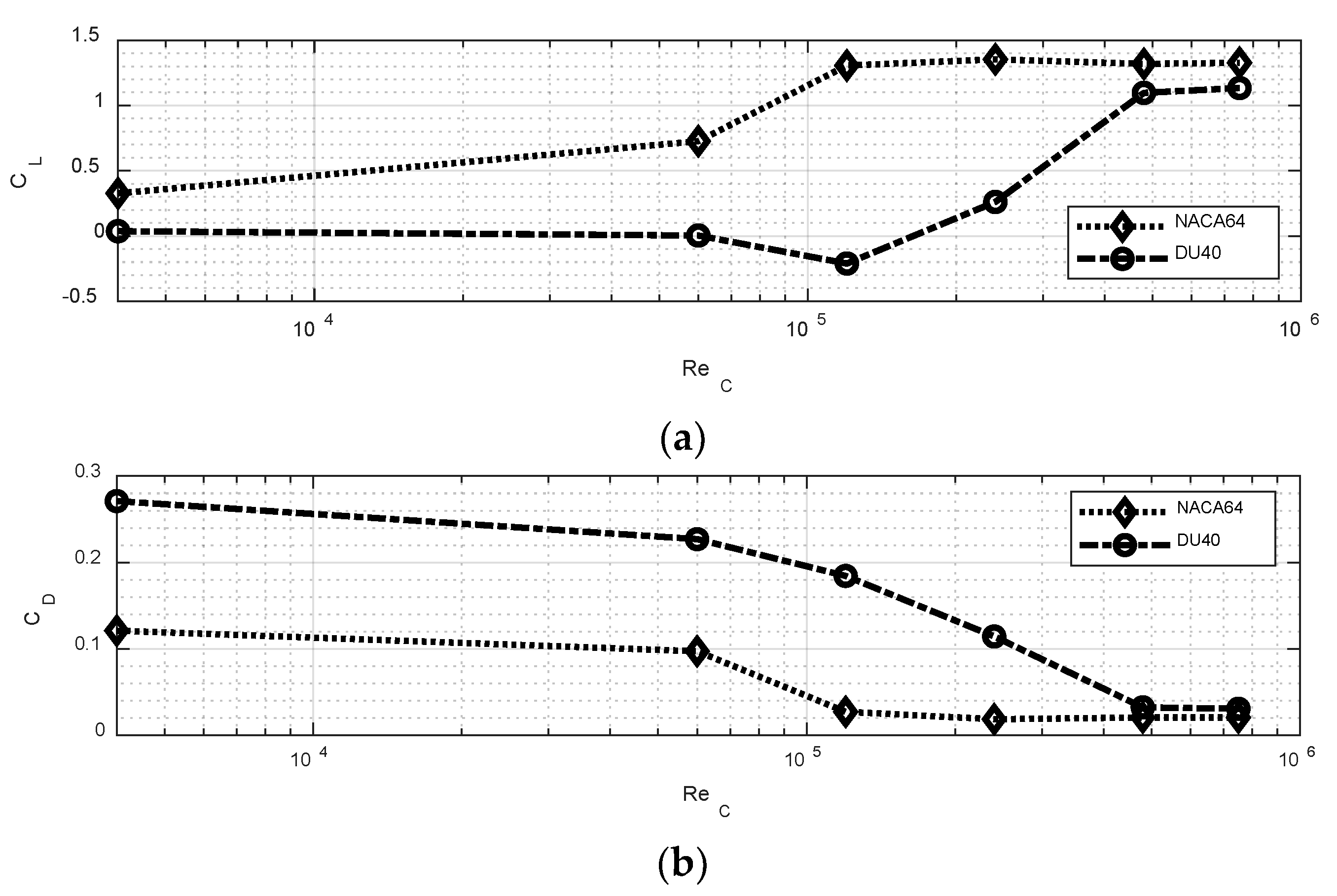
3.1. VPM and XFOIL Simulations—NACA64 Airfoil
3.2. VPM and XFOIL Simulations—DU40 Airfoil
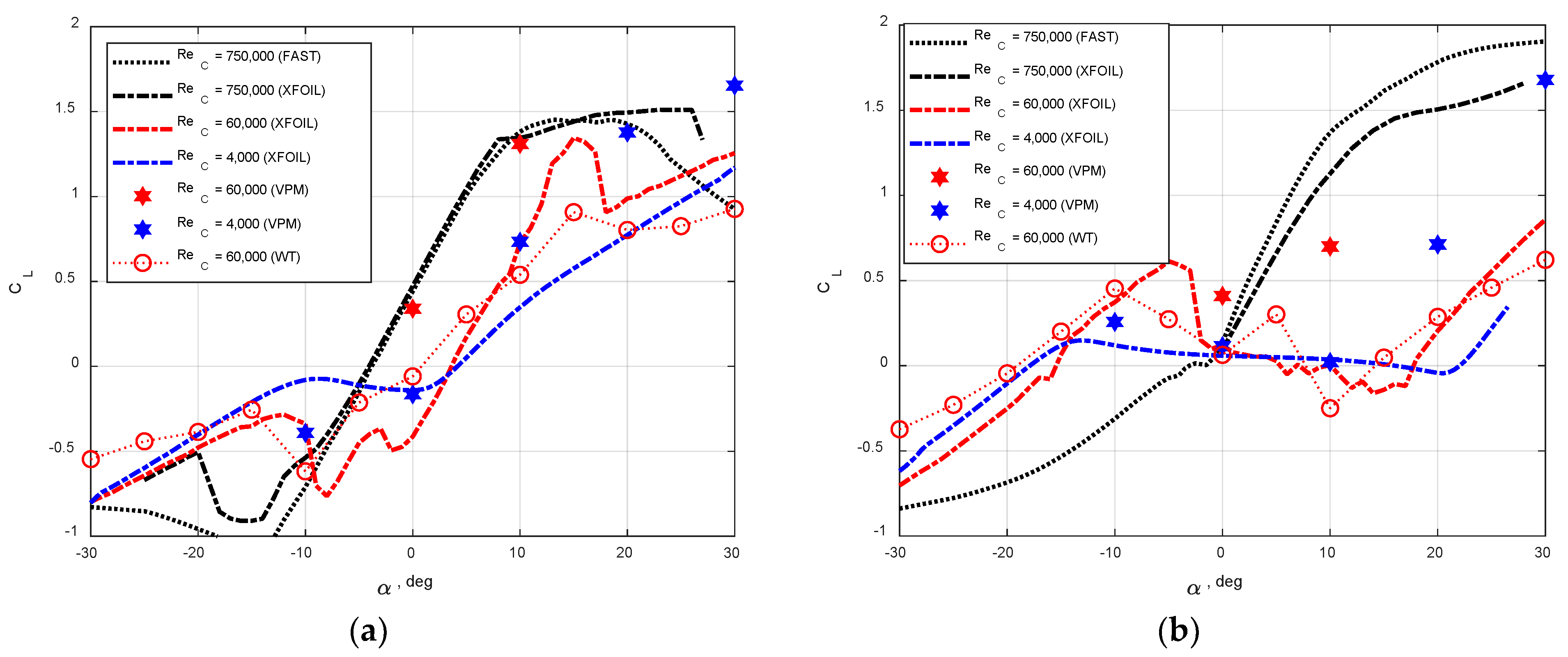
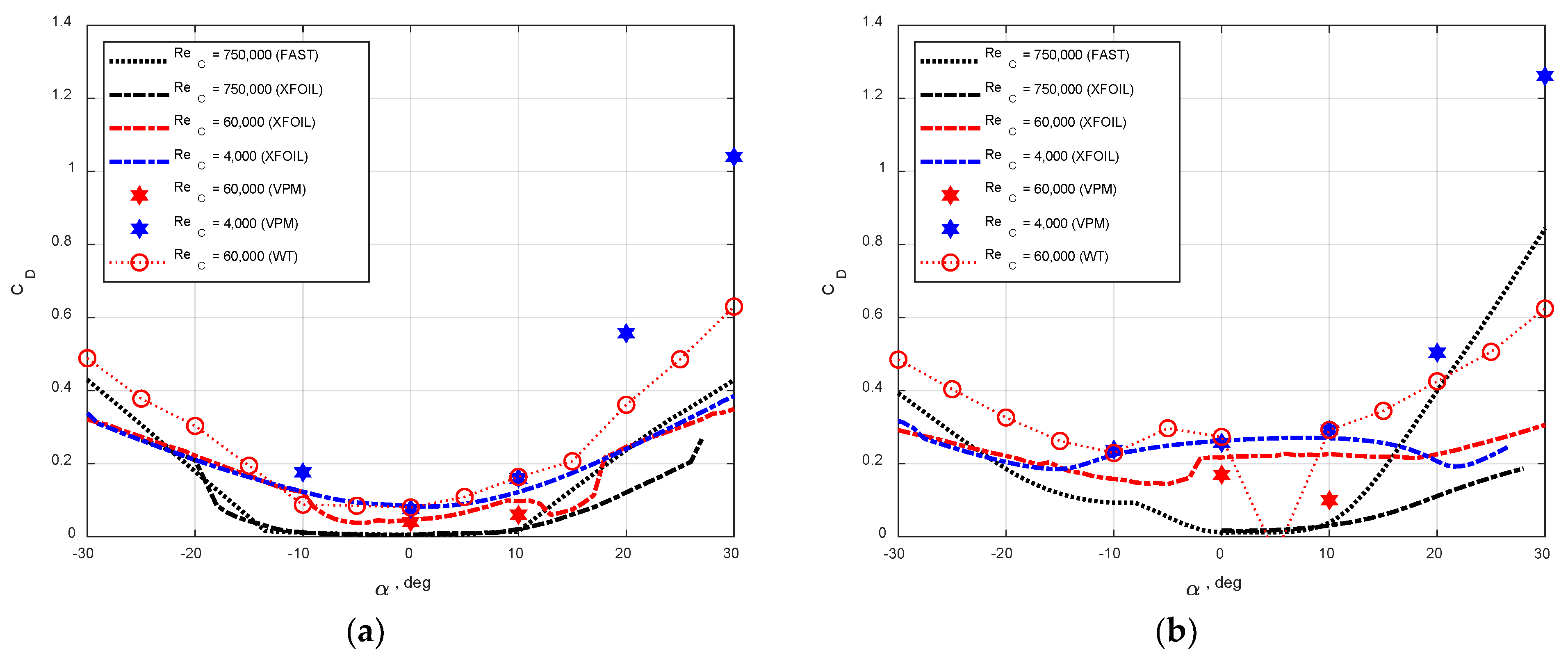
3.3. Comparison with Experiments and Other Data
3.4. Discussion
4. Conclusions
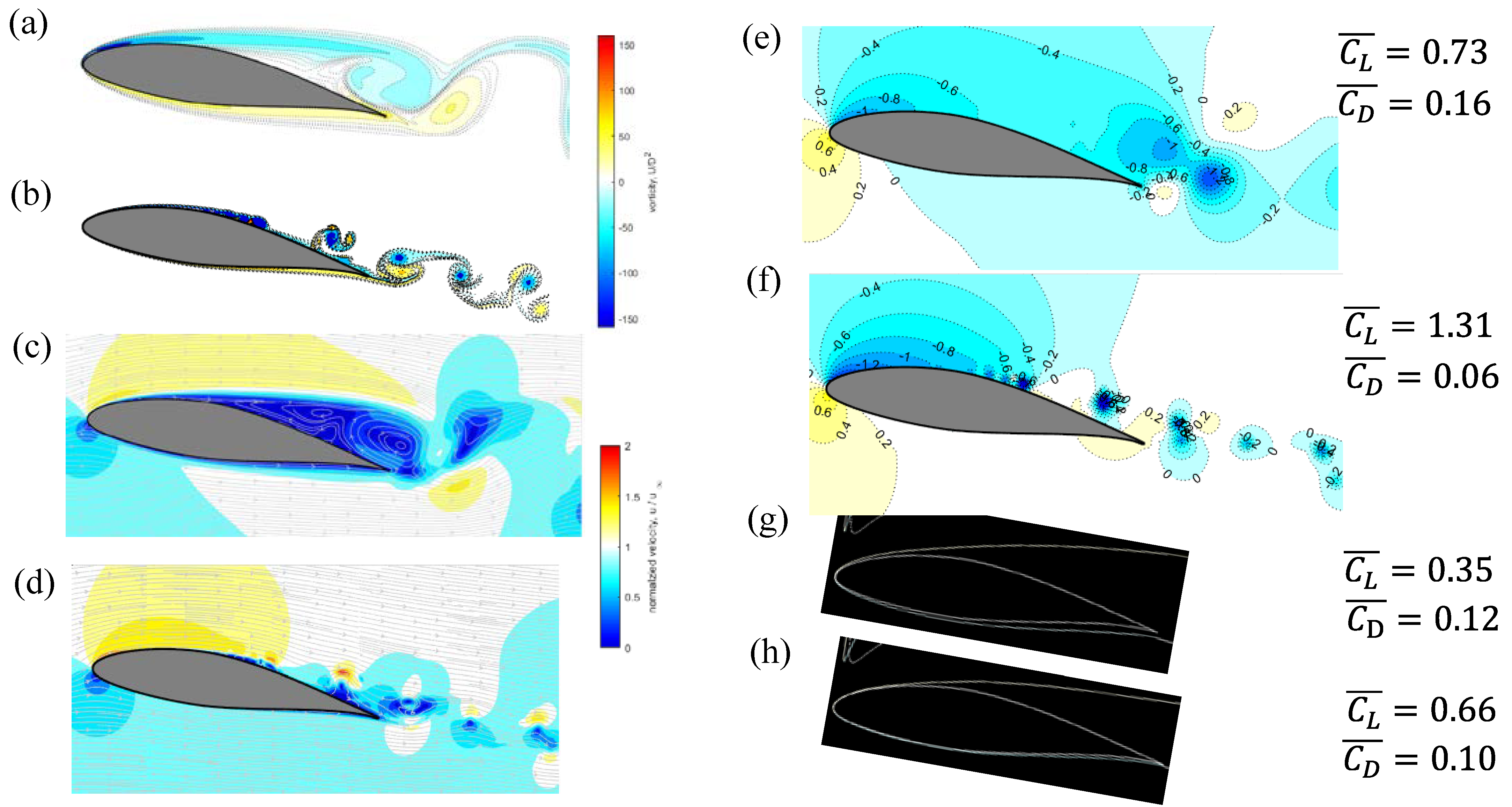
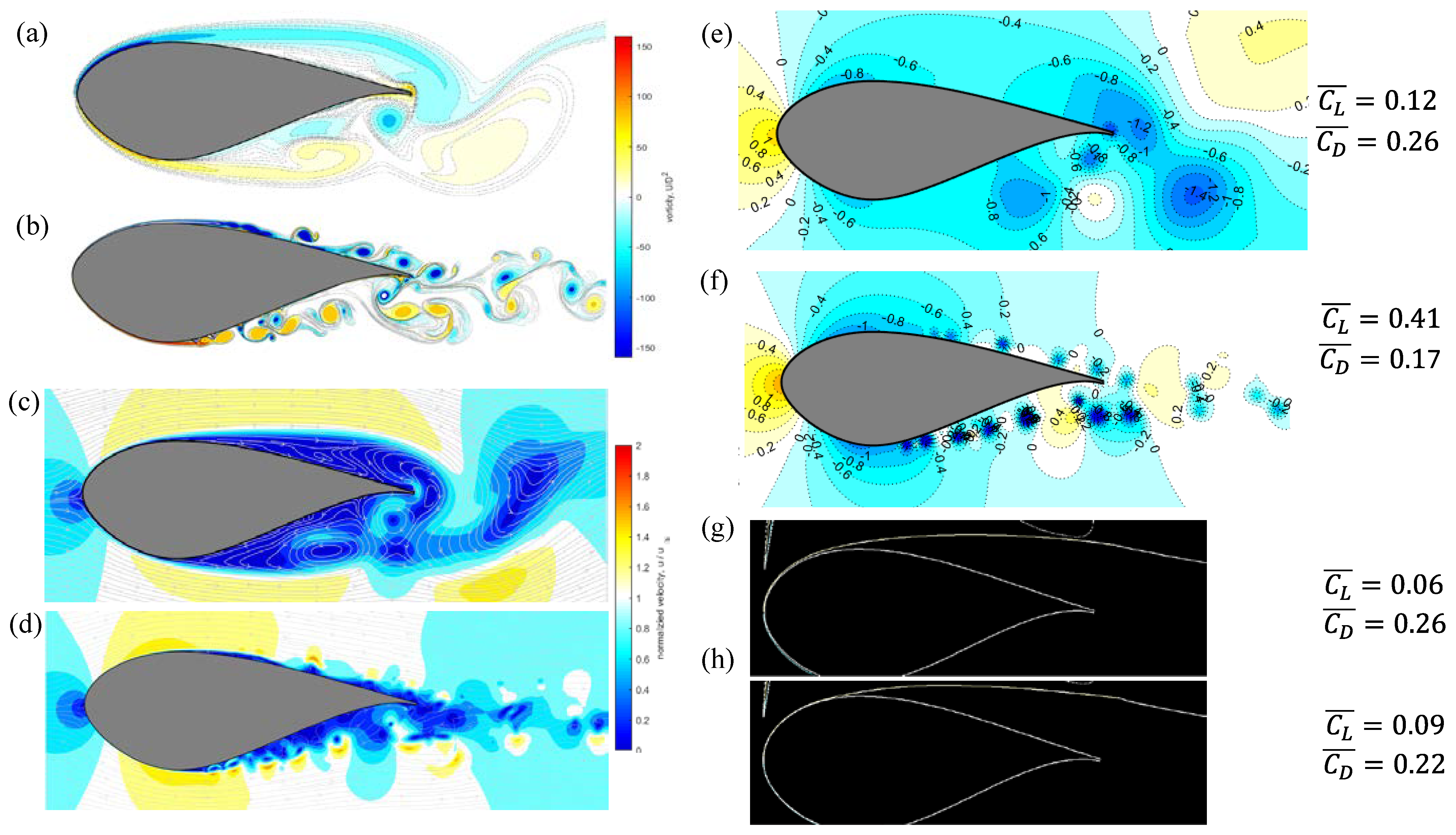
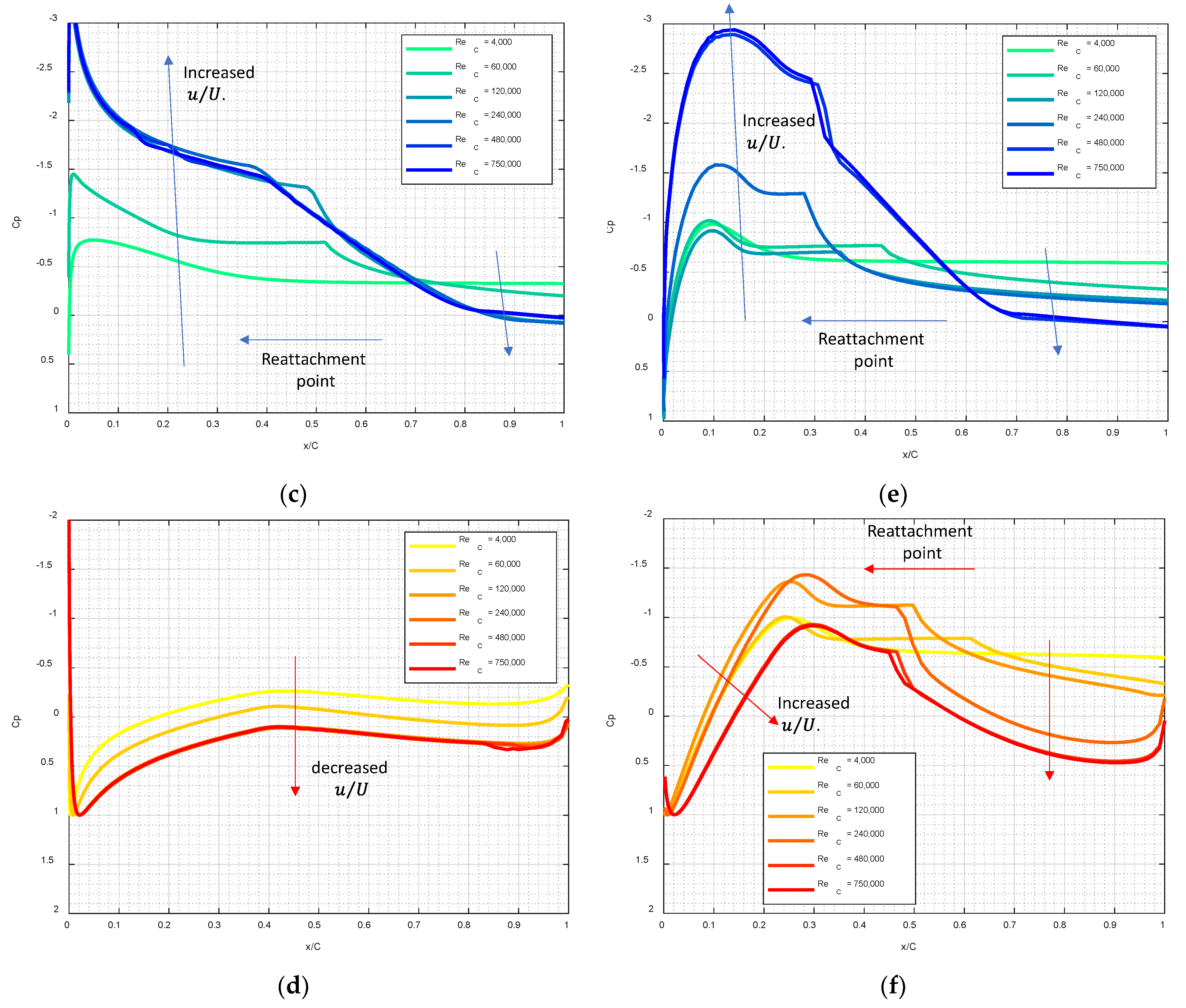
- As the Reynolds number increases, the laminar boundary layers become thinner before separation, and the separated flow may reattach, forming separation bubbles, vortex roll-ups, and irregular wake vortices of reduced length scales.
- These kinematic observations are related to variations of the surface pressure distributions, increased lifts, and reduced drags.
- Above the upstream portion of the upper airfoil surface, higher normalized wind speed occurs as ReC increases, leading to significant increases in suction coefficients. Below the lower airfoil surface, the reduced normalized wind speed occurs as ReC increases, leading to increased positive pressure coefficients. These two observations are the main causes that increase the lift coefficients.
- As ReC increases, stronger pressure recoveries induced by the flow reattachments are observed downstream of the separation bubble, leading to reduced drag coefficients.
- At the lower Reynolds number, i.e., ReC = 4000, the VPM-simulated unsteady wake vortices are larger and more organized, leading to larger wavelengths of surface pressure fluctuations and lower frequencies of aerodynamic force fluctuations.
- At the higher Reynolds number, i.e., ReC = 60,000, small-scale roll-up vortices shed downstream to form the wake, causing significant spatial pressure fluctuations on the downstream surfaces and more irregular force fluctuations at higher frequencies.
- The wind tunnel measurements of the mean integral forces at ReC = 60,000 are similar to VPM and XFOIL simulations at ReC = 4000, implying little changes in aerodynamics in this range of Reynolds numbers, i.e., 4000 < ReC < 60,000.
- It is not clear at this point why the pressure recoveries are stronger as the ReC increases. The 2D VPM simulations at intermediate Reynolds numbers, i.e., 4000 < ReC < 60,000, may assist in explaining this mechanism.
- To increase the airfoil performance at low Reynolds numbers, adding roughness near the separation point may be a feasible way, since it may promote the roll-up of separating vorticity and thus the reattachments, higher lift, and reduced drag coefficients. However, this mechanism needs to be validated.
- The 2D VPM simulations are shown to ‘overestimate’ the effects of the increasing Reynolds number at ReC = 60,000. At higher angles of attack, i.e., , reduced accuracy of VPM simulations is observed. These deficiencies are possibly due to the missing consideration of the 3D effects, which may be considered in future models. Although less accurate, the 2D VPM model is valuable in terms of its capability at a reduced cost to reflect the aerodynamics with Reynolds numbers at low angles of attack.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| C | Chord length of the airfoil. Unit: meter (m). |
| Drag force coefficient, . | |
| Lift force coefficient, . | |
| ReC | Reynolds number based on airfoil chord length, i.e., . |
| t | Time. Unit: second (s). |
| U | Freestream wind speed. Unit: m/s. |
| Angle of attack. Unit: degree (o). | |
| Kinematic viscosity. Unit: m2/s. | |
| Air density. Unit: kg/m3. |
References
- Moran, J. An Introduction to Theoretical and Computational Aerodynamics; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine; Danish Wind Power Research: Fredericia, Denmark, 2013; (Sound/Visual production (digital)). [Google Scholar]
- Bayati, I.; Belloli, M.; Bernini, L.; Giberti, H.; Zasso, A. Scale model technology for floating offshore wind turbines. IET Renew. Power Gener. 2016, 11, 1120–1126. [Google Scholar] [CrossRef] [Green Version]
- Kapoulas, I.K.; Statharas, J.C.; Hatziefremidis, A.; Baldoukas, A.K. Fast Airfoil Selection Methodology for Small Unmanned Aerial Vehicles. Appl. Sci. 2022, 12, 9328. [Google Scholar] [CrossRef]
- Dwivedi, Y.D.; Wahab, A.; Pallay, A.D.; Shesham, A. Effect of surface roughness on aerodynamic performance of the wing with NACA 4412 airfoil at Reynolds number 1.7 × 105. Mater. Today Proc. 2022, 56, 468–476. [Google Scholar] [CrossRef]
- Moraes, P.G.d.; Alcântara Pereira, L.A. Surface Roughness Effects on Flows Past Two Circular Cylinders in Tandem Arangement at Co-Shedding Regime. Energies 2021, 14, 8237. [Google Scholar] [CrossRef]
- Koehler, C.; Wischgoll, T.; Dong, H.; Gaston, Z. Vortex Visualization in Ultra Low Reynolds Number Insect Flight. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2071–2079. [Google Scholar] [CrossRef] [PubMed]
- Mueller, T.J. Aerodynamic measurements at low Reynolds numbers for fixed wing micro-air vehicles. In RTO AVT/VKI Special Course on Development and Operation of UAVs for Military and Civil Applications; Von-Karman Institute: Brussels, Belgium, 1999. [Google Scholar]
- Leloudas, S.N.; Eskantar, A.I.; Lygidakis, G.N.; Nikolos, I.K. Low Reynolds airfoil family for small horizontal axis wind turbines based on RG15 airfoil. SN Appl. Sci. 2020, 2, 371. [Google Scholar] [CrossRef] [Green Version]
- Boermans, L.M.M.; van Garrel, A. Design and Wind Tunnel Test Results of a Flapped Laminar Flow Airfoil for High Performance Sailplane Applications; XXIV OSTIV Congress: Onmrama, New Zealand, 1995. [Google Scholar]
- Addy, H.E.; Broeren, A.P.; Zoeckler, J.G.; Le, S. A wind tunnel study of icing effects on a business jet airfoil. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NE, USA, 6–9 January 2003. [Google Scholar]
- Arena, A.V.; Mueller, T.J. Laminar separation, transition, and turbulent reattachment near the leading edge of airfoils. AIAA J. 1980, 18, 79-0004R. [Google Scholar] [CrossRef]
- Selig, M.S.; McGranahan, B.D. Wind tunnel aerodynamic tests of six airfoils for use on small wind turbines. Trans. ASME 2004, 126, 986–1001. [Google Scholar] [CrossRef]
- Hu, H.; Yang, Z. An experimental study of the laminar flow separation on a low-Reynolds-number airfoil. J. Fluids Eng. 2008, 130, 051101. [Google Scholar] [CrossRef] [Green Version]
- Yarusevch, S.; Sullivan, P.; Kawall, J. On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 2009, 632, 245–271. [Google Scholar] [CrossRef]
- Mahbub Alam, M.; Zhou, Y.; Yang, H.X.; Guo, H.; Mi, J. The ultra-low Reynolds number airfoil wake. Exp. Fluids 2010, 48, 81–103. [Google Scholar] [CrossRef]
- Katz, J. A Discrete Vortex Method for the Non-Steady Separated Flow over an Airfoil. J. Fluid Mech. 1981, 102, 315–328. [Google Scholar] [CrossRef]
- Lin, J.C.M.; Pauley, L.L. Low-Reynolds-number separation on an airfoil. AIAA J. 1996, 34, 1570–1577. [Google Scholar] [CrossRef]
- Akbari, M.H.; Price, S.J. Simulation of dynamic stall for a NACA 0012 airfoil using a vortex method. J. Fluids Struct. 2003, 17, 855–874. [Google Scholar] [CrossRef]
- Kurtulus, D.F. On the wake pattern of symmetric airfoils for different incidence angles at Re = 1000. Int. J. Micro Air Veh. 2016, 8, 109–139. [Google Scholar] [CrossRef] [Green Version]
- Winslow, J.; Hikaru, O.; Govindarajan, B.; Chopra, I. Basic Understanding of Airfoil Characteristics at Low Reynolds Numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Błoński, D.; Strzelecka, K.; Kudela, H. Vortex Trapping Cavity on Airfoil: High-Order Penalized Vortex Method Numerical Simulation and Water Tunnel Experimental Investigation. Energies 2021, 14, 8402. [Google Scholar] [CrossRef]
- Ploumhans, P.; Winckelmans, G.S. Vortex methods for high-resolution simulations of viscous flow past bluff bodies of general geometry. J. Comput. Phys. 2000, 165, 354–406. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics, Proceedings of the Conference, Notre Dame, IN, USA, 5–7 June 1989; University of Notre Dame: Notre Dame, IN, USA, 1989; Volume 54, pp. 1–12. [Google Scholar]
- XFOIL. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 22 September 2022).
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Noca, F.; Shiels, D.; Jeon, D. A comparison of methods for evaluating time-dependent fluid dynamic forces on bodies, using only velocity fields and their derivatives. J. Fluid. Struct. 1999, 13, 551–578. [Google Scholar] [CrossRef]
- Wu, C.-H.; Kopp, G.A. Two-dimensional vortex particle simulation of the separated flows induced by impulsively started cylinder. In Proceedings of the 14th Americas Conference on Wind Engineering, Lubbock, TX, USA, 17–19 May 2022. [Google Scholar]
- Rae, W.H., Jr.; Pope, A. Low-Speed Wind Tunnel Testing, 2nd ed.; Wiley: New York, NY, USA, 1984; Volume 176, pp. 344–444. [Google Scholar]
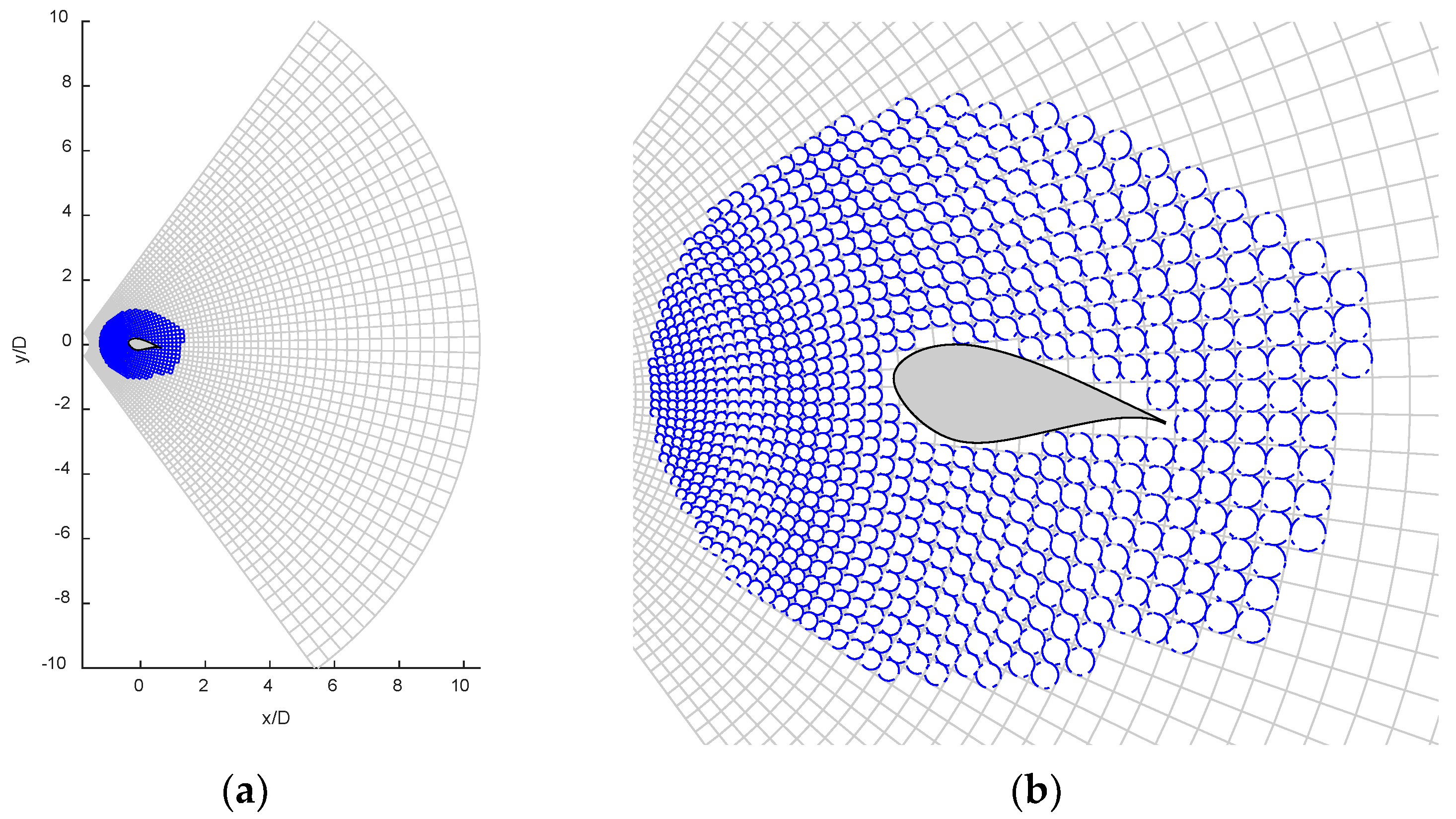



| Reynolds number, ReC | 4000 | 60,000 | ||
| Time increment, (sec) | 0.005 | 0.002 | ||
| Particle spacing at the center of the airfoil, | ||||
| Airfoils | NACA64 | DU40 | NACA64 | DU40 |
| Surface panel length, | 0.6~1.8 | 0.4~1.7 | 0.32~0.9 | |
| Azimuthal division of the redistribution grid, Nm | 8024 | 49217 | ||
| Control volume for integral force calculation, Equation (12) | ||||
| Control volume limits in x-dir, [xmin, xmax] (m) | [−0.8, 1.5] | |||
| Control volume limits in y-dir, [ymin, ymax] (m) | [−1.2, 1.2] | |||
| Eulerian grid for pressure Poisson solution, Equation (13) | ||||
| Domain limits in x-dir, [xmin, xmax] (m) | [−1.5, 5] | [−0.8, 1.3] | ||
| Domain limits in y-dir, [ymin, ymax] (m) | [–3, 3] | [−0.8, 0.8] | ||
| Grid spacing, | 1.6 | 0.26 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-H.; Chen, J.-Z.; Lo, Y.-L.; Fu, C.-L. Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers. Appl. Sci. 2023, 13, 1478. https://doi.org/10.3390/app13031478
Wu C-H, Chen J-Z, Lo Y-L, Fu C-L. Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers. Applied Sciences. 2023; 13(3):1478. https://doi.org/10.3390/app13031478
Chicago/Turabian StyleWu, Chieh-Hsun, Jing-Zong Chen, Yuan-Lung Lo, and Chung-Lin Fu. 2023. "Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers" Applied Sciences 13, no. 3: 1478. https://doi.org/10.3390/app13031478
APA StyleWu, C.-H., Chen, J.-Z., Lo, Y.-L., & Fu, C.-L. (2023). Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers. Applied Sciences, 13(3), 1478. https://doi.org/10.3390/app13031478






