Semi-Analytical Solution for the Vertical Vibration of a Single Pile Embedded in a Frozen Poroelastic Half-Space

Abstract

The theory of vertical pile vibration is the essential basis for pile integrity determination and dynamic analysis. The pile vibration characteristics are inevitably affected when the surrounding soil is frozen due to the low environmental temperature. Therefore, the investigation of pile vibration considering the surrounding soil as a saturated frozen porous medium is of great importance. In this paper, an analytical model for vertical pile vibration was established by employing the theory of composite saturated porous media, that is, by simplifying the upper frozen soil layer as a homogeneous isotropic saturated frozen porous medium and the foundation soil beneath the pile as an elastic half-space subjected to the motion of a rigid disk. By employing the integral transform and variable separation method, analytical solutions for the proposed model were derived under the three-dimensional axisymmetric condition. The analytical model and its solutions were verified by comparing them with the existing solutions for an end-bearing pile embedded in a homogeneously frozen soil layer as well as for a saturated half-space. A parametric study was conducted by utilizing the proposed solutions, and the results indicated that the pile bottom stiffness, the freezing temperature, the shear modulus of the unfrozen soil, etc., had a significant influence on the dynamic responses of the vertical pile vibration in both the frequency and the time domains.

1. Introduction

With the wide application of pile foundations in transportation and civil and energy engineering, more and more researchers have paid attention to the topics of pile foundation vibration [1,2,3,4,5,6]. The transmission of dynamic loads in an elastic half-space is the theoretical basis for studying specific problems such as pile vibration. This topic has received much attention and stimulated research efforts, which have resulted in beneficial findings [7,8,9,10,11,12]. From the perspective of the saturated porous media theory, some researchers have studied the vibration of piles in saturated soil and investigated the important influence of the liquid phase of the soil layer on pile vibration [4,13,14]. In the published studies, the piles were treated as a one-dimensional elastic rods [3,15] or beams [6,16,17,18]. The Biot’s elastic model [19,20] and poroelastic model [21,22,23], as well as the viscoelastic model [11,24,25,26] were adopted to simulate the saturated soil around a pile. The influences of the parameters of the saturated soil, the dimensions of the pile, and the Poisson’s ratio of the pile vibration were further analyzed [6,19,20,21,22]. Some studies also analyzed the relationship between the soil layer structure around the pile and the vibration response of the pile [27,28,29]. The above works have greatly promoted the development of pile dynamics and provided theoretical support for the dynamic design of pile foundations.

It is noted that in alpine and high-latitude regions, the upper soil layers are always frozen; this is a special kind of soil, with complex properties. When the soil layers are affected by the environmental temperature, especially by a temperature below the freezing point, frozen soil is formed because part of the water it contains turns into ice. Since changes in the ice content of soil have a significant impact on the soil properties, they could also affect the dynamic response of a pile foundation. Therefore, many scholars have also paid attention to the vibration of a pile foundation in a frozen soil layer covering the upper layer of an elastic half-space. Li et al. [30,31] adopted Leclaire’s frozen porous medium and Biot’s porous medium models to simulate frozen and unfrozen soil layers, respectively, realizing a dynamic analysis of end-bearing piles in single- and double-layer frozen porous media. They found that the properties of frozen soil have a great influence on the dynamic response of a pile foundation. Cao et al. [32] assumed that the water in soil gradually condenses into ice when the temperature is close to the freezing point and analyzed the influence of the change in soil ice content on the cementation between solid particles and the dynamic characteristics of a pile foundation. Due to the difference in the thickness of frozen soil layers, there is a large number of non-end-bearing piles that are utilized in frozen soil areas. The engineering importance of non-end-bearing piles has promoted a significant research progress in recent years [33,34,35]; however, to the authors’ knowledge, there are few research results available on the vertical vibration of non-end-bearing piles in frozen soil layers.

To investigate the vertical vibration characteristics of a floating pile in frozen soil areas, this study examined the vertical vibration of a pile embedded in a frozen poroelastic half-space based on the theory of frozen saturated porous media. At first, vertical vibration solutions for the pile in the frozen porous medium were derived by using analytical approaches. Then, the influence of the frozen soil parameters on the dynamic response of the pile were discussed in detailed. The innovation of this paper is the derivation of a theoretical solution for the vertical vibration of a single pile with any type of pile-end support condition in frozen soil. The reported research results have important reference value for analyzing the vibration characteristics of a pile under the effect of changes in ambient temperature and for developing a vibration theory of pile foundation in frozen soil areas.

2. Mathematical Model

In this paper, a pile embedded in frozen soil was studied. The bottom of the pile was assumed to be an elastic half-space, and the top of the pile was subjected to an arbitrary vertical excitation load. The overlying frozen soil layer is described as a homogeneous and isotropic frozen saturated porous medium composed of soil particles, ice and water. By ignoring the interaction between the solid and the ice phases, the governing equation is [30,36,37,38,39,40]:

$$\overline{R}\nabla \nabla \cdot \overrightarrow{u}-\overline{\mu }\nabla \times \nabla \times \overrightarrow{u}=\overline{\rho }\frac{{\partial }^2\overrightarrow{u}}{\partial t^2}+\overline{A}\frac{\partial \overrightarrow{u}}{\partial t}$$

(1)

where $\overrightarrow{u}$ is the displacement field vector, and $\overrightarrow{u}={\left\{{\overrightarrow{u}}^{(s)},{\overrightarrow{u}}^{(f)},{\overrightarrow{u}}^{(i)}\right\}}^{\mathrm{T}}$ represents the solid, liquid and ice displacements of the saturated frozen porous medium, respectively. $\overline{R}$, $\overline{\mu }$, $\overline{\rho }$ and $\overline{A}$ are coefficients of the frozen saturated porous medium, which can be expressed as:

$$\overline{R}=\left[\begin{array}{ccc}{R}_{11}& R_{12}& 0\\ R_{21}& R_{22}& R_{23}\\ 0& R_{32}& R_{33}\end{array}\right]$$

(2)

$$\overline{\mu }=\left[\begin{array}{ccc}{\mu }_{11}& 0& 0\\ 0& 0& 0\\ 0& 0& {\mu }_{33}\end{array}\right]$$

(3)

$$\overline{\rho }=\left[\begin{array}{ccc}{\rho }_{11}& {\rho }_{12}& 0\\ {\rho }_{21}& {\rho }_{22}& {\rho }_{23}\\ 0& {\rho }_{32}& {\rho }_{33}\end{array}\right]$$

(4)

$$\overline{A}=\left[\begin{array}{ccc}{b}_{11}& -b_{11}& 0\\ -b_{11}& b_{11}+b_{33}& -b_{33}\\ 0& -b_{33}& b_{33}\end{array}\right]$$

(5)

where $R_{11}=K_1+\frac{4}{3}{\mu }_{11}$, $R_{12}=R_{21}=C_{12}$, $R_{22}=K_2$, $R_{23}=R_{32}=C_{23}$, $R_{33}=K_3+\frac{4}{3}{\mu }_{33}$. $K_1$, $K_2$ and $K_3$ represent the bulk moduli of solid, pore fluid and ice, respectively. $C_{12}$ and $C_{23}$ denote the elastic coupling coefficients of pore fluid and solid and ice, respectively; ${\rho }_{11}$ is the density of the soil particles, ${\rho }_{22}$ is the density of the fluid, ${\rho }_{33}$ is the density of ice, ${\rho }_{12}={\rho }_{21}$ is the density of solid–liquid interaction, ${\rho }_{23}={\rho }_{32}$ is the interaction density of ice and liquid phases; $b_{11}$ and $b_{33}$ are the viscosity coupling coefficients of soil skeleton and pore fluid, and ice skeleton and pore fluid, respectively; ${\mu }_{11}$ and ${\mu }_{33}$ are the shear moduli of soil skeleton and ice, respectively.

According to the previous research results of pile dynamics [2,3,10,27], for most concrete solid piles with large slenderness (i.e., the slenderness of the pile is greater than 10), the pile can be assumed to be an elastic and circular homogeneous one-dimensional rod. $H$, $a$, ${\rho }_{\mathrm{b}}$ and $E_{\mathrm{b}}$ are the length, diameter, body density and elastic modulus of the pile, respectively. The governing equation of the vertical vibration of the pile can be written as [30]:

$$E_{\mathrm{b}}\mathsf{\pi }{a}^2\frac{{\mathrm{d}}^2{w}_{\mathrm{b}}}{\mathrm{d}{z}^2}-{\rho }_b\mathsf{\pi }{a}^2\frac{{\mathrm{d}}^2{w}_{\mathrm{b}}}{\mathrm{d}{t}^2}=f(z)$$

(6)

where $w_{\mathrm{b}}$ denotes the displacement of the pile, $f(z)=-2\mathsf{\pi }a[{\tau }_{zr}^{(s)}(a,z)+{\tau }_{zr}^{(i)}(a,z)]$ is the friction stress around the pile, and ${\tau }_{zr}^{(s)}$ and ${\tau }_{zr}^{(i)}$ denote the traction of the pile shaft produced by the soil skeleton and the ice skeleton, respectively.

In this paper, the interaction of the pile–soil system was simplified by considering it as the combination of the upper homogeneous isotropic saturated frozen porous medium and the underlying elastic half-space, as shown in Figure 1a. As shown in Figure 1b, the interaction between the overlying soil layer and the half-space was simplified by the Winkler model, whose parameters can be obtained by an inverse analysis of the soil properties at interface of half-space and its upper soil layer [40,41,42]. The soil surface was free, and the pile top was subject to an arbitrary exciting force $P(t)$. To simplify the solving process, the pile bottom was assumed to be an elastic support with the corresponding stiffness coefficient $k_{\mathrm{b}}$. As shown in Figure 1c, the application of the rigid disk solution to the elastic half-space implied that there was no lateral displacement of the soil around the pile; therefore, the soil and the pile were perfectly bonded. The friction resistance at the pile shaft is the combined force $f(z)$ of soil particles and ice. The initial condition was static, and the displacement and velocity of the system were zero; the boundary conditions are expressed as follows:

$${\left.{\sigma }_z^{(s)}\right|}_{z=0}=0, {\left.{\sigma }_z^{(i)}\right|}_{z=0}=0, {\left.{\sigma }^{(f)}\right|}_{z=0}=0, {\left.{\tau }_z^{(s)}\right|}_{z=0}=0, {\left.{\tau }_z^{(i)}\right|}_{z=0}=0, {\left.{\tau }^{(f)}\right|}_{z=0}=0$$

(7)

$$E_{\mathrm{s}}^{(av)}\frac{\partial u_z^{(s)}}{\partial z}(r,H)+k_{\mathrm{s}}{u}_z^{(s)}(r,H)=0$$

(8)

$${\left.u_r^{(s)}\right|}_{r=\infty }=0, {\left.u_z^{(s)}\right|}_{z=\infty }=0, {\left.{\sigma }_r^{(s)}\right|}_{r=\infty }=0, {\left.{\sigma }_z^{(s)}\right|}_{z=\infty }=0$$

(9)

$${\left.u_r^{(s)}\right|}_{r=a}=0, {\left.u_r^{(i)}\right|}_{r=a}=0, {\left.u_r^{(f)}\right|}_{r=a}=0$$

(10)

$$f(z)=-2\mathsf{\pi }a({\tau }_{zr}^{(s)}(a,z)+{\tau }_{zr}^{(i)}(a,z)), u_z^{(s)}(a,z)=w_{\mathrm{b}}(z), {\overline{u}}_z^{(i)}(a,z)=w_{\mathrm{b}}(z)$$

(11)

$${\left.(E_{\mathrm{b}}\mathsf{\pi }{a}^2\frac{\partial w_{\mathrm{b}}}{\partial z}+k_{\mathrm{b}}{w}_{\mathrm{b}})\right|}_{z=H}=0, {\left.\frac{\partial w_{\mathrm{b}}}{\partial z}\right|}_{z=0}=\frac{P(t)}{E_{\mathrm{b}}\mathsf{\pi }{a}^2}$$

(12)

where $k_{\mathrm{s}}$ and $k_{\mathrm{b}}$ represent the bearing coefficients of the bottom of the soil layer and the pile, respectively.

3. Analytical Solutions for the Vertical Vibration of the Pile

By using the method provided in [28], Equation (1) was transformed into the frequency domain by using Laplace transformation, in which the vector Helmholtz decomposition was introduced as:

$$\tilde{\overrightarrow{u}}=\nabla \tilde{\varphi }+\nabla \times \tilde{\overrightarrow{\psi }}=\nabla \tilde{\varphi }+\nabla \times [\tilde{\chi }{e}_z+\nabla \times (\tilde{\eta }{e}_z)], \nabla \cdot (\tilde{\eta }{e}_z)=0$$

(13)

where $\tilde{\phi }$ and $\tilde{\overrightarrow{\psi }}$ represent the displacement scalar and the vector potentials, respectively.

By using the operator decomposition method, combined with the axisymmetric loading conditions, Equation (13) can be expressed in a dimensionless form as follows:

$$\begin{array}{l}{\tilde{u}}_r^{(k)}=-{\displaystyle \sum _{l=1}^3{g}_{l1}{K}_1(g_{l1}r)(C_l^{(k)}{\mathrm{e}}^{g_{l2}z}+D_l^{(k)}{\mathrm{e}}^{-g_{l2}z})}\\ -g_{41}{g}_{42}{K}_1(g_{41}r)(C_6^{(k)}{\mathrm{e}}^{g_{42}z}-D_6^{(k)}{\mathrm{e}}^{-g_{42}z})-g_{51}{g}_{52}{K}_1(g_{51}r)(C_7^{(k)}{\mathrm{e}}^{g_{52}z}-D_7^{(k)}{\mathrm{e}}^{-g_{52}z})\end{array}$$

(14)

$$\begin{array}{l}{\tilde{u}}_z^{(k)}={\displaystyle \sum _{l=1}^3{g}_{l2}{K}_0(g_{l1}r)(C_l^{(k)}{\mathrm{e}}^{g_{l2}z}-D_l^{(k)}{\mathrm{e}}^{-g_{l2}z})}\\ -g_{41}^2{K}_0(g_{41}r)(C_6^{(k)}{\mathrm{e}}^{g_{42}z}+D_6^{(k)}{\mathrm{e}}^{-g_{42}z})-g_{51}^2{K}_0(g_{51}r)(C_7^{(k)}{\mathrm{e}}^{g_{52}z}+D_7^{(k)}{\mathrm{e}}^{-g_{52}z})\end{array}$$

(15)

where $g_{l1}^2+g_{l2}^2={\beta }_l^2$, $l=1, 2, 3, 4, 5$; ${\beta }_1^2$, ${\beta }_2^2$, ${\beta }_3^2$ and ${\beta }_{4,5}^2$ meet the following relationships, $-({\beta }_1^2+{\beta }_2^2+{\beta }_3^2)=d_1$, ${\beta }_1^2{\beta }_2^2+{\beta }_2^2{\beta }_3^2+{\beta }_1^2{\beta }_3^2=d_2$, $-{\beta }_1^2{\beta }_2^2{\beta }_3^2=d_3$, ${\beta }_{4,5}^2=\frac{d_4\pm \sqrt{d_4^2-4d_5}}{2}$. $K_0(\cdot )$ and $K_1(\cdot )$ are the modified Bessel functions of the second kind of order zero and order one, respectively. $C_1^{(k)}$, $C_2^{(k)}$, $C_3^{(k)}$; $D_1^{(k)}$, $D_2^{(k)}$, $D_3^{(k)}$, $C_4^{(k)}$, $C_5^{(k)}$, $C_6^{(k)}$, $C_7^{(k)}$; $D_4^{(k)}$, $D_5^{(k)}$, $D_6^{(k)}$, $D_7^{(k)}$ are undetermined coefficients, $k=s, f, i$ represent the solid phase, liquid phase and ice phase, respectively. $R_{ij}^{\ast }=\frac{R_{ij}}{{\mu }_{11}}$, ${\mu }_{33}^{\ast }=\frac{{\mu }_{33}}{{\mu }_{11}}$, $\delta =\sqrt{\frac{{\rho }_{11}}{{\mu }_{11}}}sa$, ${\rho }_{ij}^{\ast }=\frac{{\rho }_{ij}}{{\rho }_{11}}$, $b_{ij}^{\ast }=\frac{b_{ij}a}{\sqrt{{\rho }_{11}{\mu }_{11}}}$. It is noted that the coordinates should be converted to a dimensionless form, i.e., $\overline{r}=r/a$, $\overline{z}=z/a$.

The stress field can be obtained from the stress–strain relationship of the axisymmetric condition as:

$$\begin{array}{l}{{\tilde{\sigma }}_z^{(s)}|}_{z=0}=\left\{[({\overline{\lambda }}_1{\beta }_1^2+2g_{12}^2){\xi }_l+C_{12}^{*}{\beta }_1^2]C_1^{(f)}+[({\overline{\lambda }}_1{\beta }_1^2+2g_{12}^2){\xi }_l+C_{12}^{*}{\beta }_1^2]D_1^{(f)}\right\}{k}_0(g_{11}r)\\ +\left\{[({\overline{\lambda }}_1{\beta }_2^2+2g_{22}^2){\xi }_l+C_{12}^{*}{\beta }_2^2]C_2^{(f)}+[({\overline{\lambda }}_1{\beta }_2^2+2g_{22}^2){\xi }_l+C_{12}^{*}{\beta }_2^2]D_2^{(f)}\right\}{k}_0(g_{21}r)\\ +\left\{[({\overline{\lambda }}_1{\beta }_3^2+2g_{32}^2){\xi }_l+C_{12}^{*}{\beta }_3^2]C_3^{(f)}+[({\overline{\lambda }}_1{\beta }_3^2+2g_{32}^2){\xi }_l+C_{12}^{*}{\beta }_3^2]D_2^{(f)}\right\}{k}_0(g_{31}r)\\ -2g_{41}^2{g}_{42}{\zeta }_6(C_6^{(f)}-D_6^{(f)})k_0(g_{41}r)-2g_{51}^2{g}_{52}{\zeta }_7(C_7^{(f)}-D_7^{(f)})k_0(g_{51}r)=0\end{array}$$

(16)

$$\begin{array}{l}{\left.{\tilde{\sigma }}^{(f)}\right|}_{z=0}=\\ (C_{12}^{*}{\xi }_1+K_2^{*}+C_{23}^{*}{{\xi }^{\prime }}_1){\beta }_1^2(C_1^{(f)}+D_1^{(f)})k_0(g_{11}r)+(C_{12}^{*}{\xi }_2+K_2^{*}+C_{23}^{*}{{\xi }^{\prime }}_2){\beta }_2^2(C_2^{(f)}+D_2^{(f)})k_0(g_{21}r)\\ +(C_{12}^{*}{\xi }_3+K_2^{*}+C_{23}^{*}{{\xi }^{\prime }}_3){\beta }_3^2(C_3^{(f)}+D_3^{(f)})k_0(g_{31}r)=0\end{array}$$

(17)

$$\begin{array}{l}{\left.{\sigma }_z^{(i)}\right|}_{z=0}=[({\overline{\lambda }}_3{\beta }_1^2+2{\mu }_{33}^{*}{g}_{12}^2){{\xi }^{\prime }}_1+C_{23}^{*}{\beta }_1^2](C_1^{(f)}+D_1^{(f)})k_0(g_{11}r)\\ +[({\overline{\lambda }}_3{\beta }_2^2+2{\mu }_{33}^{*}{g}_{22}^2){{\xi }^{\prime }}_2+C_{23}^{*}{\beta }_2^2](C_2^{(f)}+D_2^{(f)})k_0(g_{21}r)+[({\overline{\lambda }}_3{\beta }_3^2+2{\mu }_{33}^{*}{g}_{32}^2){{\xi }^{\prime }}_3+C_{23}^{*}{\beta }_3^2](C_3^{(f)}+D_3^{(f)})k_0(g_{31}r)\\ -2{\mu }_{33}^{*}{g}_{41}^2{g}_{42}{{\zeta }^{\prime }}_6(C_6^{(f)}-D_6^{(f)})k_0(g_{41}r)-2{\mu }_{33}^{*}{g}_{51}^2{g}_{52}{{\zeta }^{\prime }}_7(C_7^{(f)}-D_7^{(f)})k_0(g_{51}r)=0\end{array}$$

(18)

where ${\tilde{\sigma }}_{ij}^{(s)}={\sigma }_{ij}^{(s)}/{\mu }_{11}$, ${\tilde{\sigma }}_{}^{(f)}={\sigma }_{}^{(f)}/{\mu }_{11}$, ${\tilde{\sigma }}_{ij}^{(i)}={\sigma }_{ij}^{(i)}/{\mu }_{11}$, $K_1^{*}=K_1/{\mu }_{11}$, $K_2^{*}=K_2/{\mu }_{11}$, $K_3^{*}=K_3/{\mu }_{11}$, ${\mu }_3^{*}={\mu }_3/{\mu }_{11}$, $C_{12}^{*}=C_{12}/{\mu }_{11}$, $C_{23}^{*}=C_{23}/{\mu }_{11}$, ${\mu }_{11}={\mu }_1$, ${\mu }_{33}={\mu }_3$.

Substituting the boundary conditions into Equations (16)–(18), the correlations of the unknown coefficients in Equations (16)–(18) can be determined as:

$$\left\{\begin{array}{l}(C_1^{(f)}+D_1^{(f)})=0; (C_2^{(f)}+D_2^{(f)})=0; (C_3^{(f)}+D_3^{(f)})=0;\\ (C_6^{(f)}-D_6^{(f)})=0; (C_7^{(f)}-D_7^{(f)})=0; \end{array}\right.$$

(19)

Therefore, the shear stress and vertical displacement at the pile–soil interface are expressed as follows:

$${\left.{\overline{\tau }}_{zr}^{(s)}\right|}_{\overline{r}=1}={\displaystyle \sum _{n=1}^{\infty }({\eta }_{1n}{C}_1^{(f)}+{\eta }_{2n}{C}_3^{(f)})\cosh (h_{n}z)}$$

(20)

where

$\begin{array}{l}{\eta }_{1n}=2[-2g_{11}{g}_{12}{k}_1(g_{11}){\xi }_1-2g_{21}{g}_{22}{k}_1(g_{21}){\xi }_2{\alpha }_{21}\\ +(g_{41}^3-g_{41}{g}_{42}^2)k_1(g_{41}){\zeta }_6{\alpha }_{61}+(g_{51}^3-g_{51}{g}_{52}^2)k_1(g_{51}){\zeta }_7{\alpha }_{71}]\end{array}$,

$\begin{array}{l}{\eta }_{2n}=2[-2g_{31}{g}_{32}{k}_1(g_{31}){\xi }_3-2g_{21}{g}_{22}{k}_1(g_{21}){\xi }_2{\alpha }_{23}\\ +(g_{41}^3-g_{41}{g}_{42}^2)k_1(g_{41}){\zeta }_6{\alpha }_{63}+(g_{51}^3-g_{51}{g}_{52}^2)k_1(g_{51}){\zeta }_7{\alpha }_{73}]\end{array}$.

$${\left.{\overline{\tau }}_{zr}^{(i)}\right|}_{\overline{r}=1}={\displaystyle \sum _{n=1}^{\infty }({\eta }_{3n}{C}_1^{(f)}+{\eta }_{4n}{C}_3^{(f)})\cosh (h_{n}z)}$$

(21)

where

${\eta }_{3n}=2\left[\begin{array}{l}-2{\mu }_{33}^{*}{g}_{11}{g}_{12}{k}_1(g_{11}){{\xi }^{\prime }}_1-2{\mu }_{33}^{*}{g}_{21}{g}_{22}{k}_1(g_{21}){{\xi }^{\prime }}_2{\alpha }_{21}\\ +{\mu }_{33}^{*}(g_{41}^3-g_{41}{g}_{42}^2)k_1(g_{41}){{\varsigma }^{\prime }}_6{\alpha }_{61}+{\mu }_{33}^{*}(g_{51}^3-g_{51}{g}_{52}^2)k_1(g_{51}){{\varsigma }^{\prime }}_7{\alpha }_{71}\end{array}\right]$,

${\eta }_{4n}=2\left[\begin{array}{l}-2{\mu }_{33}^{*}{g}_{31}{g}_{32}{k}_1(g_{31}){{\xi }^{\prime }}_3-2{\mu }_{33}^{*}{g}_{21}{g}_{22}{k}_1(g_{21}){{\xi }^{\prime }}_2{\alpha }_{23}\\ +{\mu }_{33}^{*}(g_{41}^3-g_{41}{g}_{42}^2)k_1(g_{41}){{\varsigma }^{\prime }}_6{\alpha }_{63}+{\mu }_{33}^{*}(g_{51}^3-g_{51}{g}_{52}^2)k_1(g_{51}){{\varsigma }^{\prime }}_7{\alpha }_{73}\end{array}\right]$.

$${\left.{\overline{u}}_z^{(s)}\right|}_{\overline{r}=1}={\displaystyle \sum _{n=1}^{\infty }({\eta }_{5n}{C}_1^{(f)}+{\eta }_{6n}{C}_3^{(f)})\cosh (h_{n}z)}$$

(22)

where

${\eta }_{5n}=2[g_{12}{k}_0(g_{11}){\xi }_1+g_{22}{k}_0(g_{21}){\xi }_2{\alpha }_{21}-g_{41}^2{k}_0(g_{41}){\zeta }_6{\alpha }_{61}-g_{51}^2{k}_0(g_{51}){\zeta }_7{\alpha }_{71}]$,

${\eta }_{6n}=2[g_{32}{k}_0(g_{31}){\xi }_3+g_{22}{k}_0(g_{21}){\xi }_2{\alpha }_{23}-g_{41}^2{k}_0(g_{41}){\zeta }_6{\alpha }_{63}-g_{51}^2{k}_0(g_{51}){\zeta }_7{\alpha }_{73}]$.

$${\left.{\overline{u}}_z^{(i)}\right|}_{\overline{r}=1}={\displaystyle \sum _{n=1}^{\infty }({\eta }_{7n}{C}_1^{(f)}+{\eta }_{8n}{C}_3^{(f)})\cosh (h_{n}z)}$$

(23)

where

${\eta }_{7n}=2[g_{12}{k}_0(g_{11}){{\xi }^{\prime }}_1+g_{22}{k}_0(g_{21}){{\xi }^{\prime }}_2{\alpha }_{21}-g_{41}^2{k}_0(g_{41}){{\varsigma }^{\prime }}_6{\alpha }_{61}-g_{51}^2{k}_0(g_{51}){{\varsigma }^{\prime }}_7{\alpha }_{71}]$,

${\eta }_{8n}=2[g_{32}{k}_0(g_{31}){{\xi }^{\prime }}_3+g_{22}{k}_0(g_{21}){{\xi }^{\prime }}_2{\alpha }_{23}-g_{41}^2{k}_0(g_{41}){{\varsigma }^{\prime }}_6{\alpha }_{63}-g_{51}^2{k}_0(g_{51}){{\varsigma }^{\prime }}_7{\alpha }_{73}]$,

${\alpha }_{21}=\frac{\left[{{\xi }^{\prime }}_1({\varsigma }_6-{\varsigma }_7)-{{\varsigma }^{\prime }}_6({\xi }_1-{\varsigma }_7)+{{\varsigma }^{\prime }}_7({\xi }_1-{\varsigma }_6)\right]g_{11}{k}_1(g_{11})}{\left[{{\xi }^{\prime }}_2({\varsigma }_6-{\varsigma }_7)-{{\varsigma }^{\prime }}_6({\xi }_2-{\varsigma }_7)+{{\varsigma }^{\prime }}_7({\xi }_2-{\varsigma }_6)\right]g_{21}{k}_1(g_{21})}$,

${\alpha }_{23}=\frac{\left[{{\xi }^{\prime }}_3({\varsigma }_6-{\varsigma }_7)-{{\varsigma }^{\prime }}_6({\xi }_3-{\varsigma }_7)+{{\varsigma }^{\prime }}_7({\xi }_3-{\varsigma }_6)\right]g_{31}{k}_1(g_{31})}{\left[{{\xi }^{\prime }}_2({\varsigma }_6-{\varsigma }_7)-{{\varsigma }^{\prime }}_6({\xi }_2-{\varsigma }_7)+{{\varsigma }^{\prime }}_7({\xi }_2-{\varsigma }_6)\right]g_{21}{k}_1(g_{21})}$,

${\alpha }_{61}=\frac{g_{11}{k}_1(g_{11})({\xi }_1-{\varsigma }_7)+g_{21}{k}_1(g_{21})({\xi }_2-{\varsigma }_7){\alpha }_{21}}{g_{41}{g}_{42}{k}_1(g_{41})({\varsigma }_7-{\varsigma }_6)}$,

${\alpha }_{63}=\frac{g_{31}{k}_1(g_{31})({\xi }_3-{\varsigma }_7)+g_{21}{k}_1(g_{21})({\xi }_2-{\varsigma }_7){\alpha }_{23}}{g_{41}{g}_{42}{k}_1(g_{41})({\varsigma }_7-{\varsigma }_6)}$,

${\alpha }_{71}=\frac{g_{11}{k}_1(g_{11})({\xi }_1-{\varsigma }_6)+g_{21}{k}_1(g_{21})({\xi }_2-{\varsigma }_6){\alpha }_{21}}{g_{51}{g}_{52}{k}_1(g_{51})({\varsigma }_6-{\varsigma }_7)}$,

${\alpha }_{73}=\frac{g_{31}{k}_1(g_{31})({\xi }_3-{\varsigma }_6)+g_{21}{k}_1(g_{21})({\xi }_2-{\varsigma }_6){\alpha }_{23}}{g_{51}{g}_{52}{k}_1(g_{51})({\varsigma }_6-{\varsigma }_7)}$.

By assuming that $h_n=g_{12}=g_{22}=g_{32}=g_{42}=g_{52}$, the following transcendental equations can be satisfied:

$$(h_n+k_{\mathrm{s}}^{*})e^{h_n\theta }-(h_n-k_s^{*})e^{-h_n\theta }=0 \mathrm{or} h_n\sinh (h_n\theta )+k_s^{*}\cosh (h_n\theta )=0$$

(24)

The specific forms of the coefficients ${\xi }_1$, ${\xi }_2$, ${\varsigma }_6$, ${\varsigma }_7$, ${{\xi }^{\prime }}_1$, ${{\xi }^{\prime }}_2$, ${{\varsigma }^{\prime }}_6$, ${{\varsigma }^{\prime }}_7$ are provided in Appendix A. $\theta =H/a$ denotes the slenderness of the pile, $k_{\mathrm{s}}^{*}=k_{s}a/E_s$ is the dimensionless bearing coefficient of the bottom of the soil layer.

The vertical vibration of the pile, described by Equation (6), can be solved by using the Laplace transformation and can be expressed in a dimensionless manner as:

$$\frac{{\mathrm{d}}^2{\overline{w}}_{\mathrm{b}}}{\mathrm{d}{\overline{z}}^2}-\frac{{\rho }_b^{*}{\delta }^2}{E_{\mathrm{b}}^{*}}{\overline{w}}_{\mathrm{b}}+\frac{2}{E_{\mathrm{b}}^{*}}[{\tau }_{zr}^{(s)}(1,z)+{\tau }_{zr}^{(i)}(1,z)]=0$$

(25)

where ${\left.{\overline{\tau }}_{zr}^{(s)}\right|}_{\overline{r}=1}+{\left.{\overline{\tau }}_{zr}^{(i)}\right|}_{\overline{r}=1}={\displaystyle \sum _{n=1}^{\infty }}[({\eta }_{1n}+{\eta }_{3n})C_1^{(f)}+({\eta }_{2n}+{\eta }_{4n})C_3^{(f)}]\cosh (h_{n}z)$, ${\rho }_b^{\ast }={\rho }_b/{\rho }_{11}$, $E_b^{\ast }=E_b/{\mu }_{11}$.

$${\overline{w}}_{\mathrm{b}}=A_1{\mathrm{e}}^{\kappa \overline{z}}+B_1{\mathrm{e}}^{-\kappa \overline{z}}+{\displaystyle \sum _{n=1}^{\infty }\frac{-2[({\eta }_{1n}+{\eta }_{3n})C_1^{(f)}+({\eta }_{2n}+{\eta }_{4n})C_3^{(f)}]}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}\cosh (h_{n}z)$$

(26)

Substituting Equations (22), (23) and (26) into Equation (11) yields:

$${\overline{w}}_{\mathrm{b}}(z)=A_1\left\{{\mathrm{e}}^{\kappa \overline{z}}+{\displaystyle \sum _{n=1}^{\infty }\frac{-E_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}\cosh (h_{n}z)\right\}+B_1\left\{{\mathrm{e}}^{-\kappa \overline{z}}+{\displaystyle \sum _{n=1}^{\infty }\frac{-F_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}\cosh (h_{n}z)\right\}$$

(27)

where

$E_n=\frac{\frac{{\mathrm{e}}^{(\kappa +h_n)\theta }-1}{2(\kappa +h_n)}+\frac{{\mathrm{e}}^{(\kappa -h_n)\theta }-1}{2(\kappa -h_n)}}{\left[\frac{({\eta }_{5n}{\eta }_{8n}-{\eta }_{6n}{\eta }_{7n})}{2[({\eta }_{2n}+{\eta }_{4n})({\eta }_{5n}-{\eta }_{7n})+({\eta }_{1n}+{\eta }_{3n})({\eta }_{8n}-{\eta }_{6n})]}+\frac{1}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}\right]\left[\frac{\theta }{2}+\frac{\sinh (2h_n\theta )}{4h_n}\right]}$,

${F^{\prime }}_n=-\frac{\frac{{\mathrm{e}}^{-(\kappa -h_n)\theta }-1}{2(\kappa -h_n)}+\frac{{\mathrm{e}}^{-(\kappa +h_n)\theta }-1}{2(\kappa +h_n)}}{\left[\frac{({\eta }_{5n}{\eta }_{8n}-{\eta }_{6n}{\eta }_{7n})}{2[({\eta }_{2n}+{\eta }_{4n})({\eta }_{5n}-{\eta }_{7n})+({\eta }_{1n}+{\eta }_{3n})({\eta }_{8n}-{\eta }_{6n})]}+\frac{1}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}\right]\left[\frac{\theta }{2}+\frac{\sinh (2h_n\theta )}{4h_n}\right]}$.

Equation (12) can be transformed as:

$${\left.(\frac{\partial {\overline{w}}_{\mathrm{b}}}{\partial z}+k_{\mathrm{b}}^{*}{\overline{w}}_{\mathrm{b}})\right|}_{z=\theta }=0, {\left.\frac{\partial w_{\mathrm{b}}}{\partial z}\right|}_{z=0}=\frac{\overline{P}(s)}{E_{\mathrm{b}}^{*}{\mu }_{11}}$$

(28)

where $k_{\mathrm{b}}^{*}=k_{\mathrm{b}}/E_{\mathrm{b}}\mathsf{\pi }a$ denotes the dimensionless bearing coefficient of the pile bottom.

Substituting Equation (27) into Equation (28) gives:

$$\begin{array}{l}{A}_1=\frac{\frac{{\overline{P}}^{*}}{E_{\mathrm{b}}^{*}\kappa }[(k_{\mathrm{b}}^{*}-\kappa ){\mathrm{e}}^{-\kappa \theta }+{\displaystyle \sum _{n=1}^{\infty }\frac{-F_n{G}_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]}{(k_{\mathrm{b}}^{*}+\kappa ){\mathrm{e}}^{\kappa \theta }+(k_{\mathrm{b}}^{*}-\kappa ){\mathrm{e}}^{-\kappa \theta }+{\displaystyle \sum _{n=1}^{\infty }\frac{-(E_n+F_n)G_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}}\\ B_1=-\frac{\frac{{\overline{P}}^{*}}{E_{\mathrm{b}}^{*}\kappa }[(k_{\mathrm{b}}^{*}+\kappa ){\mathrm{e}}^{\kappa \theta }+{\displaystyle \sum _{n=1}^{\infty }\frac{-E_n{G}_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]}{(k_{\mathrm{b}}^{*}+\kappa ){\mathrm{e}}^{\kappa \theta }+(k_{\mathrm{b}}^{*}-\kappa ){\mathrm{e}}^{-\kappa \theta }+{\displaystyle \sum _{n=1}^{\infty }\frac{-(E_n+F_n)G_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}}\end{array}$$

(29)

where $G_n=h_n\sinh (h_n\theta )+k_{\mathrm{b}}^{*}\cosh (h_n\theta )$.

Thus, the displacement of the pile body was determined. Meanwhile, the complex impedance of the pile top can be defined as:

$$Z_u=\frac{1}{A_1[1+{\displaystyle \sum _{n=1}^{\infty }\frac{-E_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]+B_1[1+{\displaystyle \sum _{n=1}^{\infty }\frac{-F_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]}$$

(30)

Therefore, the displacement mobility of pile top was obtained as:

$$G_u=\frac{1}{Z_u}=A_1[1+{\displaystyle \sum _{n=1}^{\infty }\frac{-E_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]+B_1[1+{\displaystyle \sum _{n=1}^{\infty }\frac{-F_n}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}]$$

(31)

Setting $s=\mathrm{i}\omega$ (in which $s$ is the parameter of the Fourier transform domain, $\mathrm{i}$ is an imaginary unit, $\omega$ is the circular frequency), the complex dynamic stiffness of the pile top and the velocity response of the pile top in the frequency domain can be separately obtained as:

$$k_d(\mathrm{i}\omega )=Z_u(\mathrm{i}\omega )$$

(32)

$$\left|H_v(\mathrm{i}\omega )\right|=\left|\mathrm{i}\omega G_u(\mathrm{i}\omega )\right|$$

(33)

It should be noted that the complex dynamic stiffness of the pile top is mainly utilized for the dynamic design of the pile foundation and the velocity response of the pile top is used for the nondestructive testing of piles by the mechanical impedance method. Therefore, the concerning frequency range may be 0–40 Hz in the design process of the dynamic foundation and in the nondestructive testing of piles by the mechanical impedance method.

Consider the half–sine impulse:

$$q(t)=q_{\max }\sin \frac{2\mathsf{\pi }}{T}t[H(t-\frac{T}{2})-H(t)], t\in (0, \frac{T}{2})$$

(34)

where $T$ is the pulse period. Thus, when the half–sine transient force acts on the pile top, the velocity response of the pile top in the time domain can be obtained by using the convolution theorem and the Fourier inverse transformation:

$$V(t)=IFT[Q(\mathrm{i}\omega )\cdot H_v(\mathrm{i}\omega )]=\frac{q_{\max }}{2\mathsf{\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\frac{2\mathsf{\pi }T}{4{\mathsf{\pi }}^2-T^2{\omega }^2}(1+{\mathrm{e}}^{-\mathrm{i}\omega T/2})H_v(\mathrm{i}\omega ){\mathrm{e}}^{\mathrm{i}\omega t}\mathrm{d}\omega }$$

(35)

4. Verification

4.1. Comparison and Verification of an End-Bearing Pile in a Single-Layer Frozen Soil

By using the displacement mobility of the pile top defined in Equation (31), the degradation problem of the presented solutions can be discussed. When the bottom of the soil layer and the underlying layer of the pile are bedrock, the elastic half-space is transformed into a rigid one; thus, $k_b^{*} k_{\mathrm{s}}^{*}\to \infty$, and $G_n=h_n\sinh (h_n\theta )+k_b^{*}\cosh (h_n\theta ) 0$. At the same time, the eigenvalue $\cosh (h_n\theta ) 0$ is the same as that of the end-bearing pile, and Equation (31) can be reduced to:

$$G_u=-\frac{\tanh (\kappa \theta )}{E_{\mathrm{b}}^{*}\kappa }+{\displaystyle \sum _{n=1}^{\infty }\frac{-4}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)\theta [\frac{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)({\eta }_{5n}{\eta }_{8n}-{\eta }_{6n}{\eta }_{7n})}{\begin{array}{l}{\eta }_{1n}{\eta }_{8n}+{\eta }_{3n}{\eta }_{8n}-{\eta }_{1n}{\eta }_{6n}-{\eta }_{3n}{\eta }_{6n}\\ -{\eta }_{2n}{\eta }_{7n}-{\eta }_{4n}{\eta }_{7n}+{\eta }_{2n}{\eta }_{5n}+{\eta }_{4n}{\eta }_{5n}\end{array}}+2]}}$$

(36)

The first item on the right of Equation (36) is just the displacement admittance of an elastic rod with one free and one fixed end under any excitation force, and it is noted that:

$$-\frac{\tanh (\kappa \theta )}{E_{\mathrm{b}}^{*}\kappa }=\frac{2}{\theta }{\displaystyle \sum _{n=1}^{\infty }\frac{1}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)}}$$

(37)

Therefore, Equation (36) can be simplified as:

$$G_u=\frac{2}{\theta }{\displaystyle \sum _{n=1}^{\infty }\frac{1}{E_{\mathrm{b}}^{*}(h_n^2-{\kappa }^2)+2{\alpha }_n}}$$

(38)

where ${\alpha }_n=({\eta }_{1n}{\eta }_{8n}+{\eta }_{3n}{\eta }_{8n}-{\eta }_{1n}{\eta }_{6n}-{\eta }_{3n}{\eta }_{6n}-{\eta }_{2n}{\eta }_{7n}-{\eta }_{4n}{\eta }_{7n}+{\eta }_{2n}{\eta }_{5n}+{\eta }_{4n}{\eta }_{5n})/({\eta }_{5n}{\eta }_{8n}-{\eta }_{6n}{\eta }_{7n})$.

It can be seen that if the bottom of the pile is supported on bedrock and the bottom is rigid, Equation (34) is completely consistent with Equation (36) in [28] for the end-bearing pile. Therefore, the elastic pile problem is transformed into an end–bearing pile problem. In other words, the solution in [28] is a special case of the present solutions.

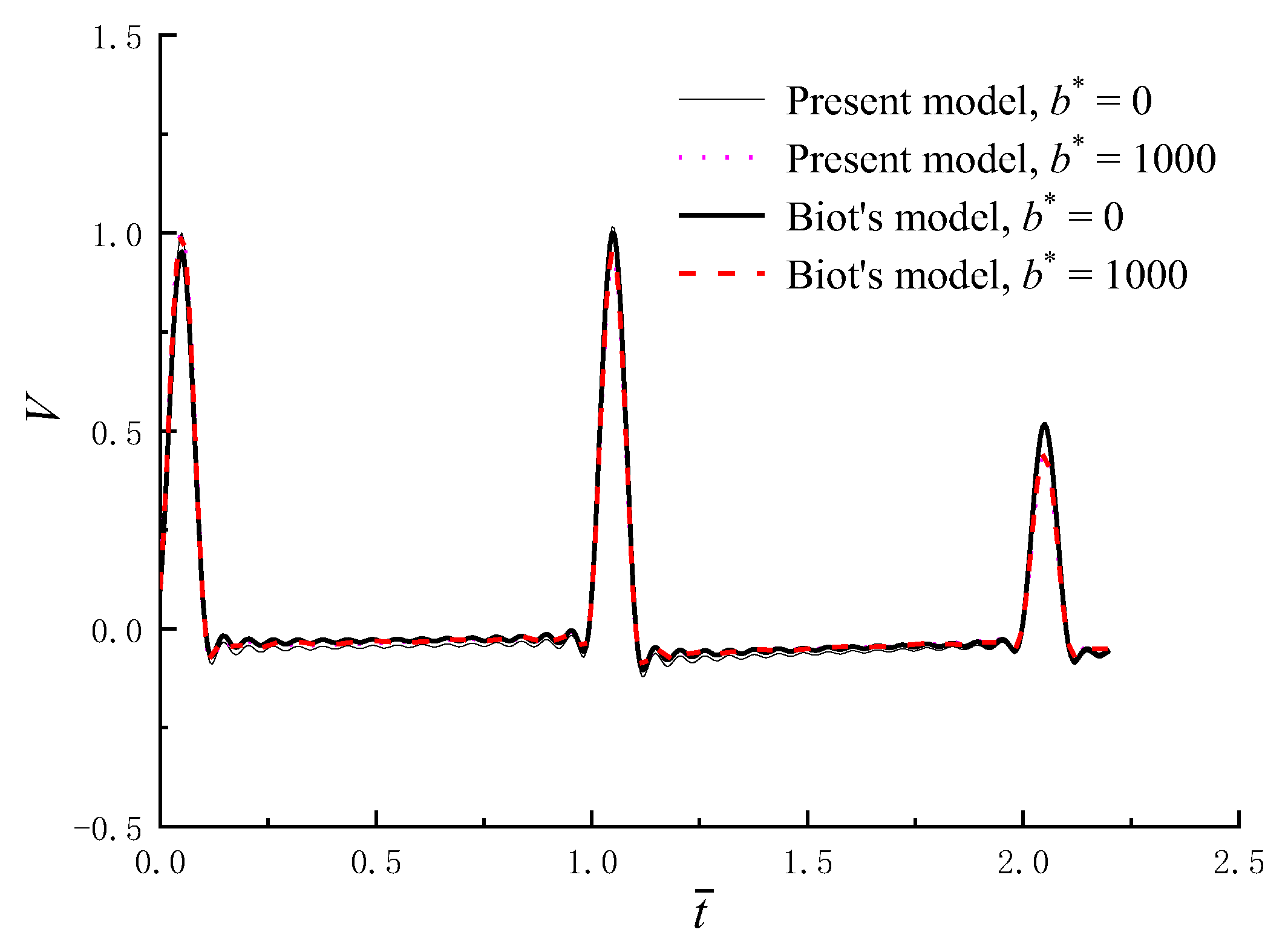
4.2. Verification of the Solution for a Saturated Half–Space

To further verify the validity of the proposed solutions, a comparison of the complex dynamic stiffness of the pile in frozen and saturated soils is provided in this section. The complex dynamic stiffness of the pile in saturated soil was calculated according to the rigorous formulation of the porous elastic mechanics integral through a virtual pile method described by Zeng and Rajapakse [15]. When the temperature in the analysis was set as T = −0.15 °C, the ice content was approximately zero, and the frozen soil was equivalent to the saturated soil. Figure 2 shows the results obtained from the simplified model of the present solutions and the Biot’s model of Zeng and Rajapakse [15] within the low-frequency range, where the horizontal axis represents the dimensionless frequency $b_1=\omega /{\omega }_{\mathrm{g}}$, and the vertical axis denotes the dimensionless complex dynamic stiffness of the pile top $k_d^{\prime }$, which can be decomposed into a real part and an imaginary part. ${\omega }_{\mathrm{g}}$ is the natural frequency of the free vibration of an elastic bearing pile, meeting the following characteristic equation $\frac{{\omega }_{\mathrm{g}}}{v_{\mathrm{p}}}=k_{\mathrm{b}}\cot \left(\frac{{\omega }_{\mathrm{g}}}{v_{\mathrm{p}}}H\right)$ in which $v_{\mathrm{p}}$ is the longitudinal wave velocity of the pile. To ensure consistency with the calculation conditions provided in reference [15], the bearing coefficient of the pile bottom was taken as $k_{\mathrm{b}}=4\mu a/(1-\nu )$, according to the analytical solution for the rigid disk in an elastic half-space through theoretical derivation and experimental data inversion [15]. It can be seen in Figure 2 that under the conditions of two different seepage forces (i.e., $b^{*}=0$ indicates a free support condition, and $b^{*}=1000$ indicates a fixed support condition), the curves corresponding to the real and the imaginary parts of the simplified model and the reference curves [15] are in good agreement. This confirms that when the temperature is close to the freezing point, the solution proposed in this paper can be reduced to the strict solution for the vertical vibration of the pile in saturated soil. Furthermore, Figure 3 shows a comparison of the reflected signals obtained for the two aforementioned models in the time domain, and it can be seen that these curves are almost identical. In Figure 3, $\overline{t}=tc/2H$ denotes the dimensionless time.

5. Parametric Study

In this section, the bearing coefficient of the pile bottom, the freezing temperature, and the shear modulus of the soil in relation to the complex dynamic stiffness of the pile top is investigated in detailed. The complex dynamic stiffness of pile top can be divided into a real part $k_{\mathrm{d}}$ and an imaginary part $c_{\mathrm{d}}$, which represent the dynamic stiffness and dynamic damping of the pile, respectively. In order to facilitate the comparative analysis with static stiffness, the dynamic stiffness was replaced by the dynamic stiffness factor ${\overline{k}}_{\mathrm{d}}=k_{\mathrm{d}}/k_{\mathrm{d}0}$, in which $k_{\mathrm{d}0}$ is the static stiffness of the pile top.

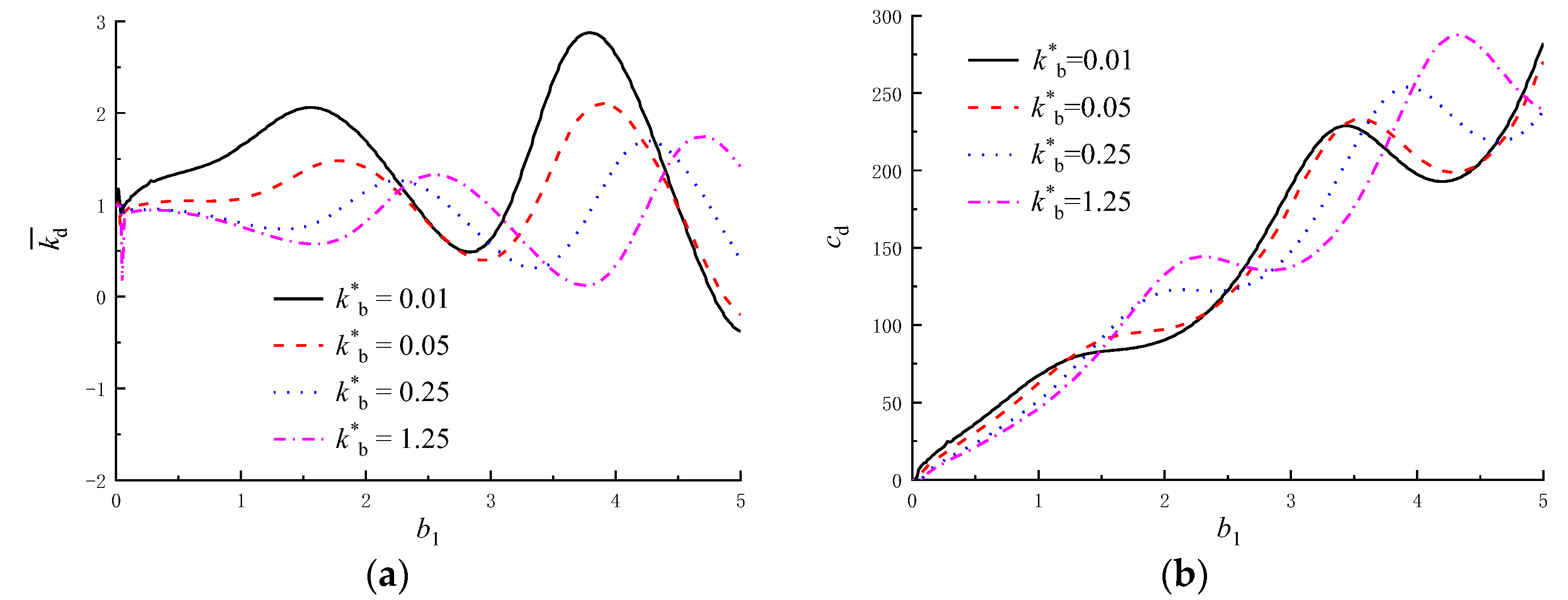
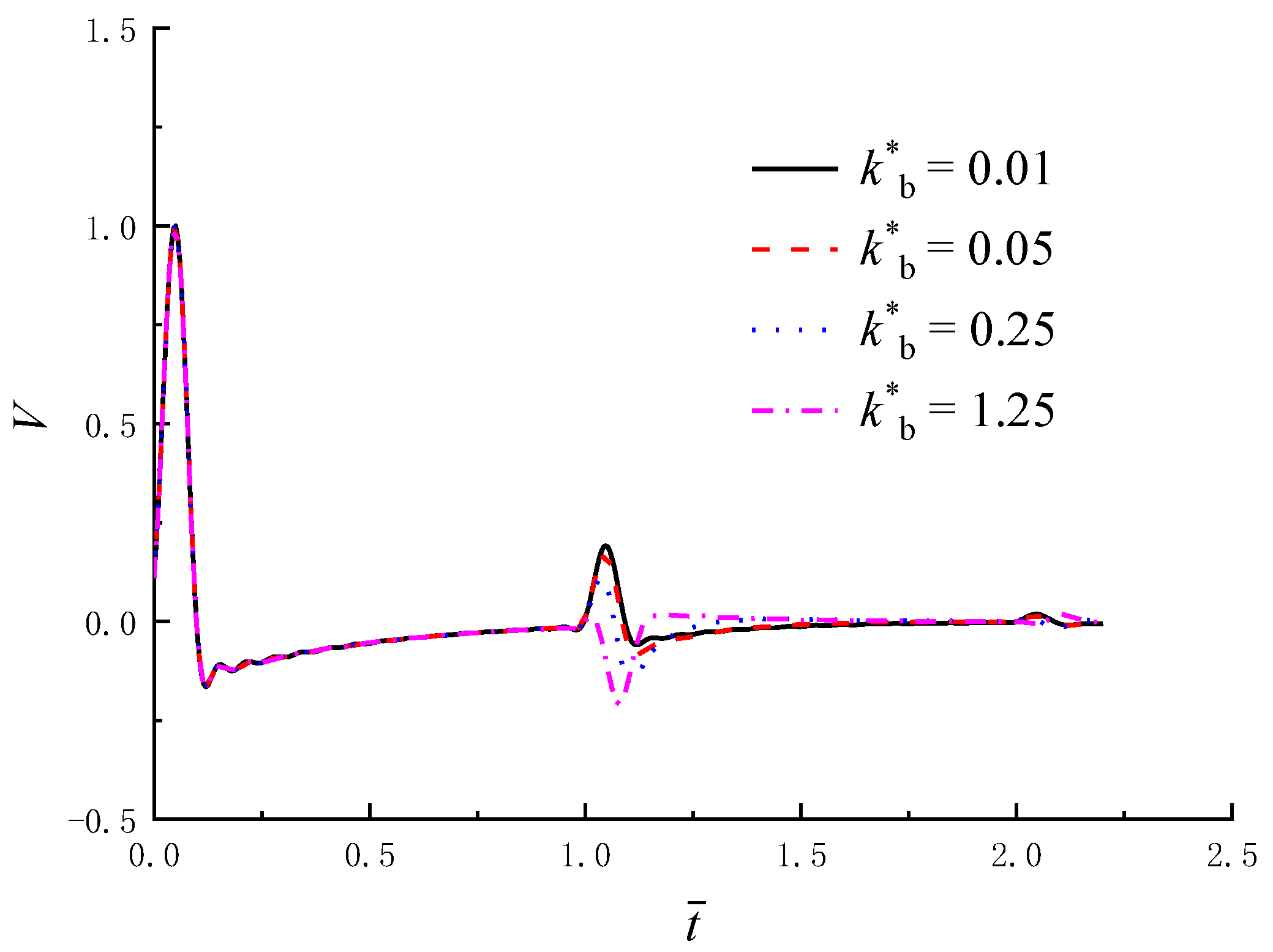
5.1. Influence of the Bearing Coefficient of the Pile Bottom

The bearing coefficient of the pile bottom was used to reflect the degree of softness or stiffness of the pile bottom soil. As shown in Figure 4, when the bearing coefficient of the pile bottom was large enough, the curves obtained by the present solutions were close to those of the end-bearing pile. The resonance amplitudes of the dynamic stiffness and damping increased with the decrease in the bearing coefficient of the pile bottom. The resonance frequency of the dynamic stiffness and damping increased with the increase in the bearing coefficient of the pile bottom.

As shown in Figure 5, the variation of the bearing coefficient of the pile bottom had an obvious influence on the reflected wave curves of the pile top. When the support of the pile bottom was rigid, i.e., the bearing coefficient of the pile bottom was large enough ($k_{\mathrm{b}}^{*}\ge 1.25$), the first reflected wave signal was opposite to the incident wave. On the contrary, when the support of the pile bottom was free, namely, the bearing coefficient of the pile bottom was small enough ($k_{\mathrm{b}}^{*}\le 0.01$), the first reflected wave signal was in the same direction as that of the incident wave. When the support of the pile bottom was between rigid and free ($0.01<k_{\mathrm{b}}^{*}<1.25$), the reflected signal at the pile bottom usually appears first in the same direction as the head wave, followed by the reverse reflected signal.

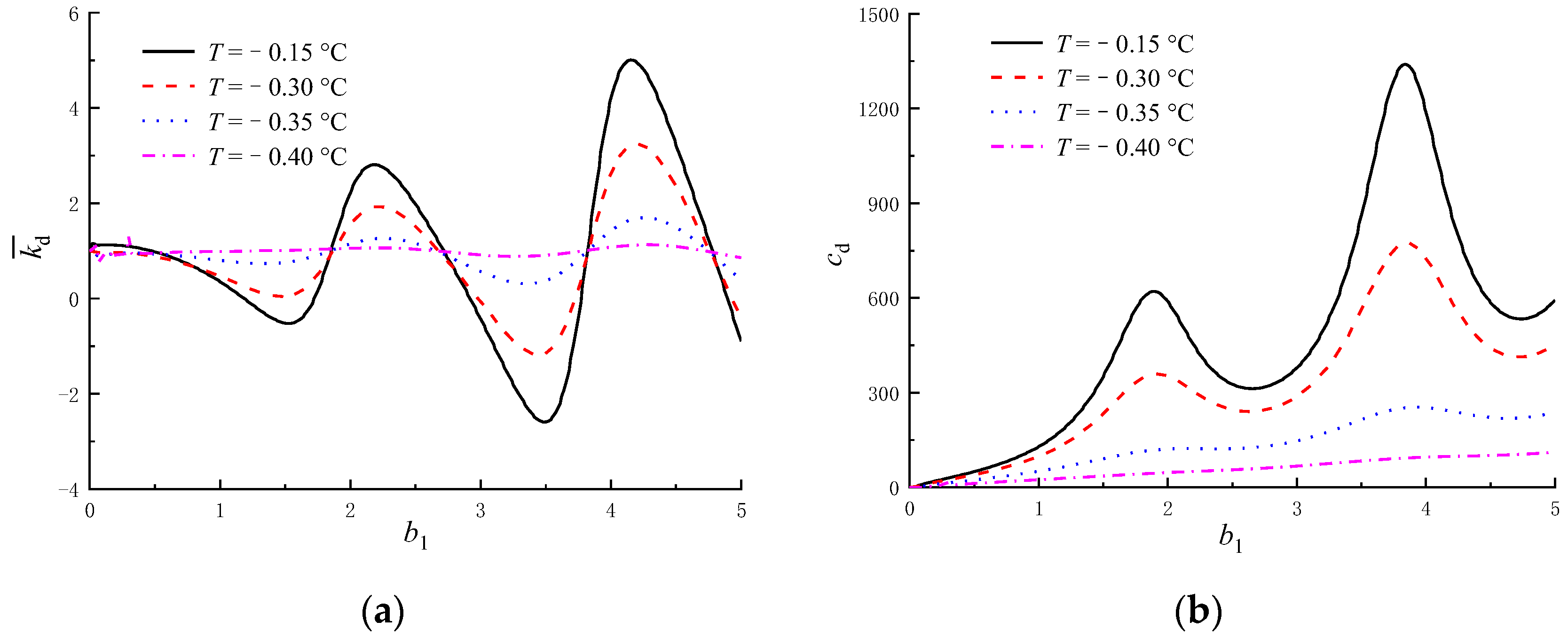
5.2. Influence of the Temperature

As the temperature decreased, the unfrozen water content of the soil decreased, and the ice content increased. Meanwhile, the influence of temperature on unfrozen water is closely related to other factors, such as the size of the soil particles, the size and distribution of pores, and the salt content of pore water. In this section, the influence of the temperature on the vibration response of a pile with a certain pore distribution was investigated. During the analysis, we only considered liquid phase damping, disregarding the damping of other materials. As shown in Figure 6, the resonance the amplitudes of the dynamic stiffness and damping decreased with the decrease in temperature. The reason for this phenomenon is that the damping caused by the relative motion of the water phase and the two solid phases also decreased with the decrease of the unfrozen water content. In other words, as the ice content increased, the relative amount of pile-surrounding soil decreased. Therefore, from the perspective of vibration, it is more advantageous that a pile is located in permafrost.

As shown in Figure 7, when the temperature was close to the freezing point, i.e., the soil condition was close to that of saturated unfrozen soil, the reflected signal with a big amplitude at the pile bottom usually appears first in the same direction as the head wave, followed by the reverse reflected signal. With the decrease in temperature, the amplitudes of the same-direction and reverse-direction reflected signals of the first reflected wave signal gradually decreased. When the temperature was −0.40 °C, the amplitudes of the signals were very small and almost difficult to capture. Therefore, the reduction of the temperature caused some difficulties in the identification of the reflected wave signal of the pile bottom.

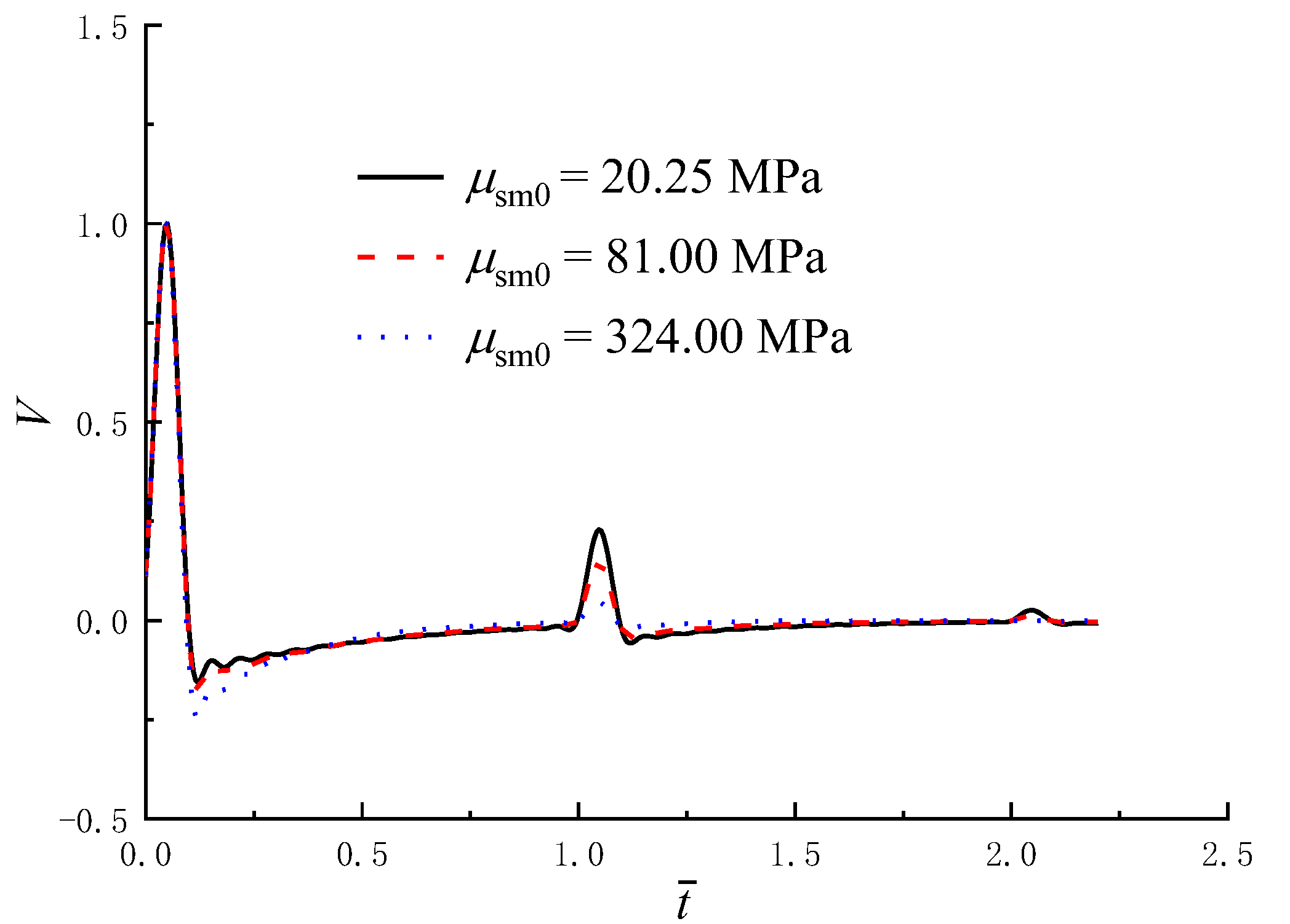
5.3. Influence of the Shear Modulus of the Pile-Surrounding Soil

In this section, the shear moduli of the frozen soil layer surrounding the pile and the lower elastic half-space are considered the same. As shown in Figure 8, the increase in the shear modulus of the pile-surrounding soil led to a decrease in the resonance amplitudes of dynamic stiffness and damping, but did not affect their resonance frequency. The reason for this phenomenon is similar to that reported in the analysis of the effect of the temperature. The larger the shear modulus of the pile-surrounding soil, the stronger the constraint on the pile, resulting in a reduction in the amplitudes of dynamic stiffness and damping.

As shown in Figure 9, the first reflected wave signals were in the same direction as that of the incident waves. The amplitude of the first reflected wave signal decreased as the shear modulus of the pile-surrounding soil increased, as a larger shear modulus of the pile-surrounding soil caused a stronger constraint on the pile.

6. Conclusions

In this paper, an analytical model for the vertical vibration of a non-end-bearing pile embedded in a frozen poroelastic half-space was established, and analytical solutions of the vertical dynamic response of the pile in the frequency and time domains were derived. The solutions can be reduced to those for the vertical vibration of an end-bearing pile in a frozen soil layer. The rationality of the present solutions was also verified by comparing them with the solutions for a pile in a saturated porous medium half–space modeled by the Biot’s theory. The conclusions can be summarized as follows:

(1)

The smaller the support stiffness of the pile bottom, the greater the amplitudes of dynamic stiffness and damping. When the support stiffness of the pile bottom is large enough, the results calculated by the present solutions are consistent with those for an end-bearing pile.

(2)

The lower the temperature, the smaller amplitudes of dynamic stiffness and damping. The amplitude of the first reflected wave signal also decreases with the decrease in the temperature.

(3)

The increase in the shear modulus of the pile-surrounding soil results in the decrease of dynamic stiffness and damping amplitudes. The amplitude of the first reflected wave signal also decreases with the increase of the shear modulus of the pile-surrounding soil.