Comparative Analysis for Slope Stability by Using Machine Learning Methods
Abstract
:Featured Application
Abstract
1. Introduction
- -
- They use hyperplane, nodes, and neurons, which act like a decision boundary between different classes;
- -
- Options and choices are set out logically at the same time, and costs are considered as well as potential benefits, which leads to calculating the capabilities and errors;
- -
- There is the possibility of measuring the amount of error and the accuracy of calculations depending on the complexity level of the analysis;
- -
- There is a reduction of calculation time and the possibility of using it in all stages of evaluation and stabilization;
- -
- They provide a higher level of accuracy in predicting outcomes, which automatically reduces the error rate;
- -
- They are easy to understand and provide tangible results.
2. Analysis Methods Principles
3. Methods and Materials
3.1. Analysis Method
3.2. Data Preparations
3.3. Model Implementations
3.4. Models Validations
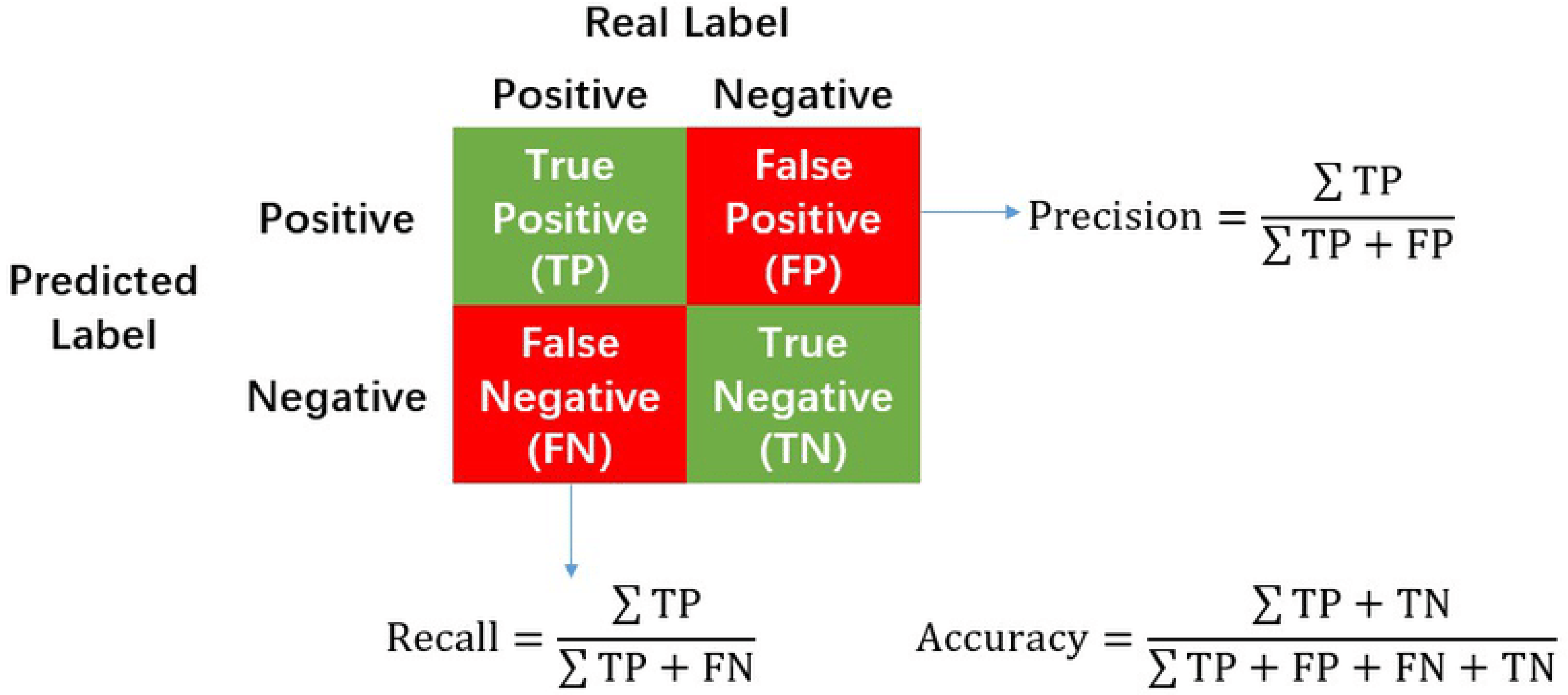
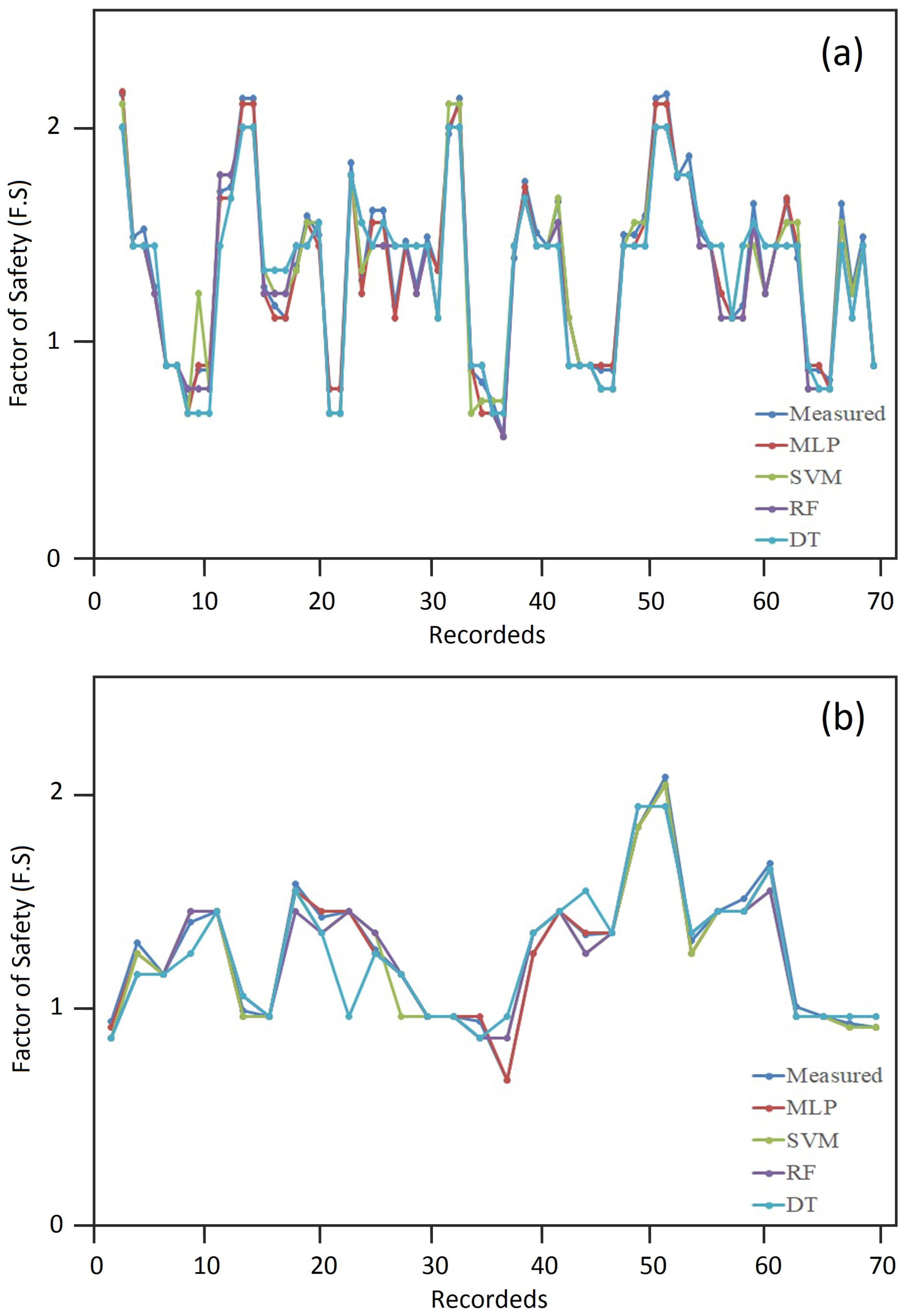
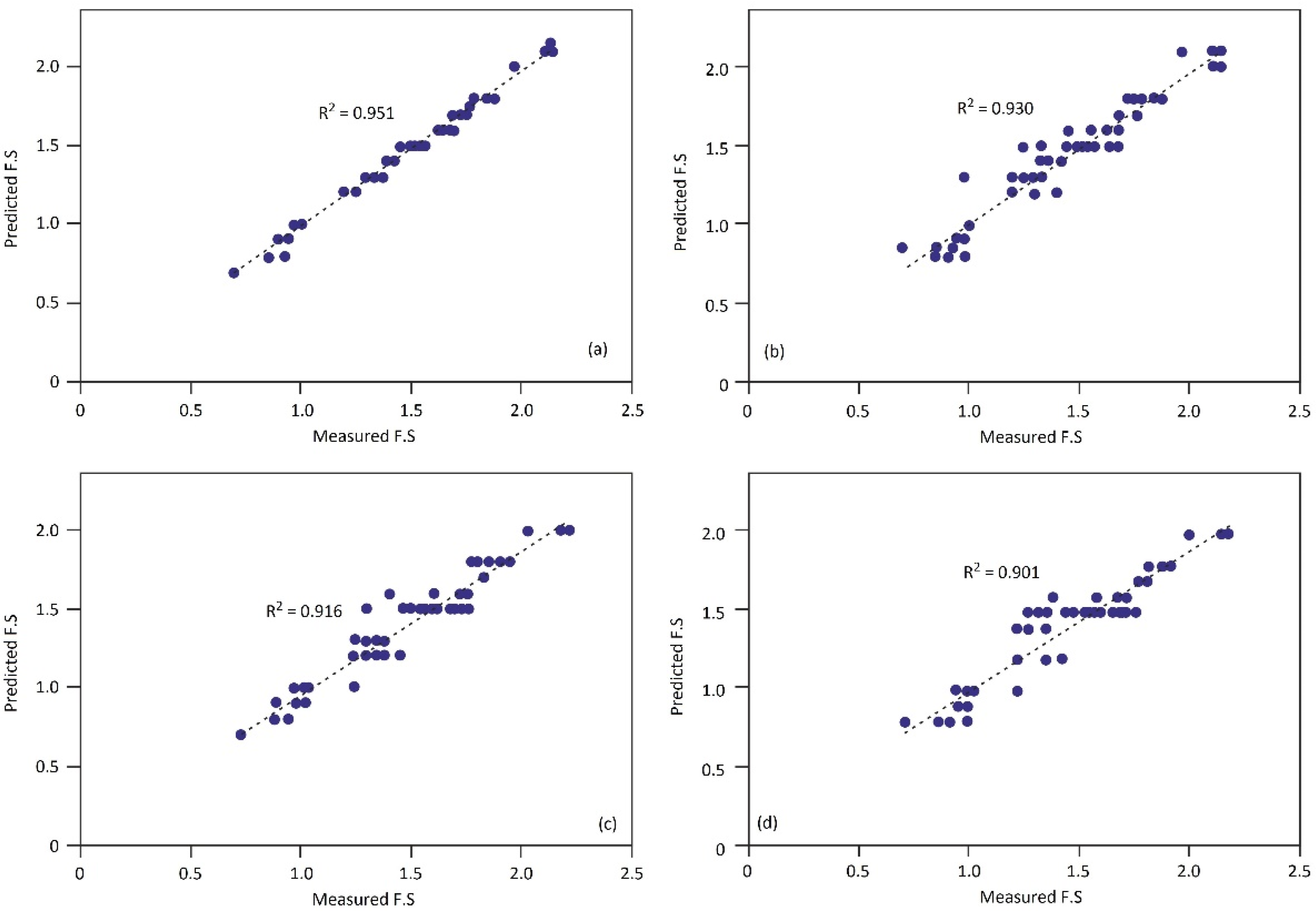
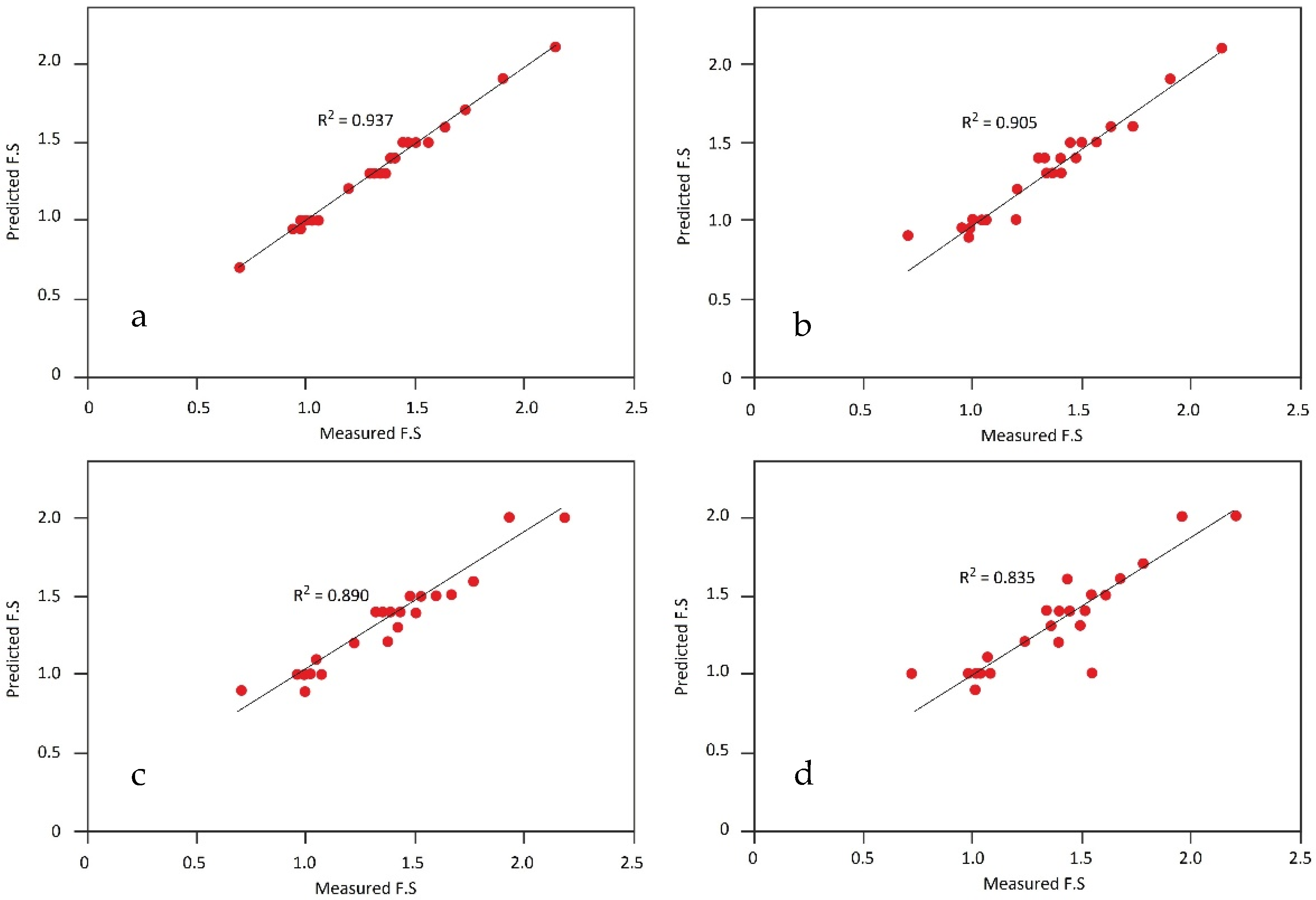
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Y.H. Slope Stability Analysis by the Limit Equilibrium Method; ASCE Publications: Reston, VA, USA, 2014. [Google Scholar]
- Bromhead, E. The Stability of Slopes; Spon Press: New York, NY, USA, 1992. [Google Scholar]
- Akgün, H.; Koçkar, M.K. Design of Anchorage and Assessment of the Stability of Openings in Silty, Sandy Limestone: A Case Study in Turkey. Int. J. Rock Mech. Min. Sci. 2004, 41, 37–49. [Google Scholar] [CrossRef]
- Abramson, L.W.; Lee, T.S.; Sharma, S.; Boyce, G.M. Slope Stability Concepts: Slope Stabilization and Stabilization Methods, 2nd ed.; Wiley-Interscience: Millburn, NJ, USA, 2001. [Google Scholar]
- Azarafza, M.; Hajialilue Bonab, M.; Derakhshani, R. A novel empirical classification method for weak rock slope stability analysis. Sci. Rep. 2022, 12, 14744. [Google Scholar] [PubMed]
- Azarafza, M.; Akgün, H.; Ghazifard, A.; Asghari-Kaljahi, E.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis by limit equilibrium approaches–a review. Int. J. Digital Earth 2021, 14, 1918–1941. [Google Scholar] [CrossRef]
- Bordoni, M.; Vivaldi, V.; Lucchelli, L.; Ciabatta, L.; Brocca, L.; Galve, J.P.; Meisina, C. Development of a data-driven model for spatial and temporal shallow landslide probability of occurrence at catchment scale. Landslides 2021, 18, 1209–1229. [Google Scholar]
- Rotigliano, E.; Martinello, C.; Hernandéz, M.A.; Agnesi, V.; Conoscenti, C. Predicting the landslides triggered by the 2009 96E/Ida tropical storms in the Ilopango caldera area (El Salvador, CA): Optimizing MARS-based model building and validation strategies. Environ. Earth Sci. 2019, 78, 210. [Google Scholar] [CrossRef]
- Kaur, A.; Sharma, R.K. Slope stability analysis techniques: A review. Int. J. Eng. Appl. Sci. Technol. 2016, 1, 52–57. [Google Scholar]
- Albataineh, N. Slope Stability Analysis Using 2D and 3D Methods; University of Akron: Akron, OH, USA, 2006. [Google Scholar]
- Azarafza, M.; Akgün, H.; Feizi-Derakhshi, M.-R.; Azarafza, M.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis under blocky structural sliding by fuzzy key-block analysis method. Heliyon 2020, 6, e03907. [Google Scholar]
- Chen, Z.; Mi, H.; Zhang, F.; Wang, X. A Simplified Method for 3D Slope Stability Analysis. Canadian Geotech. J. 2003, 40, 675–683. [Google Scholar] [CrossRef]
- Kliche, C.A. Rock Slope Stability, 2nd ed.; Society for Mining, Metallurgy, and Exploration Press: Englewood, NJ, USA, 2018. [Google Scholar]
- Fellenius, W. Calculation of the Stability of Earth Dams. In Proceedings of the 2nd Transaction Congress on Large Dams (ICOLD), Washington, DC, USA, 1936. [Google Scholar]
- Bishop, A.W. The use of Failure Circle in the Stability Analysis of Slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Nonveiller, E. The Stability Analysis of Slopes with a Slide Surface of General Shape. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965. [Google Scholar]
- Fredlund, D.D.; Krahn, J.; Pufahl, D.E. The relationship between limit equilibrium slope stability methods. In Proceedings of the International Conference on Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981. [Google Scholar]
- Janbu, N. Application of Composite Slip Surface for Stability Analysis. In Proceedings of the European Conference on Stability Analysis, Stockholm, Sweden, 1954. [Google Scholar]
- Janbu, N.; Bjerrum, L.; Kjaernsli, B. Soil Mechanics Applied to Some Engineering Problems; Norwegian Geotechnical Institute Publication: Oslo, Norway, 1956. [Google Scholar]
- US Army Corps of Engineers, USACE. Slope Stability: Engineering and Design; US Army Corps of Engineers Publications: Washington, DC, USA, 2003. [Google Scholar]
- Lowe, J.; Karafiath, L. Stability of Earth Dams Upon Drawdown. In Proceedings of the 1st Pan American Conference on Soil Mechanic and Foundation Engineering, São Paulo, Mexico, 1960. [Google Scholar]
- Sarma, S.K. Stability Analysis of Embankments and Slopes. Geotechnique 1973, 23, 423–433. [Google Scholar] [CrossRef]
- Spencer, E. A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar]
- Correia, R.M. A limit equilibrium method of slope stability analysis. In Proceedings of the 5th International Symposium on Landslides, Lausanne, Switzerland, 10–15 July 1988. [Google Scholar]
- Wyllie, D.C.; Duncan, C.; Mah, C. Rock Slope Engineerin, 4th ed.; Spon Press: London, UK, 2004. [Google Scholar]
- Zhu, D.Y.; Lee, C.F.; Jiang, H.D. Generalized Framework of Limit Equilibrium Methods for Slope Stability Analysis. Geotechnique 2003, 53, 377–395. [Google Scholar] [CrossRef]
- Ahangari Nanehkaran, Y.; Pusatli, T.; Chengyong, J.; Chen, J.; Cemiloglu, A.; Azarafza, M.; Derakhshani, R. Application of Machine Learning Techniques for the Estimation of the Safety Factor in Slope Stability Analysis. Water 2022, 14, 3743. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, X.L. Soil-slope stability considering effect of soil-strength nonlinearity. Int. J. Geomech. 2019, 19, 04018201. [Google Scholar] [CrossRef]
- Mathe, L.; Ferentinou, M. Rock slope stability analysis adopting Eurocode 7, a limit state design approach for an open pit. IOP Conf. Series: Earth Environ. Sci. 2021, 833, 012201. [Google Scholar]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media: Sebastopol, CA, USA, 2016. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Azarafza, M.; Hajialilue Bonab, M.; Derakhshani, R. A Deep Learning Method for the Prediction of the Index Mechanical Properties and Strength Parameters of Marlstone. Materials 2022, 15, 6899. [Google Scholar] [CrossRef]
- Vang-Mata, R. Multilayer Perceptrons: Theory and Applications; Nova Publications: Hauppauge, NY, USA, 2020. [Google Scholar]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: New York, NY, USA, 2015. [Google Scholar]
- Cortes, C.; Vapnik, V.N. Support-vector networks. Machine Learning 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sheppard, C. Tree-Based Machine Learning Algorithms: Decision Trees, Random Forests, and Boosting; Createspace Independent Publishing: Scotts Valley, CA, USA, 2017. [Google Scholar]
- Pavlov, Y.L. Random Forests; De Gruyter Press: Berlin, Germany, 2018. [Google Scholar]
- Ma, J.; Ding, Y.; Cheng, J.C.; Tan, Y.; Gan, V.J.; Zhang, J. Analyzing the leading causes of traffic fatalities using XGBoost and grid-based analysis: A city management perspective. IEEE Access 2019, 7, 148059–148072. [Google Scholar] [CrossRef]
- ASTM D2166; Standard Test Method for Unconfined Compressive Strength of Cohesive Soil. ASTM International: West Conshohocken, PA, USA, 2006.
- ASTM D3080; Standard Test Method for Direct Shear Test of Soils under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 2004.
- ASTM C830; Standard Test Methods for Apparent Porosity, Liquid Absorption, Apparent Specific Gravity, and Bulk Density of Refractory Shapes by Vacuum Pressure. ASTM International: West Conshohocken, PA, USA, 2016.
- Labuz, J.F.; Zang, A. Mohr–Coulomb failure criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar]
- Yang, X.L.; Yin, J.H. Slope stability analysis with non-linear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar]
- Barvor, Y.J.; Bacha, S.; Qingxiang, C.; Zhao, C.S.; Siddique, M. Surface mines composite slope deformation mechanisms and stress distribution. Min. Mineral Dep. 2020, 14, 1–16. [Google Scholar] [CrossRef]
- Sedina, S.; Altayeva, A.; Shamganova, L.; Abdykarimova, G. Rock mass management to ensure safe deposit development based on comprehensive research within the framework of the geomechanical model development. Min. Mineral Dep. 2022, 16, 103–109. [Google Scholar] [CrossRef]
- Barvor, Y.J.; Bacha, S.; Qingxiang, C.; Zhao, C.S.; Mohammad, N.; Jiskani, I.M.; Khan, N.M. Research on the coupling effect of the composite slope geometrical parameters. Min. Mineral Dep. 2021, 15, 35–46. [Google Scholar] [CrossRef]
| Classifier | Hyperparameters | Elements |
|---|---|---|
| MLP | Hidden layers’ size Learning rate Optimization | Activation = ’relu’; Optimization = rmsprop; Loss_function = ’mse’; Metrics = ’mae’ |
| SVM | Kernels C value | Kernel =‘poly’; Degree = 2 C = 100; Epsilon = 0.1 |
| DT | Max depth Random state | Criterion = ‘gini’; Max_depth = 5 Ccp_alpha = 0.0; Min_samples_leaf = 1 Random_state = 100 |
| RF | Number of estimators Max depth | Criterion = ‘entropy’; N_estimators = 10; Max_depth = 5; Min_samples_leaf = 1; Min_sanmples_split = 2 |
| Parameter | Unit | Max | Min | Mean | St.Dv. |
|---|---|---|---|---|---|
| Slope height (H) | m | 25 | 5.5 | 15.25 | 9.75 |
| Slope angle (β) | Degree | 73 | 30 | 51.5 | 21.25 |
| Slope topography * | - | Rough | Smooth | - | - |
| Water level in slope | m | 3 | 0 | 1.5 | 1.5 |
| Layers number | - | 1 | 1 | 1 | 0 |
| Tensile crack depth | m | 1.75 | 0.12 | 0.935 | 0.815 |
| Sliding surfaces depth ** | m | 27.4 | 1.3 | 14.35 | 13.05 |
| Parameter | Unit | Max | Min | Mean | St.Dv. |
|---|---|---|---|---|---|
| Water content | % | 37.2 | 5.44 | 21.32 | 22.457 |
| Specific gravity (Gs) | - | 2.63 | 2.60 | 2.61 | 0.0212 |
| γd | kN/m3 | 19 | 17 | 18 | 1.4142 |
| Slope height | m | 25 | 12 | 18.5 | 9.1923 |
| Slope angle | Degree | 72 | 40 | 56 | 22.627 |
| Cohesion (c) | kPa | 185 | 93 | 139 | 63.053 |
| Friction (φ) | Degree | 35 | 32 | 33.5 | 2.1213 |
| Poisson’s ratio (υ) | - | 0.35 | 0.33 | 0.034 | 0.0141 |
| No. | Slope Location | Gs | γd (kN/m3) | H (m) | β (o) | c (kPa) | φ (o) | F.S |
|---|---|---|---|---|---|---|---|---|
| 1 | Tehran | 2.62 | 18.22 | 12 | 45 | 124 | 35 | 1.65 |
| 2 | Fars | 2.63 | 18.71 | 10 | 60 | 117 | 33 | 1.57 |
| 3 | Fars | 2.60 | 18.20 | 7 | 63 | 93 | 33 | 0.98 |
| 4 | Isfahan | 2.60 | 18.20 | 15 | 52 | 117 | 35 | 1.54 |
| 5 | Tehran | 2.62 | 17.93 | 17 | 45 | 128 | 35 | 1.42 |
| 6 | Fars | 2.62 | 18.00 | 20 | 63 | 155 | 32 | 1.57 |
| 7 | Fars | 2.60 | 18.22 | 10 | 67 | 155 | 32 | 1.65 |
| 8 | Tehran | 2.60 | 18.70 | 15 | 40 | 142 | 33 | 1.25 |
| 9 | Tehran | 2.60 | 17.57 | 7 | 45 | 120 | 35 | 1.73 |
| 10 | Isfahan | 2.63 | 18.00 | 17 | 52 | 117 | 35 | 1.33 |
| Classifier | Dataset | Assessment Score | Accuracy | ||
|---|---|---|---|---|---|
| Precision | Recall | F1-Score | |||
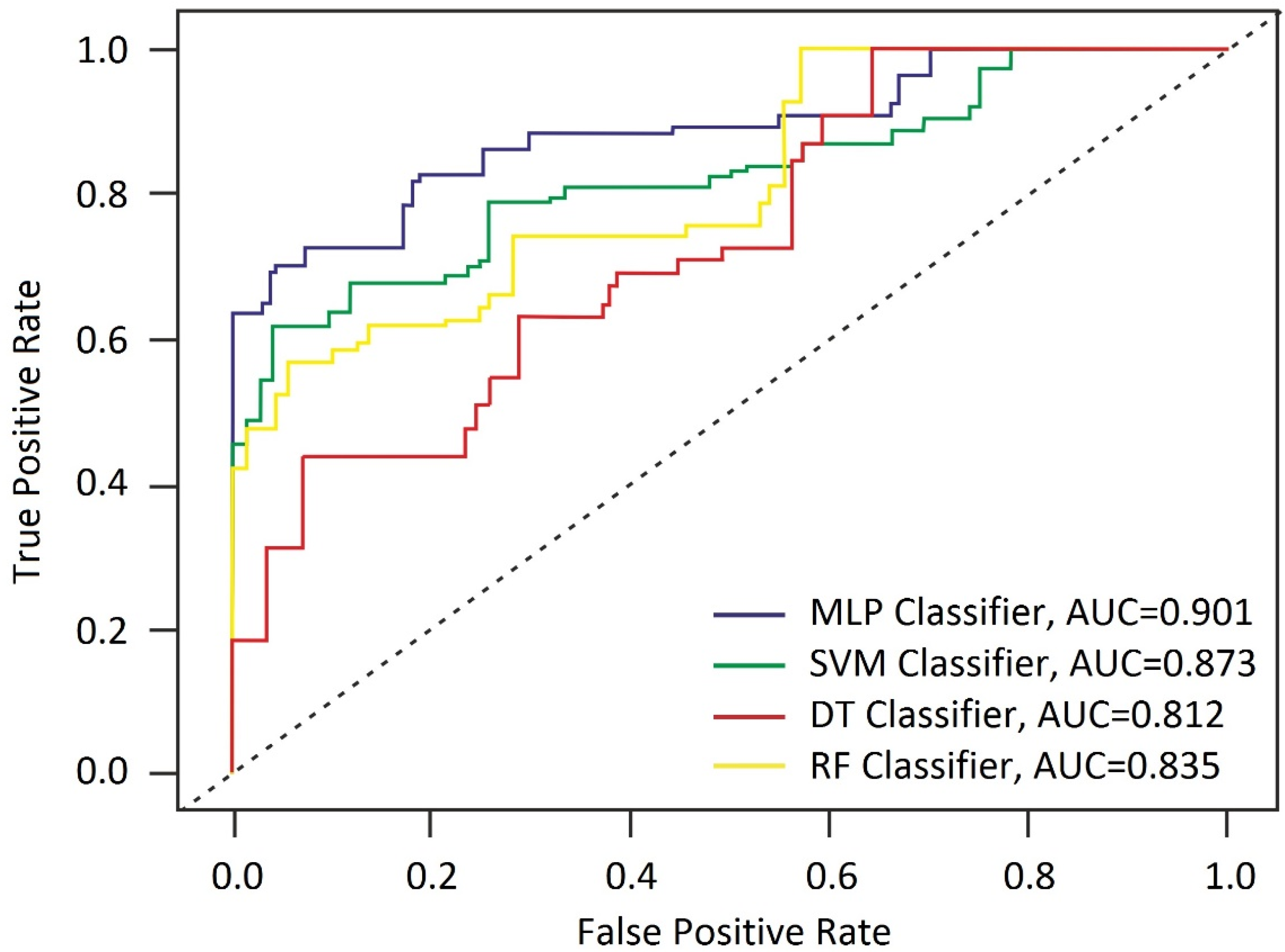
| MLP | Training | 0.90 | 0.90 | 0.91 | 0.901 |
| Testing | 0.91 | 0.85 | 0.91 | ||
| SVM | Training | 0.85 | 0.85 | 0.87 | 0.873 |
| Testing | 0.85 | 0.87 | 0.87 | ||
| DT | Training | 0.81 | 0.83 | 0.83 | 0.812 |
| Testing | 0.80 | 0.80 | 0.80 | ||
| RF | Training | 0.85 | 0.83 | 0.83 | 0.835 |
| Testing | 0.83 | 0.83 | 0.85 | ||
| Classifier | Maximum Loss | Minimum Loss | Mean Loss |
|---|---|---|---|
| MLP | 0.4873650 | 0.1104769 | 0.298921 |
| SVM | 0.5798631 | 0.2546394 | 0.417251 |
| DT | 0.7506439 | 0.4934867 | 0.622065 |
| RF | 0.6007535 | 0.3010182 | 0.450886 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nanehkaran, Y.A.; Licai, Z.; Chengyong, J.; Chen, J.; Anwar, S.; Azarafza, M.; Derakhshani, R. Comparative Analysis for Slope Stability by Using Machine Learning Methods. Appl. Sci. 2023, 13, 1555. https://doi.org/10.3390/app13031555
Nanehkaran YA, Licai Z, Chengyong J, Chen J, Anwar S, Azarafza M, Derakhshani R. Comparative Analysis for Slope Stability by Using Machine Learning Methods. Applied Sciences. 2023; 13(3):1555. https://doi.org/10.3390/app13031555
Chicago/Turabian StyleNanehkaran, Yaser A., Zhu Licai, Jin Chengyong, Junde Chen, Sheraz Anwar, Mohammad Azarafza, and Reza Derakhshani. 2023. "Comparative Analysis for Slope Stability by Using Machine Learning Methods" Applied Sciences 13, no. 3: 1555. https://doi.org/10.3390/app13031555
APA StyleNanehkaran, Y. A., Licai, Z., Chengyong, J., Chen, J., Anwar, S., Azarafza, M., & Derakhshani, R. (2023). Comparative Analysis for Slope Stability by Using Machine Learning Methods. Applied Sciences, 13(3), 1555. https://doi.org/10.3390/app13031555







