Multi-Layered and Homogenized Models for In-Plane Guided Wave Excitation, Sensing, and Scattering in Anisotropic Laminated Composites
Abstract
:1. Introduction
2. Mathematical Models
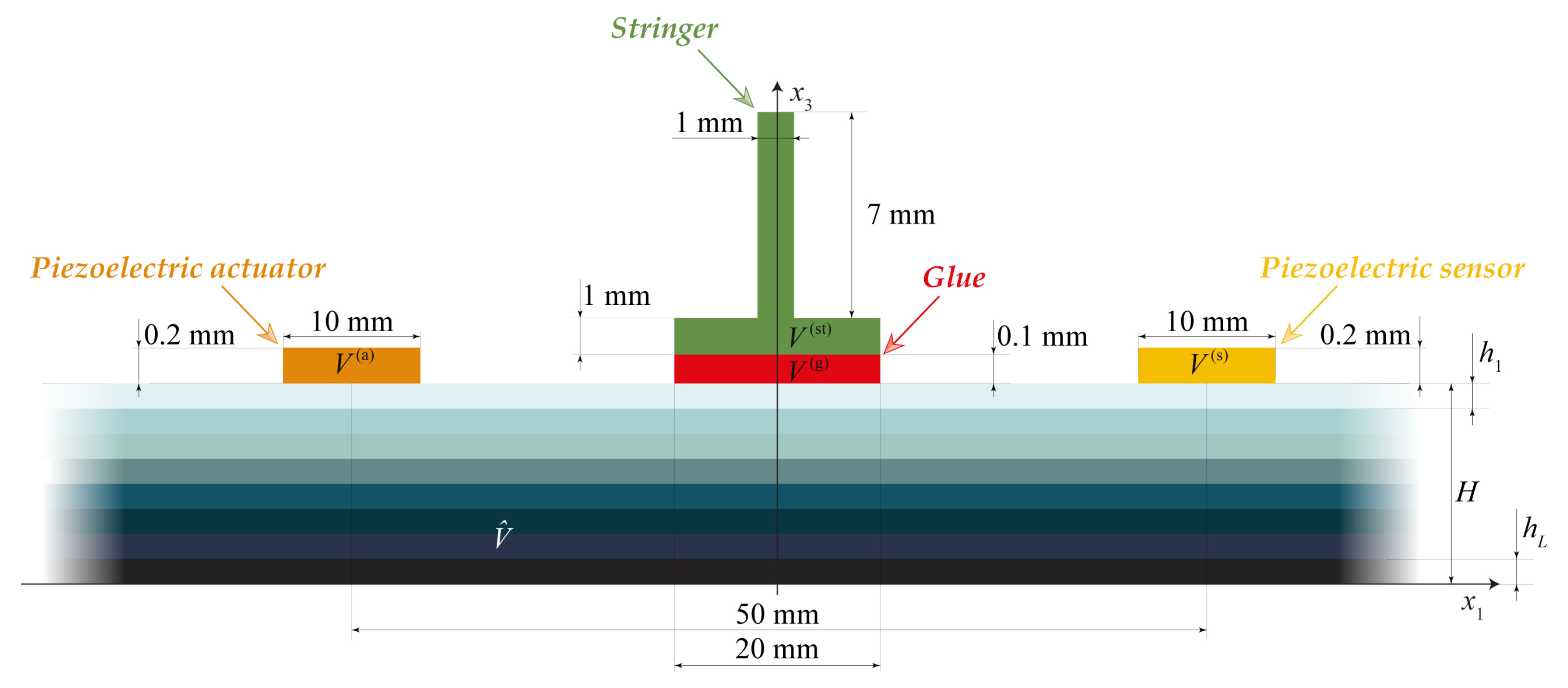
2.1. General Problem Statement
2.1.1. Multi-Layered Waveguide
2.1.2. Homogenized Waveguide
2.2. Guided Waves Excitation, Sensing, and Scattering
3. Comparison of the Models
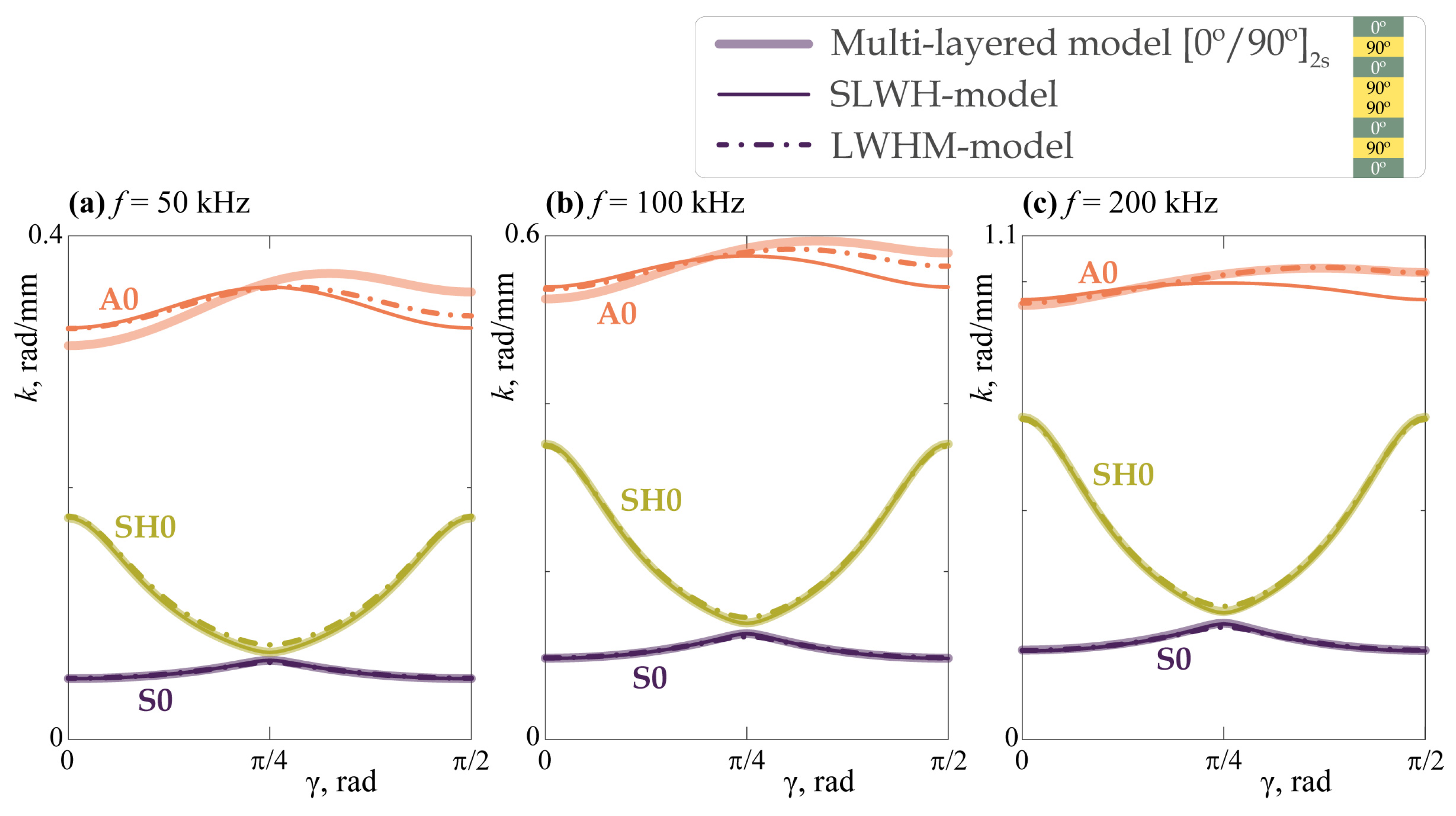
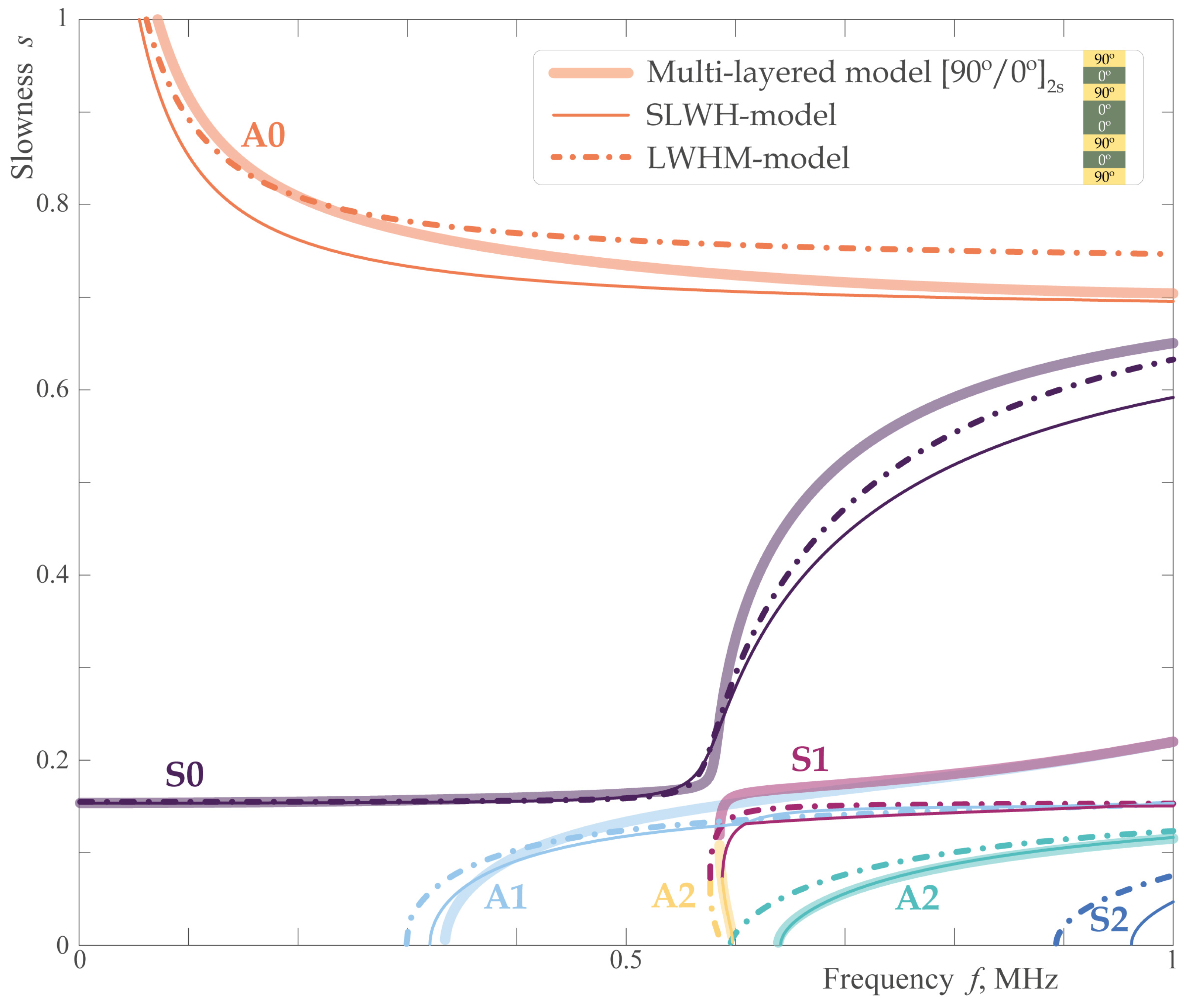
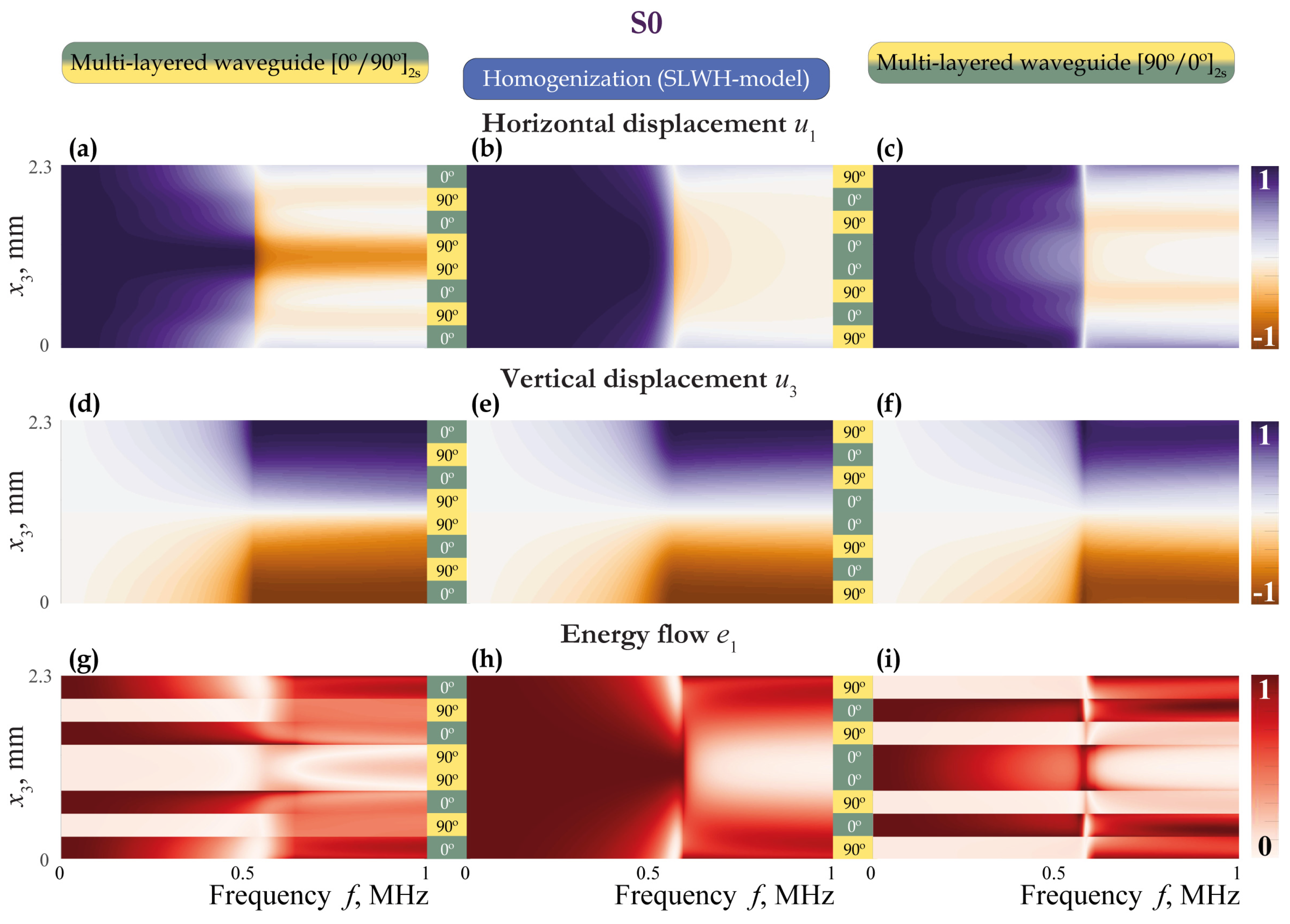
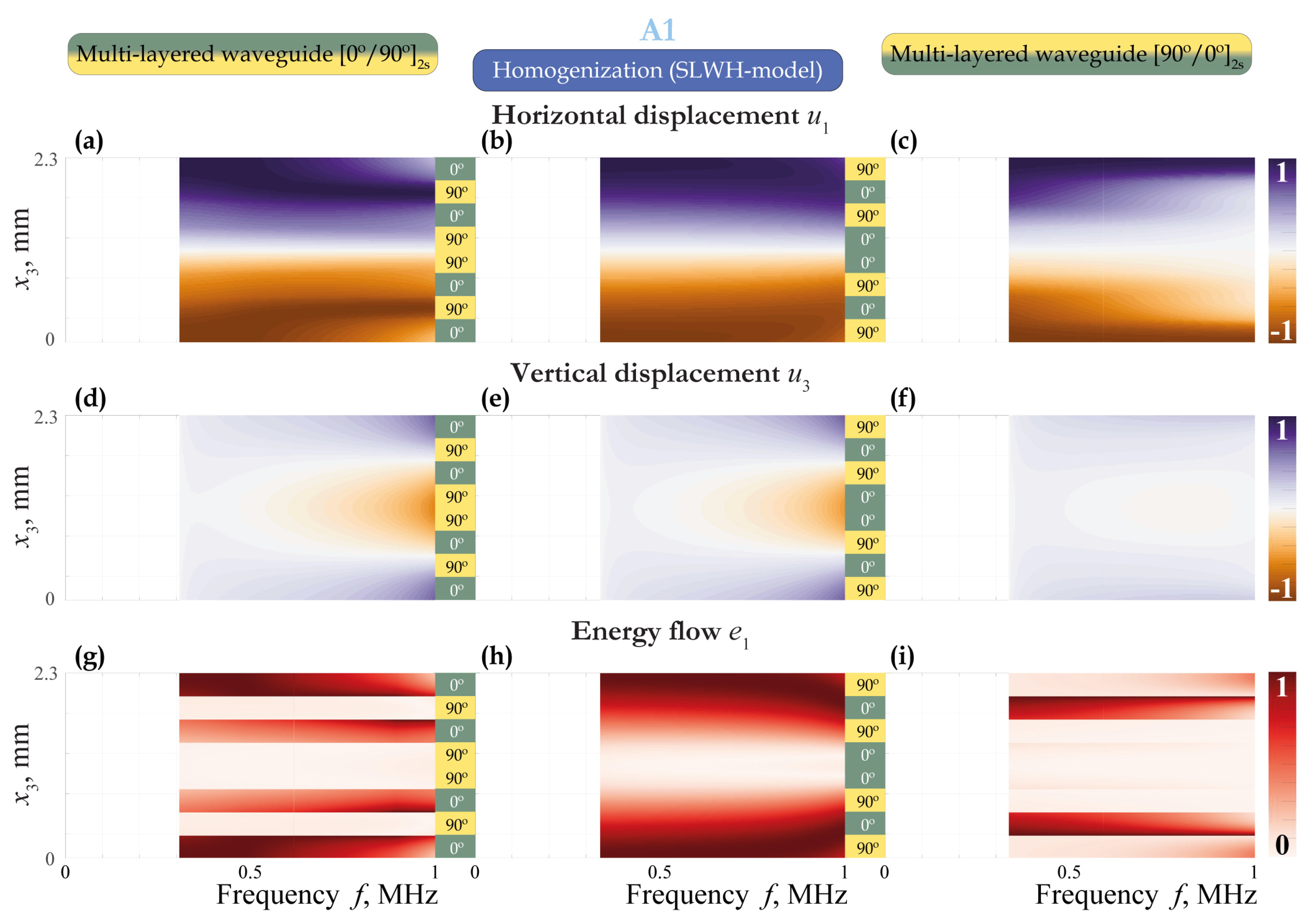
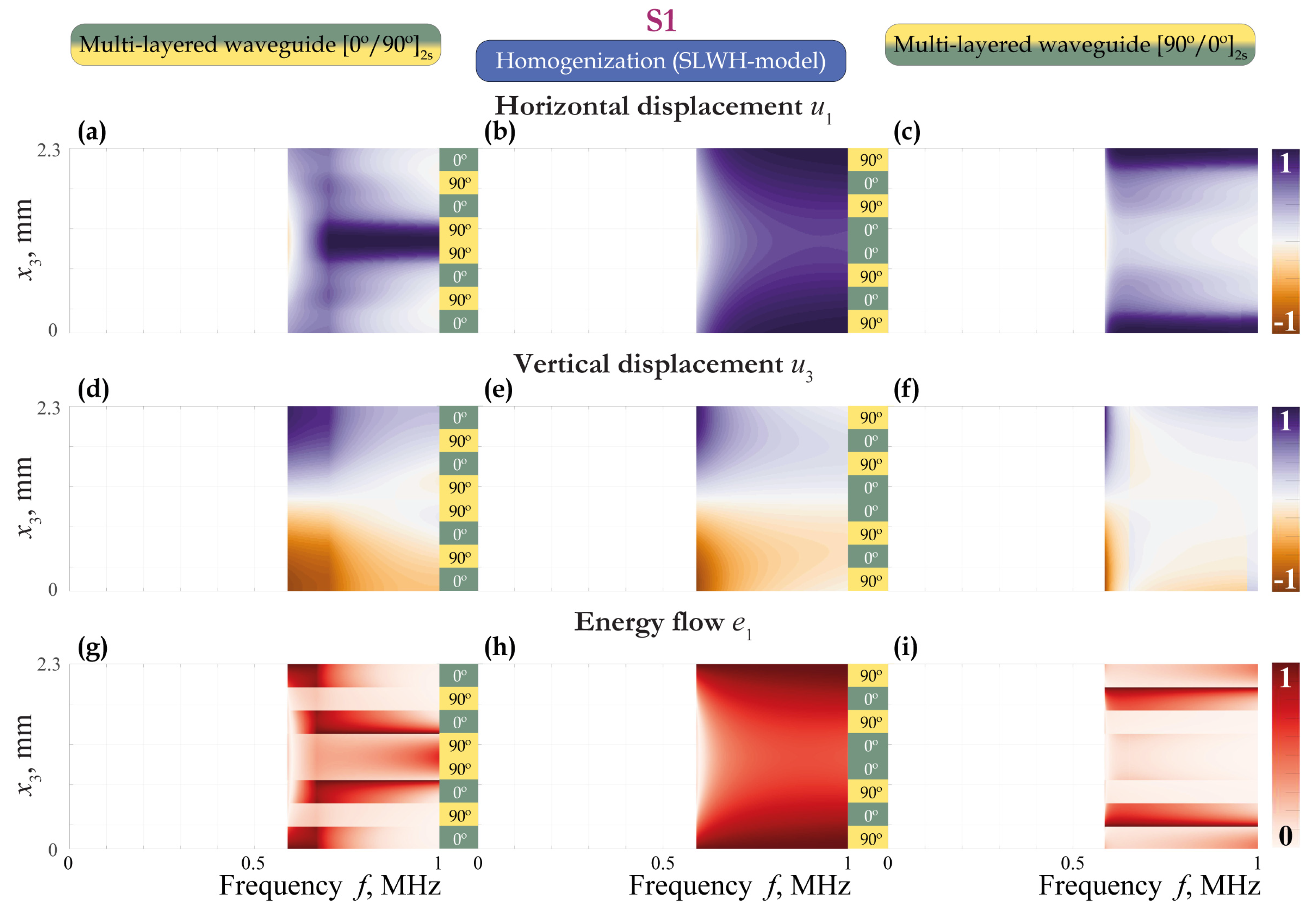
3.1. EGW Dispersion Characteristics
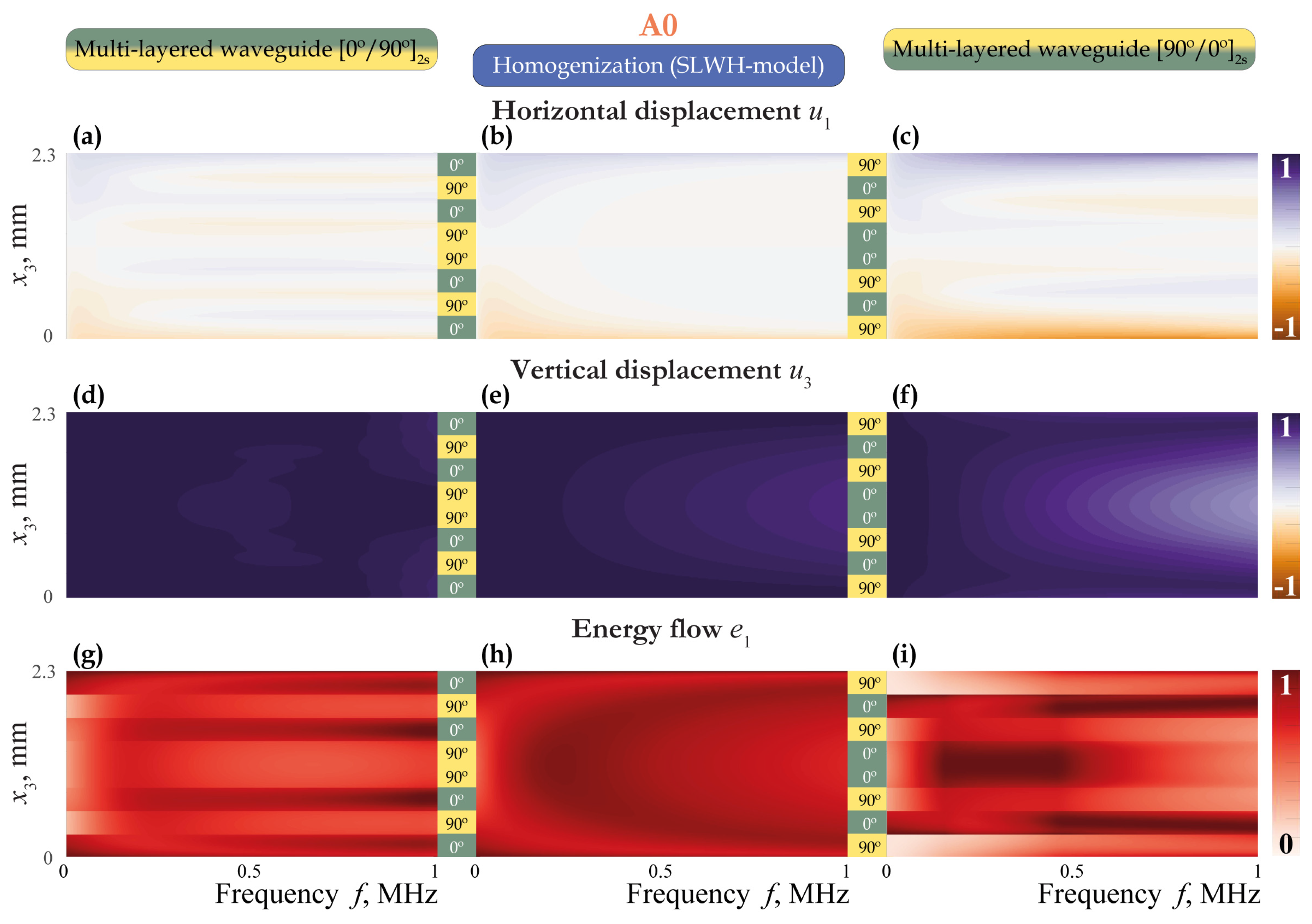
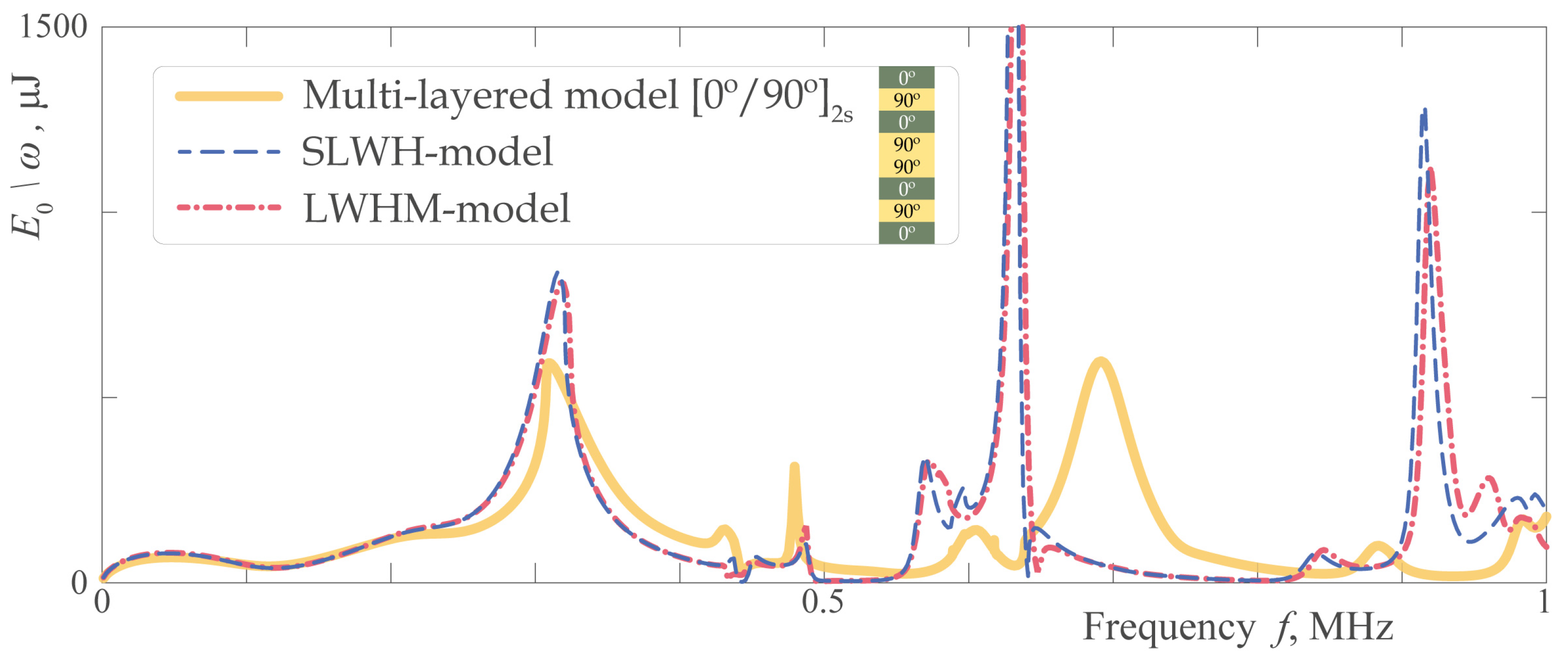
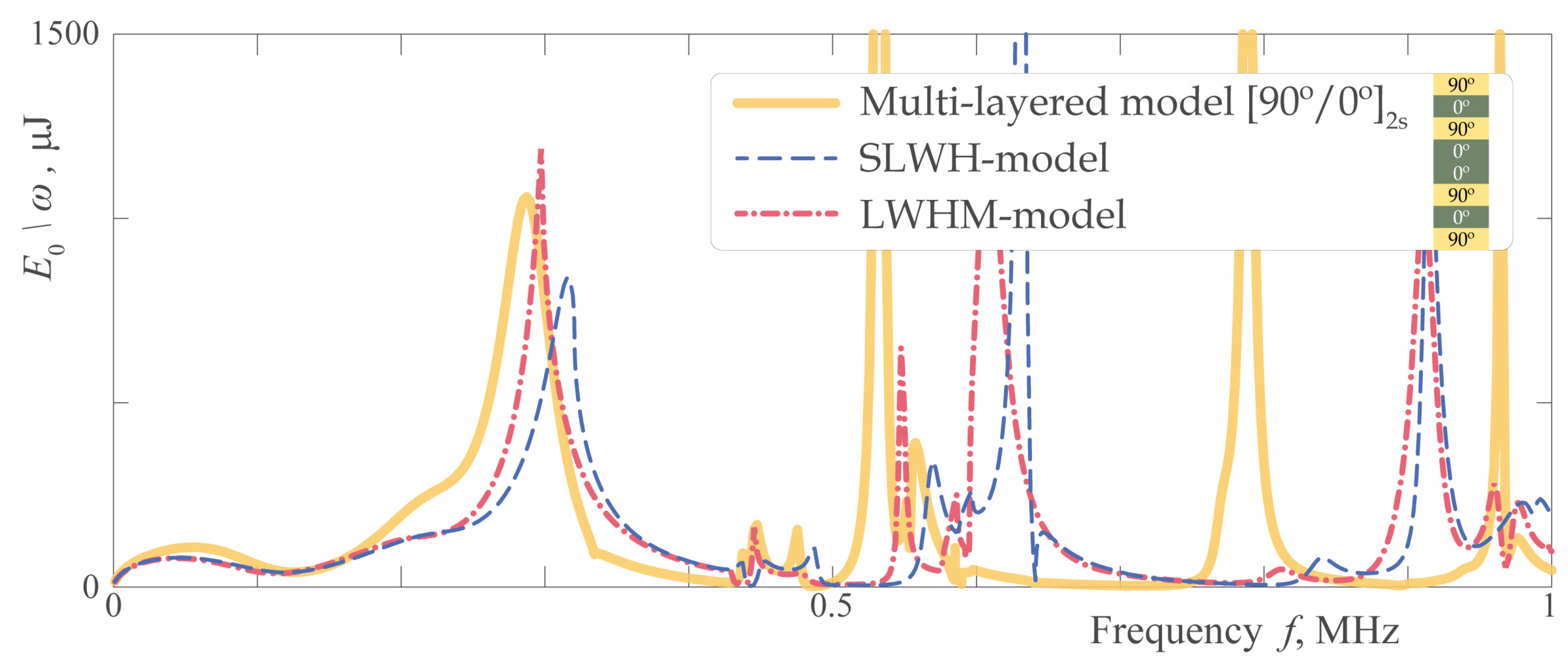
3.2. Excitation of EGWs
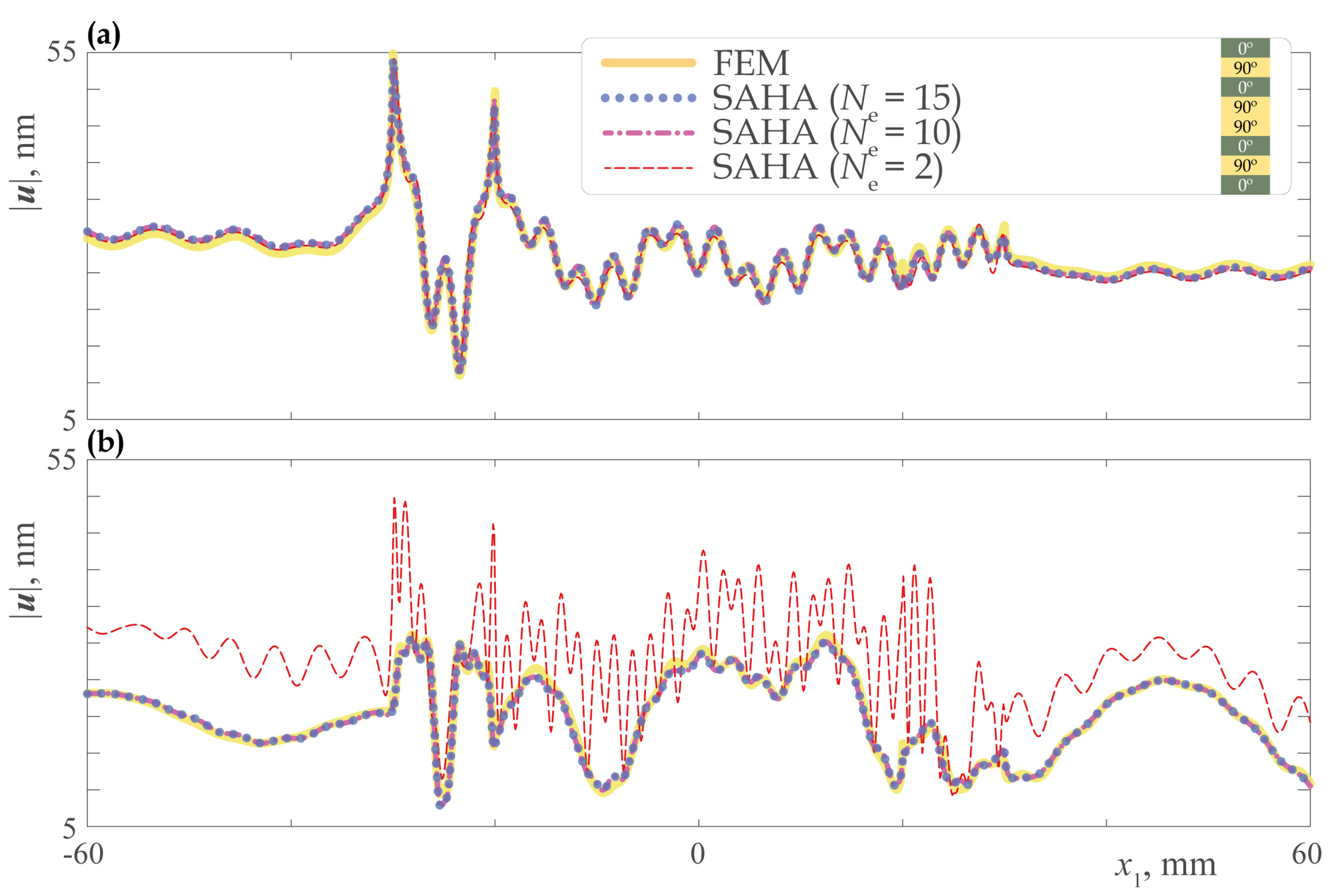
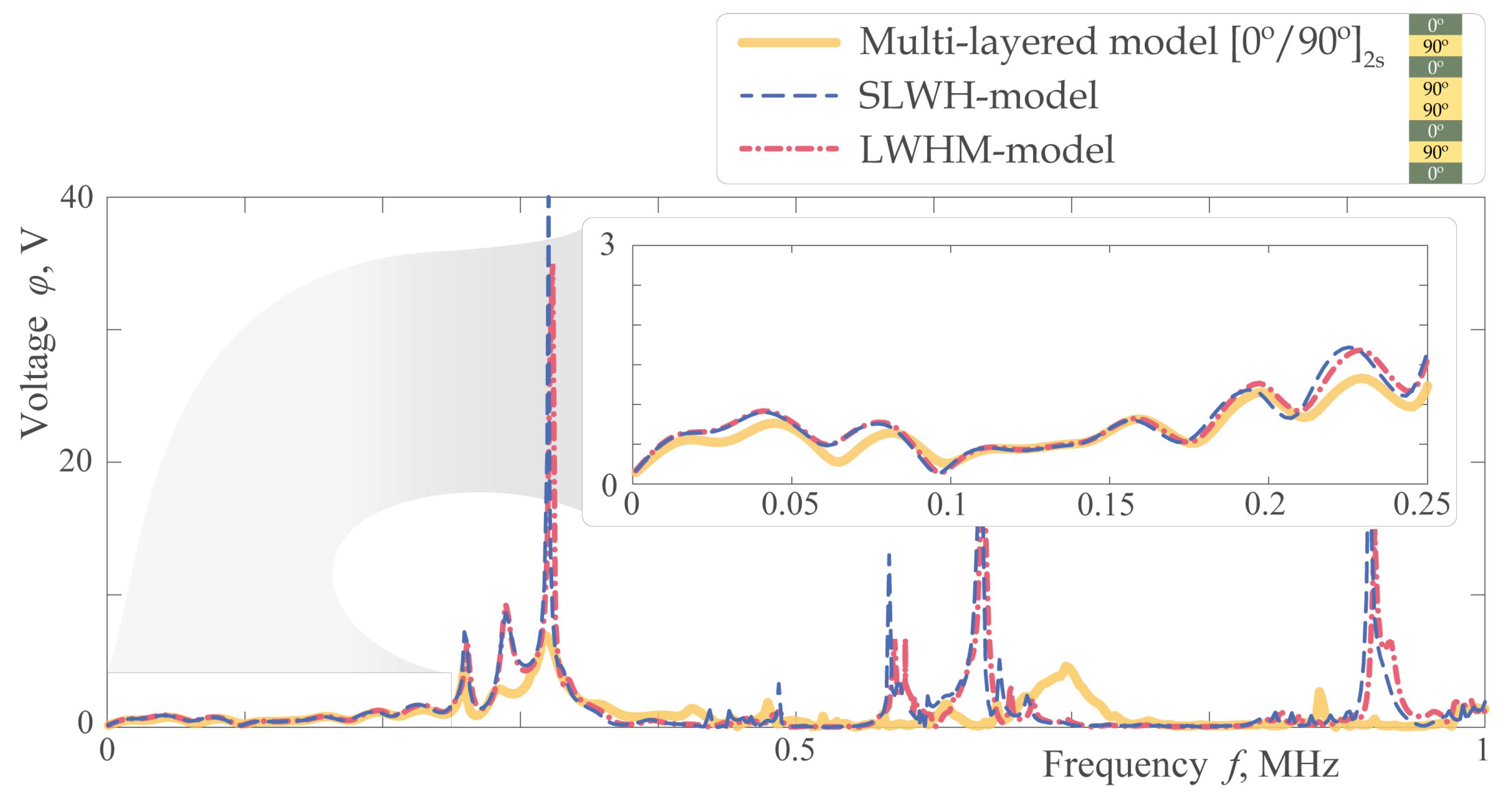
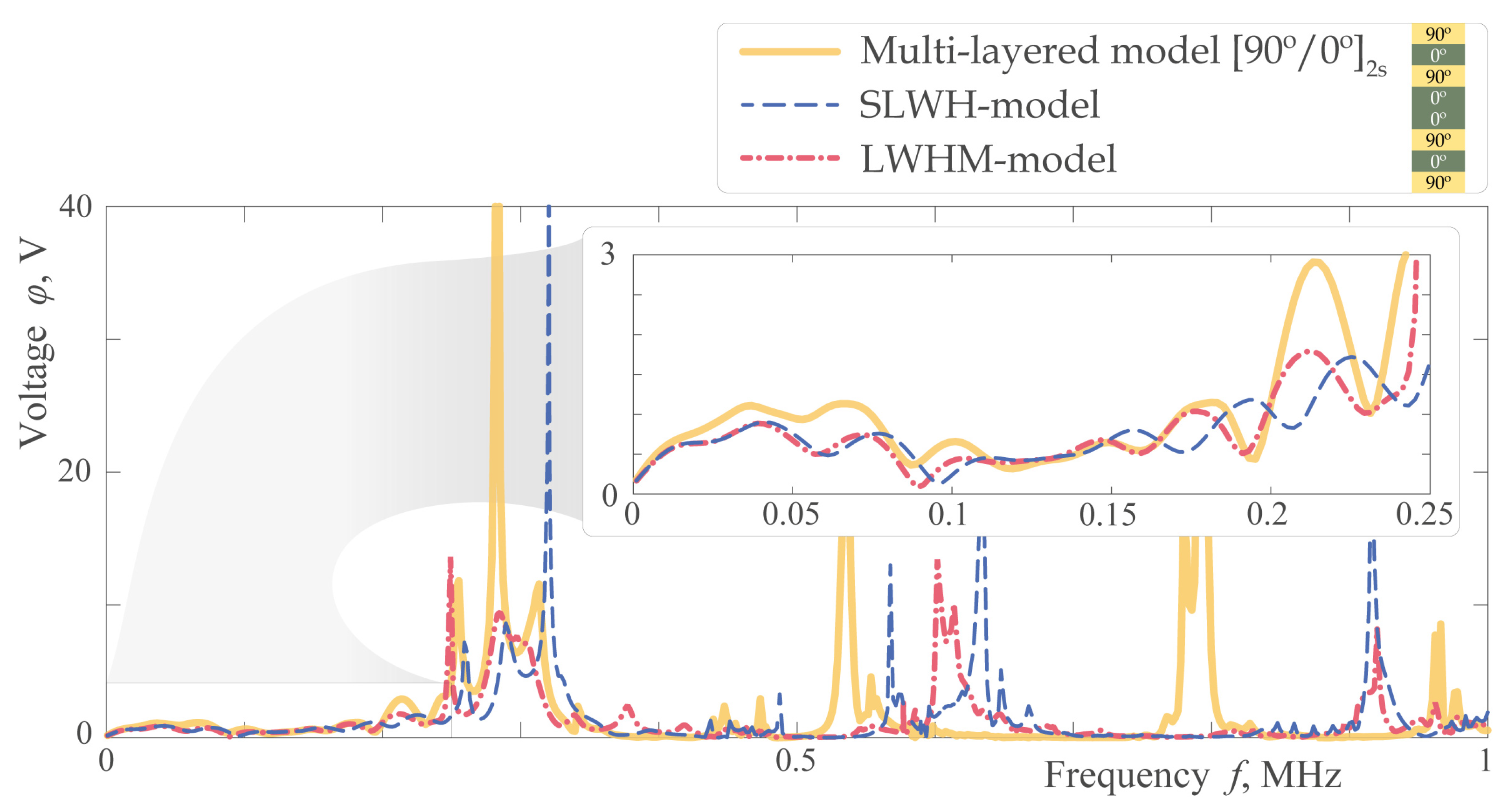
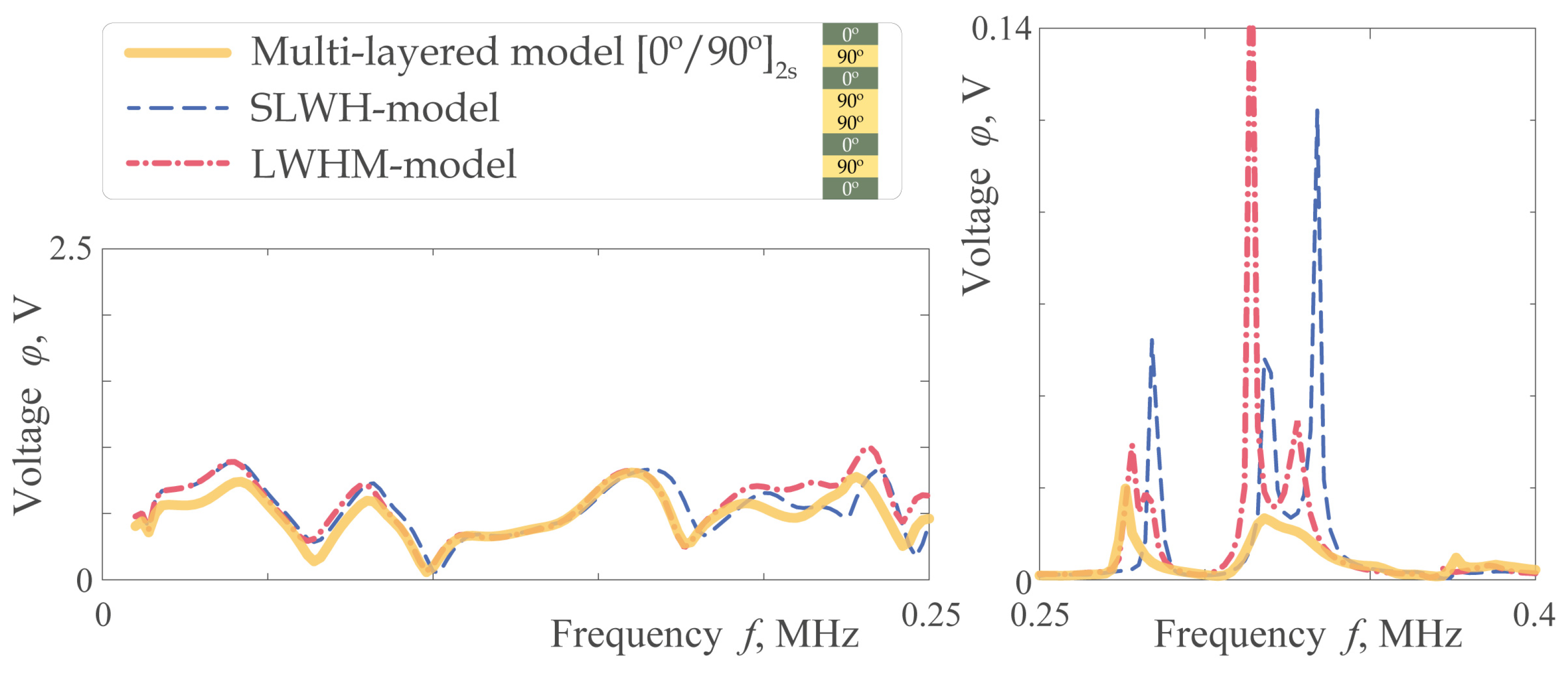
3.3. Sensing and Scattering of EGWs
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Irving, P.; Soutis, C. (Eds.) Polymer Composites in the Aerospace Industry; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Branner, K.; Petersen, H.N.; Beauson, J.; McGugan, M.; Sorensen, B.F. Materials for Wind Turbine Blades: An Overview. Materials 2017, 10, 1285. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Yu, R.; Sun, H.; Chen, Z. Lightweight multilayer composite structure for hydrogen storage tank. Int. J. Hydrogen Energy 2016, 41, 15812–15816. [Google Scholar] [CrossRef]
- Elsheikh, A. Bistable Morphing Composites for Energy-Harvesting Applications. Polymers 2022, 14, 1893. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Anand Raj, M.K.; Muthusamy, S.; Panchal, H.; Mahmoud Ibrahim, A.M.; Alsoufi, M.S.; Elsheikh, A.H. Investigation of mechanical properties of dual-fiber reinforcement in polymer composite. J. Mater. Res. Technol. 2022, 18, 3908–3915. [Google Scholar] [CrossRef]
- Wang, B.; Zhong, S.; Lee, T.L.; Fancey, K.S.; Mi, J. Non-destructive testing and evaluation of composite materials/structures: A state-of-the-art review. Adv. Mech. Eng. 2020, 12, 1687814020913761. [Google Scholar] [CrossRef] [Green Version]
- Güemes, A.; Fernandez-Lopez, A.; Pozo, A.R.; Sierra-Perez, J. Structural Health Monitoring for Advanced Composite Structures: A Review. J. Compos. Sci. 2020, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 53001. [Google Scholar] [CrossRef]
- Ricci, F.; Monaco, E.; Boffa, N.; Maio, L.; Memmolo, V. Guided waves for structural health monitoring in composites: A review and implementation strategies. Prog. Aerosp. Sci. 2022, 129, 100790. [Google Scholar] [CrossRef]
- Humeida, Y.; Pinfield, V.J.; Challis, R.E.; Wilcox, P.D.; Li, C. Simulation of ultrasonic array imaging of composite materials with defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 1935–1948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glushkov, E.; Glushkova, N.; Eremin, A.; Lammering, R.; Neumann, M. Frequency dependent directivity of guided waves excited by circular transducers in anisotropic composite plates. J. Acoust. Soc. Am. 2012, 132, EL119–EL124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, X.; Ratassepp, M.; Rajagopal, P.; Fan, Z. Anisotropic effects on ultrasonic guided waves propagation in composite bends. Ultrasonics 2016, 72, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Cesnik, C.E.S. Hybrid local FEM/global LISA modeling of damped guided wave propagation in complex composite structures. Smart Mater. Struct. 2016, 25, 95021. [Google Scholar] [CrossRef]
- Castaings, M.; Singh, D.; Viot, P. Sizing of impact damages in composite materials using ultrasonic guided waves. NDT E Int. 2012, 46, 22–31. [Google Scholar] [CrossRef]
- Liu, Y.; Hong, X.; Zhang, B. A novel velocity anisotropy probability imaging method using ultrasonic guided waves for composite plates. Measurement 2020, 166, 108087. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W. Impact induced damage assessment by means of Lamb wave image processing. Mech. Syst. Signal Process. 2018, 102, 23–36. [Google Scholar] [CrossRef]
- Yang, C.; Liang, K.; Zhang, X.; Geng, X. Sensor placement algorithm for structural health monitoring with redundancy elimination model based on sub-clustering strategy. Mech. Syst. Signal Process. 2019, 124, 369–387. [Google Scholar] [CrossRef]
- Mueller, I.; Memmolo, V.; Tschöke, K.; Moix-Bonet, M.; Möllenhoff, K.; Golub, M.V.; Venkat, R.S.; Lugovtsova, Y.; Eremin, A.A.; Moll, J. Performance Assessment for a Guided Wave-Based SHM System Applied to a Stiffened Composite Structure. Sensors 2022, 22, 7529. [Google Scholar] [CrossRef]
- Maio, L.; Fromme, P. On ultrasound propagation in composite laminates: Advances in numerical simulation. Prog. Aerosp. Sci. 2022, 129, 100791. [Google Scholar] [CrossRef]
- De Luca, A.; Perfetto, D.; De Fenza, A.; Petrone, G.; Caputo, F. Guided waves in a composite winglet structure: Numerical and experimental investigations. Compos. Struct. 2019, 210, 96–108. [Google Scholar] [CrossRef]
- Voß, M.; Ilse, D.; Hillger, W.; Vallee, T.; Eppmann, M.; de Wit, J.; von Dungern, F. Numerical simulation of the propagation of Lamb waves and their interaction with defects in C-FRP laminates for non-destructive testing. Adv. Compos. Mater. 2020, 29, 423–441. [Google Scholar] [CrossRef]
- Leckey, C.A.; Wheeler, K.R.; Hafiychuk, V.N.; Hafiychuk, H.; Timucin, D.A. Simulation of guided-wave ultrasound propagation in composite laminates: Benchmark comparisons of numerical codes and experiment. Ultrasonics 2018, 84, 187–200. [Google Scholar] [CrossRef] [PubMed]
- Kudela, P.; Moll, J.; Fiborek, P. Parallel spectral element method for guided wave based structural health monitoring. Smart Mater. Struct. 2020, 29, 95010. [Google Scholar] [CrossRef]
- Kudela, P.; Zak, A.; Krawczuk, M.; Ostachowicz, W. Modelling of wave propagation in composite plates using the time domain spectral element method. J. Sound Vib. 2007, 302, 728–745. [Google Scholar] [CrossRef]
- Willberg, C.; Duczek, S.; Vivar Perez, J.; Schmicker, D.; Gabbert, U. Comparison of different higher order finite element schemes for the simulation of Lamb waves. Comput. Methods Appl. Mech. Eng. 2012, 241–244, 246–261. [Google Scholar] [CrossRef]
- Maio, L.; Memmolo, V.; Ricci, F.; Boffa, N.; Monaco, E.; Pecora, R. Ultrasonic wave propagation in composite laminates by numerical simulation. Compos. Struct. 2015, 121, 64–74. [Google Scholar] [CrossRef]
- Nanda, N.; Kapuria, S.; Gopalakrishnan, S. Spectral finite element based on an efficient layerwise theory for wave propagation analysis of composite and sandwich beams. J. Sound Vib. 2014, 333, 3120–3137. [Google Scholar] [CrossRef]
- Orta, A.H.; Vandendriessche, J.; Kersemans, M.; Van Paepegem, W.; Roozen, N.B.; Van Den Abeele, K. Modeling lamb wave propagation in visco-elastic composite plates using a fifth-order plate theory. Ultrasonics 2021, 116, 106482. [Google Scholar] [CrossRef] [PubMed]
- Chou, P.; Carleone, J.; Hsu, C. Elastic Constants of Layered Media. J. Compos. Mater. 1972, 6, 80–93. [Google Scholar] [CrossRef]
- Sun, C.; Li, S. Three-Dimensional Effective Elastic Constants for Thick Laminates. J. Compos. Mater. 1988, 22, 629–639. [Google Scholar] [CrossRef]
- Whitcomb, J.; Noh, J. Concise Derivation of Formulas for 3D Sublaminate Homogenization. J. Compos. Mater. 2000, 34, 522–535. [Google Scholar] [CrossRef]
- Wang, L.; Rokhlin, S.I. Floquet wave homogenization of periodic anisotropic media. J. Acoust. Soc. Am. 2002, 112, 38–45. [Google Scholar] [CrossRef]
- Karunasena, W.; Shah, A.H.; Datta, S.K. Wave Propagation in a Multilayered Laminated Cross-Ply Composite Plate. J. Appl. Mech. 1991, 58, 1028–1032. [Google Scholar] [CrossRef]
- Datta, S.; Ju, T.H.; Bratton, R.; Shah, A. Transient response of a laminated composite plate: Results from homogenization and discretization. Int. J. Solids Struct. 1992, 29, 1711–1721. [Google Scholar] [CrossRef]
- Golub, M.V.; Shpak, A.N. Semi-analytical hybrid approach for the simulation of layered waveguide with a partially debonded piezoelectric structure. Appl. Math. Model. 2019, 65, 234–255. [Google Scholar] [CrossRef]
- Golub, M.V.; Eremin, A.A.; Shpak, A.N.; Lammering, R. Lamb wave scattering, conversion and resonances in an elastic layered waveguide with a surface-bonded rectangular block. Appl. Acoust. 2019, 155, 442–452. [Google Scholar] [CrossRef]
- Golub, M.V.; Shpak, A.N.; Mueller, I.; Fomenko, S.I.; Fritzen, C.P. Lamb wave scattering analysis for interface damage detection between a surface-mounted block and elastic plate. Sensors 2021, 21, 860. [Google Scholar] [CrossRef]
- Sveshnikov, A.G. The limit absorption principle for a waveguide. Dokl. Akad. Nauk. USSR 1951, 80, 345–347. [Google Scholar]
- Glushkov, E.V.; Glushkova, N.V. On the efficient implementation of the integral equation method in elastodynamics. J. Comput. Acoust. 2001, 9, 889–898. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A. Forced wave propagation and energy distribution in anisotropic laminate composites. J. Acoust. Soc. Am. 2011, 129, 2923–2934. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Wave Propagation in Layered Anisotropic Media with Applications to Composites; Elsevier Academic Press: Amsterdam, The Netherlands, 1995; p. 696. [Google Scholar]
- Lu, L.; Charron, E.; Glushkov, E.; Glushkova, N.; Bonello, B.; Julien, F.H.; Gogneau, N.; Tchernycheva, M.; Boyko, O. Probing elastic properties of nanowire-based structures. Appl. Phys. Lett. 2018, 113, 161903. [Google Scholar] [CrossRef] [Green Version]
- Golub, M.V.; Doroshenko, O.V.; Arsenov, M.; Bareiko, I.; Eremin, A.A. Identification of material properties of elastic plate using guided waves based on the matrix pencil method and laser Doppler vibrometry. Symmetry 2022, 14, 1077. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-genetic algorithms for stationary and non-stationary function optimization. In Intelligent Control and Adaptive Systems; Rodriguez, G., Ed.; International Society for Optics and Photonics: Philadelphia, PA, USA, 1990; Volume 1196, pp. 289–296. [Google Scholar] [CrossRef]
- Eremin, A.; Miakisheva, O.; Glushkov, E.; Glushkova, N.; Lammering, R. Advanced characterization of laminate fiber-reinforced composite materials with elastic guided waves and non-contact measurement techniques. In Advanced Materials: Techniques, Physics, Mechanics and Applications; Parinov, I.A., Chang, S.H., Jani, M.A., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 285–292. [Google Scholar] [CrossRef]
- Tiersten, H.F. Electromechanical coupling factors and fundamental material constants of thickness vibrating piezoelectric plates. Ultrasonics 1970, 8, 19–23. [Google Scholar] [CrossRef]
- Shi, L.; Liu, N.; Zhou, J.; Zhou, Y.; Wang, J.; Liu, Q. Spectral element method for band-structure calculations of 3D phononic crystals. J. Phys. Appl. Phys. 2016, 49, 605. [Google Scholar] [CrossRef]
- Xu, H.; Cantwell, C.D.; Monteserin, C.; Eskilsson, C.; Engsig-Karup, A.P.; Sherwin, S.J. Spectral/hp element methods: Recent developments, applications, and perspectives. J. Hydrodyn. 2018, 30, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Vatulyan, A.; Baranov, I. Determination of the crack configuration in an anisotropic elastic medium. Acoust. Phys. 2005, 51, 385–391. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, F. Group velocity and characteristic wave curves of Lamb waves in composites: Modeling and experiments. Compos. Sci. Technol. 2007, 67, 1370–1384. [Google Scholar] [CrossRef]



| Material | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| , ply | 122.4 | 11.5 | 11.5 | 4.13 | 4.13 | 6.47 | 2.51 | 4.85 | 4.85 |
| Model 1, SLWH | 67.0 | 67.0 | 11.5 | 4.13 | 5.30 | 5.30 | 3.31 | 3.31 | 4.85 |
| Model 2, LWHM | 64.8 | 64.8 | 11.1 | 7.99 | 3.63 | 3.90 | 2.85 | 3.39 | 4.92 |
| Material | ||||
|---|---|---|---|---|
| ply | 122.4 | 4.13 | 11.5 | 4.85 |
| ply | 11.5 | 6.47 | 11.5 | 2.51 |
| Model 1, plane | 67.0 | 5.30 | 11.5 | 3.31 |
| Model 1, plane | 67.0 | 5.30 | 11.5 | 3.31 |
| Model 2, plane | 64.8 | 3.63 | 11.1 | 3.39 |
| Model 2, plane | 64.8 | 3.90 | 11.1 | 2.85 |
| Material | Elastic Constants [GPa] | Piezoelectric Constants [C/m2] | Dielectric Constants [F/m] | Density [kg/m3] |
|---|---|---|---|---|
| Piezoeletric | 7800 | |||
| material | ||||
| PWTs | ||||
| (PIC 155) |
| Material | Young’s Modulus [GPa] | Poisson’s Ratio | Density [kg/m3] |
|---|---|---|---|
| Aluminum (stringer) | 70.0 | 0.33 | 2700 |
| Adhesive | 3.0 | 0.4 | 1248 |
| SAHA, (1 Core), s | FEM (COMSOL) (14 Cores), s | |
|---|---|---|
| f = 200 kHz | ||
| SLWH | 40 | 51 |
| Multi-layered | 182 | 161 |
| f = 400 kHz | ||
| SLWH | 37 | 51 |
| Multi-layered | 170 | 161 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eremin, A.A.; Golub, M.V.; Fomenko, S.I.; Evdokimov, A.A.; Nets, P.A. Multi-Layered and Homogenized Models for In-Plane Guided Wave Excitation, Sensing, and Scattering in Anisotropic Laminated Composites. Appl. Sci. 2023, 13, 1698. https://doi.org/10.3390/app13031698
Eremin AA, Golub MV, Fomenko SI, Evdokimov AA, Nets PA. Multi-Layered and Homogenized Models for In-Plane Guided Wave Excitation, Sensing, and Scattering in Anisotropic Laminated Composites. Applied Sciences. 2023; 13(3):1698. https://doi.org/10.3390/app13031698
Chicago/Turabian StyleEremin, Artem A., Mikhail V. Golub, Sergey I. Fomenko, Alexander A. Evdokimov, and Polina A. Nets. 2023. "Multi-Layered and Homogenized Models for In-Plane Guided Wave Excitation, Sensing, and Scattering in Anisotropic Laminated Composites" Applied Sciences 13, no. 3: 1698. https://doi.org/10.3390/app13031698
APA StyleEremin, A. A., Golub, M. V., Fomenko, S. I., Evdokimov, A. A., & Nets, P. A. (2023). Multi-Layered and Homogenized Models for In-Plane Guided Wave Excitation, Sensing, and Scattering in Anisotropic Laminated Composites. Applied Sciences, 13(3), 1698. https://doi.org/10.3390/app13031698







