1. Introduction
Solitary waves—physical waves that maintain their shape and move with a constant velocity due to a cancellation of nonlinear effects and dispersive processes in the medium [
1]—have been a long-term subject of fundamental and applied research studies in the fields of optics [
2], fluid dynamics [
3], magnetism [
4], acoustics [
5], electronics [
6], and biology [
7,
8]. However, despite a good understanding of the physical properties of solitary waves of different kinds, their experimental studies often involve expensive and difficult-to-operate equipment, such as intense laser beams and nonlinear-optical materials in the field of optics [
2] and sources of high-power microwave radiation in the field of magnetism [
4]. Yet, in some systems, such as biological nerve fibres [
7,
8], the observation of solitary-like waves requires significant preparatory works and is possible mostly when a number of specific experimental conditions are satisfied. Such technical challenges complicate both fundamental studies and the verification of numerous theoretical works predicting that solitary waves could be used in communication [
9,
10], sensing [
11], and data-processing [
12] devices and systems.
There also exists a class of material solitary-like surface waves that originate from spatio-temporal evolution of falling liquid films [
13,
14]. Since the equipment needed to create falling liquid films is, in general, simpler than that used in experiments in the fields of optics and magnetism, the waves of this kind have attracted the attention of many scientists [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28] following the pioneering experiments conducted by the Kapitzas [
29]. In fact, while such solitary-like surface waves share many physical features with the other known types of solitary waves, they can exhibit unique physical properties not observed in other systems [
24,
30,
31]. For instance, they can merge instead of passing through each other without significant change, with the latter being the case of two solitary waves governed by the well-known KdV equation [
3,
32]. The analysis of solitary-like surface waves in flowing liquid films is also important because liquid films, as well as similar physical systems [
33,
34,
35], are often encountered in the fields of earth and planetary sciences [
36,
37] and in technological processes [
38], where the liquids of interest can also experience temperature gradients [
14,
28] and vibrations [
39,
40,
41]. Given this, the effect of vibrations on the wave dynamics of film flows has become an independent subject of fundamental and applied research [
42,
43,
44,
45,
46]. In particular, it has been shown that vibrations can suppress certain waves on the surface of flowing liquid films [
42] but in a relevant experiment [
47] it has been demonstrated that vibrations can promote unusual regimes of spontaneous drop movement. Speaking broadly, the study of the effect of vibrations should also help develop communication, sensing and data processing systems that are immune to undesirable mechanical impacts on devices that use liquids as a medium and provide the critical functionality (see, e.g., [
48,
49,
50]).
Although, traditionally, greater attention has been paid to the wave dynamics on free-falling vertical liquid films [
13,
14], studies of surface waves on liquid films flowing over slightly inclined planes have also been conducted, given them having essentially the same physics as in the case of vertical systems [
24,
42]. However, reports on experimental results involving the effect of vibrations are rather scarce and scattered in the literature sources [
39,
40,
45]. In particular, in [
39] it was shown that the vibration of a horizontal tube with a liquid thin film flowing over it results in the appearance of ripple waves at the vibration frequency. The amplitude of the so-created waves depends on the vibration amplitude and can reach the amplitude of periodic waves existing on the film surface without vibration. Subsequently, high-amplitude vibrations result in an increase in the film thickness and a concomitant increase in the speed of the waves. However, the opposite conclusions were drawn in [
40], which is, most likely, a result of the differences in the system (a liquid film under two-phase flow conditions) investigated in that paper. It is also well-known that in horizontal liquid layers a harmonic vibration excites two different types of standing surface waves: harmonic waves that oscillate at the vibration frequency and subharmonic waves that oscillate at half of the vibration frequency [
51]. However, the presence of a mean flow across the layer changes the response frequency of the excited waves [
42,
43,
44]. Surface waves excited by harmonic vibration in a liquid film flowing over a vertical plane were investigated experimentally in [
45] and the results obtained in that work validated the linear theory developed in [
42,
43,
44].
Thus, the experimental work [
45] mostly represents an attempt to systematically study the physics of wave motion on a vibrated plane. However, in general, building a setup involving liquids flowing down a vibrated vertical surface requires non-standard equipment built according to demanding technical specifications. In particular, the liquid should be supplied to the inlet located at the upper part of the plane so that the flow rate is not affected by the vibration. This is because the thickness of the liquid film is known to be very sensitive to external disturbances, including vibrations caused by the pump used to deliver the liquid from a reservoir to the inlet [
22]. Moreover, the shaker producing the vibration should be connected to the vertically positioned surface via a vibration transmission structure. Some of the engineering challenges of creating such a structure are the need to move a considerable total mass of the supporting structure and liquid with high precision, and to ensure that the amplitude of the vibration across the plane area is uniform [
45]. To resolve the problem of non-uniform vibration amplitude, in [
45] it is was suggested that qualitatively similar results could be obtained vibrating just one side of the plane, i.e., vibrating just a portion of the liquid, thus also significantly reducing the total mass that needs to be moved by the shaker.
In this paper, we present and discuss a technically simple and compact experimental setup for the investigation of solitary-like surface waves on a slightly inclined plane positioned on top of a vibrating table and equipped with an auxiliary channel that recycles the liquid used in the experiment, thus decreasing the chance of spills of the liquid and its unwanted contact with the measurement and imaging equipment, and also decreasing the total mass that needs to be moved by the shaker. We employ this setup to demonstrate that the instabilities of the thin liquid film caused by the vibrations result in a decrease in the peak amplitude of the solitary-like surface waves. We conclude that, despite these changes, the speed of the solitary-like waves does not appreciably change due to vibration. As a result, these waves can propagate for long distances without changing their shape and, therefore, can be used in the practical applications discussed in this work. We also demonstrate the advantage of using frequency-wavevector dispersion maps for the analysis of the properties of rolling waves, thus extending the toolbox of researchers working on this class of wave motion phenomena. Our experimental results are validated using the Shkadov model [
52,
53]: a boundary-layer hydrodynamic model derived from the Navier–Stokes equation under the assumption of self-similar parabolic longitudinal velocity flow field across the layer.
2. Background and Experimental Methods
When a single-layer liquid film flows down an inclined plane with a no-slip boundary, the resulting Nusselt flat film flow profile assumes a parabolic longitudinal velocity shape, having the largest velocity at the free surface [
13,
14,
24]. In this flow regime, a long-wavelength surface instability develops when the average flow rate exceeds a certain critical value [
15]. When the disturbances are excited naturally, in general four regimes of different wave behaviour can be observed in the downstream regions of the inclined plane [
13]. The first regime is observed in a section of the plane that is adjacent to the inlet of the liquid, where small disturbances caused by the inlet structure are amplified while moving downstream and forming predominantly monochromatic waves. The second regime is observed in the following downstream region, where the monochromatic waves grow in amplitude and then develop higher-order frequency harmonics due to nonlinear effects. Then, as a result of complex nonlinear interactions, two-dimensional solitary-like waves are formed, and then they propagate further downstream exhibiting unique properties that, in part, coincide with those of other known solitary waves but, in general, are unique [
24]. Finally, three-dimensional waves start to form due to transverse variations [
13,
14].
It is noteworthy that not all aforementioned regimes can necessarily be observed in practice [
13]. Yet, it is well-known that when the initial natural disturbance at the inlet is nearly monochromatic, the waves emerging in the region located immediately after the inlet can first inherit the frequency of the disturbance and then evolve into a solitary-like wave far downstream [
13,
14,
24]. However, when either the thickness of the liquid film or the fluid flow is periodically modulated at the inlet, solitary-like surface waves develop almost immediately after leaving the inlet area [
14,
24], which indicates that the nonlinear evolution of the flow over an inclined plane is dominated by solitary-like waves independently of whether their formation was deliberately forced or resulted naturally.
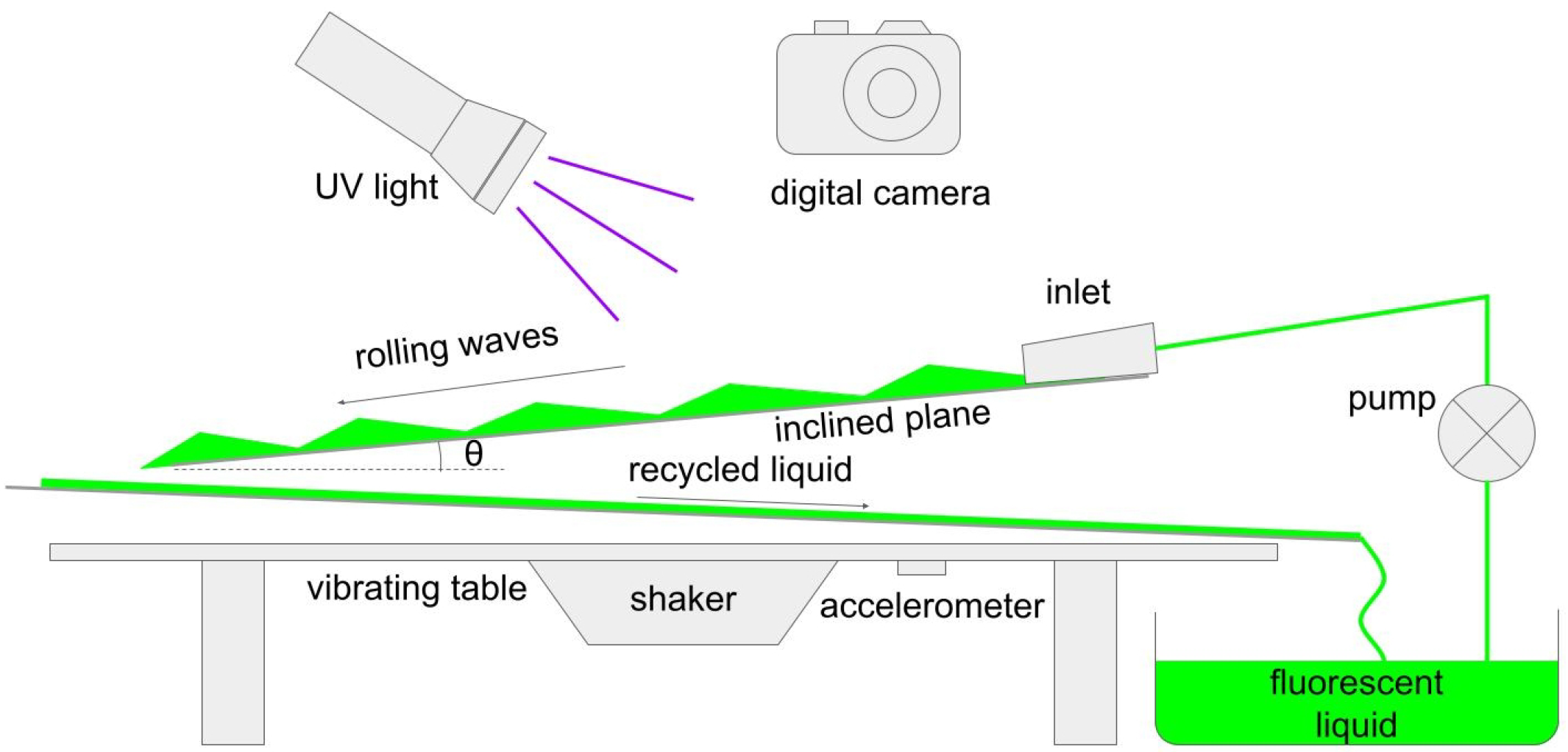
Figure 1 shows a sketch of the setup that enables observing the formation of both forced and natural (unforced) solitary-like surface waves. The setup is assembled on a vibrating table that is driven by a shaker (35 W, 20–80 Hz response, Dayton Audio, OH, USA). The electric signal applied to the shaker is produced using a digital signal generator that has the frequency tuning accuracy of
μHz. The vibration amplitude is measured by an analog accelerometer (ADXL326, Analog Devices, OH, USA) that has the accuracy of
g. The inclined plane, where the waves are observed, is a 5-cm-wide and 50-cm-long rigid aluminium plate. The surface of the plate was chemically treated to improve the formation of the liquid film. In general, the inclination angle
must be relatively small to suppress the three-dimensional instabilities of the rolling waves that are known to develop at relatively large flow rates [
54]. Subsequently, for the fluid parameters used in this work, we choose
and experimentally verify that in the absence of vibration the observed two-dimensional rolling waves remain stable during the entire observation period. The inclined plate was mounted on top of wider open channel used to recycle the liquid by redirecting it to the main reservoir. A low-vibration DC voltage pump driven via a customised electronic circuit was used to supply water from the reservoir to the inlet. The electronic modulation of the pump flow rate enabled controlling the thickness of the liquid film and the creation of solitary-like waves. Based on the pump flow rate, the width of the channel and the average speed of the flow close to the inlet, the estimated thickness
h of the liquid layer varies in the range
mm.
At the stage of preparation of the experiments, an organic fluorescent dye (Tintex, Australia) was added to tap water in the concentration of 1 g per litre, thus leading to the emission of bright green fluorescence light when the surface of the inclined plate was illuminated with UV-A light. All experiments were conducted in a darkened, acoustically isolated room with environmental humidity and temperature levels. An overhead digital camera, capable of recording videos in a slow motion regime, was used and the resulting videos were post-processed in FFmpeg and Octave software using customised computational procedures enabling the extraction of the wave amplitude from the intensity profile of the fluorescence images. In brief, FFmpeg software was used to extract every frame from the recorded videos. The pixel size of each resulting image was calibrated with the real dimensions of the inclined plate. Then, all so-obtained frame images were processed in Octave software using the following procedure: a linear averaging filter (function wiener2) was first applied to the input image and then function impixel was used to return the pixel values at the selected image coordinates, thus producing an intensity profile based on the pixel values from the RGB colour triples. The resulting data were stored as two-dimensional arrays. Plotted as an image, these two-dimensional arrays correspond to false-colour maps, where spatiotemporal traces of solitary-like waves can be seen, as discussed below. The application of a Hann window to both dimensions of these arrays and the use of the two-dimensional Fourier transformation function fft2 results in the dispersion maps of the solitary-like waves.
3. Experimental Results
Figure 2 shows the representative images of the solitary-like surface waves propagating over a downstream section of the inclined plate, when the vibration is turned off (
Figure 2a) and when the plate is vibrated with the frequency of 48 Hz and the peak amplitude is 1 g (
Figure 2b), g being the gravitational acceleration. The frequency of the forcing of the solitary-like waves is 2 Hz in both panels of
Figure 2. The images were obtained from the selected individual fluorescence frames of the recorded videos of the propagating waves. Without vibration (
Figure 2a), we can observe a train of downstream-propagating solitary pulses. A closer inspection also reveals the existence of periodic waves with an amplitude that is much smaller than that of solitary-like waves. When the plate is subjected to vibration (
Figure 2b), we continue observing a train of solitary pulses with approximately the same pulse periodicity as in
Figure 2a. However, the peak amplitude of the pulses is lower than in the case without vibration. Yet, in agreement with the relevant theory [
42,
44] and experiment on the vertical plane [
45], we also observe the short wavelength ripples arising due to the onset of the Faraday instability.
Using our fluorescence intensity analysis software, we register the profiles of the waves at the points located on the centre line of the inclined plate along the downstream direction, and we plot the so-obtained data as a function of time. The resulting spatiotemporal false-colour maps are plotted in
Figure 3 with the observation period of 2 s for the scenario of no vibration (
Figure 3a) and with the 48 Hz vibration (
Figure 3b). In those figures, we can see the traces of several solitary-like waves that propagate in the downstream direction. The traces are more distinguishable and have higher false-colour amplitudes in the case of no vibration than with the vibration, which confirms our observation of a decrease in the peak amplitude of the solitary pulses due to the vibration in
Figure 2. The ripple waves caused by the vibration-induced Faraday instabilities can also be seen in
Figure 3b. It is noteworthy that the separation between the traces and the relative position of the traces in the time-downstream coordinate space are very similar with and without the vibration. This indicates that, even though the peak amplitude of the solitary-like waves is affected by the vibration, in general the vibration does not change the shape of the soliton pulses.
Then, we apply a two-dimensional Fourier transformation to the spatiotemporal data to obtain the dispersion maps as a function of frequency
f and wavevector
k. Since the speed of a wave is given by
, using the resulting dispersion maps we can identify the bands of constant
ratio that correspond to waves travelling along the incline plate at a constant speed. However, we apply the standard f-k filtering procedures to remove noise from the dispersion characteristics [
55].
Figure 4 shows the dispersion maps for the case of no vibration (
Figure 4a) and with the 48 Hz vibration (
Figure 4b). While the negative frequency regions of the dispersion maps originate from the mathematical properties of the Fourier transformation, the sign of the wavevector has the physical meaning as it determines the direction of the wave propagation.
We first analyse the dispersion map in
Figure 4a and its magnified image presented in
Figure 5a, where we can see a set of high-magnitude discrete bands that are superimposed on a broader continuum band of a lower magnitude. The frequencies of the discrete bands correspond to the forcing frequency of the solitary-like waves of 2 Hz and its higher-order harmonics of 4, 6 and 8 Hz and so forth. The origin of the harmonics is due to the nonlinear effects, as discussed below. The spectrum of the discrete bands changes as the frequency of forcing of the solitary-like waves is changed. When the modulation of the pump flow was turned off, i.e., with no wave forcing, the discrete bands completely disappeared. However, a continuum band was always observed independently of whether the forcing was turned on or off. Subsequently, we associate the continuum band with natural periodic rolling waves propagating on the surface of the liquid film flowing over the inclined surface. According to the frequency–wavevector spectral analysis theory [
55], a fit of the observed bands with a straight line produces the velocity of the solitary-like wave of
m/s.
When the plate is vibrated (
Figure 4b), in addition to the dispersion bands discussed in
Figure 4a we observe two new isolated bands that can be associated with the Faraday instability. Moreover, the close-up of the dispersion map (
Figure 5b) shows that the magnitude of the discrete modes decreased due to the vibration, which is an observation that is consistent with our conclusions made earlier in the text. Yet, the bands in
Figure 5b can also be fitted with a straight line that corresponds to the wave velocity of
m/s.
Empirically, the presence of the discrete bands at the forcing frequency of 2 Hz and its higher-order harmonics can be explained using the well-established analogy between rolling waves and acoustic waves [
56]. Indeed, the solitary-like surface waves in
Figure 2 can be regarded as large-amplitude shock-like disturbances (in the sub-field of physically similar roll waves in open channel such a discontinuity is called the hydraulic jump [
14,
21,
34]). Shock waves are also well-known in the field of nonlinear acoustics, where their formation is accompanied by strong nonlinear effects such as the generation of higher-order harmonic frequencies [
50]. Considering longitudinal acoustic waves that can be described as alternating areas of compression and rarefaction in the medium, we can show that the points of the crests of an acoustic wave travel faster than the speed of sound in the medium, but the points of the wave troughs travel slower [
50]. This physical process underpins the formation of an acoustic shock wave [
56]. In turn, in the field of rolling waves, the crest of a large-amplitude solitary-like wave is connected to its trough by a discontinuity, where the flow regime abruptly changes from a supercritical condition and where the fluid moves faster than the wave, to a subcritical one, where the fluid moves slower [
14,
34]. As a result, the spectrum of the wave becomes enriched by the higher-order harmonic of the frequency of forcing.
Qualitatively similar results were obtained at the vibration frequencies in the range from 30 Hz to 50 Hz, and they were validated by our theoretical analysis, the results of which are presented in the following section. As a technical note, we established that in our measurements the resonance frequency of the mounted shaker was approximately 40 Hz and that the analysis of results obtained at this frequency and at the frequencies close to it required several additional post-processing signal filtering steps compared with the analysis of the results at the frequencies that are far from the resonance, including 48 Hz, the results for which have been discussed above.
4. Theory
The theoretical description of a non-steady flow in the presence of deformable interfaces, such as the flow in a thin liquid layer down a vibrated incline, is a notoriously difficult hydrodynamic problem. The exact analysis is only available in the linear case, i.e., when the deformation amplitude of the liquid-air interface is much smaller than the average film thickness [
42]. In the general case, when a harmonic vibration is applied both in the perpendicular and parallel directions with respect to the inclined plate, the unperturbed base flow is given by a superposition of a steady Nusselt flow and of an additional harmonically oscillating flow parallel to the incline with a flat free surface [
42]. The Navier–Stokes equation for an incompressible fluid can be linearised about the base flow and the Floquet theory-based stability analysis determines if the flow is stable or unstable. The linear stability of a flat film flowing down an incline under the combined action of the longitudinal and orthogonal vibration has been investigated in Ref. [
43] using a theoretical approach based on the exact linearisation of the Navier–Stokes equation [
42].
The full nonlinear problem with a large amplitude deformation of the film surface can only be studied approximately using simplified hydrodynamic models. Here we use the well-known Shkadov model [
52,
53], which can be derived from the Navier–Stokes equation by assuming a self-similar parabolic longitudinal velocity profile. The model developed by Shkadov was used earlier to study nonlinear solitary waves in falling liquid films in the absence of vibration [
22,
23] and to investigate the onset of Faraday waves in vertically vibrated isolated liquid drops [
57].
Despite a long history of the boundary layer models and other simplified hydrodynamic models in thin liquid films dynamics, the nonlinear behaviour of the surface waves in a liquid film flowing down an incline in the presence of both the longitudinal and orthogonal vibrations remains largely unexplored. Indeed, earlier studies have mainly focused either on the nonlinear Faraday waves in liquid films on a horizontal plate subjected to horizontal and vertical vibrations [
58] or on liquid films falling down a vertical plate with the vibration applied orthogonally to the plate surface [
44,
45]. In this work, we use the Shkadov model [
52,
53] to study linear stability and nonlinear dynamics of the surface waves in liquid layers on a slightly inclined plate mounted on a vertically vibrated table. In this situation, the driving force due to gravity is not as dominating as in falling liquid films and the inclination of the plate leads to a redistribution of the vibration into the longitudinal and orthogonal components. Our theoretical analysis presented below is used to validate the experimental results and to explain the nonlinear interaction between the long-wave gravitational instability mode and the short-wave Faraday mode.
Thus, we consider a liquid film with the local film thickness
flowing down an inclined solid plate that makes an angle
with the horizontal, as shown in
Figure 1. In our model, the
x-axis is chosen to be parallel to the plate with the positive direction pointing down the incline. To capture rolling waves, we use a one-dimensional version of the Shkadov model, which is formulated as a set of two coupled nonlinear equations for
and the local flux across the layer
, where
is the longitudinal flow velocity and
z-axis is perpendicular to the incline
where
is the dynamic viscosity,
is the liquid–air surface tension, and the time-dependent gravity acceleration due to vibration is
. The inclination of the plate leads to a re-distribution of the vertical vibration into a longitudinal
and an orthogonal
components, respectively.
The base flow corresponds to a time-periodic spatially homogeneous flux
and a flat film surface
. From Equation (
1) we obtain the following expression by setting
:
where
represents the length of the acoustic boundary layer.
In the absence of vibration, i.e., when
, the base flow is the time-independent Nusselt flow, where the linear stability is well-known in the case of a falling film, i.e., at
[
22,
23]. For an arbitrary inclination angle
, the instability sets in when
, where
is the Reynolds number. To put this condition into perspective, for a water film on a
incline, the flow is unstable when
mm. The corresponding instability is called gravitational instability and it leads to the onset of long surface waves propagating downstream. The wavelength of unstable waves is longer than
, where
is the critical wavevector of the gravitational instability
Neutrally stable waves with the wavelength propagate downstream with a speed c, which is twice as large as the surface speed in the Nusselt flow, i.e., .
When the vibration is switched on, the Faraday instability mode develops and it competes with the gravitational instability mode. To study the stability of the base flow Equation (
2) we use the standard plane-wave ansatz
and
, where
k is the wavevector of the small-amplitude perturbation. By differentiating the second equation in Equation (
1) with respect to time and the first equation with respect to
x, the flux perturbation
can be eliminated to yield a complex-valued Mathieu-like equation for the film thickness perturbation
with
and
.
According to the Floquet theory, the solution of Equation (
4) is given by
, where
is some bounded periodic function with the period
and
is the Floquet exponent. The solution is stable when the real part of the largest Floquet exponent is negative, i.e.,
and it is unstable otherwise. The Floquet exponents are related to the monodromy matrix
via
, where
is the eigenvalue of
. The
complex-valued monodromy matrix
is given by the fundamental solution matrix that is obtained by writing Equation (
4) as a system of two first-order equations and integrating it over one period
T with the unit
matrix as the initial condition.
For the inclination angle
, we choose the thickness of the water film
mm, which is slightly above the critical value for the gravitational instability of
mm. The corresponding Reynolds number in the absence of vibration is
. The definition of the Froude number
depends on the source and according to [
23] is given by
in the absence of vibration. When the vibration is switched on, the characteristic flow speed changes so that the Reynolds and Froude numbers must be redefined. Thus, according to [
44],
, when vibrated at
Hz.
The marginal stability curves that correspond to
are shown in
Figure 6 for four different vibration frequencies
Hz. The critical wavevector of the gravitational instability Equation (
3) is marked by
in
Figure 6d and it remains unaffected by the vibration. The shaded regions in
Figure 6d indicate the unstable areas. The Faraday instability sets in at the vibration amplitude
that corresponds to the tip of the lowest Faraday tongue. The value of
, as extracted from
Figure 6, slightly increases with
f, namely:
for
Hz,
for
Hz,
for
Hz and
for
Hz. This observation confirms the earlier statement that, for the range of frequencies between 30 Hz and 50 Hz, the surface waves are much more sensitive to the changes of the vibration amplitude
a than to the changes of the vibration frequency
f. Indeed, comparing
Figure 6c,d we see only a marginal difference in the critical amplitude
when the frequency is doubled. On the other hand, increasing the value of
a from
to
will significantly broaden the band of unstable wavevectors of the Faraday instability, thus significantly changing the dynamics of the surface waves.
To better understand the temporal signature of the surface waves in response to vibration, we compute the imaginary part of the Floquet exponent , where, as before, is the eigenvalue of the monodromy matrix and n is an arbitrary integer. Any neutrally stable wave, i.e., , can be represented in the form , where is a bounded -periodic function. Therefore, the temporal spectrum of such a neutrally stable wave contains delta peaks located at . The temporal spectrum of a growing wave with contains the same delta peaks that will appear slightly smeared.
At this stage, it is important to emphasise that the temporal response of the surface waves that develop on the surface of a liquid layer on a vibrated incline is not necessarily harmonic (frequencies
) or subharmonic (frequencies
). This feature is in stark contrast to the standard Faraday instability in horizontal liquid layers, when the neutrally stable waves are always harmonic or subharmonic standing waves [
51]. In some special cases, however, such as that discussed in [
45] for transversally vibrated falling liquid films, the magnitude of
may be close to zero or
, leading to an almost harmonic or subharmonic response. For the fluid parameters used in the present study, the frequency of the Faraday mode is significantly shifted from
or
, as shown in
Figure 4b.
Next, we simulate the experimental conditions at which the results shown in
Figure 4b were obtained to gain a better understanding of how the vibration changes the dynamics of the waves in the early stages of evolution. Thus, we numerically integrate Equation (
1) over the time interval of 3 s in the system of length of 60 cm with periodic boundaries. The vibration amplitude is
, and the other parameters are the same as in
Figure 6d. As the initial conditions, we use zero flux and random initial perturbation of the flat film surface with the amplitude of
mm. The dispersion map is obtained by taking the two-dimensional Fourier transformation of the solution
. The contour lines of the dispersion map that correspond to the level of 3% of its maximum are shown by the thick lines in
Figure 7. The thin solid lines in
Figure 7 correspond to the dispersion curves
, computed from Equation (
4) for
and
Hz. It can be seen that the results of the direct simulation of the full system Equation (
1) are in perfect agreement with the dispersion curves of the small-amplitude surface waves.
The dispersion map in
Figure 7 is dominated by the delta peaks located at
and
Hz, thus confirming that the primary response of the liquid film to a harmonic vibration is neither harmonic, nor subharmonic. Qualitatively, the shift of the response frequency away from the standard for the Faraday instability subharmonic mode can be explained as follows. In a horizontal layer vibrated at frequency
, the Faraday instability sets in the form of a standing wave oscillating at the subharmonic frequency
. Any standing wave can be represented as a superposition of two plane waves travelling at the phase speed of
in the opposite directions, i.e.,
. When the layer is slightly inclined with the positive direction pointing downstream, it would be reasonable to assume that the plane wave propagating downstream will increase its phase speed by some amount
, but the wave propagating upstream will decrease its phase speed by the same amount
. Assuming that the wavevector remains unaffected by a small inclination angle, the resulting solution is represented by
. Therefore, the temporal spectrum of
will contain delta peaks located at
and
, in agreement with
Figure 7.
Alongside the delta peaks, the dispersion map in
Figure 7 also contains a band of linearly unstable plane waves with the wavevectors
. These long waves are amplified as the result of the gravitational instability mode. It can be seen that the gravitational band falls perfectly on the central dispersion curve that passes through the origin. The central dispersion branch in
Figure 7 is almost indistinguishable from the dispersion curve in the absence of vibration (not shown). This allows us to conclude that a relatively strong vibration (sufficiently strong to excite Faraday waves) has almost no effect on the phase speed
of the long gravitational surface waves.
To study the interaction between the Faraday waves and gravitational surface waves in the nonlinear regime, we solve Equation (
1) over the time interval of 15 s with and without vibration and compare the respective dispersion maps in
Figure 8.
It is evident from
Figure 8 that vibration leads to a suppression of the long surface waves. Indeed, the magnitude of the dispersion band that corresponds to the gravitational waves is significantly smaller when the film is vibrated. This result is in qualitative agreement with
Figure 2.
5. Conclusions
In conclusion, our experiments with a sub-millimetre-thick water layer on a slightly inclined vertically vibrated plate demonstrate that low-frequency vibration in the range between 30 and 50 Hz suppresses the development of long rolling surface waves propagating downstream. These surface waves appear as the result of the long-scale gravitational instability of the base flow in the absence of vibration [
15,
16] and may also be excited by mechanically perturbing the flow at the inlet. A relatively small thickness of the water layer (under 1 mm) is required to suppress the three-dimensional instability of the rolling waves that is known to develop at large flow rates. Experimental findings are verified using a boundary-layer hydrodynamic model [
52,
53] obtained from the Navier–Stokes equation by assuming a self-similar parabolic longitudinal flow velocity. Linear stability and nonlinear dynamics of the surface waves obtained with the model qualitatively confirm the main experimental findings.
Without vibration, the Fourier content of surface waves is represented by a broad band of unstable wavevectors
, where
is a critical cut-off wavevector of the gravitational instability (see Equation (
3)). As the instability unfolds, the wavelength of the dominant wave quickly increases until it develops into a solitary-like wave [
24]. For fluids with a relatively small viscosity, such as water, the characteristic time required for solitary rolling waves to develop on a 3
o incline is in the order of several seconds. In the nonlinear regime, the Fourier content of the surface waves is dominated by solitary-like waves characterised by a small wavevector with a background of smaller amplitude shorter waves, which is shown in
Figure 4a and
Figure 8a.
We observe that the properties of the surface waves change dramatically when the layer is vibrated. Thus, a relatively weak vibration (the vibration amplitude
) leads to the onset of the secondary Faraday instability in the form of short waves with a wavelength of
mm when vibrated at
Hz. In agreement with the earlier theoretical studies [
42,
43,
44], the temporal frequency of the Faraday waves is shifted away from the harmonic (48 Hz) and subharmonic (24 Hz) response that is typical of Faraday instability in horizontal liquid layers. In fact, the inclination angle of the plate acts as a wave filter, splitting a standing Faraday wave into two plane waves: one propagating upstream and one propagating downstream. Similarly to the Doppler effect, the wave that propagates downstream increases its speed and, therefore, increases its temporal frequency, while the wave that propagates upstream decreases its speed and frequency. For water layers vibrated at 48 Hz, we observe the following shifts in frequency away from the subharmonic response: from 24 Hz to approximately 40 Hz for the downstream wave and from 24 Hz to approximately 8 Hz for the upstream wave.
In the nonlinear regime, the interaction between shorter Faraday waves and longer gravitational waves leads to the broadening of their respective bands in the f-k dispersion map. Most importantly, we find that the average and peak amplitudes of the long-scale gravitational waves are significantly reduced when vibration is applied. This result is rather intriguing since the total influx of energy is larger in the vibrated system when both gravity and vibration together drive the flow, unlike in the non-vibrated case, where the only source of energy is due to gravity. Yet, nonlinear wave interaction leads to an uneven re-distribution of energy amongst the Faraday and gravitational waves in favour of the former. The physical mechanism responsible for the suppression of gravitational waves remains an open question; however, it is plausible to assume that the fast-oscillating fluid flow in the form of circulation patterns [
59] in pulsating Faraday waves may slow down the redistribution of fluid on the large scale, required for the growth and development of the gravitational waves.
Apart from a contribution of the fundamental knowledge, the results presented in this work may be used to better understand and further improve certain technological processes that rely on falling liquid films. Yet, the demonstrated immunity of the solitary-like waves to external vibration and their intriguing nonlinear dynamical behaviour will be of interest to researchers working on emergent technologies, where both solitary waves and fluid systems play an important role [
7,
8,
12,
48,
60,
61,
62].