Online Walking Speed Estimation Based on Gait Phase and Kinematic Model for Intelligent Lower-Limb Prosthesis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase-Based Step Frequency Estimator
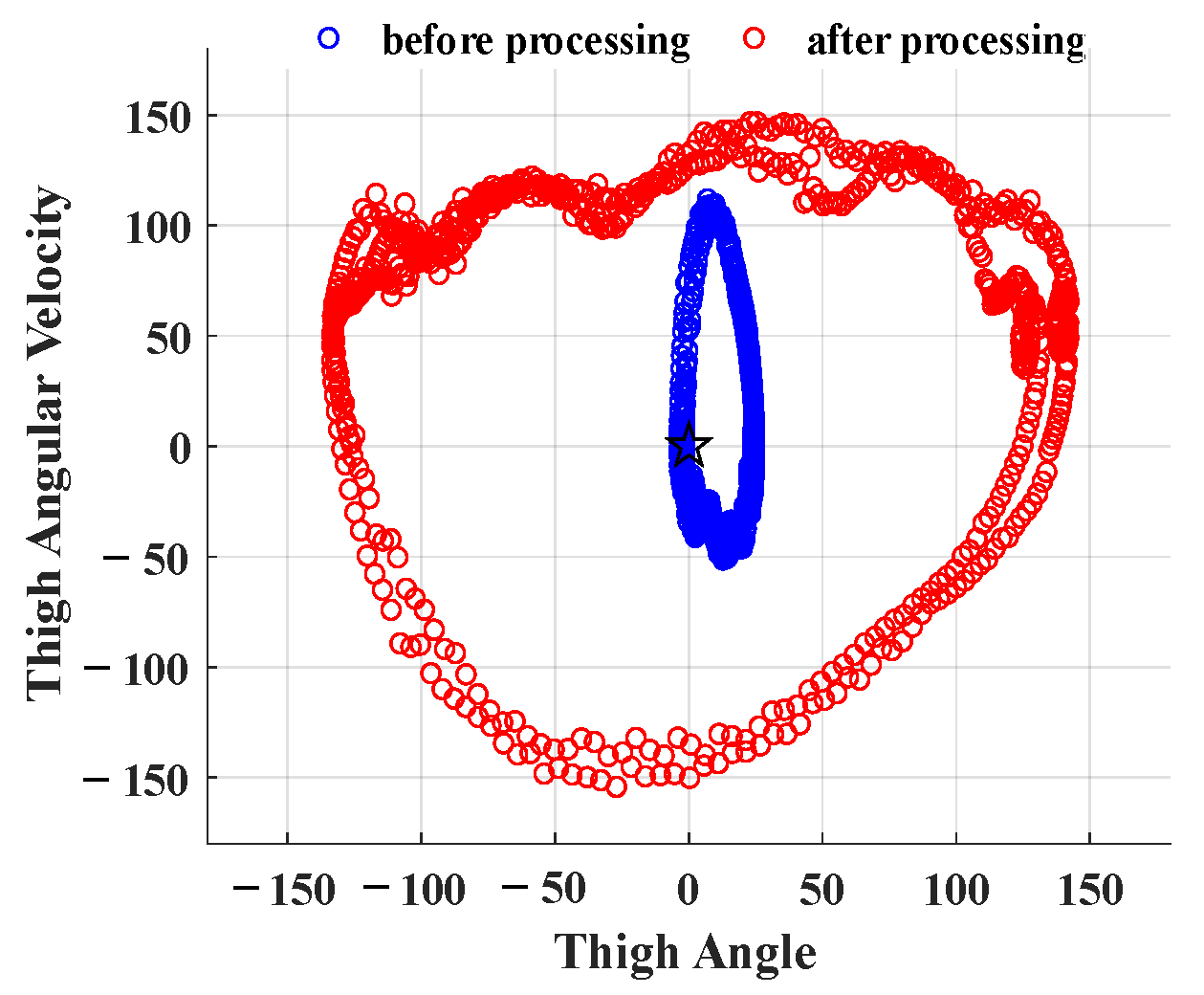
2.1.1. Gait Phase Variable of Thigh Motion
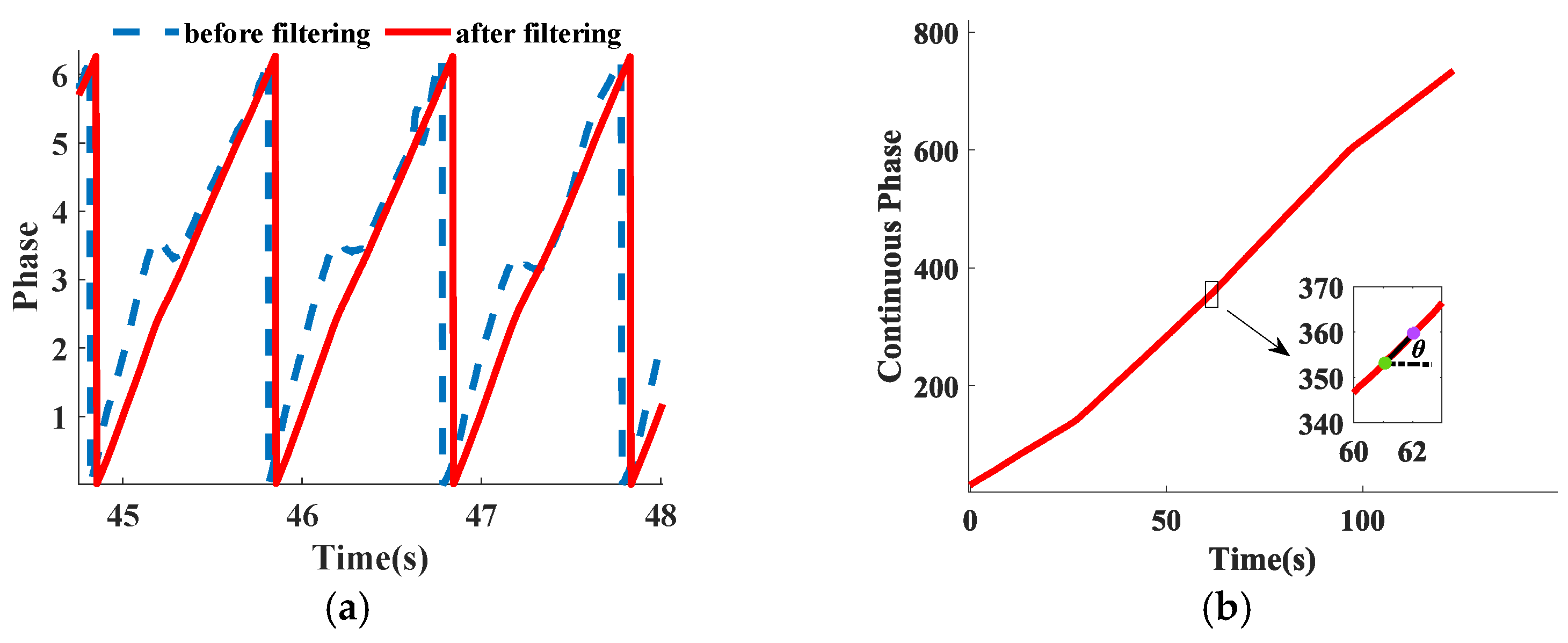
2.1.2. Real-Time Step Frequency Computation
2.2. Stride Estimator Based on Inverted Pendulum Model
3. Results
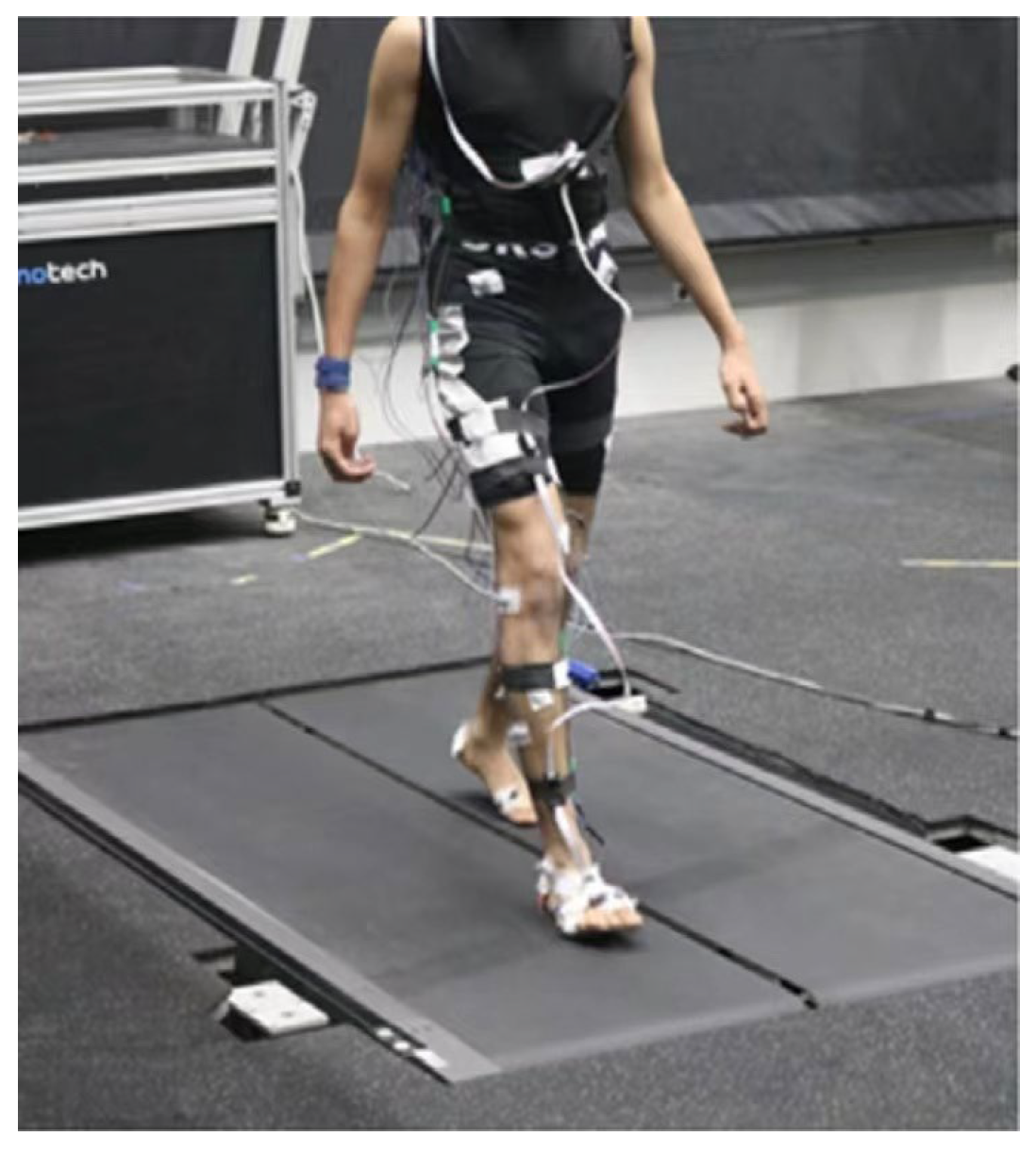
3.1. Data Acquisition
3.1.1. AB (the Able-Bodied) Dataset
3.1.2. PW (Prosthetic Wearer) Dataset
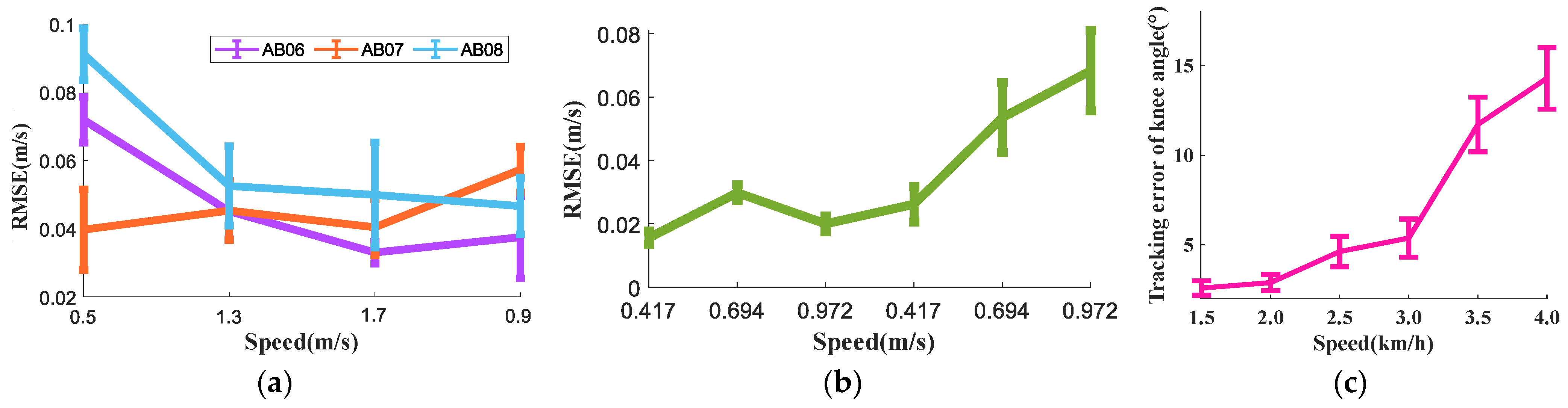
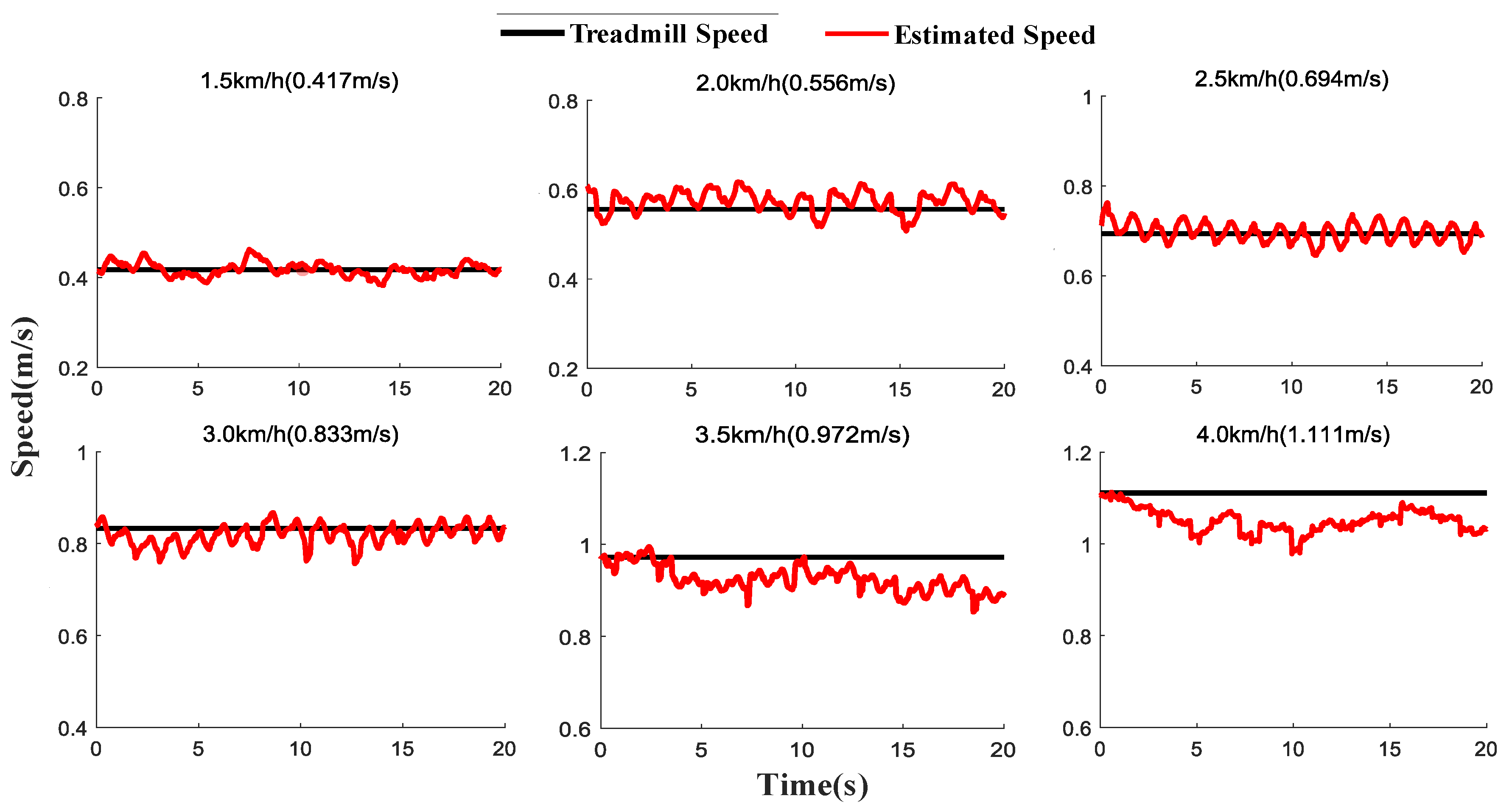
3.2. Dynamic Speed Tracking Validation
3.3. Static Speed Tracking of PW Dataset
3.4. Comparison of Previous Works
4. Discussion
4.1. Speed Switch
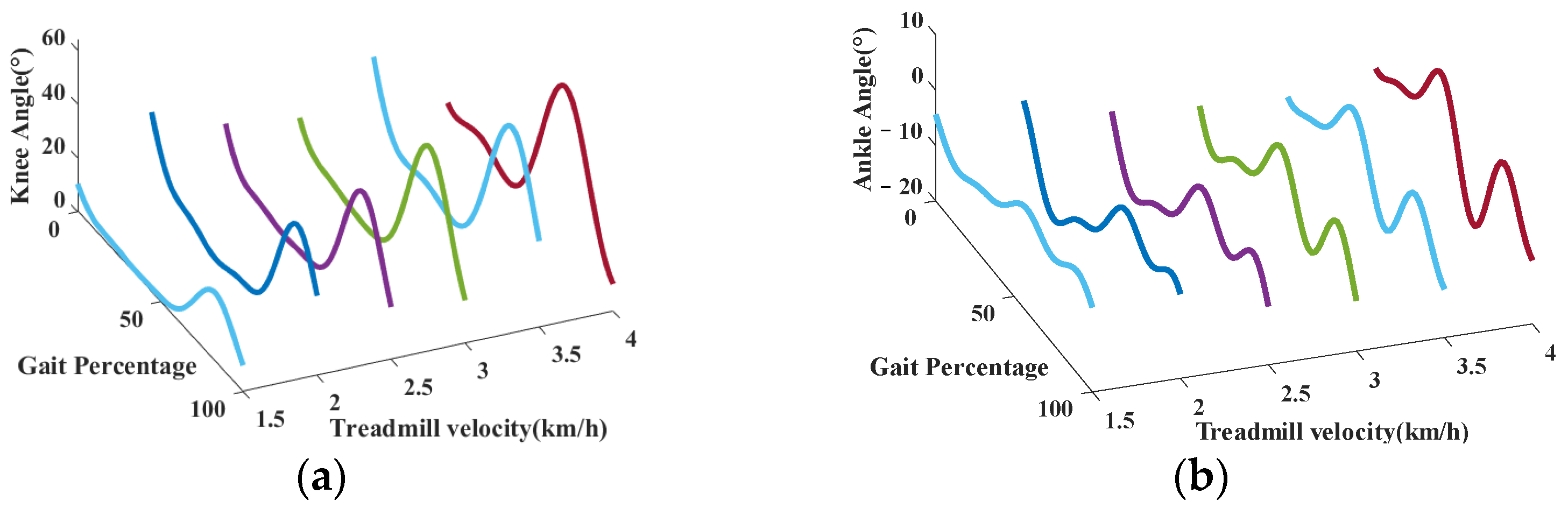
4.2. Gait Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Asif, M.; Tiwana, M.I.; Khan, U.S.; Qureshi, W.S.; Iqbal, J.; Rashid, N.; Naseer, N. Advancements, Trends and Future Prospects of Lower Limb Prosthesis. IEEE Access 2021, 9, 85956–85977. [Google Scholar] [CrossRef]
- Au, S.K.; Weber, J.; Herr, H. Powered ankle-foot prosthesis improves walking metabolic economy. IEEE Trans. Robot. 2009, 25, 51–66. [Google Scholar] [CrossRef]
- Robert, G.; Kerry, A.; Julie, C.; Jennifer, K.; Mariah, R. Review of secondary physical conditions associated with lower-limb amputation and long-term prosthesis use. J. Rehabil. Res. Dev. 2008, 45, 15–30. [Google Scholar]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O. Control strategies for active lower extremity prosthetics and orthotics: A review. J. NeuroEng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Kang, I.; Molinaro, D.D.; Duggal, S.; Chen, Y.; Kunapuli, P.; Young, A.J. Real-Time Gait Phase Estimation for Robotic Hip Exoskeleton Control During Multimodal Locomotion. IEEE Robot. Autom. Lett. 2021, 6, 3491–3497. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; An, H.; Liu, Y.; Huang, Y.; Ma, H.; Wei, Q. Phase-based Dynamic Movement Primitives for Powered Knee-Ankle Prosthesis Control. In Proceedings of the 6th International Conference on Robotics and Automation Sciences (ICRAS), Wuhan, China, 25 April 2022. [Google Scholar]
- Embry, K.R.; Villarreal, D.J.; Macaluso, R.L.; Gregg, R.D. Modeling the Kinematics of Human Locomotion over Continuously Varying Speeds and Inclines. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2342–2350. [Google Scholar] [CrossRef] [PubMed]
- Lawson, B.E.; Ruhe, B.; Shultz, A.; Goldfarb, M. A Powered Prosthetic Intervention for Bilateral Transfemoral Amputees. IEEE Trans. Biomed. Eng. 2015, 62, 1042–1050. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of walking features from foot inertial sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.-S.; Sun, K.-C.; Cheng, C.-Y. A Kinematic Human-Walking Model for the Normal-Gait-Speed Estimation Using Tri-Axial Acceleration Signals at Waist Location. IEEE Trans. Biomed. Eng. 2013, 60, 2271–2279. [Google Scholar] [PubMed]
- Bhakta, K.; Camargo, J.; Compton, W.; Herrin, K.; Young, A. Evaluation of Continuous Walking Speed Determination Algorithms and Embedded Sensors for a Powered Knee & Ankle Prosthesis. IEEE Robot. Autom. Lett. 2021, 6, 4820–4826. [Google Scholar]
- Quintero, D.; Lambert, D.J.; Villarreal, D.J.; Gregg, R.D. Real-Time continuous gait phase and speed estimation from a single sensor. Control Technol. Appl. IEEE 2017, 2017, 847–852. [Google Scholar]
- Villarreal, D.J.; Poonawala, H.A.; Gregg, R.D. A Robust Parameterization of Human Gait Patterns Across Phase-Shifting Perturbations. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Camargo, J.; Ramanathan, A.; Flanagan, W.; Young, A. A comprehensive, open-source dataset of lower limb biomechanics in multiple conditions of stairs, ramps, and level-ground ambulation and transitions. J. Biomech. 2021, 119, 110320. [Google Scholar] [CrossRef] [PubMed]
- Dauriac, B.; Bonnet, X.; Pillet, H.; Lavaste, F. Estimation of the walking speed of individuals with transfemoral amputation from a single prosthetic shank-mounted IMU. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 931–937. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Young, M.; Naing, V.; Donelan, J. Walking speed estimation using a shank-mounted inertial measurement unit. J. Biomech. 2010, 43, 1640–1643. [Google Scholar] [CrossRef] [PubMed]
- Quintero, D.; Villarreal, D.J.; Lambert, D.J.; Kapp, S.; Gregg, R.D. Continuous-Phase Control of a Powered Knee–Ankle Prosthesis: Amputee Experiments Across Speeds and Inclines. IEEE Trans. Robot. 2018, 99, 686–701. [Google Scholar] [CrossRef]
- Thatte, N.; Shah, T.; Geyer, H. Robust and Adaptive Lower Limb Prosthesis Stance Control via Extended Kalman Filter-Based Gait Phase Estimation. IEEE Robot. Autom. Lett. 2019, 4, 3129–3136. [Google Scholar] [CrossRef]
- Martin, C.L.; Phillips, B.A.; Kilpatrick, T.J.; Butzkueven, H.; Tubridy, N.; McDonald, E.; Galea, M.P. Gait and balance impairment in early multiple sclerosis in the absence of clinical disability. Mult. Scler. J. 2006, 12, 620–628. [Google Scholar] [CrossRef] [PubMed]
- Waters, R.L.; Mulroy, S. The energy expenditure of normal and pathologic gait. Gait Posture 1999, 9, 231. [Google Scholar] [CrossRef] [PubMed]




| Authors | N Subject | Sensors | Method | Statistical Analysis | RMSE (m/s) |
|---|---|---|---|---|---|
| Sabatini [9] | 5 AB | a foot IMU | Direct integration method | Standard regression tool | 0.05 |
| Boris [16] | 9 TF | IMU installed on shank | Kinematic model | Not mentioned | 0.09 |
| Li [15] | 8 AB | IMU installed on shank | Direct integration method combined with kinematic model | ANOVA (p < 0.05) | 0.07 |
| Bhakta [11] | 6 TF | IMU on the thigh | Machine learning models including LR, XGBoost and NN (<0.9 m/s) | ANOVA (p < 0.05) and Bonferroni post-hoc correction | DEP: 0.014 ± 0.001 IND: 0.070 ± 0.007 |
| This paper | 11 AB 6 PW | IMU on the thigh | Phased-based method combined with kinematic model | ANOVA (p < 0.05) | AB: 0.051 ± 0.016 PW:0.036 ± 0.021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; An, H.; Ma, H.; Wei, Q. Online Walking Speed Estimation Based on Gait Phase and Kinematic Model for Intelligent Lower-Limb Prosthesis. Appl. Sci. 2023, 13, 1893. https://doi.org/10.3390/app13031893
Liu Y, An H, Ma H, Wei Q. Online Walking Speed Estimation Based on Gait Phase and Kinematic Model for Intelligent Lower-Limb Prosthesis. Applied Sciences. 2023; 13(3):1893. https://doi.org/10.3390/app13031893
Chicago/Turabian StyleLiu, Yi, Honglei An, Hongxu Ma, and Qing Wei. 2023. "Online Walking Speed Estimation Based on Gait Phase and Kinematic Model for Intelligent Lower-Limb Prosthesis" Applied Sciences 13, no. 3: 1893. https://doi.org/10.3390/app13031893
APA StyleLiu, Y., An, H., Ma, H., & Wei, Q. (2023). Online Walking Speed Estimation Based on Gait Phase and Kinematic Model for Intelligent Lower-Limb Prosthesis. Applied Sciences, 13(3), 1893. https://doi.org/10.3390/app13031893







