Biomechanical Modeling of Human–Robot Accident Scenarios: A Computational Assessment for Heavy-Payload-Capacity Robots
Abstract
:1. Introduction
2. Material and Methods
2.1. Design of Finite Element Human Hand Model
2.2. Material of FE Human Hand Model
2.3. Meshing
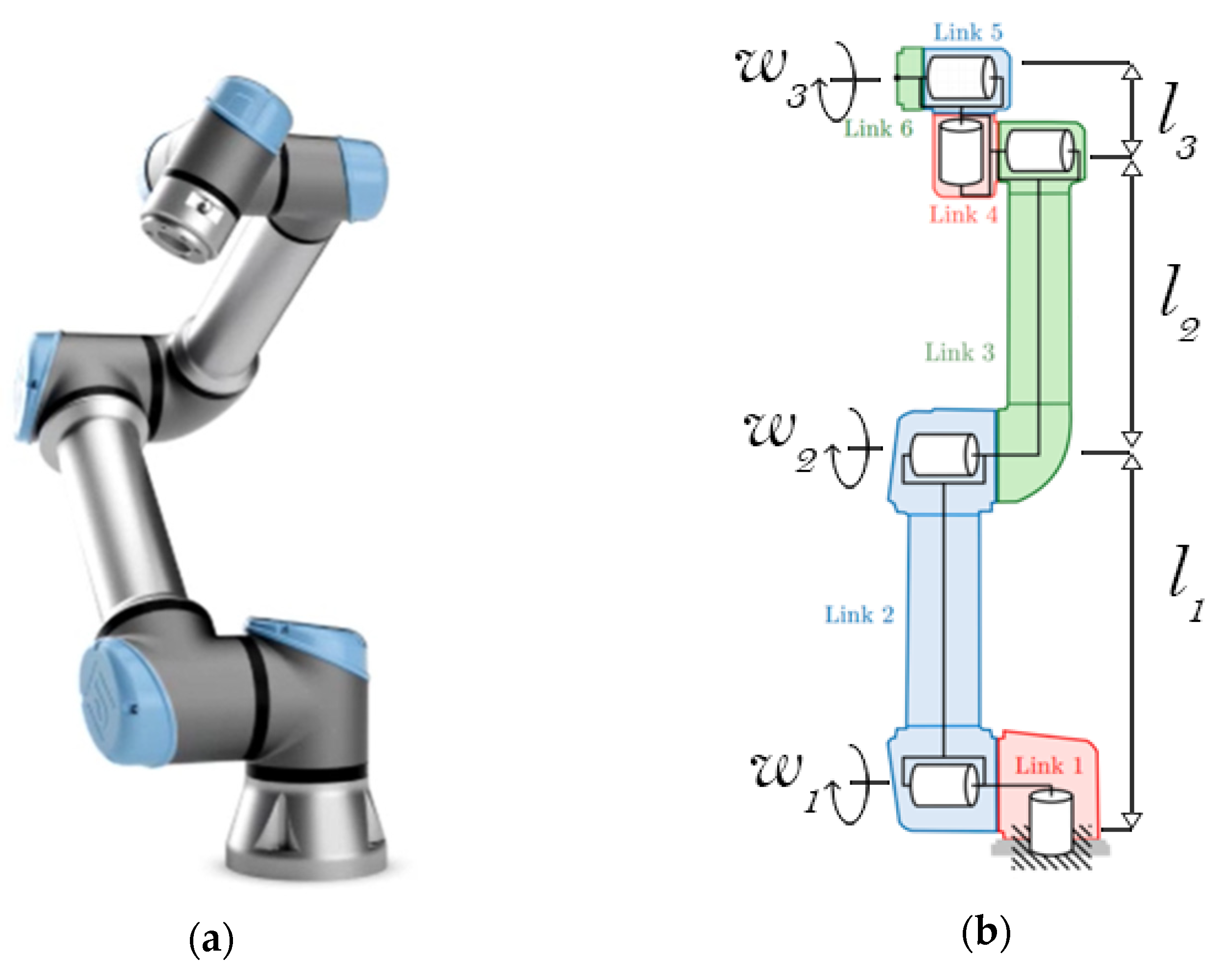
3. Virtual Experiment Setup for Human–Robot Collaboration
3.1. Setup for Quasi-Static Simulations
3.2. Setup for Dynamic Simulations
4. Analysis and Results
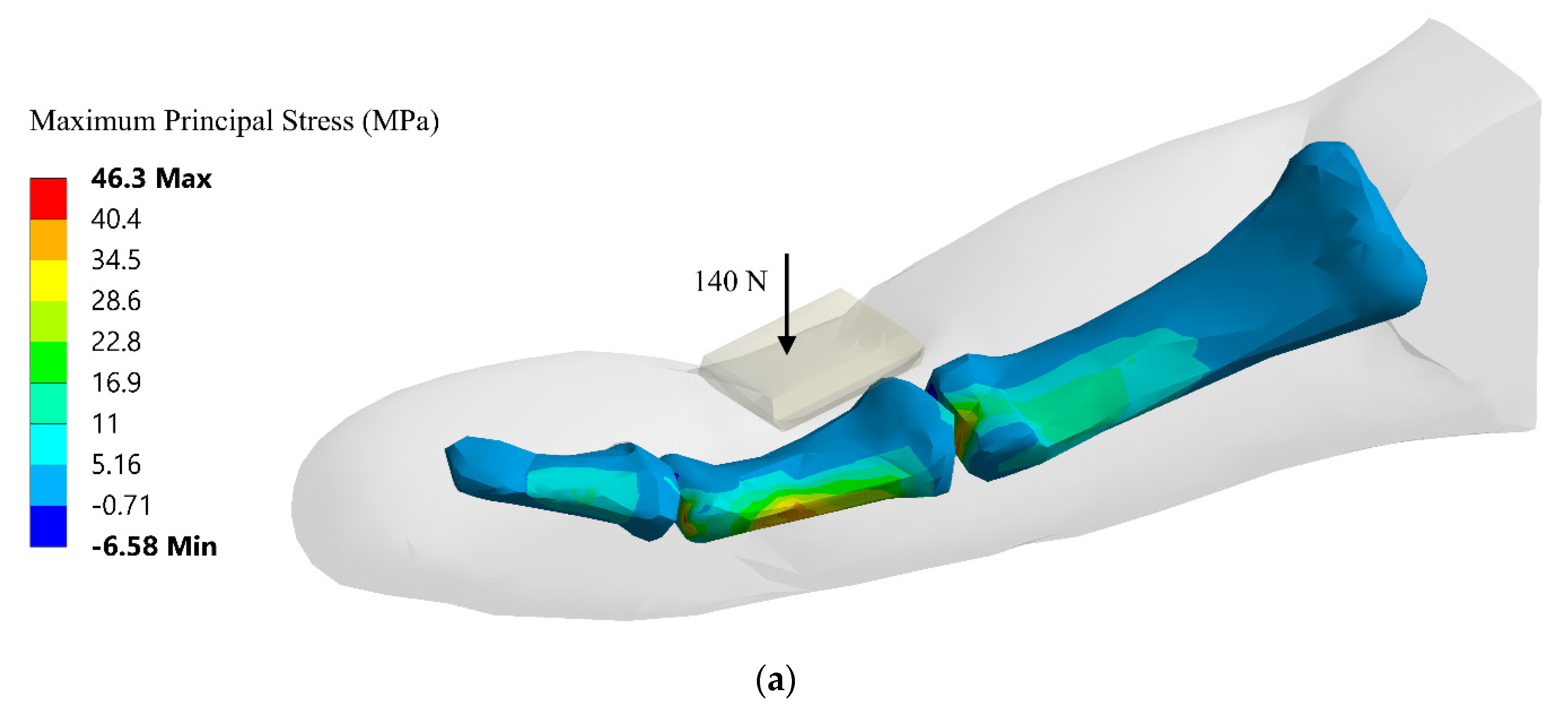
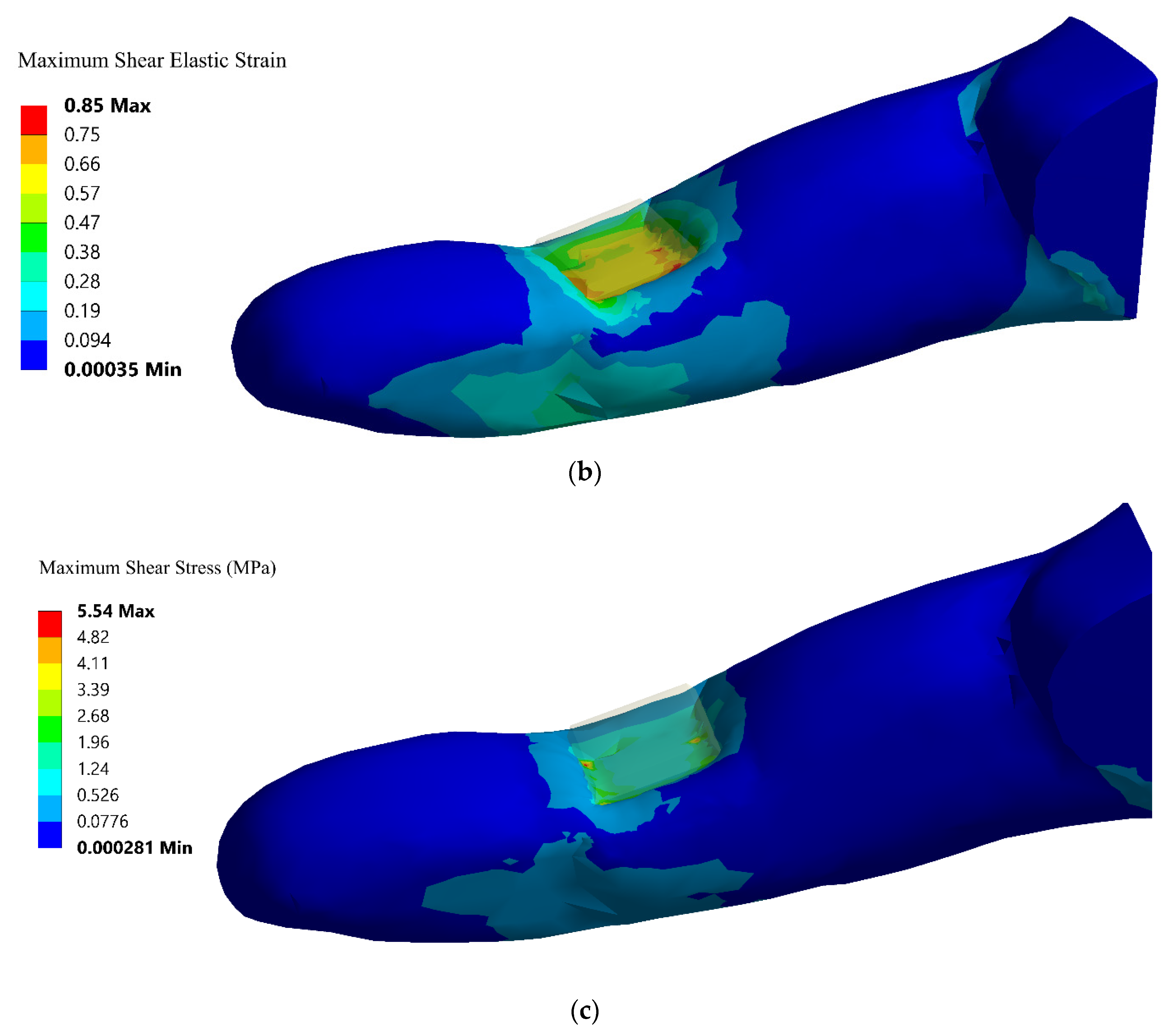
4.1. Quasi-Static Analysis
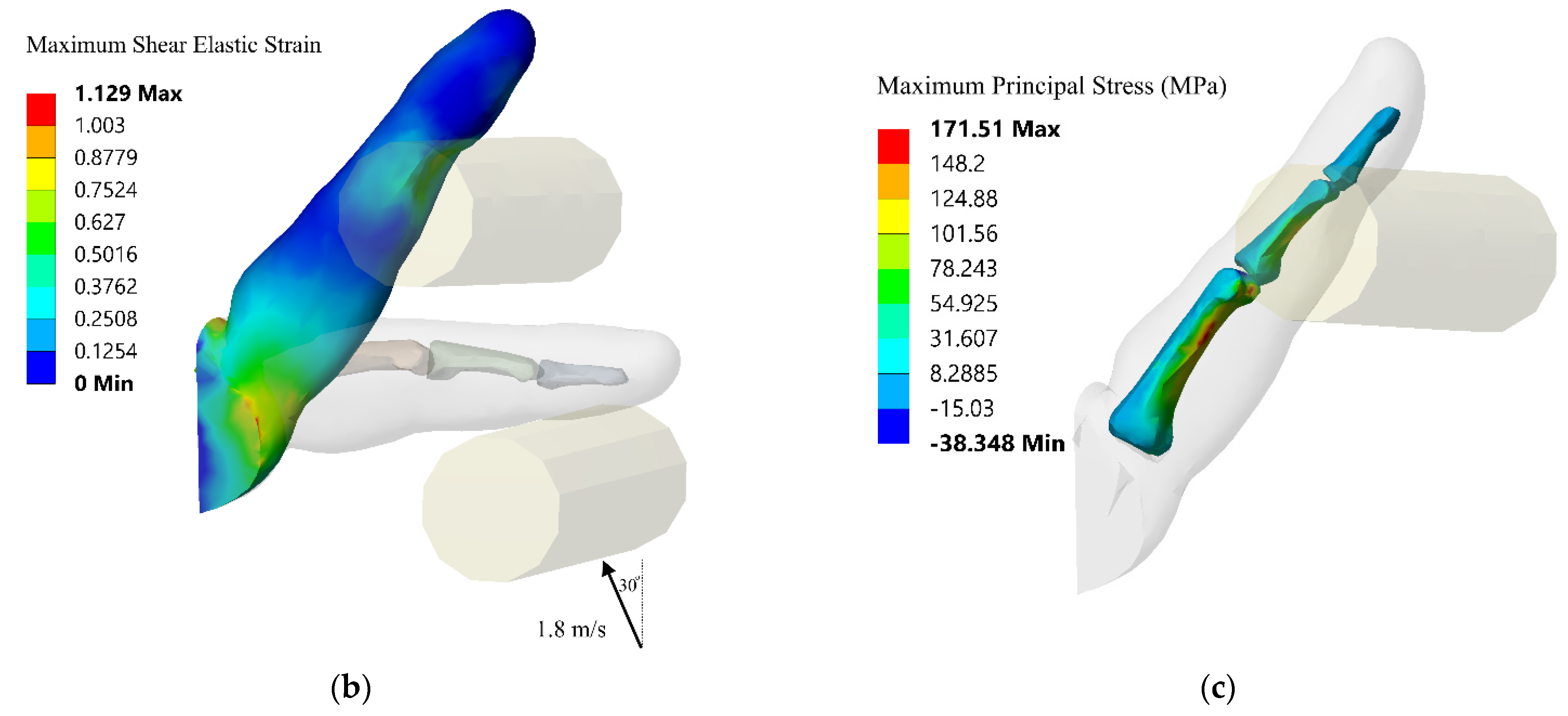
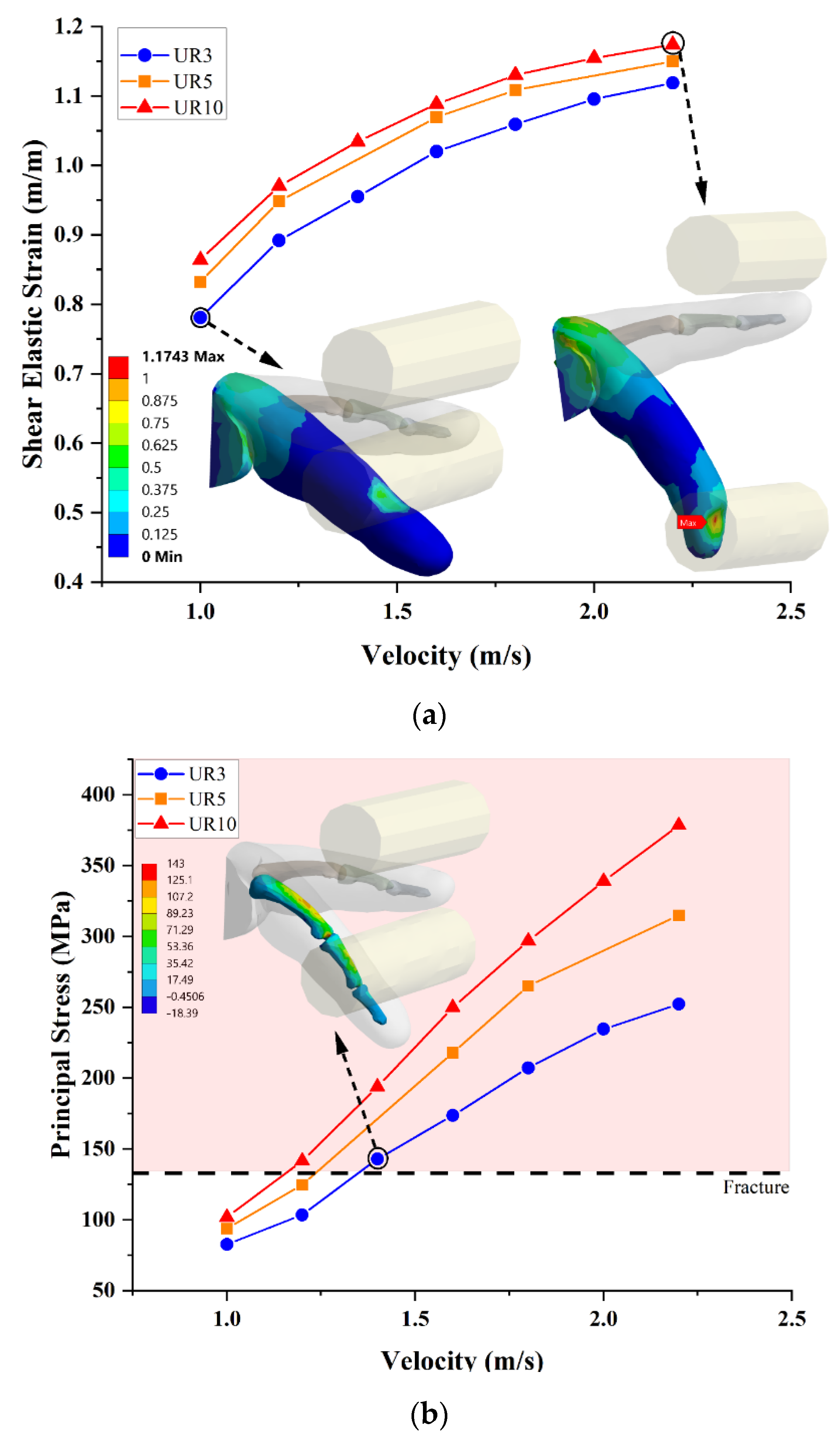
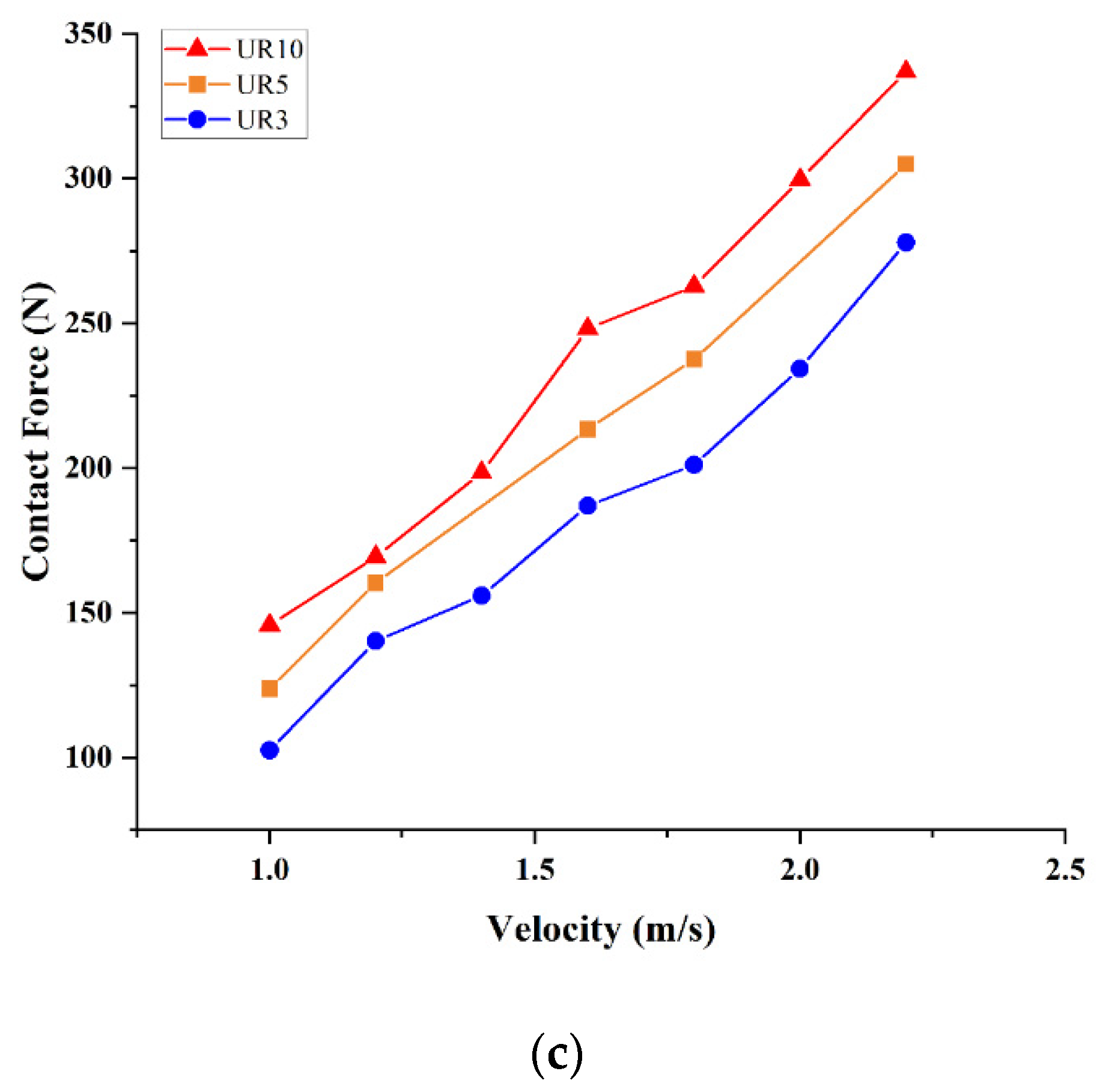
4.2. Dynamic Analysis
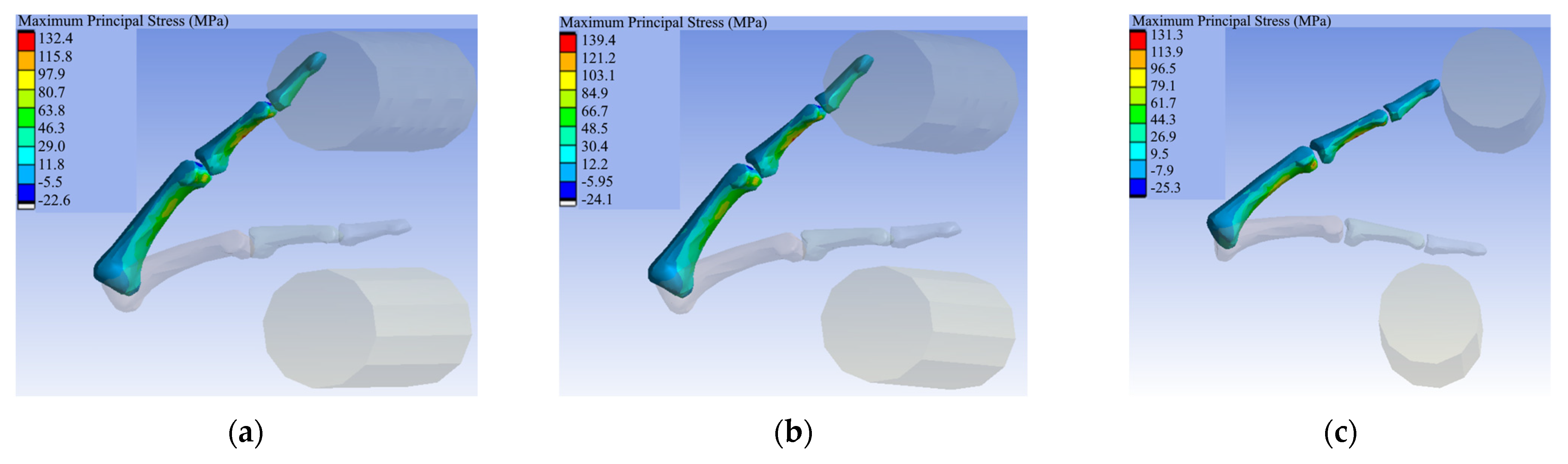
4.2.1. Case I—Hyperextension
4.2.2. Case II—Flexion
4.2.3. Case III—Abduction
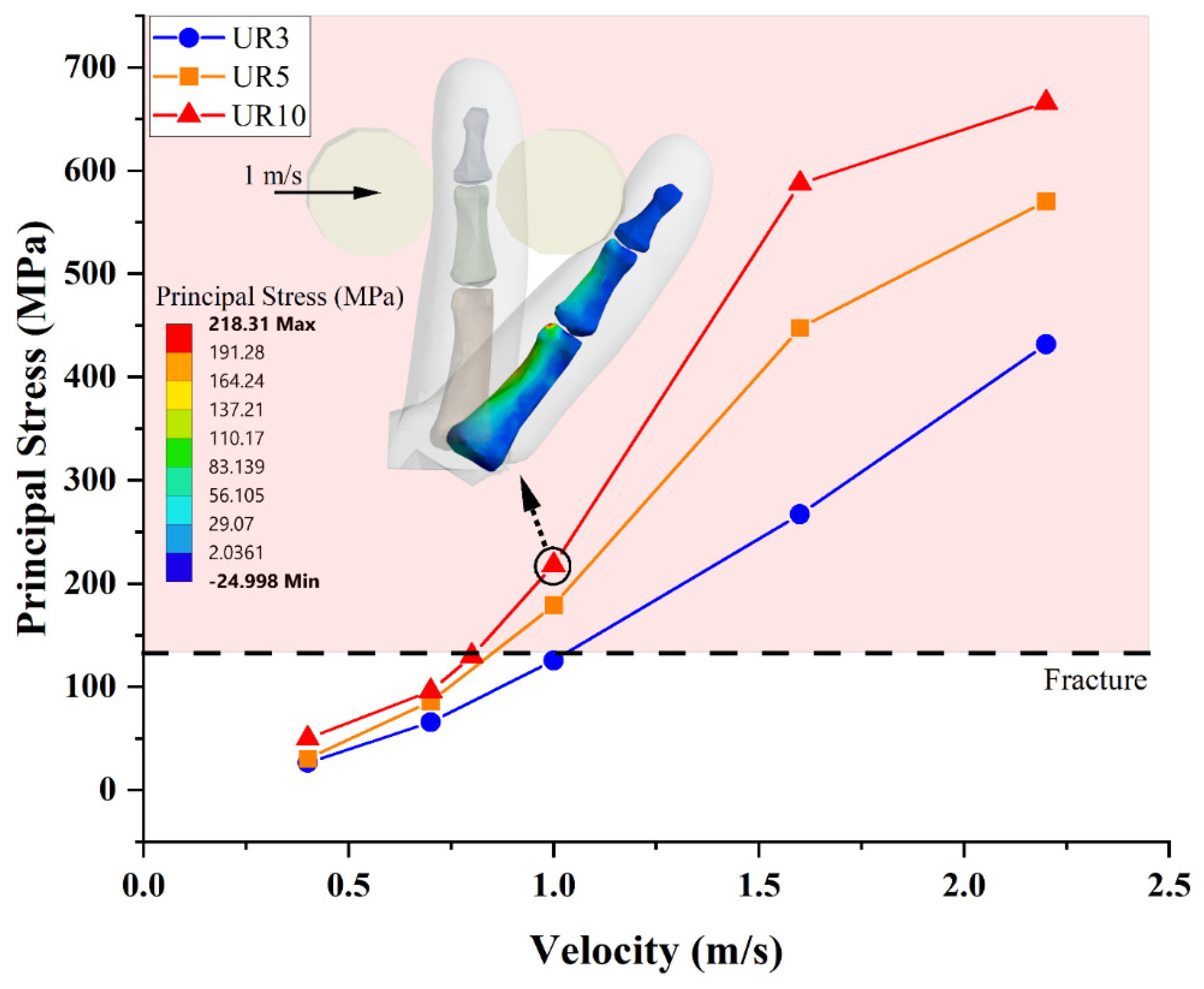
4.2.4. Case IV: Full Hand Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Strain Energy Potential | Robot Effective Mass | ||
| Principal stretches | Robot effective payload | ||
| No. of terms in hyperelastic model | Robot link lengths | ||
| , | Experimentally determined material parameters | Robot link-length Ratios | |
| Compressibility | Sum of robot link lengths | ||
| Elastic Volume Ratio | Robot actuator mass | ||
| Total mass of robot moving parts | Distributed mass of robot links |
References
- Executive Summary World Robotics 2018 Industrial Robots (No Date). Available online: https://ifr.org/downloads/press2018/Executive_Summary_WR_2018_Industrial_Robots.pdf (accessed on 19 March 2022).
- Executive Summary World Robotics 2020 Industrial Robots (No Date). Available online: https://ifr.org/img/worldrobotics/Executive_Summary_WR_2020_Industrial_Robots_1.pdf (accessed on 4 April 2022).
- Kriaa, S.; Pietre-Cambacedes, L.; Bouissou, M.; Halgand, Y. A Survey of Approaches Combining Safety and Security for Industrial Control Systems. In Reliability Engineering and System Safety; Elsevier Ltd.: Amsterdam, The Netherlands, 2015; pp. 156–178. [Google Scholar] [CrossRef]
- Khalid, A.; Kirisci, P.; Ghrairi, Z.; Pannek, J.; Thoben, K.D. Safety Requirements in Collaborative Human–Robot Cyber-Physical System. In Lecture Notes in Logistics; Springer Science and Business Media: Berlin, Germany, 2017; pp. 41–51. [Google Scholar] [CrossRef]
- Vysocky, A.; Novak, P. Human—Robot collaboration in industry. MM Sci. J. 2016, 2016, 903–906. [Google Scholar] [CrossRef]
- Rüßmann, M.; Lorenz, M.; Gerbert, P.; Waldner, M.; Justus, J.; Engel, P.; Harnisch, M. Industry 4.0: The Future of Productivity and Growth in Manufacturing Industries. Boston Consult. Group 2015, 9, 54–89. [Google Scholar]
- Islam, S.O.B.; Lughmani, W.A.; Qureshi, W.S.; Khalid, A.; Mariscal, M.A.; Garcia-Herrero, S. Exploiting visual cues for safe and flexible cyber-physical production systems. Res. Artic. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Thumm, J.; Althoff, M. Provably Safe Deep Reinforcement Learning for Robotic Manipulation in Human Environments. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]
- Liu, Q.; Liu, Z.; Xiong, B.; Xu, W.; Liu, Y. Deep reinforcement learning-based safe interaction for industrial human-robot collaboration using intrinsic reward function. Adv. Eng. Inform. 2021, 49, 1360. [Google Scholar] [CrossRef]
- Choi, S.H.; Park, K.-B.; Roh, D.H.; Lee, J.Y.; Mohammed, M.; Ghasemi, Y.; Jeong, H. An integrated mixed reality system for safety-aware human-robot collaboration using deep learning and digital twin generation. Robot. Comput. Integr. Manuf. 2022, 73, 102258. [Google Scholar] [CrossRef]
- Khalid, A.; Kirisci, P.; Khan, Z.H.; Ghrairi, Z.; Thoben, K.-D.; Pannek, J. Security framework for industrial collaborative robotic cyber-physical systems. Comput. Ind. 2018, 97, 132–145. [Google Scholar] [CrossRef]
- Lasota, P.A.; Rossano, G.F.; Shah, J.A. Toward Safe Close-Proximity Human-Robot Interaction with Standard Industrial Robots. In 2014 IEEE International Conference on Automation Science and Engineering (CASE); IEEE: Piscataway, NJ, USA, 2014; pp. 339–344. [Google Scholar] [CrossRef]
- Cherubini, A.; Passama, R.; Crosnier, A.; Lasnier, A.; Fraisse, P. Collaborative manufacturing with physical human-robot interaction. Robot. Comput. Integr. Manuf. 2016, 40, 1–13. [Google Scholar] [CrossRef]
- Chinniah, Y. Robot Safety: Overview of Risk Assessment and Reduction. Adv. Robot. Autom. 2016, 5, 139. [Google Scholar] [CrossRef]
- Pellegrinelli, S.; Moro, F.L.; Pedrocchi, N.; Tosatti, L.M.; Tolio, T. A probabilistic approach to workspace sharing for human–robot cooperation in assembly tasks. CIRP Ann. 2016, 65, 57–60. [Google Scholar] [CrossRef]
- Jiang, B.C.; Gainer, C.A. A cause-and-effect analysis of robot accidents. J. Occup. Accid. 1987, 9, 27–45. [Google Scholar] [CrossRef]
- Fryman, J.; Matthias, B. Safety of Industrial Robots: From Conventional to Collaborative Applications. In Proceedings of the ROBOTIK 2012 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; pp. 1–5. [Google Scholar]
- Accident Search Results Page|Occupational Safety and Health Administration (No Date). Available online: https://www.osha.gov/pls/imis/AccidentSearch.search?acc_keyword=%22Robot%22&keyword_list=on (accessed on 4 April 2022).
- Oberer, S.; Malosio, M.; Schraft, R.D. Investigation of robot human impact. VDI Berichte 1956 2006, 15, 87. [Google Scholar]
- Khalid, A.; Kirisci, P.; Ghrairi, Z.; Thoben, K.D.; Pannek, J. Towards implementing Safety and Security Concepts for Human-Robot Collaboration in the context of Industry 4.0. In Proceedings of the 39th International MATADOR Conference on Advanced Manufacturing, Manchester, UK, 17–19 August 2017. [Google Scholar]
- Suita, K.; Yamada, Y.; Tsuchida, N.; Imai, K.; Ikeda, H.; Sugimoto, N. A Failure-to-Safety “Kyozon” System with Simple Contact Detection and Stop Capabilities for Safe Human-Autonomous Robot Coexistence. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 3, pp. 3089–3096. [Google Scholar] [CrossRef]
- Povse, B.; Koritnik, D.; Kamnik, R.; Bajd, T.; Munih, M. Industrial Robot and Human Operator Collision. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2663–2668. [Google Scholar] [CrossRef]
- Haasper, C.; Junge, M.; Ernstberger, A.; Brehme, H.; Hannawald, L.; Langer, C.; Nehmzow, J.; Otte, D.; Sander, U.; Krettek, C.; et al. The Abbreviated Injury Scale (AIS). Options and problems in application. Unfallchirurg 2020, 113, 366–372. [Google Scholar] [CrossRef] [PubMed]
- ISO 15066; Robots and Robotic Devices-Collaborative Robots. International Organisation of Standardisation: Genewa, Switzerland, 2016.
- Mallon, W.J.; Brown, H.R.; Nunley, J.A. Digital ranges of motion: Normal values in young adults. J. Hand Surg. 1991, 16, 882–887. [Google Scholar] [CrossRef]
- Joodaki, H.; Panzer, M.B. Skin mechanical properties and modeling: A review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 323–343. [Google Scholar] [CrossRef]
- Harih, G.; Tada, M. Development of a feasible finite element digital human hand model. DHM Posturography 2019, 273–286. [Google Scholar] [CrossRef]
- Shergold, O.A.; Fleck, N.A. Mechanisms of deep penetration of soft solids, with application to the injection and wounding of skin. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 3037–3058. [Google Scholar] [CrossRef]
- Kamper, D.G.; George Hornby, T.; Rymer, W.Z. Extrinsic flexor muscles generate concurrent flexion of all three finger joints. J. Biomech. 2002, 35, 1581–1589. [Google Scholar] [CrossRef]
- Completo, A.; Duarte, R.; Fonseca, F.; Simões, J.; Ramos, A.; Relvas, C. Biomechanical evaluation of different reconstructive techniques of proximal tibia in revision total knee arthroplasty: An in-vitro and finite element analysis. Clin. Biomech. 2013, 28, 291–298. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Y.; Tai, B.L.; Chen, R.K.; Shih, A.J. Bone geometry on the contact stress in the shoulder for evaluation of pressure ulcers: Finite element modeling and experimental validation. Med. Eng. Phys. 2015, 37, 187–194. [Google Scholar] [CrossRef]
- Aubert, K.; Germaneau, A.; Rochette, M.; Ye, W.; Severyns, M.; Billot, M.; Rigoard, P.; Vendeuvre, T. Development of Digital Twins to Optimize Trauma Surgery and Postoperative Management. A Case Study Focusing on Tibial Plateau Fracture. Front. Bioeng. Biotechnol. 2021, 9, 722275. [Google Scholar] [CrossRef]
- Bahraminasab, M.; Bin Sahari, B.; Edwards, K.; Farahmand, F.; Hong, T.S.; Arumugam, M.; Jahan, A. Multi-objective design optimization of functionally graded material for the femoral component of a total knee replacement. Mater. Des. 2014, 53, 159–173. [Google Scholar] [CrossRef]
- Maas, S.A.; Ellis, B.J.; Rawlins, D.S.; Weiss, J.A. Finite Element Simulation of Articular Contact Mechanics with Quadratic Tetrahedral Elements HHS Public Access. J. Biomech. 2016, 49, 659–667. [Google Scholar] [CrossRef] [PubMed]
- Elsheikh, A.H.; Showaib, E.A.; Asar, E.M. Artificial Neural Network Based Forward Kinematics Solution for Planar Parallel Manipulators Passing through Singular Configuration. Adv. Robot. Autom. 2013, 106, 2. [Google Scholar]
- UR5 Collaborative Robot Arm|Flexible and Lightweight Cobot (No Date). Available online: https://www.universal-robots.com/products/ur5-robot/ (accessed on 23 March 2022).
- Welford, W.T.; Brebner, J.M.; Kirby, N. Reaction Times; Welford, A.T., Ed.; Academic Press: London, UK, 1980. [Google Scholar]
- Khalid, A.; Kirisci, P.; Ghrairi, Z.; Thoben, K.D.; Pannek, J. A methodology to develop collaborative robotic cyber physical systems for production environments. Logist. Res. 2016, 9, 1–15. [Google Scholar] [CrossRef]
- Hart, N.H.; Nimphius, S.; Rantalainen, T.; Ireland, A.; Siafarikas, A.; Newton, R.U. Mechanical basis of bone strength: Influence of bone material, bone structure and muscle action. J. Musculoskelet. Neuronal Interact. 2017, 17, 114. [Google Scholar]
- Berx, N.; Decré, W.; Pintelon, L. Examining the Role of Safety in the Low Adoption Rate of Collaborative Robots. Procedia CIRP 2022, 106, 51–57. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, Z.H.; Idrees, M.; Kirisci, P.; Ghrairi, Z.; Thoben, K.-D.; Pannek, J. Understanding vulnerabilities in cyber physical production systems. Int. J. Comput. Integr. Manuf. 2021, 35, 569–582. [Google Scholar] [CrossRef]
- Fan, J.; Zheng, P.; Li, S. Vision-based holistic scene understanding towards proactive human–robot collaboration. Robot. Comput. Integr. Manuf. 2022, 75, 102304. [Google Scholar] [CrossRef]
- McCalden, R.W.; A McGeough, J.; Barker, M.B.; Court-Brown, C.M. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. J. Bone Jt. Surg. Am. Vol. 1993, 75, 1193–1205. [Google Scholar] [CrossRef]


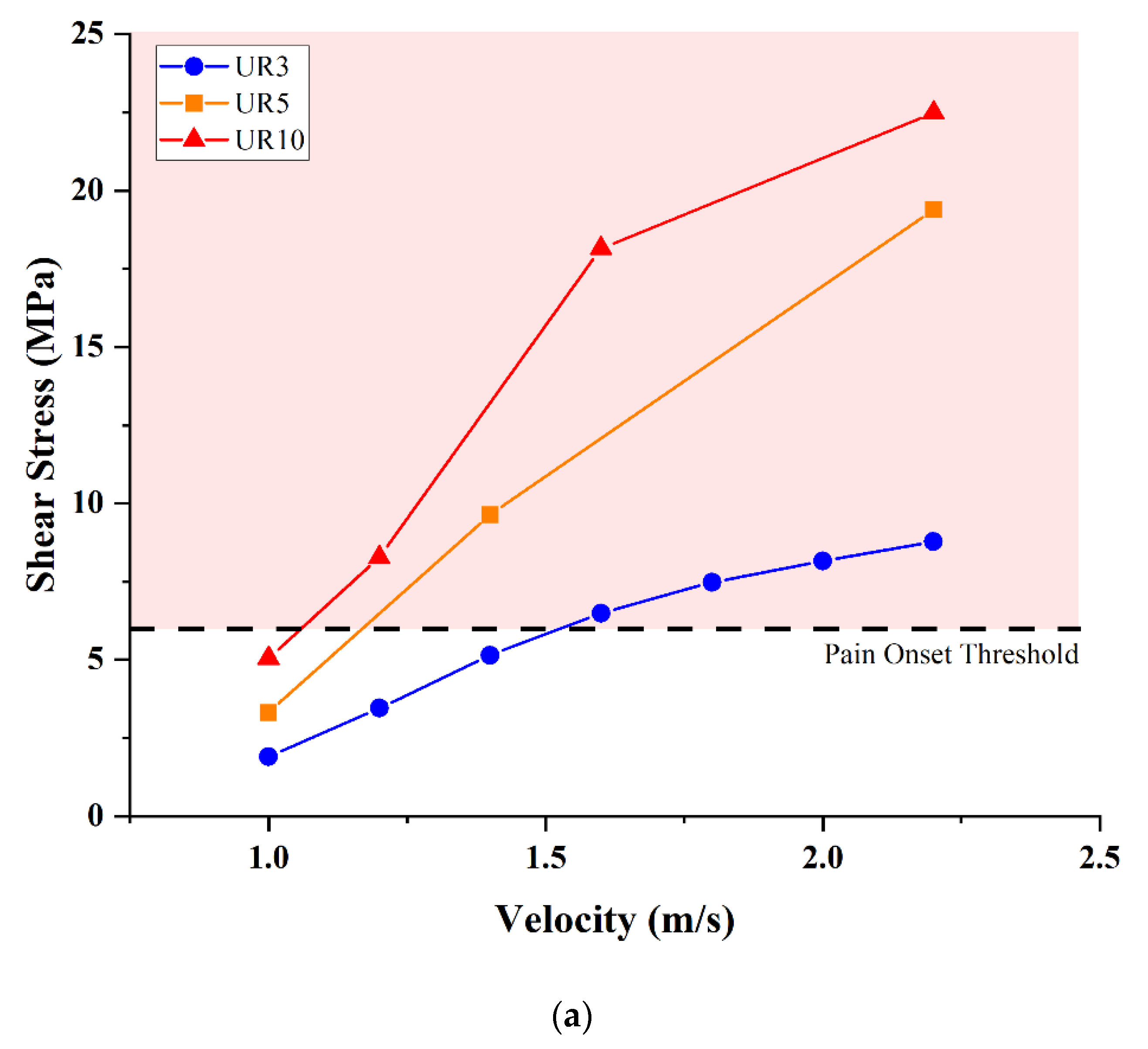
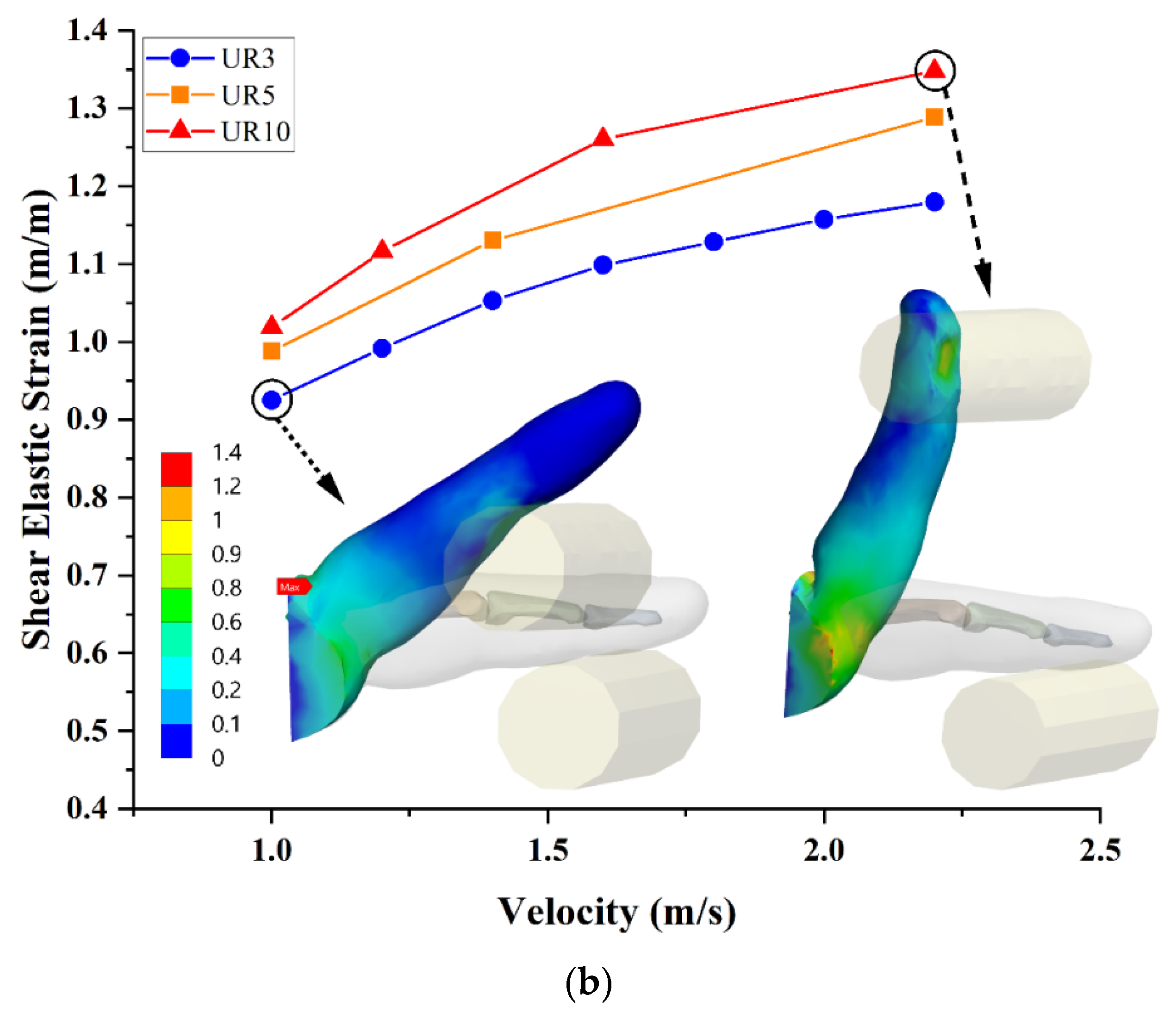
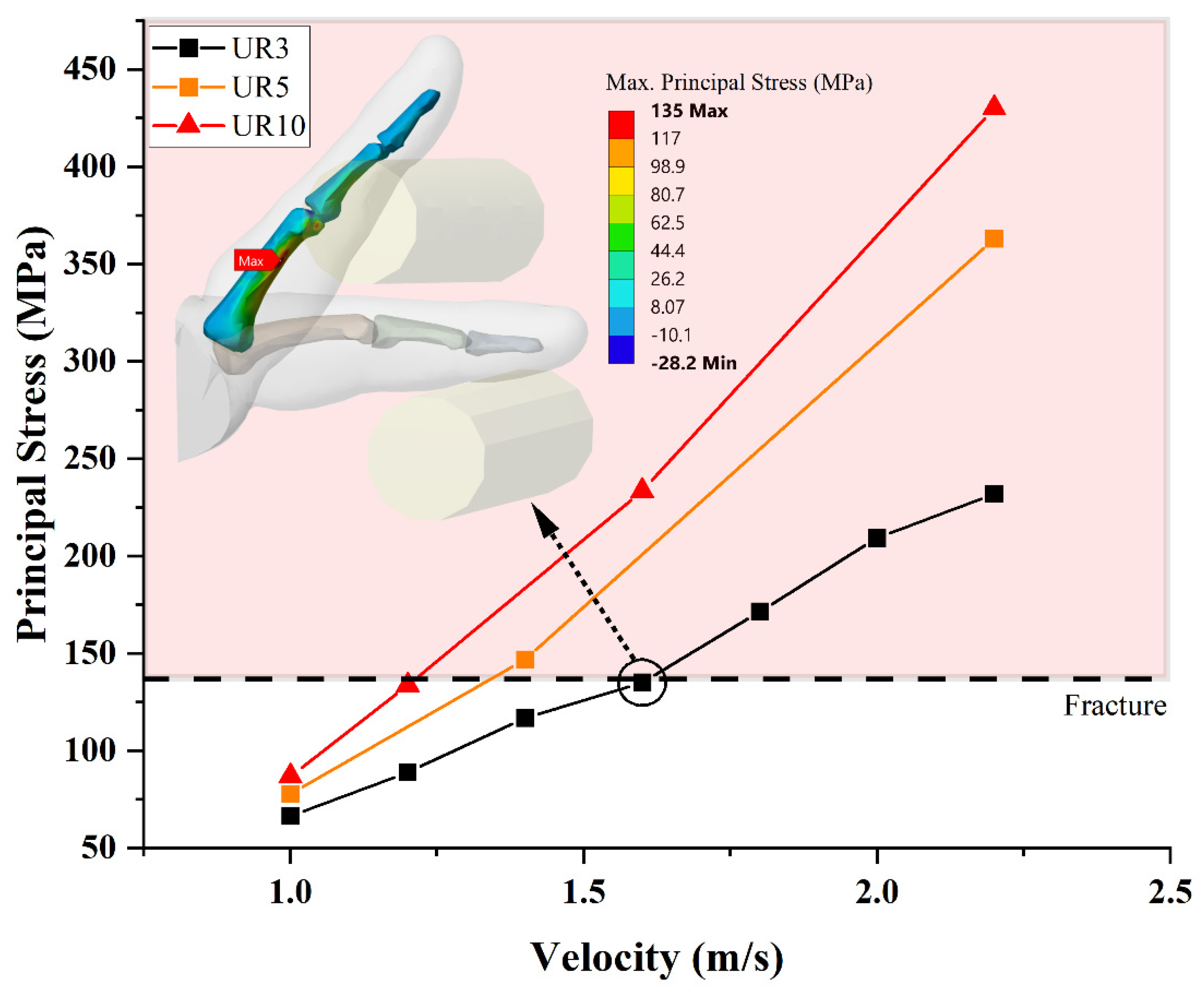

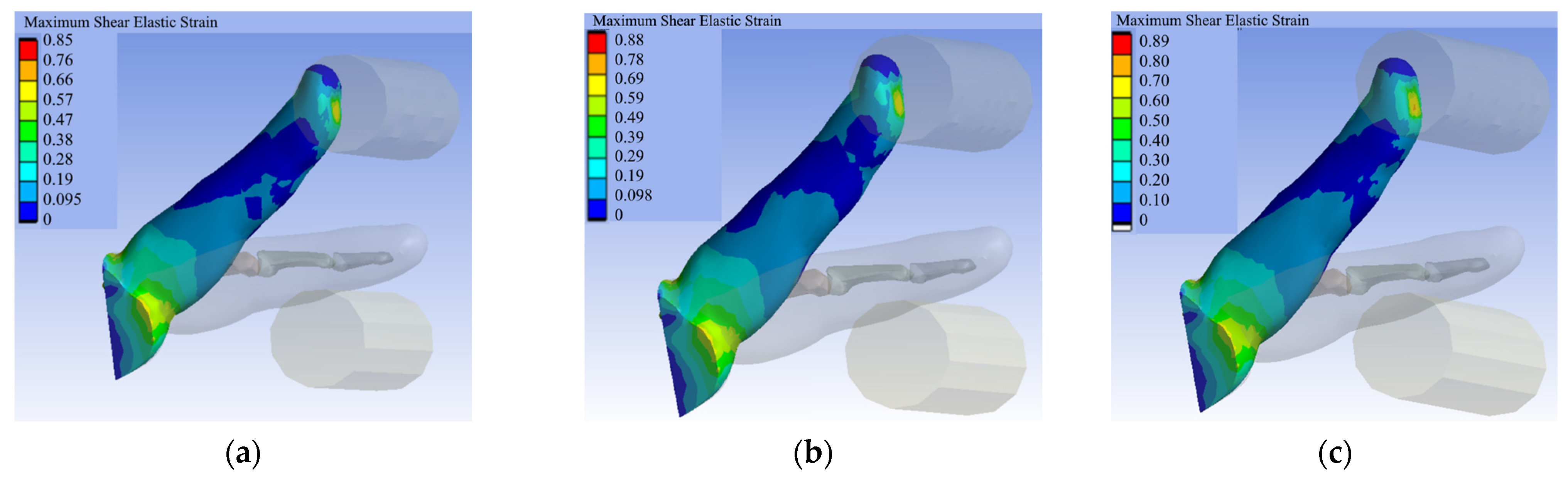



| Bone | |
| Young’s Modulus | 17 GPa |
| Poisson’s Ratio | 0.3 |
| Density, | 2000 kg/m3 |
| Skin | |
| Material Parameter, | 9 |
| Material Parameter, | 0.11 MPa |
| Compressibility, | 2 MPa−1 |
| Density, | 1040 kg/m3 |
| Joints | |
| Stiffness | 142 N·mm/° |
| Damping | 2.4 N·mm·s/° |
| Robot Size/Effective Mass | Velocity Range | Mode of Loading |
|---|---|---|
| UR3; Effective Mass: 3.6 kg | 1000 to 2200 mm/s | Flexion |
| UR5; Effective Mass: 7.2 kg | Hyper-Extension | |
| UR10; Effective Mass: 14.4 kg | Abduction |
| S# | Robot Size | Hyperextension | Flexion | Abduction |
|---|---|---|---|---|
| 1 | UR3; Effective Mass: 3.6 kg | 1520 mm/s | 1360 mm/s | 1000 mm/s |
| 2 | UR5; Effective Mass: 7.2 kg | 1300 mm/s | 1250 mm/s | 850 mm/s |
| 3 | UR10; Effective Mass: 14.4 kg | 1200 mm/s | 1150 mm/s | 800 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, U.; Rasheed, S.; Lughmani, W.A.; Kazim, T.; Khalid, A.; Pannek, J. Biomechanical Modeling of Human–Robot Accident Scenarios: A Computational Assessment for Heavy-Payload-Capacity Robots. Appl. Sci. 2023, 13, 1957. https://doi.org/10.3390/app13031957
Asad U, Rasheed S, Lughmani WA, Kazim T, Khalid A, Pannek J. Biomechanical Modeling of Human–Robot Accident Scenarios: A Computational Assessment for Heavy-Payload-Capacity Robots. Applied Sciences. 2023; 13(3):1957. https://doi.org/10.3390/app13031957
Chicago/Turabian StyleAsad, Usman, Shummaila Rasheed, Waqas Akbar Lughmani, Tayyaba Kazim, Azfar Khalid, and Jürgen Pannek. 2023. "Biomechanical Modeling of Human–Robot Accident Scenarios: A Computational Assessment for Heavy-Payload-Capacity Robots" Applied Sciences 13, no. 3: 1957. https://doi.org/10.3390/app13031957
APA StyleAsad, U., Rasheed, S., Lughmani, W. A., Kazim, T., Khalid, A., & Pannek, J. (2023). Biomechanical Modeling of Human–Robot Accident Scenarios: A Computational Assessment for Heavy-Payload-Capacity Robots. Applied Sciences, 13(3), 1957. https://doi.org/10.3390/app13031957











