Seismic Upgrade of Steel Frame Buildings by Using Damped Braces
Abstract
:1. Introduction
2. Modeling Approaches for Steel Structures in OpenSees
3. Description of the Case-Study Frames
4. Numerical Model in OpenSees
5. Design of the Seismic Rehabilitation
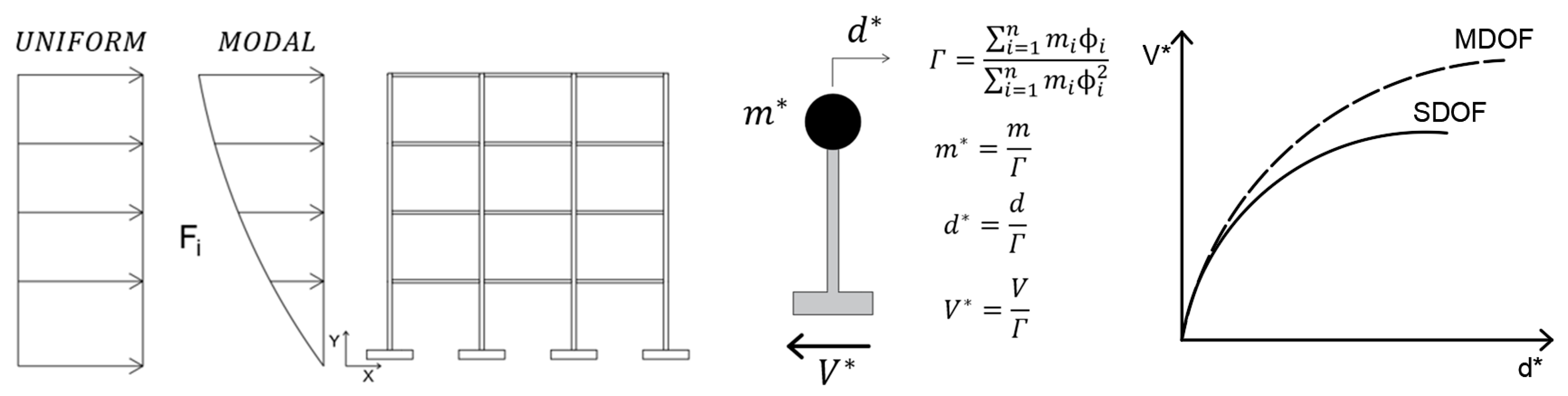
5.1. Step 1: Definition of the Main Frame Capacity Curve
5.2. Step 2: Definition of the Target Displacement and Construction of the Equivalent Bilinear Capacity Curve of the Main Frame
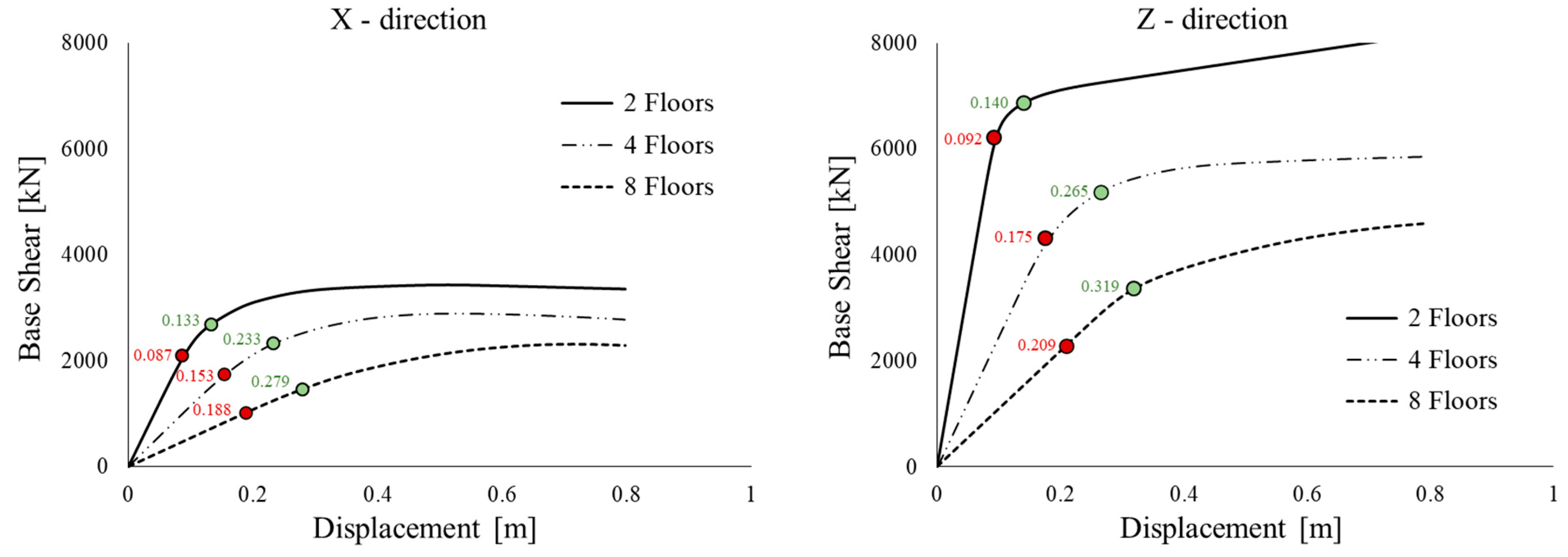
5.3. Step 3: Performance Check of the Main Frame
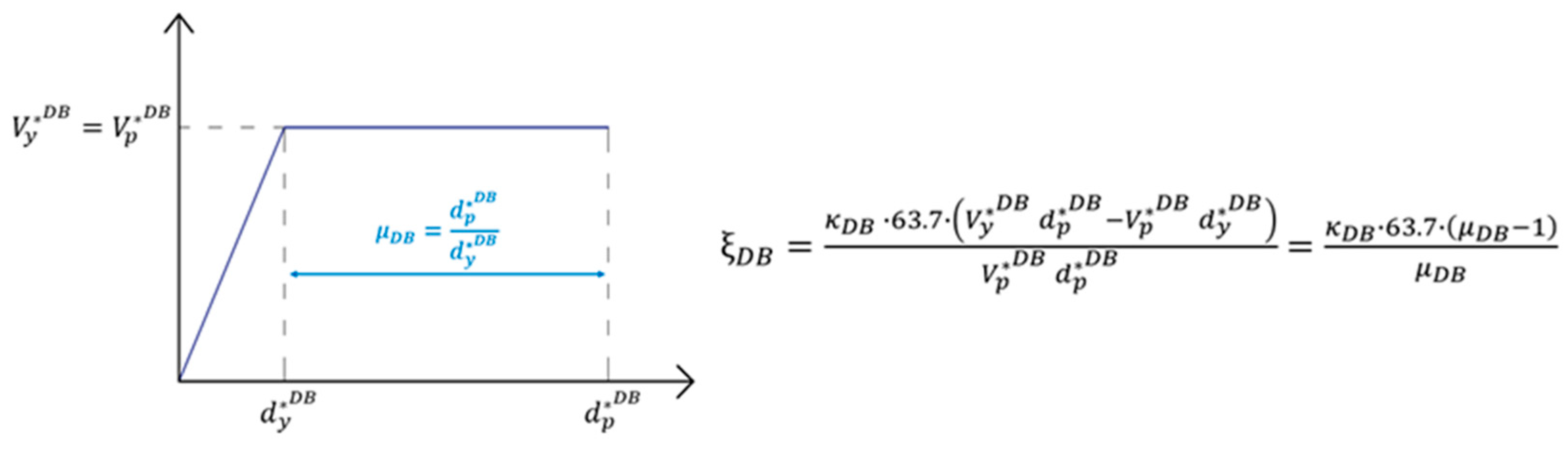
5.4. Step 4: Determination of the Equivalent Damped Brace System
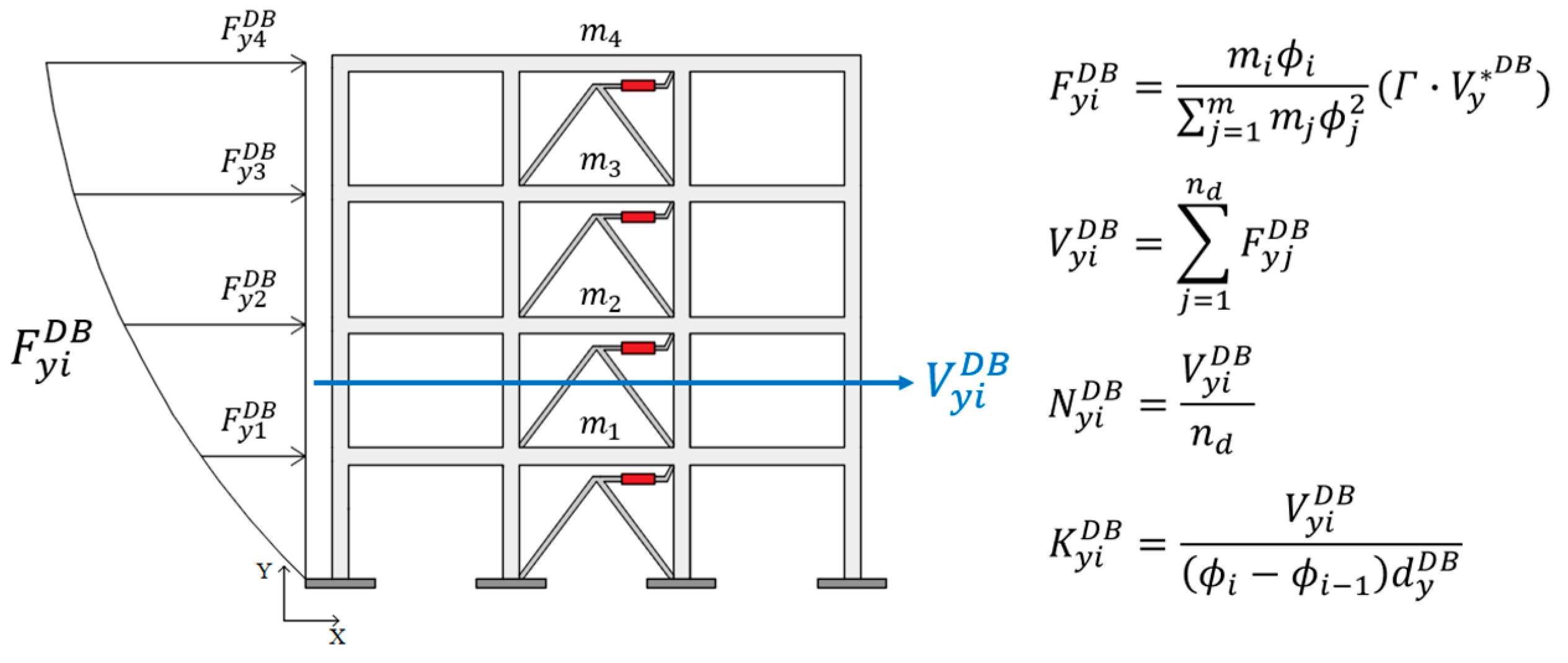
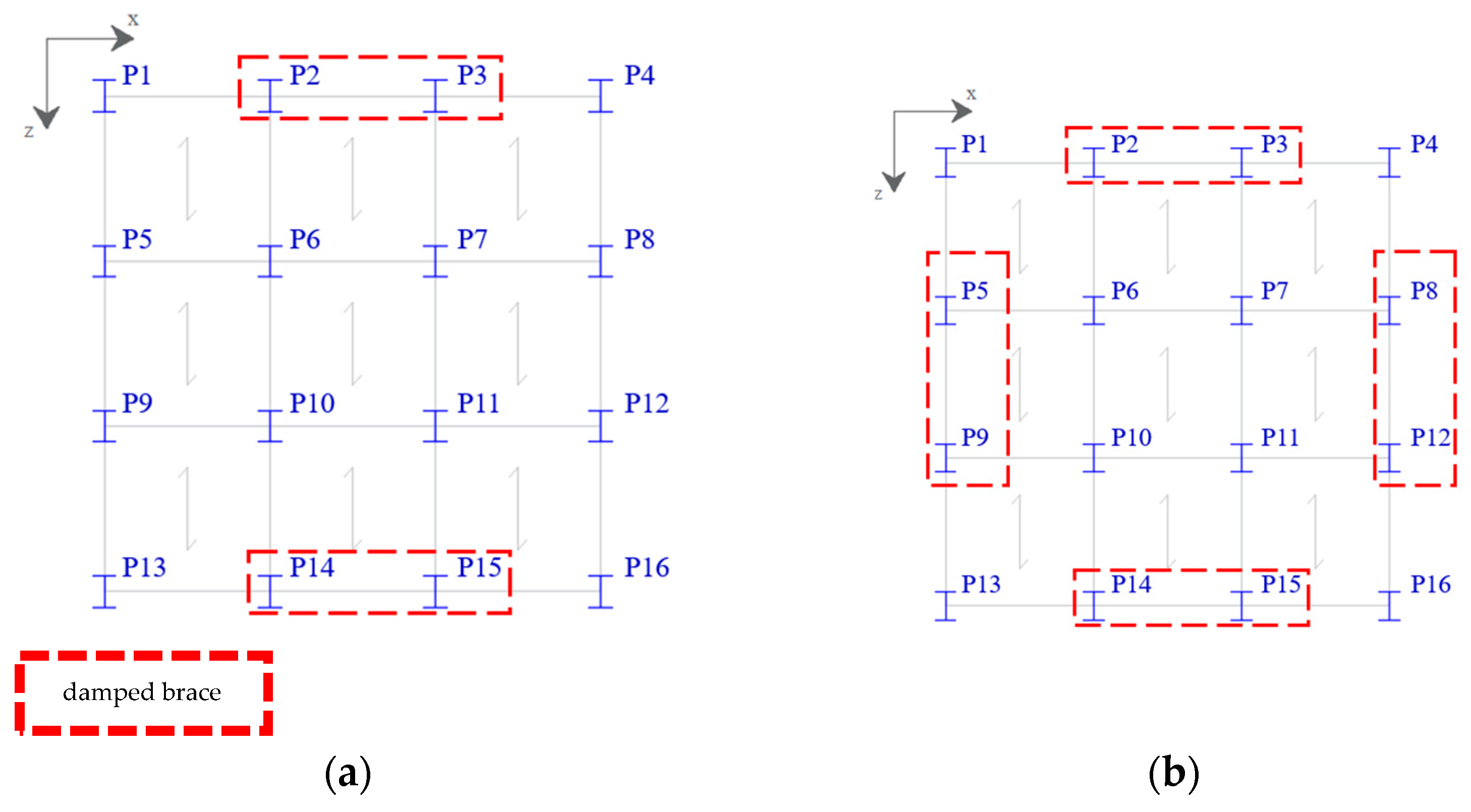
5.5. Step 5: Distribution of the Damped Braces across the Frame
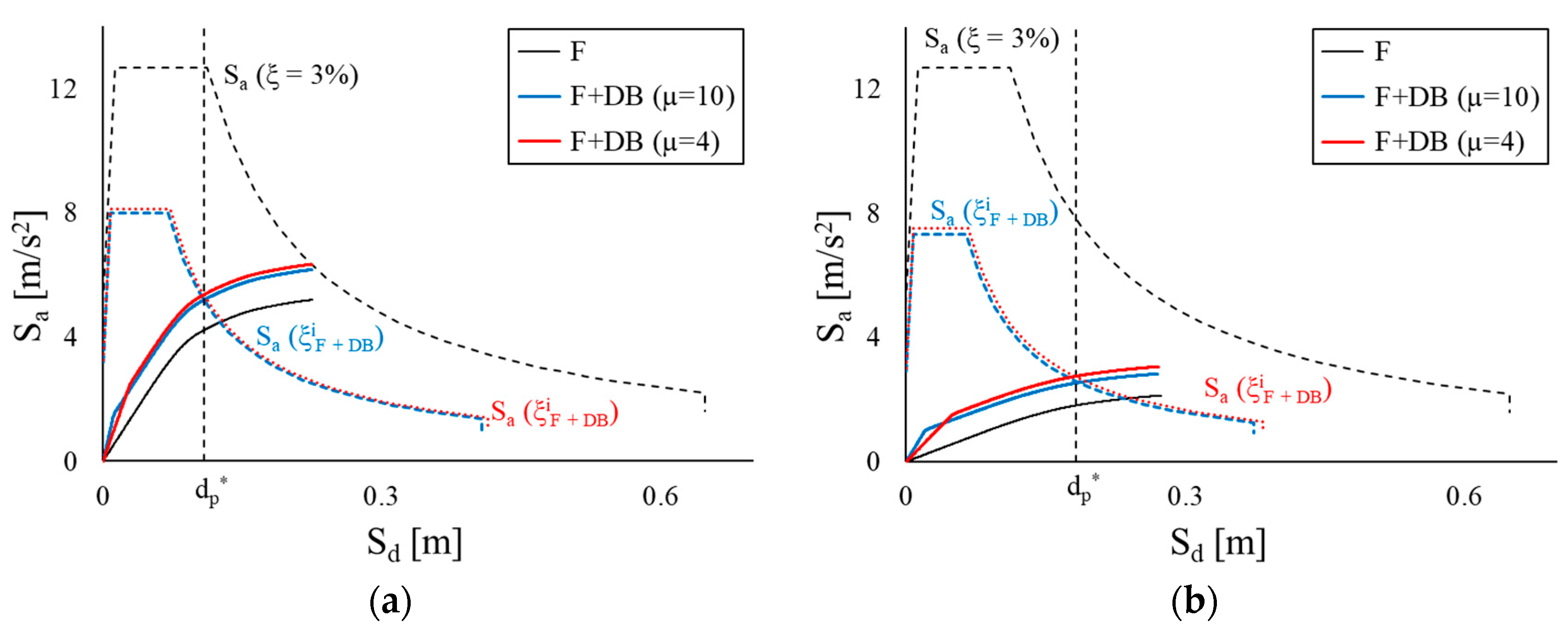
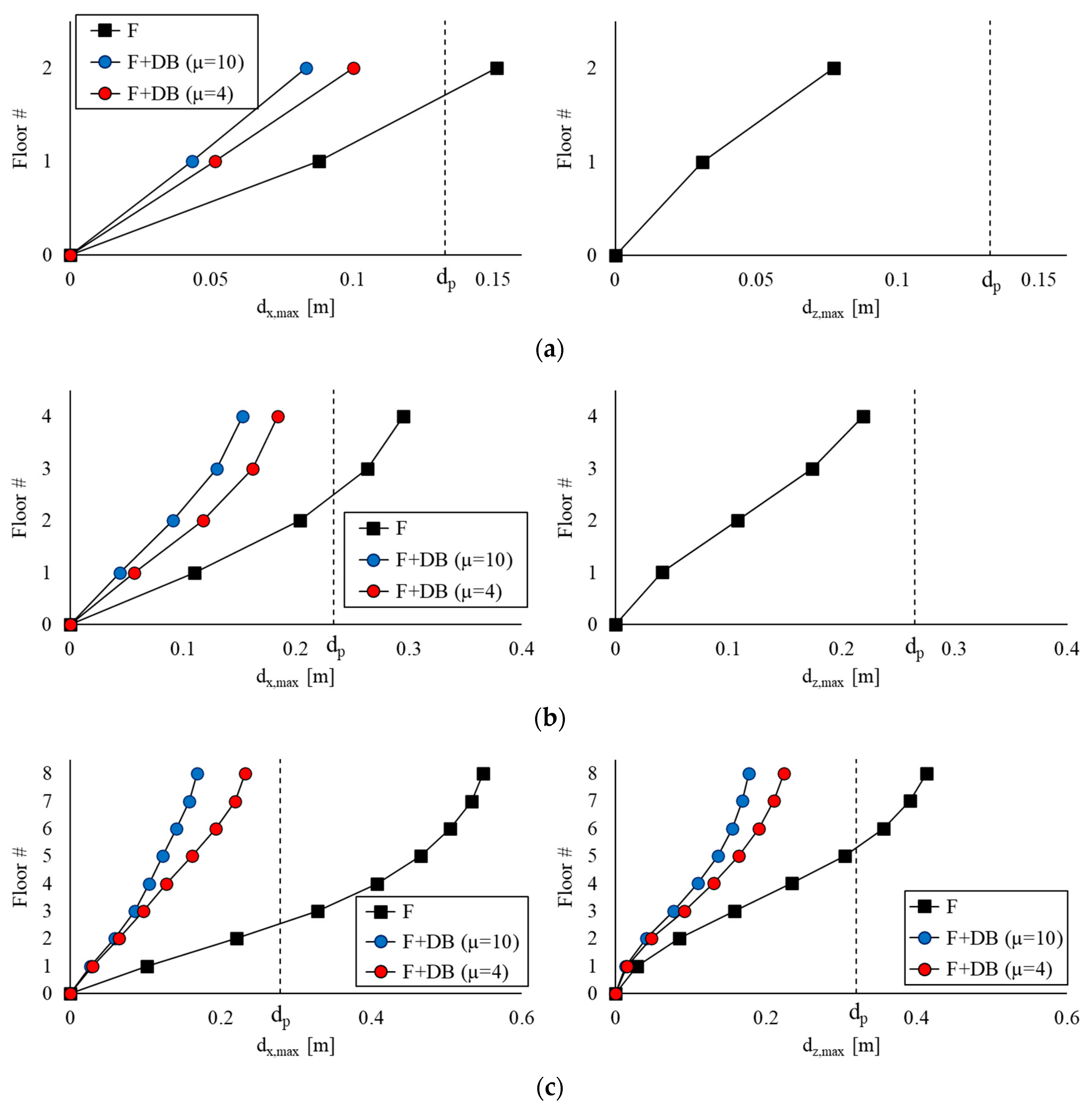
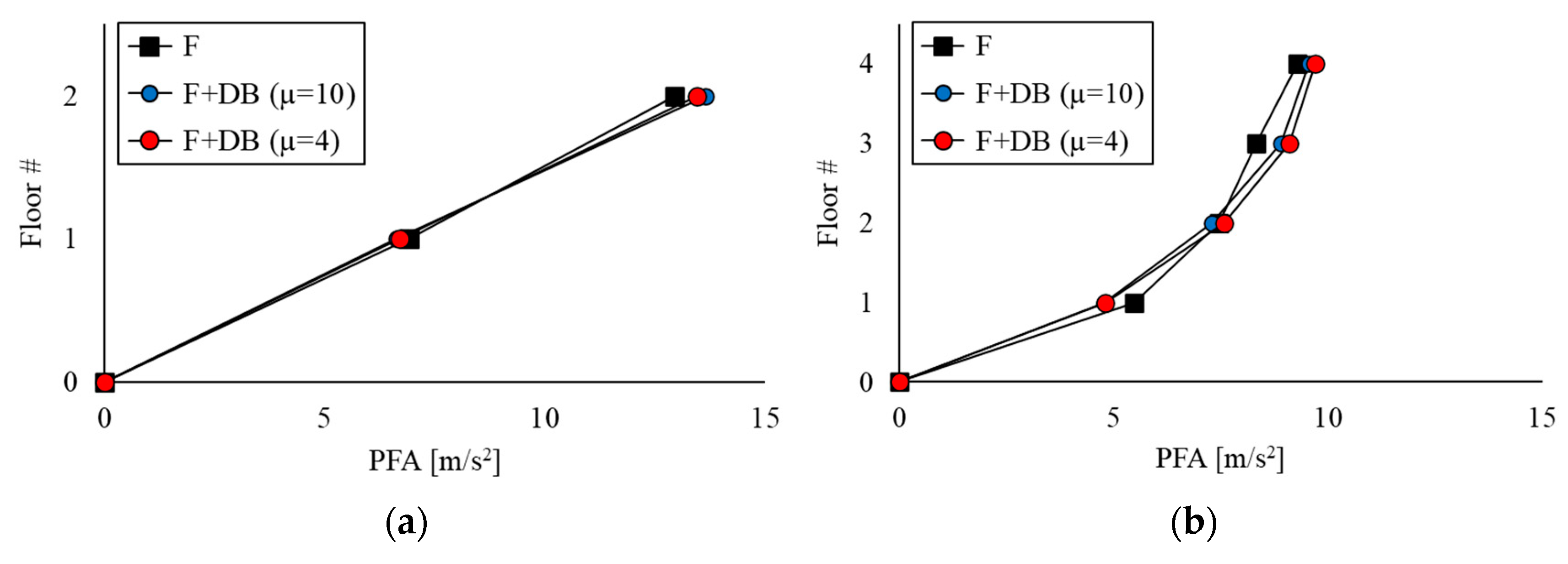
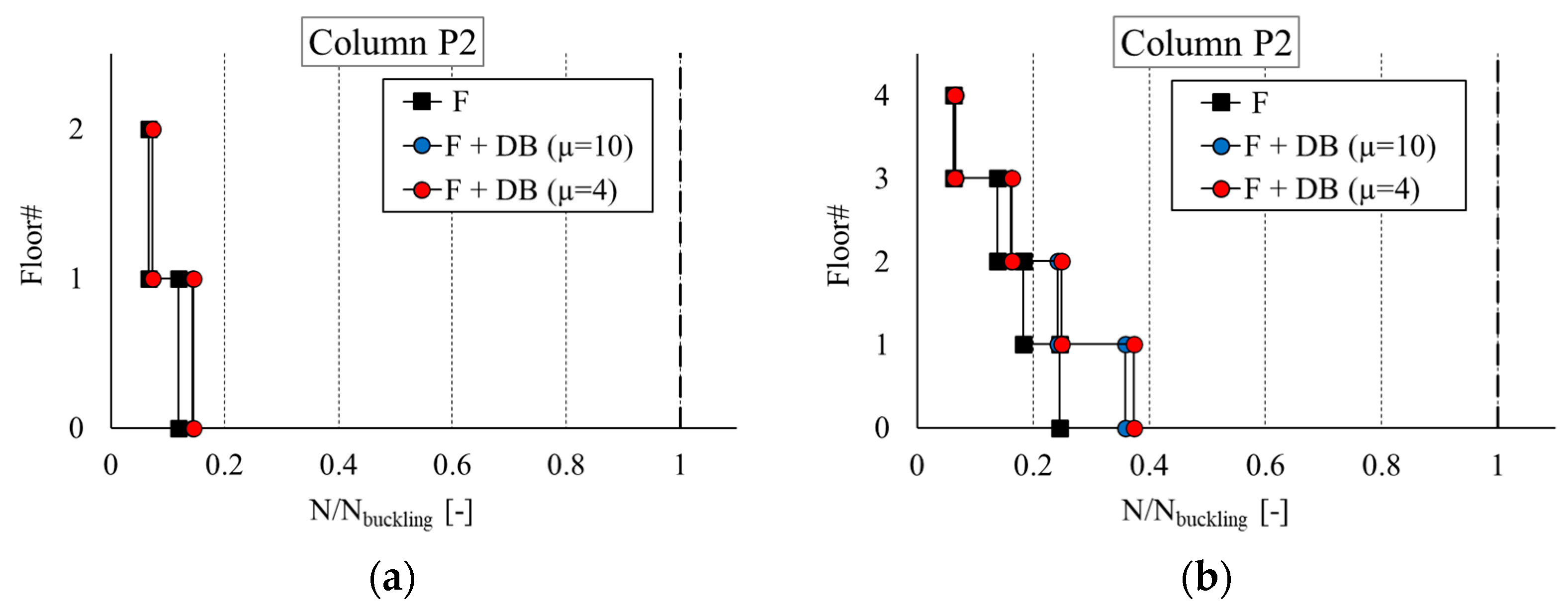
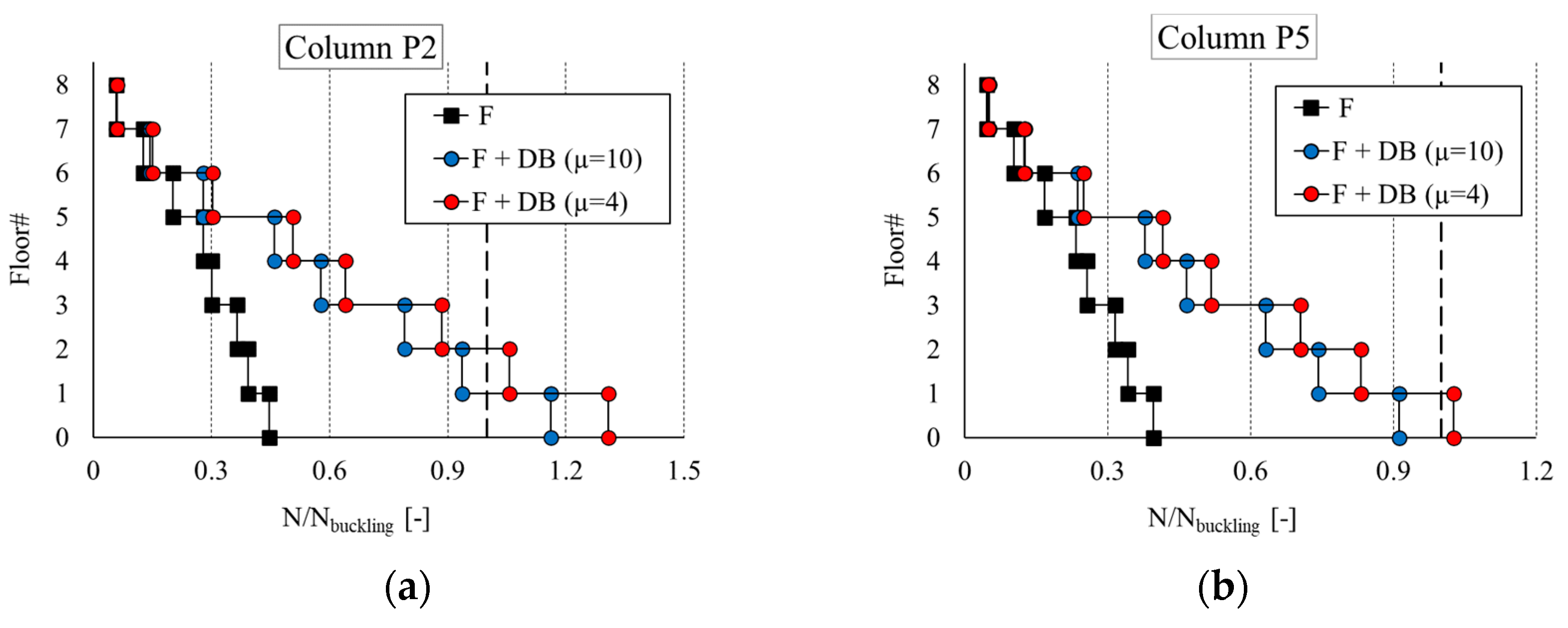
6. Seismic Response Assessment
7. Conclusions
- (1)
- The proposed procedure proved to be a viable means for proportioning the damped braces of the low- and mid-rise steel frames in order to achieve a target performance defined in terms of the maximum lateral displacement of the frame.
- (2)
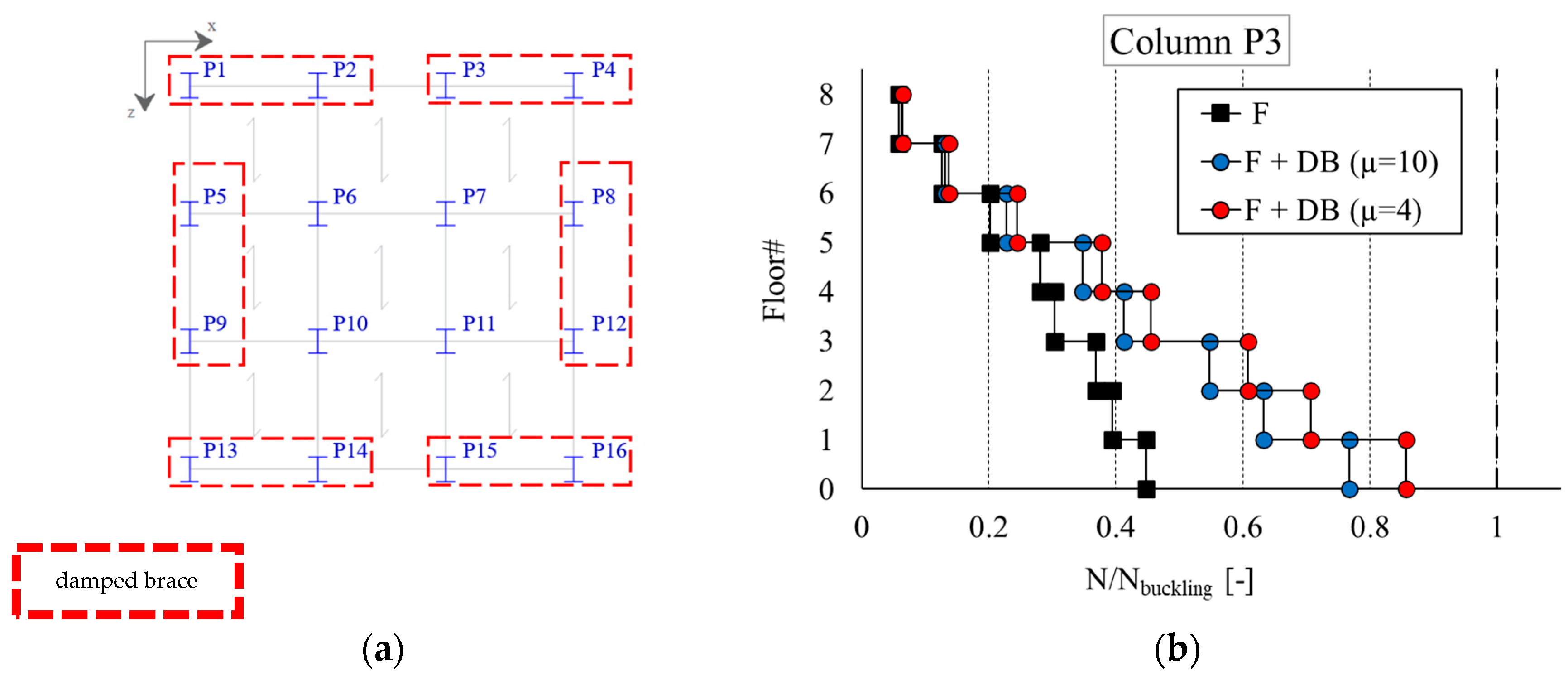
- The design of an effective dissipation brace system for a steel frame must take into account also the ensuing increase in the internal forces of the structural members of the bays where the braces are introduced. For mid-rise buildings, an issue is represented by the increase in axial force and possible buckling of the columns for the seismic loads. For these buildings, it is recommended to explore different layouts for the brace system, especially at the lower stories.
- (3)
- In this study, two ductility factors, representing the upper and lower bounds for the conventional hysteretic dampers, were examined. For low-rise buildings, the performance of the upgraded structure was scarcely affected by the characteristic of the dampers, while for the mid-rise frame a non-negligible influence of the ductility factor of the damper system was highlighted from the NLDAs.
- (4)
- The analyses showed that the design procedure is conservative, and that the structural displacement calculated via the NLDAs is significantly smaller than the design target; this difference tends to increase as the ductility of the dampers increases.
- (5)
- Even though more cases need to be examined to validate these outcomes, the study provides some guidance to professionals who have to tackle with the seismic upgrading of steel frames with damped brace systems, by illustrating a handy procedure for the design and dimensioning of the damper layout and giving some practical suggestions for the assessment of the overall structural response.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landolfo, R.; Formisano, A.; Di Lorenzo, G.; Di Filippo, A. Classification of european building stock in technological and typological classes. J. Build. Eng. 2022, 45, e103482. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P.; Stramondo, P. A multi-performance design method for seismic upgrading of existing RC frames by BRBs. Earthq. Eng. Struct. Dyn. 2017, 46, 1099–1119. [Google Scholar] [CrossRef]
- Cao, X.Y.; Shen, D.; Feng, D.C.; Wang, C.L.; Qu, Z.; Wu, G. Seismic retrofitting of existing frame buildings through externally attached sub-structures: State of the art review and future perspectives. J. Build. Eng. 2022, 57, 104904. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Li, Y. Assessment of various seismic fragility analysis approaches for structures excited by non-stationary stochastic ground motions. Mech. Syst. Signal. Process. 2023, 186, 109838. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Wu, G.; Wang, Z. Experimental and theoretical investigations of the existing reinforced concrete frames retrofitted with the novel external SC-PBSPC BRBF sub-structures. Eng. Struct. 2022, 256, 113982. [Google Scholar] [CrossRef]
- Bergami, A.V.; Nuti, C. A design procedure of dissipative braces for seismic upgrading structures. Earthq. Struct. 2013, 4, 85–105. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Displacement-Based Design procedure of damped braces for the seismic retrofitting of RC framed buildings. Bull. Earthq. Eng. 2015, 13, 2121–2143. [Google Scholar] [CrossRef]
- Mazza, F.; Mazza, M.; Vulcano, A. Displacement-Based seismic Design of hysteretic damped braces for retrofitting in-elevation irregular RC framed buildings. Soil Dyn. Earthq. Eng. 2015, 69, 115–124. [Google Scholar] [CrossRef]
- Di Cesare, A.; Ponzo, F.C. Seismic retrofit of reinforced concrete frame buildings with hysteretic bracing systems: Design procedure and behaviour factor. Shock. Vib. 2017, 2017, e2639361. [Google Scholar] [CrossRef]
- Nuzzo, I.; Losanno, D.; Caterino, N. Seismic design and retrofit of frames structures with hysteretic dampers: A simplified displacement-based procedure. Bull. Earthq. Eng. 2019, 17, 2787–2819. [Google Scholar] [CrossRef]
- Bruschi, E.; Quaglini, V.; Calvi, P.M. A simplified design procedure for seismic upgrade of frame structures equipped with hysteretic dampers. Eng. Struct. 2021, 251, e113504. [Google Scholar] [CrossRef]
- Bruschi, E. Seismic Retrofit of RC Framed Buildings with Supplementary Energy Dissipation: Modelling and Application of a Novel Lead Damper. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2021. [Google Scholar]
- Quaglini, V.; Pettorruso, C.; Bruschi, E. Experimental and numerical assessment of prestressed lead extrusion dampers. Int. J. Earthq. Eng. 2021, XXXVIII, 46–69. [Google Scholar]
- Quaglini, V.; Bruschi, E. Controllo passivo mediante controventi dissipativi. Principi generali, requisiti normativi ed evoluzione dei principali dispositivi a comportamento dipendente dallo spostamento. Structural 2022, 240, 09. [Google Scholar] [CrossRef]
- Freddi, F.; Tubaldi, E.; Ragni, L.; Dall’Asta, A. Probabilistic performance assessment of low-ductility reinforced concrete frames retrofitted with dissipative braces. Earthq. Eng. Struct. Dyn. 2013, 42, 993–1011. [Google Scholar] [CrossRef]
- Freddi, F.; Ghosh, J.; Kotoky, N.; Raghunandan, M. Device uncertainty propagation in low-ductility RC frame retrofitted with BRBs for seismic risk mitigation. Earthq. Eng. Struct. Dyn. 2021, 50, 2488–2509. [Google Scholar] [CrossRef]
- American Institute of Steel Construction. Seismic Provisions for Structural Steel Buildings; ANSI/AISC 341-16, ANSI/AISC 341-16; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE/SEI 7–16; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- EN 1993-1-1; Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- EN 1998–1; Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Building. European Committee for Standardization: Brussels, Belgium, 2005.
- Tartaglia, R.; D’Aniello, M.; Landolfo, R. Numerical simulation to predict the seismic performance of a 2-story steel moment-resisting frame. Materials 2020, 13, 4831. [Google Scholar] [CrossRef]
- Reinhorn, A.M. The Northridge, California Earthquaake of January 17, 1994: General Reconnaissance Report; Report No. NCEER-94-0005; National Centre for Earthquake Engineering Research: Buffalo, NY, USA, 1994. [Google Scholar]
- Youssef, N.F.G.; Bonowitz, D.; Gross, J.L. A Survey of Steel Moment-Resisting Frame Buildings Affected by the 1994 Northridge Earthquake; Report No. NISTR 56254; National Institute for Science and Technology: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Watanabe, E.; Sugiura, K.; Nagata, K.; Kitane, Y. Performances and damages to steel structures during 1995 Hyogoken–Nanbu earthquake. Eng. Struct. 1998, 20, 282–290. [Google Scholar] [CrossRef]
- Federal EmergencyManagement Agency. State of the Art Report on Past Performance of Steel Moment-Frame Buildings in Earthquakes; FEMA 355E; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Di Sarno, L.; Paolacci, F.; Sextos, A.G. Seismic performance assessment of existing steel buildings: A case study. Key Eng. Mater. 2018, 763, 1067–1076. [Google Scholar] [CrossRef]
- Di Sarno, L.; Freddi, F.; D’Aniello, M.; Kwon, O.S.; Wu, J.R.; Gutierrez-Urzua, F.; Landolfo, R.; Park, J.; Palios, X.; Strepelias, E. Assessment of existing steel frames: Numerical study, pseudo-dynamic testing and influence of masonry infills. J. Constr. Steel Res. 2021, 185, 106873. [Google Scholar] [CrossRef]
- Gutiérrez-Urzúa, F.; Freddi, F.; Di Sarno, L. Comparative analysis of code-based approaches for seismic assessment of existing steel moment resisting frames. J. Constr. Steel Res. 2021, 181, 106589. [Google Scholar] [CrossRef]
- Güneyisi, E.M. Seismic reliability of steel moment resisting framed buildings retrofitted with buckling restrained braces. Earthq. Eng. Struct. Dyn. 2012, 41, 853–874. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Fluid viscous damper-based seismic retrofit strategies of steel structures: General concepts and design applications. Adv. Steel Constr. 2009, 5, 322–339. [Google Scholar]
- Mazza, F.; Vulcano, A. Control of the earthquake and wind dynamic response of stee-framed buildings by using additional braces and/or viscoelastic dampers. Earthq. Eng. Struct. Dyn. 2011, 40, 155–174. [Google Scholar] [CrossRef]
- Ismail, M. Seismic retrofit of steel frame structures. Int. J. Eng. Inf. Sci. 2020, 15, 106–117. [Google Scholar] [CrossRef]
- Gutiérrez-Urzúa, F.; Freddi, F. Influence of the design objectives on the seismic performance of steel moment resisting frames retrofitted with buckling restrained braces. Earthq. Eng. Struct. Dyn. 2022, 51, 3131–3153. [Google Scholar] [CrossRef]
- Freddi, F.; Tubaldi, E.; Zona, A.; Dall’Asta, A. Seismic performance of dual systems coupling moment-resisting and buckling-restrained braced frames. Earthq. Eng. Struct. Dyn. 2021, 50, 329–353. [Google Scholar] [CrossRef]
- INNOSEIS. European Commission Research Programme of the Research Fund for Coal and Steel. Valorization of Innovative Anti-Seismic Devices. Work Package 4—Deliverable 4.3: Volume on Case Studies for Upgrading Existing Buildings. Available online: http://innoseis.ntua.gr/deliverables/INNOSEIS_D4.2_MidHighRiseCaseStudies.pdf (accessed on 6 June 2022).
- Kim, J.; Choi, H. Displacement-Based Design of supplemental dampers for seismic retrofit of a framed structure. J. Struct. Eng. 2006, 132, 873–883. [Google Scholar] [CrossRef]
- Lavan, O.; Dargush, G.F. Multi-objective evolutionary seismic design with passive energy dissipation systems. J. Earthq. Eng. 2009, 13, 758–790. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Design of hysteretic damped braces to improve the seismic performance of steel and R.C. framed structures. Int. J. Earthq. Eng. 2014, XXXI, 5–16. [Google Scholar]
- Ragni, L.; Zona, A.; Dall’Asta, A. Analytical expressions for preliminary design of dissipative bracing systems in steel frames. J. Constr. Steel Res. 2011, 67, 102–113. [Google Scholar] [CrossRef]
- Xie, Q. State of the art of buckling-restrained braces in Asia. J. Constr. Steel Res. 2005, 61, 727–748. [Google Scholar] [CrossRef]
- Freddi, F.; Galasso, C.; Cremen, G.; Dall’Asta, A.; Di Sarno, L.; Giaralis, A.; Gutiérrez-Urzúa, F.; Málaga-Chuquitaype, F.; Mitoulis, S.A.; Petrone, C.; et al. Innovations in earthquake risk reduction for resilience: Recent advances and challenges. Int. J. Disaster Risk Reduct. 2021, 60, 102267. [Google Scholar] [CrossRef]
- Tremblay, R.; Poncet, L.; Bolduc, P.; Neville, R.; DeVall, R. Testing and design of buckling restrained braces for canadian application. In Proceedings of the 13th World Conference in Earthquake Engineering 2004, Vancouver, BC, Canada, 1–6 August 2004; p. 200. [Google Scholar]
- Maley, T.J.; Sullivan, T.J.; Della Corte, G. Development of a displacement-based design method for steel dual systems with buckling-restrained braces and moment-resisting frames. J. Earthq. Eng. 2010, 14, 106–140. [Google Scholar] [CrossRef]
- Kalapodis, N.A.; Mucho, E.V.; Beskos, D.E. Seismic design of plane steel MRFS, EBFS and BRBFS by improved direct displacement-based design method. Soil Dyn. Earthq. Eng. 2022, 153, 107111. [Google Scholar] [CrossRef]
- Ferraioli, M.; Lavino, A. A Displacement-Based Design Method for seismic retrofit of RC buildings using dissipative braces. Math. Probl. Eng. 2018, 5364564, 28. [Google Scholar] [CrossRef]
- Kim, J.; Seo, Y. Seismic design of low-rise steel frames with buckling-restrained braces. Eng. Struct. 2004, 26, 543–551. [Google Scholar] [CrossRef]
- Quaglini, V.; Bruschi, E.; Pettorruso, C. Dimensionamento di dispositivi dissipativi per la riabilitazione sismica di strutture intelaiate. Structural 2021, 237. paper 25. [Google Scholar] [CrossRef]
- Bruschi, E.; Quaglini, V.; Calvi, P.M. A simplified design procedure to improve the seismic performance of RC framed buildings with hysteretic damped braces. In Proceedings of the New Metropolitan Perspectives 2022—5th International Symposium “Post COVID Dynamics: Green and Digital Transition, between Metropolitan and Return to Villages’ Perspectives”, Reggio Calabria, Italy, 25–27 May 2022; Calabrò, F., Della Spina, F., Piñeira Mantiñán, M.J., Eds.; Springer: Reggio Calabria, Italy, 2022; Volume 482, pp. 2173–2182, ISBN 978-3-031-06825-6. [Google Scholar]
- ATC-40; Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council: Redwood City, CA, USA, 1996.
- Fajfar, P. Capacity spectrum method based on inelastic demand spectra. Earthq. Eng. Struct. Dyn. 1999, 28, 979–993. [Google Scholar] [CrossRef]
- Italian Council of Public Works. Technical Standards on Constructions; Italian Council of Public Works: Rome, Italy, 2018. (In Italian) [Google Scholar]
- Italian Council of Public Works. Commentary on the Technical Standards on Constructions; Italian Council of Public Works: Rome, Italy, 2019. (In Italian) [Google Scholar]
- EN 1998–3; Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Vamvatsikos, D.; Bakalis, K.; Kohrangi, M.; Pyrza, S.; Castiglioni, C.A.; Kanyilmaz, A.; Morelli, F.; Stratan, A.; D’Aniello, M.; Calado, L.; et al. A risk-consistent approach to determine EN1998 behaviour factors for lateral load resisting systems. Soil Dyn. Earthq. Eng. 2020, 131, 106008. [Google Scholar] [CrossRef]
- De Domenico, D.; Gandelli, E.; Quaglini, V. Cyclic engagement of hysteretic steel dampers in braced buildings: A parametric investigation. Bull. Earthq. Eng. 2021, 19, 5219–5251. [Google Scholar] [CrossRef]
- McKenna, F.; Fenves, G.I.; Scott, M.H. Open System for Earthquake Engineering Simulation; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2000. [Google Scholar]
- OpenSeesWiki Online Manual. Available online: https://opensees.berkeley.edu/wiki/index.php/Main_Page (accessed on 9 April 2022).
- Bosco, M.; Tirca, L. Numerical simulation of steel I-shaped beams using a fiber-based damage accumulation model. Constr. Steel Res. 2017, 133, 241–255. [Google Scholar] [CrossRef]
- Ribeiro, F.L.; Barbosa, A.R.; Scott, M.H.; Neves, L.C. Deterioration modeling of steel moment-resisting frames using finite-length plastic hinge force based beam columns elements. J. Struct. Eng. 2015, 141, e04014112. [Google Scholar] [CrossRef]
- Bruschi, E.; Calvi, P.M.; Quaglini, V. Concentrated plasticity modelling of RC frames in time-history analyses. Eng. Struct. 2021, 243, e112716. [Google Scholar] [CrossRef]
- Ferraioli, M. Evaluation of dynamic increase factor in progressive collapse analysis of steel frame structures considering catenary action. Steel Comp. Struct. 2019, 30, 253–269. [Google Scholar] [CrossRef]
- Mohebi, B.; Chegini, A.H.; Miri, A.R. A new damage index for steel MRFs based on incremental dynamic analysis. J. Constr. Steel Res. 2019, 156, 137–154. [Google Scholar] [CrossRef]
- Pandikkadavath, M.S.; Shaijal, K.M.; Mangalathu, S.; Davis, R. Seismic robustness assessment of steel moment resisting frames employing material uncertainty incorporated incremental dynamic analysis. J. Constr. Steel Res. 2022, 191, e107200. [Google Scholar] [CrossRef]
- Guan, X.; Burton, H.; Shokrabadi, M. A database of seismic design nonlinear models, and seismic responses for steel moment resisting frame buildings. Earthq. Spectra 2021, 37, 1199–1222. [Google Scholar] [CrossRef]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 2005, 34, 1489–1511. [Google Scholar] [CrossRef]
- Chopra, A.K.; McKenna, F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation. Earthq. Eng. Struct. Dyn. 2016, 45, 193–211. [Google Scholar] [CrossRef]
- Ferraioli, M. Multi-mode pushover procedure for deformation demand estimates of steel moment-resisting frames. Int. J. Steel Struct. 2017, 17, 653–676. [Google Scholar] [CrossRef]
- Jin, S.; Du, H.; Bai, J. Seismic performance assessment of steel frame structures equipped with buckling-restrained slotted steel plate shear walls. J. Constr. Steel Res. 2021, 182, e106699. [Google Scholar] [CrossRef]
- Mirjalili, M.R.; Rofooei, F.R. The modified dynamic-based pushover analysis of steel moment resisting frames. Struct. Des. Tall Spec. Build. 2017, 26, e1378. [Google Scholar] [CrossRef]
- Di Sarno, L.; Wu, J.R. Fragility assessment of existing low-rise steel moment-resisting frames with masonry infills under mainshock-aftershock earthquake sequences. Bull. Earthq. Eng. 2021, 19, 2483–2504. [Google Scholar] [CrossRef]
- Scott, M.H.; Fenves, G.L. Plastic hinge integration methods for force-based beam-column elements. J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Lignos, D.G.; Krawinkler, H. Development and utilization of structural component databases for performance-based earthquake engineering. J. Struct. Eng. 2013, 139, 1382–1394. [Google Scholar] [CrossRef]
- Gioncu, V.; Pectu, D. Available rotation capacity of wide-flange beams and beam-columns Part 1. Theoretical approaches. J. Constr. Steel Res. 1997, 43, 161–217. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Lisbon, Portugal; 1973; Volume 11, pp. 15–22. [Google Scholar]
- Barbagallo, F.; Bosco, M.; Ghersi, A.; Marino, E.M.; Rossi, P.P. Seismic assessment of steel MRFs by cyclic pushover analysis. Open Constr. Build. Tech. J. 2019, 13, 12–26. [Google Scholar] [CrossRef]
- EN 1990; Basis of Structural Design. Eurocode 1. European Committee for Standardization: Brussels, Belgium, 2005.
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Seismic design and performance of dual structures with BRBs and semi-rigid connections. J. Constr. Steel Res. 2019, 158, 306–316. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Achieving a more effective concentric braced frame by the double-stage yield BRB. Eng. Struct. 2019, 186, 484–497. [Google Scholar] [CrossRef]
- Uriz, P.; Mahin, S.A. Toward Earthquake-Resistant Design of Concentrically Braced Steel-Frame Structures; PEER Report 2008/08; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2008. [Google Scholar]
- Xuewei, C.; Xiaolei, H.; Cheang, J.; Shengyi, L.; Guiniu, M. Dynamic inelastic numerical simulation for a shaking table test of a full scale steel moment frame structure based on OpenSEES. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Report EERC 83-19; Earthquake Engineering Research Center: Berkeley, CA, USA, 1983. [Google Scholar]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Sullivan, T.; Maley, T.; Calvi, G.M. Seismic response of steel moment resisting frames designed using a Direct DBD procedure. In Proceedings of the 8th International Conference on Structural Dynamics, EURODYN 2011, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Keykhosravi, A.; Aghayari, R. Evaluating response modification factor (R) of reinforced concrete frames with chevron brace equipped with steel slit damper. KSCE J. Civil. Eng. 2017, 21, 1417–1423. [Google Scholar] [CrossRef]
- Fahiminia, M.; Ghaderi, M.R.; Zahrai, S.M. Seismic performance of chevron braced frames with shape memory alloy vertical shear link. Struct. Des. Tall. Spec. Build. 2019, 28, e1658. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Lago, A. Towards a simplified Direct DBD procedure for the seismic design of moment resisting frames with viscous dampers. Eng. Struct. 2012, 35, 140–148. [Google Scholar] [CrossRef]
- Sullivan, T.J. Direct displacement-base seismic design of steel eccentrically braced frame structures. Bull. Earthq. Eng. 2013, 11, 2197–2231. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Di Cesare, A.; Telesca, A.; Pavese, A.A.; Furinghetti, M. Advanced modelling and risk analysis of RC buildings with sliding isolation systems designed by the Italian Seismic Code. Appl. Sci. 2021, 11, 1938. [Google Scholar] [CrossRef]
- Gandelli, E.; Taras, A.; Distl, J.; Quaglini, V. Seismic retrofit of hospitals by means of hysteretic braces: Influence on acceleration-sensitive non-structural components. Front. Built. Environ. 2019, 5, e100. [Google Scholar] [CrossRef]
- Scozzese, F.; Gioiella, L.; Dall’Asta, A.; Ragni, L.; Tubaldi, E. Influence of viscous dampers ultimate capacity on the seismic reliability of building structures. Struct. Saf. 2021, 91, e102096. [Google Scholar] [CrossRef]
- Castaldo, P.; Tubaldi, E.; Selvi, F.; Gioiella, L. Seismic performance of an existing RC structure retrofitted with buckling restrained braces. J. Build. Eng. 2021, 33, 101688. [Google Scholar] [CrossRef]
- Greco, A.; Caddemi, S.; Caliò, I.; Fiore, I. A Review of Simplified Numerical Beam-like Models of Multi-Storey Framed Buildings. Buildings 2022, 12, 1397. [Google Scholar] [CrossRef]
- SIMQKE (SIMulation of Earthquake Ground Motions). Available online: https://gelfi.unibs.it/software/simqke/simqke_gr.htm (accessed on 10 July 2022).
- Bruschi, E.; Quaglini, V. Assessment of a novel hysteretic friction damper for the seismic retrofit of reinforced concrete frame structures. Structures 2022, 46, 793–811. [Google Scholar] [CrossRef]
- Bungale, S.T. Wind and Earthquake Resistant Buildings Structural Analysis and Design, 1st ed.; Marcel Dekker: New York, NY, USA, 2005; ISBN 978-04-2909-603-7. [Google Scholar]
- MacRae, G.A.; Urmson, C.R.; Walpole, W.R.; Moss, P.; Hyde, K.; Clifton, C. Axial shortening of steel columns in buildings subjected to earthquakes. Bull. N. Z. Soc. Earthq. Eng. 2009, 42, 275–287. [Google Scholar] [CrossRef]
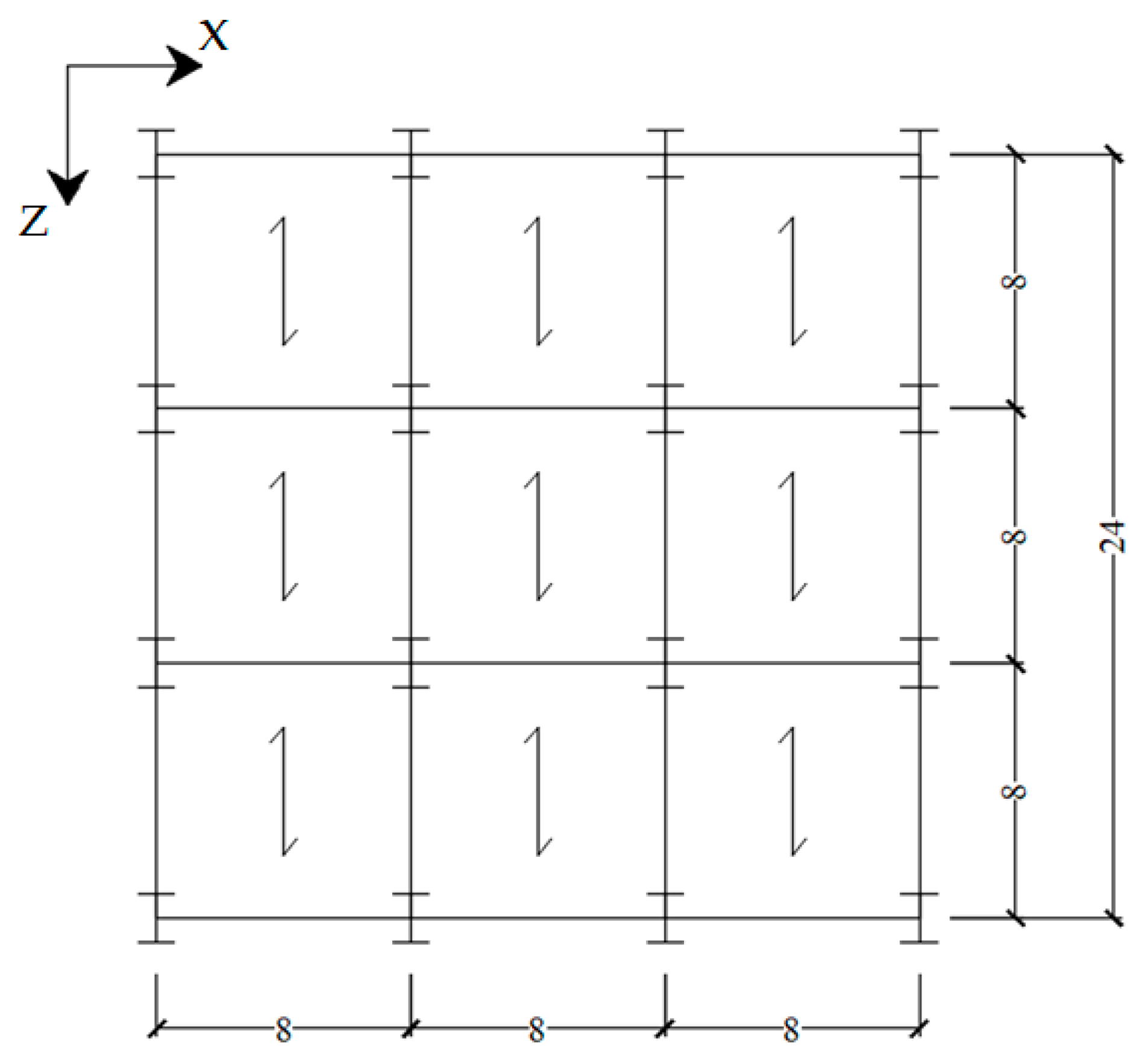
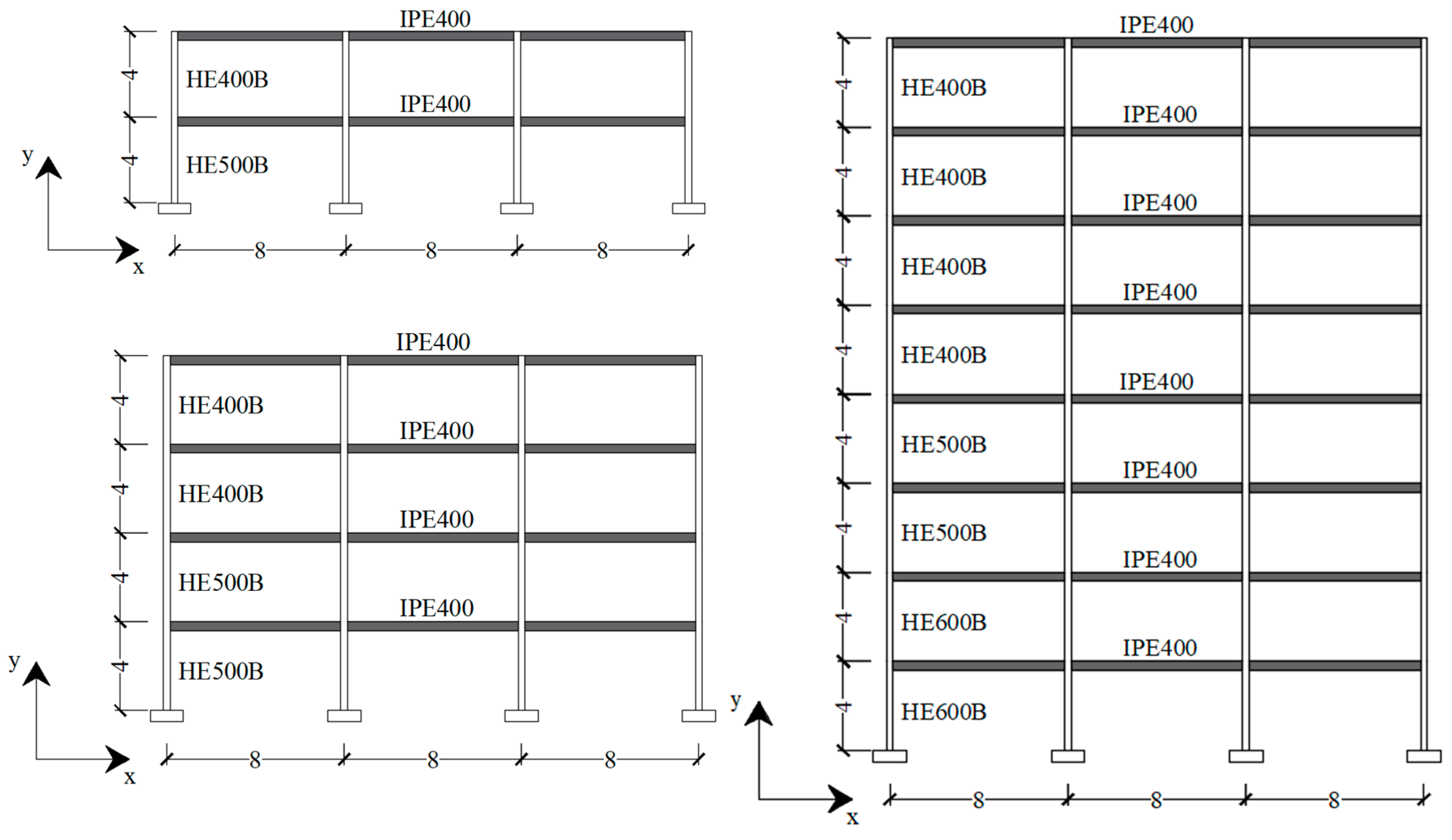





| Story | G [kN/m2] | Q [kN/m2] |
|---|---|---|
| 1 to n − 1 | 4.11 | 3.80 |
| n (roof) | 3.74 | 3.80 |
| Case-Study MRF | Direction | Γ [-] | [ton] | [m] | [kN] | [m] | [kN] | [%] |
|---|---|---|---|---|---|---|---|---|
| two-story | 1.22 | 523.4 | 0.072 | 1729.0 | 0.109 | 2210.8 | 8.11 | |
| 1.22 | 523.4 | 0.076 | 5085.2 | 0.0115 | 5616.6 | 15.77 | ||
| four-story | 1.27 | 1019.9 | 0.120 | 1380.7 | 0.183 | 1824.6 | 6.43 | |
| 1.31 | 994.22 | 0.134 | 3306.6 | 0.203 | 3967.0 | 10.94 | ||
| eight-story | 1.29 | 2046.55 | 0.146 | 793.9 | 0.217 | 1141.0 | 1.48 | |
| 1.31 | 2011.13 | 0.160 | 1750.4 | 0.244 | 2572.6 | 1.62 |
| Case-Study MRF | Direction | [m] | [m] | [kN] | [kN/mm] | [kN/mm] | |
|---|---|---|---|---|---|---|---|
| Two-story | X | 4 | 0.027 | 0.11 | 588.93 | 21.57 | 5.39 |
| 10 | 0.011 | 0.11 | 503.50 | 46.10 | 4.61 | ||
| Four-story | X | 4 | 0.046 | 0.18 | 951.52 | 20.80 | 5.20 |
| 10 | 0.018 | 0.18 | 810.93 | 44.32 | 4.43 | ||
| Eight-story | X | 4 | 0.054 | 0.22 | 2212.45 | 40.77 | 10.19 |
| Z | 0.061 | 0.24 | 1657.90 | 27.15 | 6.79 | ||
| X | 10 | 0.022 | 0.22 | 1888.77 | 87.01 | 8.70 | |
| Z | 0.024 | 0.24 | 1413.71 | 57.87 | 5.79 |
| Story | ||||
|---|---|---|---|---|
[kN/mm] | [kN] | [kN/mm] | [kN] | |
| 2nd | 29.5 | 232.7 | 63.1 | 199.0 |
| 46.7 | 357.9 | 99.7 | 306.0 | |
| Story | ||||
|---|---|---|---|---|
[kN/mm] | [kN] | [kN/mm] | [kN] | |
| 4th | 52.5 | 214.1 | 111.9 | 182.5 |
| 3rd | 55.4 | 412.3 | 118.0 | 351.4 |
| 2nd | 61.3 | 547.5 | 130.6 | 466.6 |
| 88.2 | 606.4 | 187.9 | 516.8 | |
| X-Direction | Z-Direction | |||||||
|---|---|---|---|---|---|---|---|---|
| Story | ||||||||
[kN/mm] | [kN] | [kN/mm] | [kN] | [kN/mm] | [kN] | [kN/mm] | [kN] | |
| 8th | 282.2 | 370.0 | 602.3 | 315.9 | 139.8 | 290.2 | 298.0 | 247.4 |
| 7th | 300.5 | 756.3 | 641.3 | 645.6 | 168.9 | 588.3 | 360.1 | 501.6 |
| 6th | 302.6 | 1111.6 | 645.8 | 949.0 | 173.5 | 857.0 | 369.9 | 730.8 |
| 5th | 303.7 | 1421.7 | 648.1 | 1213.7 | 175.2 | 1084.1 | 373.4 | 924.4 |
| 4th | 325.3 | 1675.0 | 694.2 | 1429.9 | 193.7 | 1259.6 | 413.0 | 1074.1 |
| 3rd | 327.8 | 1865.3 | 699.6 | 1592.4 | 213.5 | 1380.5 | 455.1 | 1177.2 |
| 2nd | 349.0 | 1985.3 | 744.9 | 1694.9 | 274.1 | 1446.7 | 584.2 | 1233.6 |
| 1st | 510.8 | 2034.9 | 1090.2 | 1737.2 | 585.5 | 1468.1 | 1248.2 | 1251.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruschi, E.; Quaglini, V.; Zoccolini, L. Seismic Upgrade of Steel Frame Buildings by Using Damped Braces. Appl. Sci. 2023, 13, 2063. https://doi.org/10.3390/app13042063
Bruschi E, Quaglini V, Zoccolini L. Seismic Upgrade of Steel Frame Buildings by Using Damped Braces. Applied Sciences. 2023; 13(4):2063. https://doi.org/10.3390/app13042063
Chicago/Turabian StyleBruschi, Eleonora, Virginio Quaglini, and Luca Zoccolini. 2023. "Seismic Upgrade of Steel Frame Buildings by Using Damped Braces" Applied Sciences 13, no. 4: 2063. https://doi.org/10.3390/app13042063
APA StyleBruschi, E., Quaglini, V., & Zoccolini, L. (2023). Seismic Upgrade of Steel Frame Buildings by Using Damped Braces. Applied Sciences, 13(4), 2063. https://doi.org/10.3390/app13042063







