A Robust Health Prognostics Technique for Failure Diagnosis and the Remaining Useful Lifetime Predictions of Bearings in Electric Motors
Abstract
:Featured Application
Abstract
1. Introduction
2. Background
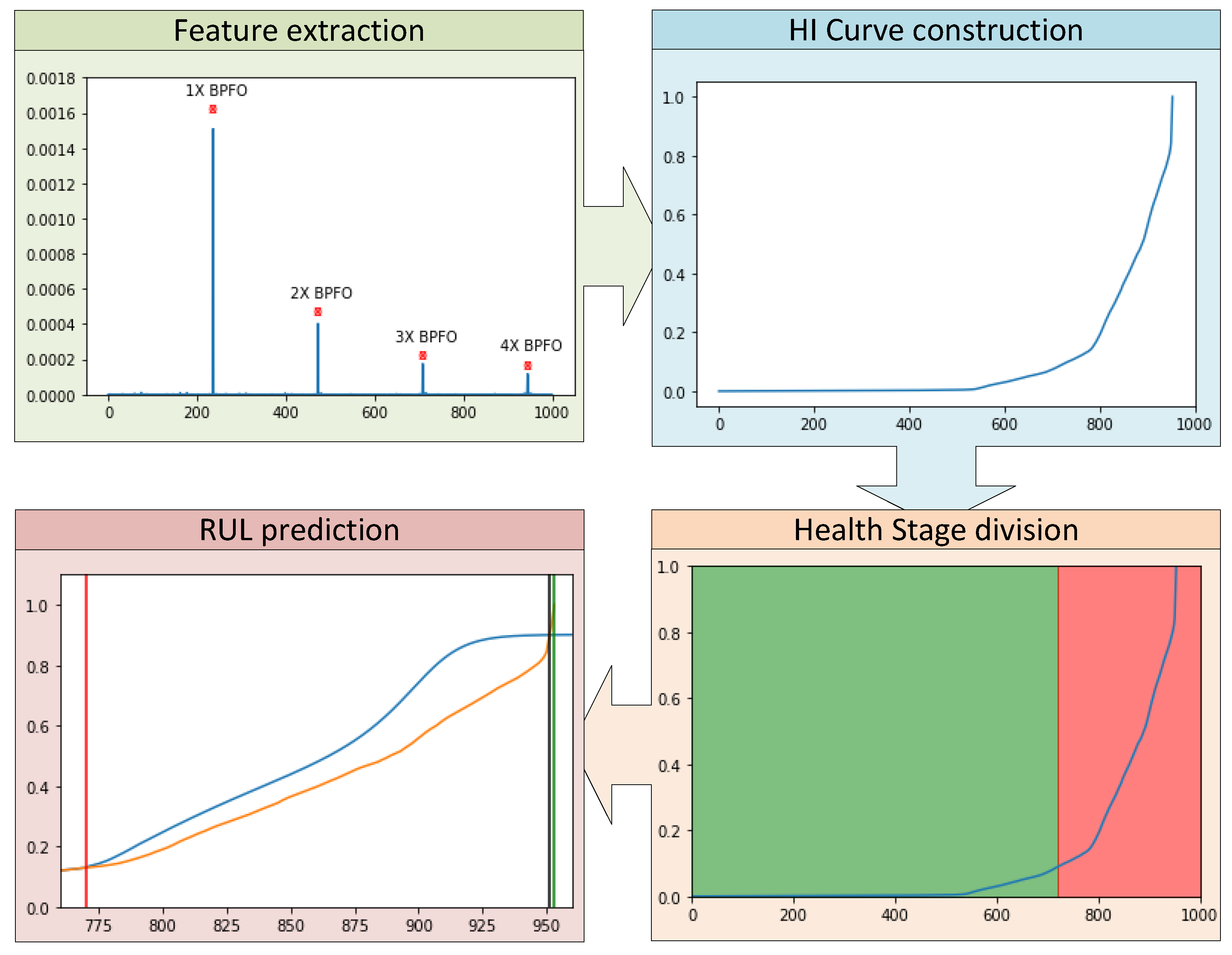
3. Proposed Solution
3.1. Feature Extraction
3.2. HI Curve Construction
3.3. Health Stage Division
3.4. RUL Prediction
4. Results
4.1. Model Training
4.2. Model Testing
4.3. Model Discrimination
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hashemian, H. Wireless sensors for predictive maintenance of rotating equipment in research reactors. Ann. Nucl. Energy 2011, 38, 665–680. [Google Scholar] [CrossRef]
- Bazurto, A.J.; Quispe, E.C.; Mendoza, R.C. Causes and failures classification of industrial electric motor. In Proceedings of the 2016 IEEE ANDESCON, Arequipa, Peru, 19–21 October 2016; pp. 1–4. [Google Scholar]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Lu, B.; Durocher, D.B.; Stemper, P. Predictive maintenance techniques. IEEE Ind. Appl. Mag. 2009, 15, 52–60. [Google Scholar] [CrossRef]
- Zonta, T.; Da Costa, C.A.; da Rosa Righi, R.; de Lima, M.J.; da Trindade, E.S.; Li, G.P. Predictive maintenance in the Industry 4.0: A systematic literature review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Liao, R.; Zheng, X.; Dai, W. Integrated predictive maintenance approach for multistate manufacturing system considering geometric and non-geometric defects of products. Reliab. Eng. Syst. Saf. 2022, 228, 108793. [Google Scholar] [CrossRef]
- Gholaminejad, A.; Bidgoli, F.S.; Poshtan, J.; Poshtan, M. A novel kurtogram-based health index for induction motor fault diagnosis. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019; pp. 85–92. [Google Scholar]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Ansari, F.; Glawar, R.; Nemeth, T. PriMa: A prescriptive maintenance model for cyber-physical production systems. Int. J. Comput. Integr. Manuf. 2019, 32, 482–503. [Google Scholar] [CrossRef]
- Kordestani, M.; Saif, M.; Orchard, M.E.; Razavi-Far, R.; Khorasani, K. Failure prognosis and applications—A survey of recent literature. IEEE Trans. Reliab. 2019, 70, 728–748. [Google Scholar] [CrossRef]
- Baur, M.; Albertelli, P.; Monno, M. A review of prognostics and health management of machine tools. Int. J. Adv. Manuf. Technol. 2020, 107, 2843–2863. [Google Scholar] [CrossRef]
- Magadán, L.; Suárez, F.; Granda, J.; García, D. Low-Cost Industrial IoT System for Wireless Monitoring of Electric Motors Condition. Mob. Netw. Appl. 2022, 1–10. [Google Scholar] [CrossRef]
- Aruquipa, G.; Diaz, F. An IoT architecture based on the control of Bio Inspired manufacturing system for the detection of anomalies with vibration sensors. Procedia Comput. Sci. 2022, 200, 438–450. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Tang, L.; Zhai, W. Skidding dynamic performance of rolling bearing with cage flexibility under accelerating conditions. Mech. Syst. Signal Process. 2021, 150, 107257. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics—A comprehensive review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Antonino-Daviu, J.A.; Cureño-Osornio, J.; Saucedo-Dorantes, J.J. Gradual Wear Diagnosis of Outer-Race Rolling Bearing Faults through Artificial Intelligence Methods and Stray Flux Signals. Electronics 2021, 10, 1486. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–22 June 2012; pp. 1–8. [Google Scholar]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Lee, C.Y.; Huang, T.S.; Liu, M.K.; Lan, C.Y. Data science for vibration heteroscedasticity and predictive maintenance of rotary bearings. Energies 2019, 12, 801. [Google Scholar] [CrossRef]
- Lee, M.S.; Shifat, T.A.; Hur, J.W. Kalman Filter Assisted Deep Feature Learning for RUL Prediction of Hydraulic Gear Pump. IEEE Sens. J. 2022, 22, 11088–11097. [Google Scholar] [CrossRef]
- Motahari-Nezhad, M.; Jafari, S.M. Bearing remaining useful life prediction under starved lubricating condition using time domain acoustic emission signal processing. Expert Syst. Appl. 2021, 168, 114391. [Google Scholar] [CrossRef]
- AlShorman, O.; Alkahatni, F.; Masadeh, M.; Irfan, M.; Glowacz, A.; Althobiani, F.; Kozik, J.; Glowacz, W. Sounds and acoustic emission-based early fault diagnosis of induction motor: A review study. Adv. Mech. Eng. 2021, 13, 1687814021996915. [Google Scholar] [CrossRef]
- Belmiloud, D.; Benkedjouh, T.; Lachi, M.; Laggoun, A.; Dron, J. Deep convolutional neural networks for Bearings failure predictionand temperature correlation. J. Vibroeng. 2018, 20, 2878–2891. [Google Scholar] [CrossRef]
- Shifat, T.A.; Yasmin, R.; Hur, J.W. A Data Driven RUL Estimation Framework of Electric Motor Using Deep Electrical Feature Learning from Current Harmonics and Apparent Power. Energies 2021, 14, 3156. [Google Scholar] [CrossRef]
- Dameshghi, A.; Refan, M.H. Combination of condition monitoring and prognosis systems based on current measurement and PSO-LS-SVM method for wind turbine DFIGs with rotor electrical asymmetry. Energy Syst. 2021, 12, 203–232. [Google Scholar] [CrossRef]
- Zheng, L.; He, Y.; Chen, X.; Pu, X. Optimization of Dilated Convolution Networks with Application in Remaining Useful Life Prediction of Induction Motors. Measurement 2022, 200, 111588. [Google Scholar] [CrossRef]
- Cao, R.; Yunusa-Kaltungo, A. An Automated Data Fusion-Based Gear Faults Classification Framework in Rotating Machines. Sensors 2021, 21, 2957. [Google Scholar] [CrossRef]
- Han, T.; Pang, J.; Tan, A.C. Remaining useful life prediction of bearing based on stacked autoencoder and recurrent neural network. J. Manuf. Syst. 2021, 61, 576–591. [Google Scholar] [CrossRef]
- Lin, M.; Shan, M.; Zhou, J.; Pan, Y. A Data-Driven Fault Diagnosis Method Using Modified Health Index and Deep Neural Networks of a Rolling Bearing. J. Comput. Inf. Sci. Eng. 2022, 22, 021005. [Google Scholar] [CrossRef]
- Shen, Z.; He, Z.; Chen, X.; Sun, C.; Liu, Z. A monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time. Sensors 2012, 12, 10109–10135. [Google Scholar] [CrossRef]
- Xu, X.; Li, X.; Ming, W.; Chen, M. A novel multi-scale CNN and attention mechanism method with multi-sensor signal for remaining useful life prediction. Comput. Ind. Eng. 2022, 169, 108204. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Senanayaka, J.S.L.; Van Khang, H.; Robbersmyr, K.G. Autoencoders and recurrent neural networks based algorithm for prognosis of bearing life. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; pp. 537–542. [Google Scholar]
- Wang, G.; Li, H.; Zhang, F.; Wu, Z. Feature Fusion based Ensemble Method for remaining useful life prediction of machinery. Appl. Soft Comput. 2022, 129, 109604. [Google Scholar] [CrossRef]
- Chen, C.; Lu, N.; Jiang, B.; Xing, Y.; Zhu, Z.H. Prediction interval estimation of aeroengine remaining useful life based on bidirectional long short-term memory network. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Calabrese, F.; Regattieri, A.; Bortolini, M.; Gamberi, M.; Pilati, F. Predictive maintenance: A novel framework for a data-driven, semi-supervised, and partially online prognostic health management application in industries. Appl. Sci. 2021, 11, 3380. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, J.; Lu, F. Reduced kernel recursive least squares algorithm for aero-engine degradation prediction. Mech. Syst. Signal Process. 2017, 95, 446–467. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Addepalli, S. Remaining useful life prediction using deep learning approaches: A review. Procedia Manuf. 2020, 49, 81–88. [Google Scholar] [CrossRef]
- Kumar, S.; Dutta, S.K.; Ghoshal, S.K.; Das, J. Model-Based Adaptive Prognosis of a Hydraulic System. In Recent Advances in Mechanical Engineering; Springer: Singapore, 2020; pp. 375–391. [Google Scholar]
- Qian, Y.; Yan, R.; Gao, R.X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. Enhancing the abilities in assessing slurry pumps’ performance degradation and estimating their remaining useful lives by using captured vibration signals. J. Vib. Control 2017, 23, 1925–1937. [Google Scholar] [CrossRef]
- Jin, X.; Sun, Y.; Que, Z.; Wang, Y.; Chow, T.W. Anomaly detection and fault prognosis for bearings. IEEE Trans. Instrum. Meas. 2016, 65, 2046–2054. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, Z.; Ke, X.; Wang, W.; Sun, Y. Remaining useful life prediction for an adaptive skew-Wiener process model. Mech. Syst. Signal Process. 2017, 87, 294–306. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Wang, X.z. Reliability estimation and remaining useful lifetime prediction for bearing based on proportional hazard model. J. Cent. South Univ. 2015, 22, 4625–4633. [Google Scholar] [CrossRef]
- Scalabrini Sampaio, G.; Vallim Filho, A.R.d.A.; Santos da Silva, L.; Augusto da Silva, L. Prediction of motor failure time using an artificial neural network. Sensors 2019, 19, 4342. [Google Scholar] [CrossRef] [PubMed]
- Shifat, T.A.; Hur, J.W. ANN assisted multi sensor information fusion for BLDC motor fault diagnosis. IEEE Access 2021, 9, 9429–9441. [Google Scholar] [CrossRef]
- Chen, J.; Jing, H.; Chang, Y.; Liu, Q. Gated recurrent unit based recurrent neural network for remaining useful life prediction of nonlinear deterioration process. Reliab. Eng. Syst. Saf. 2019, 185, 372–382. [Google Scholar] [CrossRef]
- Ding, N.; Li, H.; Xin, Q.; Wu, B.; Jiang, D. Multi-source domain generalization for degradation monitoring of journal bearings under unseen conditions. Reliab. Eng. Syst. Saf. 2022, 230, 108966. [Google Scholar] [CrossRef]
- Lu, B.L.; Liu, Z.H.; Wei, H.L.; Chen, L.; Zhang, H.; Li, X.H. A deep adversarial learning prognostics model for remaining useful life prediction of rolling bearing. IEEE Trans. Artif. Intell. 2021, 2, 329–340. [Google Scholar] [CrossRef]
- Xiao, D.; Huang, Y.; Qin, C.; Shi, H.; Li, Y. Fault diagnosis of induction motors using recurrence quantification analysis and LSTM with weighted BN. Shock Vib. 2019, 2019, 8325218. [Google Scholar] [CrossRef]
- Kang, R.; Wang, J.; Chen, J.; Zhou, J.; Pang, Y.; Guo, L.; Cheng, J. A method of online anomaly perception and failure prediction for high-speed automatic train protection system. Reliab. Eng. Syst. Saf. 2022, 226, 108699. [Google Scholar] [CrossRef]
- Yu, J. Machine health prognostics using the Bayesian-inference-based probabilistic indication and high-order particle filtering framework. J. Sound Vib. 2015, 358, 97–110. [Google Scholar] [CrossRef]
- Du, S.; Lv, J.; Xi, L. Degradation process prediction for rotational machinery based on hybrid intelligent model. Robot. Comput.-Integr. Manuf. 2012, 28, 190–207. [Google Scholar] [CrossRef]
- Liu, X.; Song, P.; Yang, C.; Hao, C.; Peng, W. Prognostics and health management of bearings based on logarithmic linear recursive least-squares and recursive maximum likelihood estimation. IEEE Trans. Ind. Electron. 2017, 65, 1549–1558. [Google Scholar] [CrossRef]
- Yoo, Y.; Baek, J.G. A novel image feature for the remaining useful lifetime prediction of bearings based on continuous wavelet transform and convolutional neural network. Appl. Sci. 2018, 8, 1102. [Google Scholar] [CrossRef]
- Saufi, M.S.R.M.; Hassan, K.A. Remaining useful life prediction using an integrated Laplacian-LSTM network on machinery components. Appl. Soft Comput. 2021, 112, 107817. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Q.; Shen, Y.; Xu, F.; Zhu, Q. RUL prediction for rolling bearings based on Convolutional Autoencoder and status degradation model. Appl. Soft Comput. 2022, 130, 109686. [Google Scholar] [CrossRef]
- Kong, W.; Li, H. Remaining useful life prediction of rolling bearing under limited data based on adaptive time-series feature window and multi-step ahead strategy. Appl. Soft Comput. 2022, 129, 109630. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Xu, L. Study on Fault Detection of Rolling Element Bearing Based on Translation-Invariant Denoising and Hilbert-Huang Transform. J. Comput. 2012, 7, 1142–1146. [Google Scholar] [CrossRef]
- Sharma, M.; Sarma, K.K.; Mastorakis, N. AE and SAE Based Aircraft Image Denoising. In Proceedings of the 2018 5th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Corfu, Greece, 25–27 August 2018; pp. 81–85. [Google Scholar]
- Nguyen, C.D.; Prosvirin, A.E.; Kim, C.H.; Kim, J.M. Construction of a sensitive and speed invariant gearbox fault diagnosis model using an incorporated utilizing adaptive noise control and a stacked sparse autoencoder-based deep neural network. Sensors 2020, 21, 18. [Google Scholar] [CrossRef]
- Li, Y.H.; Harfiya, L.N.; Purwandari, K.; Lin, Y.D. Real-time cuffless continuous blood pressure estimation using deep learning model. Sensors 2020, 20, 5606. [Google Scholar] [CrossRef]







| SAE Structure | 3–2–1–2–3 |
|---|---|
| Activation function | ReLu |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Epochs | 20 |
| BiLSTM Structure | 1-5-60-5-1 |
|---|---|
| Activation function | ReLu |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Epochs | 1000 |
| Name | Samples | Total Time | Bearing Type | Shaft Frequency | Load | BPFO | Used in |
|---|---|---|---|---|---|---|---|
| IMS dataset no. 2 | 984 | 6 d 20 h | Rexnord ZA-2115 | 33.33 Hz | 26.69 kN | 236 Hz | Training |
| IMS dataset no. 3 | 4448 | 31 d 10 h | Testing | ||||
| FEMTO Bearing1_3 | 2376 | 6 h 36 m | NSK 6804-DD | 30 Hz | 4 kN | 168.34 Hz | Testing |
| FEMTO Bearing1_4 | 1429 | 3 h 58 m | |||||
| FEMTO Bearing1_7 | 2260 | 6 h 16 m | |||||
| XJTU-SY Bearing2_5 | 339 | 5 h 39 m | LDK UER204 | 37.5 Hz | 11 kN | 115.61 Hz | Testing |
| XJTU-SY Bearing3_1 | 2538 | 42 h 18 m | 40 Hz | 10 kN | 123.32 Hz |
| Prediction Error (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Dataset | Proposed Model | [33] | [56] | [57] | [58] | [59] | [60] | |||
| IMS dataset no. 3 | 6174 | 6315 | 6314 | 0.71 | - | - | - | - | - | - |
| FEMTO Bearing 1_3 | 2200 | 2376 | 2374 | 0.91 | 43.28 | 2.58 | 1.05 | −0.69 | −2.62 | - |
| FEMTO Bearing 1_4 | 1247 | 1428 | 1427 | 1.75 | 67.55 | −9.14 | 20.35 | 3.10 | 17.40 | - |
| FEMTO Bearing 1_7 | 2030 | 2260 | 2254 | 2.08 | 17.83 | −0.70 | 29.19 | 7.00 | 1.06 | - |
| XJTU-SY Bearing 2_5 | 265 | 338 | 338 | 1.52 | - | - | - | - | - | 8.95 |
| XJTU-SY Bearing 3_1 | 2433 | 2527 | 2525 | 1.06 | - | - | - | - | - | 10.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magadán, L.; Suárez, F.J.; Granda, J.C.; delaCalle, F.J.; García, D.F. A Robust Health Prognostics Technique for Failure Diagnosis and the Remaining Useful Lifetime Predictions of Bearings in Electric Motors. Appl. Sci. 2023, 13, 2220. https://doi.org/10.3390/app13042220
Magadán L, Suárez FJ, Granda JC, delaCalle FJ, García DF. A Robust Health Prognostics Technique for Failure Diagnosis and the Remaining Useful Lifetime Predictions of Bearings in Electric Motors. Applied Sciences. 2023; 13(4):2220. https://doi.org/10.3390/app13042220
Chicago/Turabian StyleMagadán, Luis, Francisco J. Suárez, Juan C. Granda, Francisco J. delaCalle, and Daniel F. García. 2023. "A Robust Health Prognostics Technique for Failure Diagnosis and the Remaining Useful Lifetime Predictions of Bearings in Electric Motors" Applied Sciences 13, no. 4: 2220. https://doi.org/10.3390/app13042220





