Prediction of the Absorption Characteristics of Non-Uniform Acoustic Absorbers with Grazing Flow
Abstract
:1. Introduction
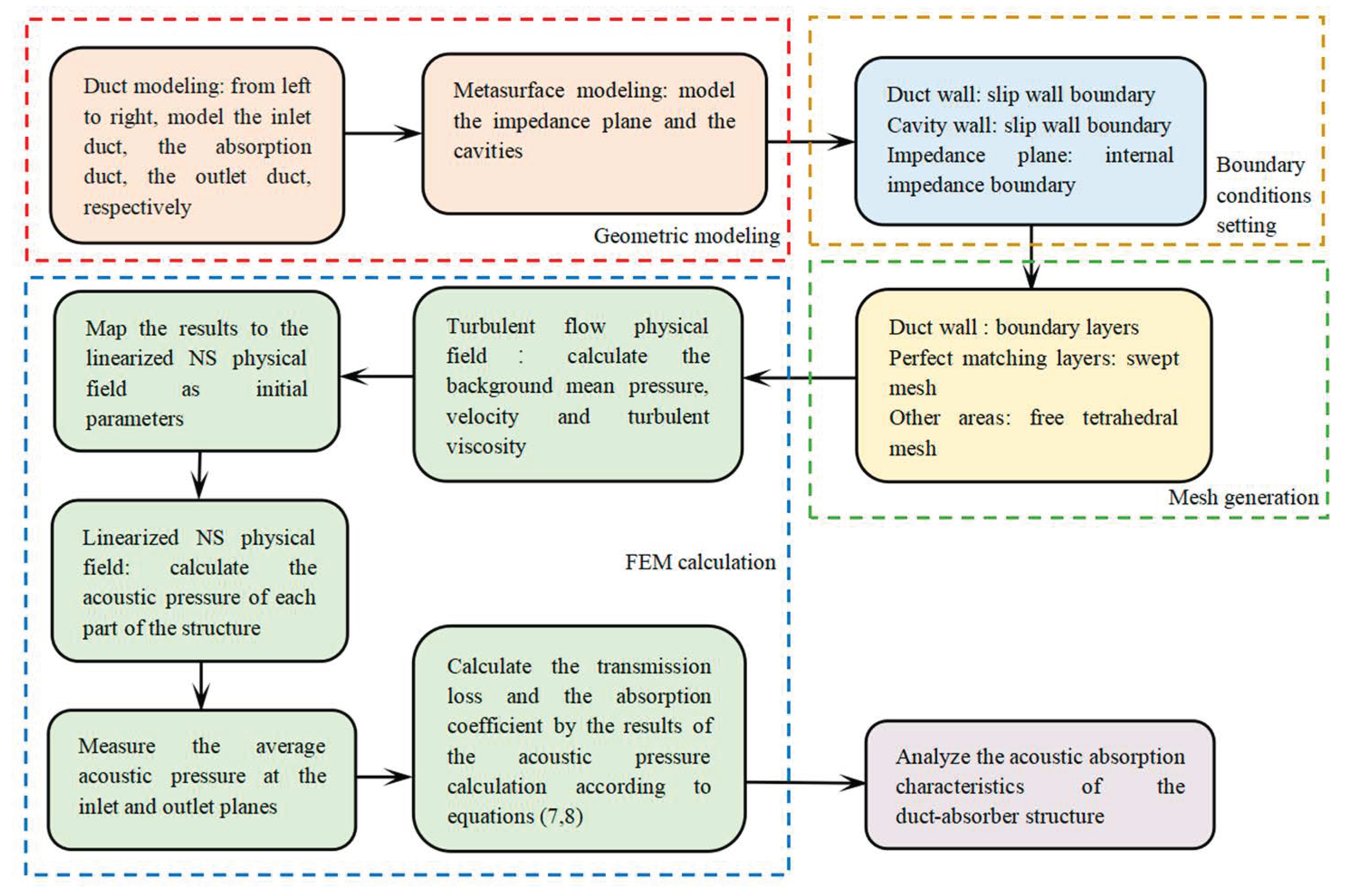
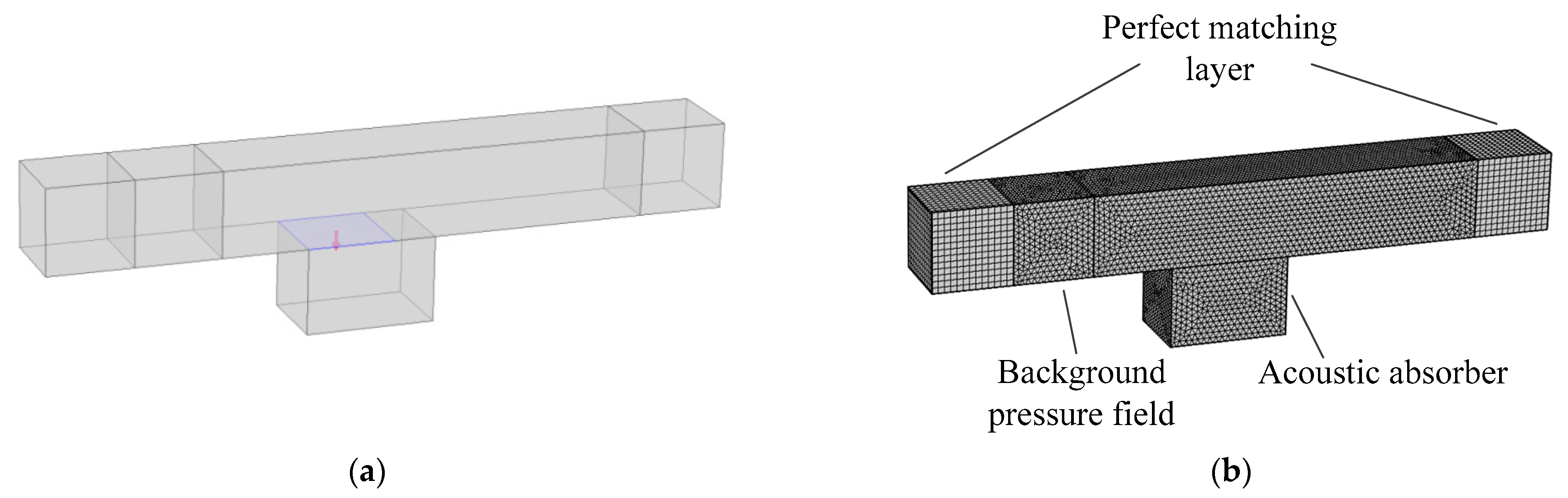
2. Full Navier–Stokes Equations (FNSE) Method
3. Impedance Boundary Navier–Stokes Equations (IBNSE) Method
3.1. Semi-Empirical Impedance Models of the Perforated Plate under Grazing Flow
3.1.1. Eversman Model
3.1.2. Guess Model
3.1.3. Lee Model
3.1.4. Goodrich Model
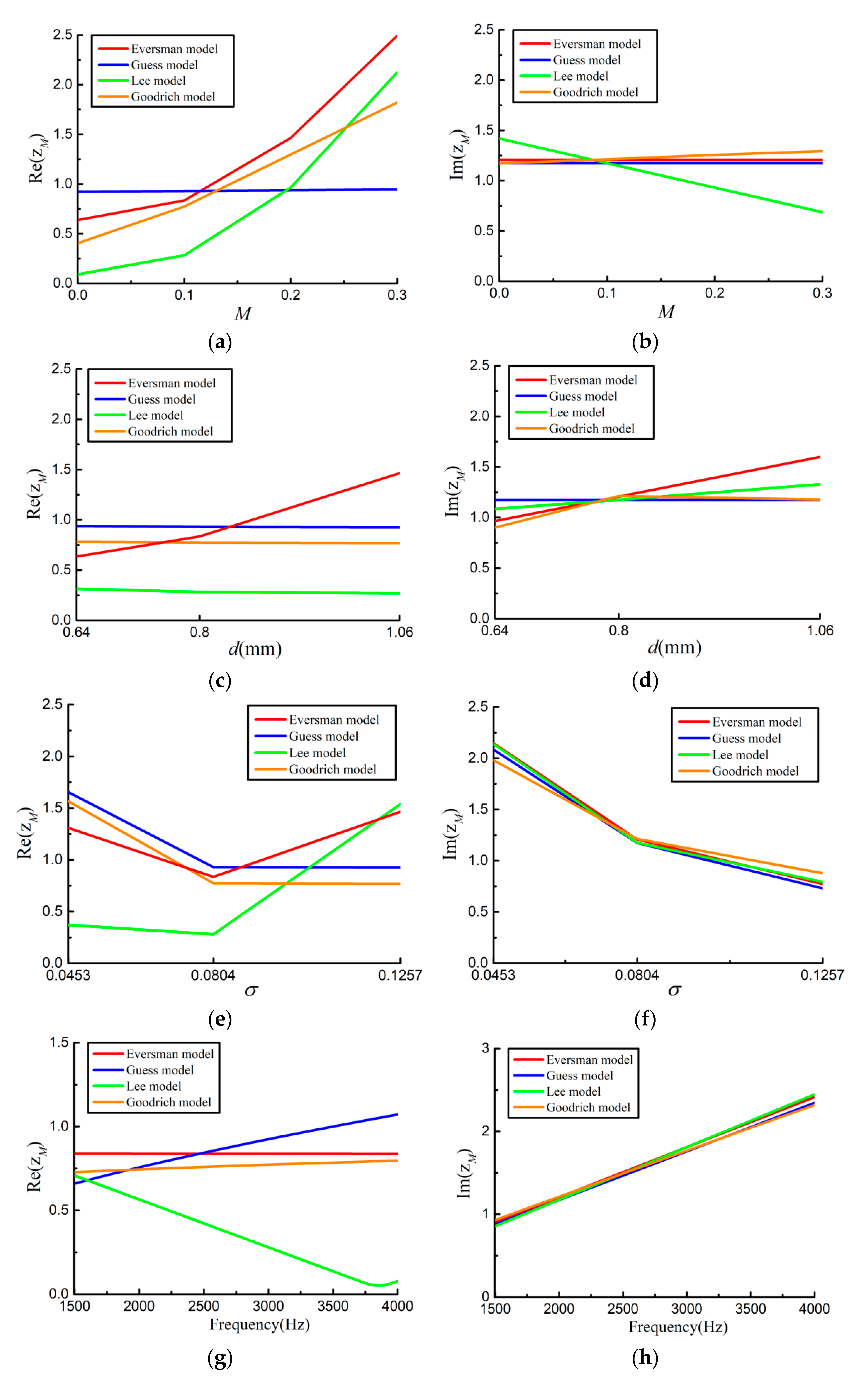
3.2. Comparisons of Different Impedance Models
3.3. IBNSE Method Using Semi-Empirical Impedance Model
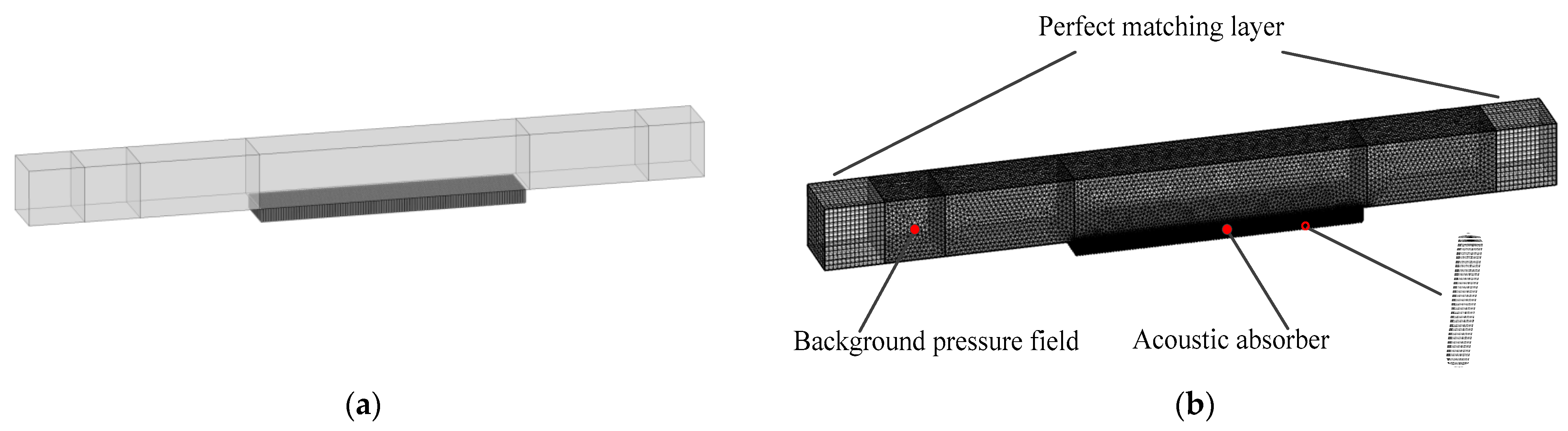
3.4. Comparisons with Published Experimental Results
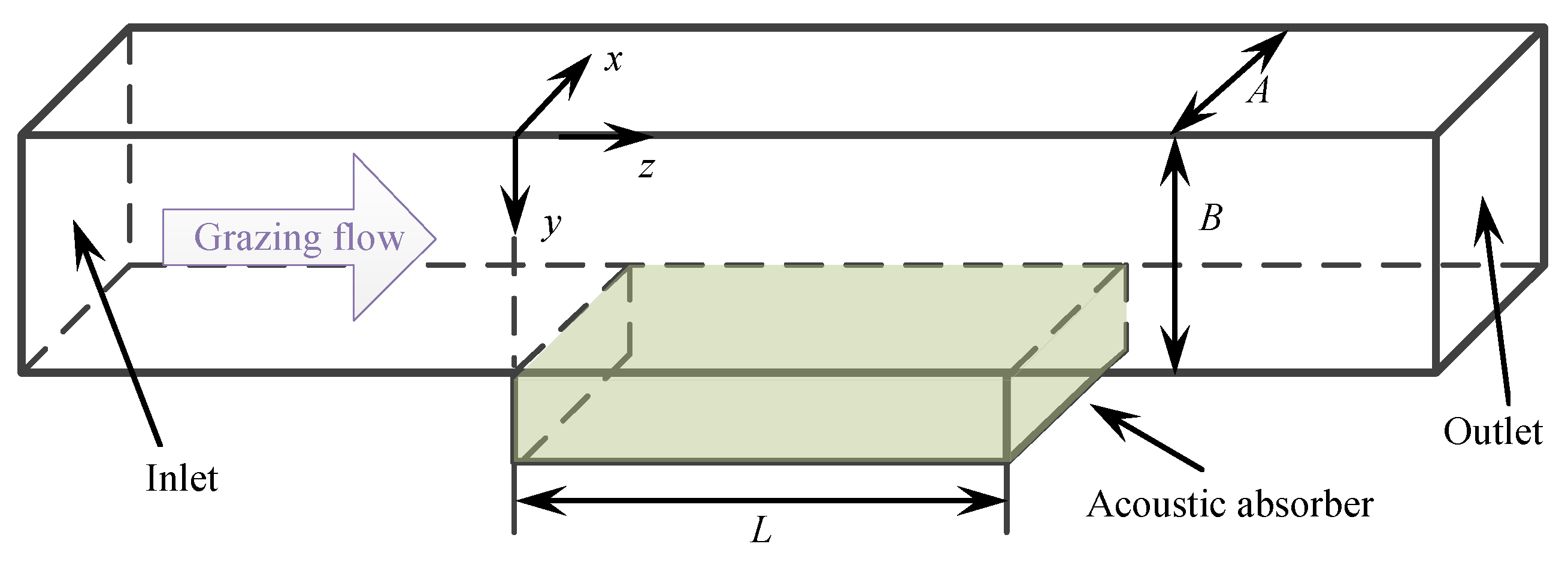
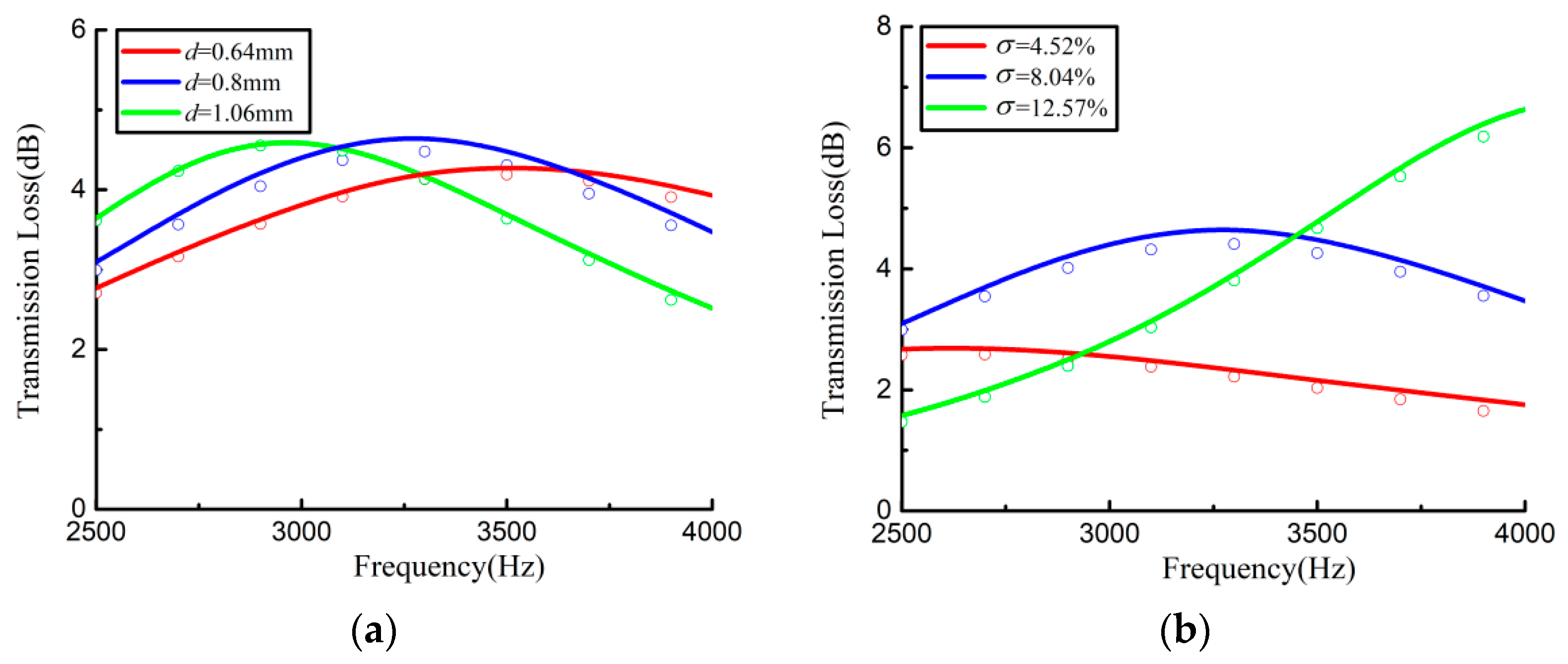
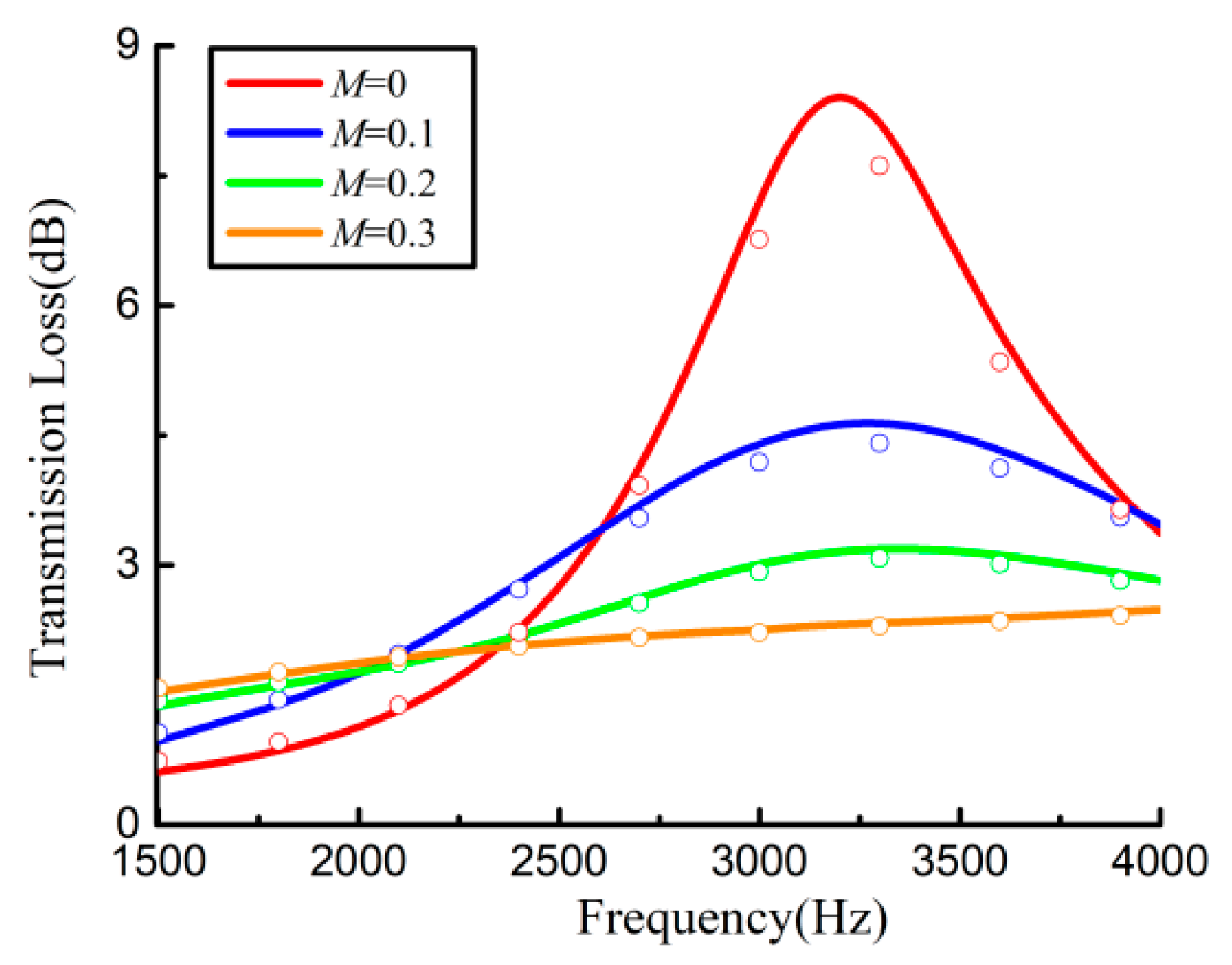
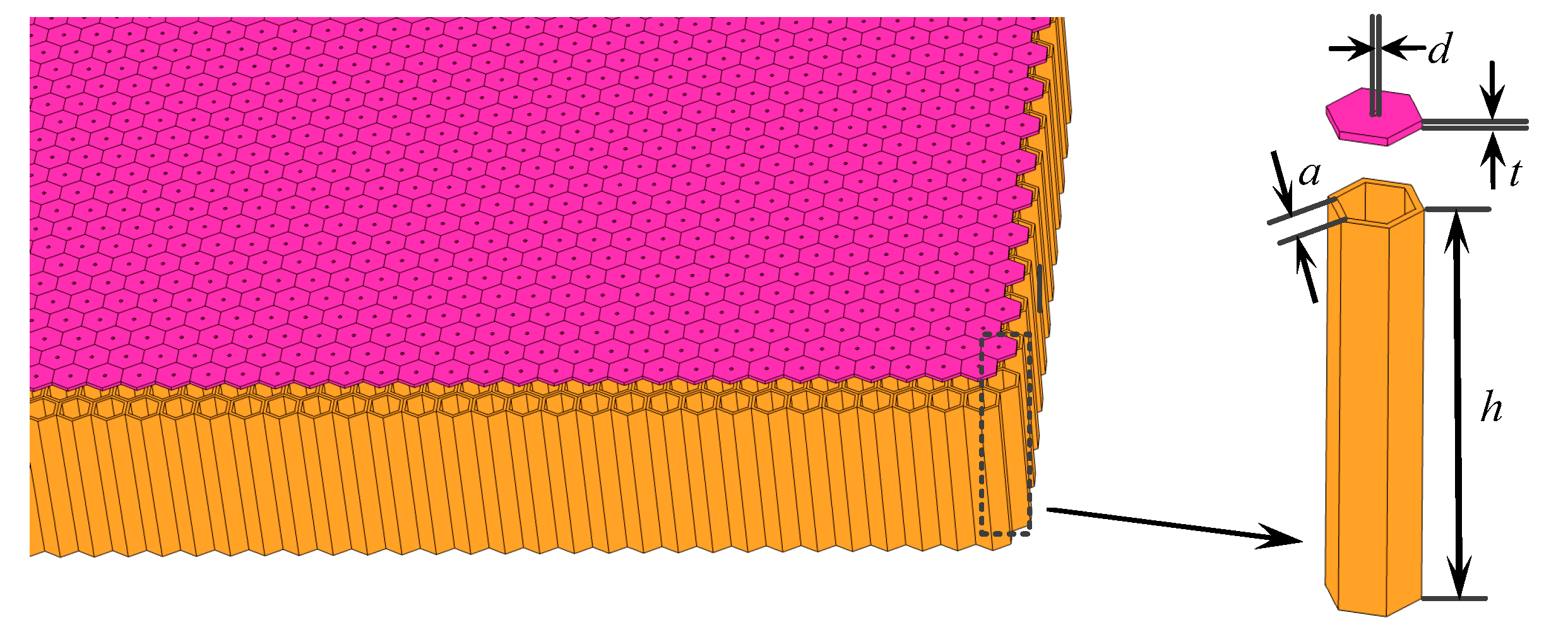
4. Absorption Characteristics of the Duct–Acoustic Absorber System
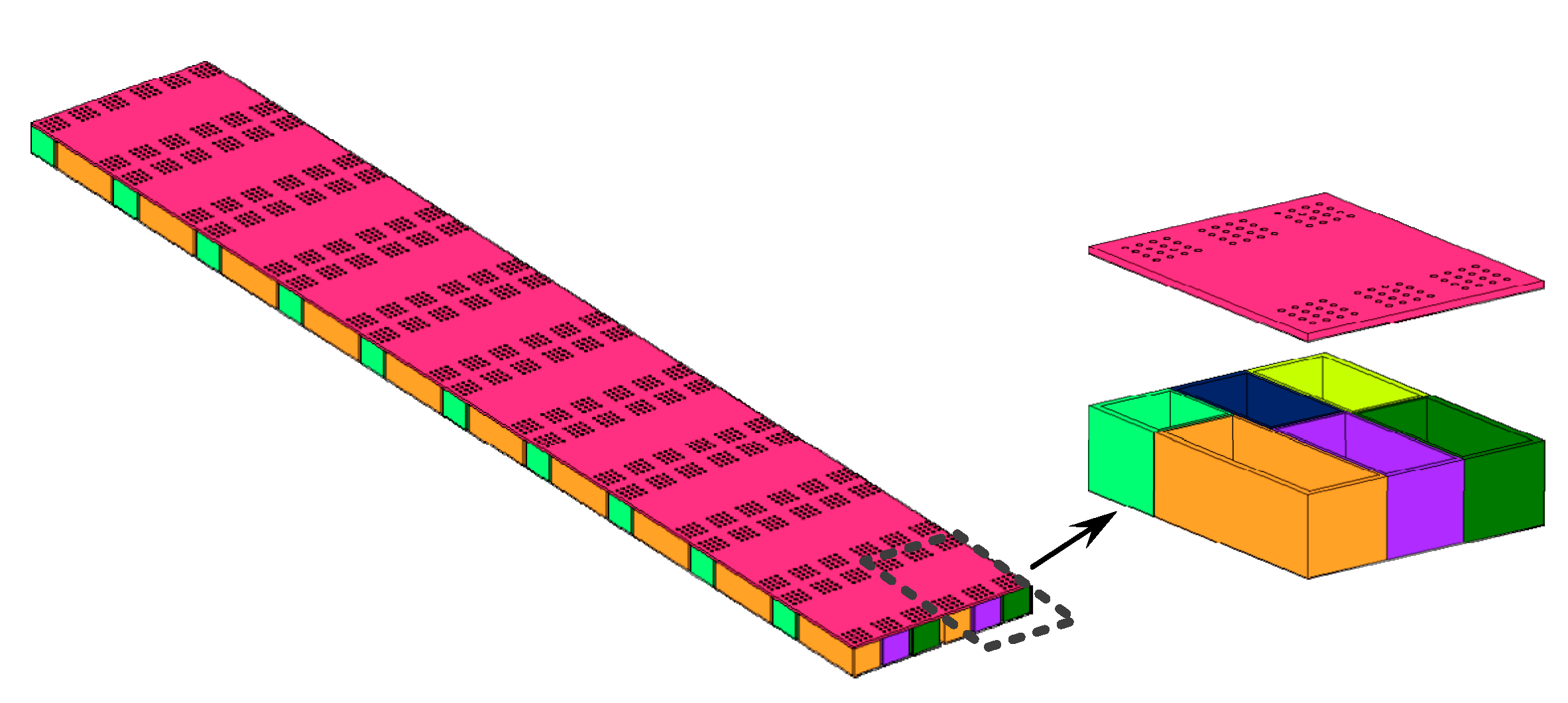
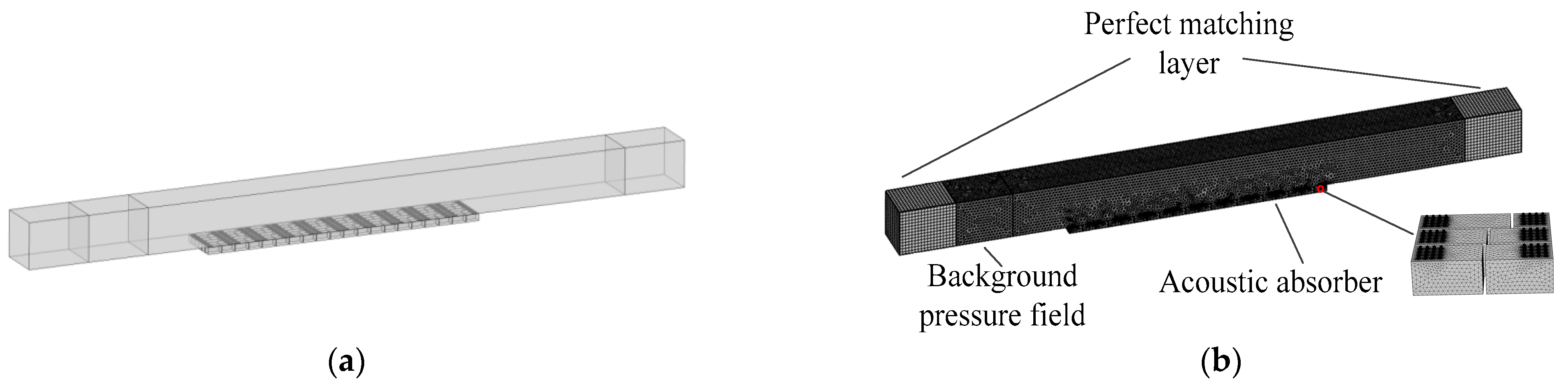
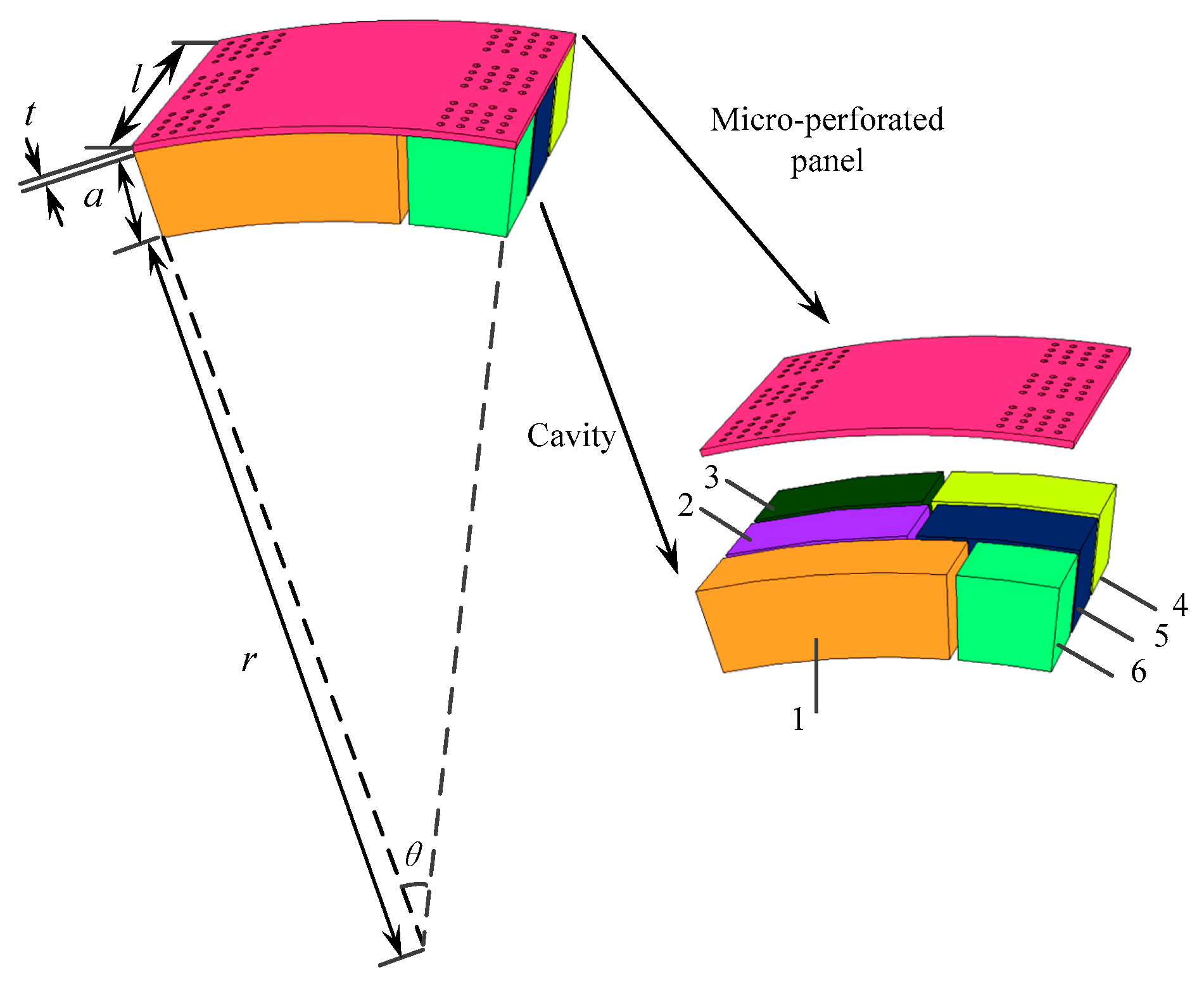
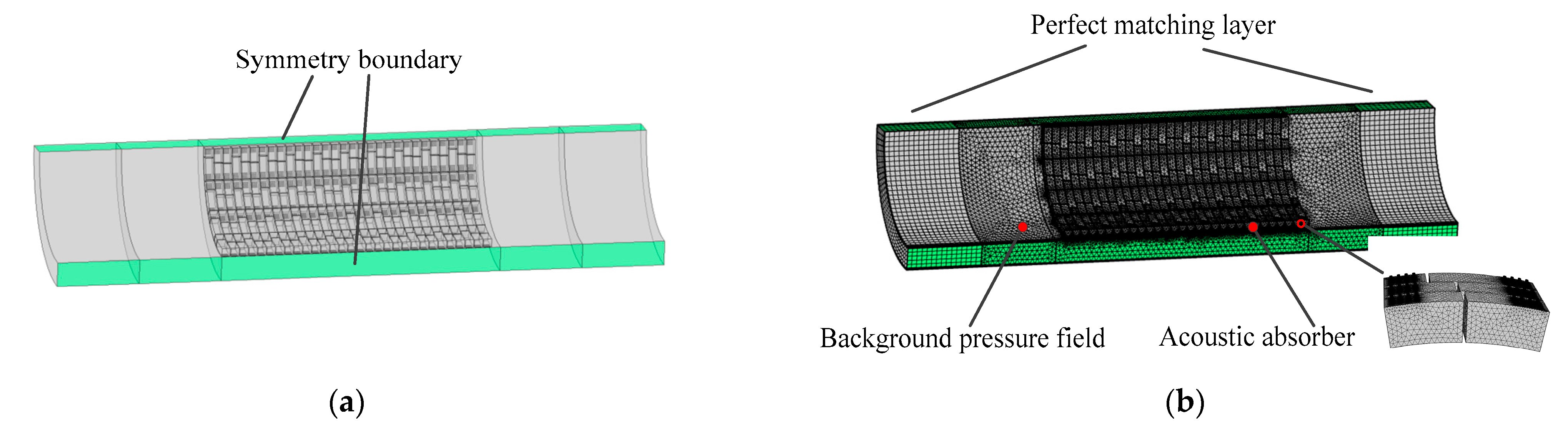
4.1. Rectangular Duct Acoustic Absorber
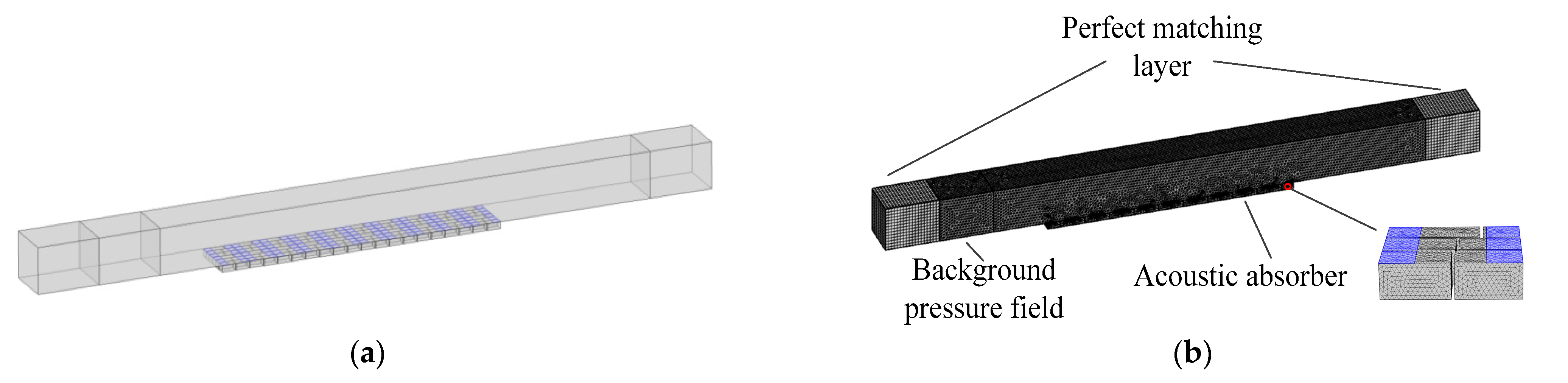
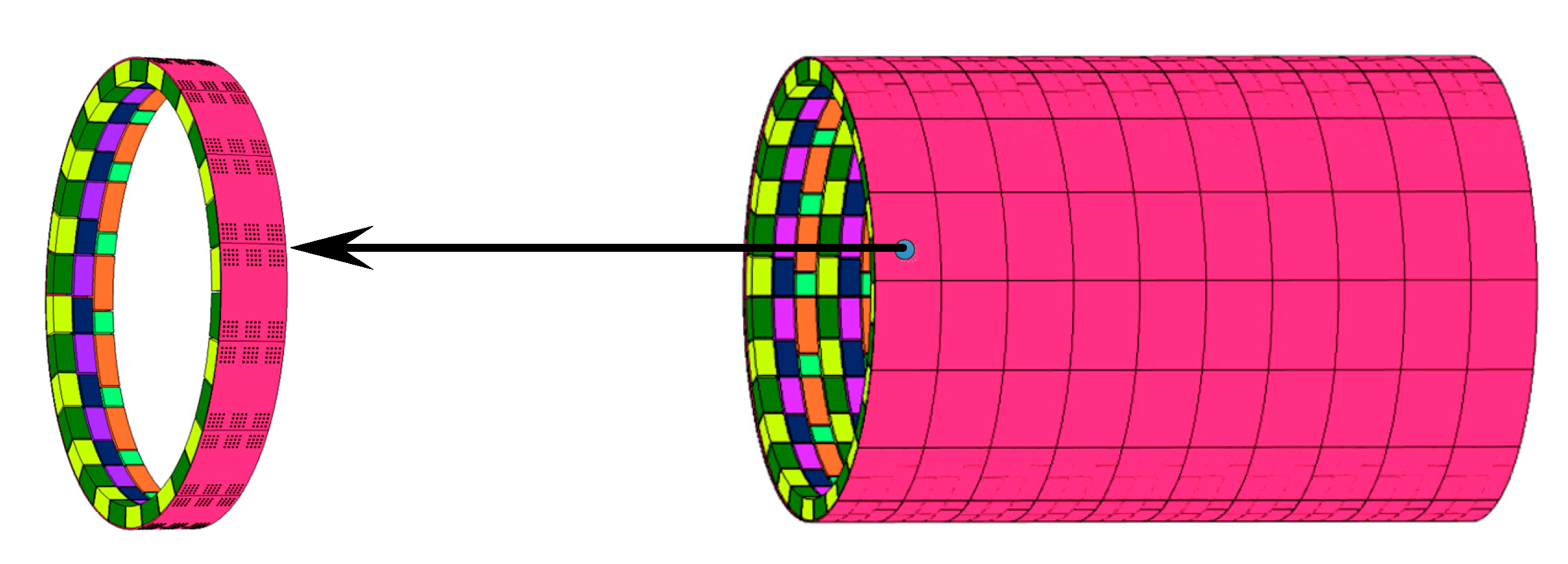
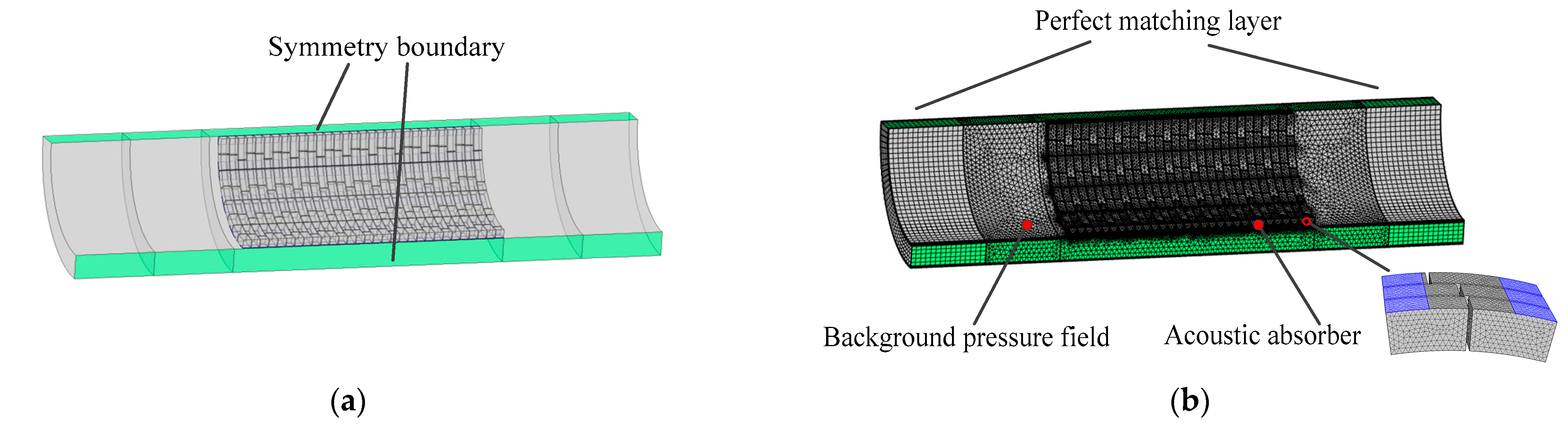
4.2. Annular Duct Acoustic Absorber
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maa, D.Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Liu, C.; Wu, J.; Yang, Z.; Ma, F. Ultra-broadband acoustic absorption of a thin microperforated panel metamaterial with multi-order resonance. Compos. Struct. 2020, 246, 112366. [Google Scholar]
- Zhong, J.; Zhao, H.; Yang, H.; Wang, Y.; Yin, J.; Wen, J. Theoretical requirements and inverse design for broadband perfect absorption of low-frequency waterborne sound by ultrathin metasurface. Sci. Rep. 2019, 9, 1181. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Xiao, Y.; Yu, D.; Zhao, H.; Wang, Y.; Wen, J. Low-frequency sound absorption of hybrid absorber based on micro-perforated panel and coiled-up channels. Appl. Phys. Lett. 2019, 114, 151901. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, Y.; Guo, X.; Shen, Y.; Zhang, D. Low-frequency anechoic metasurface based on coiled channel of gradient cross-section. Appl. Phys. Lett. 2019, 114, 083501. [Google Scholar] [CrossRef]
- Li, Y.; Assouar, B. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Patel, S.K.; Udayakumar, A.K.; Mahendran, G.; Vasudevan, B.; Surve, J.; Parmar, J. Highly efficient, perfect, large angular and ultrawideband solar energy absorber for UV to MIR range. Sci. Rep. 2022, 12, 18044. [Google Scholar] [CrossRef]
- Ciaburro, G.; Parente, R.; Iannace, G.; Romero, V.P. Design Optimization of three-layered metamaterial acoustic absorbers based on PVC reused membrane and metal washers. Sustainability 2022, 14, 4218. [Google Scholar] [CrossRef]
- Jiang, X.; Liang, B.; Cheng, J.; Qiu, C. Twisted acoustics: Metasurface-enabled multiplexing and demultiplexing. Adv. Mater. 2018, 30, 1800257. [Google Scholar] [CrossRef]
- Liu, L.; Chang, H.; Zhang, C.; Hu, X. Single-channel labyrinthine metasurfaces as perfect sound absorbers with tunable bandwidth. Appl. Phys. Lett. 2017, 111, 083503. [Google Scholar] [CrossRef]
- Song, G.; Cheng, Q.; Cui, T.; Jing, Y. Acoustic planar surface retroreflector. Phys. Rev. Mater. 2018, 2, 065201. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, X.; Liang, B.; Zhang, L. Metascreen-based acoustic passive phased array. Phys. Rev. Appl. 2015, 4, 024003. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Cheng, L.; Cui, F. Vibroacoustic modeling of an acoustic resonator tuned by dielectric elastomer membrane with voltage control. J. Sound Vib. 2017, 387, 114–126. [Google Scholar] [CrossRef]
- Fleury, R.; Alù, A. Extraordinary sound transmission through density-near-zero ultranarrow channels. Phys. Rev. Lett. 2013, 111, 055501. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, L. Acoustic silencing in a flow duct with micro-perforated panel liners. Appl. Acoust. 2020, 167, 107382. [Google Scholar] [CrossRef]
- Drevon, E. Measurement methods and devices applied to A380 nacelle double degree-of-freedom acoustic liner development. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004. [Google Scholar]
- Yan, S.; Wu, J.; Chen, J.; Mao, X. Design of Honeycomb Microperforated Structure with Adjustable Sound Absorption Performance. Shock Vib. 2021, 2021, 6613701. [Google Scholar] [CrossRef]
- Gautam, A.; Celik, A.; Meek, H.; Azarpeyvand, M. Double degree of freedom Helmholtz resonator based acoustic liners. AIAA AVIATION 2021 FORUM 2021. Available online: https://arc.aiaa.org/doi/abs/10.2514/6.2021-2205 (accessed on 28 July 2021).
- Watson, W. An acoustic evaluation of circumferentially segmented duct liners. AIAA J. 1984, 22, 1229–1233. [Google Scholar] [CrossRef]
- Brown, M.C.; Jones, M.G. Evaluation of variable facesheet liner configurations for broadband noise reduction. AIAA AVIATION 2020 FORUM 2020. Available online: https://arc.aiaa.org/doi/abs/10.2514/6.2020-2616 (accessed on 8 June 2020).
- Palani, S.; Murray, P.; McAlpine, A.; Richter, C. Optimisation of slanted septum core and multiple folded cavity acoustic liners for aero-engines. AIAA AVIATION 2021 FORUM 2021. Available online: https://arc.aiaa.org/doi/10.2514/6.2021-2172 (accessed on 28 July 2021).
- McAlpine, A.; Astley, A.; Hii, V.J.T.; Baker, N.J.; Kempton, A.J. Acoustic scattering by an axially-segmented turbofan inlet duct liner at supersonic fan speeds. J. Sound Vib. 2006, 294, 780–806. [Google Scholar] [CrossRef]
- Schiller, N.H.; Jones, M.G.; Howerton, B.M.; Nark, D.M. Initial developments of a low drag variable depth acoustic liner. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- McAlpine, A.; Wright, M.C.M. Acoustic scattering by a spliced turbofan inlet duct liner at supersonic fan speeds. J. Sound Vib. 2006, 292, 911–934. [Google Scholar] [CrossRef]
- Bi, W.P.; Pagneux, V.; Lafarge, D.; Aurégan, Y. Modelling of sound propagation in a non-uniform lined duct using a multi-modal propagation method. J. Sound Vib. 2006, 289, 1091–1111. [Google Scholar] [CrossRef]
- Law, T.R.; Dowling, A.P. Reduction of aeroengine tonal noise using scattering from a multi-segmented liner. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference, Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Bi, W.P.; Pagneux, V.; Lafarge, D.; Aurégan, Y. An improved multimodal method for sound propagation in nonuniform lined ducts. J. Acoust. Soc. Am. 2007, 122, 280–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Wang, X.; Huang, L.; Sun, X. Calculation model for sound propagation in duct with circumferentially non-uniform liner. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–7 June 2017. [Google Scholar]
- Namba, M.; Fukushige, K. Application of the equivalent surface source method to the acoustics of duct systems with non-uniform wall impedance. J. Sound Vib. 1980, 73, 125–146. [Google Scholar] [CrossRef]
- Wright, M.C.M. Hybrid analytical/numerical method for mode scattering in azimuthally non-uniform ducts. J. Sound Vib. 2006, 292, 583–594. [Google Scholar] [CrossRef]
- Schiller, N.H.; Jones, M.G.; Bertolucci, B. Experimental evaluation of acoustic engine liner models developed with COMSOL Multiphysics. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–7 June 2017. [Google Scholar]
- Winkler, J.; Mendoza, J.M.; Reimann, C.A.; Homma, K.; Alonso, J.S. High fidelity modeling tools for engine liner design and screening of advanced concepts. Int. J. Aeroacoustics 2021, 20, 530–560. [Google Scholar] [CrossRef]
- Scofano, A.; Murray, P.B.; Ferrante, P. Back-calculation of liner impedance using duct insertion loss measurements and fem predictions. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 21–23 May 2007. [Google Scholar]
- Zhang, Q.; Bodony, D.J. Numerical simulation of two-dimensional acoustic liners with high-speed grazing flow. AIAA J. 2011, 49, 365–382. [Google Scholar] [CrossRef]
- Ji, C.; Zhao, D. Lattice Boltzmann investigation of acoustic damping mechanism and performance of an in-duct circular orifice. J. Acoust. Soc. Am. 2014, 135, 3243–3251. [Google Scholar] [CrossRef]
- Casalino, D.; Hazir, A.; Mann, A. Turbofan broadband noise prediction using the lattice boltzmann method. AIAA J. 2018, 56, 609–628. [Google Scholar] [CrossRef]
- Dassé, J.; Mendez, S.; Nicoud, F. Large-eddy simulation of the acoustic response of a perforated plate. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference, Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Jensen, M.J.H.; Shaposhnikov, K.; Svensson, E. Using the linearized navier-stokes equations to model acoustic liners. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Tang, Y.; He, W.; Xin, F.; Lu, T. Nonlinear sound absorption of ultralight hybrid-cored sandwich panels. Mech. Syst. Signal Process. 2020, 135, 106428. [Google Scholar] [CrossRef]
- Eversman, W.; Drouin, M.; Locke, J.; McCartney, J. Impedance models for single and two degree of freedom linings and correlation with grazing flow duct testing. Int. J. Aeroacoustics 2021, 20, 497–529. [Google Scholar] [CrossRef]
- Guess, A.W. Calculation of perforated plate liner parameters from specified acoustic resistance and reactance. J. Sound Vib. 1975, 40, 119–137. [Google Scholar] [CrossRef]
- Lee, S.H.; Ih, J.G. Empirical model of the acoustic impedance of a circular orifice in grazing mean flow. J. Acoust. Soc. Am. 2003, 114, 98–113. [Google Scholar] [CrossRef]
- Yu, J.; Ruiz, M.; Kwan, H.W. Validation of Goodrich perforate liner impedance model using NASA Langley test data. In Proceedings of the 14th AIAA/CEAS aeroacoustics conference (29th AIAA aeroacoustics conference), Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Yu, X.; Cheng, L.; You, X. Hybrid silencers with micro-perforated panels and internal partitions. J. Acoust. Soc. Am. 2014, 137, 951–962. [Google Scholar] [CrossRef] [Green Version]
- Selamet, E.; Selamet, A.; Iqbal, A.; Kim, H. Effect of flow on Helmholtz resonator acoustics: A three-dimensional computational study vs. Experiments. SAE Tech. Pap. 2011. Available online: https://www.sae.org/publications/technical-papers/content/2011-01-1521/ (accessed on 17 May 2011).









| Impedance Models | ||||
|---|---|---|---|---|
| Eversman model | 8.38% | 4.22% | 5.65% | 5.86% |
| Guess model | 9.68% | 3.59% | 3.77% | 8.86% |
| Lee model | 14.07% | 7.15% | 10.32% | 11.66% |
| Goodrich model | 2.45% | 1.63% | 3.22% | 3.28% |
| Methods | Average Error | Peak Frequency Error | Peak Value Error |
|---|---|---|---|
| IBNSE | 5.87% | 1.75% | 4.69% |
| FNSE | 4.24% | 1.67% | 2.50% |
| Methods | Average Error | Peak Frequency Error | Peak Value Error |
|---|---|---|---|
| IBNSE | 4.06% | 2.48% | 0.71% |
| FNSE | 3.89% | 2.40% | 1.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Zhao, Y. Prediction of the Absorption Characteristics of Non-Uniform Acoustic Absorbers with Grazing Flow. Appl. Sci. 2023, 13, 2256. https://doi.org/10.3390/app13042256
Ou Y, Zhao Y. Prediction of the Absorption Characteristics of Non-Uniform Acoustic Absorbers with Grazing Flow. Applied Sciences. 2023; 13(4):2256. https://doi.org/10.3390/app13042256
Chicago/Turabian StyleOu, Yang, and Yonghui Zhao. 2023. "Prediction of the Absorption Characteristics of Non-Uniform Acoustic Absorbers with Grazing Flow" Applied Sciences 13, no. 4: 2256. https://doi.org/10.3390/app13042256
APA StyleOu, Y., & Zhao, Y. (2023). Prediction of the Absorption Characteristics of Non-Uniform Acoustic Absorbers with Grazing Flow. Applied Sciences, 13(4), 2256. https://doi.org/10.3390/app13042256





