Use of Land Gravity Data in Small Areas to Support Structural Geology, a Case Study in Eskişehir Basin, Turkey
Abstract
:1. Introduction
2. Geological Setting of the Study Area
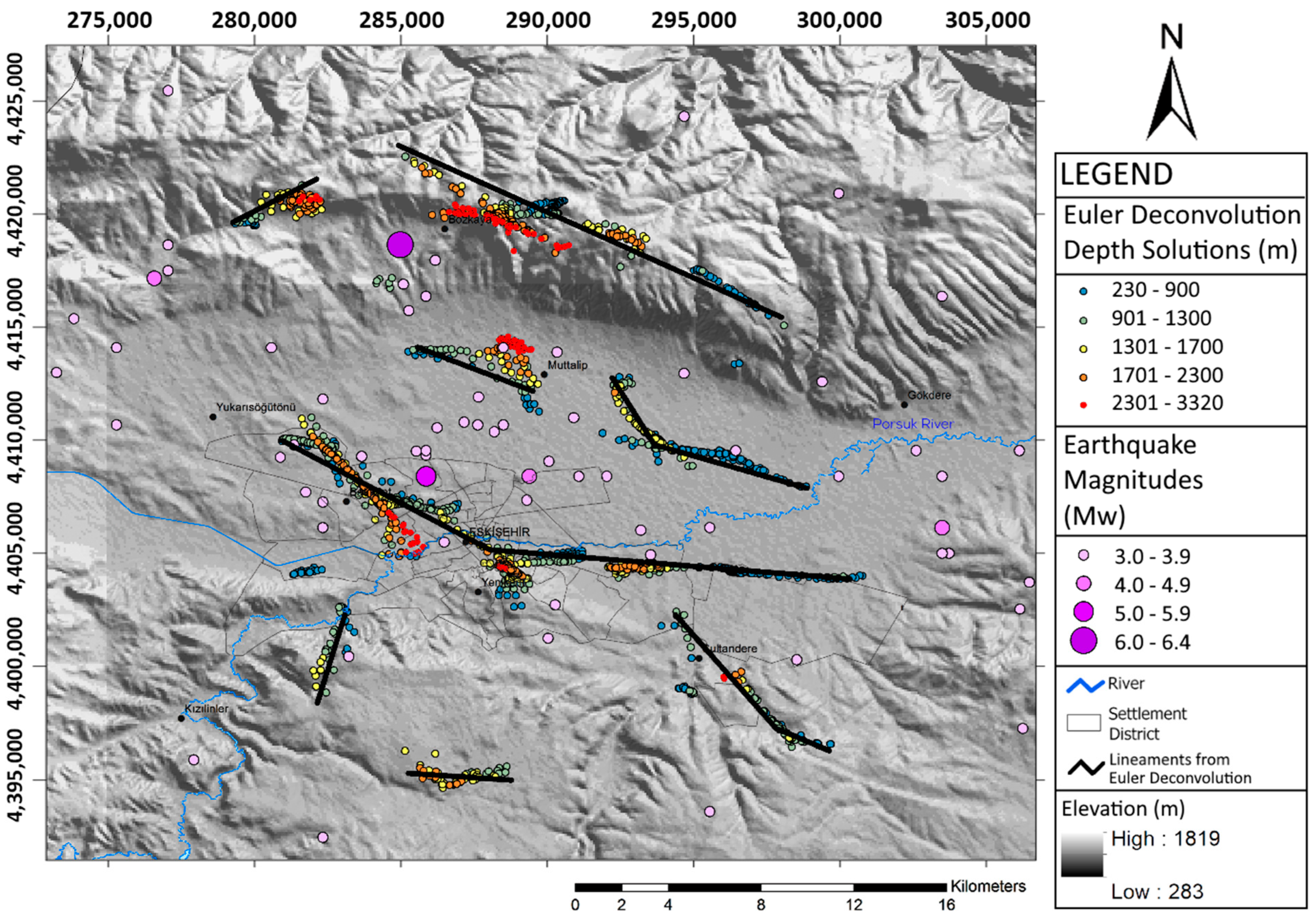
3. Earthquake Distribution in the Study Area
4. Methodology
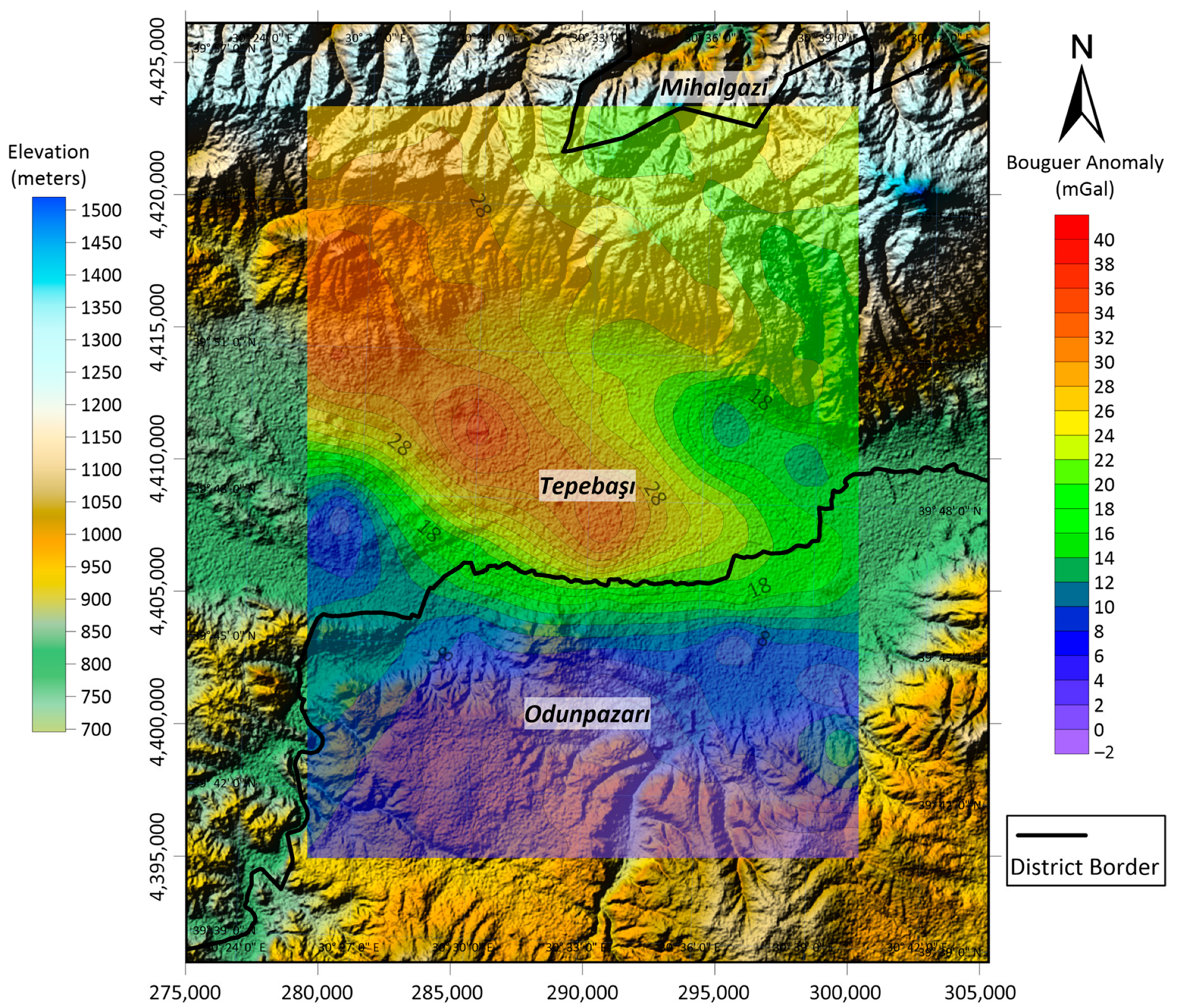
4.1. Gravity Field Survey and Bouguer Gravity Anomaly Data
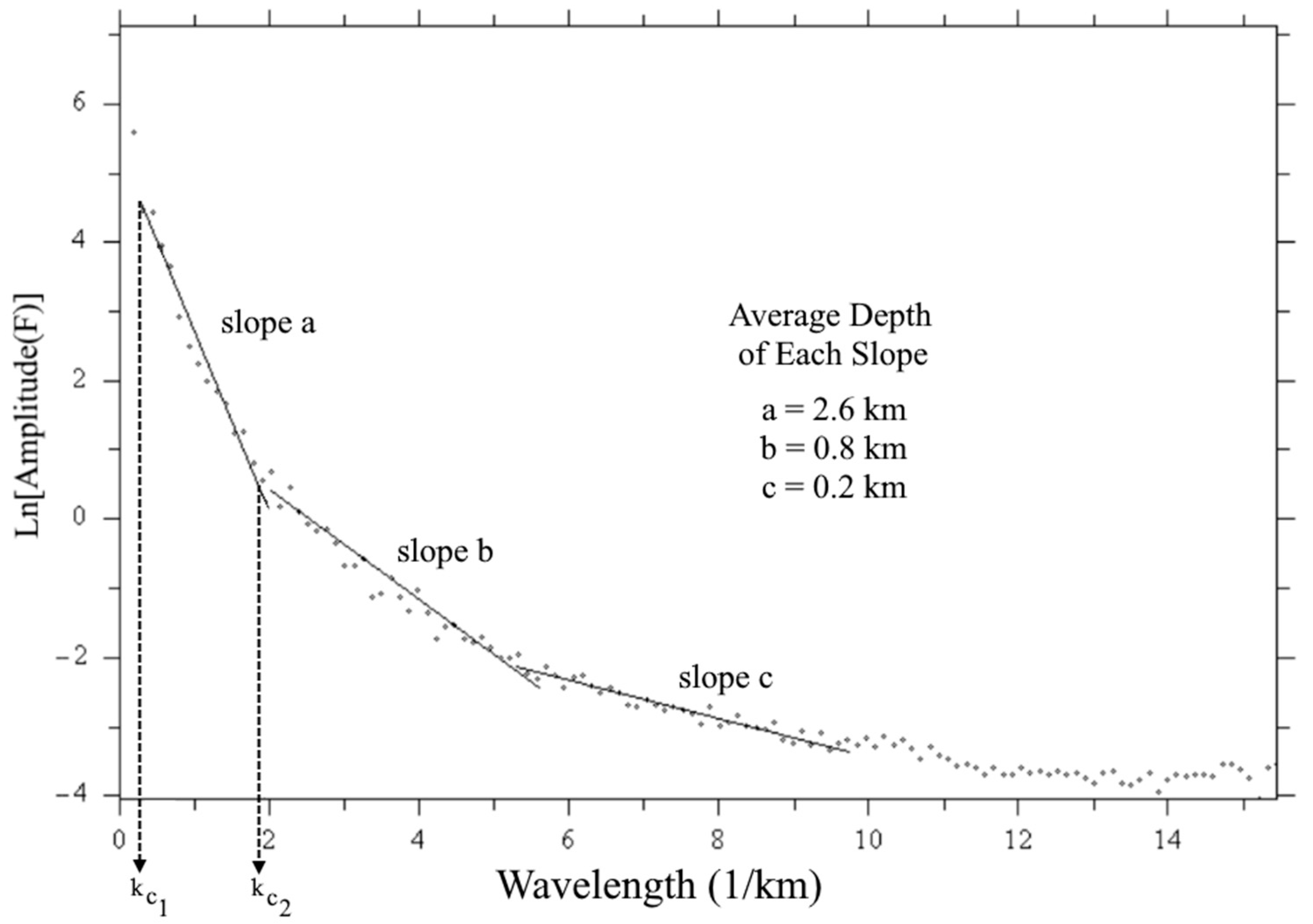
4.2. Spectral Analysis
4.3. Edge Detection
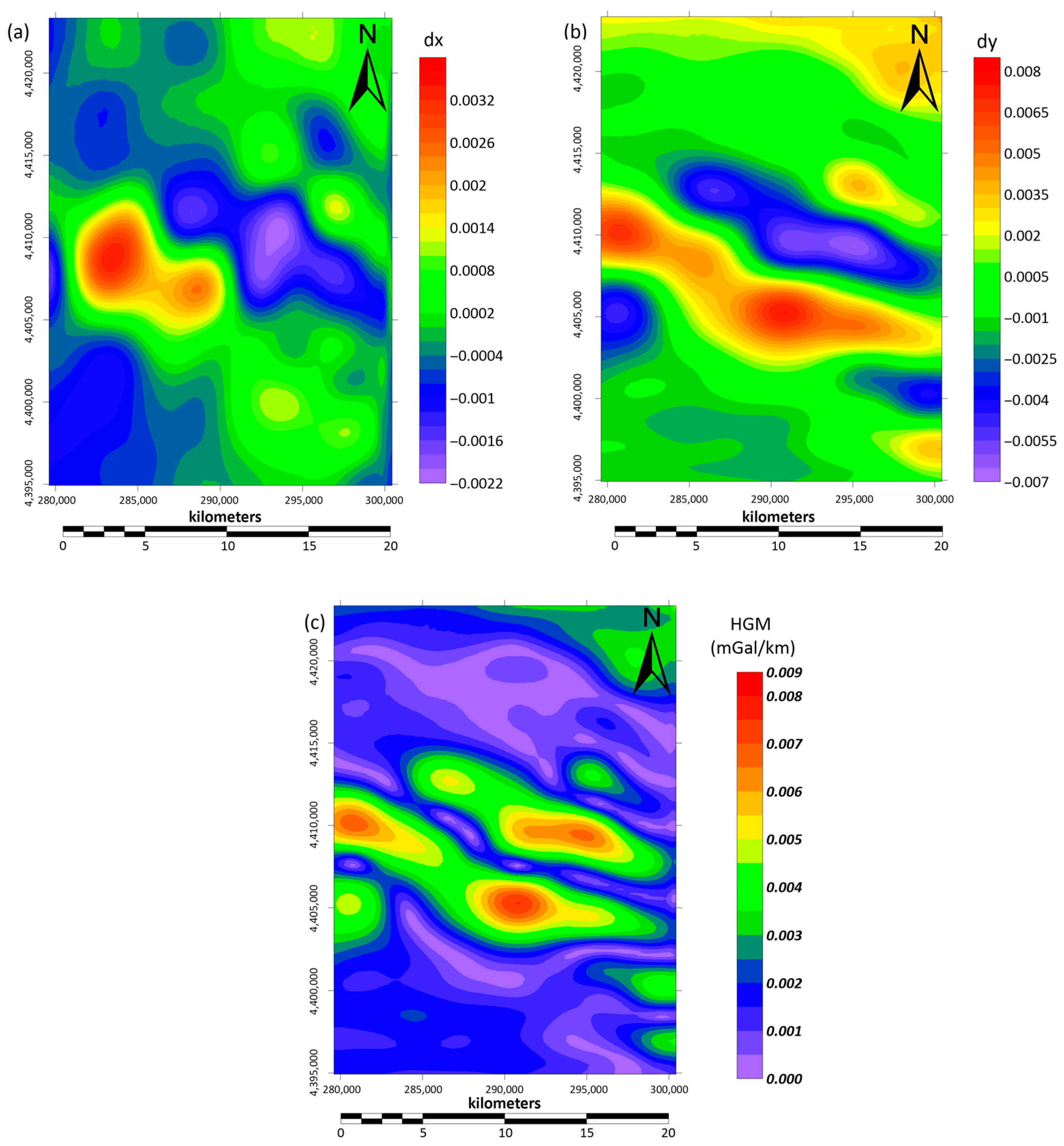
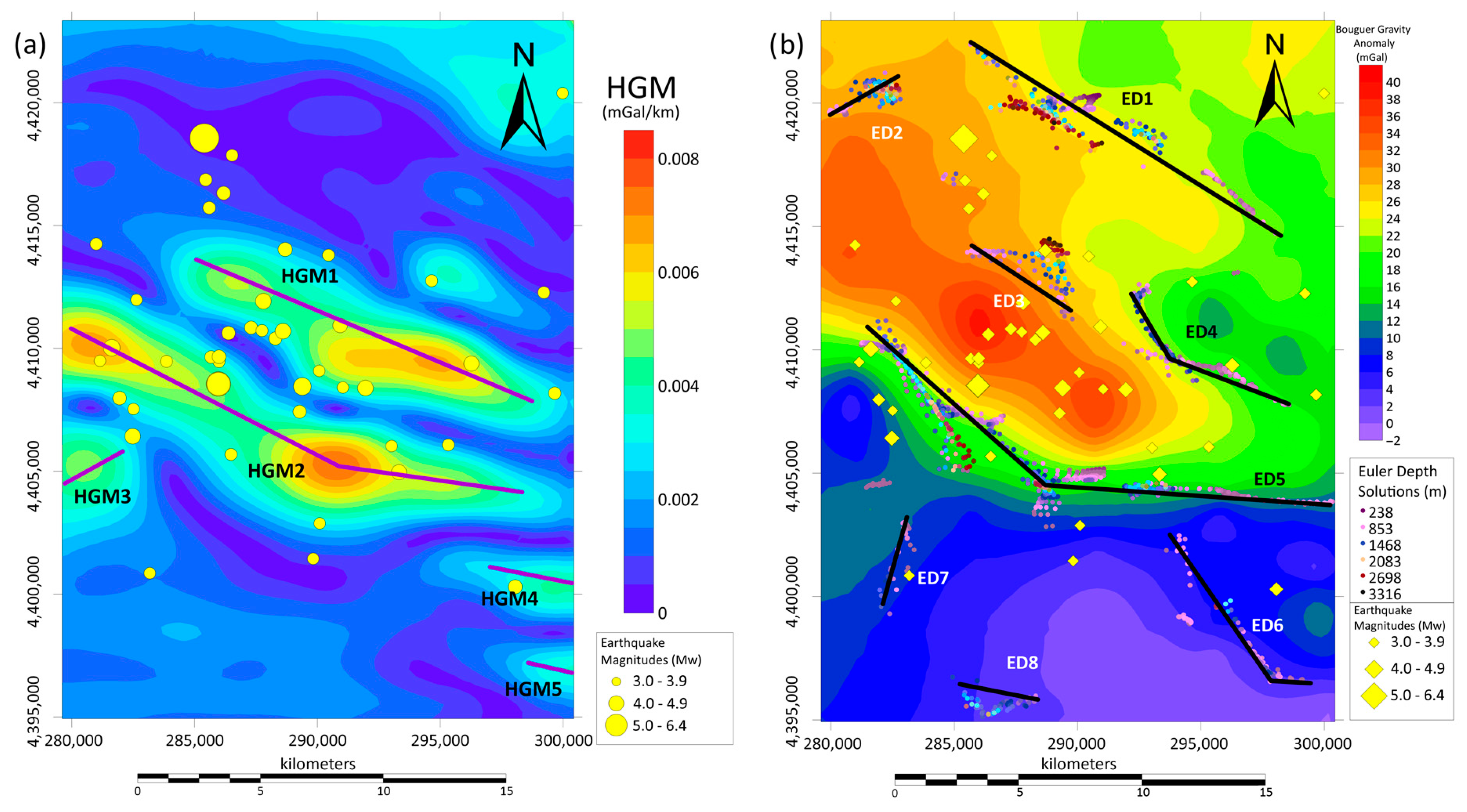
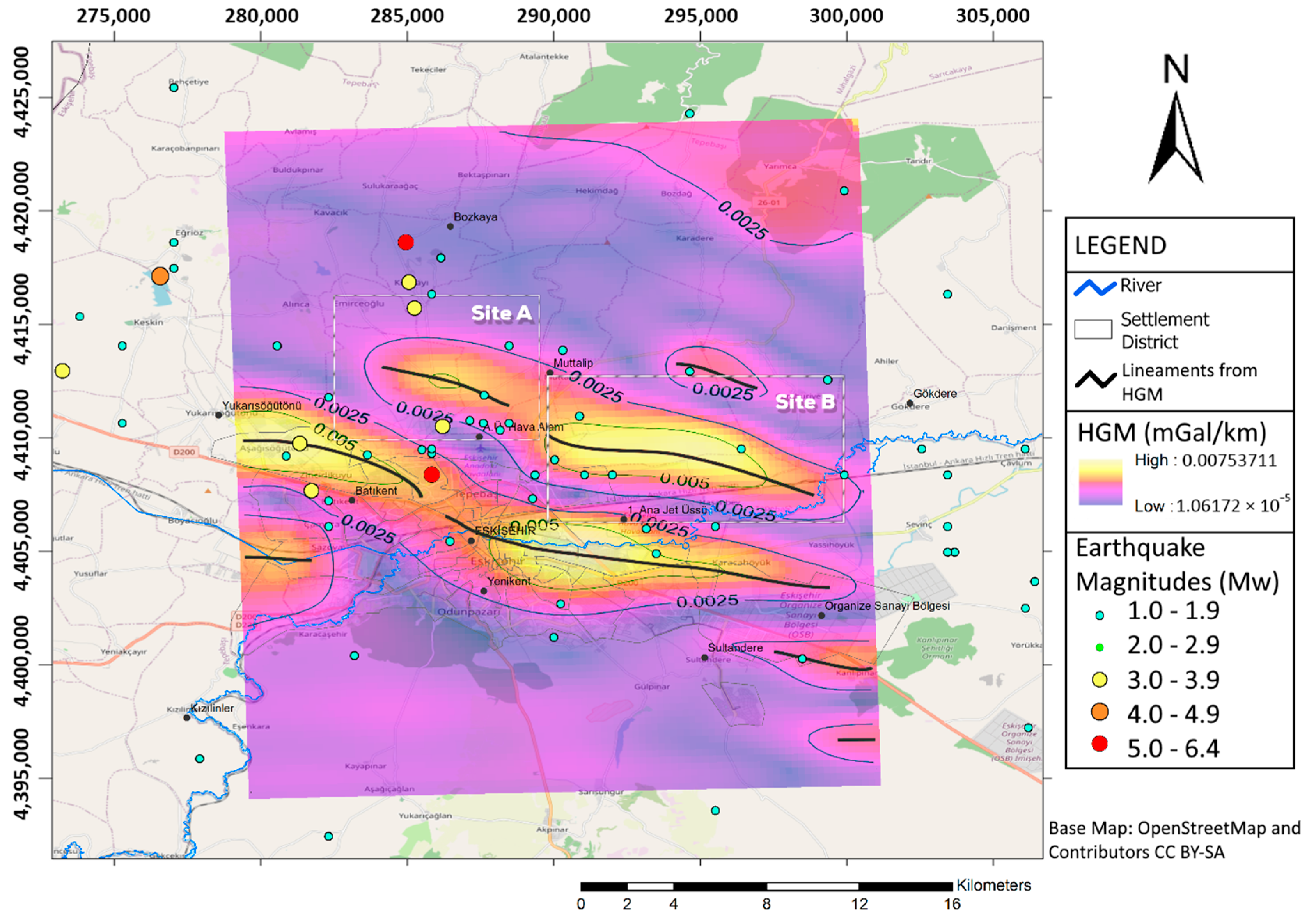
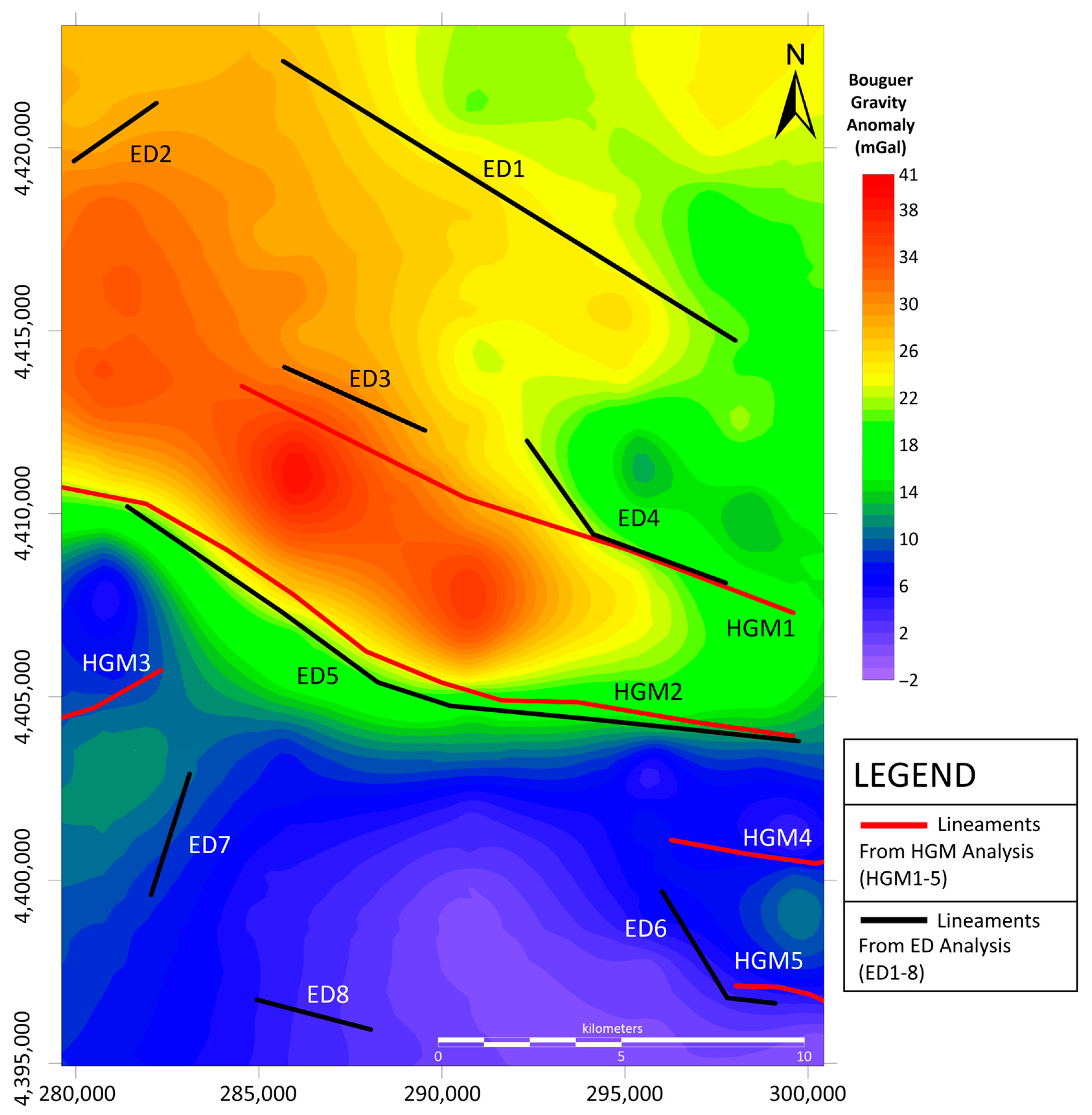
4.3.1. Horizontal Gradient Magnitude (HGM)
4.3.2. Euler Deconvolution (ED)
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pekkan, E.; Tun, M.; Guney, Y.; Mutlu, S. Integrated seismic risk analysis using simple weighting method: The case of residential Eskisehir, Turkey. Nat. Hazards Earth Syst. Sci. 2015, 15, 1123–1133. [Google Scholar] [CrossRef]
- Özmen, H.B. Seismic Hazard Analysis of Eskişehir. Master’s Thesis, Anadolu University, Eskişehir, Turkey, 2018. [Google Scholar]
- Ketin, İ. Relations between general tectonic features and the main earthquake regions of Turkey. Maden Tetk. Ve Aram. Derg. 1968, 71, 129–135. [Google Scholar]
- Ocakoğlu, F. A re-evaluation of the Eskişehir Fault Zone as a Recent extensional structure in NW Turkey. J. Asian Earth Sci. 2007, 31, 91–103. [Google Scholar] [CrossRef]
- Koçyiğit, A. The Denizli graben-horst system and the eastern limit of western Anatolian continental extension: Basin fill, structure, deformational mode, throw amount and episodic evolutionary history, SW Turkey. Geodin. Acta 2005, 18, 167–208. [Google Scholar] [CrossRef]
- Şaroğlu, F.; Emre, Ö.; Boray, A. Active Faults and Seismicity of Turkey; Report No: 8174; General Directorate of Mineral Research and Exploration Ankara: Ankara, Turkey, 1987; p. 51. [Google Scholar]
- Koçyiğit, A. Orta Anadolu’nun genel neotektonik özellikleri ve depremselliği. TPJD (Türkiye Pet. Jeologları Derneği) Bülteni Özel Sayı 2003, 5, 1–26. [Google Scholar]
- Ocakoğlu, F.; Altunel, E.; Yalçıner, Ç. Eskişehir Bölgesinin Neotektonik dönemdeki tektono-stratigrafik ve Sedimantolojik Gelişimi; Osmangazi Üniversitesi, Osmangazi Üniversitesi Bilimsel Araştırma Projeleri Komisyonu: Odunpazarı, Turkey, 2005; p. 122. [Google Scholar]
- Tokay, F.; Altunel, E. Neotectonic activity of Eskişehir fault zone in vicinity of İnönü–Dodurga area. Bull. Miner. Res. Explor. Inst. Turk. 2005, 130, 1–15. [Google Scholar]
- Altunel, E.; Barka, A. Eskişehir fay zonimun İnönü-Sultandere arasında neotektonik aktivitesi. Geol. Bull. Turk. 1998, 41, 41–52. [Google Scholar]
- Seyitoğlu, G.; Ecevitoğlu, G.B.; Kaypak, B.; Güney, Y.; Tün, M.; Esat, K.; Uyar Aldaş, G.G. Determining the main strand of the Eskisehir strike-slip fault zone using subsidiary structures and seismicity: A hypothesis tested by seismic reflection studies. Turk. J. Earth Sci. 2015, 24, 1. [Google Scholar] [CrossRef]
- Gözler, M.; Cevher, F.; Ktieijkayman, A. Geology and hotsprings of Eskisehir. MTA Inst. Rep. 1985, 103, 40–50. [Google Scholar]
- Orhan, A.; Seyrek, E.; Tosun, H. A probabilistic approach for earthquake hazard ssessment of the Province of Eskisehir. Nat. Hazards Earth Syst. Sci. 2007, 7, 607–614. [Google Scholar] [CrossRef]
- Gözler, M.; Cevher, F.; Ergül, E.; Asutay, H.J. Orta Sakarya ve Güneyinin Jeolojisi; MTA Genel Müdürlüğü: Eskişehir, Turkey, 1996. [Google Scholar]
- Blakely, R.J.; Simpson, R.W. Approximating edges of source bodies from magnetic or gravity anomalies. Geophysics 1986, 51, 1494–1498. [Google Scholar] [CrossRef]
- Wilsher, W. A Structural İnterpretation of the Witwatersrand Basin through the Application of the Automated Depth Algorithms to both Gravity and Aeromagnetic Data. Master’s Thesis, University of Witwatersrand, Johannesburg, South Africa, 1987. [Google Scholar]
- Huang, D.; Gubbins, D.; Clark, R.; Whaler, K. Combined study of Euler’s homogeneity equation for gravity and magnetic field. In Proceedings of the 57th EAGE Conference and Exhibition, Glasgow, UK, 29 May–2 June 1995; p. cp–90-00372. [Google Scholar]
- Ma, Z.J.; Gao, X.L.; Song, Z.F. Analysis and tectonic interpretation to the horizontal-gradient map calculated from Bouguer gravity data in the China mainland. Chin. J. Geophys. 2006, 49, 95–106. [Google Scholar] [CrossRef]
- Oruç, B.; Keskinsezer, A. Structural setting of the northeastern Biga Peninsula (Turkey) from tilt derivatives of gravity gradient tensors and magnitude of horizontal gravity components. Pure Appl. Geophys. 2008, 165, 1913–1927. [Google Scholar] [CrossRef]
- Oruç, B. Depth estimation of simple causative sources from gravity gradient tensor invariants and vertical component. Pure Appl. Geophys. 2010, 167, 1259–1272. [Google Scholar] [CrossRef]
- Oruç, B. Edge detection and depth estimation using a tilt angle map from gravity gradient data of the Kozaklı-Central Anatolia Region, Turkey. Pure Appl. Geophys. 2011, 168, 1769–1780. [Google Scholar] [CrossRef]
- Eysteinsson, H. Elevation and gravity changes at geothermal fields on the Reykjanes Peninsula, SW Iceland. In Proceedings of the World Geothermal Congress 2000, Kyushu-Tohoku, Japan, 28 May–10 June 2000; pp. 559–564. [Google Scholar]
- Sugihara, M.; Sato, T.; Takemura, T. Measurement and use of the vertical gravity gradient in correcting repeat microgravity measurements for the effects of ground subsidence in geothermal systems. Geothermics 2002, 31, 19. [Google Scholar] [CrossRef]
- Bektaş, Ö.; Ravat, D.; Buyuksarac, A.; Bilim, F.; Ates, A. Regional Geothermal Characterisation of East Anatolia from Aeromagnetic, Heat Flow and Gravity Data. Pure Appl. Geophys. 2007, 164, 975–997. [Google Scholar] [CrossRef]
- Atef, H.; Abd El-Gawad, A.; Zaher, M.A.; Farag, K. The contribution of gravity method in geothermal exploration of southern part of the Gulf of Suez–Sinai region, Egypt. NRIAG J. Astron. Geophys. 2016, 5, 173–185. [Google Scholar] [CrossRef]
- Yılmaz, Y. Interpretation of Gravity Data of Bergama-Dikili Geothermal Field. Master’s Thesis, Dokuz Eylul University, İzmir, Turkey, 2018. [Google Scholar]
- Emre, Ö.; Duman, T.Y.; Özalp, S.; Şaroğlu, F.; Olgun, Ş.; Elmacı, H.; Çan, T. Active fault database of Turkey. Bull. Earthq. Eng. 2018, 16, 3229–3275. [Google Scholar] [CrossRef]
- Tün, M. Mikrobölgeleme Çalışmalarında Yer Tepkisi ve Kayma Dalga Hız Yapısının Yorumlanması: Eskişehir Örneği. Ph.D. Thesis, İistanbul Üniversitesi, İistanbul, Turkey, 2013. [Google Scholar]
- Esen, E.; Yakal, M.; Gökçen, M.; Mumcu, N.; Türkman, M.; Dirik, M.; Çuhadar, G. Eskişehir ve İnönü Ovaları Hidrojeoloji Haritası; TC Enerji Ve Tabii Kaynaklar Bakanlığı DSİ Jeoteknik Hizmetler Ve Yeraltısuları Dairesi Başkanlığı: Ankara, Turkey, 1976. [Google Scholar]
- Ölmez, E.; Demirel, Z.; Uzel, Ö.F. ESKİŞEHİR ES-1 ve ES-2 SICAKSU SONDAJLARI KUYU BİTİRME RAPORU; Maden Tetkik ve Arama Genel Müdürlüğü; Enerji Hammadde Etüd ve Arama Dairesi: Ankara, Turkey, 1986. [Google Scholar]
- Ölmez, E. Eskişehir Es-1 ve Es-2 Sıcaksu Sondajları Kutu Bitirme Raporu; Enerji Hammade Edüd Arama Dairesi; Maden Tetkik ve Arama Genel Müdürlüğü: Eskişehir, Turkey, 1986. [Google Scholar]
- Ölmez, E.; Yücel, B. Eskişehir ve Yöresinin Jeotermal Enerji Olanakları; Maden Tetkik ve Arama Genel Müdürlüğü; Enerji Hammadde Etüd ve Arama Dairesi Başkanlığı: Ankara, Turkey, 1985. [Google Scholar]
- Yıldırım, A.; Gürsoy, T. Eskişehir İl Merkezi ve Yakın Çevresi Detay Jeotermal Gravite Etüdü; Maden Tetkik ve Arama Genel Müdürlüğü: Eskişehir, Turkey, 1985. [Google Scholar]
- Sarıiz, K.; Oruç, N. Eskişehir Yöresi’nin Jeolojisi ve Jeotermal Özellikleri. Anadolu Üniversitesi Müh. Ve Mimar. Fak. Derg. 1989, 2, 59–81. [Google Scholar]
- Yücel, B. Eskişehir Sıcaksu Sondajı (ES-3) Kuyu Bitirme Raporu; Enerji Hammadde Etüd ve Arama Dairesi Başkanlığı; MTA Genel Müdürlüğü: Eskişehir, Turkey, 1986. [Google Scholar]
- Emre, Ö.; Doğan, A.; Duman, T.; Özalp, S. Eskişehir (NJ 36-1) Quadrangle. 1: 250.000 Scale Active Fault Map Series of Turkey 2011. Available online: http://www.mta.gov.tr/v3.0/hizmetler/yenilenmis-diri-fay-haritalari (accessed on 1 February 2023).
- Özmen, B. Ağustos 1999 İzmit Körfezi Depreminin Hasar Durumu (Rakamsal Verilerle). Türkiye Deprem Vakfı 2000, TDV/DR 010-53, 132. [Google Scholar]
- Şaroğlu, F.; Emre, Ö.; Boray, A. Active Faults and Seismicity of Turkey; MTA Report; MTA: Ankara, Turkey, 1987. [Google Scholar]
- Sengör, A.; Görür, N.; Saroglu, F. Strike-slip deformation, basin formation and sedimentation: Strike-slip faulting and related basin formation in zones of tectonic escape: Turkey as a case study. Soc. Econ. Paleontol. Mineral. Spec. Publ. 1985, 37, 227–264. [Google Scholar]
- Şaroğlu, F.; Emre, Ö.; Doğan, A.; Yıldırım, C. Eskişehir Fay Zonu ve Deprem Potansiyeli. Eskişehir Fay Zonu Ve Lişkili Sist. Depremselliği Çalıştayı 2005, 28–30. [Google Scholar]
- Barka, A.; Reilinger, R.; Şaroğlu, F.; Şengör, A. The Isparta Angle: Its importance in the neotectonics of the Eastern Mediterranean Region. Int. Earth Sci. Colloqium Aegean Reg. 1995, 1, 3–17. [Google Scholar]
- Nyquist, H. Certain factors affecting telegraph speed. Trans. Am. Inst. Electr. Eng. 1924, 43, 412–422. [Google Scholar] [CrossRef]
- Balkan, E.; Tün, M. DATA S1: Bouguer Gravity Anomaly Data of Eskişehir Basin; Eskişehir Technical University: Eskişehir, Turkey, 2016. [Google Scholar]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Oruç, B. Yeraltı Kaynak Aramalarında Gravite Yöntemi:(Matlab Kodları ve Cözümlü Örnekler); Umuttepe Yayınları: Istanbul, Turkey, 2013. [Google Scholar]
- Nagy, D. The prism method for terrain corrections using digital computers. Pure Appl. Geophys. 1966, 63, 31–39. [Google Scholar] [CrossRef]
- Bhattacharyya, B.K. Some general properties of potential fields in space and frequency domain; a review. Geoexploration 1967, 5, 127–243. [Google Scholar] [CrossRef]
- Pirttijärvi, M. FOURPOT-Potential Field Data Processing and Analysis of Using 2-D Fourier Transform; University of Oulu: Oulu, Finland, 2014; Volume 1, p. 54. [Google Scholar]
- Cordell, L. Sedimentary facies and gravity anomaly across master faults of the Rio Grande rift in New Mexico. Geology 1979, 7, 201–205. [Google Scholar] [CrossRef]
- Grauch, V.; Cordell, L. Limitations of determining density or magnetic boundaries from the horizontal gradient of gravity or pseudogravity data. Geophysics 1987, 52, 118–121. [Google Scholar] [CrossRef]
- Sharpton, V.; Grieve, R.; Thomas, M.; Halpenny, J. Horizontal gravity gradient: An aid to the definition of crustal structure in North America. Geophys. Res. Lett. 1987, 14, 808–811. [Google Scholar] [CrossRef]
- Thompson, D. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics 1982, 47, 31–37. [Google Scholar] [CrossRef]
- Reid, A.B.; Allsop, J.; Granser, H.; Millett, A.t.; Somerton, I. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef]
- Cooper, G. Euler deconvolution with improved accuracy and multiple different structural indices. J. China Univ. Geosci. 2008, 19, 72–76. [Google Scholar] [CrossRef]
- Noutchogwe, C.T.; Koumetio, F.; Manguelle-Dicoum, E. Structural features of South-Adamawa (Cameroon) inferred from magnetic anomalies: Hydrogeological implications. Comptes Rendus Geosci. 2010, 342, 467–474. [Google Scholar] [CrossRef]
- Clotilde, O.A.M.L.; Tabod, T.C.; Séverin, N.; Victor, K.J.; Pierre, T.K.A. Delineation of lineaments in south cameroon (central africa) using gravity data. Open J. Geol. 2013, 2013, 36618. [Google Scholar] [CrossRef]
- Singh, A.; Singh, U.K. Continuous wavelet transform and Euler deconvolution method and their application to magnetic field data of Jharia coalfield, India. Geosci. Instrum. Methods Data Syst. 2017, 6, 53. [Google Scholar] [CrossRef]
- FitzGerald, D.; Milligan, P.; Reid, A. Integrating Euler solutions into 3D geological models-automated mapping of depth to magnetic basement. In SEG Technical Program Expanded Abstracts 2004; Society of Exploration Geophysicists: Houston, TX, USA, 2004; pp. 738–741. [Google Scholar]
- Tün, M.; Pekkan, E.; Özel, O.A.; Güney, Y. An investigation into the bedrock depth in the Eskisehir Quaternary Basin (Turkey) using the microtremor method. Geophys. J. Int. 2016, 207, 589–607. [Google Scholar] [CrossRef] [Green Version]


| Source | Structural Index (N) | ||
|---|---|---|---|
| Data Used for ED | |||
| Gravity | 1st Degree Vertical Derivative of Gravity | 2nd Degree Vertical Derivative of Gravity | |
| Sphere | 2 | 3 | 4 |
| Horizontal Cylinder | 1 | 2 | 3 |
| Half-Infinite Thin Layer or Step | 0 | 1 | 2 |
| Half-Infinite Contact | −1 | 0 | 1 |
| Half-Infinite Thin Dyke | 1 | 2 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balkan, E.; Tün, M. Use of Land Gravity Data in Small Areas to Support Structural Geology, a Case Study in Eskişehir Basin, Turkey. Appl. Sci. 2023, 13, 2286. https://doi.org/10.3390/app13042286
Balkan E, Tün M. Use of Land Gravity Data in Small Areas to Support Structural Geology, a Case Study in Eskişehir Basin, Turkey. Applied Sciences. 2023; 13(4):2286. https://doi.org/10.3390/app13042286
Chicago/Turabian StyleBalkan, Emir, and Muammer Tün. 2023. "Use of Land Gravity Data in Small Areas to Support Structural Geology, a Case Study in Eskişehir Basin, Turkey" Applied Sciences 13, no. 4: 2286. https://doi.org/10.3390/app13042286
APA StyleBalkan, E., & Tün, M. (2023). Use of Land Gravity Data in Small Areas to Support Structural Geology, a Case Study in Eskişehir Basin, Turkey. Applied Sciences, 13(4), 2286. https://doi.org/10.3390/app13042286








