The Stationary Thermal Field in a Multilayer Elliptic Cylinder

Abstract

An analytical–numerical method for determining the two-dimensional (2D) thermal field in a layer-inhomogeneous elliptic cylinder (elliptical roller) was developed in the article. A mathematical model was formulated in the form of a boundary problem for Poisson equations with an external boundary condition of the third kind (Hankel’s). The conditions of continuity of temperature and heat flux increment were assumed at the inner boundaries of material layers. The eigenfunctions of the boundary problem were determined analytically. Hankel’s condition was subjected to appropriate mathematical transformations. As a result, a system of algebraic equations with respect to the unknown coefficients of the eigenfunctions was obtained. The above-mentioned system of equations was solved numerically (iteratively). As an example of an application of the aforementioned method, an analysis of the thermal field in an elliptical electric wire was presented. The system consists of an aluminum core and two layers of insulation (PVC and rubber). In addition to the field distribution, the steady-state current rating was also determined. The thermal conductivities of PVC and rubber are very similar to each other. For this reason, apart from the real model, a test system was also considered. Significantly different values of thermal conductivity were assumed in individual layers of the test model. The temperature distributions were presented graphically. The graphs showed that the temperature drop is almost linear in the insulation of an electrical conductor. On the other hand, in the analogous area of the test model, a broken line was observed. It was also found that the elliptical layer boundaries are not isothermal. The results obtained by the method presented in this paper were verified numerically.

1. Introduction

Multilayer systems composed of different materials are often found in technology. By combining different physical and materials properties of individual layers, elements of improved parameters as compared to the homogeneous structure are obtained. The multilayer systems under discussion are found in the automotive and building industries, as well as in thermal and nuclear engineering and many other applications.

Multilayer systems can be investigated using analytical and numerical methods. The latter form the basis for numerous commercial software programs (such as Comsol Multiphysics [1], Nisa [2]). With their help, the nonlinearity and inhomogeneity of the medium can be easily considered. In the study of multilayer systems, analytical methods are also willingly used. Their main advantages include: the results in the form of formulas, higher accuracy, no need for a discretizing grid and better physical interpretation, compared to numerical methods. In the present study, a computer-aided analytical method was developed. For this reason, the literature review below applies exclusively analytical methods employed in the calculation of multilayer systems.

Many authors have analyzed one-dimensional (1D) distributions of temperature in multilayer flat, cylindrical and spherical systems. For solving one-dimensional problems, the orthogonal expansion technique [3,4,5,6], the Green function method [6,7,8], the Laplace transform technique [9,10,11], as well as other methods [12,13,14] were used. For example, in [15], an analytical solution of the heat conduction equation in a one-dimensional bar was presented. A combination of the method of separation of variables with the orthogonal expansion technique was used therein. Reference [16] examined a multilayer flat structure with the asymmetric boundary conditions of the third kind and with heat sources. The multilayer structure was reduced to a single layer, whose properties were continuous by sections. Study [17] also examined a one-dimensional thermal field in a layered flat solid body. An arbitrary heat source and time-dependent boundary conditions were considered. The method of separation of variables was employed. In turn, the multilayer structure of a hollow cylinder was analyzed in [18]. The coefficients of the one-dimensional heat conduction equation were assumed to be constant in each layer. Heat exchange on the inner and outer surfaces of the system was described using the convection condition. The Fourier method, the modified method of eigenfunctions and the concept of quasi derivative were employed.

More mathematically advanced methods are the analyses of the two-dimensional (2D) thermal field in multilayer systems. In this respect, a flat configuration was dealt with in reference [19]. In [19], the method of separation of variables and the boundary conditions of the third kind were used. The solution was the product of two separate one-dimensional solutions. In turn, two-dimensional cylindrical configurations, examined in polar coordinates (r, φ), were shown in references [20,21]. The subject of investigation in [20] was a multilayer sector of an annulus, while [21] dealt with a solid multilayer annulus. Both of the aforementioned studies employed the method of separation of variables and the superpositions of states, and different boundary conditions were assumed.

Multilayer spherical configurations were examined in papers [22,23]. In [22], transient heat flow was modelled in spherical coordinates (r, Θ). A hollow spherical body of an arbitrary number of layers was considered. The inhomogeneous boundary conditions of the first, second and third kind, respectively, were applied at the inner and outer borders of concentric layers. The method of separation of variables was employed. The solution was given for a hemisphere and full-sphere multilayer configuration. Paper [23] provided an analytical solution to the heat conduction equation, which modeled the steady distribution of temperature in a multilayer spherical structure. The boundary conditions corresponded to different combinations of conduction, convection and radiation. The method of separation of variables was used. The coefficients in the obtained Fourier–Lagrange series were determined from the system of equations using the Thomson recurrent algorithm [23].

Studies devoted to three-dimensional (3D) multilayer systems are rarely found. An example could be paper [24]. Study [24] determined the transient three-dimensional thermal field in a cylinder composed of multiple radial layers. The eigenfunction expansion method was employed. In the angular and axial directions, an arbitrary combination of the homogeneous boundary conditions of the first and third kind was assumed. In the radial direction, in turn, the inhomogeneous boundary conditions of the third kind were assumed. An example of a different configuration was examined in reference [25]. A transient thermal field in two flat plates with a contact resistance between them was analyzed. On the upper and lower bases of the system, the boundary conditions of the first, second and third kind were assumed. On the vertical (lateral) walls, the boundary conditions of the first and second kind were assumed. The Green function method was employed.

To the authors’ knowledge, only homogeneous elliptic systems with Dirichlett and Neumann boundary conditions have been calculated by analytical methods in the literature. The following papers [26,27,28,29,30,31] fall within this scope.

In [26], an analysis of thermally developing forced convection flow of water in aluminum metal-aluminum foam elliptic annulus was presented. The stationary heat equation with velocity term was solved. The following boundary conditions were assumed: adiabatic, the Dirichlet (first-type) and the Neumann (second-type). The boundary problem was solved using the superposition method with separation of variables.

In [27], an elliptical duct heat exchanger model with periodically varying inlet temperature was considered. The heat equation with velocity terms was solved. Adiabatic conditions and conditions of the first kind (Dirichlet) were assumed. The generalized integral transform technique (GITT) method was used.

In the paper [28], the transient heating of an elliptical annulus was considered. On its inner surface, boundary conditions of the first (Dirichlet) or second (Neumann) type were assumed. A constant temperature (i.e., conditions of the first type) was assumed on the outer surface of the elliptical annulus. The heat equation was solved using Fourier series and separation of variables methods.

The textbook [29] considered elliptically shaped systems (an elliptical hole in a wide plate and a vacuum diode). In the first case, the Laplace equation was solved and in the second case, the Poisson equation. These equations also described the stationary heat flow. In the first example, a condition analogous to adiabatic was assumed. In turn, in the case of the diode, boundary conditions of the first type (Dirichlet) were used. The separation of variables method was used.

In the paper [30], the hydrodynamic pressure distribution exerted on a hollow elliptical cylinder by water during an earthquake was calculated analytically. The pressure distribution was described in an elliptical coordinate system using the Laplace equation (analogous to the stationary heat equation). The right-hand side of the boundary condition equations does not depend on the pressure distribution sought. The problem was solved using the separation of variables method.

The paper [31] presented the derivation of the Green’s function of the wave equation in an elliptic region with boundary conditions of the first type. The mentioned function was presented in the form of a double series of Mathew functions. They were eigenfunctions of the Helmholtz operator in the elliptic region under consideration.

The above and wider literature reviews show that multilayer systems of an elliptical structure have not been calculated analytically. This gap was partially filled by the present study. Its purpose was to perform the analysis of the stationary two-dimensional thermal field in a layered elliptical cylinder with boundary conditions of the third kind on the outer surface. The eigenfunctions of the heat conduction equation were determined using the method of separation of variables. In turn, the coefficients of the eigenfunctions resulted from the system of algebraic equations obtained from the Hankel condition.

2. Physical and Mathematical Models

The subject of the study was a multilayer elliptical system, as shown in Figure 1, where η, ψ are the elliptical–cylindrical coordinates, whereas a₁, a₂ … a_N and b₁, b₂ … b_N are, respectively, the successive semi-major and semi-minor axes of ellipses. All ellipses making up the model have common focuses (±c,0), and their individual perimeters are described with the equations η = η_i = const_i for i = 1, 2 … N. In each layer of the system (Figure 1), there is a uniform heat source of efficiency g_i for i = 1, 2 … N. It is assumed that the length l of the system under consideration in the z axis direction is much greater than the length of the external ellipse axis (l >> 2a_N). This means that the thermal field is two-dimensional and depends on the coordinates η, ψ.

The mathematical model of the thermal field was formulated with respect to increments v_i(η, ψ) related to ambient temperature T_a

$$v_i(\eta ,\psi )=T_i(\eta ,\psi )-T_a,$$

(1)

where T_i(η, ψ) is the two-dimensional stationary distribution of the thermal field in the i-th layer of the system. The stationary temperature increment in the model’s i-th layer is described by the heat equation (Poisson’s) [3,32,33,34], which, in the elliptical–cylindrical system and assuming λ_i = const_i, has the following form

$$\frac{1}{c^2({\cosh }^2\eta -{\cos }^2\psi )}\left(\frac{{\partial }^2{v}_i\left(\eta ,\psi \right)}{\partial {\eta }^2}+\frac{{\partial }^2{v}_i\left(\eta ,\psi \right)}{\partial {\psi }^2}\right)=-\frac{g_i}{{\lambda }_i},\mathrm{for}{\eta }_{i-1}\le \eta \le {\eta }_i,0\le \psi \le 2\pi ,i=1,2,\dots N$$

(2)

where η₀ = 0, λ_i is the thermal conductivity of the i-th layer.

It is assumed that on the system’s external surface for η = η_N, the exchange of heat with the environment takes place according to Newton’s law [3]. The above-mentioned energy exchange is described by the Hankel boundary condition [3,33], which in the elliptical–cylindrical coordinates has the following form

$$\frac{1}{c\sqrt{({\cosh }^2\eta -{\cos }^2\psi )}}{\left.\frac{\partial v_N\left(\eta ,\psi \right)}{\partial \eta }\right|}_{\eta ={\eta }_N}=-\frac{\alpha }{{\lambda }_N}{v}_N(\eta ={\eta }_N,\psi ),\hspace{1em}\mathrm{for}0\le \psi \le 2\pi ,$$

(3)

where α is the total heat transfer coefficient (the sum of the convective and radiative coefficients [34]).

The proposed method also enables the analysis of a system with the boundary condition of the first kind (Dirichlet’s). For this purpose, it is necessary to substitute α→∞ in Equation (3). After making the respective transformation, this will lead to the relationship T_N(η = η_N, ψ) = T_a. In physical interpretation, the latter equation corresponds to a system with constant temperature on the system’s outer perimeter, η = η_N.

Individual elliptic layers (Figure 1) adhere closely to each other. Therefore, the conditions of the continuity of increment in temperature and heat flux at the interface η = η_i between the layers i and i + 1 are satisfied

$$v_i({\eta }_i,\psi )=v_{i+1}({\eta }_i,\psi ) \mathrm{for} 0\le \psi \le 2\pi , i=1,2,\dots N-1,$$

(4)

$${\lambda }_i{\left.\frac{\partial v_i\left(\eta ,\psi \right)}{\partial \eta }\right|}_{\eta ={\eta }_i}={\lambda }_{i+1}{\left.\frac{\partial v_{i+1}\left(\eta ,\psi \right)}{\partial \eta }\right|}_{\eta ={\eta }_i}\mathrm{for}0\le \psi \le 2\pi , i=1,2,\dots N-1.$$

(5)

Formulas (1)–(5) form a mathematical model of the temperature field in the system.

The solution of Equation (2) is the sum of its particular and general integrals [29]. The particular integral has been determined by the method of variation of parameters [29], while the general integral has been determined using the method of separation of variables [29,32]. Ultimately, the following was obtained:

$$\begin{array}{ll}{v}_i\left(\eta ,\psi \right)=\hfill & -\frac{g_i{c}^2}{8{\lambda }_i}[\cosh (2\eta )+\cos (2\psi )]+(A_i+B_i\eta )(C_i+D_i\psi )+\hfill \\ & +{\displaystyle \sum _{n=1}^{\infty }[A_{ni}\cosh (n\eta )+B_{ni}\sinh (n\eta )][C_{ni}\cos (n\psi )+D_{ni}\sin (n\psi )]}\hfill \\ & \mathrm{for} {\eta }_{i-1}\le \eta \le {\eta }_i,0\le \psi \le 2\pi ,i=1,2,\dots N\hfill \end{array}$$

(6)

where A_i, B_i, C_i, D_i, A_ni, B_ni, C_ni and D_ni are either constants or coefficients, η₀ = 0, whereas in sourceless regions it is necessary to take g_i = 0.

The singular points of solution (6) (i.e., focuses) should always be examined. This leads to the elimination of non-physical solutions. Moreover, if a field exhibits a symmetry or asymmetry relative to the coordinate system, then some constants and coefficients of appropriate terms (even or odd) of series (6) can additionally be zeroed. Such simplified solutions are substituted in the conditions of continuity of temperature and flux in (4) and (5). This leads to a further reduction in the number of unknown coefficients. At the next stage, the reduced series (6) for i = N should be substituted in Hankel’s condition (3). The relationship thus obtained is multiplied by respective trigonometric functions and then integrated with respect to the ψ coordinate using the orthogonality conditions. As a result, a system of equations is obtained, which ultimately enables the determination of the coefficients and constants in (6) that are sought.

3. Calculation Example—Electric Conductor with Double Insulation

An example of the application of the method described above is the analysis of the stationary temperature field in an elliptical electric wire. The conductor is composed of a conducting core carrying alternating current and of two different layers of insulation (Figure 1 for N = 3). The conductor core was modeled as a porous body [35,36,37] consisting of helically stranded wires with air between them. The efficiency of the heat source in the core is defined as below

$$g_1=\frac{P_1}{V_1}=\frac{k_s{k}_n{R}_{DC}{\left|I\right|}^2}{\pi a_1{b}_{1}l}=k_s{k}_n\rho (T_{max})\frac{{\left|I\right|}^2}{S_1\cdot \pi a_1{b}_1},$$

(7)

where P₁ is the power of heat losses released in the core due to the alternating current flowing through it, with root-mean-square value |I|; V₁ denotes the volume of conductor core length l; R_DC is the direct current resistance of conductor core length l; ρ(T_max) denotes the electrical resistivity of the core at sustained temperature T_max; S₁ denotes the sum of the cross-sections of core forming bundles (S₁ < πa₁b₁); k_n is the skin effect coefficient; and k_s is the coefficient that takes into account the elongation of the core caused by twisting the bundles [38]. No heat sources (g₂ = g₃ = 0) in double insulation were assumed (displacement currents were omitted at low frequency).

An important factor affecting the reliability of electrical wires is the thermal field. Too high a temperature (greater than T_max) can cause a number of disadvantageous phenomena. This includes, for example, internal mechanical stresses that can cause the wires to shift more or less. In the case of short circuits, the temperature can be so high that the delaminated wires form a kind of cage in the conductor. High temperature is also highly damaging to electrical insulating materials. It accelerates the ageing of these materials and, in extreme cases, destroys them. For the reasons mentioned above, thermal field analysis is an important technical task.

The geometry of the system (Figure 1, N = 3) and the assumed constant value of coefficient α on the outer perimeter η = η₃ imply that relationships (6) must be both periodical and even with respect to the ψ coordinate of the elliptical–cylindrical system. This results in zeroing of the constants and coefficients D_i = D_ni = 0 for i = 1, 2, 3. In addition, the heat flux cannot take on an infinite value at the focus (for η = 0, ψ = 0). In order to verify this condition, the heat flux ${\overrightarrow{q}}_1$ in the core was calculated based on the Fourier law ${\overrightarrow{q}}_1=-{\lambda }_1\cdot grad[T_a+v_1(\eta ,\psi )]$ and relationship (6) for i = 1. It turned out that, at the singular point (focus), the limit ${\overrightarrow{q}}_1$ existed in infinity. Therefore, the η and sinh(nη) functions were rejected in solution (6) (it was assumed B₁ = B_n1 = 0 in (6)). Upon taking into account the above remarks and introducing new constants and coefficients, the following reduced solutions were obtained in all conductor zones (in addition, g₂ = g₃ = 0 occurs in the insulations)

$$v_1\left(\eta ,\psi \right)=-\frac{g_1{c}^2}{8{\lambda }_1}[\cosh (2\eta )+\cos (2\psi )]+A_0+{\displaystyle \sum _{n=1}^{\infty }{A}_n\cosh (n\eta )\cos (n\psi )}\mathrm{for}0\le \eta \le {\eta }_1,0\le \psi \le 2\pi ,$$

(8)

$$v_2\left(\eta ,\psi \right)=B_0+C_0\eta +{\displaystyle \sum _{n=1}^{\infty }\left[F_n\cosh (n\eta )+G_n\sinh (n\eta )\right]\cos (n\psi )}\mathrm{for}{\eta }_1\le \eta \le {\eta }_2,0\le \psi \le 2\pi ,$$

(9)

$$v_3\left(\eta ,\psi \right)=D_0+E_0\eta +{\displaystyle \sum _{n=1}^{\infty }\left[P_n\cosh (n\eta )+Q_n\sinh (n\eta )\right]\cos (n\psi )}\mathrm{for}{\eta }_2\le \eta \le {\eta }_3,0\le \psi \le 2\pi .$$

(10)

In the solutions (8)–(10) given above, it is possible to reduce the number of unknown constants and coefficients by using the condition of the continuity of increment in temperature (4) and flux (5) for i = 1, 2. For this reason, (8)–(10) were substituted in (4)–(5) for i = 1, 2, thus obtaining

$$\begin{array}{c}-\frac{g{c}^2}{8{\lambda }_1}[\cosh (2{\eta }_1)+\cos (2\psi )]+A_0+{\displaystyle \sum _{n=1}^{\infty }{A}_n\cosh (n{\eta }_1)\cos (n\psi )}=\hfill \\ \hfill =B_0+C_0{\eta }_1+{\displaystyle \sum _{n=1}^{\infty }\left[F_n\cosh (n{\eta }_1)+G_n\sinh (n{\eta }_1)\right]\cos (n\psi )},\hfill \end{array}$$

(11)

$$\begin{array}{c}{\lambda }_1\left\{-\frac{g_1{c}^2}{4{\lambda }_1}\sinh (2{\eta }_1)+{\displaystyle \sum _{n=1}^{\infty }n{A}_n\sinh (n{\eta }_1)\cos (n\psi )}\right\}=\hfill \\ \hfill ={\lambda }_2\left\{C_0+{\displaystyle \sum _{n=1}^{\infty }n\left[F_n\sinh (n{\eta }_1)+G_n\cosh (n{\eta }_1)\right]\cos (n\psi )}\right\},\hfill \end{array}$$

(12)

$$\begin{array}{c}{B}_0+C_0{\eta }_2+{\displaystyle \sum _{n=1}^{\infty }\left[F_n\cosh (n{\eta }_2)+G_n\sinh (n{\eta }_2)\right]\cos (n\psi )}=\hfill \\ \hfill =D_0+E_0{\eta }_2+{\displaystyle \sum _{n=1}^{\infty }\left[P_n\cosh (n{\eta }_2)+Q_n\sinh (n{\eta }_2)\right]\cos (n\psi )},\hfill \end{array}$$

(13)

$$\begin{array}{c}{\lambda }_2\left\{C_0+{\displaystyle \sum _{n=1}^{\infty }n\left[F_n\sinh (n{\eta }_2)+G_n\cosh (n{\eta }_2)\right]\cos (n\psi )}\right\}=\hfill \\ \hfill ={\lambda }_3\left\{E_0+{\displaystyle \sum _{n=1}^{\infty }n\left[P_n\sinh (n{\eta }_2)+Q_n\cosh (n{\eta }_2)\right]\cos (n\psi )}\right\}.\hfill \end{array}$$

(14)

Then, the constants and expressions multiplied by cos(nψ) were compared side by side in (11)–(14). In this way, a system of equations was obtained that, after being solved, made it possible to make the coefficients B₀, C₀, D₀, E₀, F_n, G_n, P_n, Q_n in (9) and (10) dependent on A₀, A_n. As a result, the following were obtained:

$$\begin{array}{ll}{v}_2\left(\eta ,\psi \right)=\hfill & A_0-\frac{g_1{c}^2}{8{\lambda }_1}\cosh (2{\eta }_1)+({\eta }_1-\eta )\frac{g_1{c}^2}{4{\lambda }_2}\sinh (2{\eta }_1)-\frac{g_1{c}^2}{8{\lambda }_1}\cos (2\psi )\cosh [2(\eta -{\eta }_1)]+\hfill \\ & +{\displaystyle \sum _{n=1}^{\infty }{A}_n\left[f(n)\cosh (n\eta )+g(n)\sinh (n\eta )\right]\cos (n\psi )},\hfill \end{array}$$

(15)

$$\begin{array}{ll}{v}_3\left(\eta ,\psi \right)=\hfill & A_0-\frac{g_1{c}^2}{8{\lambda }_1}\cosh (2{\eta }_1)+({\eta }_1-{\eta }_2)\frac{g_1{c}^2}{4{\lambda }_2}\sinh (2{\eta }_1)+({\eta }_2-\eta )\frac{g_1{c}^2}{4{\lambda }_3}\sinh (2{\eta }_1)-\hfill \\ & -\frac{g_1{c}^2}{8{\lambda }_1}\cosh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-\eta )]\cos (2\psi )+\hfill \\ & +\frac{g_1{c}^2{\lambda }_2}{8{\lambda }_1{\lambda }_3}\sinh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-\eta )]\cos (2\psi )+\hfill \\ & +{\displaystyle \sum _{n=1}^{\infty }{A}_n\left[p(n)\cosh (n\eta )+q(n)\sinh (n\eta )\right]\cos (n\psi )},\hfill \end{array}$$

(16)

where

$$f(n)={\cosh }^2(n{\eta }_1)-\frac{{\lambda }_1}{{\lambda }_2}{\sinh }^2(n{\eta }_1),$$

(17)

$$g(n)=\frac{{\lambda }_1-{\lambda }_2}{2{\lambda }_2}\sinh (2n{\eta }_1),$$

(18)

$$\begin{array}{l}p(n)=\frac{({\lambda }_1-{\lambda }_2)({\lambda }_3-{\lambda }_2)}{4{\lambda }_2{\lambda }_3}\sinh 2(n{\eta }_1)\sinh 2(n{\eta }_2)+\\ \hfill +\left[1+\frac{{\lambda }_3-{\lambda }_2}{{\lambda }_3}{\sinh }^2(n{\eta }_2)\right]\left[1+\frac{{\lambda }_2-{\lambda }_1}{{\lambda }_2}{\sinh }^2(n{\eta }_1)\right],\hfill \end{array}$$

(19)

$$\begin{array}{c}q(n)=\frac{{\lambda }_2-{\lambda }_3}{2{\lambda }_3}\sinh 2(n{\eta }_2)\left[1+\frac{{\lambda }_2-{\lambda }_1}{{\lambda }_2}{\sinh }^2(n{\eta }_1)\right]+\hfill \\ \hfill +\frac{{\lambda }_1-{\lambda }_2}{2{\lambda }_3}\sinh 2(n{\eta }_1)\left[1+\frac{{\lambda }_2-{\lambda }_3}{{\lambda }_2}{\sinh }^2(n{\eta }_2)\right].\hfill \end{array}$$

(20)

Next, the coefficients A₀, A_n in (8), (15) and (16) were determined. For this purpose, Hankel’s boundary condition (3) was used for N = 3. The summation of series (8), (15) and (16) was limited to a finite number L of terms. Then, the truncated series (16) was substituted in (3) for N = 3. Ultimately, the following was obtained:

$$\begin{array}{l}\frac{1}{c\sqrt{{\cosh }^2({\eta }_3)-{\cos }^2(\psi )}}\left(-\frac{g_1{c}^2}{4{\lambda }_3}\sinh (2{\eta }_1)+\frac{g_1{c}^2}{4{\lambda }_1}\cosh [2({\eta }_2-{\eta }_1)]\right.\sinh [2({\eta }_2-{\eta }_3)]\cos (2\psi )-\\ -\frac{g_1{c}^2{\lambda }_2}{4{\lambda }_1{\lambda }_3}\sinh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]\cos (2\psi )+\\ \left.+{\displaystyle \sum _{n=1}^{L}n{A}_n\left\{f(n)\sinh (n{\eta }_3)+g(n)\cosh (n{\eta }_3)\right\}\cos (n\psi )}\right)=\\ =-\frac{\alpha }{{\lambda }_3}\left(A_0-\frac{g_1{c}^2}{8{\lambda }_1}\cosh (2{\eta }_1)+({\eta }_1-{\eta }_2)\frac{g_1{c}^2}{4{\lambda }_2}\sinh (2{\eta }_1)+({\eta }_2-{\eta }_3)\frac{g_1{c}^2}{4{\lambda }_3}\sinh (2{\eta }_1)-\right.\\ -\frac{g_1{c}^2}{8{\lambda }_1}\cosh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]\cos (2\psi )+\\ +\frac{g_1{c}^2{\lambda }_2}{8{\lambda }_1{\lambda }_3}\sinh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-{\eta }_3)]\cos (2\psi )+\\ +{\displaystyle \sum _{n=1}^L{A}_n\left[p(n)\cosh (n{\eta }_3)+q(n)\sinh (n{\eta }_3)\right]\cos (n\psi )}.\end{array}$$

(21)

Next, relationship (21) was multiplied by {cos(mψ)} and then integrated by sides with respect to the angular coordinate ψ in the range <0, 2π>. Thus, Equation (22) was obtained for m = 1, 2… L. A subsequent Equation (23) was obtained by a double-sided integrating relationship (21) with respect to the angular coordinate ψ in the range <0, 2π>. In this way, L + 1 equations were obtained with respect to the coefficients A₀ …A_n.

$$\left\{\begin{array}{}\mathrm{(22)}\hfill & {\displaystyle \sum _{n=1}^L{A}_n{I}_1(m,n)}=I_2(m)\mathrm{for}m=1,2\dots \mathrm{L},\hfill \mathrm{(23)}\hfill & {\displaystyle \sum _{n=1}^L{A}_n{I}_3(n)+}{A}_0\frac{2\pi \alpha }{{\lambda }_3}=I_4\hfill \end{array}\right.$$

where

$$I_1(m,n)=r(n)\cdot h(m,n)\mathrm{for}m\ne n,$$

(24)

$$I_1(m=n)=r(m)\cdot h(m=n)+\frac{\pi \alpha }{{\lambda }_3}\left[p(m)\cosh (m{\eta }_3)+q(m)\sinh (m{\eta }_3)\right],$$

(25)

$$\begin{array}{cc}{I}_2(m)=\hfill & \frac{g_{1}c\sinh (2{\eta }_1)}{4{\lambda }_3}\cdot h(m,n=0)-\frac{g_{1}c\cosh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1}\cdot h(m,n=2)+\hfill \\ & +\frac{g_{1}c{\lambda }_2\sinh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1{\lambda }_3}\cdot h(m,n=2)\mathrm{for}m\ne 2,\hfill \end{array}$$

(26)

$$\begin{array}{cc}{I}_2(m=2)\hfill & =\frac{g_{1}c\sinh (2{\eta }_1)}{4{\lambda }_3}\cdot h(m=2,n=0)-\hfill \\ & -\frac{g_{1}c\cosh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1}\cdot h(m=2,n=2)+\hfill \\ & +\frac{g_{1}c{\lambda }_2\sinh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1{\lambda }_3}\cdot h(m=2,n=2)+\hfill \\ & +\frac{\pi g_1{c}^2\alpha }{8{\lambda }_1{\lambda }_3}\cosh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]-\hfill \\ & -\frac{\pi g_1{c}^2{\lambda }_2\alpha }{8{\lambda }_1{\lambda }_3^2}\sinh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-{\eta }_3)],\hfill \end{array}$$

(27)

$$I_3(n)=r(n)\cdot h(m=0,n),$$

(28)

$$\begin{array}{c}{I}_4=\frac{g_{1}c\sinh (2{\eta }_1)}{4{\lambda }_3}\cdot h(m=n=0)-\frac{g_{1}c\cosh [2({\eta }_2-{\eta }_1)]\sinh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1}\cdot h(m=2,n=0)+\\ +\frac{g_{1}c{\lambda }_2\sinh [2({\eta }_2-{\eta }_1)]\cosh [2({\eta }_2-{\eta }_3)]}{4{\lambda }_1{\lambda }_3}\cdot h(m=2,n=0)+\frac{\pi g_1{c}^2\alpha }{4{\lambda }_1{\lambda }_3}\cosh (2{\eta }_1)-\\ -\frac{\pi ({\eta }_2-{\eta }_1)g_1{c}^2\alpha }{2{\lambda }_2{\lambda }_3}\sinh (2{\eta }_1)-\frac{\pi ({\eta }_2-{\eta }_3)g_1{c}^2\alpha }{2{\lambda }_3^2}\sinh (2{\eta }_1),\end{array}$$

(29)

$$h(m,n)={\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos (m\psi )\cos (n\psi )d\psi }{\sqrt{{\cosh }^2({\eta }_3)-{\cos }^2(\psi )}}},$$

(30)

$$r(n)=\frac{n}{c}\left[p(n)\sinh (n{\eta }_3)+q(n)\cosh (n{\eta }_3)\right].$$

(31)

where p(n) and q(n) are determined by the Formulas (19) and (20).

After the numerical calculation of integrals (30), the system of Equations (22) and (23) should be solved with respect to the coefficients A_n and the constant A₀. In Formulas (8), (15) and (16), the ambient temperature T_a was taken into account (according to formula (1)). In this way, the sought field distributions were obtained.

The calculations were performed for the case of an aluminum core of twisted bundles with a total active cross-sectional area of S₁ = 270 mm² (the aluminum fills 90% of the area of the πa₁b₁ ellipse). Materials for the inner and outer insulation were, respectively, PVC and rubber. The following set of data was adopted:

b₁ = 0.00690988 m, a₁ = 2b₁, b₂ = 0.0114796 m, a₂ = 0.0165837 m, b₃ = 0.0158993 m,
a₃ = 0.0199005 m, λ₁ = 180 W/(mK), λ₂ = 0.17 W/(mK), λ₃ = 0.16 W/(mK), α = 14.9 W/(m²K), ρ(70 °C) = 3.39592 × 10⁻⁸ Ωm, T_max = 70 °C, T_a = 25 °C, k_s = 1.02, k_n = 1.02.

(32)

Using the data set (32), additional parameters were calculated: abscissa of the ellipse focus $c=\sqrt{a_1^2-b_1^2}$ and the equations for the perimeters of individual ellipses, η_i = arcsinh(b_i/c) for i = 1, 2, 3 [29].

For the determination of the field distributions (8), (15) and (16), a computer program was developed in the Mathematica package [39]. The program computes numerically the integrals h in (24)–(30), solves iteratively the system of Equations (22) and (23) and sums the truncated series (8), (15) and (16). The above-mentioned series turned out to be strong converging. During summing of more than 12 terms, the computation results varied at the sixth decimal point at different points on the conductor. Therefore, only 12 terms were summed in series (8), (15) and (16). After completing the computation, the program visualized the results.

The key parameter of the conductor is current-carrying capacity (or ampacity). This parameter is defined as the maximum amount of current the insulation can withstand before it heats up above its maximum operating temperature. The most sensitive point of insulation is the contact with the conductor (η = η₁) at the point closest to the center of the heat source (ψ = π/2). The greatest thickness of b₃ – b₁ insulation above this point also speaks in favor of this location (Figure 1). Indeed, a thick insulation hampers the dissipation of heat from the core to the environment. For the aforementioned reasons, the hottest points of the perimeter η = η₁ are the upper and lower co-vertices of the core surface. So, to find the current-carrying capacity, I_cr, one should simply solve the following equation:

$$T_1(\eta ={\eta }_1,\psi =\frac{\pi }{2},I_{cr})=T_{max}.$$

(33)

Equation (33) was solved iteratively. Taking into account the data set (32), I_cr = 553.51 A was obtained. Then, with the current value given above, the respective field distributions in the elliptical conductor were determined. The corresponding field distribution were plotted in the Cartesian coordinate system x = c∙coshη∙cosψ, y = c∙sinhη∙sinψ. Figure 2 and Figure 3 illustrate the variation of temperature, respectively, on the major semi-axis (y = 0, Figure 2) and on the minor semi-axis (x = 0, Figure 3) of the ellipse η = η₃. In turn, Figure 4 shows the two-dimensional distribution of the temperature field in the first quarter of the conductor cross-section with the current given above.

As the thermal conductivities of PVC (λ₂ = 0.17 W/(mK)) and rubber (λ₃ = 0.16 W/(mK)) are very similar to each another, the temperature distributions were also calculated in the test model for λ₂ = 1.8 W/(mK) and λ₃ = 0.18 W/(mK). Appropriate diagrams are shown in Figure 5 and Figure 6.

4. Verification of the Results

The verification of the presented method was also performed. For this purpose, using the finite element method [40], problem (1)–(5) converted to temperature was again solved. Next, the relative differences in temperature increments were calculated from the formula

$${\delta }_{Ti}=\frac{[T_i(x,y)-T_a]-[T_i^{(FE)}(x,y)-T_a]}{T_i(x,y)-T_a}100\%\mathrm{for}i=1,2,3,$$

(34)

where $T_i(x,y)$ is the distribution of temperature in the i-th zone obtained by the analytical-numerical method presented in this paper, while $T_i^{(FE)}(x,y)$ is the distribution of temperature in the i-th zone calculated by the finite element method. Figure 7 and Figure 8 illustrate relationship (34), respectively, on the major semi-axis (y = 0, Figure 7) and on the minor semi-axis (x = 0, Figure 8) of the system. Beyond axes (x ≠ 0 and y ≠ 0), the relationships (34) are similar to those shown in Figure 7 and Figure 8.

5. Conclusions

• An analytical–numerical method for the determination of the thermal field in a multilayer elliptical system was presented in the paper. An example of application is the analysis of the thermal field in a double-insulation conductor. The eigenfunctions (6) were computed analytically by the superposition of the general and particular solutions of the Poisson Equation (2) [29] and by the variable-separation method. In turn, the coefficients of the eigenfunctions were computed by the iterative solution of the system of Equations (22) and (23) after numerical computation of the integrals in (24)–(30).
• Compared to the numerical methods, the technique presented in the article has the following advantages:

  -

  no need for area discretization;

  -

  no need for area discretization;

  -

  the possibility of calculating field values at any point in the system and not only at grid nodes;

  -

  Formulas (8), (15) and (16) support the physical interpretation and discussion of the influence of individual parameters. Moreover, they facilitate the determination of scaling laws and the fast estimation of the field at selected points;

  -

  Formulas (8), (15) and (16) enable easy calculation of the sum of series with the necessary limitation of the number of summed terms (due to the calculation time).

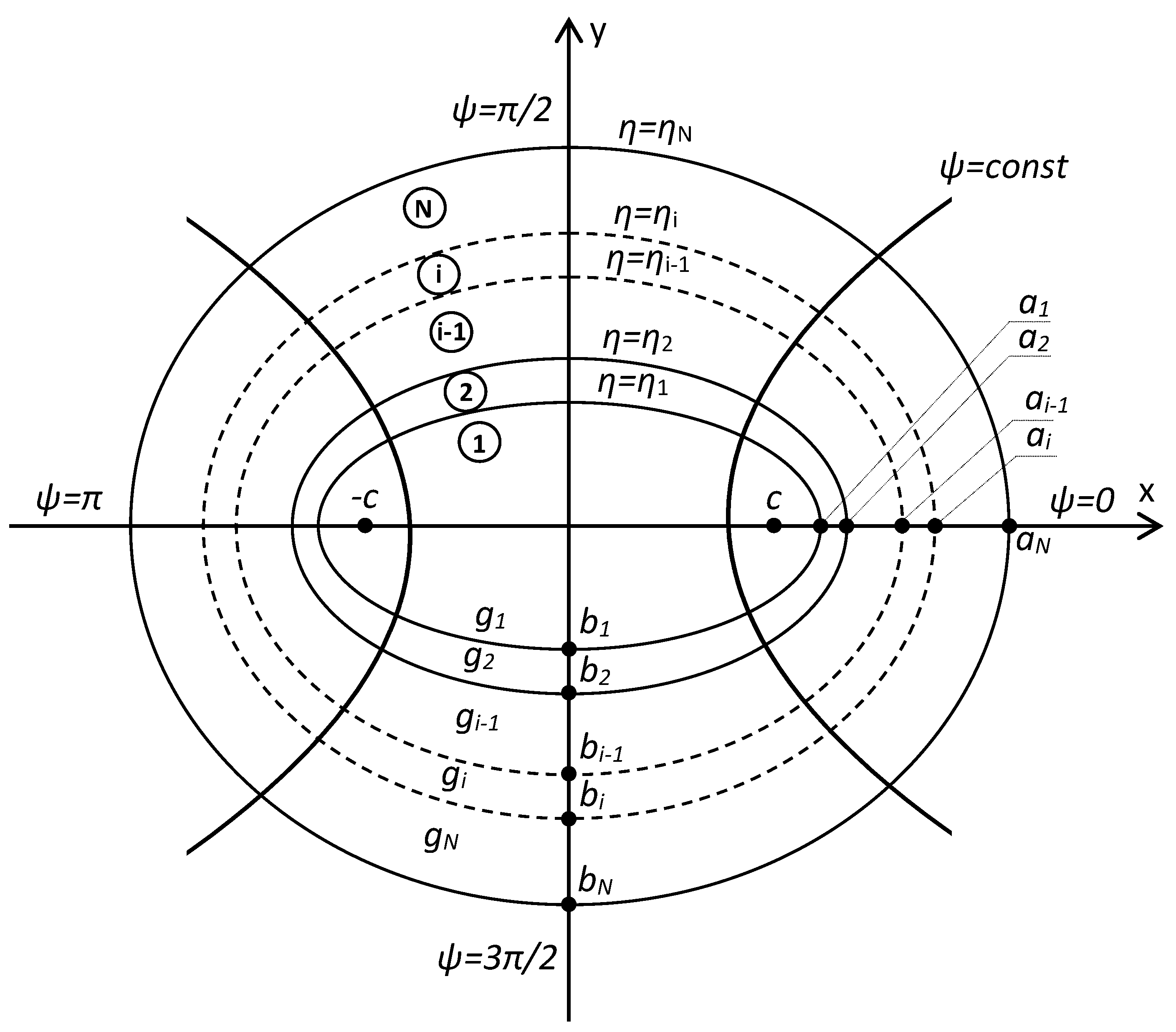
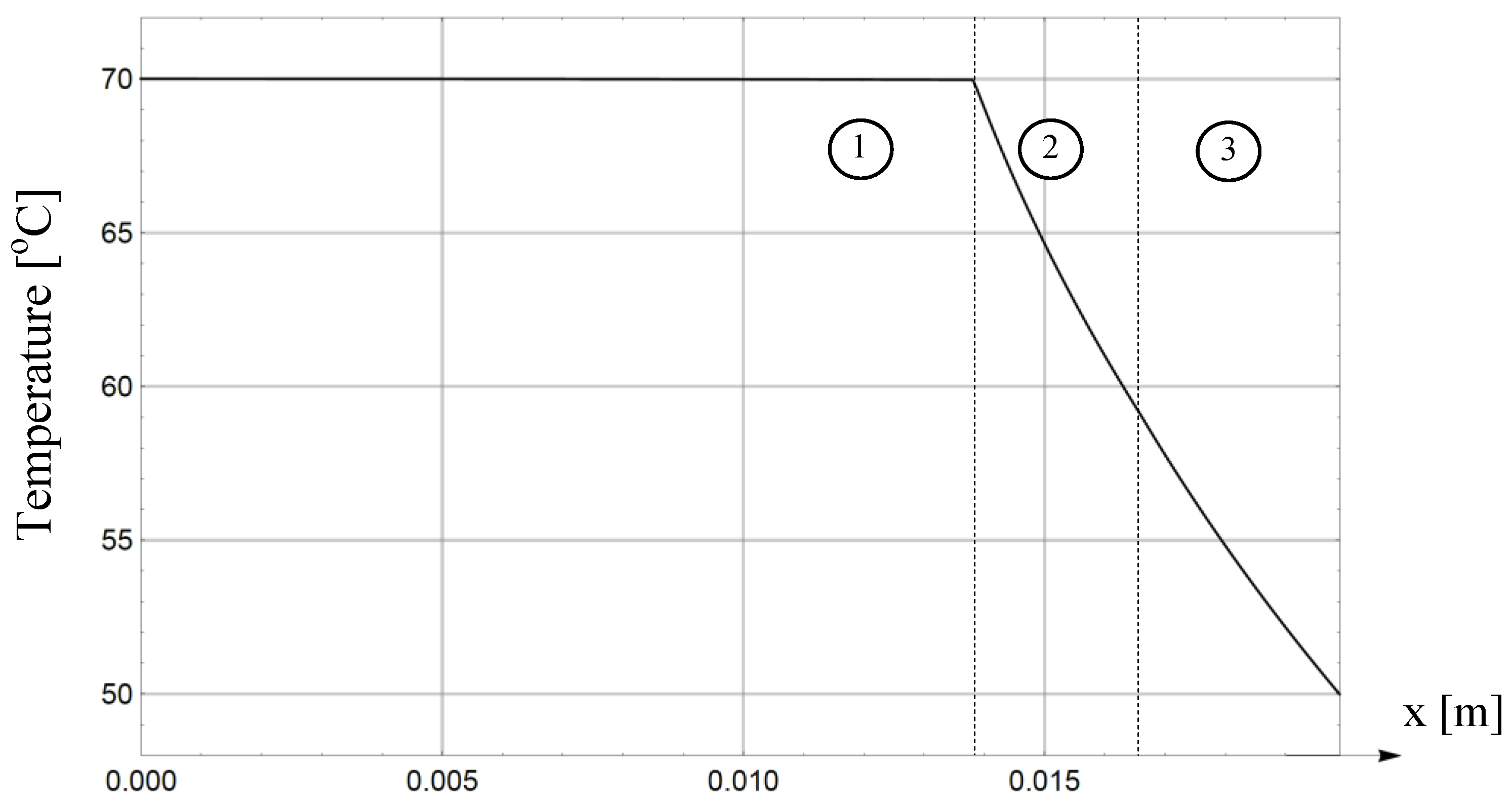
• The thermal field in the central part of the system (0 ≤ η ≤ η₁) is almost uniform. This is observed both in the conductor core (Figure 2, Figure 3 and Figure 4) and in the test model (Figure 5 and Figure 6). The maximum temperature drop in the conductor core is negligible: T₁(η = 0, ψ = π/2) − T₁(η = η₁, ψ = 0) = 0.034 °C. In the test system, the respective temperature drop is 0.033 °C. The uniformity of the field is justified by a very large thermal conductivity in the central part of the system (λ₁ = 180 W/(mK)).
• Clear temperature drops occur in regions of lower heat conductivity, compared to the central part (λ₂ << λ₁, λ₃ << λ₁). The drop increases with the increase in insulation thickness. For example, for the conductor, the following occurs: ({b₃ − b₁ ≈ 8.99 mm > a₃ − a₁ ≈ 6.08 mm} => {T₁(η = η₁, ψ = π/2) − T₃(η = η₃, ψ = π/2) = 22.09 °C > T₁(η = η₁,ψ = 0) − T₃(η = η₃, ψ = 0)= 19.99 °C})—Figure 1. The above is due to the increase in the thermal resistance of two layers of insulation with their total thickness and to thermal Ohm’s law.
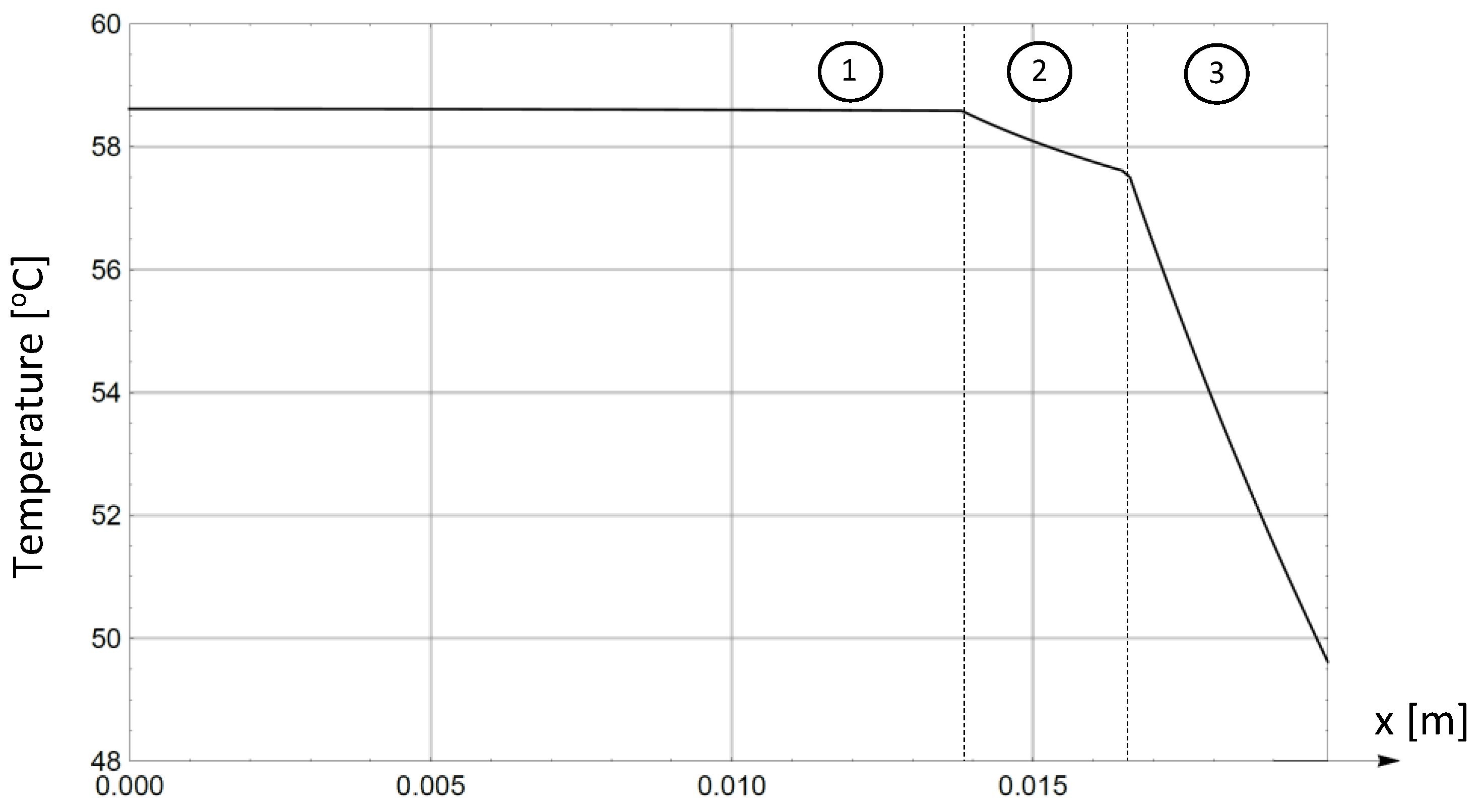
• The increase in the thermal conductivity of the middle layer λ₂ (e.g., tenfold) substantially changes the thermal field distribution. For the conductor, the temperature drop in the double insulation is almost linear (Figure 2 and Figure 3). In the test model, the temperature drop is continuous by sections (Figure 5 and Figure 6). In addition, the maximum temperature decreases from 70.01 °C (Figure 2 and Figure 3) to 58.62 °C (Figure 5 and Figure 6). This is due to better heat dissipation with the increase in λ₂.
• On the system’s outer perimeter (η = η₃), the temperature decreases from T₃(η = η₃, ψ = 0) = 49.99 °C to T₃(η = η₃, ψ = π/2) = 47.91 °C for the conductor, and from 49.61 °C to 48.22 °C for the test system. The above proves that the layer boundaries (ellipses η₁, η₂, η₃) are not isotherms. This is due to the variable distance of the points on the ellipses η₁, η₂, η₃ from the system’s center (η = 0, ψ = π/2).
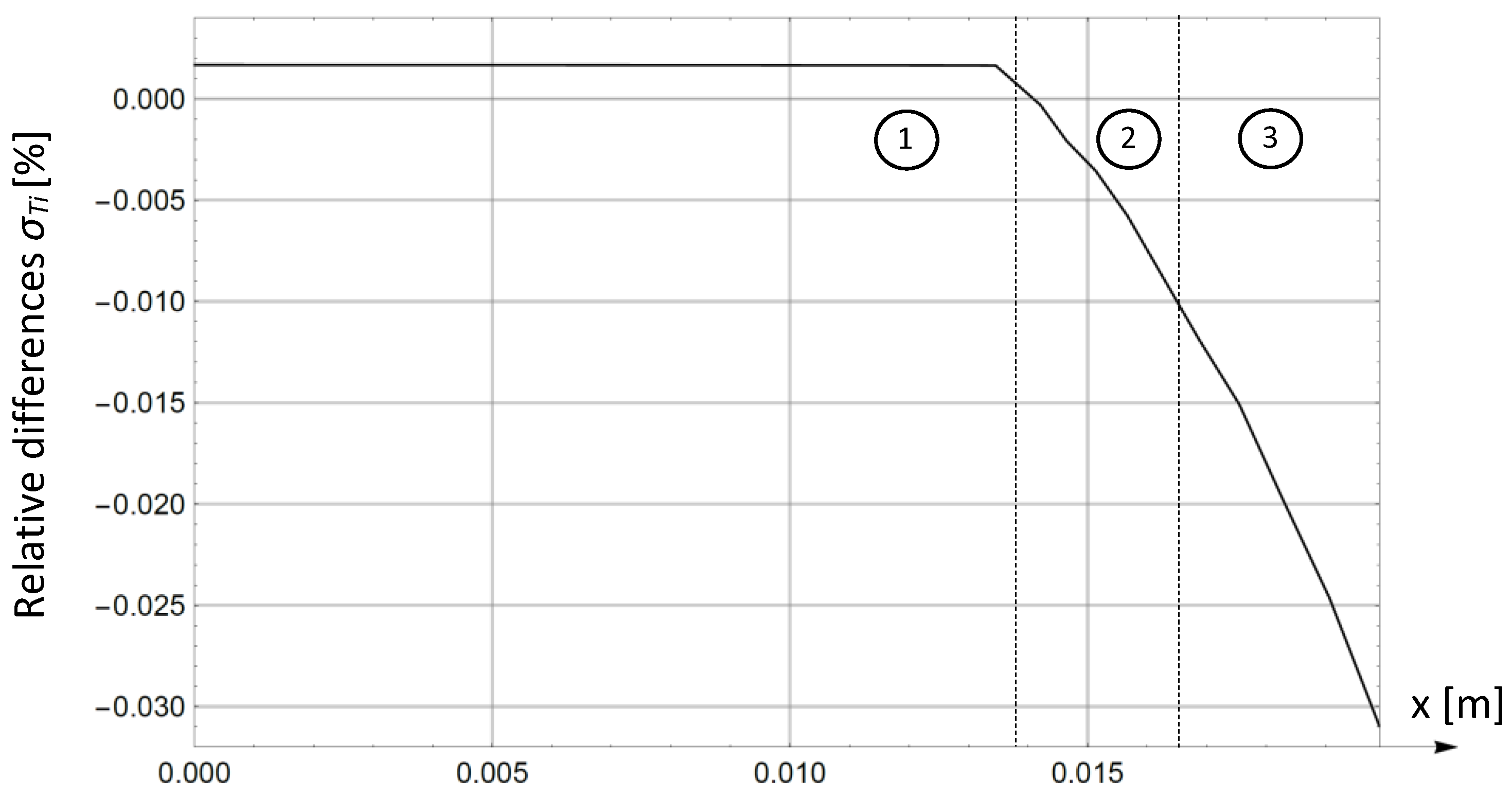
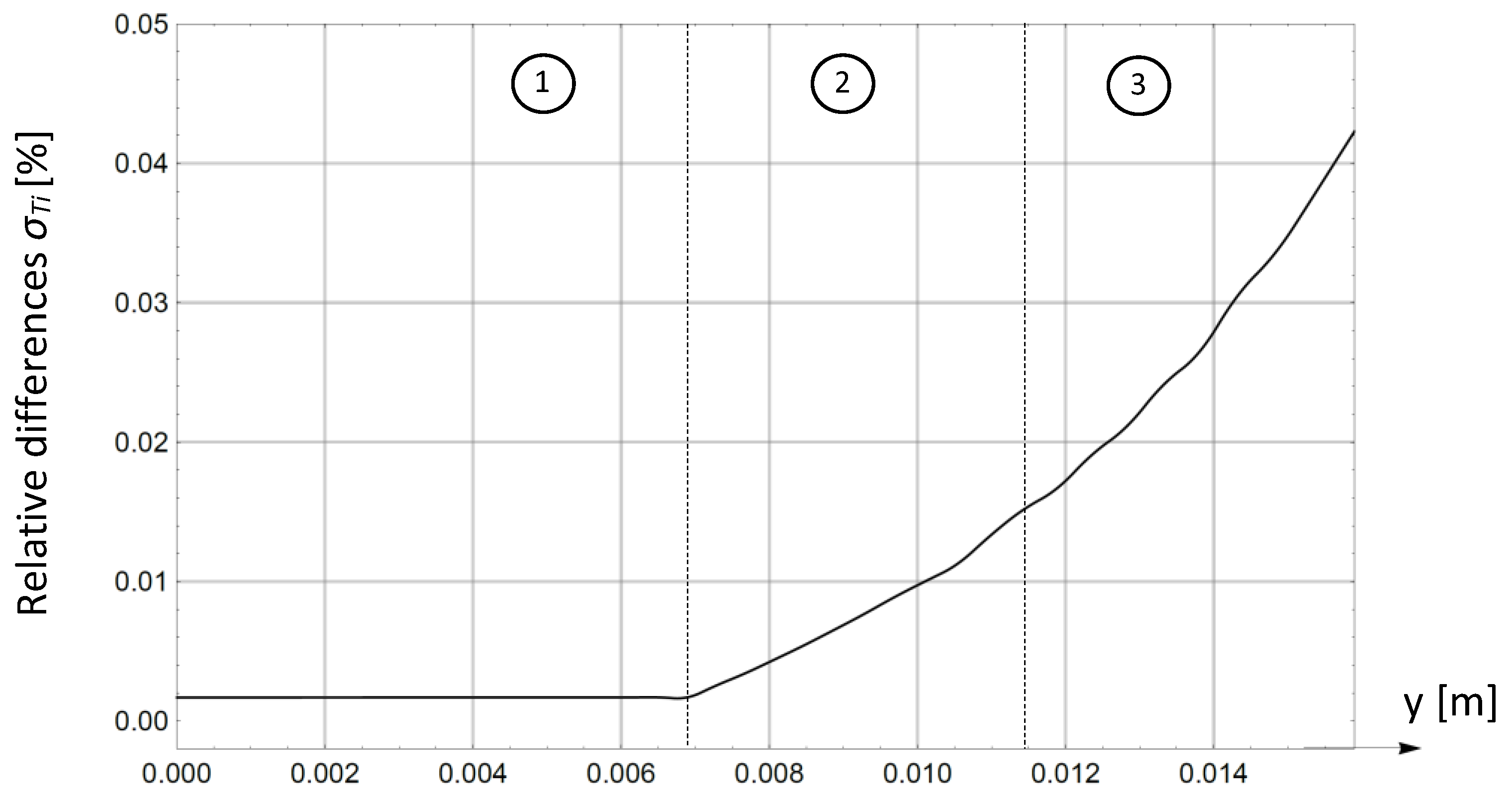
• Figure 7 and Figure 8 show that the relative differences (34) between the temperature distributions (as calculated, respectively, by the method presented in the paper and numerical method) are very small. Therefore, the above-mentioned methods give very similar results. The module of difference (34) is the smallest in the region with a uniform temperature field (0 ≤ η ≤ η₁). This is justified by the greater accuracy of the finite element method in regions with a small field gradient.
• The method presented in the paper may find application in various fields of technology. An example of this is dielectric heating of an elliptical cylinder composed of dielectric layers. Using the method described in the paper, two important parameters can be determined: the maximum temperature and the gradient of its decrease. Exceeding these parameters can result in the loss of desired properties of the dielectric charge or even its destruction. Another application is the analysis of the electrostatic field in layered elliptical systems.