Nonuniform Background Correction for Wide-Field Surveillance Camera

Abstract

Space environment surveillance is very important for space security, which is easy to be disturbed by stray light and hot pixels, and the image background presents a certain degree of nonuniformity. The existing methods can not achieve the accurate segmentation of weak targets while correcting the nonuniform background. To solve this problem, this paper presents an accurate and robust correction method for the wide-field surveillance camera, called the enhanced new top-hat transform (ENTHT). Firstly, we analyze the formation mechanism and influence of the nonuniformity background from multiple dimensions. Secondly, because of the dependence and limitations of the background suppression effect of the new top-hat transform on the selection of structural elements, we improve the new top-hat transform by designing a noise structure element (NSE). Finally, we analyze the performance and advantages of the ENTHT method. In the field experiment, the method can accurately correct the complex space nonuniform background, eliminate the stray light and hot pixels, and realize the accurate segmentation of weak targets. In the complex space environment, it brings great help to space-moving target recognition and tracking.

1. Introduction

With the development of science and technology, space exploration is becoming more and more frequent. The number of space targets has constantly been increasing since Sputnik-1 was launched in 1957 [1,2,3]. Only a small portion of the detected space targets are active satellites, and the rest can be regarded as space debris. Such a large number of space targets will pose a remarkable threat to the safety of spacecraft and human space activities [4,5]. In February of 2009, an active Iridium satellite collided with a deceased Cosmos satellite in LEO [6]. The resulting debris cloud contains hundreds of objects large enough to be tracked and potentially thousands of smaller objects that are still large enough to disable another spacecraft [7]. In order to predict and avoid these threats, it is very important to detect space targets. Space environment surveillance is very important for space security [8]. A wide-field surveillance camera can detect unidentified objects in space well. However, it is easy to be disturbed by stray light and hot pixels, and the image background presents a certain degree of nonuniformity, which makes the target signal unable to be segmented effectively. Stray light is one of the major aspects impacting the performance of optical sensors [9,10,11], which seriously affects the imaging quality and detection ability of the wide-field surveillance camera [12,13,14]. Therefore, determining how to correct the stray light nonuniform background effectively is very important for wide-field surveillance.

Stray light is usually suppressed through theoretical analysis and simulation in the process of space load design. A well-designed lens baffle that considers the working orbit and exact space task can help the wide-field surveillance camera overcome most stray light problems [15]. For example, Chen [16] analyzed the orbit characteristics and solar incidence angle distribution of a sun-synchronous orbit satellite and designed a baffle to avoid direct sunlight. However, it is often difficult to eliminate the influence of stray light in a complex space environment [17]. The strong stray light will still be received by the detector after an optical buffle. For better imaging performance, we need wide-field surveillance image post-processing.

At present, scholars have studied many nonuniformity correction algorithms in imaging systems. Flat field calibration techniques are the correction of spatial inhomogeneities in the optical sensitivity of pixel elements, which can correct the nonuniformity of camera response (PRNU). This nonuniformity is caused by the difference in photosensitive source response, noise level, quantum efficiency, etc. At the same time, if the imaging system uses coupling devices such as a fiber panel or fiber cone lens [18], it will also bring serious nonuniformity to the imaging system. These are all static scene correction algorithms; that is to say, when a camera is manufactured, these nonuniformities are fixed, and these algorithms cannot eliminate the interference of uncertain stray light [19]. Scene-based nonuniformity correction algorithms are widely used since they only need the readout image data. Mou et al. [20] proposed a method based on the neural network algorithm for real-time correction using the framework of foreground and background. Wen et al. [21] proposed a novel binarization method for nonuniformly illumination based on the curvelet transform. These neural network methods and frequency-domain methods are too complicated and need huge calculations. The amount of data taken by our camera for each task is up to hundreds of gigabytes. When the algorithm is complex, processing these images requires a lot of computing time. Space threat assessment has a high requirement for the real-time performance of the system, so the algorithms related to neural networks are not applicable to our system. There are many filtering algorithms, such as max–mean filter [22], mean iterative filtering [23], two-dimensional least mean square (tdlms) filter [24,25,26], and new top-hat transform [27,28]. These methods cannot both have high-accuracy correction of stray light nonuniform background and high-precision of target retention rate in the surveillance image [29].

Therefore, Xu et al. proposed an improved new top-hat transformation (INTHT) [29], which uses two different but related structural elements based on the new top-hat transform to retrieve the lost targets for a wide-field surveillance system in recent years. Moreover, it has higher accuracy and effectiveness in correcting a stray light nonuniform background. Xu et al. proposed an accurate stray light elimination method based on recursion multi-scale gray-scale morphology [30] for wide-field surveillance cameras in recent years. The algorithm adopts a recursion multi-scale method; that is, it increases the size of the structural operators to ensure that large stars and space targets will not be lost. This method can simultaneously have a high-precision stray light elimination effect and a high-precision target retention rate. They all have achieved good results in the stray light nonuniform background correction for wide-field surveillance. However, they rely far too much on structural elements for background suppression, resulting in the loss of space targets or stars, so their proposed methods will lose part of the weak targets. As a result, their detection rate is less than 100%. That is because, in the actual space surveillance image, in order to obtain a smooth background, it is often necessary to use larger structural elements to suppress the stray light noise. Meanwhile, the weak targets disappear. They all do not fundamentally overcome the dependence and limitations of the background suppression effect of the new top-hat transformation on the selection of structural elements. The nonuniform background of a wide-field imaging system is complex, which is usually caused by coupler devices such as optical fiber panels, dark currents, and stray light. This paper considers that these factors are important components of the nonuniform background, which seriously degrades the image quality. The first step of space target detection is star map matching. Therefore, we need to achieve nonuniform background correction and accurate star point segmentation, which will greatly help star point centroid positioning accuracy. It brings great help to space-moving target recognition and tracking. At present, the existing algorithms do not consider comprehensive facts when processing surveillance images. For weak targets, the processing ability of these algorithms is poor, and the processed images often have a large amount of residual background noise. That is to say, they cannot achieve accurate segmentation of weak targets while achieving a higher precision of nonuniform background correction.

To solve this problem, we improve the new top-hat transform by designing a noise structure element (NSE). The introduction of NSE separates the function of stray light nonuniform background suppression and noise suppression, which breaks traditional structure element selection limitations and achieves an ideal processing effect between retaining targets and suppressing nonuniform background. On the one hand, the ENTHT algorithm achieves better retention of weak targets. On the other hand, it can better suppress nonuniform noise and achieve more accurate weak target segmentation. The experimental results show that our algorithm still performs well under the worst condition. It fully demonstrates the feasibility and superiority of this algorithm in surveillance nonuniform background correction.

2. Analysis of the Space Surveillance Image

The wide-field surveillance images used in this paper are taken by a surveillance system. The sensor is a CMOS image sensor of ChangGuangChenXin company. Its Spectral response is shown in Figure 1. The sensor specifications are shown in

Table 1. The sensor specifications.

Parameter	Value
Photosensitive area	61.44 mm × 61.44 mm
Pixel size	10 µm × 10 µm
Number of active pixels	6144 (H) × 6144 (V)
Shutter type	Rolling shutter with global reset
Dark current	As shown in Figure 2

. The dark current with different temperatures is shown in Figure 2.

Firstly, we obtained surveillance images through ground-based observations. Figure 3a is the original two-dimensional image, Figure 3b is the one-dimensional image, Figure 3c is the 3D image with a size of 30 × 30 pixels, and Figure 3d is the 3D image with a size of 100 × 100 pixels, which can show more details in multiple dimensions.

From Figure 3a, we can see that the surveillance images are seriously affected by nonuniform backgrounds. This is because our wide-field imaging system uses fiber image transmission components, which will bring serious nonuniformity to the imaging system. At the same time, due to the loss of the fiber image transmission components in the image transmission process and the discrete sampling characteristics of the fiber image transmission components themselves, its application will inevitably affect the signal-to-noise ratio, modulation transfer function, and optical transmittance. Therefore, we can see from Figure 3d that the image quality of the star point is degraded seriously, which is almost submerged in the nonuniform background.

Secondly, we can also see a lot of noise in the space surveillance image. This noise mainly comes from the sensor and sensor circuit, including reset noise, quantization noise, photon shot noise, and dark current. Moreover, it will also be affected by space radiation noise. As shown in Figure 3b, space targets or stars are basically submerged in dark currents with strong energy, which is known as hot pixels. Hot pixels constitute a part of the nonuniform background of the space surveillance image.

Finally, from Figure 3b, we can also see that the background of the space surveillance image also contains the sensor defect, which is due to the fact that our sensor adopts the test piece and has a certain degree of sensor defect itself. This can simulate the possible local damage of the sensor caused by some potential factors, such as direct sunlight or space radiation, when the surveillance camera works in orbit for a long time.

The star in Figure 3c,d is the display effect of the same star in different dimensions. The star is strongly affected by the nonuniform background and is basically submerged in the nonuniform background. In general, on the one hand, wide-field and long exposure bring better target detection ability to space surveillance. On the other hand, it will also bring serious nonuniformity to the image. These factors mainly include fiber image transmission components, dark current, possible detector defects, and inevitable stray light. These factors bring serious challenges to space target detection and tracking. In order to better detect space targets, we need to correct the nonuniform background of the space surveillance image, which is also an essential part of improving the imaging performance of the surveillance camera.

3. Enhanced New Top-Hat Transform

The nonuniform background of the wide-field surveillance camera has a certain particularity. Considering the performance and complexity of the algorithm, scholars generally adopt the improved algorithm based on morphological filtering. In these algorithms, the background suppression effect and weak target retention degree have great limitations and dependence on the selection of structural elements [29]. In order to solve this problem and achieve accurate nonuniform background correction and effective target segmentation, we propose an enhanced new top-hat transform (ENTHT) correction algorithm based on mathematical morphology operation. Mathematical morphology operation is based on two basic operations: dilation operation and erosion operation, as shown in Equations (1) and (2). From dilation and erosion, the opening operation, the closing operation, and the top-hat transform in mathematical morphology operation can be obtained, respectively.

$$f\oplus S=\max \{f(i-m,j-n)+S(m,n)|(i-m),(j-n)\in D_f,(m,n)\in D_S\}$$

(1)

$$f \mathsf{\Theta } S=\min \{f(i+m,j+n)-S(m,n)|(i+m),(j+n)\in D_f,(m,n)\in D_S\}$$

(2)

where $\oplus$ and $\mathsf{\Theta }$ represents the dilation and erosion, respectively, and $S$ represents the structuring element (SE). $D_f$ and $D_S$ represent the domain of $f$ and $S$, respectively. SE is a matrix with only 1 s and 0 s of any size and shape. Dilation makes the image’s gray value larger than that of the original image, which will also increase the size of the bright region. Erosion makes the image’s gray value smaller than that of the original image, which will also decrease the size of the bright region.

The operation and principle of the proposed ENTHT correction algorithm are described as follows. Firstly, we select two morphological, structural elements: $L$ and $\Delta L$, as shown in Figure 4. Then we use the structural element $\Delta L$ to perform a dilation operation on the surveillance image to obtain the image $F_1$, as shown in Equation (3).

$$F_1=F\oplus \Delta L_{}=\max \{F(i-m,j-n)+\Delta L(m,n)|(i-m),(j-n)\in D_F,(m,n)\in D_{\Delta L_{}}\}$$

(3)

First, we choose the size of the structural element $\Delta L$. The larger $\Delta L_{ab}$ is, the stronger the background suppression will be, and the weak targets in the image will be weakened or even eliminated. In order to have a better detection ability for the wide-field surveillance camera, $\Delta L_{ab}$ should be as small as possible. In this paper, we choose the value of parameter $\Delta L_{ab}$ to be one pixel.

The purpose of this step is to replace the target pixels with the pixels around the target and transfer the target energy to the structural elements, so the size of the structural elements should be larger than the target. The larger $L_a$ is, the stronger the background suppression will be, and the weak targets in the image will be weakened or even eliminated. If $L_a$ is too small, more noise will remain in the background. The target of our interest ranges within 20 × 20 pixels. Reasonable structural elements can achieve the best suppression of the nonuniform background of the surveillance image. At the same time, the energy distribution of the target is not destroyed, i.e., no loss of weak targets and no energy loss of large targets. Therefore, $L_a$ should be larger than 20 pixels. The larger the $L_a$, the stronger the background suppression, but it will also weaken space targets. So we take the weak target with the size of 3 × 3 pixels as a reference and adjust $L_a$ appropriately to further suppress the background noise while ensuring that this target is retained intact. Finally, $L_a$ is 29 pixels and $L_b$ is 31 pixels.

Then, we use the structural element $L$ to perform an erosion operation on the image $F_1$, as shown in Equation (4). The purpose of this step is to remove the structural elements containing the target energy. The target is removed through Equation (3), and the structural elements containing the target energy are removed through Equation (4). Finally, we removed the targets and stars we were interested in and realized the preliminary estimation of the nonuniform background that needed to be eliminated. So the size of $L_c$ should be larger than the space targets or stars we care about. Since the target we are interested in is within 20 × 20 pixels. Therefore, $L_c$ should be larger than 20 pixels. The smaller the $L_c$, the stronger the background noise suppression. In order to achieve the best background suppression effect, $L_c$ is 20 pixels in this paper.

$$F_2=F_1 \mathsf{\Theta } L_{}=\min \{F_1(i+m,j+n)-L(m,n)|(i+m),(j+n)\in D_{F_1},(m,n)\in D_{L_{}}\}$$

(4)

where $F_2$ is the image with the targets and stars removed. Then, the corrected surveillance image $F_3$ is obtained by subtraction between the original image and the estimated background. Since the gray value of the background part we do not care about in $F_2$ will become larger than the original image $F$, we need to set the gray value of this part of image $F_3$ to zero, as shown in Equation (5).

$$F_3=F-\min (F,F_2)$$

(5)

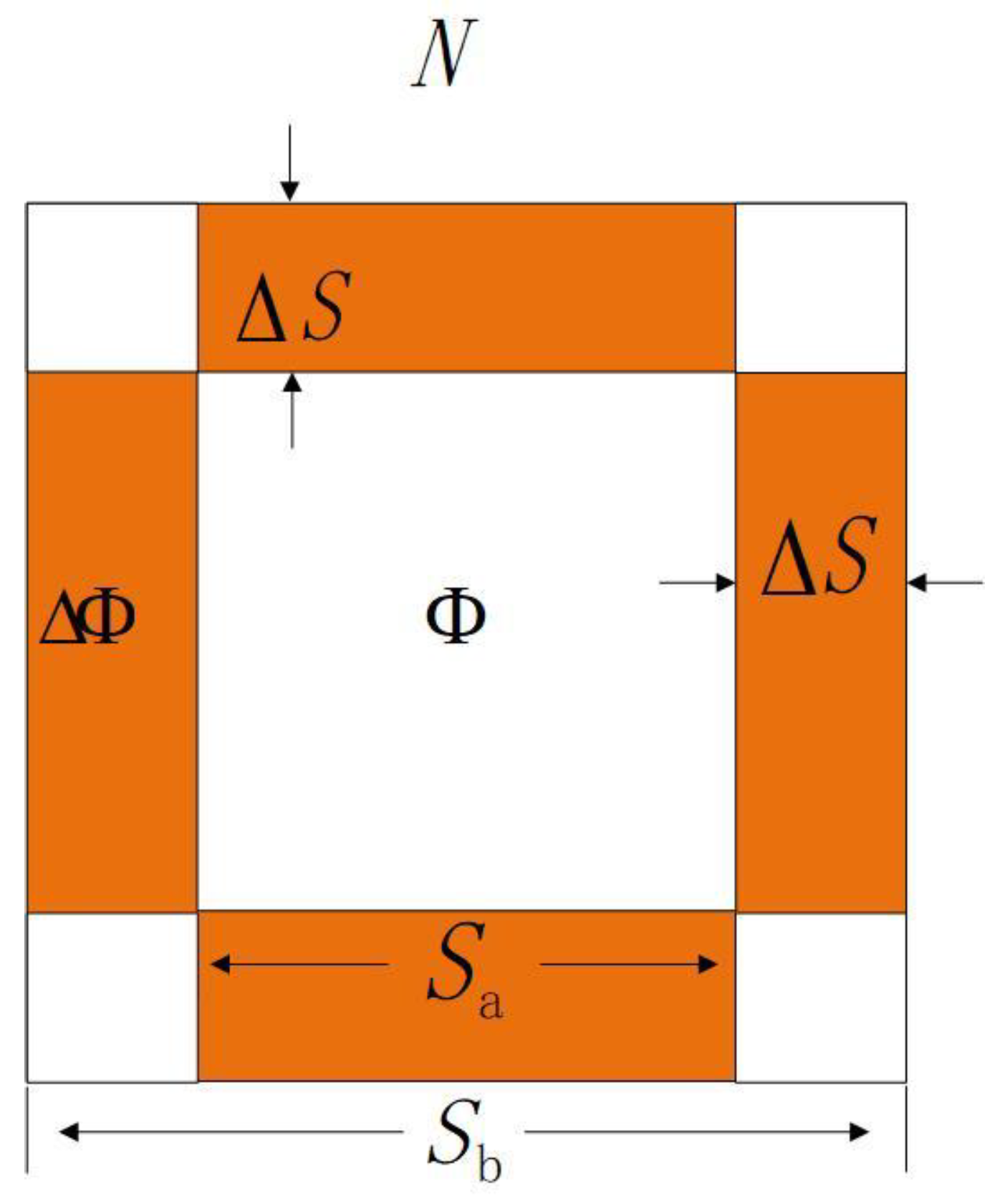
After the above steps, there will also be some residual noise, which remains in the image background. These noises appear as small isolated patches. In order to obtain a smoother background and achieve accurate segmentation of the space targets, we designed a noise structural element (NSE) N to eliminate the noise, as shown in Figure 5. NSE is a matrix with only 1 s. $\mathsf{\Phi }$ is defined as the current pixel region. $\Delta \mathsf{\Phi }$ represents the adjacent areas in the upper, lower, left, and right directions. The value of parameter $\Delta S$ is one pixel.

We define the denoising operation as follows:

$$F_4(i,j)=\{\begin{array}{ll}0,& \mathrm{in} \mathrm{case} \mathrm{that} \mathsf{\Xi }(i,j)=0 \\ F_3(i,j),& \mathrm{otherwise}\end{array}$$

(6)

$$\mathsf{\Xi }={\displaystyle \sum _{m,n}{F}_3(i-m,j-n)\times N(m,n)|(i-m,j-n)\in D_{F_3},(m,n)\in D_N}$$

(7)

where $N$ represents the noise structural element (NSE), $D_N$ represent the domain of $N$. When $\mathsf{\Xi }(i,j)$ becomes 0 after Equation (5), we consider the area $\mathsf{\Phi }$ as noise. In order to save algorithm time, the current pixel region $\mathsf{\Phi }$ is defined, as shown in Equation (8).

$$\mathsf{\Phi }(i,j)=\left\{(i,j)\right\},\left\{(i,j),(i+1,j)\right\},\left\{(i,j),(i-1,j)\right\},\left\{(i,j),(i,j+1)\right\},or\left\{(i,j),(i,j-1)\right\}$$

(8)

where $\left\{(i,j)\right\}$ represents the current pixel, $\left\{(i,j),(i+1,j)\right\}$ represents the current pixel and the right adjacent pixel, $\left\{(i,j),(i-1,j)\right\}$ represents the current pixel and the left adjacent pixel, $\left\{(i,j),(i,j+1)\right\}$ represents the current pixel and the lower adjacent pixel, and $\left\{(i,j),(i,j-1)\right\}$ represents the current pixel and the upper adjacent pixel.

Firstly, the denoising operation can properly eliminate the noise submerged in the nonuniform background. Secondly, it reduces the dependence of the noise suppression effect of the new top-hat transform on the selection of structural elements. It also reduces the sensitivity of weak targets to the selection of structural elements in the new top-hat transform and can better select more appropriate structural elements in order to retain the weak targets so as to realize the accurate segmentation of space targets in the space surveillance image.

Figure 6 shows the experimental results of background correction for the ENTHT method proposed in this paper. In Figure 6, (a1)–(a3) are different sizes of the original image, which can show more details, and (a4) is a 3D display of (a3), which can show the nonuniformity of the background more intuitively; moreover, (b1)–(b4) are the processing results of the dilation operation showing that the targets are removed and their energy is transferred to the structural elements, (c1)–(c4) are the results of the background estimation after the erosion operation showing that the structural elements containing the target energy are removed, (d1)–(d4) are the results of preliminary background correction showing that there are still some residual background noise and hot pixels around the target, and (e1)–(e4) are the results of accurate background correction by using our NSE showing almost no noise residue around the target. In general, Figure 6 shows that our algorithm achieves accurate segmentation of the target while correcting the nonuniform background image.

4. Experiments and Discussions

In this section, to verify the advantages of the proposed ENTHT correction algorithm, we use the classical new top-hat transform [27] and the latest INTHT [29] algorithm with superior performance to carry out the nonuniform background correction experiment on the same real captured image dataset. For the system in this paper, the data acquisition method is star tracking mode, in which the telescope captures the same sky area. For the convenience of research, our research object is the star point in the sky. The real surveillance images used in the experiment were taken by a surveillance system equipped with a CMOS sensor with an exposure time of 5 s, 6 K × 6 K imaging pixels, and 14 bits of gray-scale.

4.1. Accuracy of Nonuniform Background Correction

In order to analyze the performance of different algorithms, we use the background residuals [29] to evaluate the nonuniform background correction accuracy quantitatively. In background residuals, the mean and standard deviation can represent the amount of residual background noise well. We take the weak star point with the size of 3 × 3 pixels as the reference, adjust the structural elements of different algorithms to keep the reference star point with the same energy value, and then compare the performance of the algorithm for nonuniform background elimination through the background residual. The size of S(Bo) is 31/2 pixels, S(Bi) is 29/2 pixels, and S(Bb) is 20/2 pixels in the new top-hat transform [27]. The value of parameter K is 29 pixels, the value of parameter L is 31 pixels, and the value of parameter M is 20 pixels in the INTHT [29] algorithm. At the same time, compare the precision segmentation ability of different algorithms for the space weak target. The smaller the mean and the standard deviation of the corrected surveillance background, the better the performance of the correction algorithm will be. When calculating the background residuals, it is necessary to eliminate the influence of the space targets and stars. We use the method of the excluded domain [29] to eliminate the space targets and stars. In addition, in order to ensure the accurate removal of stars and targets, we will appropriately adjust the threshold with reference to the smallest star point in the surveillance image.

In this paper, the smaller the background residuals of the processed image, the better the performance of the algorithm. As shown in

Table 2. Background residuals of different algorithms.

	Method	New Top-Hat	INTHT	The Proposed ENTHT Method
Figure 7	Mean/pixel	0.5451	0.2469	0.0521
	Standard Deviation/pixel	3.9179	2.5954	1.0123

, the minimum background residual indicates the best processing performance of our algorithm. Figure 7 fully shows the background correction results of different algorithms, (a1)–(a3) are different sizes of the original images, which can show more details, and (a4) is a 3D display of (a3), which can show the nonuniformity of the background more intuitively. The target is submerged in background noise and hot pixels, as shown in Figure 7(a4). In Figure 7, (b1)–(b4) are the correction results of the new top-hat transform, (c1)–(c4) are the correction results of the INTHT algorithm, and (d1)–(d4) are the correction results of the proposed ENTHT algorithm. Figure 7(a1–d1) are images with the original size of 6 K × 6 K pixels. All algorithms can well correct the nonuniform background of surveillance images, and no obvious difference can be seen in the macro. Figure 7(a2–d2) are 512 × 512 pixels. The image background processed by our algorithm is cleaner. This is because our NSE plays a very important role. Therefore, our background residual in Table 2 is the smallest. Figure 7(a3–d3) are 30 × 30 pixels. We can see more details. The background noise processing ability of the INTHT algorithm and the new top-hat transform is poor. There are still some residual background noise and hot pixels around the target. This also leads to large background residuals of the whole image, as shown in Table 2, so the improvement in image quality is not obvious. From Figure 7(a4–d4), it can be intuitively seen that due to the introduction of NSE, our algorithm can remove hot pixels and nonuniform background noise well, and there is almost no residual background noise. This shows that the nonuniform background correction of the space surveillance image is accurate, and the precise segmentation of space objects is realized.

The new top-hat transform is a classical algorithm of background estimation based on morphological filtering. INTHT is an improved algorithm of the new top-hat transform, which adds an expansion operation step to restore the background size transformation caused by the different sizes of the structural operators in the previous step to ensure that the nonuniform background can be eliminated more thoroughly. However, these two algorithms have poor performance in processing nonuniform background residual noise. These two algorithms tend to leave isolated small residual noise in the background and are unable to solve the influence of dark current on the image, which will significantly reduce the performance in detecting space targets. Our algorithm can solve this problem well. By utilizing the NSE, our algorithm can properly remove such isolated noise. Compared with the traditional denoising algorithm based on filtering, it will not damage the energy distribution of space targets and can protect the space weak targets while removing the noise.

A good algorithm must have a strong anti-interference ability, that is, the stability of the algorithm. During the ground test, we simulated some strong stray light influence with the light source. We took some images affected by different stray lights to verify the stray light suppression performance of our algorithm. From Figure 8(a1–d1) and Figure 9(a1–d1), we can see that the three algorithms can accurately eliminate nonuniform stray light, but from the details, as shown in Figure 8(a2–d2) and Figure 9(a2–d2), our algorithm eliminates the background noise of stray light more accurately, which leads to smaller background residual of the image processed by our algorithm, as shown in

Table 3. Background residuals of different algorithms under the influence of stray light.

	Method	New Top-Hat	INTHT	The Proposed ENTHT Method
Figure 8	Mean/pixel	0.5600	0.2074	0.0639
	Standard Deviation/pixel	4.0815	2.4159	1.1563
Figure 9	Mean/pixel	0.5862	0.2212	0.0419
	Standard Deviation/pixel	4.0837	2.4280	0.8925

. The experimental results show that even under the influence of strong stray light, our algorithm can still achieve accurate segmentation of weak targets compared with other algorithms, as shown in Figure 8(a3–d3,a4–d4) and Figure 9(a3–d3,a4–d4) while correcting the nonuniform background.

The principle of our algorithm is background estimation, so it has a good correction effect for static nonuniform backgrounds and uncertain nonuniform backgrounds. Compared with other scholars’ algorithms, due to the introduction of NSE, our algorithm can eliminate noise at a deeper level and eliminate nonuniform backgrounds more accurately, thus achieving accurate target segmentation and improving the imaging quality of surveillance images. Further, compared with the traditional denoising algorithm based on filtering, our NSE will not weaken the weak targets and will not destroy the energy distribution of the targets, which is also an advantage of our algorithm.

4.2. Algorithm Time

In order to compare the calculation time of different methods, all methods implemented in MATLAB R2012a and the PC specifications include an i5-6500u (2.30 GHz) with 8 GB of main memory. The image size is 6 K × 6 K pixels. The calculation time of different methods is shown in

Table 4. Calculation time of different algorithms.

Method	New Top-Hat	INTHT	The Proposed ENTHT Method
Time(s)	14.644995	18.537087	20.092629

. Different algorithms are based on the improvement of morphological filtering. From the calculation time, it can be seen that there is little difference between the latest INTHT [29] algorithm and our algorithm. But our algorithm has a higher accuracy of nonuniform background correction.

5. Conclusions

In order to solve the problem that the existing methods can not achieve accurate background correction of space surveillance images, we propose the ENTHT algorithm. After analyzing the mechanism and influence of the nonuniform background of the wide-field surveillance camera, we improve the new top-hat transform. By defining the noise structure element (NSE) based on the structure element of mathematical morphology, we effectively reduce the dependence and limitations of the background noise suppression performance of the new top-hat transform on the selection of the structure element. For complex space surveillance images, our algorithm can not only accurately suppress the background but also remove the noise to the greatest extent. Compared with the existing algorithms, this algorithm achieves higher accuracy of nonuniform background correction and realizes accurate segmentation of space weak targets at the same time. Our algorithm will be of great help to the detection, recognition, and tracking of spatial moving objects.