Lower Bound for Sculpture Garden Problem: Localization of IoT Devices

Abstract

The purpose of the current study is to investigate a special case of art gallery problem, namely a sculpture garden problem. In this problem, for a given polygon P, the ultimate goal is to place the minimum number of guards (landmarks) to define the interior polygon P by applying a monotone Boolean formula composed of the guards. Using this problem, it can replace the operation-based method with time-consuming, pixel-based algorithms. So, the processing time of some problems in the fields of machine vision, image processing and gamification can be strongly reduced. The problem has also many applications in mobile device localization in the Internet of Things (IoT). An open problem in this regard is the proof of Eppstein’s conjecture, which has remained an open problem since 2007. According to his conjecture, in the worst case, $n-2$ vertex guards are required to describe any n-gon. In this paper, a lower bound is introduced for the special case of this problem (natural vertex guard), which shows that if a polygon can be defined with natural vertex guards, then $n-2$ is a lower bound.

1. Introduction

A large and growing body of literature about computational geometry has explored the art gallery problem. The main goal in this problem is to find the minimum number of point guards inside a polygon (P) such that the set of guards can see the whole P. Each guard can see its surroundings in 360 degrees and up to infinity (if there are no obstacles). The number of guards that suffices and is sometimes necessary for any arbitrary polygon with n vertices is $\lfloor n/3\rfloor$ [1]. The main goal in our study is to find the minimum set of angle guards by which the geometry of the polygon can be defined through two operations, $AND(.)$ and $OR(+)$. An $angleguard$ g views an infinite wedge of the plane (by going through the involved obstacles) and can be defined as a Boolean predicate, $B_g\left(p\right)$, which is $True$ for a given point, $p\in P$, if p is inside the view region of g, otherwise it is False. Given a polygon P, the aim is to place a set of angle guards on P in such a way that the monotone Boolean formula $F_P\left(p\right)$ is $True$, if and only if p is inside P or on the boundary of polygon P ($p\in \partial P$), otherwise it is $False$:

$$F_P\left(p\right)=\left\{\begin{array}{cc}True\hfill & \mathrm{if} p\in P \mathrm{or} p\in \partial P\hfill \\ False\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

There are several applications in machine vision, image processing and gamification which require the range of a shape to be determined. Various algorithms for these problems have been presented that are based on pixels, area, vertices and so on. These methods require a lot of processing time in problems that require fast processing (such as computer games and graphics). Even these methods force users to provide more powerful hardware to run a machine vision system or computer game. The method discussed in this paper is related to a problem that uses only a few points, angles and two logical operators to determine the range of a shape. Using this method, various applications in machine vision and computer games are performed much faster and with a lower number of operations. An angle guard vertex placement is considered as natural if all the guards of P have the same view of their corresponding vertices [2]. As Eppstein et al. stated, a polygon P can be demonstrated in a way that a natural angle guard vertex placement cannot fully distinguish between points on the inside and outside of P which implies that $Steiner$-point guards are sometimes necessary [2]. According to Figure 1a, even the placement of a natural angle at every vertex of the pentagon is not able to distinguish between the points x and y and at least one unnatural guard is needed to define the polygon (Figure 1b). Consequently, the polygon is defined by $F=A.B.D$.

A variety of cases of the problem is present in which the location and angle of view of the guards are different. We focus on a type of the problem that all the guards are placed on the vertices of P. It was a conjecture [3] that in the worst case, $n-2$ guards are needed to describe an n-gon. In this paper, we present an algorithm to generate a polygon for a given n which needs at least $n-2$ natural vertex guards. We do not prove Eppstein’s conjecture and this problem is still open. However, by using our algorithm, we create an n-gon for any given n, which needs exactly $n-2$ natural vertex guards.

In the next section, the sculpture garden problem is introduced and some applications are mentioned. Section 3 provides the main problem and presents an algorithm for generating the n-gon which needs exactly $n-2$ natural vertex guards to be defined. Finally, Section 4 presents the findings of the study and also some suggestions for further research.

2. Sculpture Garden Problem and Applications

As mentioned previously, the sculpture garden problem can be considered as a special case of an art gallery problem. There are various problems with similarities and differences with the sculpture garden problem. As the sculpture garden problem comes up from localization problems in wireless mobile computing, we wish to determine the position of some devices in a geometric environment.

The sculpture garden problem could be used in localization problems in which a wireless device is used to prove that it belongs to a given polygonal environment. In this case, the locators would be simple and can broadcast information inside a certain angle. In this context, the Boolean predicates could be associated with secret keys. Therefore, each angle guard g could periodically broadcast a secret key K in its transmission angle and consequently the devices in range would have knowledge of this key. The wireless localization problem with natural vertex guards is an NP-hard problem [4,5].

In another application, namely constructive solid geometry (CSG), we wish to construct a geometric shape from simple combinations of primitive shapes [6]. Solutions to the sculpture garden problem can be used to construct an efficient CSG formula that defines a given polygon P. The prison yard problem seeks a set of guards that can simultaneously see both the interior and exterior of a simple polygon, in which $\lfloor n/2\rfloor$ guards are sufficient and sometimes necessary (tight bound) [7]. Another related problem is the floodlight illumination problem, in which the vertex angle guards (called floodlights) with angles of 180 should see a simple polygon [8]. Likewise, studies have been conducted on the complexity of illuminating wedges with angle-restricted floodlights placed at a fixed set of points [9]. There is another study on a generalization of the classical problem of the illumination of polygons. Aichholzer et al. [10] modeled a wireless device whose radio signal can penetrate a given number k of walls (k-modems) and they studied the minimum number of k-modems sufficient and sometimes necessary to illuminate monotone and monotone orthogonal polygons. They showed that every monotone polygon with n vertices can be illuminated with $\lceil \frac{n-2}{2k+3}\rceil$k-modems. Ballinger et al. [11] developed lower and upper bounds for the number of k-transmitters that are necessary and sufficient to cover a given collection of line segments, polygonal chains and polygons.

In one of the applications of the problem, the wireless localization problem is considered to deal with the placement of the smallest number of broadcasting antennas required to satisfy some property within a given polygon. The antennas propagate a unique key within a certain antenna-specific angle of broadcast, so that the set of keys received at any given point is sufficient to determine whether that point is inside or outside the polygon. To ascertain this localization property, a Boolean formula must be produced along with the placement of the antennas. Crepaldi et al. [12,13] presented an exact algorithm based on integer linear programming for solving the NP-hard natural wireless localization problem. Cano et al. [14] show that $\lceil n/2\rceil$ point guards are always sufficient and sometimes necessary to guard a piecewise convex art gallery with n vertices. Karavelas et al. [15,16] showed that for monitoring a piecewise-convex polygon with $n\ge 2$ vertices, $\lfloor \frac{2n}{3}\rfloor$ vertex guards are always sufficient and sometimes necessary. They also presented a polynomial algorithm for computing the location of guards.

Since we are interested in more than simply observing the inside and outside of a polygon, solutions to the art gallery or prison yard problems would not change into solutions to the sculpture garden problem. In other words, we intend to establish the time when a point is inside a polygon using only the guards as witnesses.

Indeed, any polygon P can be triangulated and two angle guards can be used to define each of the resulting $n+2(h-1)$ triangles, where h is the number of holes in P. This would give rise to a concise formula F defining P. However, it uses at least $2n+4(h-1)$ angle guards, which is a more constant-depth formula.

Upper and Lower Bounds

The sculpture garden problem has different types due to the different restrictions as guards could be observed in varied forms including vertices, edges, interior or exterior of the polygon, and the SGP can be manifested in different types as well. However, in each case, finding the upper and lower bound is a problem that has already been investigated.

An angle guard g with angle $\alpha \in (0,360)$ is a pair $(a,{\omega }_{\alpha })$ of a point a and an infinitive wedge ${\omega }_{\alpha }$ of aperture $\alpha$ at apex a and views ${\omega }_{\alpha }$. It can be shown as a Boolean predicate $B_g\left(p\right)$, in which for a point p in the plane, $B_g\left(p\right)$ is $True$ if p is inside the angle associated with g, otherwise it is $False$. Given a polygon P with n vertices, we intend to allocate the minimum number of angle guards with arbitrary angles at vertices of P. Thus, a monotone Boolean formula, $F_P(.)$, based on the angle guard predicates, $B_g(.)$, is obtained as follows:

$$F_P\left(p\right)=\left\{\begin{array}{cc}True\hfill & \forall p\in int\left(P\right)\hfill \\ False\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

It is worth mentioning that $int\left(P\right)$ is the interior of polygon P. If $F_P\left(p\right)$ is a solution of the sculpture garden problem for a given P, P is defined by $F_P$. The complement of an angle guard $g=(a,{\omega }_{\alpha })$ is an angle guard $g^{\prime }$ at the point a with angle $2\pi -\alpha$. Hence, the wedge associated with $g^{\prime }$ is the complement of ${\omega }_{\alpha }$ in the plane. If formula F is a solution for the sculpture garden problem for polygon P, then the complement of F which is denoted by $F^{\prime }$ defines the exterior of P. To obtain $F^{\prime }$, initially, we replace every angle guard g by its complement, (i.e., $g^{\prime }$), and then swap the operations $AND$ and $OR$. In addition, we define, a pocket of a simple polygon as the areas outside of the polygon and inside of its convex hull.

As Eppstein et al. [2,3] reported, for any polygon P, a set of $n+2(h-1)$ angle guards and an associated concise formula F are present, solving the sculpture garden problem where h is the number of holes in P. So, a simple polygon can be defined with $n-2$ guards. They have conjectured a class of simple n-gons that require at least $n-2$ vertex guards. The main goal of this paper is to solve a special case of this open problem for natural vertex guards. They showed that at least $\lceil n/2\rceil$ guards are required to solve the sculpture garden problem for any polygon with no two edges lying on the same line. Furthermore, for any convex polygon P, a natural angle guard vertex placement is present whose $\lceil n/2\rceil$ guards are sufficient. They showed that $\lceil n/2\rceil +\mathcal{O}\left(1\right)$ angle guards suffice to solve the sculpture garden problem for pseudo-triangles. Moreover, for any orthogonal polygon P (which is probably the most likely real-world application), a set of $\lfloor 3(n-2)/4\rfloor$ angle guards and an associated concise formula F are available to solve the sculpture garden problem using $\lceil n/2\rceil$ natural angle guards. They gave an example of a class of simple polygons containing sculpture garden solutions that used $\mathcal{O}\left(\sqrt{n}\right)$ guards. Afterwards, they showed that the bound is optimal. On the contrary, some varied results are obtained for vertex guards. As Damian et al. demonstrated [17], a class of simple n-gons are presented that require at least $\lfloor 2n/3\rfloor -1$ guards placed at polygon vertices for localization. Through revealing the point that the maximum number of guards to describe any simple polygon on n vertices is roughly observable at $(3/5n,4/5n)$, Hoffman et al. enhanced both upper and lower bounds for the general setting [18]. Eskandari et al. [19] improved the large upper bound $n+2(h-1)$ for an arbitrary n-gon with h holes for placing guards and obtained a tight bound $(n-\lceil c/2\rceil -h)$, where c is the number of vertices of convex hull of $P$. So, in simple polygons, this bound is $n-\lceil c/2\rceil$, which is tight too. To complete the first column of

Table 1. Number of guards needed for a simple polygon with n vertices.

	$\mathit{Natural}\mathit{Vertex}$	$\mathit{Natural}$	$\mathit{Vertex}$	$\mathit{General}$
$UpperBound$	$Unknown$	$n-2$ [18]	$Unknown$	$\lfloor \frac{(4n-2)}{5}\rfloor$ [18]
$LowerBound$	$Unknown$	$n-2$ [18]	$\lfloor \frac{\left(2n\right)}{3}\rfloor -1$ [17]	$\lceil \frac{(3n-4)}{5}\rceil$ [18]

, a new class of polygons entitled Helix is introduced in the next section. In some previous documents, this type of polygon was called spiral polygon.

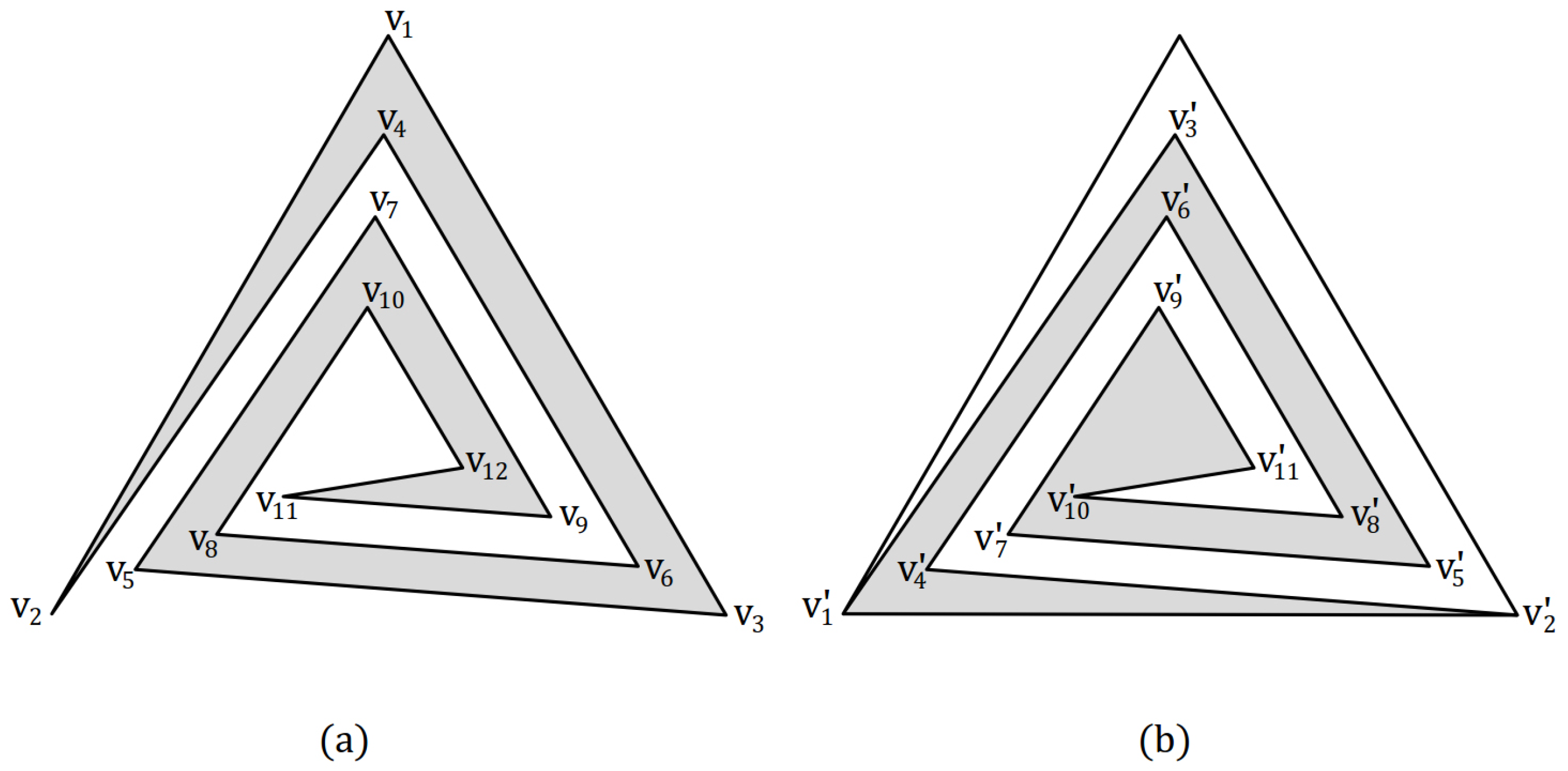
3. Helix Polygon

In this section, we explore the special class of the sculpture garden problem, where the guards are natural. We demonstrate the point that the lower bound for the problem is $n-2$. To do so, we commence with introducing a class of polygons demanding the exact number of $n-2$ natural guards to be defined. In the next section, we introduce this class of polygons named Helix (see Figure 2).

3.1. Construction of Helix

An n-gon Helix polygon (i.e., $H_n$) is constructed by an incremental method using an $n-1$-gon Helix, $H_{n-1}$. A Helix with three vertices is a triangle. By adding two new edges to $H_{n-1}$ and also removing an edge of $H_{n-1}$, $H_n$ is constructed on the basis of $H_{n-1}$, where $n\ge 4$. The details are presented in Algorithm 1 and are illustrated in Figure 3.

Algorithm 1 Constructing Helix Polygon

Input: Integer number $n\ge 3$ as the number of vertices.  Output: The Helix polygon $H_n$. 1: Construct $H_3=▵v_1{v}_2{v}_3$, which is an equilateral triangle, where $v_2{v}_3$ is horizontal and the vertices are in counterclockwise order. 2: Choose a positive real number $\delta$ so $0<\delta <\frac{|v_2{v}_3|}{2\lfloor \frac{n-1}{3}\rfloor }$ 3: $p_1=v_1; p_2=v_2; p_3=v_3$. 4: for $i=4$; $i\le n$; $i++$do 5:      $q_1=p_1$; $p_1=$ a point on $v_1{v}_2$ such that $|p_1{q}_1|=\delta$, $a=l_{13}\left(p_1\right)$; 6:      $q_2=p_2$; $p_2=$ a point on $v_2{v}_3$ such that $|p_2{q}_2|=\delta$, $b=l_{12}\left(p_2\right)$; 7:      $q_3=p_3$; $p_3=$ a point on $v_1{v}_3$ such that $|p_3{q}_3|=\delta$, $c=l_{23}\left(p_3\right)$; 8:      if $i==4$ then 9:          $l=b$; 10:    else 11:        $l=l_{24}\left(v_{i-2}\right)$; 12:    end if 13:    if $i==5$ then 14:        $l^{{}^{\prime }}=c$; 15:    else 16:        $l^{{}^{\prime }}=l_{35}\left(v_{i-2}\right)$; 17:    end if 18:    if $i==3k$ then 19:        $v_i=a\cap c$; 20:    end if 21:    if $i==3k+1$ then 22:        $v_i=c\cap l$; 23:    end if 24:    if $i==3k+2$ then 25:        $v_i=b\cap l^{{}^{\prime }}$; 26:    end if 27:    Add edges $v_i{v}_{i-1}$ and $v_i{v}_{i-2}$. 28:    Remove $v_{i-1}{v}_{i-2}$ to obtain $H_i$ 29: end for 30: Return $H_n$.

It is worth noting that the length of a line segment $pq$ is denoted by $\left|pq\right|$, and for an arbitrary point p, $l_{ij}\left(p\right)$ denotes a line parallel to $v_i{v}_j$ which passes through p.

3.2. Properties of Helix

Constructing the Helix polygon sheds light on the fact that for $i>2$, the angles made by vertices $v_{2i}$ are concave and for $i>0$, vertices $v_{2i+1}$ and $v_2$ are convex (Figure 2).

In fact, the pocket of a polygon P is defined as $CH\left(P\right)-P$ where $CH\left(P\right)$ is the convex hull of the vertices of P. The pocket of a Helix polygon with n vertices is a Helix polygon with $n-1$ vertices (Figure 4). The pocket of a polygon $H_n$ is denoted by $P\left(H_n\right)$. For i, $1\le i\le n-1$, the vertices of $P\left(H_n\right)$ are called $v_i^{{}^{\prime }}$, located on $v_{i+1}$. For $n>4$, the angle $\widehat{v_i^{{}^{\prime }}}$ in $P\left(H_n\right)$ is obtained as follows:

$$\widehat{v_i^{{}^{\prime }}}=\left\{\begin{array}{cc}\widehat{v_1{v}_2{v}_3}-\widehat{v_1{v}_2{v}_4}\hfill & i=1\hfill \\ \widehat{v_1{v}_3{v}_2}-\widehat{v_1{v}_3{v}_5}\hfill & i=2\hfill \\ 2\pi -\mathrm{interior}\mathrm{angle}\mathrm{of}{v}_{i+1}\mathrm{in}{H}_n\hfill & i\ge 3·\hfill \end{array}\right.$$

(2)

We will show that polygon $H_n$ for any given natural number $n\left(3\right),$ can be defined by $n-2$ natural vertices guards which are located on $v_1,v_2,\dots ,v_{n-3},v_n$. The Boolean formula, $F_n$, is as below:

$$F_n=\sum _{i=1}^{\lceil n/2\rceil -2}{A}_i·g_{2i}+A_{\lfloor n/2\rfloor -1}·g_n$$

(3)

where $A_1=g_1$, $A_{i+1}=A_i·g_{2i+1}$ for all $1\le i\le \lfloor n/2\rfloor -2$ and $g_i$ is the natural vertex guard located on the vertex $v_i$ of $H_n$. To clarify this point, $F_8$ can be written as follows:

$$F_8=\sum _{i=1}^2{A}_i·g_{2i}+A_5·g_8$$

(4)

where $A_1=g_1,A_2=g_1·g_3$ and $A_3=g_1·g_3·g_5$. Thus, we have

$$F_8=g_1·g_2+g_1·g_3·g_4+g_1·g_3·g_5·g_8$$

Generally, we expand $F_n$ as follows:

$$F_n=\left\{\begin{array}{cc}\sum _{i=1}^{k-1}(\prod _{j=0}^{i-1}{g}_{2j+1})·g_{2i}+(\prod _{j=0}^{k-2}{g}_{2j+1})·g_n\hfill & n=2k+1,k\in \mathbb{N}\hfill \\ \sum _{i=1}^{k-1}(\prod _{j=0}^{i-1}{g}_{2j+1})·g_{2i}+(\prod _{j=0}^{k-1}{g}_{2j+1})·g_n\hfill & n=2k+2,k\in \mathbb{N}·\hfill \end{array}\right.$$

(5)

According to Lemma 1, $F_n$ defined by Equation (5) describes $H_n$.

Lemma 1.

Helix polygon $H_n$ can be defined by $n-2$ natural vertex guards $g_i$ ($1\le i\le n;i\ne n-1,n-2$) located on $v_1,v_2,\dots v_{n-3},v_n$ and the correspondent Boolean formula is Formula 5.

Proof. 

We will prove the lemma by induction. When $n=3$, $k=1$ and $F_3=g_1·g_3$ clearly define triangle $H_3$. For $n=4$, $k=1$ and $F_4=g_1·g_4$ define $H_4$ and it implies that Lemma 1 holds for $n=3,4$. Now, for $n\ge 5$, without loss of generality, assume that $n=2k+2,k\in \mathbb{N}$. According to Property 2, $P\left(H_n\right)$ is a Helix polygon with $2k+1$ vertices. By induction hypothesis, $P\left(H_n\right)$ can be defined as follows:

$$F^{\prime }=\sum _{i=1}^{k-1}(\prod _{j=0}^{i-1}{g}_{2j+1}^{\prime })·g_{2i}^{\prime }+(\prod _{j=0}^{k-2}{g}_{2j+1}^{\prime })·g_{2k+1}^{\prime }$$

(6)

where $g_i^{\prime }$ is a natural guard on the vertex $v_i^{\prime }$ of $P\left(H_n\right)$. According to correspondence between the vertices of $H_n$ and $P\left(H_n\right)$, we have

$$g_i^{\prime }=\left\{\begin{array}{cc}{g}_{i+1}^c\hfill & i\ge 3\hfill \\ G_{i+1}·g_{i+1}^c\hfill & i=1,2·\hfill \end{array}\right.$$

(7)

in which $g^c$ is the complement of guard g and $G_2$ and $G_3$ are the guards located on $v_2$ and $v_3$ with the angles $\widehat{v_1{v}_2{v}_3}$ and $\widehat{v_1{v}_3{v}_2}$, respectively. So, we have

$$F^{\prime }=g_1^{\prime }·g_2^{\prime }+\sum _{i=2}^{k-1}(\prod _{j=0}^{i-1}{g}_{2j+1}^{\prime })·g_{2i}^{\prime }+(\prod _{j=0}^{k-2}{g}_{2j+1}^{\prime })·g_{2k+1}^{\prime }$$

$$=g_1^{\prime }·g_2^{\prime }+\sum _{i=2}^{k-1}{g}_1^{\prime }·(\prod _{j=1}^{i-1}{g}_{2j+1}^{\prime })·g_{2i}^{\prime }+g_1^{\prime }·(\prod _{j=1}^{k-2}{g}_{2j+1}^{\prime })·g_{2k+1}^{\prime }$$

$$=G_2·G_3·g_2^c·g_3^c+\sum _{i=2}^{k-1}{G}_2·g_2^c·(\prod _{j=1}^{i-1}{g}_{2j+2}^c)·g_{2i+1}^c+G_2·g_2^c·(\prod _{j=1}^{k-2}{g}_{2j+2}^c)·g_{2k+2}^c$$

$$=G_2·[G_3·g_2^c·g_3^c+\sum _{i=2}^{k-1}(\prod _{j=0}^{i-1}{g}_{2j+2}^c)·g_{2i+1}^c+(\prod _{j=0}^{k-2}{g}_{2j+2}^c)·g_{2k+2}^c]$$

$$\Rightarrow {(F^{\prime })}^c=G_2^c+(G_3^c+g_2+g_3)·(\prod _{i=2}^{k-1}(\sum _{j=0}^{i-1}{g}_{2j+2})+g_{2i+1})·(\sum _{j=0}^{k-2}{g}_{2j+2}+g_{2k+2})$$

Consider the point that $F=(g_1·g_2)·{\left(F^{\prime }\right)}^c+(g_1·g_3)·{\left(F^{\prime }\right)}^c$. By replacing ${\left(F^{\prime }\right)}^c$ from the above relation, we obtain

$$F=g_1·(g_2+g_2·g_3)·(\prod _{i=2}^{k-1}(\sum _{j=0}^{i-1}{g}_{2j+2})+g_{2i+1})·(\sum _{j=0}^{k-2}{g}_{2j+2}+g_{2k+2})$$

$$+g_1·(g_2·g_3+g_3)·(\prod _{i=2}^{k-1}(\sum _{j=0}^{i-1}{g}_{2j+2})+g_{2i+1})·(\sum _{j=0}^{k-2}{g}_{2j+2}+g_{2k+2})$$

Note that $g_1·g_2·G_2^c=g_1·g_3·G_2^c=g_1·g_2·G_3^c=g_1·g_3·G_3^c=⌀$. So, we have

$$F=(\prod _{i=2}^{k-1}(\sum _{j=0}^{i-1}{g}_{2j+2})+g_{2i+1})·(\sum _{j=0}^{k-2}(g_{2j+2}+g_{2k+2}))·(g_2+g_3)·g_1$$

Now, we show that F can define $H_n$ which contains exactly the natural guards $g_1,g_2,\dots ,g_{n-3},g_n$ and can be written in the form of $F_n$.

First, consider the definition of F which contains only natural guards. To prove that $H_n$ can be defined by F, let x be an arbitrary point inside $H_n$. We have $g_1\left(x\right)=True$ and ${\left(F^{\prime }\right)}^c\left(x\right)=True$ ( $x\in H_n\Rightarrow x\notin P\left(H_n\right)\Rightarrow F^{\prime }\left(x\right)=False\Rightarrow {\left(F^{\prime }\right)}^c\left(x\right)=True$). There are two cases:

• $g_2\left(x\right)=True\Rightarrow F\left(x\right)=(g_1\left(x\right)·g_2\left(x\right))·{\left(F^{\prime }\right)}^c\left(x\right)+(g_1\left(x\right)·g_3\left(x\right))·{\left(F^{\prime }\right)}^c\left(x\right)=True$
• $g_2\left(x\right)=False\Rightarrow g_3\left(x\right)=True\Rightarrow (g_1\left(x\right)·g_3\left(x\right))·{\left(F^{\prime }\right)}^c\left(x\right)=True\Rightarrow F\left(x\right)=True·$

Thus, F can distinguish the interior of $H_n$. Now, let $x\notin H_n$. There are two cases:

• $x\in P\left(H_n\right)\Rightarrow F^{\prime }\left(x\right)=True,{\left(F^{\prime }\right)}^c\left(x\right)=False\Rightarrow F\left(x\right)=False$
• $x\notin P\left(H_n\right)\Rightarrow x\in Ext(▵v_1{v}_2{v}_3)\Rightarrow g_1\left(x\right)=False\Rightarrow F\left(x\right)=False·$

So, F can distinguish the exterior of $H_n$ as well. Now, we show that F can be written in the form of $F_n$. Let

$$S=(g_2+g_3)·(\prod _{i=2}^{k-1}(\sum _{j=0}^{i-1}{g}_{2j+2})+g_{2i+1})·(\sum _{j=0}^{k-2}{g}_{2j+2}+g_{2k+2})$$

and

$$T=\sum _{i=1}^{k-1}(\prod _{j=1}^{i-1}\left(g_{2j+1}\right)·g_{2i})+(\prod _{j=1}^{k-1}(g_{2j+1})·g_{2k+2})$$

Note that $F_n=g_1·T$ and $F=g_1·S$. To prove $F=F_n$, it is sufficient to show that $T=S$. For all integers r where $1\le r\le k-1$, we define $S_i^{\left(r\right)}$ as follows:

$$S_i^{\left(r\right)}=\left\{\begin{array}{cc}{g}_{2i+1}+\sum _{j=r}^{i-1}{g}_{2j+2}\hfill & r\le i\le k-1\hfill \\ g_{2k+2}+\sum _{j=r}^{k-2}{g}_{2j+2}\hfill & i=k·\hfill \end{array}\right.$$

(8)

So, we have

$$S_i^{\left(1\right)}=\left\{\begin{array}{cc}{g}_{2i+1}+\sum _{j=1}^{i-1}{g}_{2j+2}\hfill & 1\le i\le k-1\hfill \\ g_{2k+2}+\sum _{j=1}^{k-2}{g}_{2j+2}\hfill & i=k·\hfill \end{array}\right.$$

(9)

By definition of $S_i^{\left(r\right)}$, it is clear that

$$S=\prod _{i=1}^k(g_2+S_i^{\left(1\right)})=g_2+\prod _{i=1}^k{S}_i^{\left(1\right)}$$

On the other hand, $S_i^{\left(r\right)}-S_i^{(r+1)}=g_{2r+2}$. Therefore we have

$$\prod _{i=r}^k{S}_i^{\left(r\right)}=S_r^{\left(r\right)}·\prod _{i=r+1}^k{S}_i^{\left(r\right)}$$

$$=g_{2r+1}·\prod _{i=r+1}^k{S}_i^{\left(r\right)}=g_{2r+1}·\prod _{i=r+1}^k(g_{2r+2}+S_i^{(r+1)})=g_{2r+1}·(g_{2r+2}+\prod _{i=r+1}^k{S}_i^{(r+1)})$$

By applying obtained recursive relation, $k-2$ times on $S=g_2+{\prod }_{i=1}^k{S}_i^{\left(1\right)}$, $S=T$. In this respect, we have

$$S=g_2+\prod _{i=1}^k{S}_i^{\left(1\right)}=g_2+g_3·(g_4+\prod _{i=2}^k{S}_i^{\left(2\right)})=g_2+g_3·g_4+g_3·\prod _{i=2}^k{S}_i^{\left(2\right)}$$

$$S=g_2+g_3·g_4+g_3·g_5·g_6+g_3·g_5·\prod _{i=3}^k{S}_i^{\left(3\right)}$$

After t times, we have

$$S=(\sum _{i=1}^{t+1}(\prod _{j=1}^{i-1}{g}_{2j+1})·g_{2i})+\prod _{j=1}^t{g}_{2j+1}·\prod _{i=t+1}^k{S}_i^{(t+1)}$$

So after $k-2$ times, we have

$$S=(\sum _{i=1}^{k-1}(\prod _{j=1}^{i-1}{g}_{2j+1})·g_{2i})+\prod _{j=1}^{k-2}{g}_{2j+1}·\prod _{i=k-1}^k{S}_i^{(k-1)}$$

Note that ${\prod }_{i=k-1}^k{S}_i^{(k-1)}=S_{k-1}^{(k-1)}·S_k^{(k-1)}=g_{2k-1}·g_{2k+2}$; therefore,

$$S=(\sum _{i=1}^{k-1}\left(\prod _{j=1}^{i-1}{g}_{2j+1}\right)·g_{2i})+\prod _{j=1}^{k-1}{g}_{2j+1}·g_{2k+2}=T·$$

$S=T$ implies $F=F_n$ which means that F can be written in the form of $F_n$ and could define $H_n$. □

3.3. Necessity of $n-2$ Natural Vertex Guards for Helix

In this section, we will prove that it is impossible to define a Helix polygon with fewer than $n-2$ natural vertex guards.

Lemma 2.

Every arbitrary set of natural vertex guards G which defines $H_n$ contains $g_1$, a natural vertex guard on $v_1$. The final formula is in the form of $F=F_1·g_1$, where $F_1$ is a Boolean expression of $G-\left\{g_1\right\}$.

Proof. 

Let G be an arbitrary set of natural guards which defines $H_n$ by Boolean formula F. Suppose for a contradiction that $g_1$ does not belong to G. Since $v_1{v}_2$ and $v_1{v}_3$ are edges of $H_n$, G should contain two natural guards on $v_2$ and $v_3$ which are called $g_2$ and $g_3$, respectively. So, F can be written in the general form $F=g_2·g_3·T_1+g_2·T_2+g_3·T_3$ where $T_i$s are Boolean formulas which do not contain $g_1$, $g_2$ and $g_3$. This will result in a contradiction, mentioned below.

Consider two regions, $R_1$ and $R_2$, as shown in Figure 5. Let x be an arbitrary point inside $R_1$ or $R_2$. So, we have $g_2\left(x\right)=True$ and $g_3\left(x\right)=False$. So,

$$F\left(x\right)=T_2\left(x\right)$$

(10)

Furthermore, note that we can expand $T_2$ in the following general form:

$$T_2=T_2^{\left(1\right)}+T_2^{\left(2\right)}+\dots +T_2^{\left(l\right)}$$

(11)

where $T_2^{\left(i\right)}$s are the multiplication of some natural guards in G. Let $x\in R_1$ be an arbitrary point. So, from Equation (10), it is implied that

$$x\in R_1\Rightarrow T_2\left(x\right)=F\left(x\right)=True$$

Therefore, at least one of the expressions of $T_2$ should be True. Without loss of generality, it can be called $T_2^{\left(1\right)}$ and is written as $T_2^{\left(1\right)}=g_{i_1}·g_{i_2}·\cdots ·g_{i_m}$, where $g_{i_j}$ is the natural guards of G and $j=1,2,3$. Since $T_2^{\left(1\right)}\left(x\right)=True$, we have

$$\forall j:1\le j\le m:g_{i_j}\left(x\right)=True$$

Regarding the structure of $H_n$, none of indices $i_j$ can be odd. This is because we know that

$$\forall i\ge 1:g_{2i+1}\left(x\right)=False$$

Now, let $y\in R_2$ be an arbitrary point. Due to the structure of $H_n$, it is inferred that for all $\forall y\in R_2$, we have

$$\forall i\ge 2:g_{2i}\left(y\right)=True·$$

So, $T_2^{\left(1\right)}\left(x\right)=True$ and from Equation (11), $T_2\left(y\right)=True$ is obtained and consequently $F\left(y\right)=T_2\left(y\right)=True$ (due to Equation (10). Nevertheless, $y\notin H_n$, which is a contradiction. With regard to the existence of $g_1$ in G, F can be written in the form of $F=g_1·T_1+T_2$, where $T_2$ does not contain $g_1$. Indeed, $g_1·T_1+g_1·T_2$ defines $H_n$ as well. Let $x\in H_n$, then $g_1\left(x\right)=True$ and $g_1\left(x\right)·T_1\left(x\right)+g_1\left(x\right)·T_2\left(x\right)=g_1\left(x\right)·T_1\left(x\right)+T_2\left(x\right)=F\left(x\right)=True$. If $y\notin H_n$ and $g_1\left(y\right)=True$, then $g_1\left(y\right)·T_1\left(y\right)+g_1\left(y\right)·T_2\left(y\right)=g_1\left(y\right)·T_1\left(y\right)+T_2\left(y\right)=F\left(y\right)=False$. On the other hand, if $g_1\left(y\right)=False$, then $g_1\left(y\right)·T_1\left(y\right)+g_1\left(y\right)·T_2\left(y\right)=False$. So, $F=g_1·(T_1+T_2)$ defines $H_n$. In other words, F can be expressed as $F=g_1·F_1$. □

Lemma 3.

Every arbitrary set of natural vertex guards G defining $H_n$ contains $g_2$ (i.e., a natural guard on $v_2$). The final formula is in the form of $F=g_1·(g_2+F_2)$, where $F_2$ is a Boolean expression of $G-\{g_1,g_2\}$.

Proof. 

Let G be an arbitrary set of natural guards which defines $H_n$ by Boolean formula F, for $n\ge 4$. Suppose a contradiction in which $g_2$ does not belong to G. From Lemma 2, we can write

$$F=g_1·(T_1+T_2+\dots +T_l)$$

where $T_i$s are Boolean expression of natural guards of G.

Consider two regions, $R_1$ and $R_3$, as shown in Figure 6. Let $x\in R_1$ be an arbitrary point. We have $F\left(x\right)=g_1\left(x\right)·(T_1\left(x\right)+T_2\left(x\right)+\dots +T_l\left(x\right))=True$. Thus, at least one of the expressions $T_i$s is True. Without loss of generality, it can be named $T_1$ and is written as $T_1=g_{i_1}·g_{i_2}\dots ·g_{i_m}$ where $g_{i_j}$s are some natural guards in G and $i_j\ne 1,2$. Since $T_1\left(x\right)=True$, we have

$$\forall j,1\le j\le m:g_{i_j}\left(x\right)=True$$

Regarding the structure of $H_n$, $i_j$s are even, because $\forall i\ge 2:g_{2i}\left(x\right)=True$.

Now, let $y\in R_3$ be an arbitrary point. Obviously, $\forall i\ge 2$, $g_{2i}\left(y\right)=True$ which implies $T_1\left(y\right)=True$. Then, $F\left(y\right)=True$. However, $y\notin H_n$, which denotes a contradiction.

In addition, F can be manifested as below:

$$F=g_1·(g_2·T_1+T_2)$$

Now note that for all points which are located in the interior (or exterior) of $H_n$, the above formula has the same value with the formula $g_1·(g_2+T_2)$. This fact can be shown easily by considering all cases. Then, $F=g_1·(g_2+F_1)$. □

Lemma 4.

It is not possible to define $H_5$ with less than 3 natural vertex guards. The formula is $F=g_1·(g_2+g_5)$.

Proof. 

Regarding Lemmas 2 and 3, F can be written as $g_1·(g_2+F_2)$. The edges $v_4{v}_5$ and $v_3{v}_5$ should have at least one guard on their endpoints. The optimal possibility is to locate a guard on $v_5$ as their intersection point. Clearly, $g_1·(g_2·g_5)$ defines $H_5$. □

Lemma 5.

Every arbitrary set of natural vertex guards G which defines $H_n$ contains $g_3$ which is a natural guard on $v_3$. The final formula is in the form of $F=g_1·(g_2+g_3·F_3)$ where $F_3$ is a Boolean expression of $G-\{g_1,g_2,g_3\}$.

Proof. 

Let G be an arbitrary set of natural guards which defines $H_n$ by Boolean formula F for $n\ge 6$. Suppose a contradiction in which $g_3$ does not belong to G. By Lemma 3, $F=g_1·(g_2+F_2)$. Assume that $F_2=T_1+T_2+\dots +T_l$, where $T_i$s are multiplication of natural guards in G.

Consider two regions, $R_3$ and $R_4$, as shown in Figure 7. Let $x\in R_4$ be an arbitrary point. We have $F\left(x\right)=F_2\left(x\right)=True$. So, at least one of $T_i$s is True. Without loss of generality, we call it $T_1$, which can be expressed as follows:

$$T_1=g_{i_1}·g_{i_2}\dots ·g_{i_m}$$

where $g_{i_j}$s are natural guards in G and $i_j\ne 1,2,3$.

Since $T_1\left(x\right)=True$, we have

$$\forall j,1\le j\le m:g_{i_j}\left(x\right)=True$$

Therefore, $i_j$s are even. Now, let $y\in R_3$ be an arbitrary point. This point casts light that for all $i\ge 2$, $g_{2i}\left(y\right)=True$, which implies $T_1\left(y\right)=True$. Then, $F\left(y\right)=True$. However, $y\notin H_n$, showing a contradiction. So, $g_3\in G$.

In addition, F can be written as below:

$$F+g_1·(g_2+g_3·F_3)$$

It can be easily obtained from equivalency of $g_1·(g_2+F_2)$ and $g_1·(g_2+g_3·F_3)$ for all points with respect to $H_n$. □

Lemma 6.

It is not possible to define $H_5$ with fewer than three natural vertex guards. The formula is $F=g_1·(g_2+g_3·g_6)$.

Proof. 

Considering Lemma 5, $H_6$ can be defined by $F=g_1·(g_2+g_3·F_3)$. Since $v_4{v}_6$ and $v_6{v}_5$ are two edges of $H_6$, it is required to place at least one guard on one of the endpoints of these two edges. The optimal placement is to place a guard on $v_6$. Obviously, $H_6$ can be defined by $F=g_1·(g_2+g_3·g_6)$. □

Lemma 7.

Every arbitrary set of natural vertex guards G which defines $H_n$, for all $n\ge 7$, contains $g_4$, a natural guard on $v_4$. The final formula is in the form of $F=g_1·(g_2+g_3·(g_4+F_4))$, where $F_4$ is a Boolean expression of $G-\{g_1,g_2,g_3,g_4\}$.

Proof. 

Let G be an arbitrary set of natural guards defining $H_n$ by Boolean formula F and $n\ge 7$. Suppose a contradiction in which $g_4$ does not belong to G. By Lemma 5, $F=g_1·(g_2+g_3·F_3)$. It is intended to show that $F_3=g_4+F_4$. Assume that $F_3=T_1+T_2+\dots +T_l$, where $T_i$s are the multiplication of natural guards of G. Consider two regions, $R_5$ and $R_6$, shown in Figure 8. Let $x\in R_5$ be an arbitrary point, then $F\left(x\right)=F_3\left(x\right)=True·$ So, at least one of $T_i$s is True. Without loss of generality, t is called $T_1$ which can be expressed as below:

$$T_1=g_{i_1}·g_{i_2}\dots ·g_{i_m}$$

where $g_{i_j}$s are natural guards and $i_j\ne 1,2,3,4$. Since $T_1\left(x\right)=True$, for all $j:1\le j\le m$, $g_{i_j}\left(x\right)=True$. Therefore, $i_j$s are even. Now, let $y\in R_6$ be an arbitrary point (see Figure 8). It is clear that for all $i\ge 2$, $g_{2i}\left(y\right)=True$, which implies $T_1\left(y\right)=True$. Then, $F\left(y\right)=True$. However, $y\notin H_n$, indicating a contradiction. So, $g_4\in G$. In addition, F can be written as below:

$$F=g_1·(g_2+g_3·(g_4+F_4))$$

It can be easily shown that $g_1·(g_2+g_3·F_3)$ is equivalent with $g_1·(g_2+g_3·(g_4+F_4))$ for all the points inside or outside of $H_n$. □

Lemma 8.

Let $H_n$ be defined by $F=g_1·(g_2+g_3·(g_4+F_4))$. Formula $F_P=g_1^{{}^{\prime }}·(g_2^{{}^{\prime }}+g_3^{{}^{\prime }}·F_4^c)$ defines the pocket of $H_n$, $P\left(H_n\right)$, where $g_i^{{}^{\prime }}$s are defined in Equation (7).

Proof. 

Let $x\in P\left(H_n\right)$ and $y\notin P\left(H_n\right)$ be two arbitrary points (see Figure 9). Then, it can be demonstrated that $F_P\left(x\right)=True$ and $F_P\left(y\right)=False$. Additionally, $g_2^{{}^{\prime }}=G_3·g_3^c$ and $g_3^{{}^{\prime }}=g_4^c$, so $x\in P\left(H_n\right)\Rightarrow g_1^{{}^{\prime }}\left(x\right)=True$ and $G_3\left(x\right)=True$. So

$$F_P\left(x\right)=g_3^c\left(x\right)+g_4^c\left(x\right)·F_4^c\left(x\right)$$

(12)

On the other hand, $x\in P\left(H_n\right)$ implies that $F\left(x\right)=False$ and $g_1\left(x\right)=True$. Hence,

$$F\left(x\right)=g_2\left(x\right)+g_3\left(x\right)·(g_4\left(x\right)+F_4\left(x\right))=False\Rightarrow g_3\left(x\right)·(g_4\left(x\right)+F_4\left(x\right))=False·$$

So,

$$g_3^c\left(x\right)+g_4^c\left(x\right)·F_4^c\left(x\right)=True$$

(13)

From Equations (12) and (13), $F_P\left(x\right)=True$ can be obtained.

If $g^{{}^{\prime }}\left(y\right)=False$, for $y\notin P\left(H_n\right)$, $F_P\left(y\right)=False$ and the process of our calculations has been completed. Assume that $g^{{}^{\prime }}\left(y\right)=True$, then as $y\notin P\left(H_n\right)$, consequently $g_2^{{}^{\prime }}\left(y\right)=False$ (see Figure 9). If $g_3^{{}^{\prime }}\left(y\right)=False$, $F_P\left(y\right)=False$. Now, suppose that $g_3^{{}^{\prime }}\left(y\right)=True$ (i.e., $g_4\left(y\right)=False$). This assumption implies that $y\in H_n$ and we have $g_1\left(y\right)=True$, $g_2\left(y\right)=False$, $g_{3}1\left(y\right)=True$ and $g_4\left(y\right)=False$. Since $y\in H_n$, $F_{(}y)=F_4\left(y\right)$ and consequently, $F_4\left(y\right)=True·$ So, we have $F_P\left(y\right)=False$. This means that $F_P$ defines $P\left(H_n\right)$. □

Theorem 1.

$H_n$ requires at least $n-2$ natural vertex guards.

Proof. 

We prove this theorem by induction. It is clear that for $n=4$, $H_4$ is a tetragon and cannot be defined by fewer than two guards. We proved this in corollaries 4 and 6 for $n-5$. Now, assume that this holds for $n-1$, and we have to prove it for n where $n\ge 7$. Let F be a Boolean formula which defines $H_n$. With regard to Lemma 7, $F=g_1·(g_2+(g_3·(g_4+F_4))$. Let m be the number of natural guards used in F. From Lemma 8, $P\left(H_n\right)$, a Helix with $n-1$ vertices, can be defined by $F_P=g_1^{{}^{\prime }}·(g_2^{{}^{\prime }}+g_3^{{}^{\prime }}·F_4^c)$ which contains $m-1$ guards. By induction hypothesis, $P\left(H_n\right)$ cannot be defined by fewer than $(n-1)-2$ natural guards. So $m-1$ cannot be less than $n-3$ and hence m cannot be fewer than $n-2$. □

Theorem 2.

$H_n$ requires exactly $n-2$ natural vertex guards.

Proof. 

From Lemma 1 and Theorem 9, it is obviously implied that $H_n$ requires exactly $n-2$ natural vertex guards. □

As we proved, there is an n-gon which needs exactly $n-2$ natural vertex guards to be defined. This implies that $n-2$ is the lower bound.

4. Conclusions

Eppstein et al. [3] in 2007 conjectured that for a given number n, at least one simple polygon is present that requires $n-2$ vertex guards to describe the polygon. This is the worst case of the sculptural garden problem which can be applied to speed up the localization approaches of mobile devices in some applications. We proved a special case of the conjecture in which the guards are natural vertex ones, by introducing a new class of polygons named Helix polygon. In further research, one can prove the general case of the conjecture. Additionally, one can investigate the bounds for special cases of polygons (e.g., orthogonal polygons).

As far as the authors know, no algorithm (deterministic or non-deterministic) has been presented to solve the sculpture garden problem. It can have many applications in security, smart cities and the Internet of Things, and it is suggested that researchers try to develop approximate or heuristic algorithms to solve the problem. To be more precise, it is expected that in the future research, an algorithm will be presented to solve the problem, in which a polygon can be described and its range defined with the least number of guards.