Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve
Abstract
1. Introduction
2. Related Work
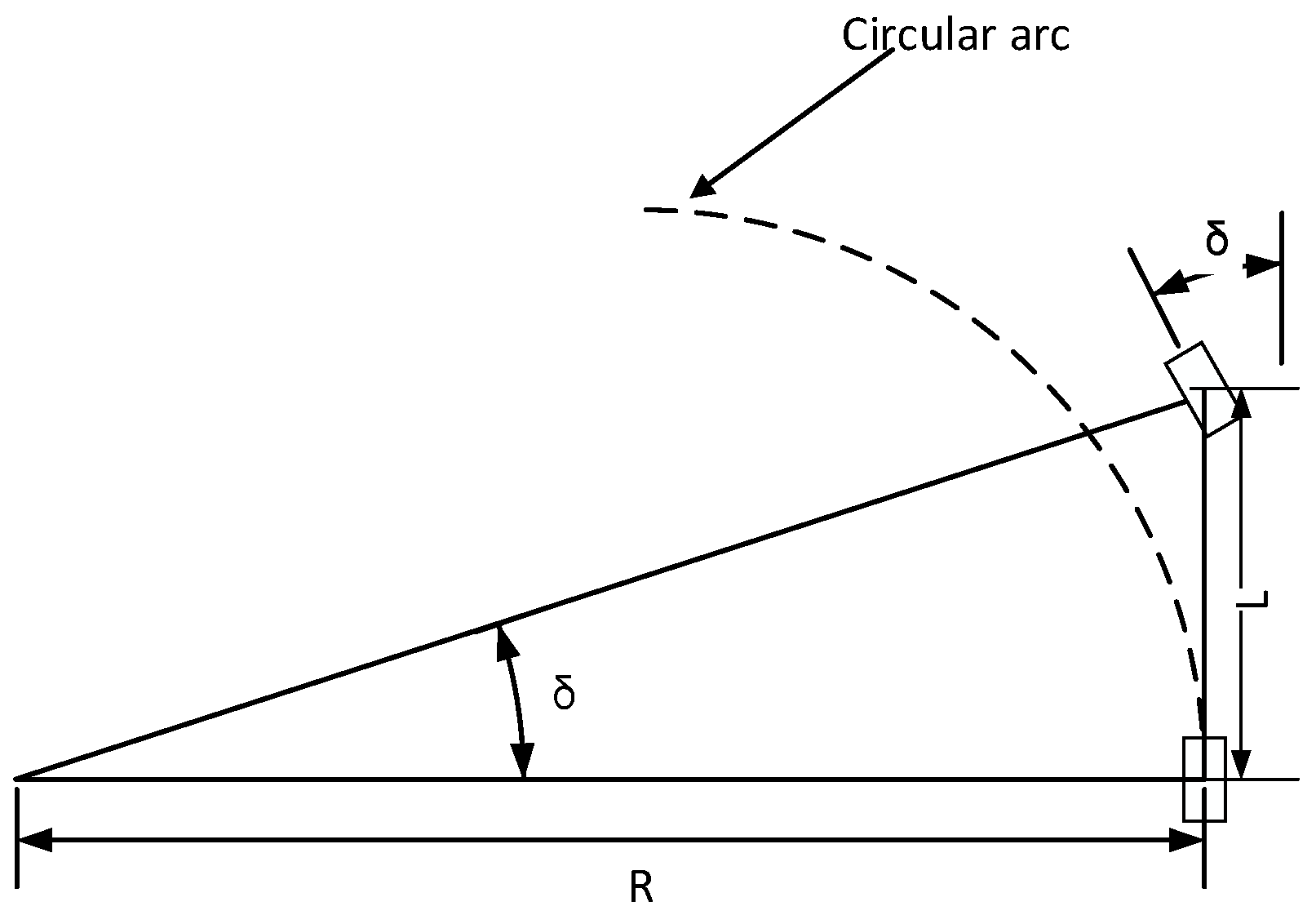
2.1. Geometric Vehicle Model
2.2. Control Curve
- When the driver controls the steering wheel, in order to ensure lateral stability, the steering wheel is generally controlled at a constant speed, which means the angular speed of the steering wheel is constant. When the speed and front wheel angle change are very small in a tiny period of time and can be ignored, the change rate of the path curvature is constant, which is consistent with the characteristics of the clothoid curve. Therefore, the planned control path constructed by the clothoid curve can ensure that the vehicle control process is stable and the jitter is tiny.
- The clothoid curve satisfies the G2 continuity conditions. Compared with the arc curve constructed by the pure pursuit tracking algorithm, the curvature of the starting point of the curve is consistent with the initial turning curvature of the vehicle, which can reduce tracking deviation at the beginning period of the path.
- Compared with the polynomial curve, because its curvature changes linearly and continuously, it is easier to control and verify the curvature and curvature change rate of the planned control path and other constraints or limitations.
2.3. Control System Delay and Hysteresis
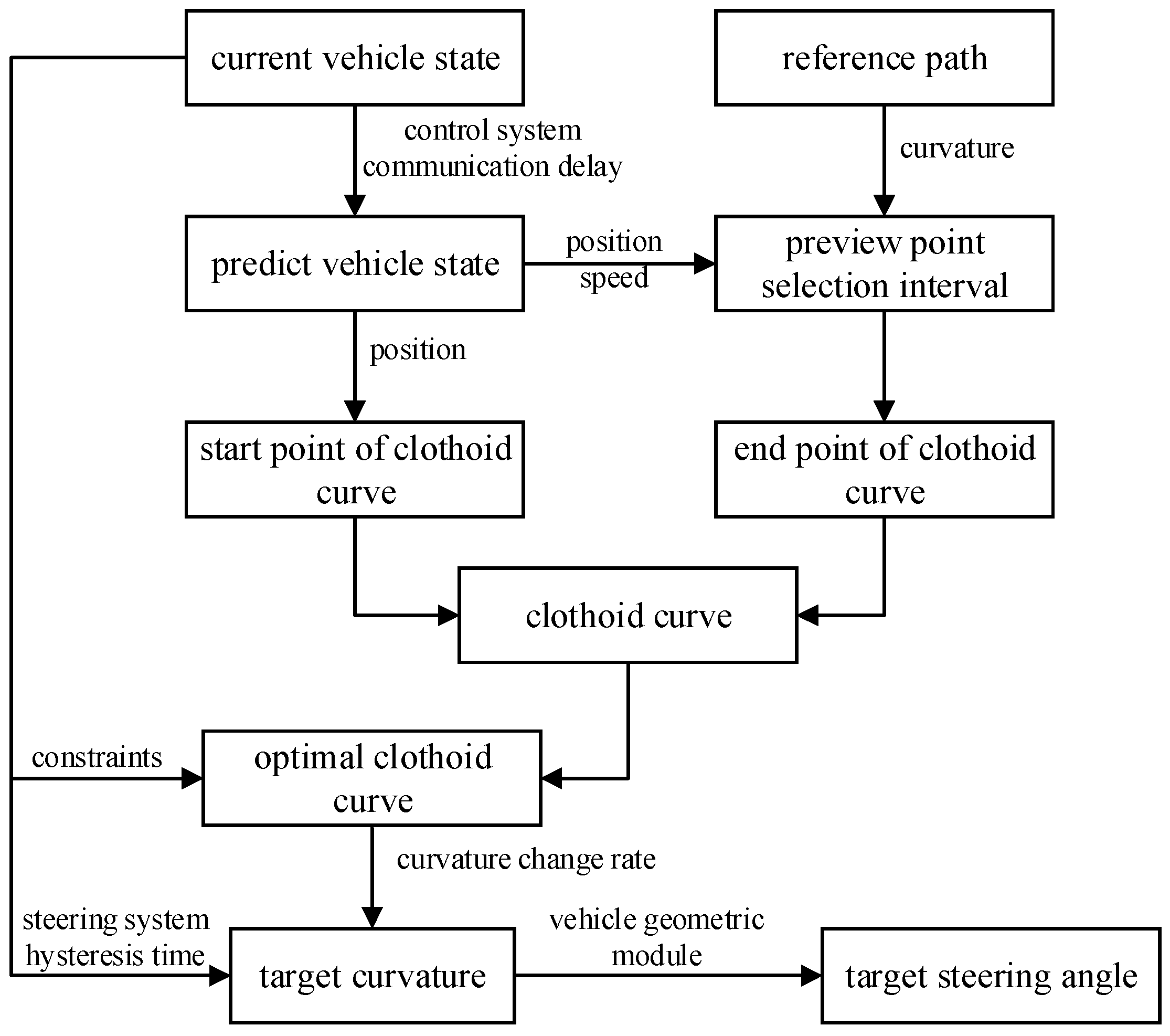
3. Tracking Control Method Using Clothoid Curve
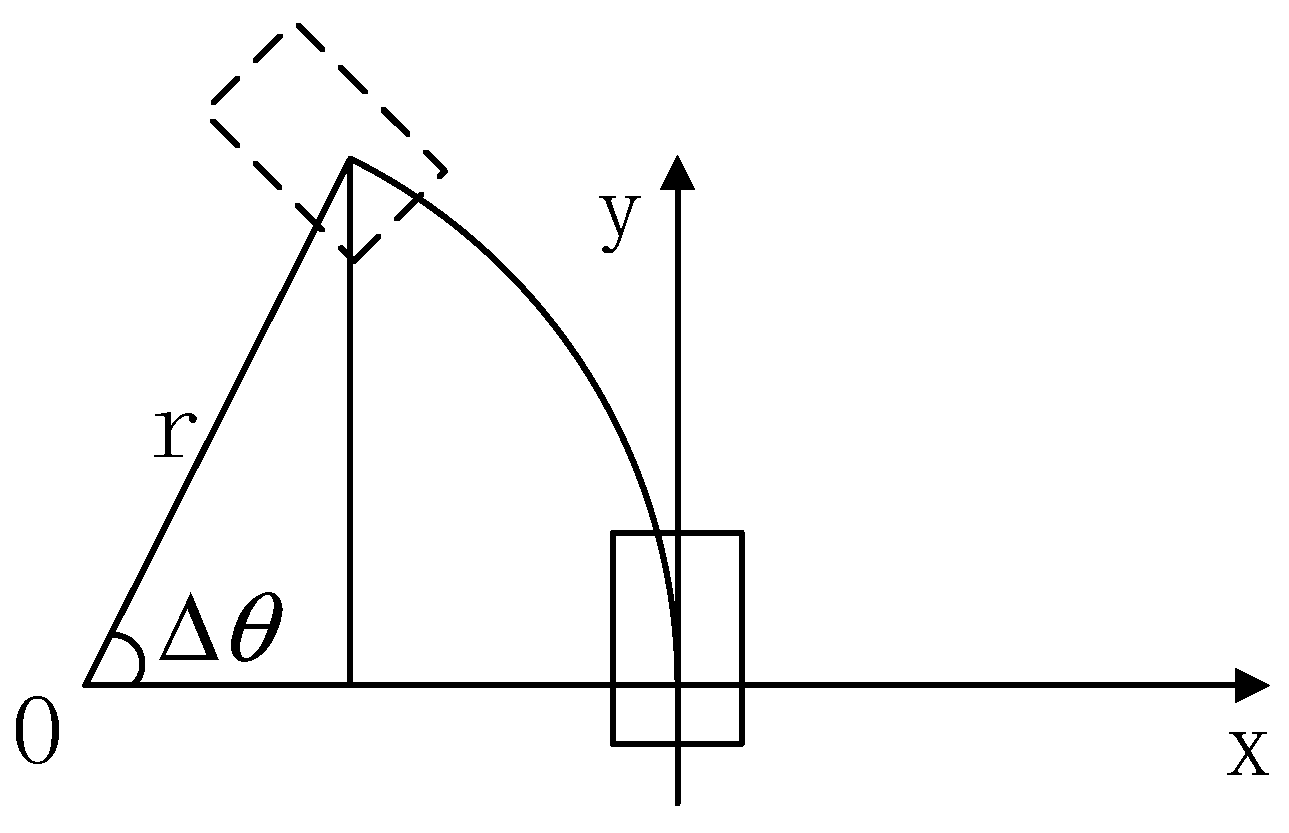
3.1. Kinematic Model of Vehicle Lateral Control
3.2. Algorithm Process
| Algorithm 1: Trajectory tracking of autonomous vehicle using clothoid curve |
 |
3.3. Vehicle State Prediction Based on Communication Delay
3.4. Preview Point Selection
| Algorithm 2: End point selection of preview point interval |
 |
3.5. Constraints
3.5.1. Curvature Constraint
3.5.2. Maximum Curvature Change Rate Constraint
3.5.3. Clothoid Curve Length Constraint
3.6. Preview Control Based on Steering System Response Hysteresis
4. Test Results and Analysis
4.1. Test Method
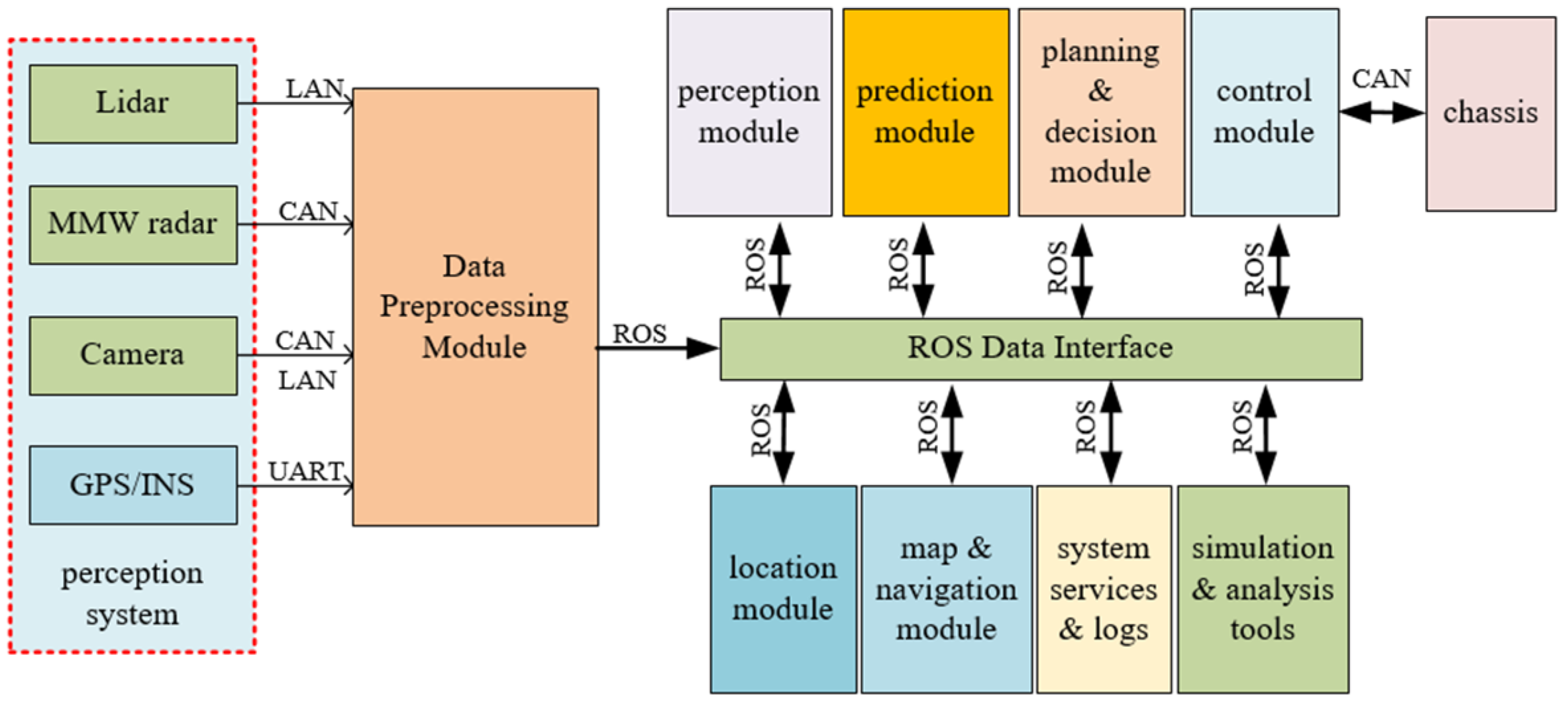
4.1.1. Test Platform
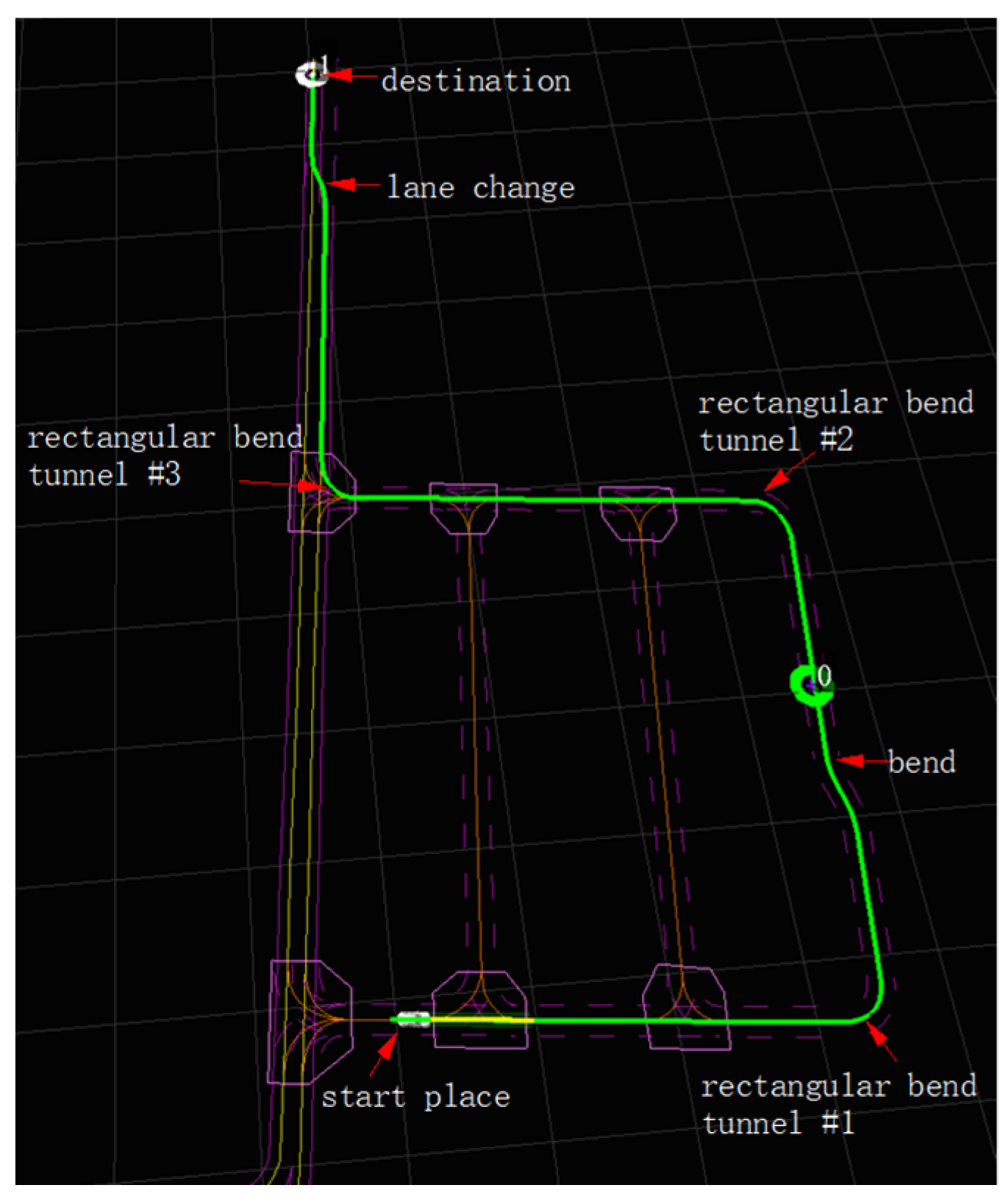
4.1.2. Test Path Design
4.1.3. Comparison Method
4.2. Test Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Du, Y. Lane-Changing Strategy Based on a Novel Sliding Mode Control Approach for Connected Automated Vehicles. Appl. Sci. 2022, 12, 11000. [Google Scholar] [CrossRef]
- Amer, N.; Zamzuri, H.; Hudha, K.; Kadir, Z.A. Modelling and Control Strategies in Path Tracking Control for Autonomous Ground Vehicles: A Review of State of the Art and Challenges. J. Intell. Robot Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Sun, Y.; Cui, B.; Ji, F.; Wei, X.; Zhu, Y. The Full-Field Path Tracking of Agricultural Machinery Based on PSO-Enhanced Fuzzy Stanley Model. Appl. Sci. 2022, 12, 7683. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Zhang, S. Review article: State-of-the-art trajectory tracking of autonomous vehicles. Mech. Sci. 2021, 12, 419–432. [Google Scholar] [CrossRef]
- Kapania, N.; Gerdes, J. Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef]
- Aicardi, M.; Casalino, G.; Bicchi, A.; Balestrino, A. Closed loop steering of unicycle like vehicles via Lyapunov techniques. IEEE Robot Autom. Mag. 1995, 2, 27–35. [Google Scholar] [CrossRef]
- Koubaa, Y.; Boukattaya, M.; Dammak, T. Adaptive Sliding-Mode Dynamic Control for Path Tracking of Nonholonomic Wheeled Mobile Robot. J. Autom. Syst. Eng. 2015, 9, 119–131. [Google Scholar]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. Adaptive-neural-network-based robust lateral motion control for autonomous vehicle at driving lim-its. Control Eng. Pract. 2018, 76, 41–53. [Google Scholar] [CrossRef]
- Park, M.; Lee, S.; Han, W. Development of Steering Control System for Autonomous Vehicle Using Geometry-Based Path Tracking Algorithm. ETRL J. 2015, 37, 617–625. [Google Scholar] [CrossRef]
- Horvath, E.; Hajdu, C.; Koros, P. Novel Pure-Pursuit Trajectory Following Approaches and their Practical Applications. In Proceedings of the 2019 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Naples, Italy, 23–25 October 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 597–602. [Google Scholar]
- Elbanhawi, M.; Simic, M.; Jazar, R. Receding horizon lateral vehicle control for pure pursuit path tracking. J. Vib. Control 2018, 24, 619–642. [Google Scholar] [CrossRef]
- Bertolazzi, E.; Frego, M. On the G 2 Hermite Interpolation Problem with clothoids. J. Comput. Appl. Math. 2018, 341, 99–116. [Google Scholar] [CrossRef]
- Krichen, M. Improving Formal Verification and Testing Techniques for Internet of Things and Smart Cities. Mobile Netw Appl. 2019, 1–12. [Google Scholar] [CrossRef]
- Medhat, N.; Moussa, S.M.; Badr, N.L.; Tolba, M.F. Tolba. A Framework for Continuous Regression and Integration Testing in IoT Systems Based on Deep Learning and Search-Based Techniques. IEEE 2022, 8, 215716–215726. [Google Scholar] [CrossRef]
- Wit, J.; Crane, C.; Armstrong, D. Autonomous ground vehicle path tracking. J. Robot. Syst. 2004, 21, 439–449. [Google Scholar] [CrossRef]
- Amidi, O.; Thorpe, C. Integrated Mobile Robot Control. In Proc. SPIE 1388; Mobile Robots V, 1 March 1991. [Google Scholar] [CrossRef]
- Girbés, V.; Armesto, L.; Tornero, J.; Solanes, J.E. Continuous-curvature kinematic control for path following problems. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4335–4340. [Google Scholar] [CrossRef]
- Shan, Y.; Yang, W.; Chen, C.; Zhou, J.; Zheng, L.; Li, B. CF-Pursuit: A Pursuit Method with a Clothoid Fitting and a Fuzzy Controller for Autono-mous Vehicles. Int. J. Adv. Robot Syst. 2015, 12, 134. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H.; Tang, Y. Preview Path Tracking Control with Delay Compensation for Autonomous Vehicles. IEEE T. Intell. Transp. Syst. 2021, 22, 2979–2989. [Google Scholar] [CrossRef]
- Zakaria, M.; Zamzuri, H.; Mamat, R.; Amri Mazlan, S. A Path Tracking Algorithm Using Future Prediction Control with Spike Detection for an Autonomous Vehicle Robot. Int. J. Adv. Robot Syst. 2013, 10, 309. [Google Scholar] [CrossRef]
- Abd Elmoniem, A.; Osama, A.; Abdelaziz, M.; Maged, .A. A path-tracking algorithm using predictive Stanley lateral controller. Int. J. Adv. Robot Syst. 2020, 17, 172988142097485. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]


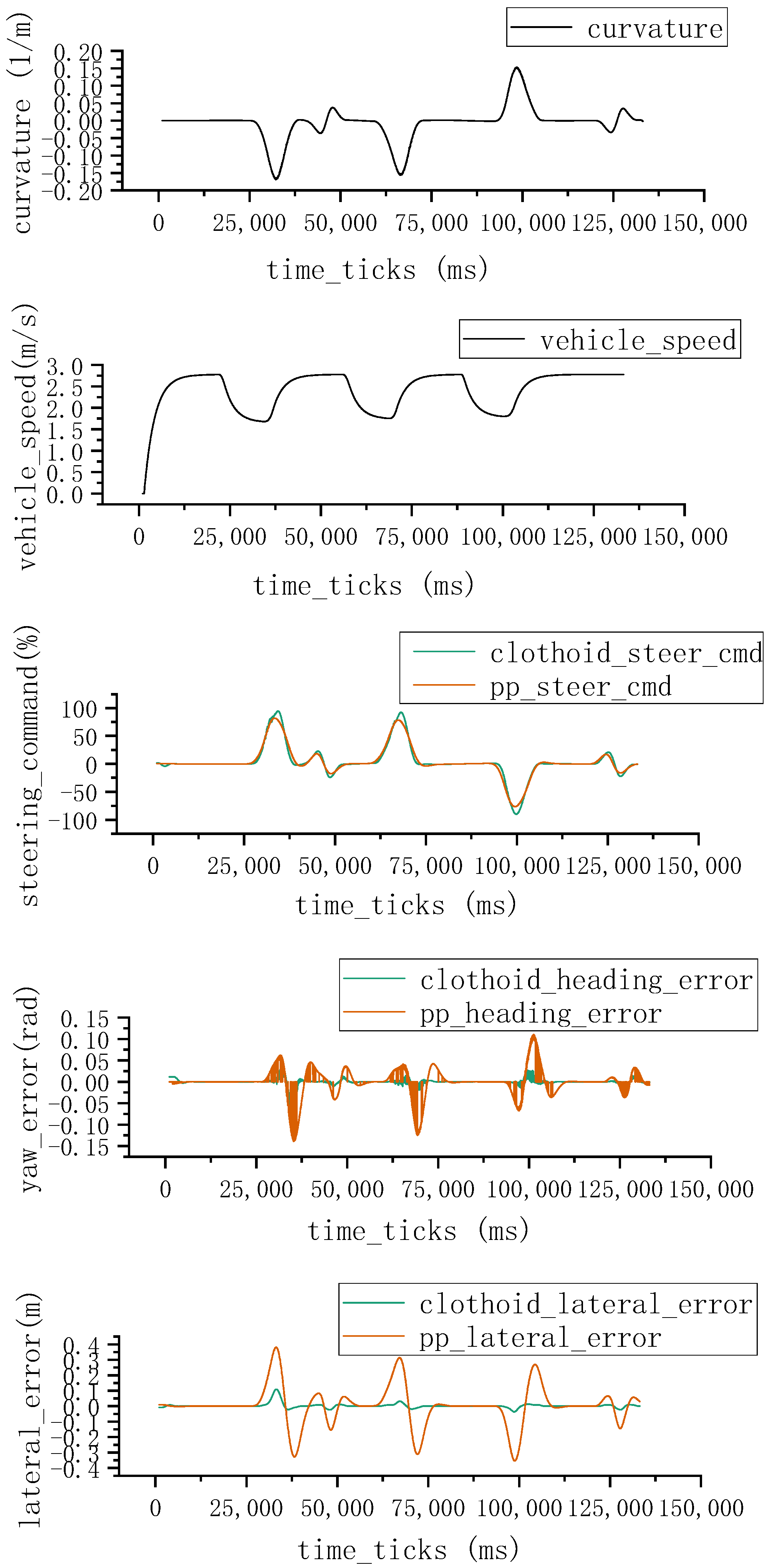
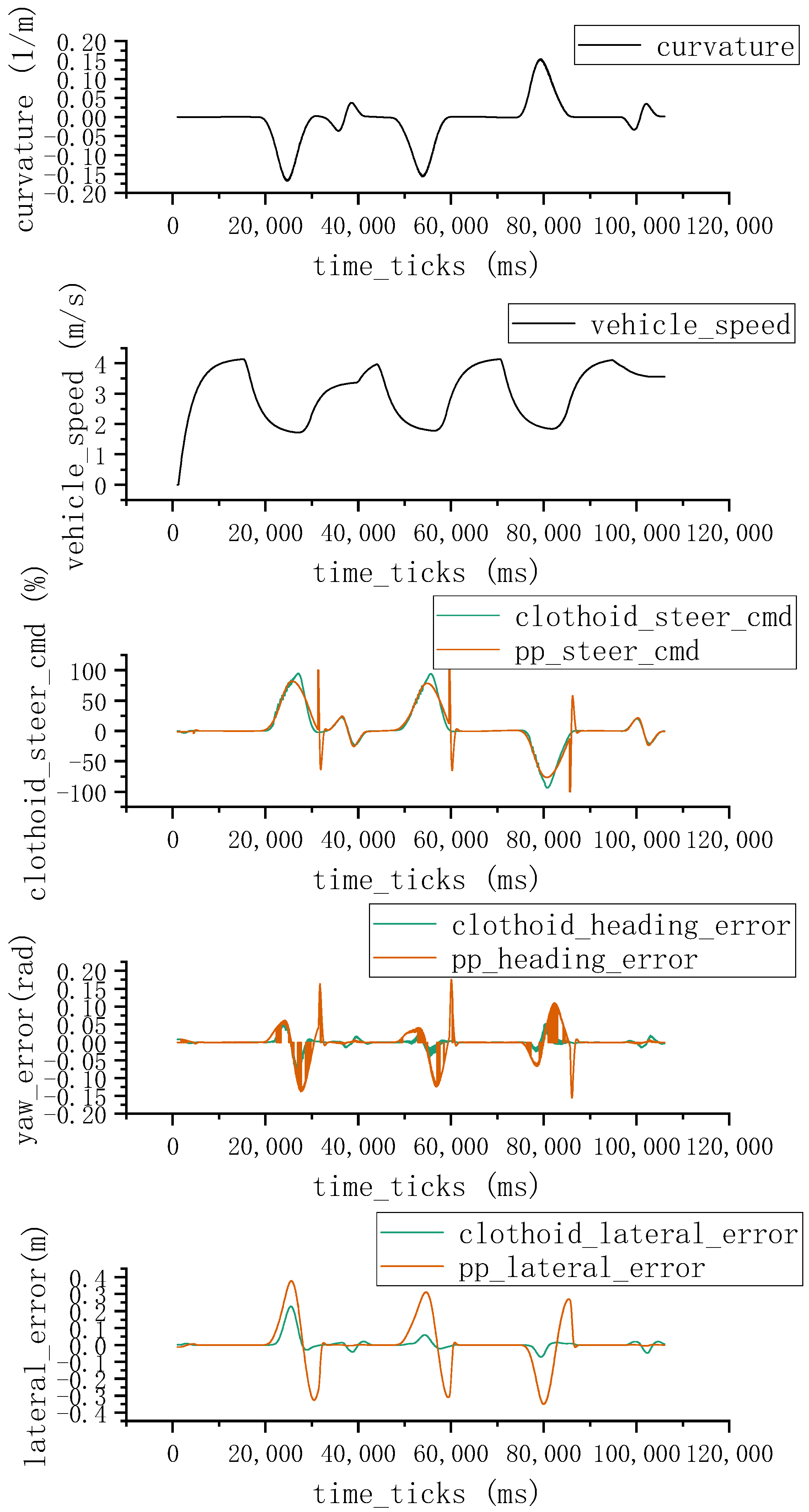

| Limited Speed (km/h) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Clothoid | PP | Clothoid | PP | Clothoid | PP | Clothoid | PP | |
| 10 | 0.109 | 0.381 | 0.0557 | 0.1390 | 0.0157 | 0.1225 | 0.0071 | 0.03148 |
| 15 | 0.227 | 0.378 | 0.0934 | 0.1753 | 0.0365 | 0.1218 | 0.0134 | 0.03662 |
| 20 | 0.232 | 0.368 | 0.0864 | 0.1727 | 0.0393 | 0.1231 | 0.0140 | 0.03754 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Lou, J.; Li, Y.; Pan, S.; Xu, Y. Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve. Appl. Sci. 2023, 13, 2733. https://doi.org/10.3390/app13042733
Li J, Lou J, Li Y, Pan S, Xu Y. Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve. Applied Sciences. 2023; 13(4):2733. https://doi.org/10.3390/app13042733
Chicago/Turabian StyleLi, Jianshi, Jingtao Lou, Yongle Li, Shiju Pan, and Youchun Xu. 2023. "Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve" Applied Sciences 13, no. 4: 2733. https://doi.org/10.3390/app13042733
APA StyleLi, J., Lou, J., Li, Y., Pan, S., & Xu, Y. (2023). Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve. Applied Sciences, 13(4), 2733. https://doi.org/10.3390/app13042733





