Band Gap Analysis for Materials with Cookie-Shaped Auxetic Microstructures, Using Finite Elements
Abstract
:Featured Application
Abstract
1. Introduction
2. State of the Art and Purpose of the Study
3. Materials and Methods
3.1. Irreducible Brillouin Zone and Periodic Structures
3.2. Applying Blovh Theorem on the Model
3.3. Setting Up the Numerical Experiment
- Dimensions of the outer ellipse: 200 × 100 (mm)
- Dimensions of the inner ellipse: 170 × 80 (mm)
- Dimensions of the cross: 150 × 150 (mm)
- Thickness for each of the cross rods: 6 (mm)
- Number of eigen frequencies: 8
- Periodic condition parameter value range: k 0–3 with step 0.08
4. Results
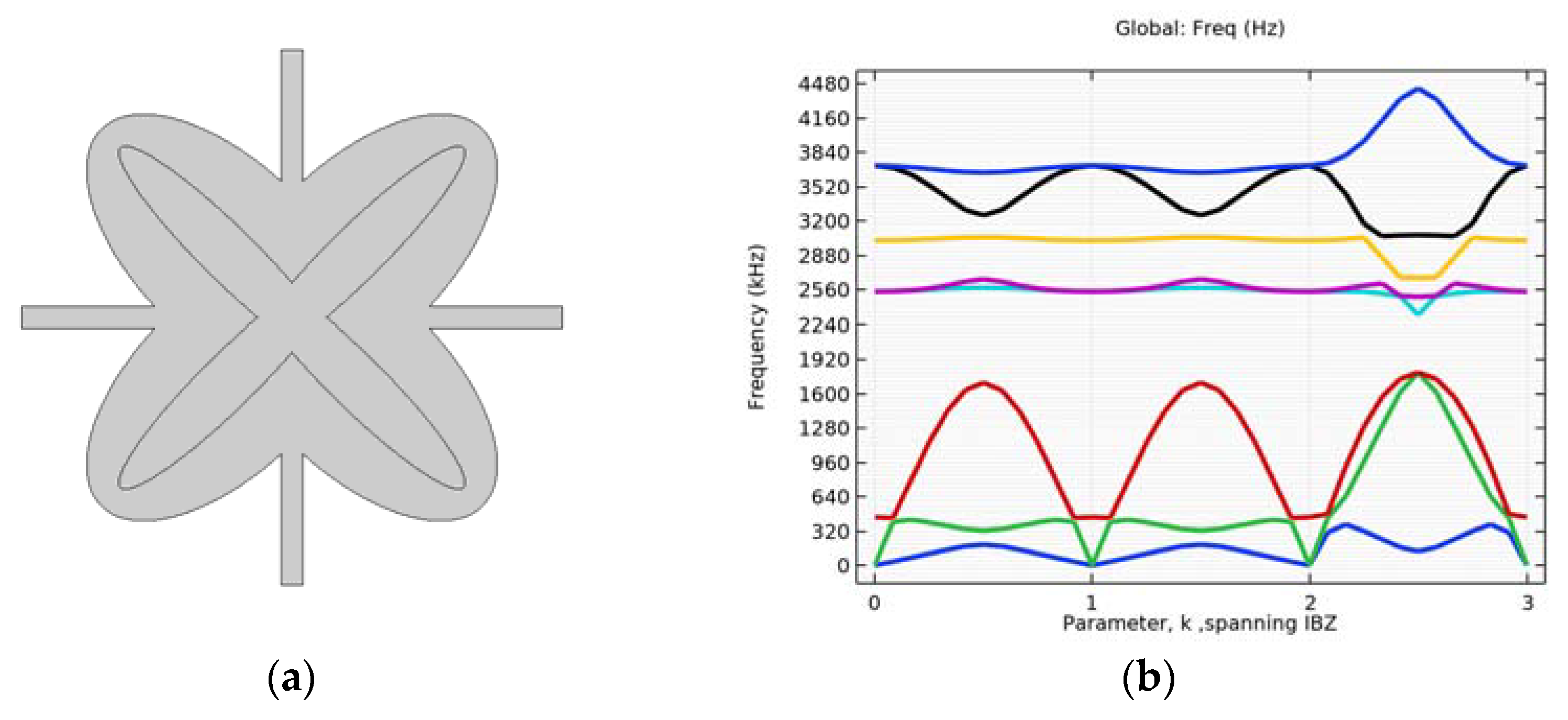
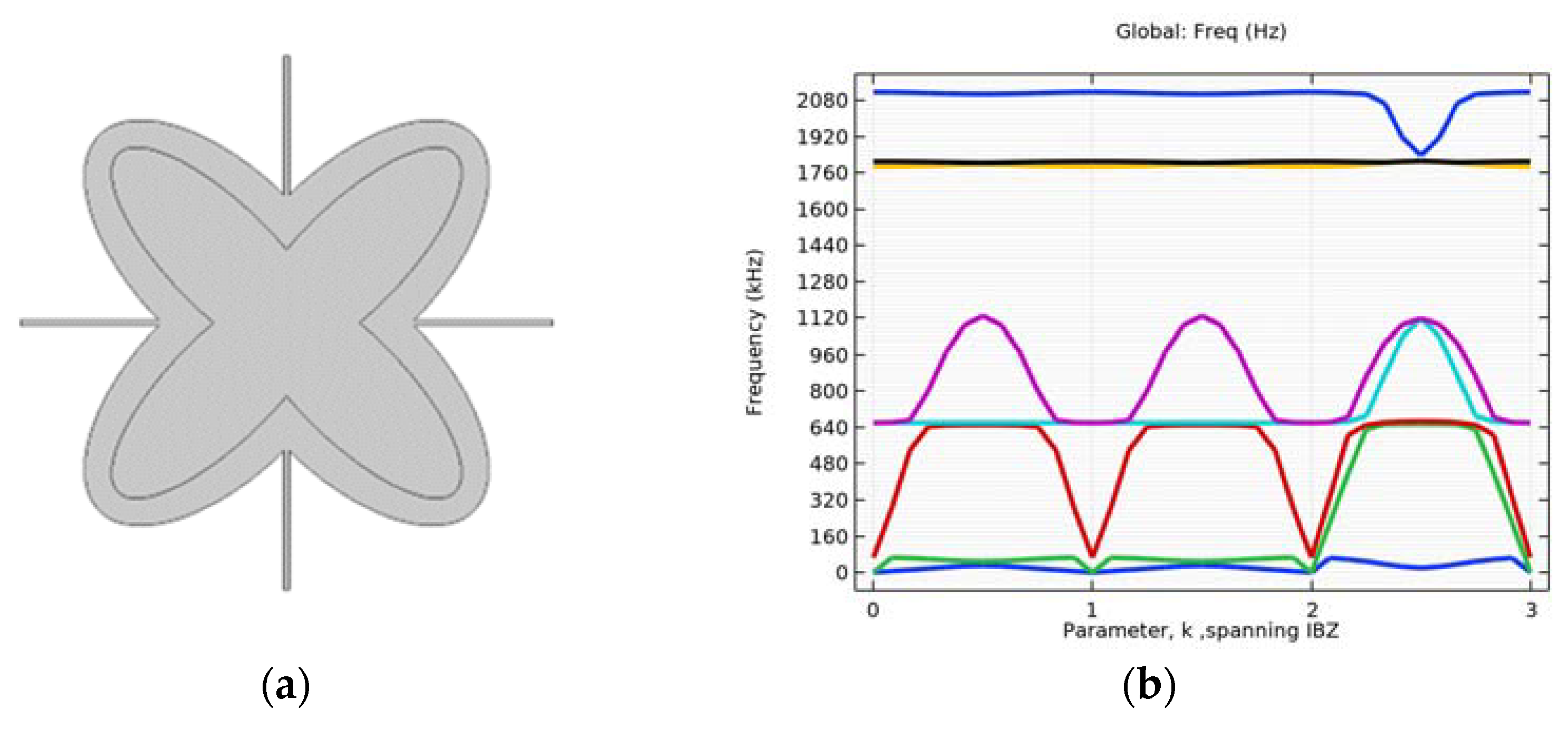
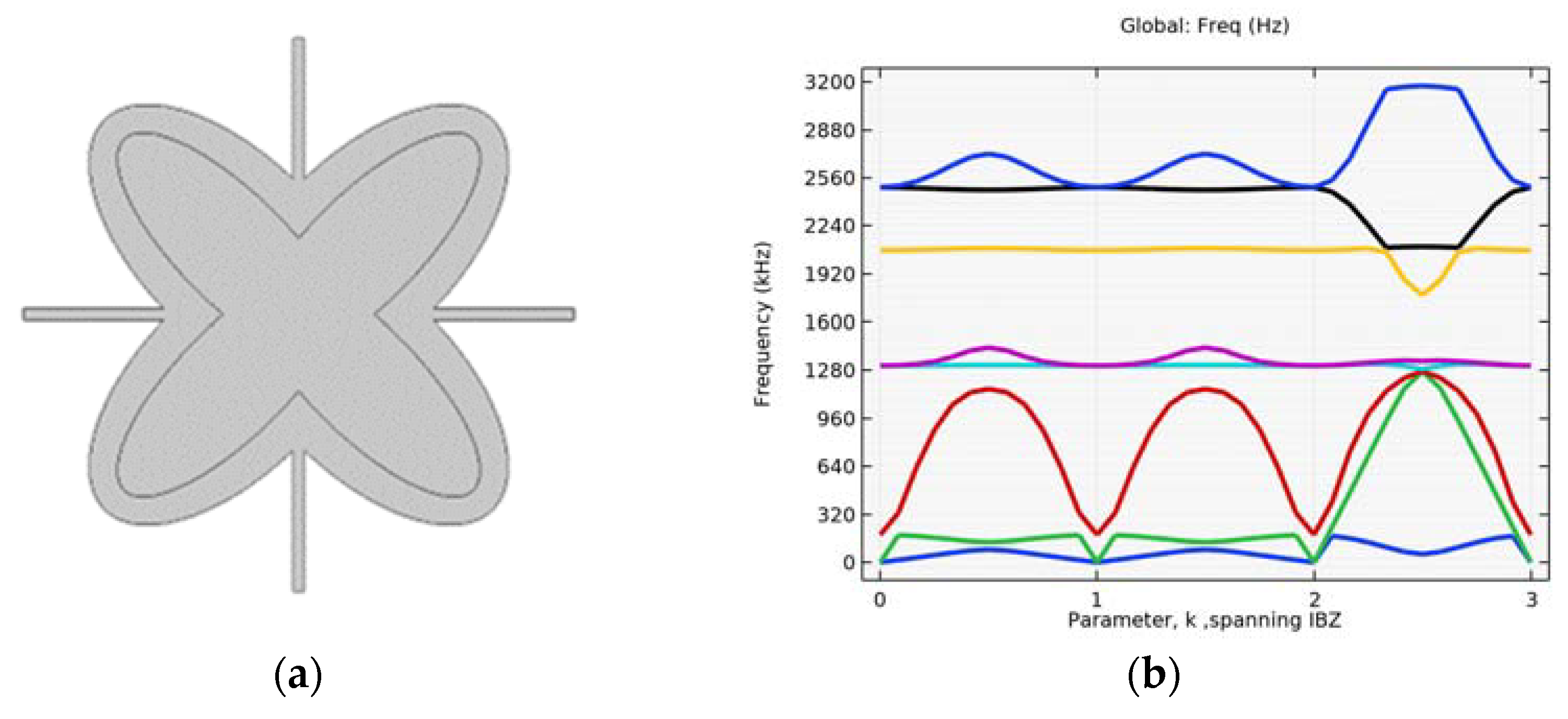
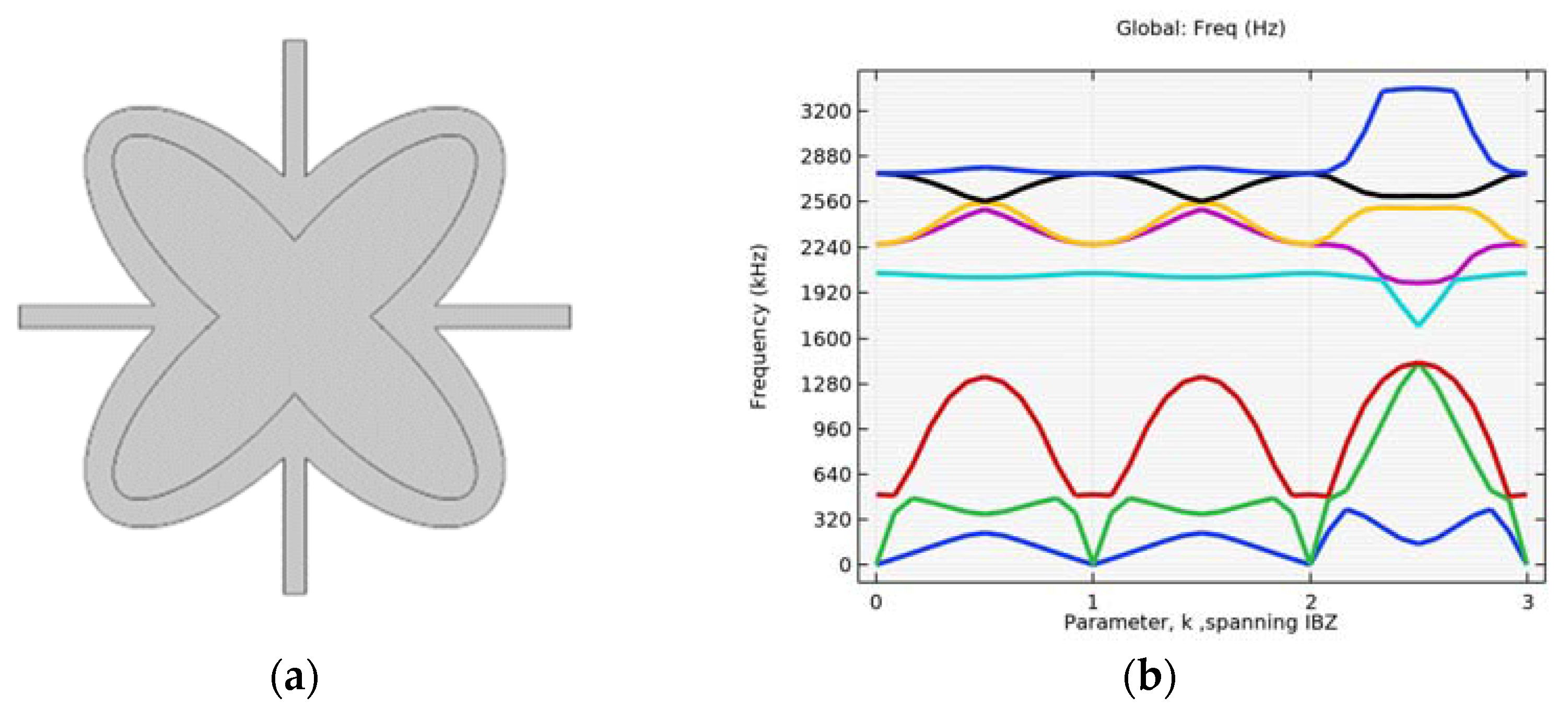
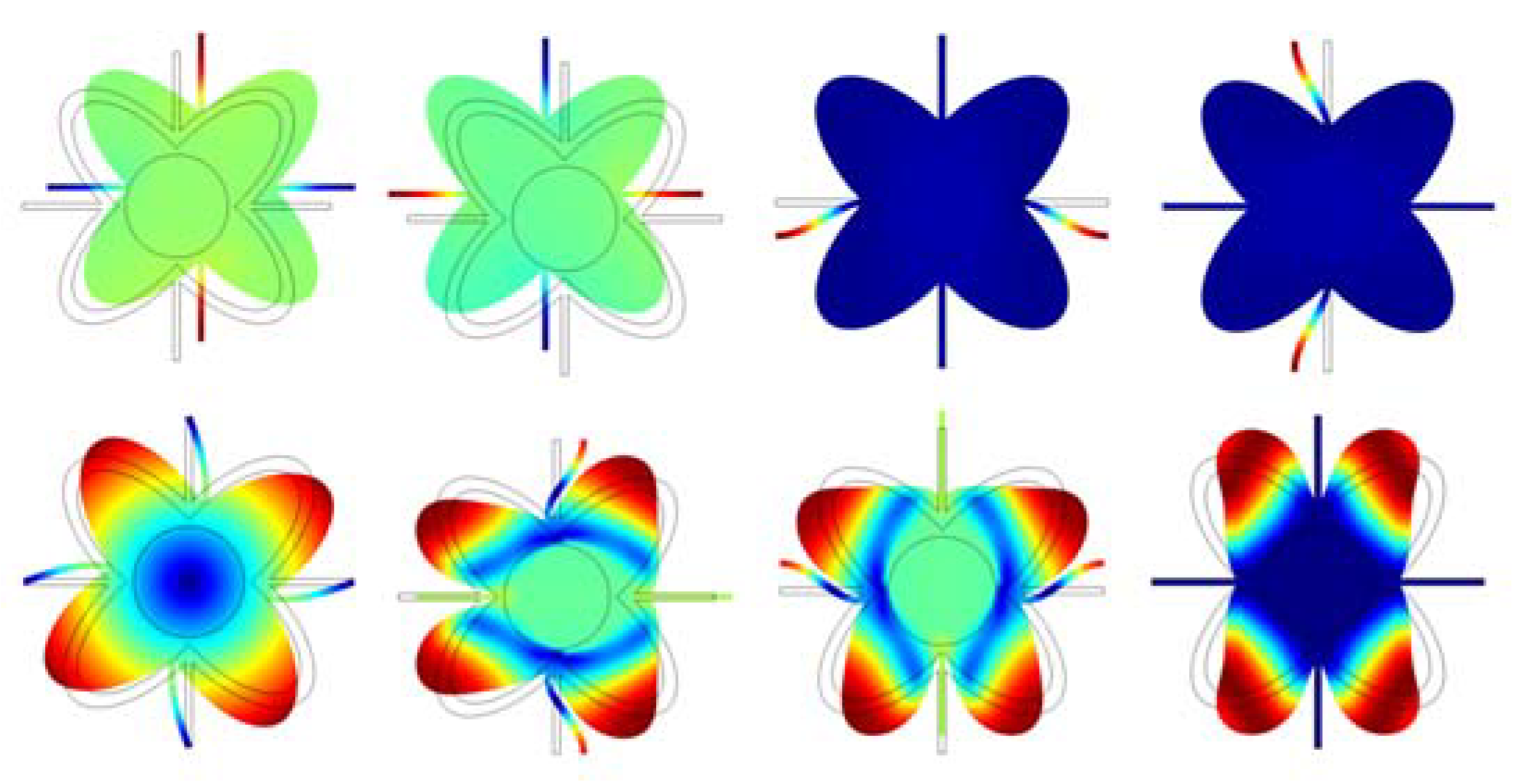
4.1. Simulation of Initial Structure with and without Circular Inclusion
4.2. Simulation with Different Alterations of the Inner Ellipse Size
4.3. Verification on a Continuum with Microstructure
- Dimensions of outer ellipse: 200 × 100 (mm)
- Dimensions of inner ellipse: 170 × 80 (mm)
- Rod thickness: 6 (mm)
4.4. Investigating the Effectiveness of Combined Microstructures
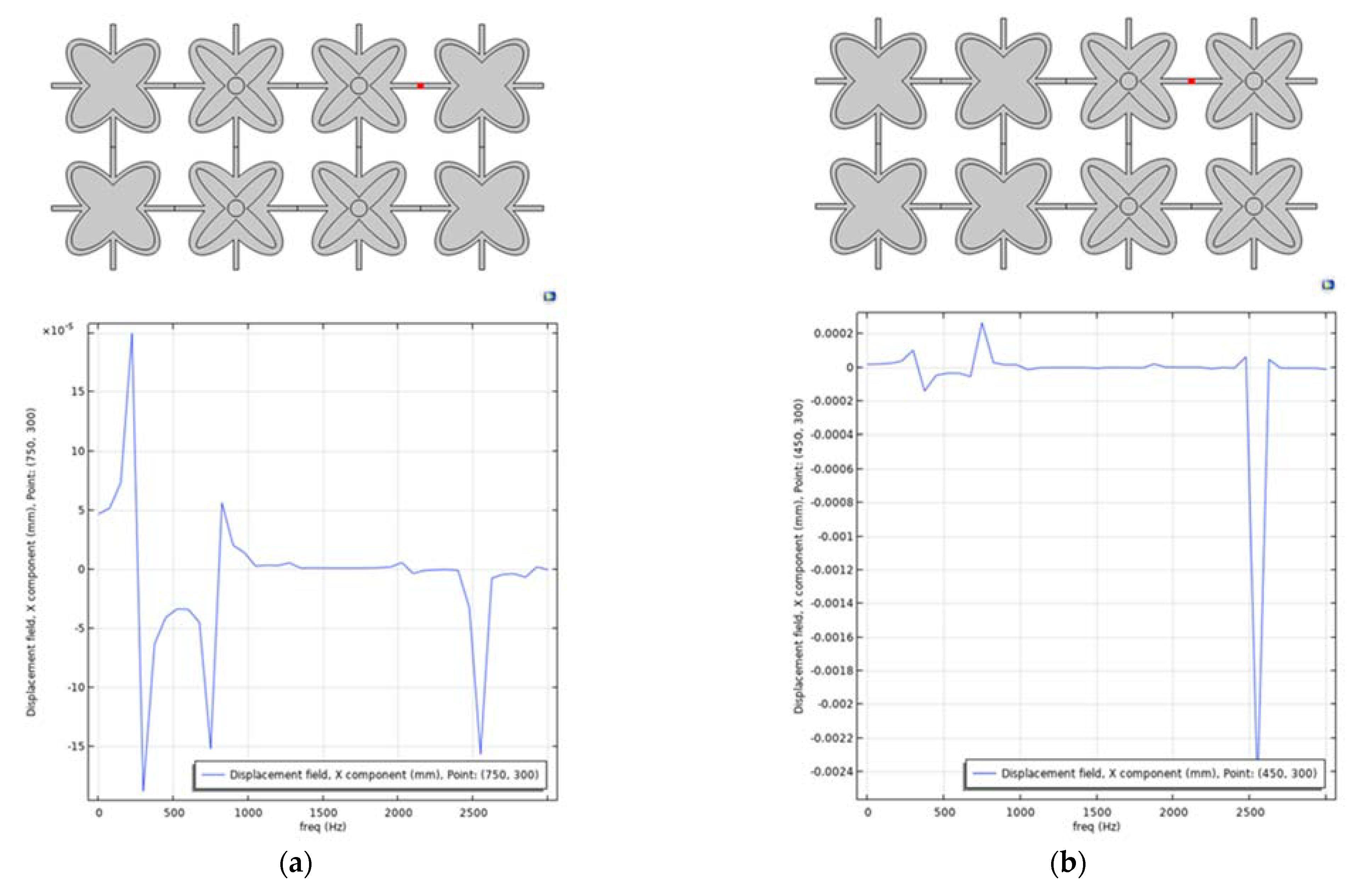
4.5. Single Layer Grid–Different Layouts of Elements
5. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Stavroulakis, G.E. Auxetic behaviour: Appearance and engineering applications. Phys. Stat. Sol. (B) 2005, 242, 710–720. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic Materials and Structures; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mariam Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496. [Google Scholar] [CrossRef] [Green Version]
- Ruzzene, M.; Mazzarella, L.; Tsopelas, P.; Scarpa, F. Wave Propagation in Sandwich Plates with Periodic Auxetic Core. J. Intell. Mater. Syst. Struct. 2002, 13, 587–597. [Google Scholar] [CrossRef]
- Ruzzene, M.; Scarpa, F. Directional and band-gap behavior of periodic auxetic lattices. Phys. Stat. Sol. (B) 2005, 242, 665–680. [Google Scholar] [CrossRef]
- Bacigalupo, A.; De Bellis, M.L. Auxetic anti-tetrachiral materials: Equivalent elastic properties and frequency band-gaps. Compos. Struct. 2015, 131, 530–544. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Zega, V.; Ardito, R.; Corigliano, A. 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep. 2018, 8, 2262. [Google Scholar] [CrossRef] [Green Version]
- Bruggi, M.; Corigliano, A. Optimal 2D auxetic micro-structures with band gap. Meccanica 2019, 54, 2001–2027. [Google Scholar] [CrossRef]
- Koutsianitis, P.K.; Tairidis, G.K.; Drosopoulos, G.A.; Stavroulakis, G.E. Conventional and star-shaped auxetic materials for the creation of band gaps. Arch. Appl. Mech. 2019, 89, 2545–2562. [Google Scholar] [CrossRef]
- Koutsianitis, P.; Tairidis, G.K.; Kougkoulos, A.; Stavroulakis, G.E. Parametric investigation of band gap effects in chiral microstructures. J. Serb. Soc. Comput. Mech. 2021, 15, 63–78. [Google Scholar] [CrossRef]
- Xiao, S.-H.; Zhang, C.; Qing-Hua, Q.-H.; Wang, H. A novel planar auxetic phononic crystal with periodic cookie-shaped cellular microstructures. Mech. Adv. Mater. Struct. 2022, 29, 3345–3358. [Google Scholar] [CrossRef]
- Chen, W.; Tian, X.; Gao, R.; Liu, S. A low porosity perforated mechanical metamaterial with negative Poisson’s ratio and band gaps. Smart Mater. Struct. 2018, 27, 115010. [Google Scholar] [CrossRef]
- Liebold-Ribeiro, Y.; Körner, C. Phononic Band Gaps in Periodic Cellular Materials. Adv. Eng. Mater. 2014, 16, 328–334. [Google Scholar] [CrossRef]
- Hou, J.; Li, D.; Dong, L. Study on Band-Gap Behaviors of 2D Hierarchical Re-Entrant Lattice Structures. Phys. Status Solidi B 2019, 256, 1800693. [Google Scholar] [CrossRef]
- Meng, J.; Deng, Z.; Zhang, K.; Xu, X.; Wen, F. Band gap analysis of star-shaped honeycombs with varied Poisson’s ratio. Smart Mater. Struct. 2015, 24, 095011. [Google Scholar] [CrossRef]
- Sheykhi, M. Vibroacoustic performance of star-shaped honeycomb-core annular cellular structures. Arch. Appl. Mech. 2022, 93, 1–20. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Qi, L.; Deng, Z. 3D chiral mechanical metamaterial for tailored band gap and manipulation of vibration isolation. Mech. Syst. Signal Process. 2022, 180, 109430. [Google Scholar] [CrossRef]
- Fei, X.; Jin, L.; Zhang, X.; Li, X.; Lu, M. Three-dimensional anti-chiral auxetic metamaterial with tunable phononic bandgap. Appl. Phys. Lett. 2020, 116, 021902. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, H.; Wang, C.; Yao, J. Design and Wave Propagation Characterization of Starchiral Metamaterials. Acta Mech. Solida Sin. 2022, 35, 215–227. [Google Scholar] [CrossRef]
- Saxena, K.K.; Das, R.; Calius, E.P. Three Decades of Auxetics Research − Materials with Negative Poisson’s Ratio: A Review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Hengsbach, S.; Lantada, A.D. Direct laser writing of auxetic structures: Present capabilities and challenges. Smart Mater. Struct. 2014, 23, 085033. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M.; Gonella, S.; Scarpa, F. Phononic properties of hexagonal chiral lattices. Wave Motion 2019, 46, 435–450. [Google Scholar] [CrossRef] [Green Version]
- Phani, A.S.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brillouin, L. Wave Propagation in Periodic Structures, 2nd ed.; Dover: New York, NY, USA, 1953. [Google Scholar]
- Kittel, C. Elementary Solid-State Physics: A Short Course, 1st ed.; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Xiong, Y.; Xu, A.; Wen, S.; Li, F.; Hosseini, S.M. Optimization of vibration band-gap characteristics of a periodic elastic metamaterial plate. Mech. Adv. Mater. Struct. 2022, 1–11. [Google Scholar] [CrossRef]
- Aage, N.; Gersborg, A.R.; Sigmund, O. Topology optimization of optical band gap effects in slab structures modulated by periodic rayleigh waves. In Proceedings of the XXII ICTAM, Adelaide, Australia, 25–29 August 2008. [Google Scholar]
- Vatanabe, S.L.; Paulino, G.H.; Silva, E.C. Maximizing phononic band gaps in piezocomposite materials by means of topology optimization. J. Acoust. Soc. Am. 2014, 136, 494–501. [Google Scholar] [CrossRef] [Green Version]
- Halkjær, S.; Sigmund, O.; Jensen, J.S. Maximizing band gaps in plate structures. Struct. Multidisc. Optim. 2006, 32, 263–275. [Google Scholar] [CrossRef]
- Quinteros, L.; Meruane, V.; Cardoso, E.L. Phononic band gap optimization in truss-like cellular structures using smooth P-norm approximations. Struct. Multidisc. Optim. 2021, 64, 113–124. [Google Scholar] [CrossRef]
- Drosopoulos, G.A.; Kaminakis, N.; Papadogianni, N.; Stavroulakis, G.E. Mechanical Behaviour of Auxetic Microstructures Using Contact Mechanics and Elastoplasticity. Key Eng. Mater. 2016, 681, 100–116. [Google Scholar] [CrossRef]
- Pyskir, A.; Collet, M.; Dimitrijevic, Z.; Lamarque, C.-H. Enhanced Vibration Isolation with Prestressed Resonant Auxetic Metamaterial. Materials 2021, 14, 6743. [Google Scholar] [CrossRef]
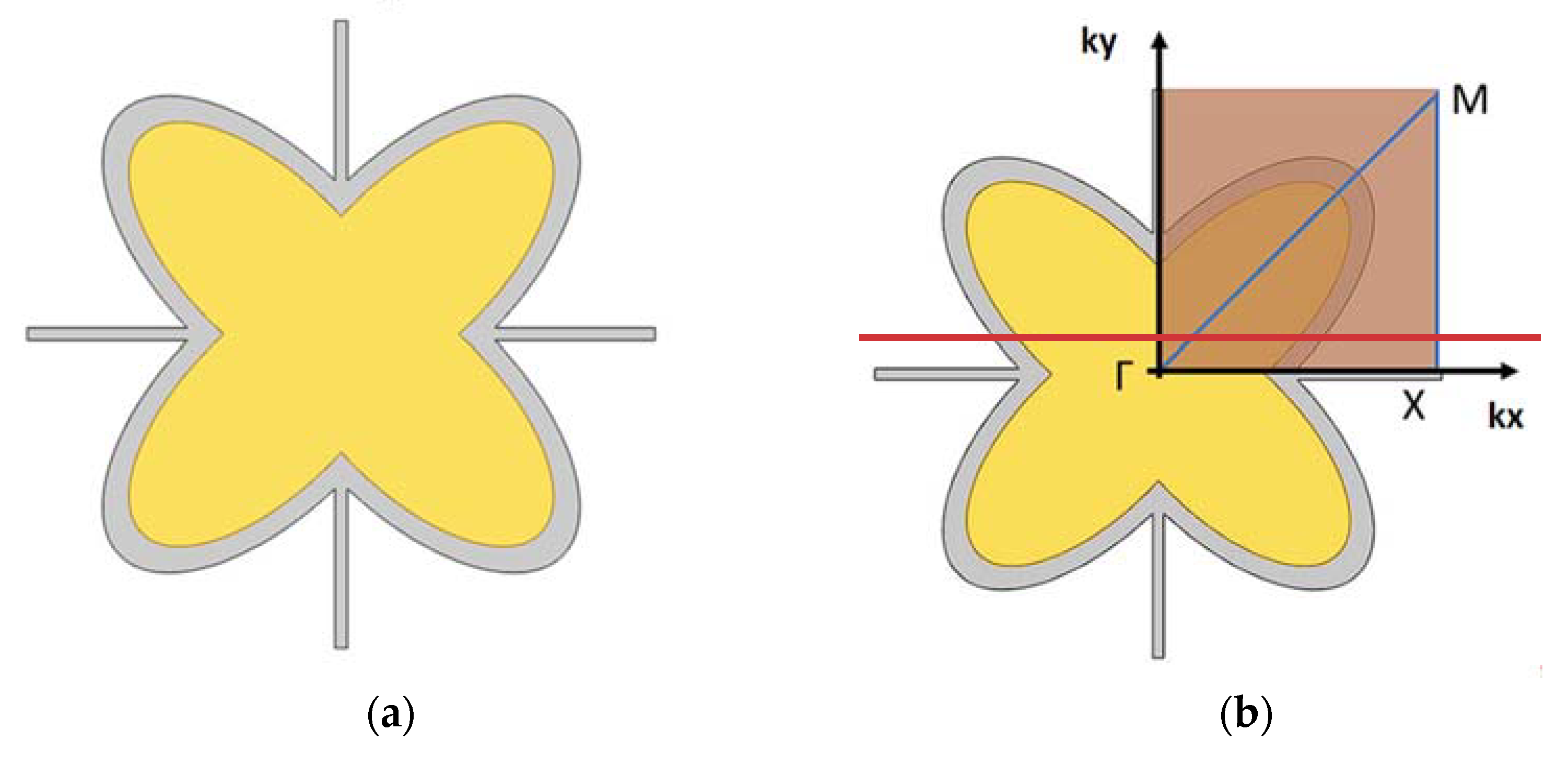

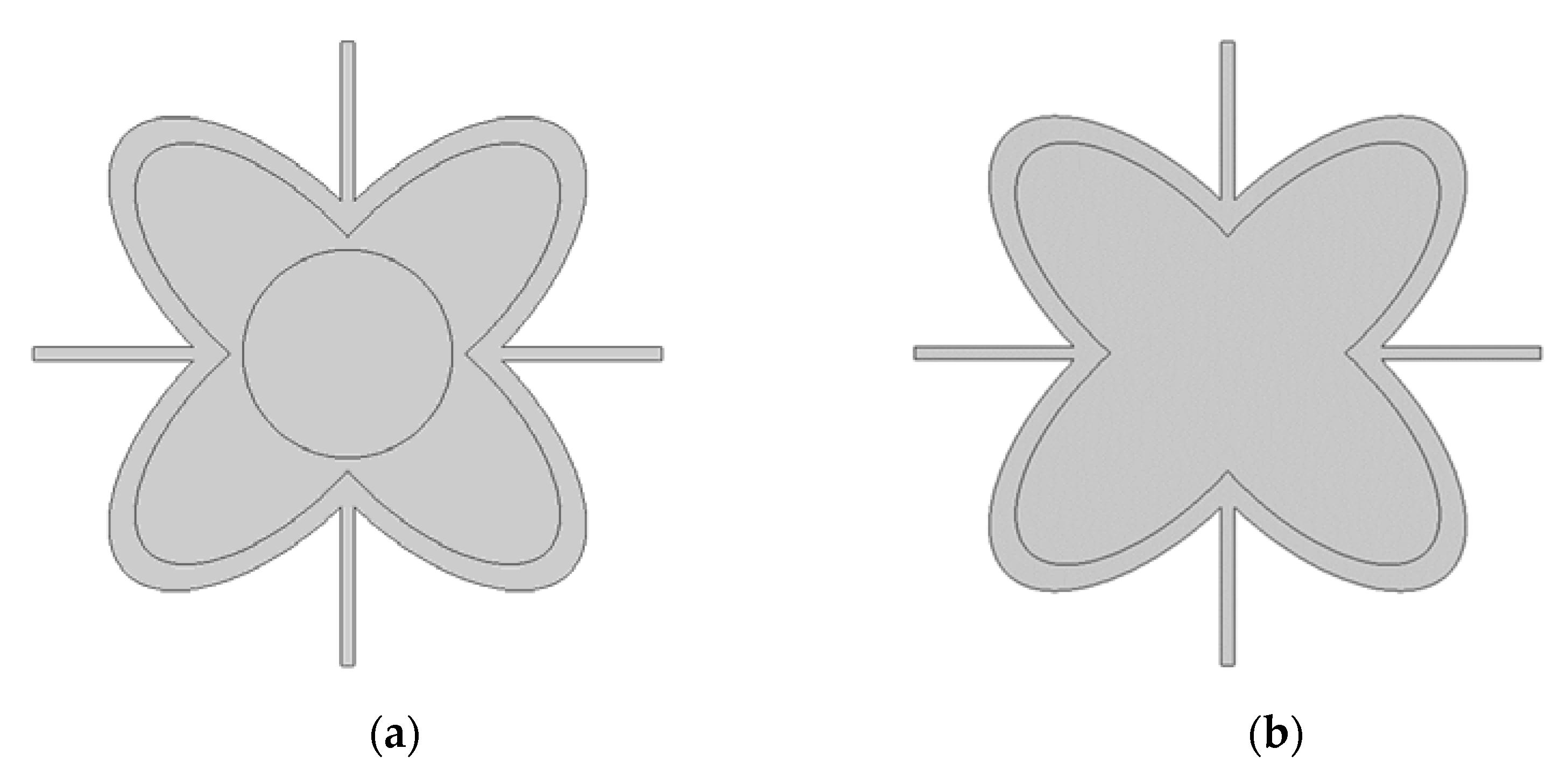
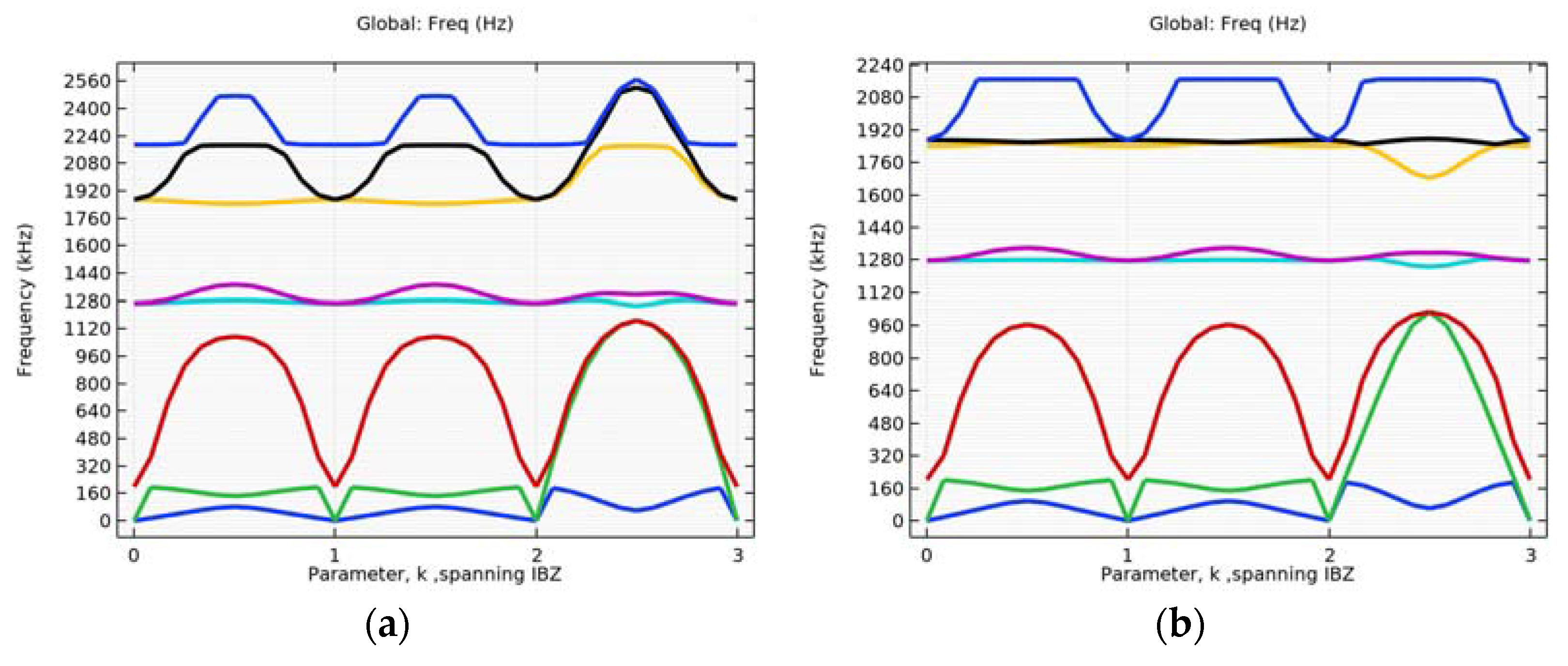

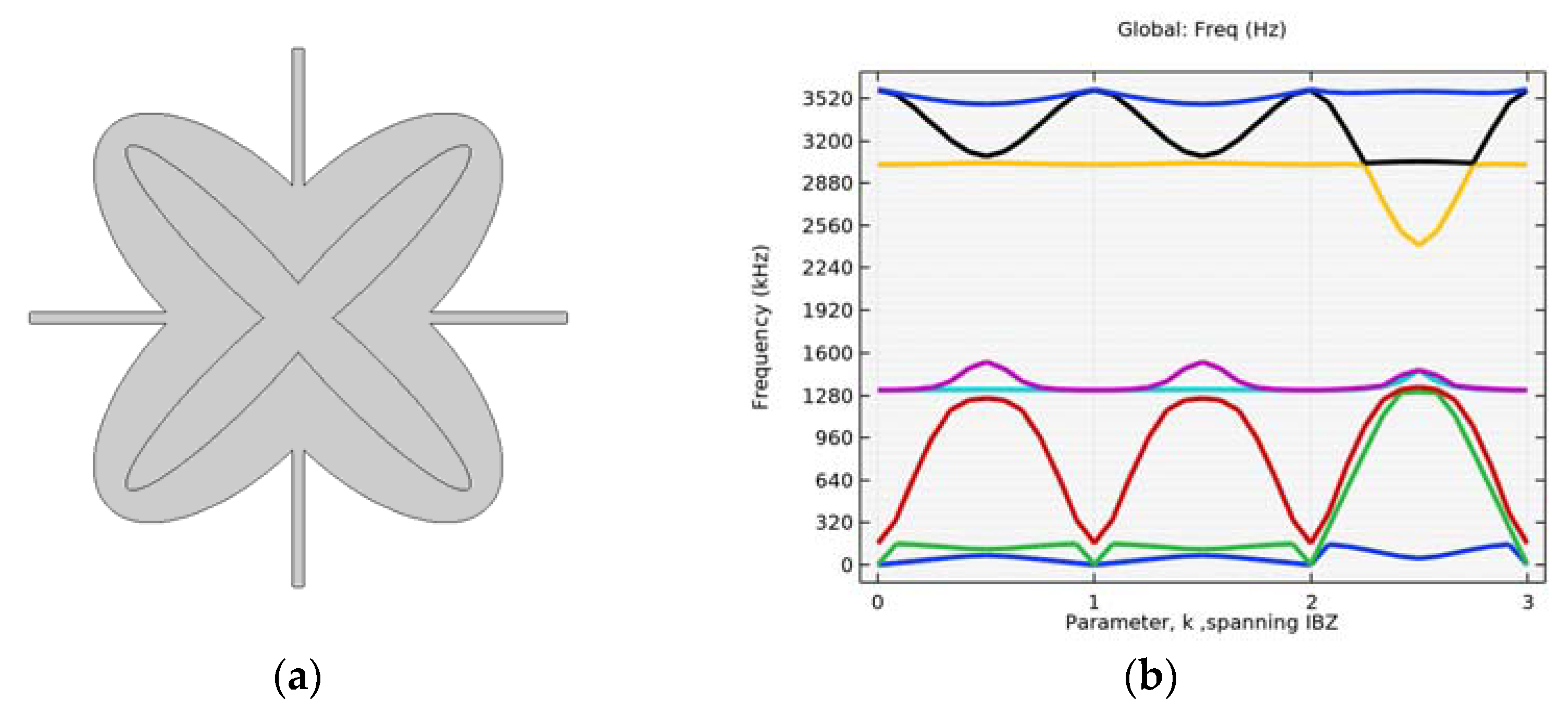
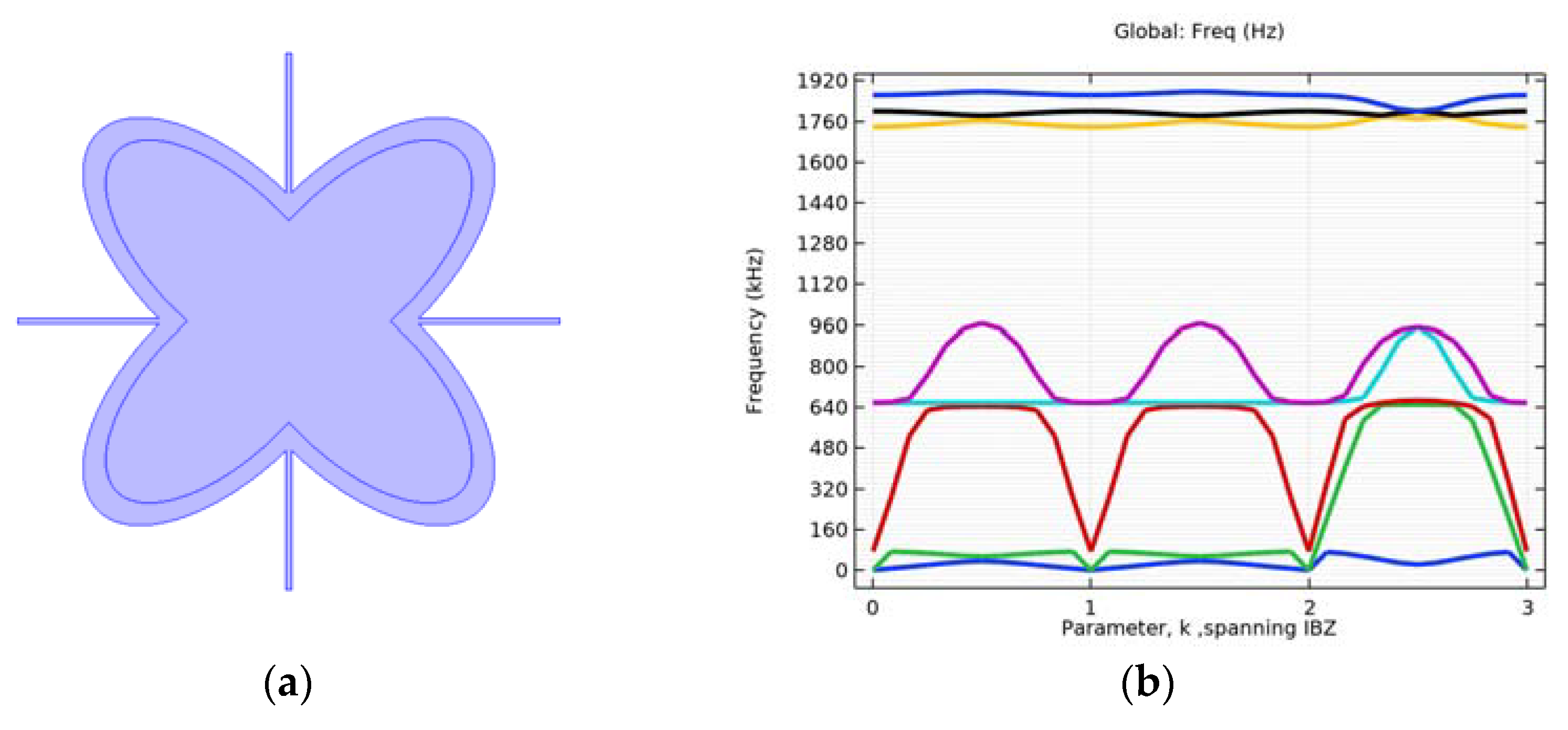
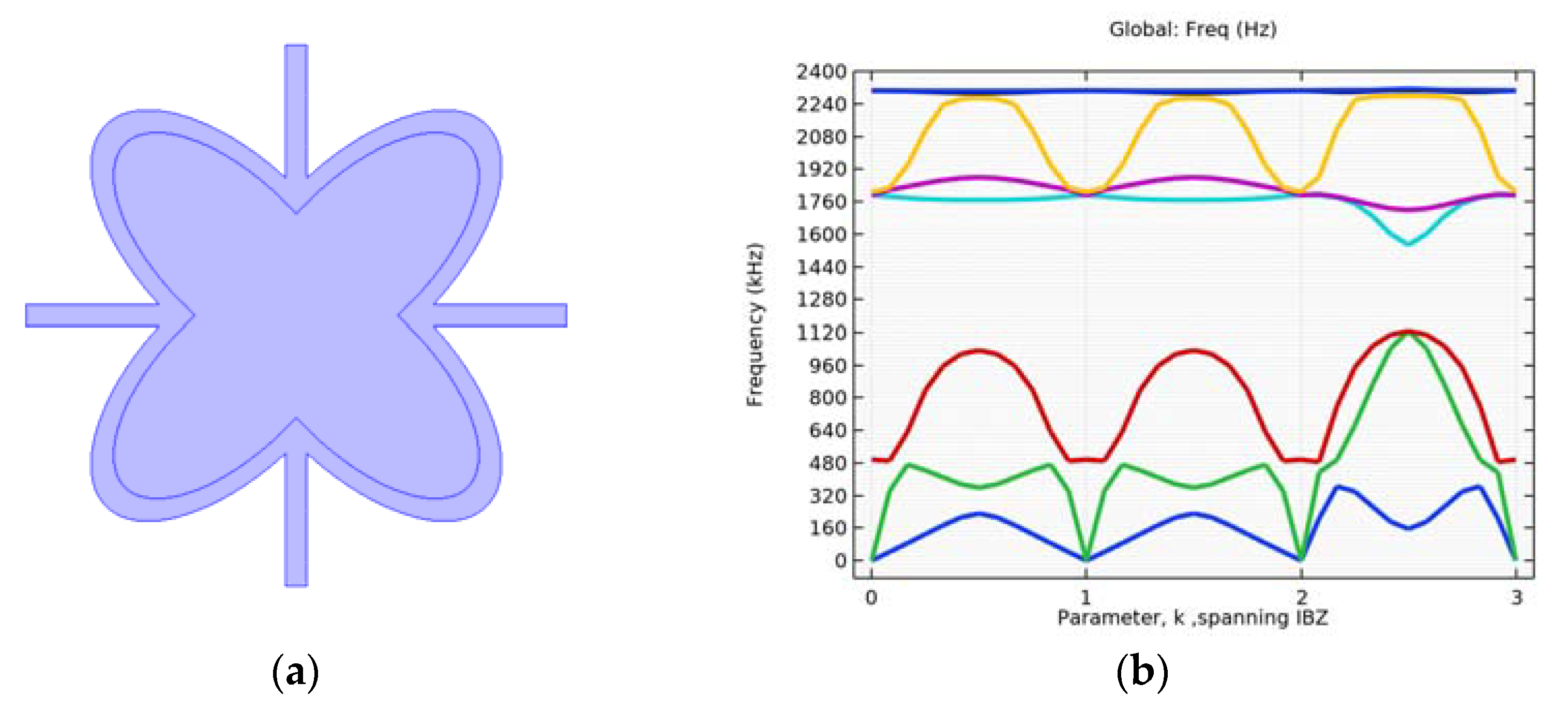
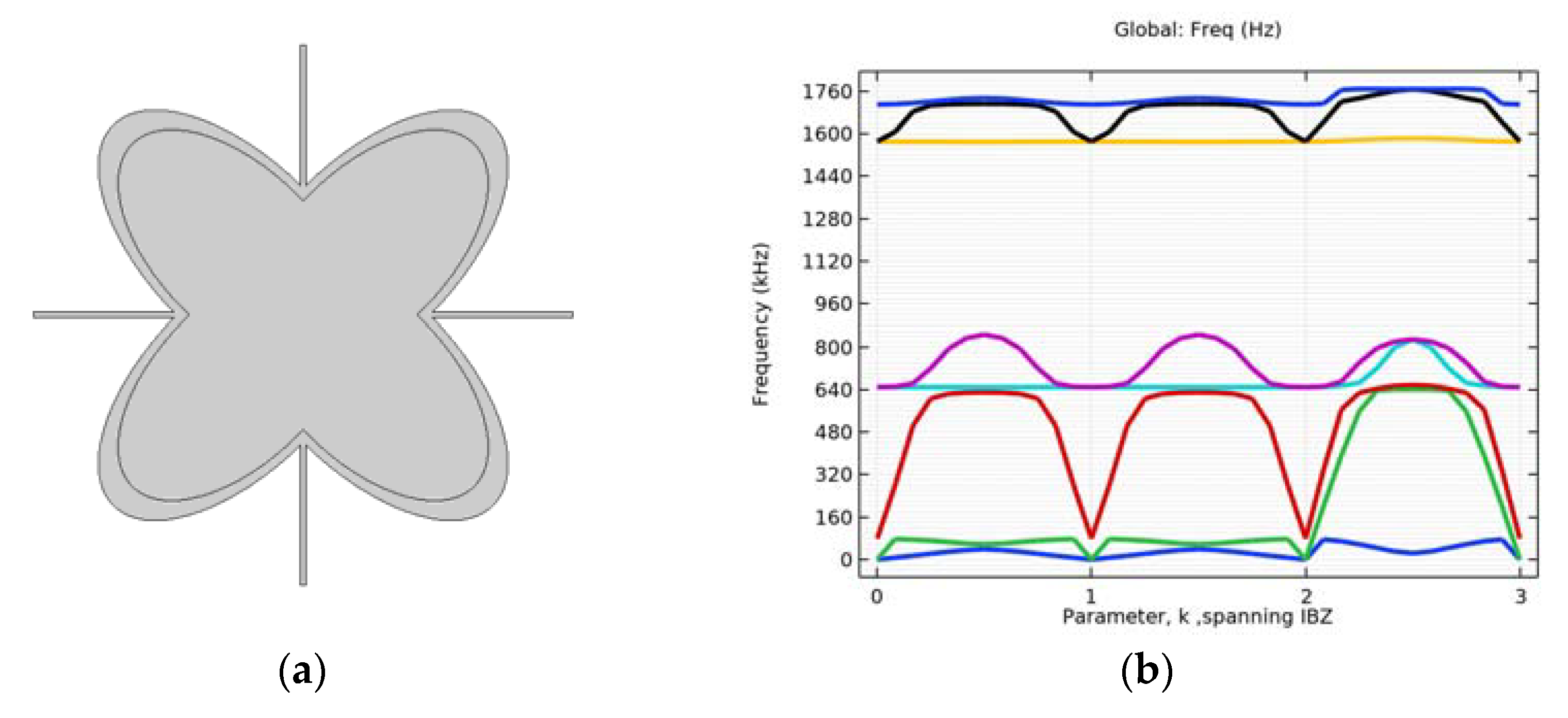
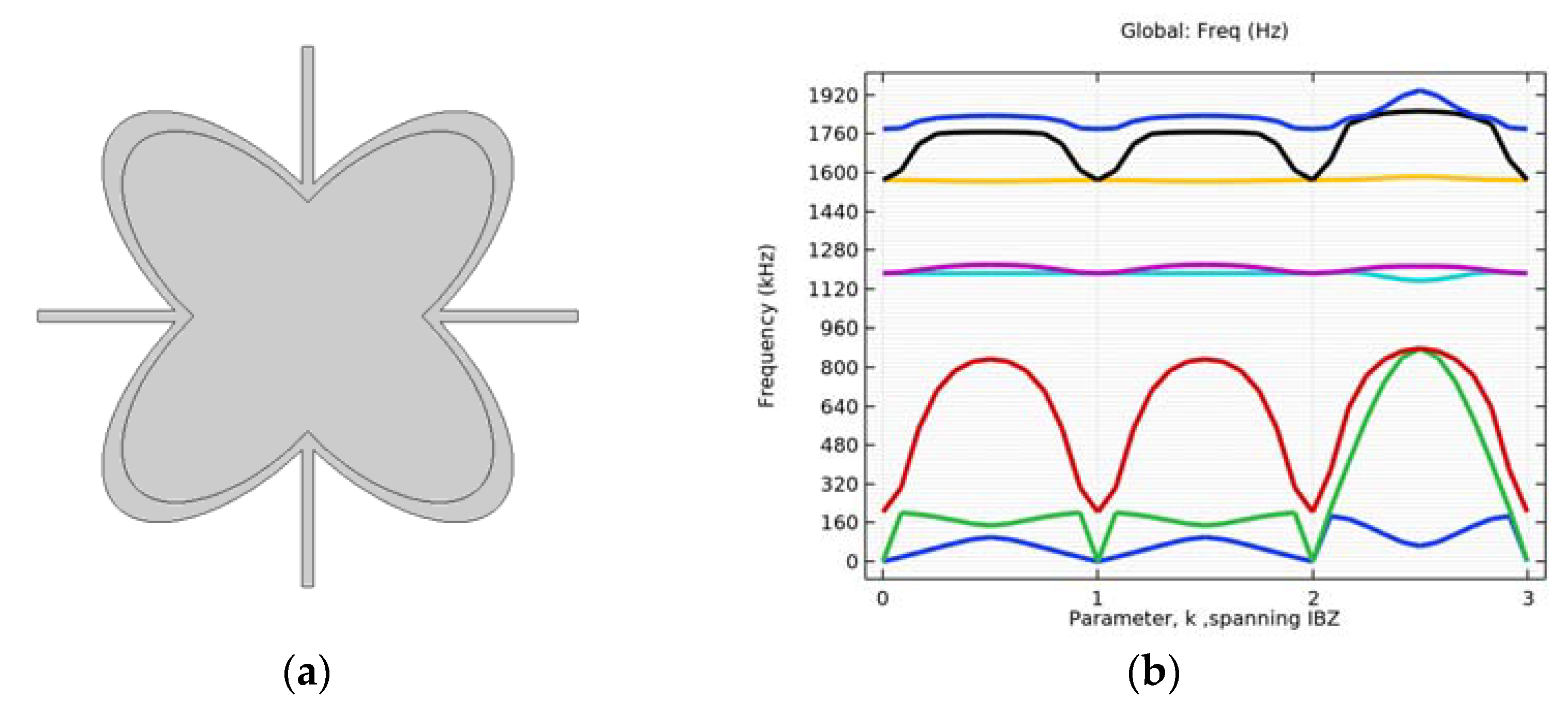
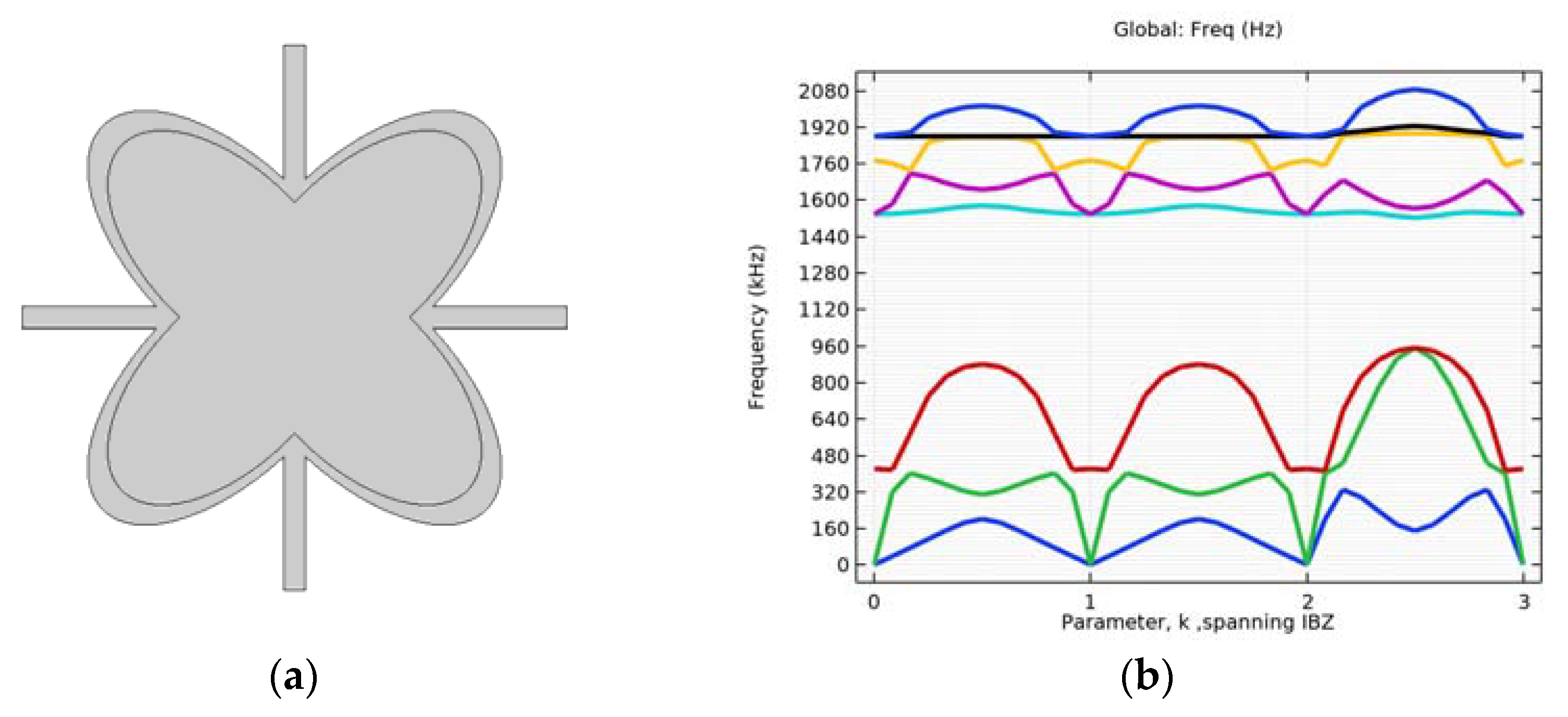
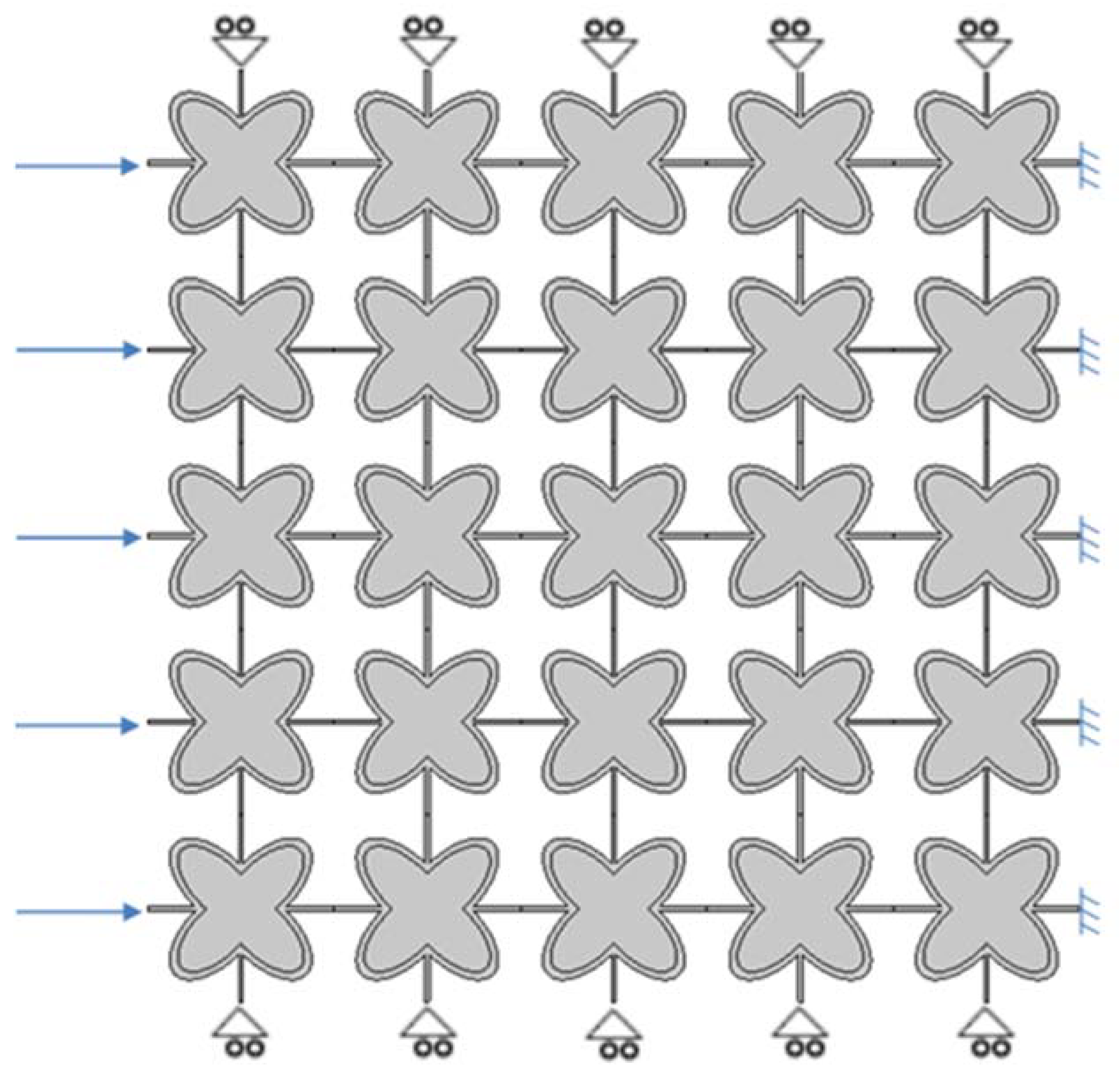

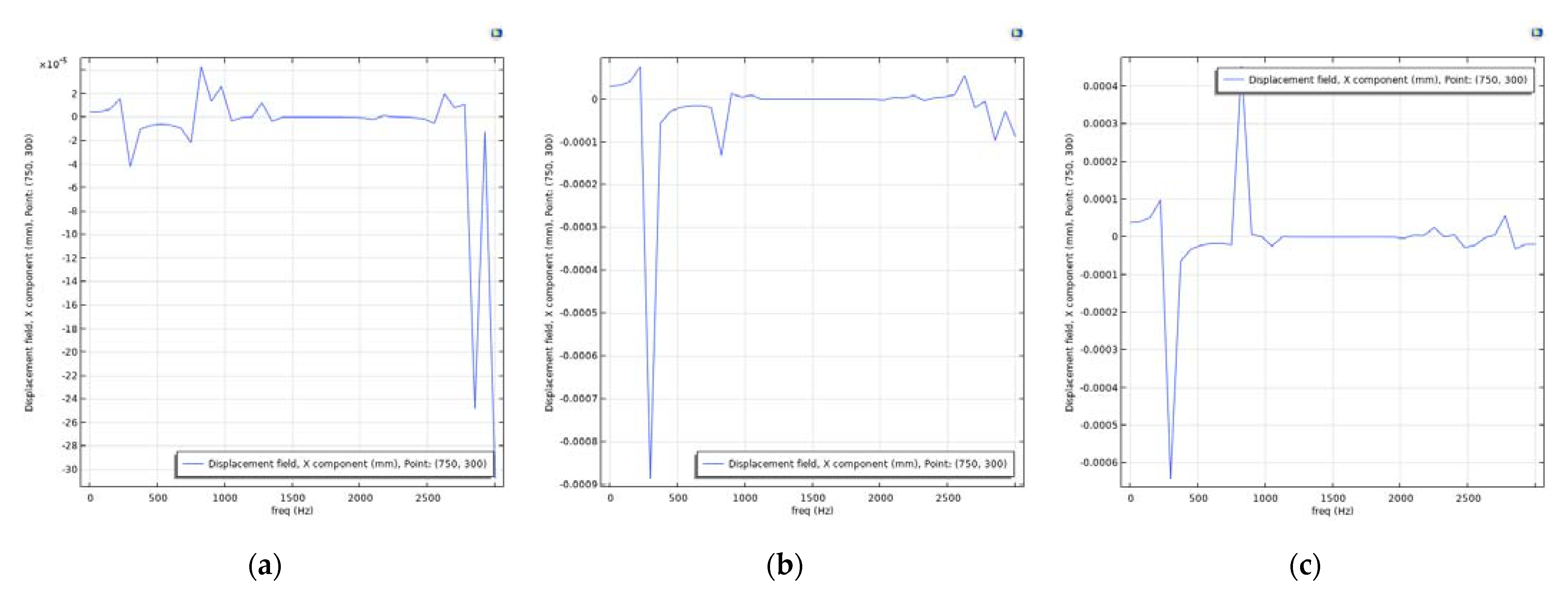

| Cartesian Coordinates | |
|---|---|
| Γ | (0,0) |
| Χ | (L1/2,0) |
| Μ | (L1/2, L1/2) |
| Material Name | Density | Poisson’s Ratio | Young’s Modulus |
|---|---|---|---|
| Material1 | 8000 kg/m3 | 0.34 | 2 × 1011 Pa |
| Material2 | 1000 kg/m3 | 0.45 | 2 × 109 Pa |
| Inner Ellipse 170 × 30 (mm) | Rod Thickness 3 mm | Rod Thickness 6 mm | Rod Thickness 12 mm |
|---|---|---|---|
| 1st bandgap | 5th–6th (1160–1800 Hz) | 5th–6th (1520–2400 Hz) | 3rd–4th (1720–2320 Hz) |
| 2nd bandgap | 7th–8th (1800–2460 Hz) | - | 7th–8th (2680–2700 Hz) |
| Inner Ellipse 170 × 60 (mm) | Rod Thickness 3 mm | Rod Thickness 6 mm | Rod Thickness 12 mm |
|---|---|---|---|
| 1st bandgap | 5th–6th (1120–1775 Hz) | 5th–6th (1440–1780 Hz) | 3rd–4th (1420–1680 Hz) |
| 2nd bandgap | 7th–8th (1805–1835 Hz) | - | - |
| Inner Ellipse 170 × 80 (mm) | Rod Thickness 3 mm | Rod Thickness 6 mm | Rod Thickness 12 mm |
|---|---|---|---|
| 1st bandgap | 5th–6th (970–1740 Hz) | 3rd–4th (1020–1240 Hz) | 3rd–4th (1050–1530 Hz) |
| 2nd bandgap | - | 5th–6th (1340–1680 Hz) | - |
| Inner Ellipse 170 × 90 (mm) | Rod Thickness 3 mm | Rod Thickness 6 mm | Rod Thickness 12 mm |
|---|---|---|---|
| 1st bandgap | 5th–6th (850–1570 Hz) | 3rd–4th (840–1160 Hz) | 3rd–4th (950–1530 Hz) |
| 2nd bandgap | - | 5th–6th (1220–1570 Hz) | - |
| Inner Ellipse 170 × 80 (mm) | Rod Thickness 6 mm | Rod Thickness 12 mm |
|---|---|---|
| 1st bandgap | 3rd–4th (1020–1240 Hz) | 3rd–4th (1050–1530 Hz) |
| 2nd bandgap | 5th–6th (1340–1680 Hz) | - |
| Inner Ellipse 170 × 40 and Circular Core | Rod Thickness 12 mm | Rod Thickness 15 mm |
|---|---|---|
| 1st bandgap | 3rd–4th (1710–2395 Hz) | 3rd–4th (1800–2540 Hz) |
| 2nd bandgap | - | 6th -7th (3185–3255 Hz) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chinis, D.; Stavroulakis, G.E. Band Gap Analysis for Materials with Cookie-Shaped Auxetic Microstructures, Using Finite Elements. Appl. Sci. 2023, 13, 2774. https://doi.org/10.3390/app13052774
Chinis D, Stavroulakis GE. Band Gap Analysis for Materials with Cookie-Shaped Auxetic Microstructures, Using Finite Elements. Applied Sciences. 2023; 13(5):2774. https://doi.org/10.3390/app13052774
Chicago/Turabian StyleChinis, Dimitrios, and Georgios E. Stavroulakis. 2023. "Band Gap Analysis for Materials with Cookie-Shaped Auxetic Microstructures, Using Finite Elements" Applied Sciences 13, no. 5: 2774. https://doi.org/10.3390/app13052774
APA StyleChinis, D., & Stavroulakis, G. E. (2023). Band Gap Analysis for Materials with Cookie-Shaped Auxetic Microstructures, Using Finite Elements. Applied Sciences, 13(5), 2774. https://doi.org/10.3390/app13052774








