Researching and Predicting the Flow Distribution of Herschel-Bulkley Fluids in Compact Parallel Channels
Abstract
:1. Introduction
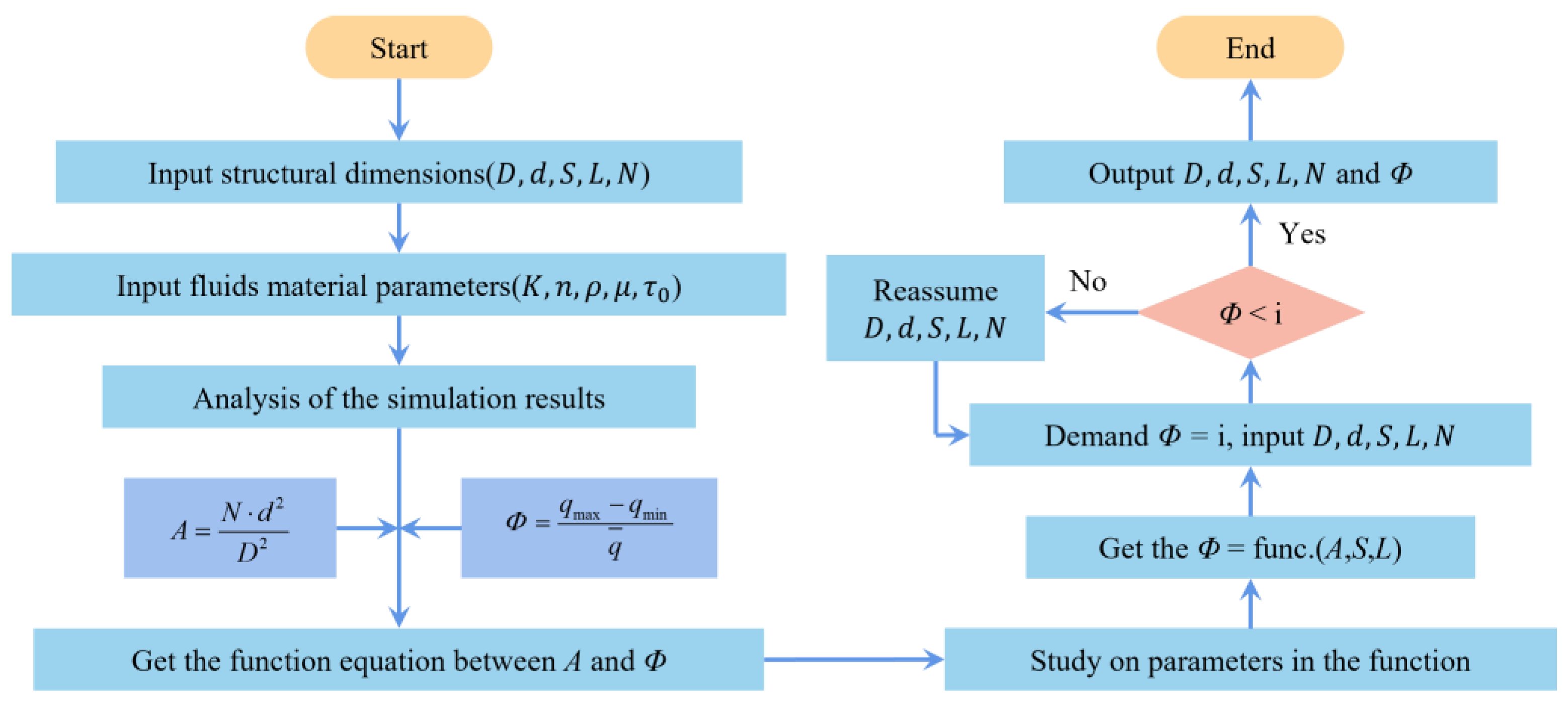
2. Physical Models
3. Numerical Simulation
3.1. The Influence of Inlet and Outlet Conditions and Structural Parameters
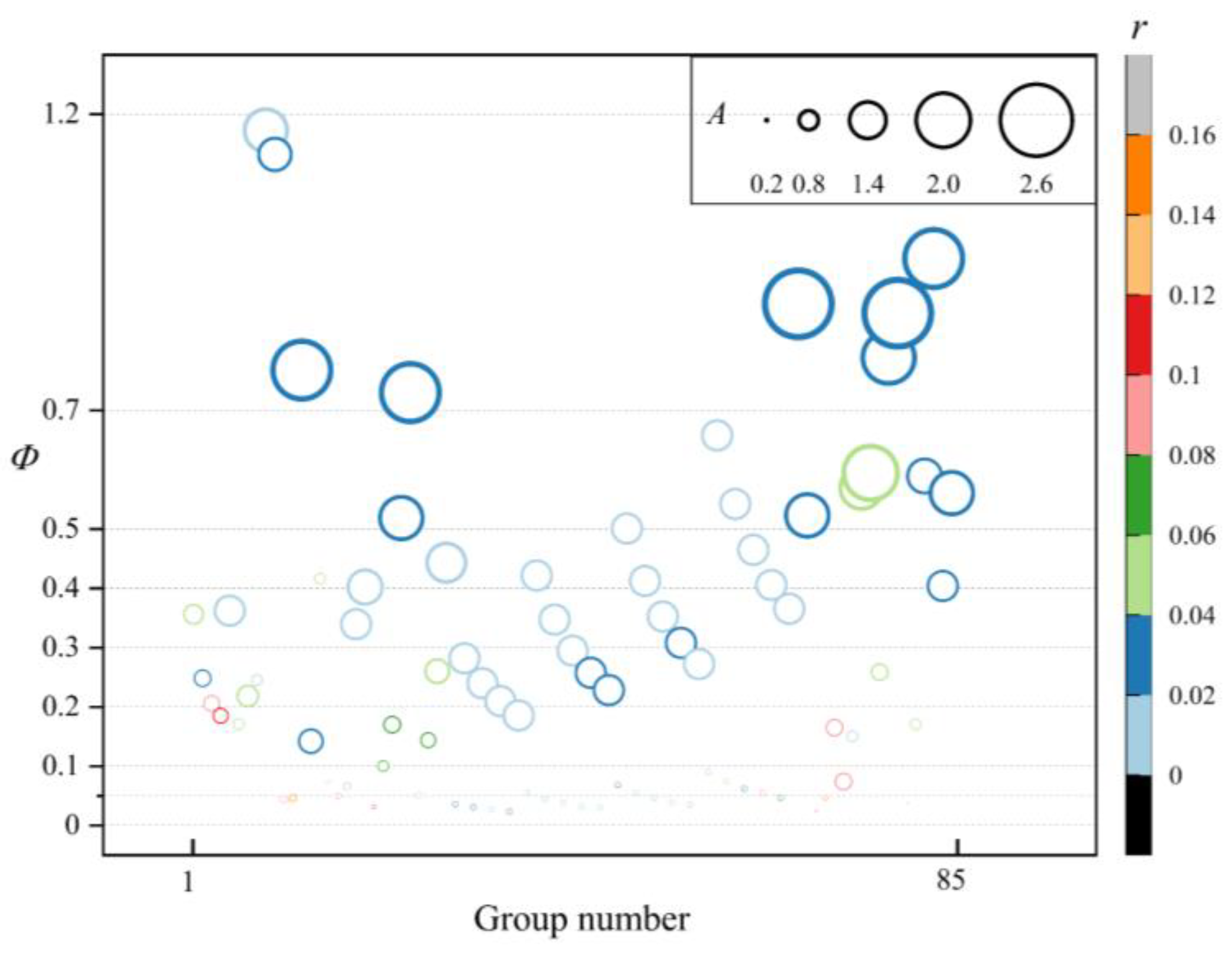
3.2. Prediction of the Influence of A, S, L on Φ Value
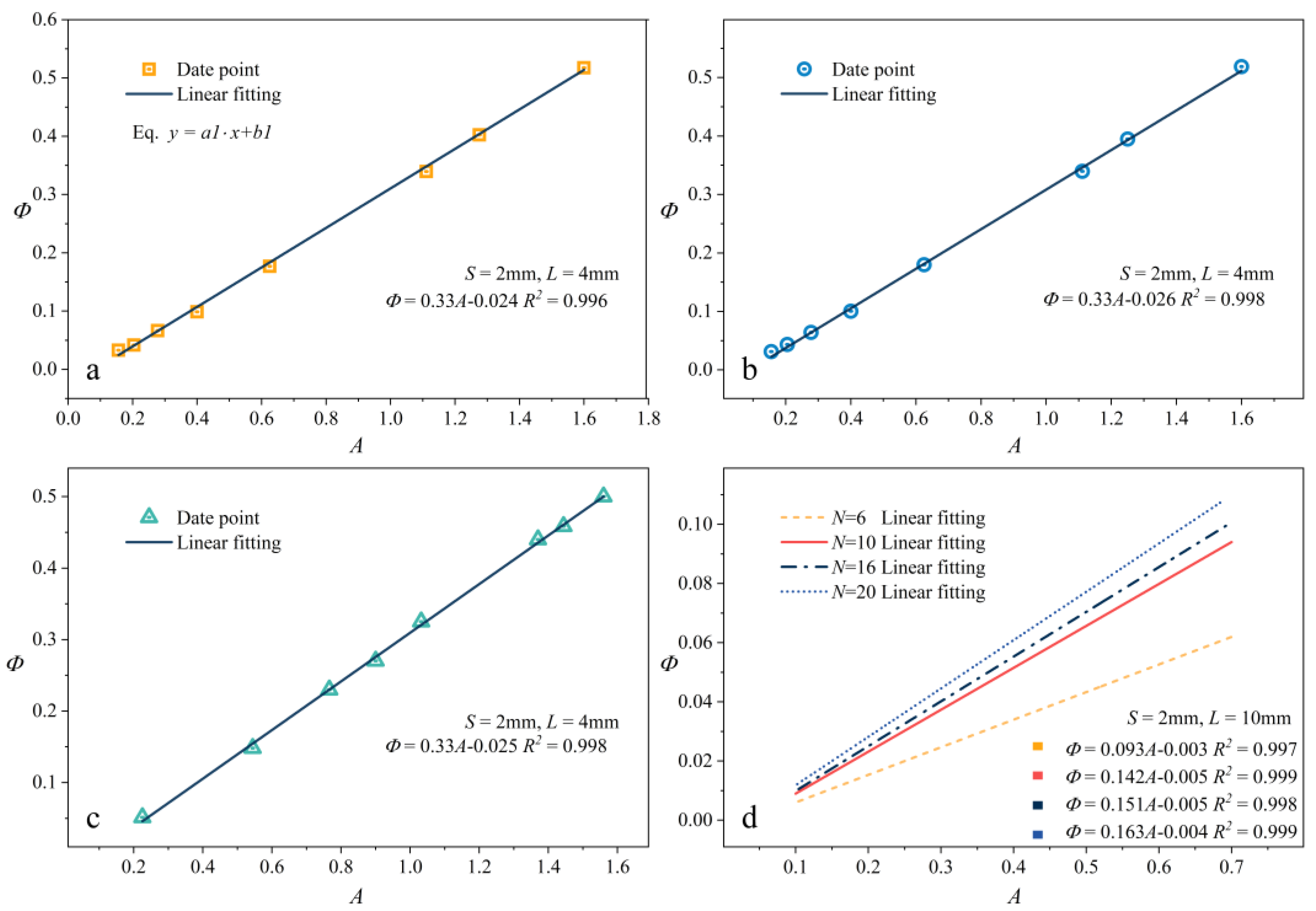
3.2.1. Study of the Functional Relationship between A and Φ
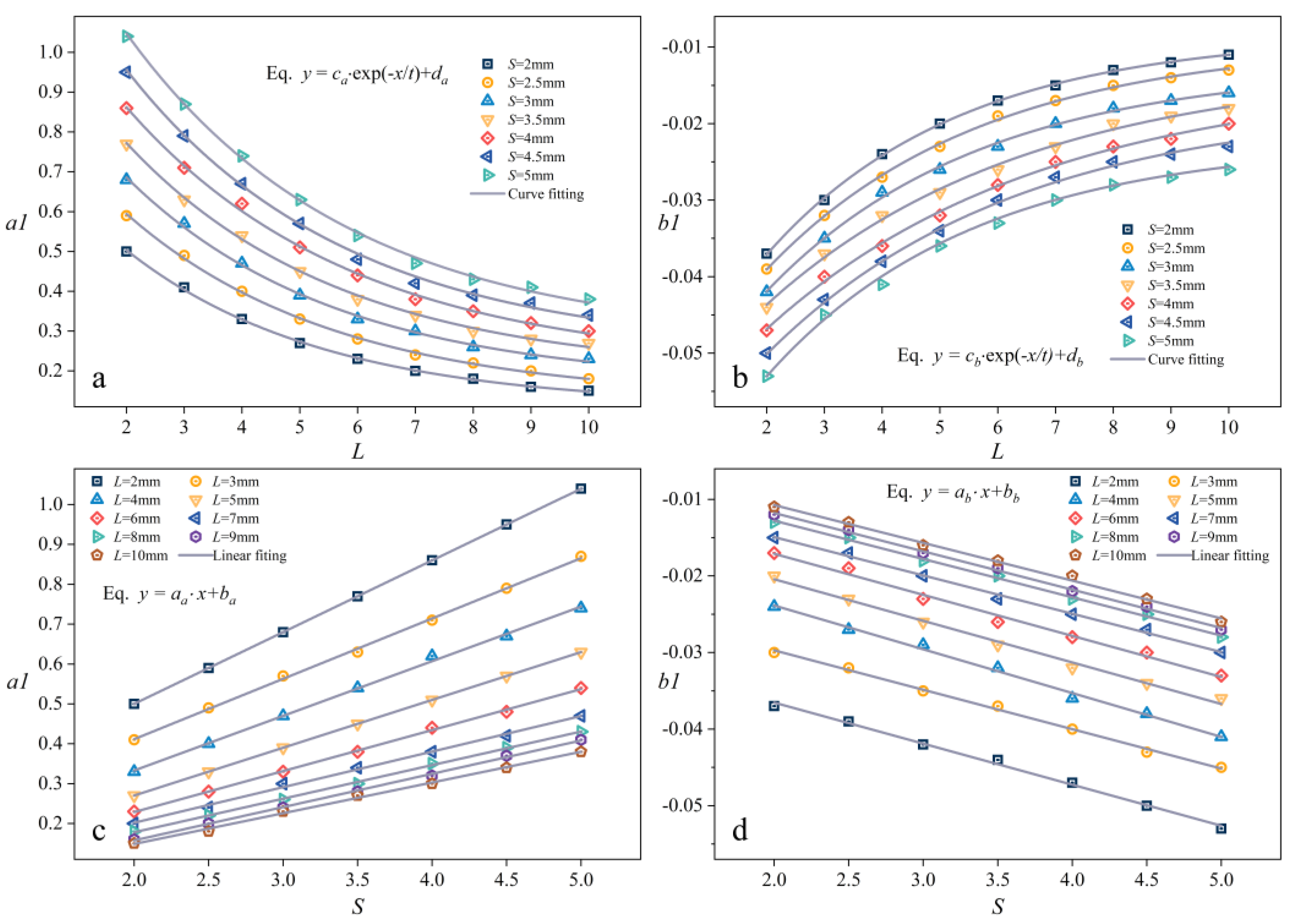
3.2.2. Study of the Functional Relationship between S, L, and Φ
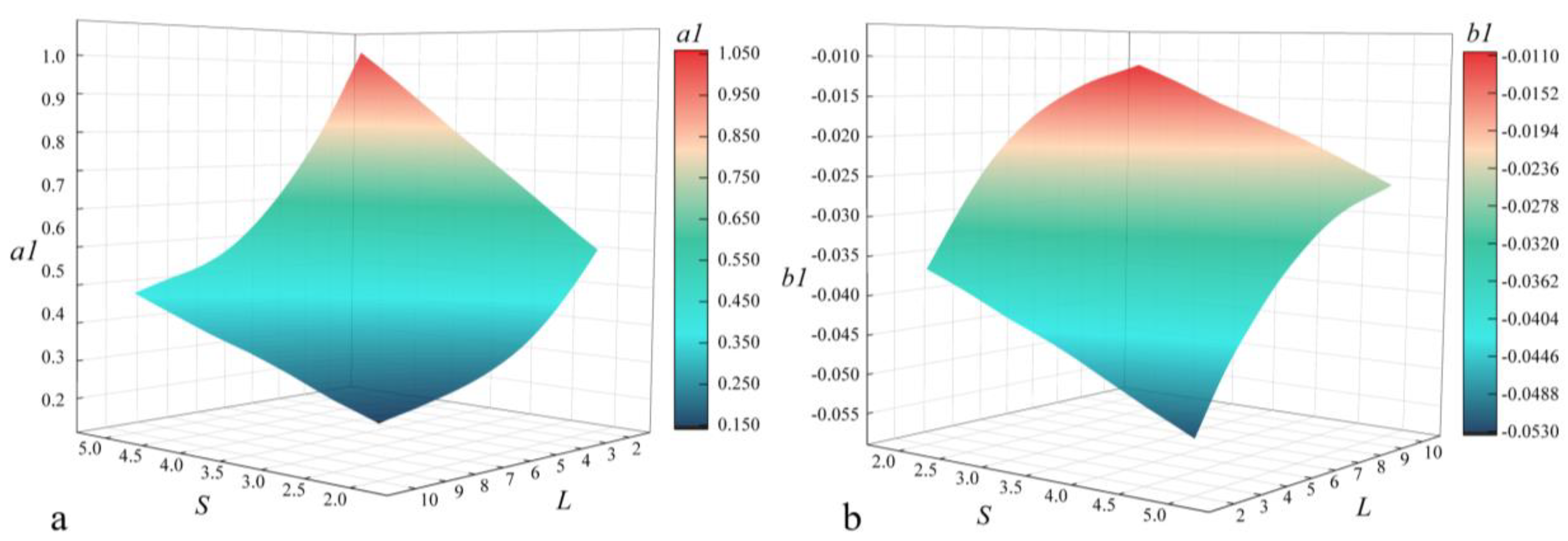
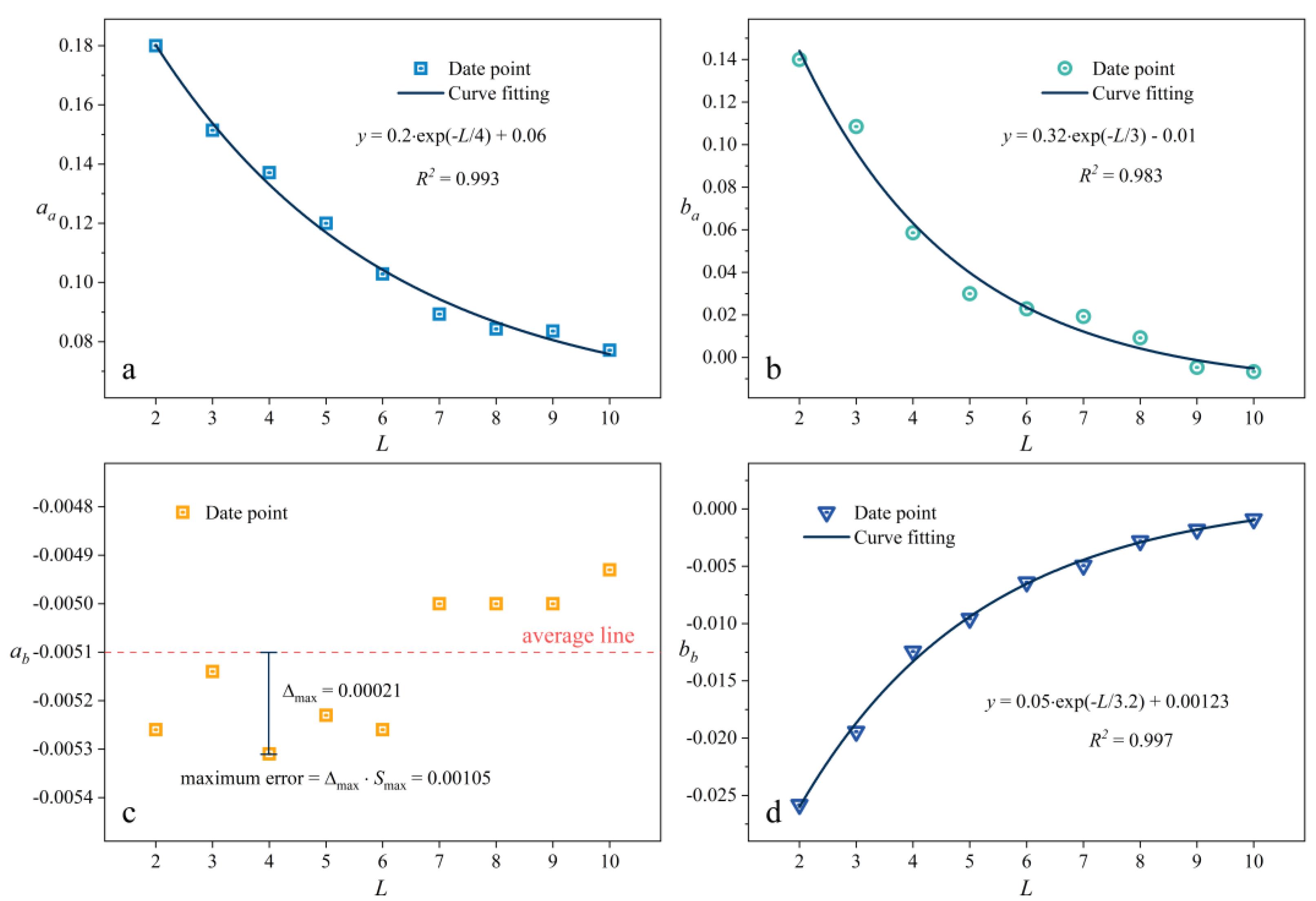
3.3. Prediction Model of Structural Parameters, A, S, and L, to Φ
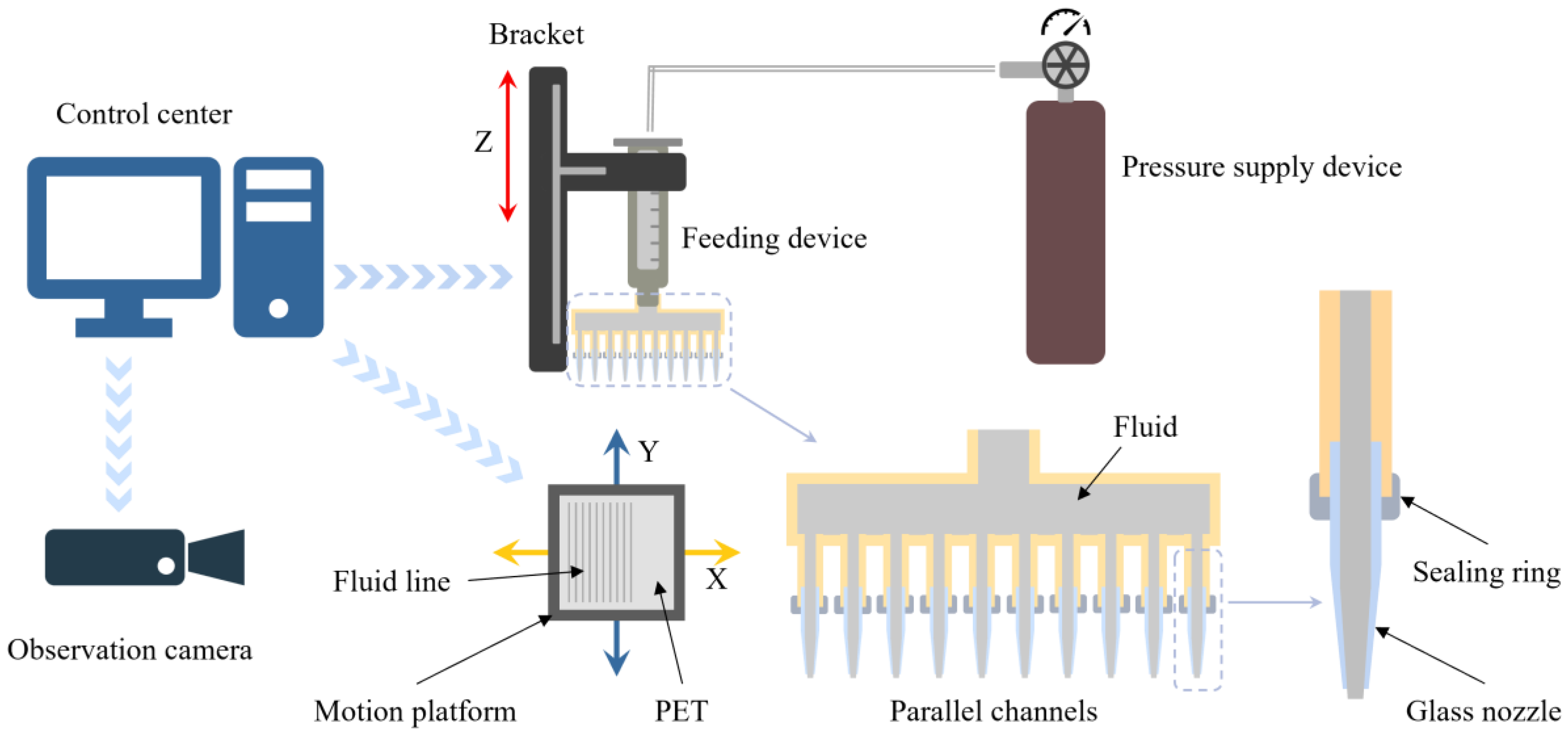
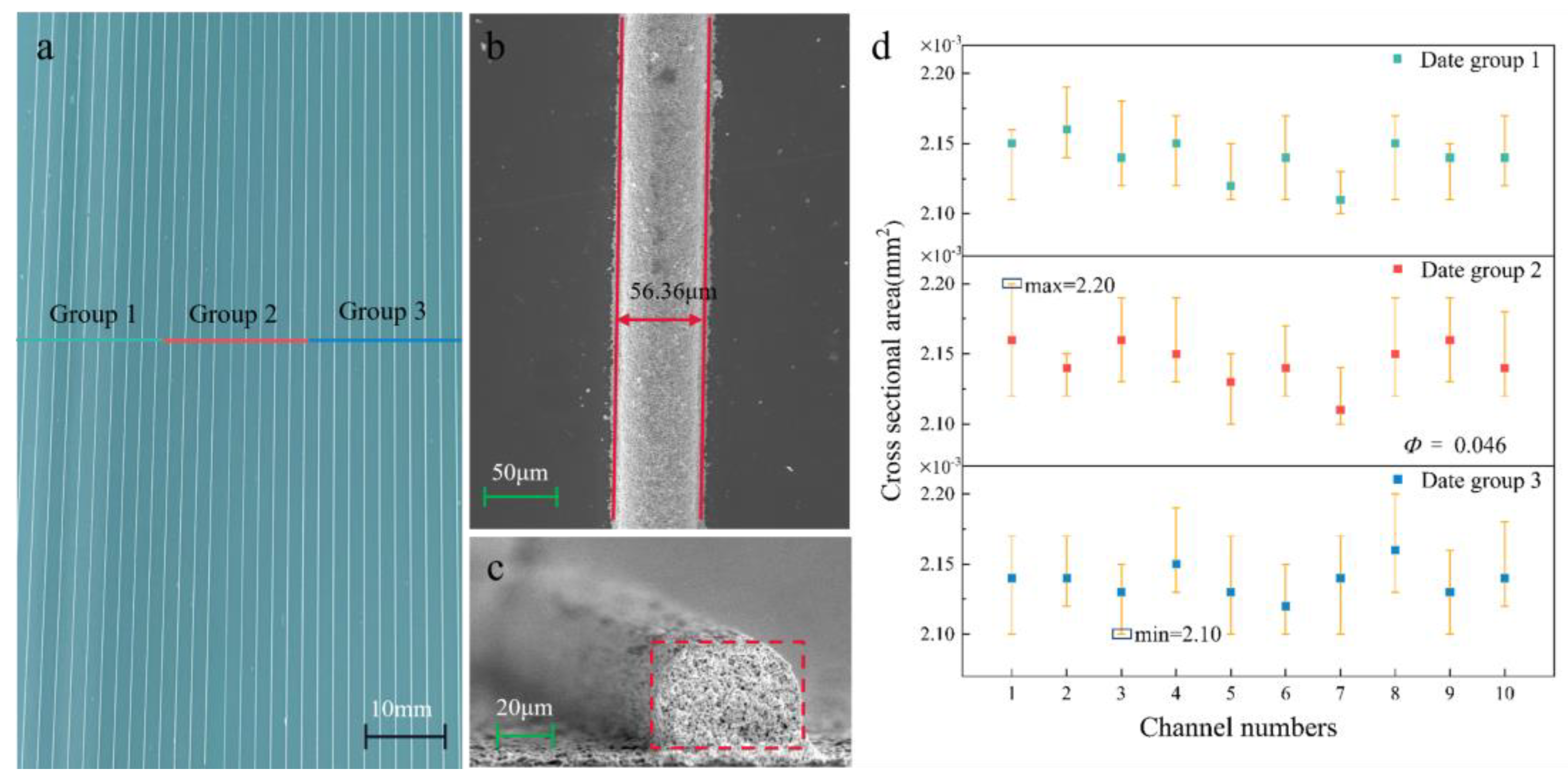
4. Experiment
5. Conclusions
- (1)
- When the Herschel-Bulkley fluid flows slowly in the compact parallel channels, within the parameter range of this study, changes in V and ∆P have negligible effects on the fluid flow distribution in the compact parallel channels, and V and ∆P have similar effects on the results of flow distribution, thus we can choose one inlet velocity (V) and inlet pressure (P) to study.
- (2)
- The maximum flow occurs in channels near the inlet and at the minimum flow occurs at the end of the cavity region. The flow decreases sequentially and the results are different from those of Newtonian fluids. In order to create uniform flow at each channel, the inlet diameter (D) and channel length (L) should be increased and the channel diameter (d) and channel spacing (S) should be reduced as much as possible within the specified dimensional parameters of the structure design. The strength of the effect on the uniform flow is: inlet diameter (D) > channel diameter (d) > channel length (L) ≈ channel spacing (S).
- (3)
- The non-uniformity flow coefficient (Φ) was defined to analyze the flow distribution in parallel channels, and the area ratio parameter (A) was defined to uniformly represent changes in the three parameters (N, D, d). According to Figure 10, Φ has a specific functional relationship with A, S, and L, which we can obtain by calculation. The functional relationship helps to design the compact parallel channel structure in order to achieve the specified flow difference.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

| Shear Rate | Sample Number | Herschel-Bulkley Model | |||||
|---|---|---|---|---|---|---|---|
| 0–13 s−1 | Sample1 | 10.28 | 64.52 | 0.51 | 5500 | 80 | |
| Sample2 | 9.85 | 60.58 | 0.54 | ||||
| Sample3 | 9.22 | 61.92 | 0.52 | ||||
| Sample4 | 10.90 | 65.63 | 0.49 | ||||
| Average | 10 | 63 | 0.52 |
Appendix C
References
- Beaucarne, G.; Schubert, G.; Tous, L.; Hoornstra, J. Summary of the 8th workshop on metallization and interconnection for crystalline silicon solar cells. J. Green Sustain. Technol. 2019, 2156, 020001. [Google Scholar]
- Oreski, G.; Stein, J.; Eder, G.; Berger, K.; Bruckman, L.S.; Vedde, J.; Weiss, K.A.; Tanahashi, T.; French, R.H.; Ranta, S. Designing New Materials for Photovoltaics: Opportunities for Lowering Cost and Increasing Performance through Advanced Material Innovations. United States. 2021. Available online: https://www.osti.gov/biblio/1779380 (accessed on 10 January 2023).
- Lossen, J.; Matusovsky, M.; Noy, A.; Maier, C.; Bähr, M. Pattern Transfer Printing (PTP™) for c-Si Solar Cell Metallization. J. Energy Procedia 2015, 67, 156–162. [Google Scholar] [CrossRef]
- Mayberry, R.; Chandrasekar, V. Metallization contributions, requirements, and effects related to pattern transfer printing (PTP™) on crystalline silicon solar cells. Int. Symp. Green Sustain. Technol. ISGST 2019, 2156, 020008. [Google Scholar]
- Schube, J.; Fellmeth, T.; Jahn, M.; Keding, R.; Glunz, S.W. Advanced Metallization with Low Silver Consumption for Silicon Heterojunction Solar Cells. Int. Symp. Green Sustain. Technol. ISGST 2019, 2156, 020007. [Google Scholar]
- Wehkamp, N.; Fell, A.; Bartsch, J.; Granek, F. Laser chemical metal deposition for silicon solar cell metallization. J. Energy Procedia 2012, 21, 47–57. [Google Scholar] [CrossRef]
- Specht, J.; Zengerle, K.; Pospischil, M.; Erath, D.; Haunschild, J.; Clement, F.; Biro, D. High Aspect Ratio Front Contacts by Single Step Dispensing of Metal Pastes. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 6–10 September 2010; pp. 1867–1870. [Google Scholar]
- Chen, X.; Church, K.; Yang, H. Highspeed non-contact printing for solar cell front side metallization. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 1343–1347. [Google Scholar]
- Chen, X.; Church, K.; Yang, H.; Cooper, I.B.; Rohatgi, A. Improved front side metallization for silicon solar cells by direct printing. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2012; pp. 003667–003671. [Google Scholar]
- Skylar-Scott, M.A.; Jochen, M.; Visser, C.W.; Jennifer, A.L. Voxelated soft matter via multimaterial multinozzle 3D printing. J. Nat. 2019, 575, 330–335. [Google Scholar] [CrossRef] [PubMed]
- Pospischil, M.; Riebe, T.; Jimenez, A.; Kuchler, M.; Tepner, S.; Geipel, T.; Ourinson, D.; Fellmeth, T.; Breitenbücher, M.; Buck, T.; et al. Applications of Parallel Dispensing in PV Metallization. Int. Symp. Green Sustain. Technol. ISGST 2019, 2156, 020005. [Google Scholar]
- Pospischil, M.; Kuchler, M.; Klawitter, M.; Rodríguez, C.; Padilla, M.; Efinger, R.; Linse, M.; Padilla, A.; Gentischer, H.; König, M.; et al. Dispensing Technology on the Route to an Industrial Metallization Process. J. Energy Procedia 2015, 67, 138–146. [Google Scholar] [CrossRef]
- Pospischil, M.; Klawitter, M.; Kuchler, M.; Specht, J.; Gentischer, H.; Efinger, R.; Kroner, C.; Luegmair, M.; König, M.; Hörteis, M.; et al. Process Development for a High-throughput Fine Line Metallization Approach Based on Dispensing Technology. J. Energy Procedia 2013, 43, 111–116. [Google Scholar] [CrossRef]
- Zemlyanaya, N.V.; Gulyakin, A.V. Analysis of Causes of Non-Uniform Flow Distribution in Manifold Systems with Variable Flow Rate along Length. J. Mater. Sci. Eng. 2017, 262, 012098. [Google Scholar]
- Lee, S.; Moon, N.; Lee, J. A study on the exit flow characteristics by the orifice configuration of multi-perforated tubes. J. Mech. Sci. Technol. 2012, 26, 2751–2758. [Google Scholar] [CrossRef]
- Junye, W. Theory of flow distribution in manifolds. Chem. Eng. J. 2011, 168, 1331–1345. [Google Scholar]
- Ke, H.; Lin, Y.; Ke, Z.; Xiao, Q.; Xu, H. Analysis Exploring the Uniformity of Flow Distribution in Multi-Channels for the Application of Printed Circuit Heat Exchangers. Symmetry 2020, 12, 314. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-C.; Yang, K.-S.; Tsai, J.-S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part I: Typical inlet header. J. Appl. Therm. Eng. 2011, 31, 3226–3234. [Google Scholar] [CrossRef]
- Wang, C.-C.; Yang, K.-S.; Tsai, J.-S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part II: Modified inlet header. J. Appl. Therm. Eng. 2011, 31, 3235–3242. [Google Scholar] [CrossRef]
- Wei, M.; Fan, Y.; Luo, L.; Flamant, G. CFD-based Evolutionary Algorithm for the Realization of Target Fluid Flow Distribution among Parallel Channels. J. Chem. Eng. Res. Des. 2015, 100, 341–352. [Google Scholar] [CrossRef]
- Zhang, W.; Li, A.; Gao, R.; Li, C. Effects of geometric structures on flow uniformity and pressure drop in dividing manifold systems with parallel pipe arrays. Int. J. Heat Mass Transf. 2018, 127, 870–881. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, P.; Shi, H.; Chen, Y.; Wang, Q. Prediction of flow maldistribution in printed circuit heat exchanger. Int. J. Heat Mass Transf. 2020, 152, 119560. [Google Scholar] [CrossRef]
- Camilleri, R.; Howey, D.; McCulloch, M. Predicting the flow distribution in compact parallel flow heat exchangers. J. Appl. Therm. Eng. 2015, 90, 551–558. [Google Scholar] [CrossRef]
- Cui, X.; Guo, J.; Huai, X.; Cheng, K.; Zhang, H.; Xiang, M. Numerical study on novel airfoil fins for printed circuit heat exchanger using supercritical CO2. Int. J. Heat Mass Transf. 2018, 121, 354–366. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Hu, Q.; Wang, W.; Xie, B.; Yu, X. Sloshing resistance and gas–liquid distribution performance in the entrance of LNG plate-fin heat exchangers. J. Appl. Therm. Eng. 2015, 82, 182–193. [Google Scholar] [CrossRef]
- Anbumeenakshi, C.; Thansekhar, M.R. Experimental investigation of header shape and inlet configuration on flow maldistribution in microchannel. J. Exp. Therm. Fluid Sci. 2016, 75, 156–161. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® 5.6. cn.comsol.com. Guangxi University, Nanning, China.
- Pigford, R.L.; Ashraf, M.; Miron, Y.D. Flow distribution in piping manifolds. J. Ind. Eng. Chem. Fundam. 1983, 22, 463–471. [Google Scholar] [CrossRef]
- Choi, S.H.; Shin, S.; Cho, Y.I. The effect of area ratio on the flow distribution in liquid cooling module manifolds for electronic packaging. J. Int. Commun. Heat Mass Transf. 1993, 20, 221–234. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Frigaard, I.A.; Ovarlez, G. Yielding to Stress: Recent Developments in Visco plastic Fluid Mechanics. J. Annu. Rev. Fluid Mech. 2014, 46, 121–146. [Google Scholar] [CrossRef]

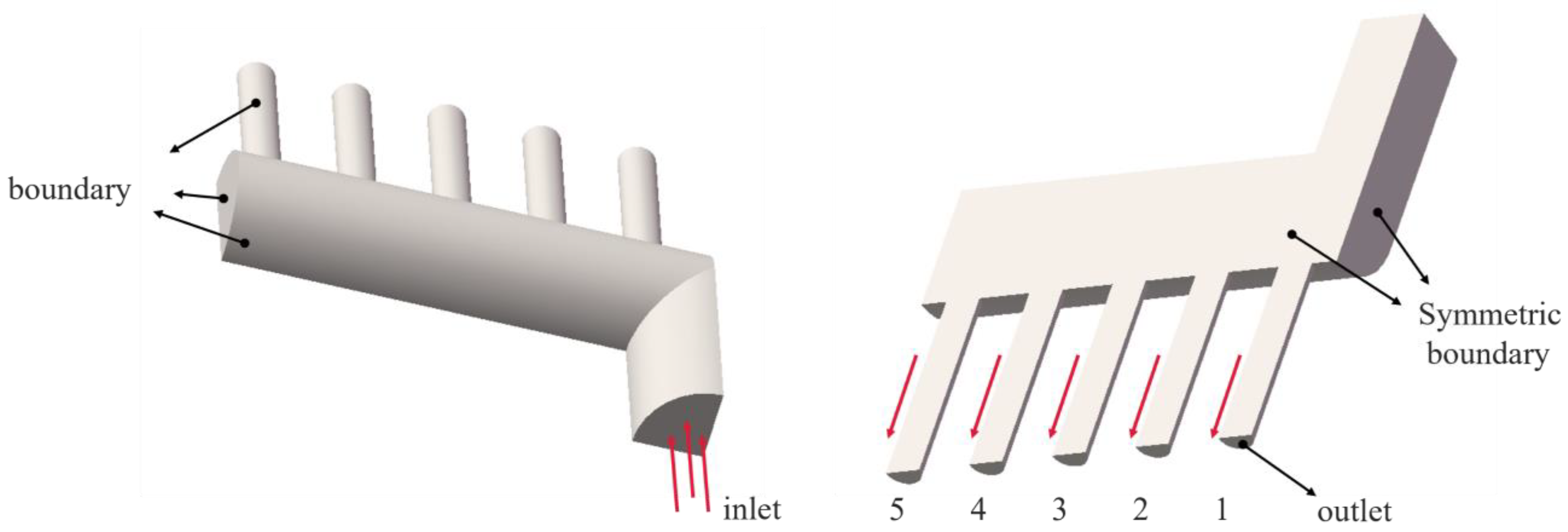
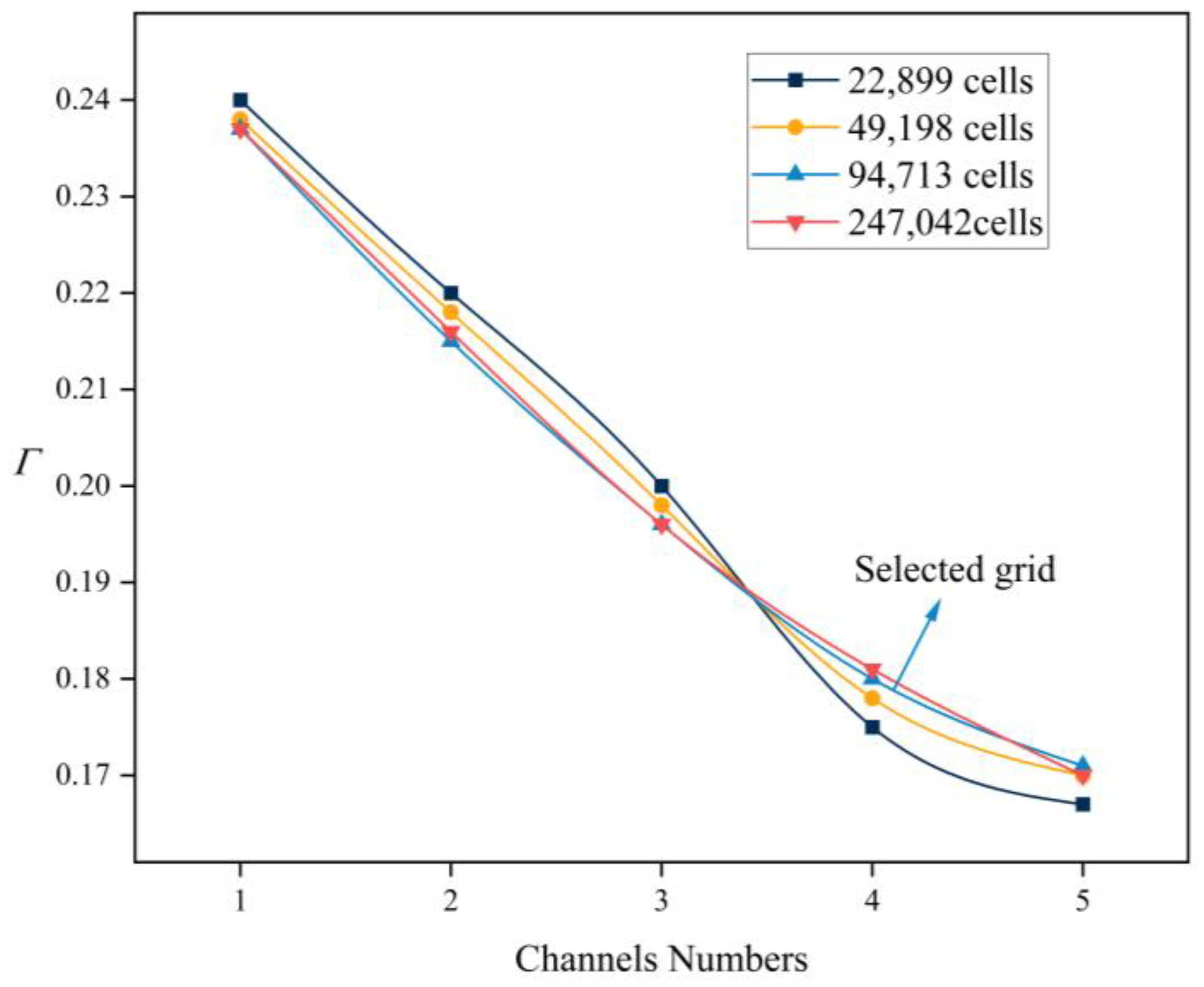
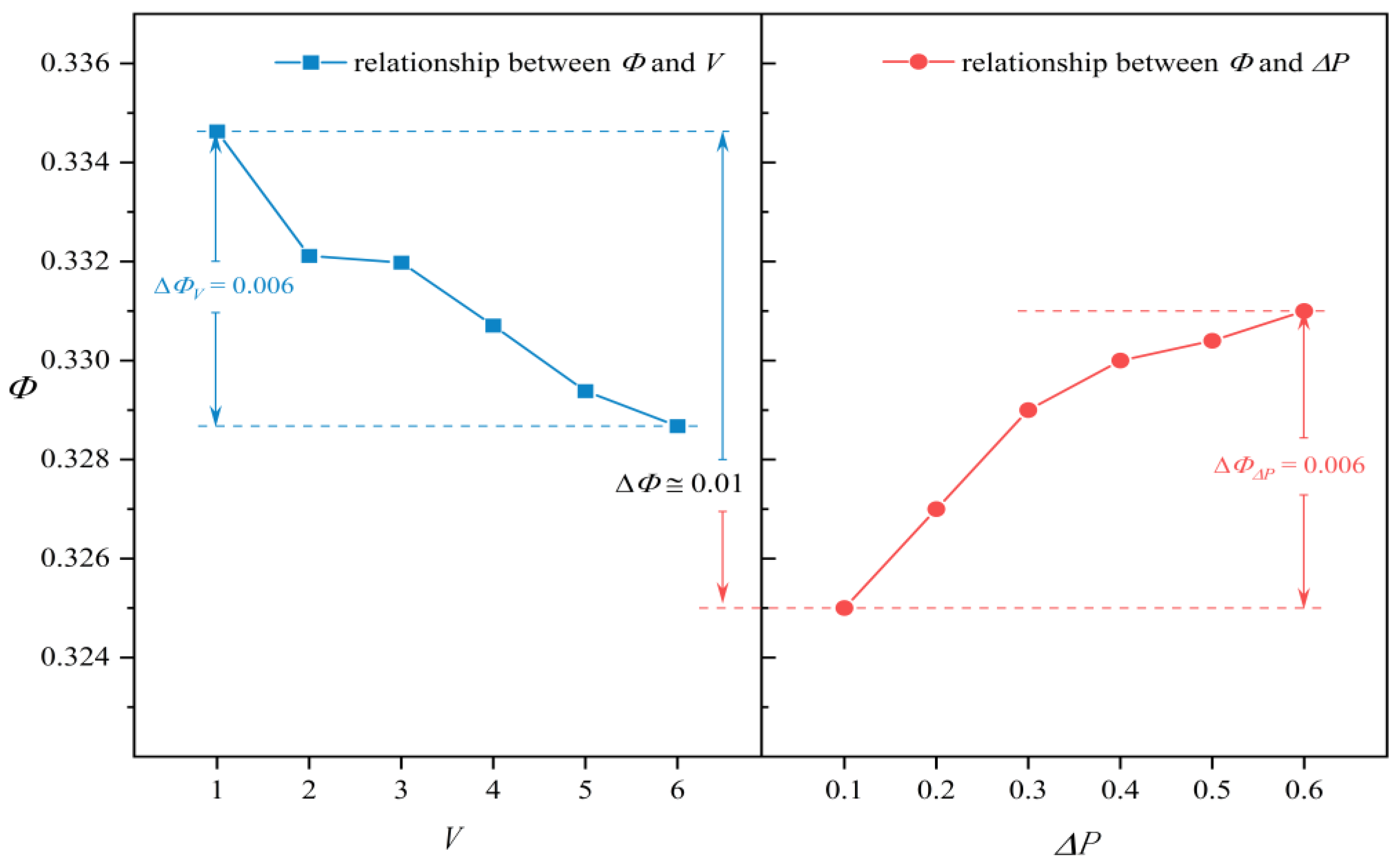
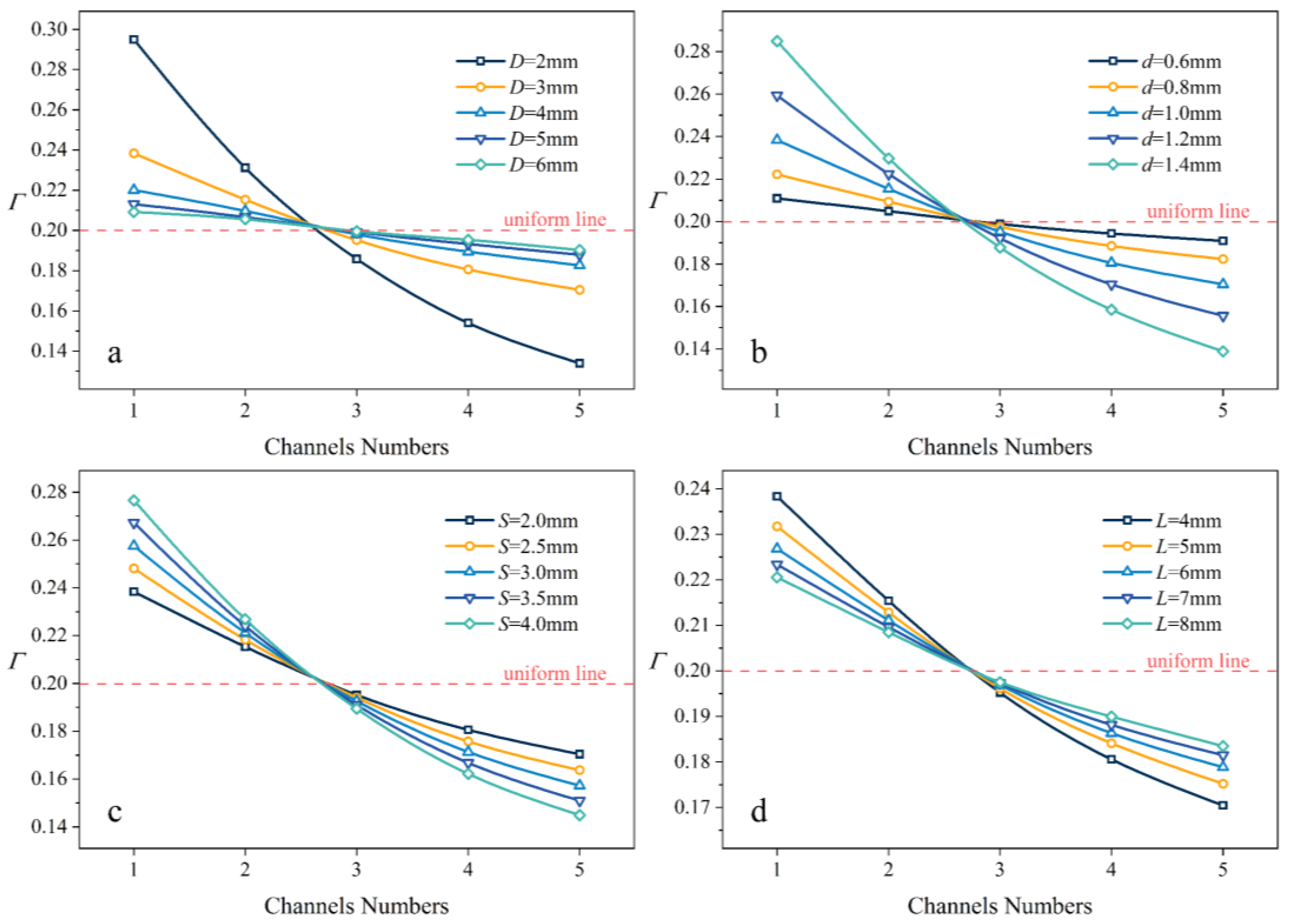
| Test Case | V [mm/s] | P2 [MPa] | D [mm] | d [mm] | S [mm] | L [mm] |
|---|---|---|---|---|---|---|
| 1 | [1:6:1] | 0.1 | 3 | 1 | 2 | 4 |
| 2 | 0 | ∆P [0.1:0.6:0.1] | 3 | 1 | 2 | 4 |
| 3 | 1 | 0.1 | [2:6:1] | 1 | 2 | 4 |
| 4 | 1 | 0.1 | 3 | [0.6:1.4:0.2] | 2 | 4 |
| 5 | 1 | 0.1 | 3 | 1 | [2:4:0.5] | 4 |
| 6 | 1 | 0.1 | 3 | 1 | 2 | [4:8:1] |
| Factor/Level | D | d | S | L |
|---|---|---|---|---|
| Inlet Diameter | Channel Diameter | Channel Spacing | Channel Length | |
| 1 | 3 | 0.8 | 2 | 2 |
| 2 | 4 | 1.0 | 3 | 4 |
| 3 | 5 | 1.2 | 4 | 6 |
| 4 | 6 | 1.4 | 5 | 8 |
| Factor | SS | df | MS | F |
|---|---|---|---|---|
| D | 0.663 | 3 | 0.221 | 2.027 |
| d | 0.405 | 3 | 0.135 | 1.239 |
| S | 0.210 | 3 | 0.070 | 0.643 |
| L | 0.285 | 3 | 0.095 | 0.870 |
| error | 0.327 | 3 | 0.109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wu, S.; Liu, Y.; Zhang, J.; Chen, Y.; Qin, Z.; Su, J.; Sun, C.; You, H. Researching and Predicting the Flow Distribution of Herschel-Bulkley Fluids in Compact Parallel Channels. Appl. Sci. 2023, 13, 2802. https://doi.org/10.3390/app13052802
Wang Z, Wu S, Liu Y, Zhang J, Chen Y, Qin Z, Su J, Sun C, You H. Researching and Predicting the Flow Distribution of Herschel-Bulkley Fluids in Compact Parallel Channels. Applied Sciences. 2023; 13(5):2802. https://doi.org/10.3390/app13052802
Chicago/Turabian StyleWang, Zedong, Shixiong Wu, Yaping Liu, Jinyu Zhang, Yuanfen Chen, Zhipeng Qin, Jian Su, Cuimin Sun, and Hui You. 2023. "Researching and Predicting the Flow Distribution of Herschel-Bulkley Fluids in Compact Parallel Channels" Applied Sciences 13, no. 5: 2802. https://doi.org/10.3390/app13052802






