Binaural Auralization of Room Acoustics with a Highly Scalable Wave-Based Acoustics Simulation
Abstract
:1. Introduction
2. Theory
2.1. Massively Parallel Room Acoustics Solver
2.1.1. Dispersion-Optimized Explicit TD-FEM
2.1.2. DDM-Based Parallel Computation
2.2. Binaural Auralization Based on Ambisonics and HRTF
2.3. Expansion Coefficient Calculation via Spatial Differentiation of the FE Shape Function
3. Scalability of Wave-Based Room-Acoustics Solver on an HPC Cloud Environment
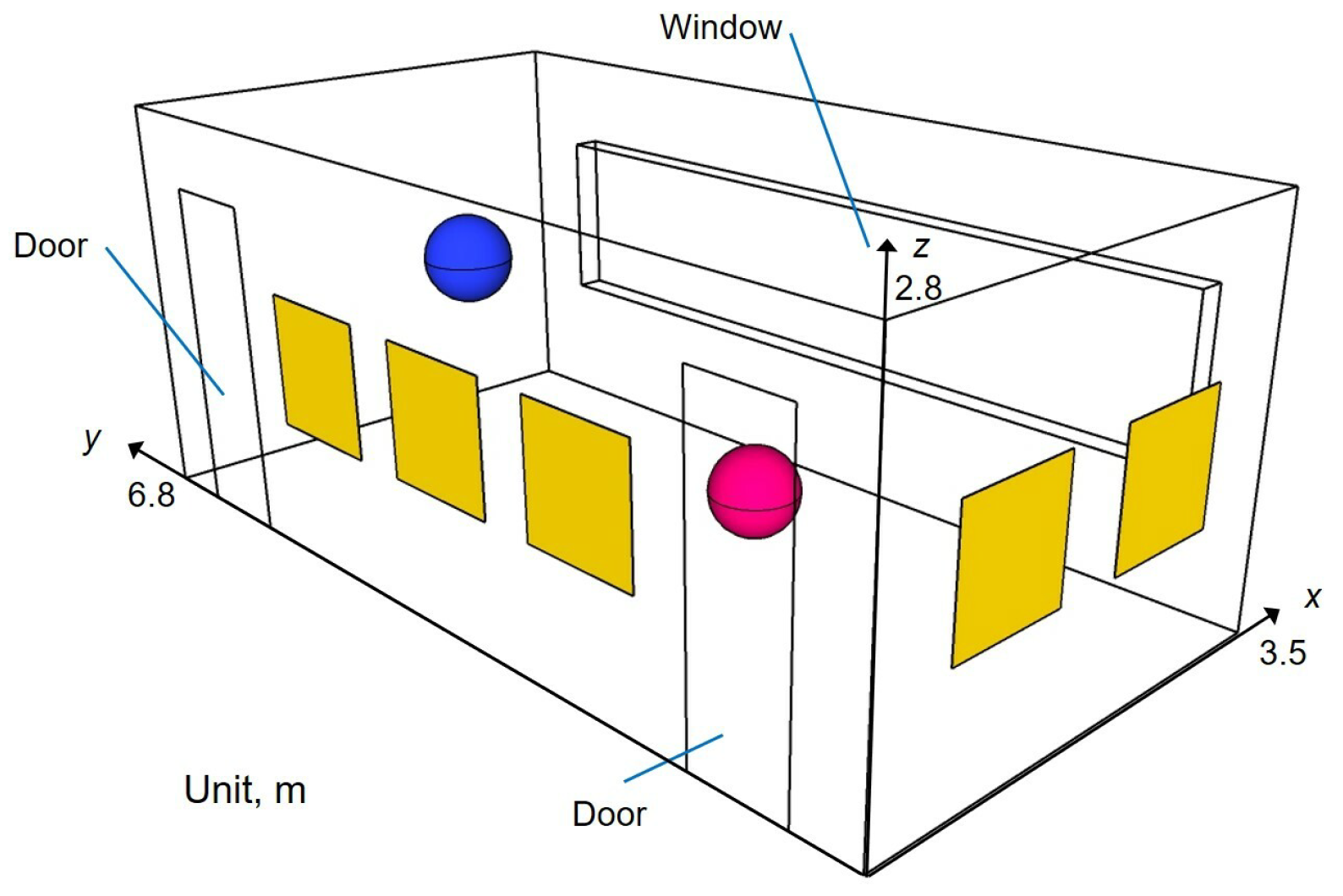
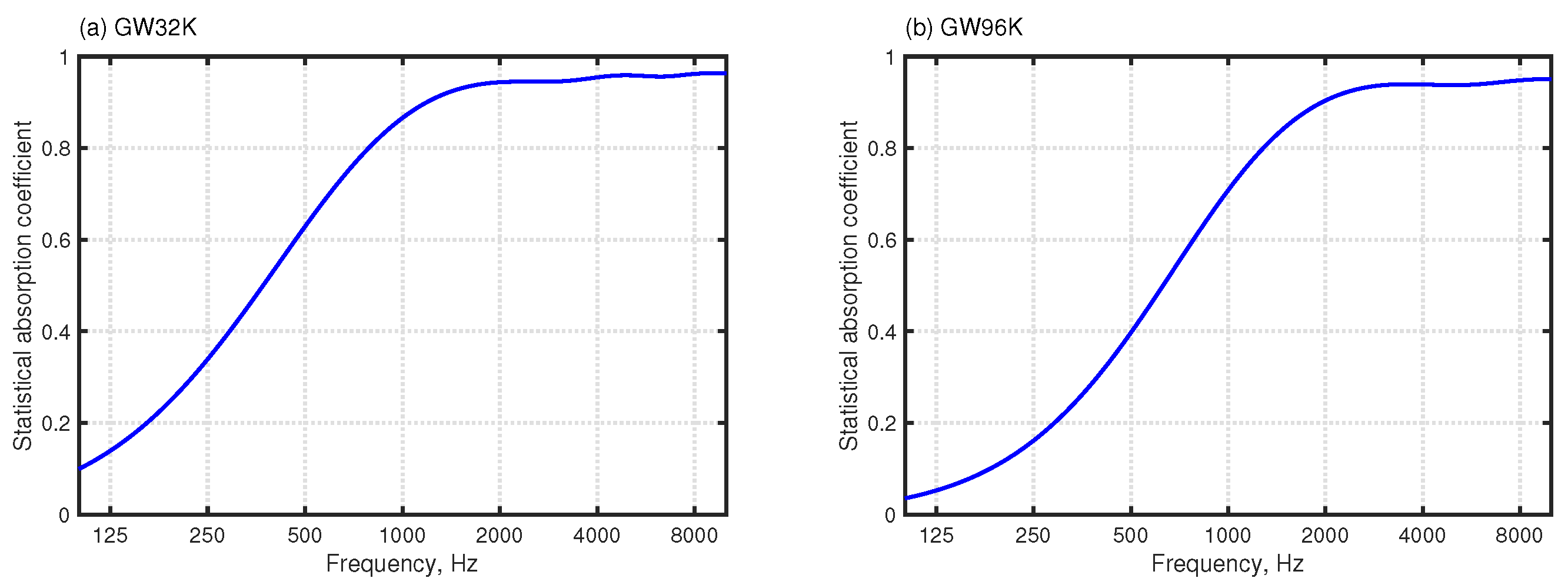
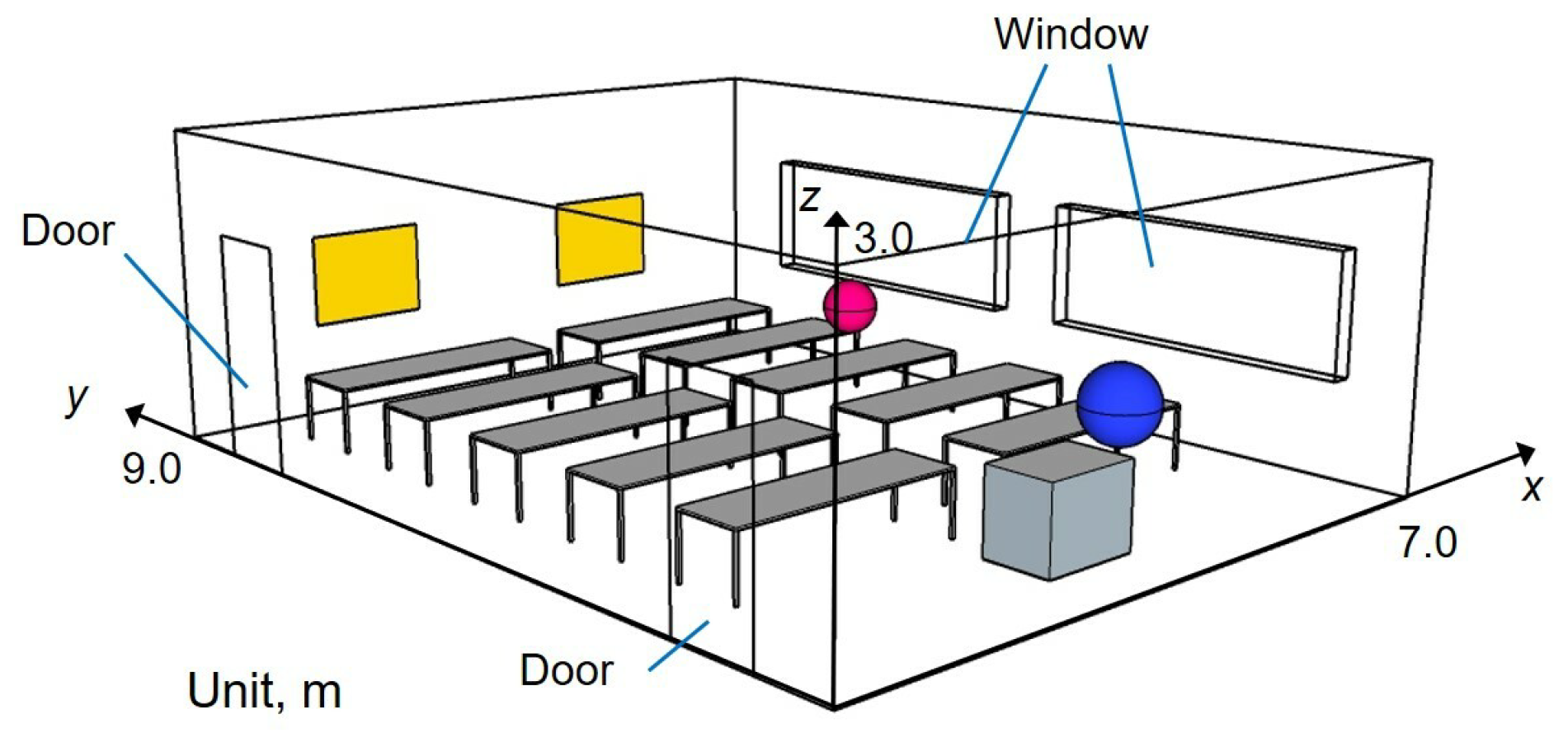
3.1. Two Room-Acoustics Problems
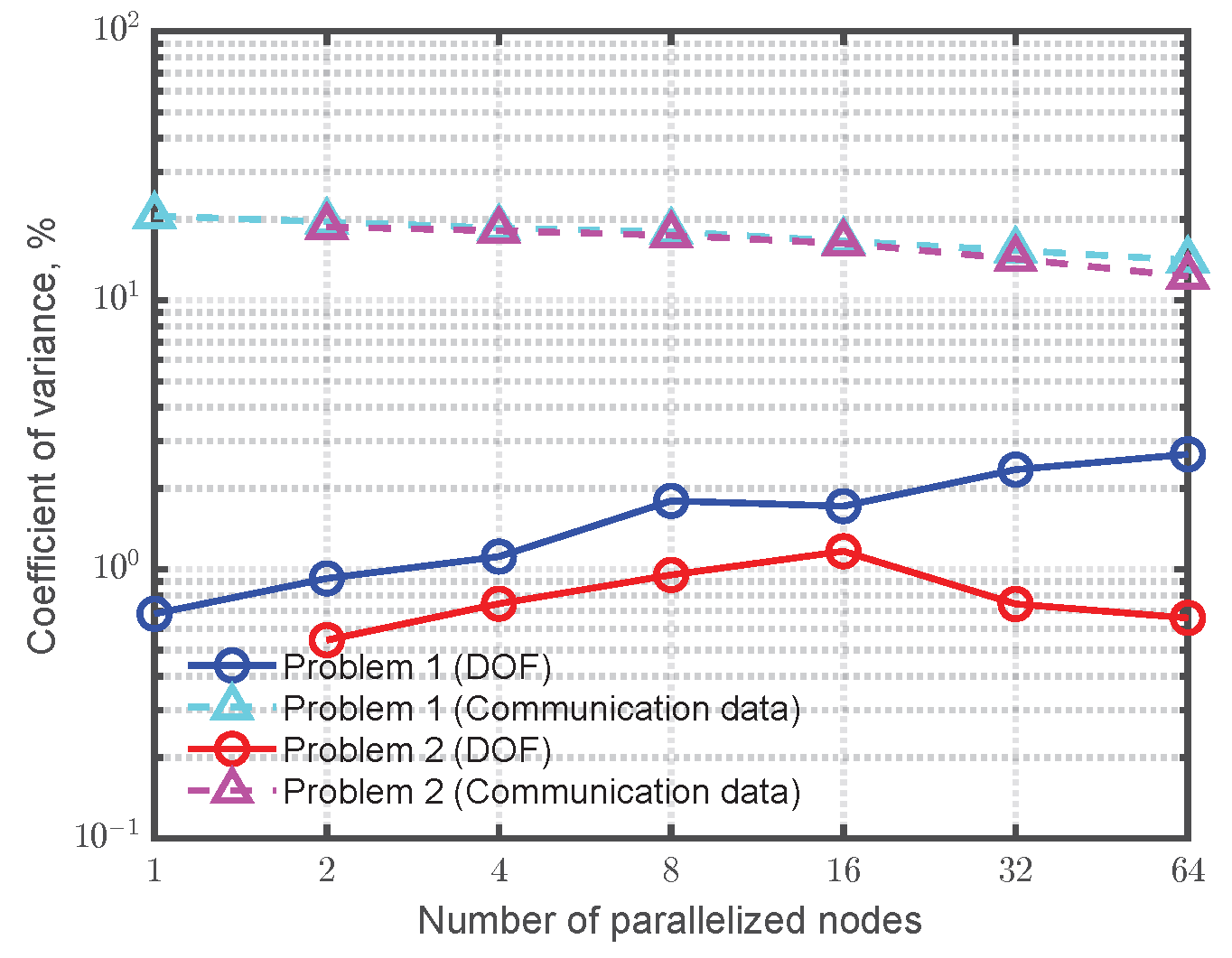
3.2. Computation Setting and Evaluation Index
3.3. Results and Discussion
4. Binaural Room-Acoustics Auralization in a Large-Scale Auditorium
4.1. Analyzed Model and Computation Setting
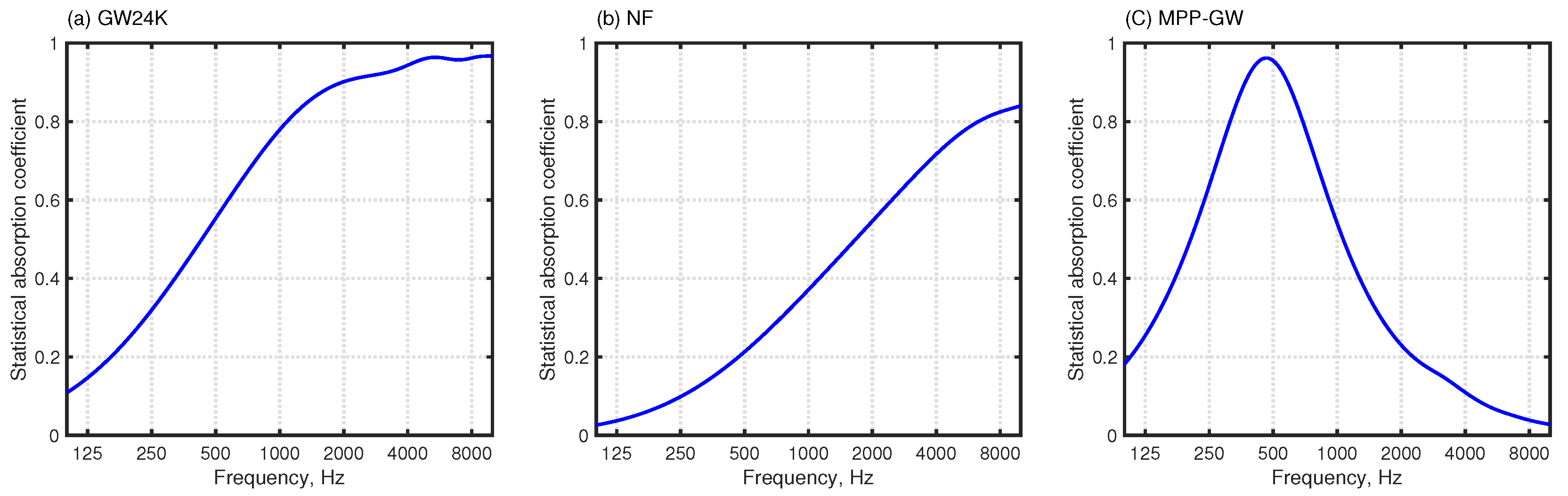
Consideration of Air Absorption
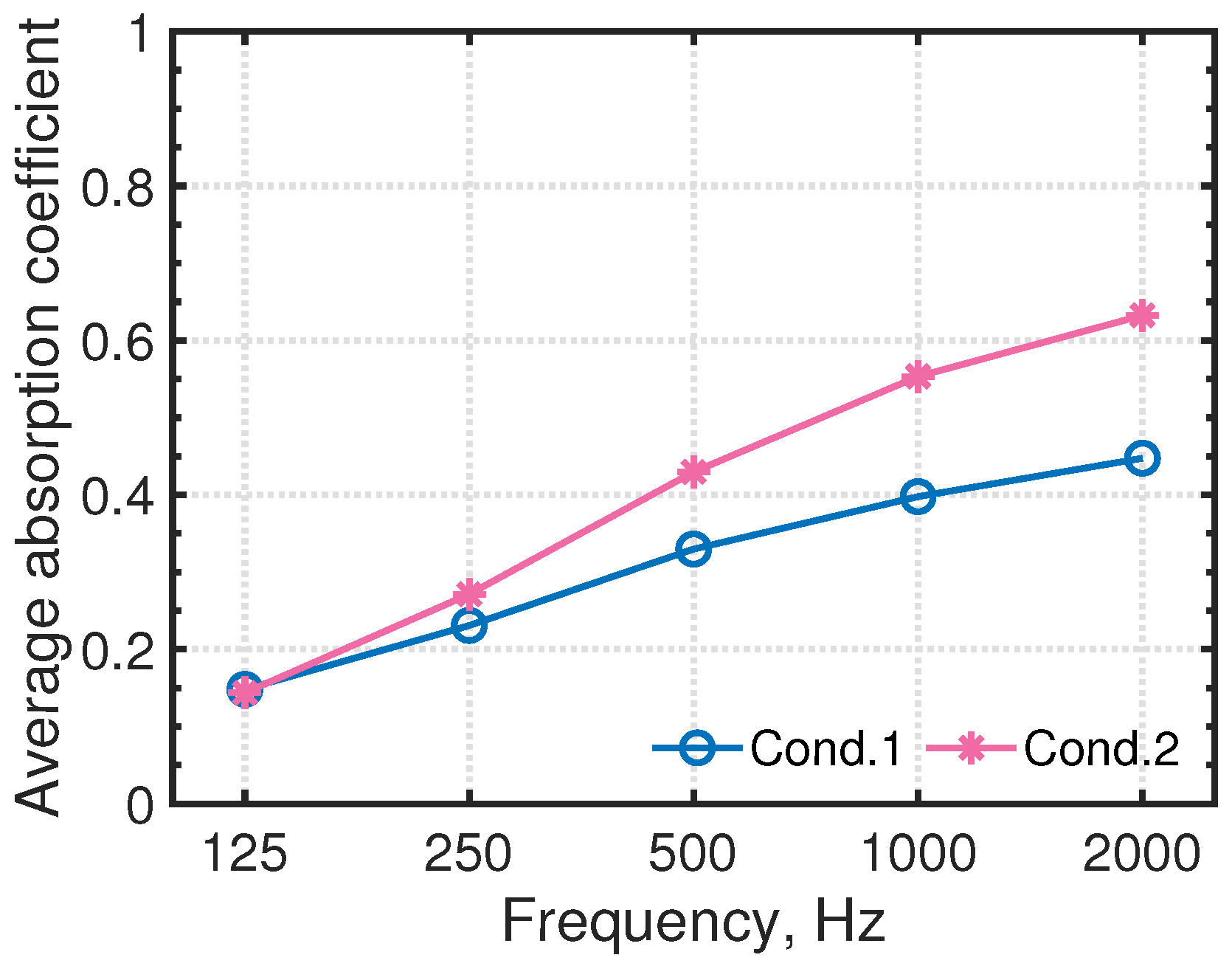
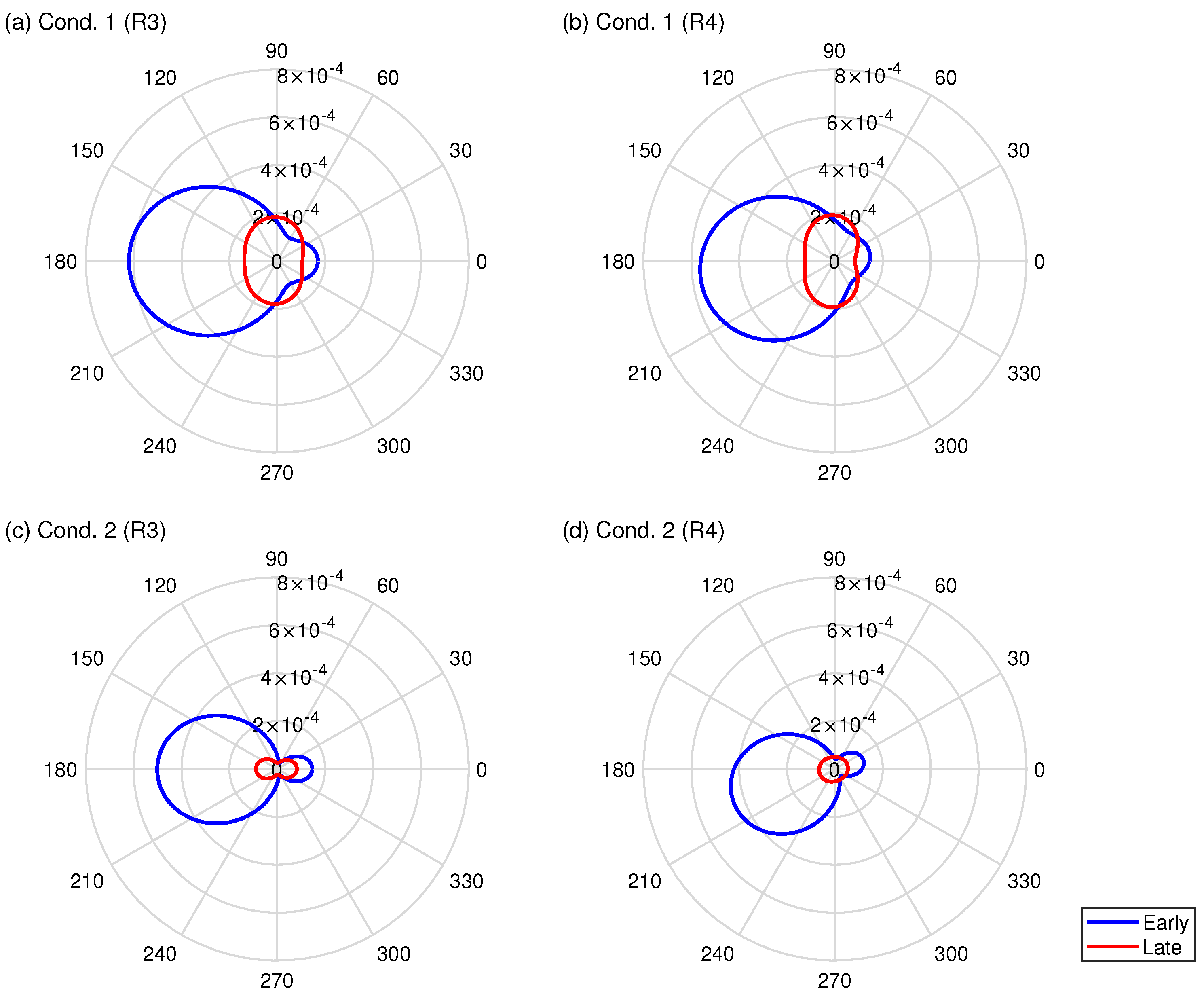
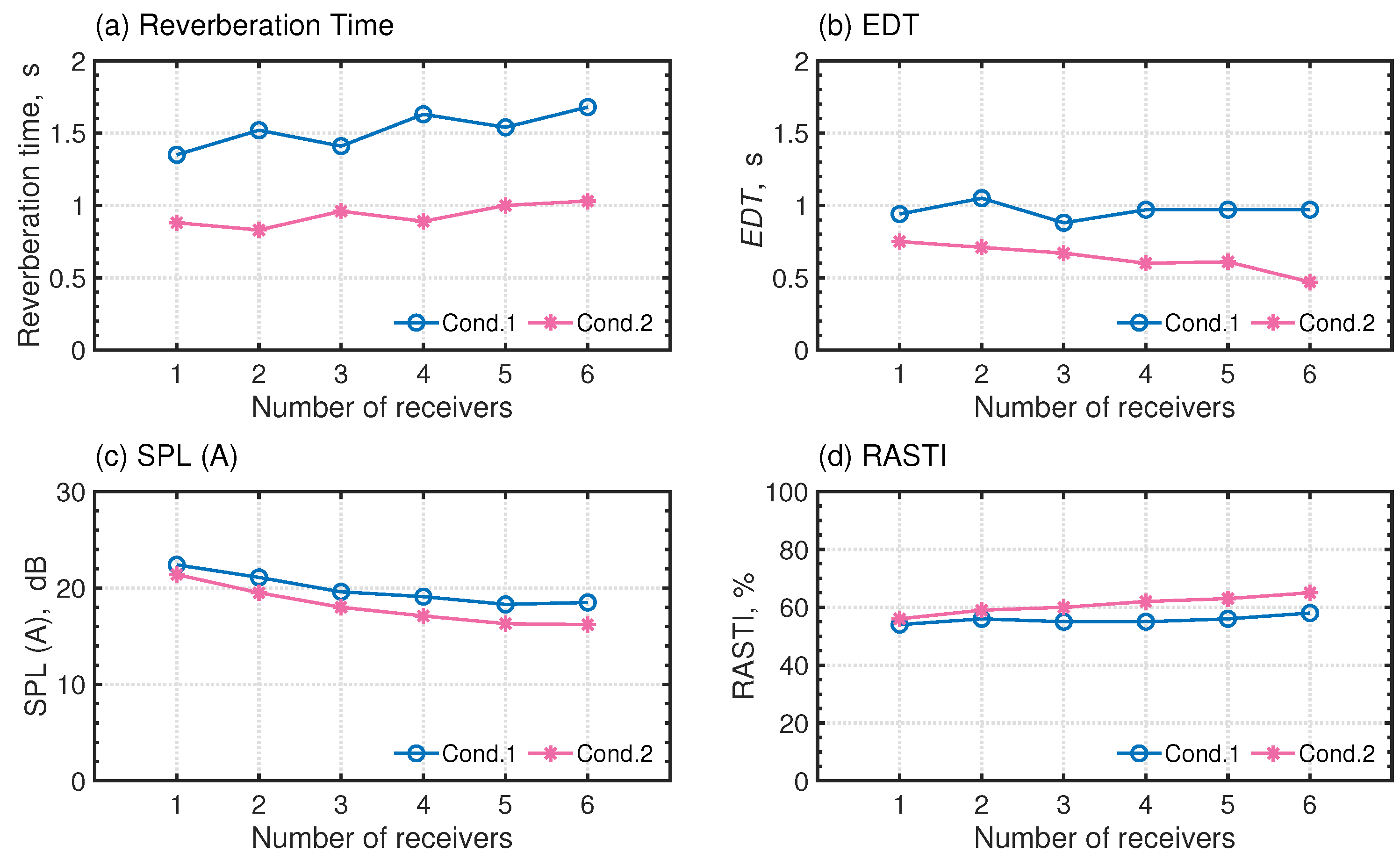
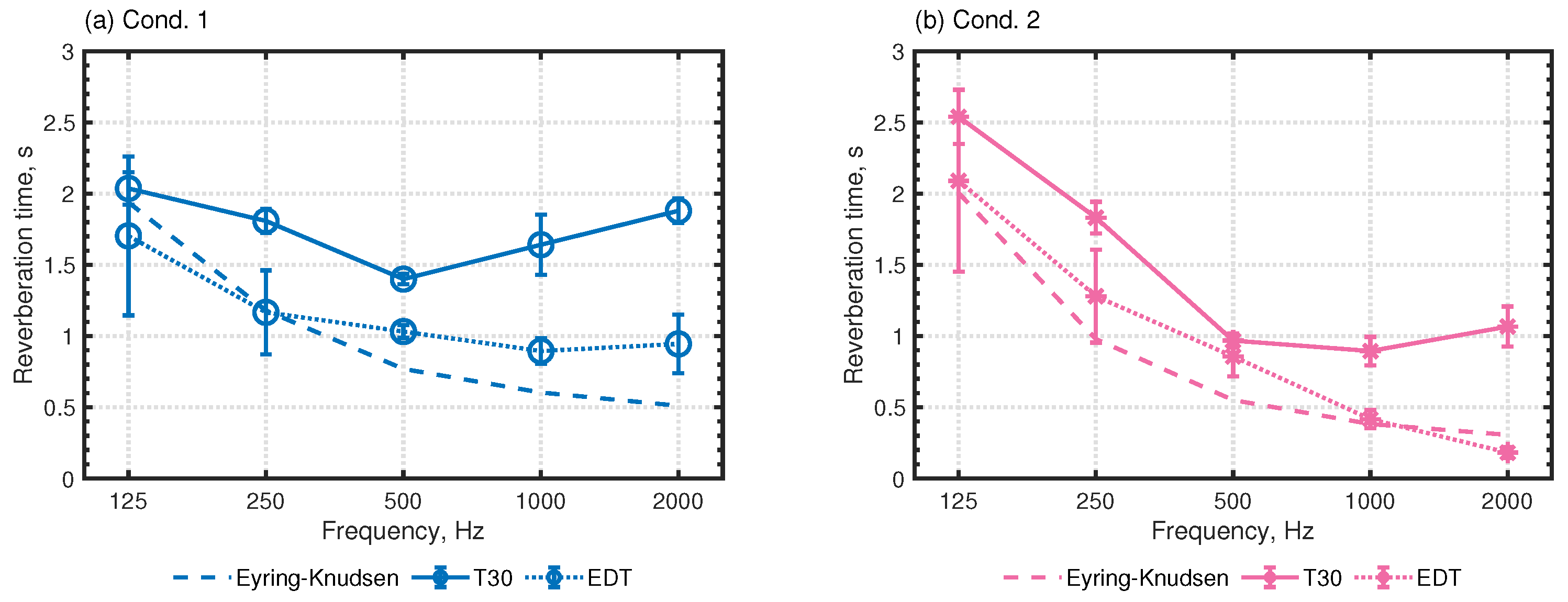
4.2. Objective Analysis of Auditorium Room Acoustics
4.3. Binaural Room-Acoustics Auralization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vorländer, M. Auralization: Fundamentals of Acoustics, Modelling, Simulation, Algorithms and Acoustic Virtual Reality; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sakuma, T.; Sakamoto, S.; Otsuru, T. (Eds.) Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Savioja, L.; Svensson, U.P. Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 2015, 138, 708–730. [Google Scholar] [CrossRef] [Green Version]
- Okuzono, T.; Otsuru, T.; Tomiku, R.; Okamoto, N.; Minokuchi, T. Speedup of time domain finite element sound field analysis of rooms. In Proceedings of the 37th International Congress and Exposition on Noise Control Engineering, Shanghai, China, 26–29 October 2008. [Google Scholar]
- Saarelma, J.; Savioja, L. An open source finite-difference time-domain solver for room acoustics using graphics processing units. In Proceedings of the Forum Acusticum 2014, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Morales, N.; Mehra, R.; Manocha, D. A parallel time-domain wave simulator based on rectangular decomposition for distributed memory architectures. Appl. Acoust. 2015, 97, 104–114. [Google Scholar] [CrossRef]
- Hamilton, B.; Webb, C.J.; Fletcher, N.; Bilbao, S. Finite difference room acoustics simulation with general impedance boundaries and viscothermal losses in air: Parallel implementation on multiple GPUs. In Proceedings of the International Symposium on Musical and Room Acoustics ISMRA 2016, La Plata, Argentina, 11–13 September 2016. [Google Scholar]
- Morales, N.; Chavda, V.; Mehra, R.; Manocha, D. MPARD: A high-frequency wave-based acoustic solver for very large compute clusters. Appl. Acoust. 2017, 121, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, T.; Okuzono, T.; Sakagami, K. A Parallel Dissipation-Free and Dispersion-Optimized Explicit Time-Domain FEM for Large-Scale Room Acoustics Simulation. Buildings 2022, 12, 105. [Google Scholar] [CrossRef]
- Yoshida, T.; Okuzono, T.; Sakagami, K. Dissipation-free and dispersion-optimized explicit time-domain finite element method for room acoustic modeling. Acoust. Sci. Technol. 2021, 42, 270–281. [Google Scholar] [CrossRef]
- Berkhout, A.J.; de Vries, D.; Vogel, P. Acoustic control by wave field synthesis. J. Acoust. Soc. Am. 1993, 93, 2764–2778. [Google Scholar] [CrossRef]
- Ise, S. A principle of sound field control based on the Kirchhoff–Helmholtz integral equation and the theory of inverse systems. Acta Acust. United Acust. 1999, 85, 78–87. [Google Scholar]
- Gerzon, M.A. Periphony: With Height Sound Reproduction. J. Audio Eng. Soc. 1972, 21, 2–10. [Google Scholar]
- Daniel, J.; Moreau, S.; Nicol, R. Further Investigations of High-Order Ambisonics and Wavefield Synthesis for Holophonic Sound Imaging. In Proceedings of the 114th Audio Engineering Society Convention, Amsterdam, The Netherlands, 22–25 March 2003. [Google Scholar]
- McKenzie, T.; Murphy, D.T.; Kearney, G. Interaural Level Difference Optimization of Binaural Ambisonic Rendering. Appl. Sci. 2019, 9, 1226. [Google Scholar] [CrossRef] [Green Version]
- Otani, M.; Shigetani, H.; Mitsuishi, M.; Matsuda, R. Binaural Ambisonics: Its optimization and applications for auralization. Acoust. Sci. Technol. 2020, 41, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Llopis, H.S.; Pind, F.; Jeong, C.-H. Development of an auditory virtual reality system based on pre-computed B-format impulse responses for building design evaluation. Build. Environ. 2020, 169, 106553. [Google Scholar] [CrossRef]
- Doggett, R.; Sander, E.J.; Birt, J.; Ottley, M.; Baumann, O. Using Virtual Reality to Evaluate the Impact of Room Acoustics on Cognitive Performance and Well-Being. Front. Virtual Real. 2021, 2, 620503. [Google Scholar] [CrossRef]
- Cirillo, E.; Martellotta, F. Sound propagation and energy relations in churches. J. Acoust. Soc. Am. 2005, 118, 232–248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merimaa, J.; Pulkki, V. Spatial impulse response rendering I: Analysis and synthesis. J. Audio Eng. Soc. 2005, 53, 1115–1127. [Google Scholar]
- Shimokura, R.; Soeta, Y. Sound field characteristics of underground railway stations: Effect of interior materials and noise source positions. J. Acoust. Soc. Am. 2012, 73, 1150–1158. [Google Scholar] [CrossRef]
- Yoshida, T.; Ueda, Y.; Mori, N.; Matano, Y. An Experimental Study of the Performance of a Crossed Rib Diffuser in Room Acoustic Control. Appl. Sci. 2021, 11, 3781. [Google Scholar] [CrossRef]
- Okuzono, T.; Yoshida, T.; Sakagami, K. Efficiency of room acoustic simulations with time-domain FEM including frequency-dependent absorbing boundary conditions: Comparison with frequency-domain FEM. Appl. Acoust. 2021, 182, 108212. [Google Scholar] [CrossRef]
- Okuzono, T.; Yoshida, T. High potential of small-room acoustic modeling with 3D time-domain finite element method. Front. Built Environ. 2022, 8, 1006365. [Google Scholar] [CrossRef]
- Dragna, D.; Pineau, P.; Blanc-Benon, P. A generalized recursive convolution method for time-domain propagation in porous media. J. Acoust. Soc. Am. 2015, 138, 1030–1042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The time dimension: Semi-discretization of field and dynamic problems. In The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth–Heinemann: Oxford, UK, 2013; pp. 382–386. [Google Scholar]
- Yoshida, T.; Okuzono, T.; Sakagami, K. Numerically stable explicit time-domain finite element method for room acoustics simulation using an equivalent impedance model. Noise Control Eng. J. 2018, 66, 176–189. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A Fast and Highly Quality Multilevel Scheme for Partitioning Irregular Graphs. SIAM J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Zotter, F.; Frank, M. Ambisonics: A Practical 3D Audio Theory for Recording, Studio Production, Sound Reinforcement, and Virtual Reality; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Sheaffer, J.; van Walstijn, M.; Rafaely, B.; Kowalczyk, K. Binaural Reproduction of Finite Difference Simulations Using Spherical Array Processing. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 2125–2135. [Google Scholar] [CrossRef] [Green Version]
- Bilbao, S.; Politis, A.; Hamilton, B. Local Time-Domain Spherical Harmonic Spatial Encoding for Wave-Based Acoustic Simulation. IEEE Signal Process. Lett. 2019, 26, 617–621. [Google Scholar] [CrossRef] [Green Version]
- Politis, A. Microphone Array Processing for Parametric Spatial Audio Techniques. Ph.D. Thesis, Aalto University, Helsinki, Finland, 2016. [Google Scholar]
- Allard, J.F.; Atalla, N. Acoustic impedance at normal incidence of fluids. Substitution of a fluid layer for a porous layer. In Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials, 2nd ed.; John Wiley & Sons: Chichester, UK, 2009; pp. 15–27. [Google Scholar]
- Miki, Y. Acoustical properties of porous materials – Modification of Delany–Bazley models. J. Acoust. Soc. Jpn. (E) 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Maa, D.-M. Microperforated-panel wideband absorbers. Noise Control Eng. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Hamilton, B.; Bilbao, S. Time-domain modeling of wave-based room acoustics including viscothermal and relaxation effects in air. JASA Express Lett. 2021, 1, 092401. [Google Scholar] [CrossRef]
- Kates, J.M.; Brandewie, E.J. Adding air absorption to simulated room acoustic models. J. Acoust. Soc. Am. 2020, 148, EL408–EL413. [Google Scholar] [CrossRef]
- ISO. 3382–1:2009; Acoustics—Measurement of Room Acoustic Parameters—Part 1: Performance Spaces. International Organization for Standardization (ISO): Geneva, Switzerland, 2009.
- Bradley, J.S.; Reich, R.; Norcross, S.G. A just noticeable difference in C50 for speech. Appl. Acoust. 1999, 58, 99–108. [Google Scholar] [CrossRef]
- Kawai, K.; Fujimoto, K.; Iwase, T.; Sakuma, T.; Hidaka, Y.; Yasuoka, H. Introduction of sound material in living environment 2004 (SMILE 2004): A sound source database for educational and practical purposes. J. Acoust. Soc. Am. 2006, 120, 3070–3071. [Google Scholar] [CrossRef]

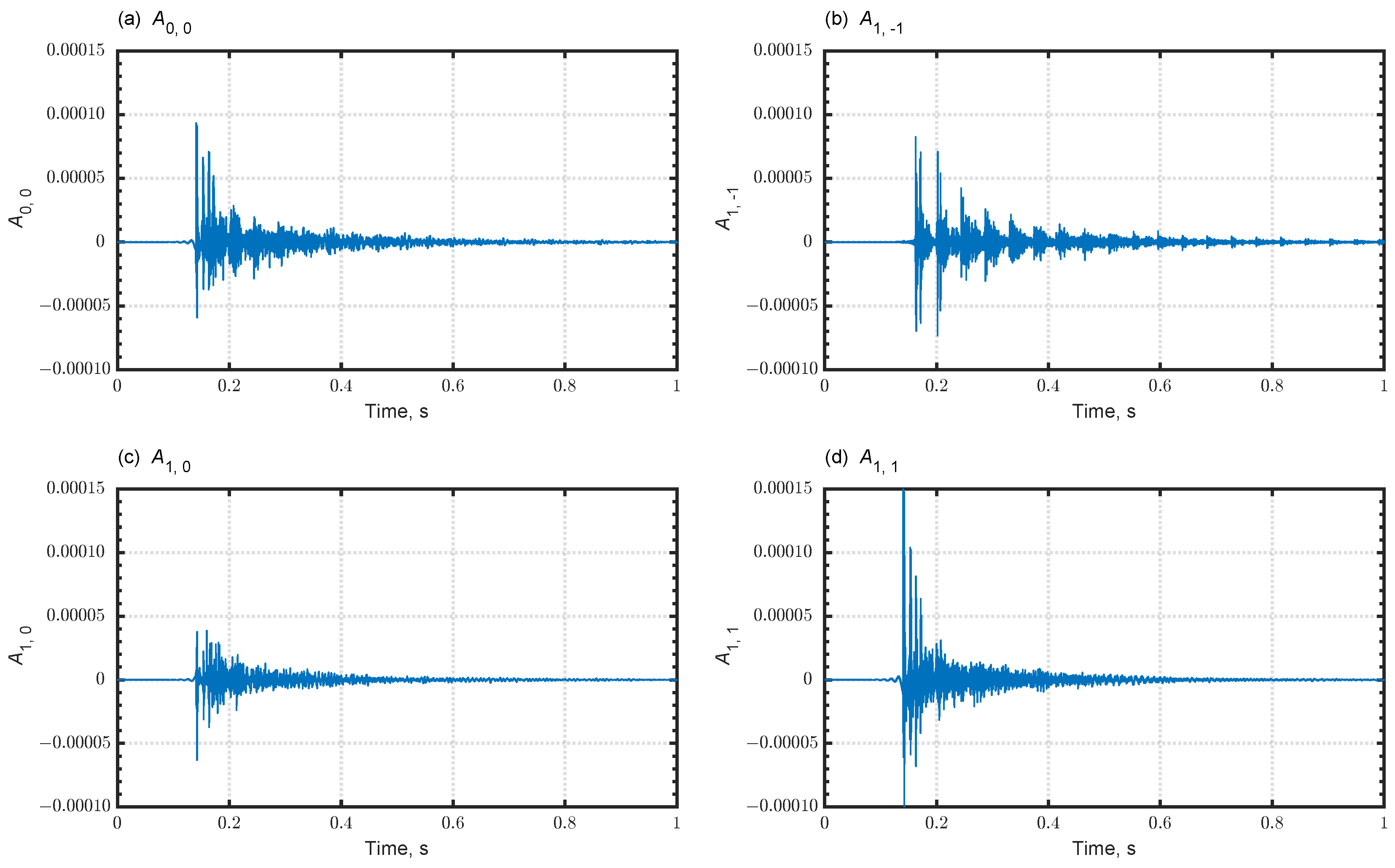
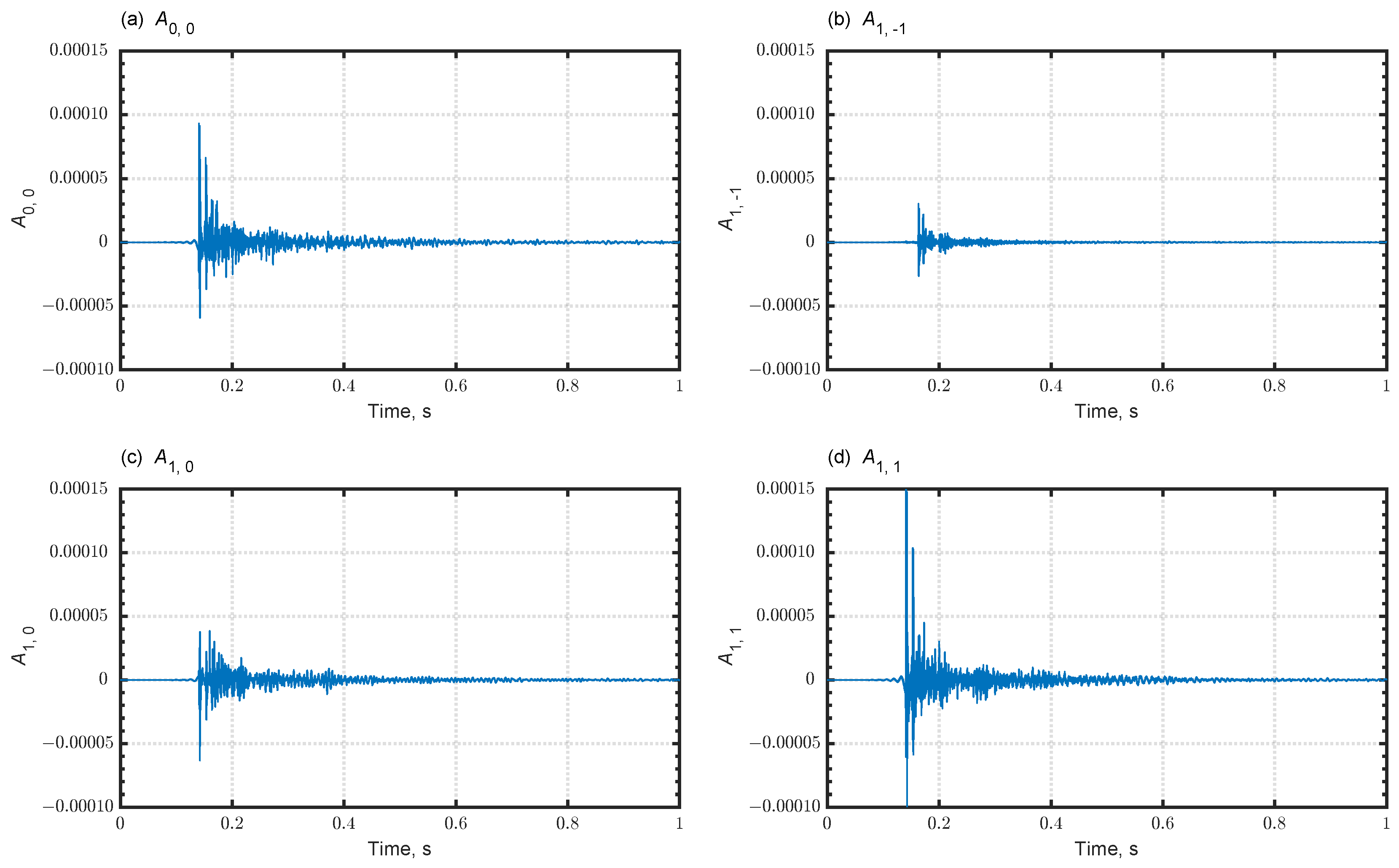

| (l, m) | ||
|---|---|---|
| (0, 0) | ||
| (1, −1) | ||
| (1, 0) | ||
| (1, 1) |
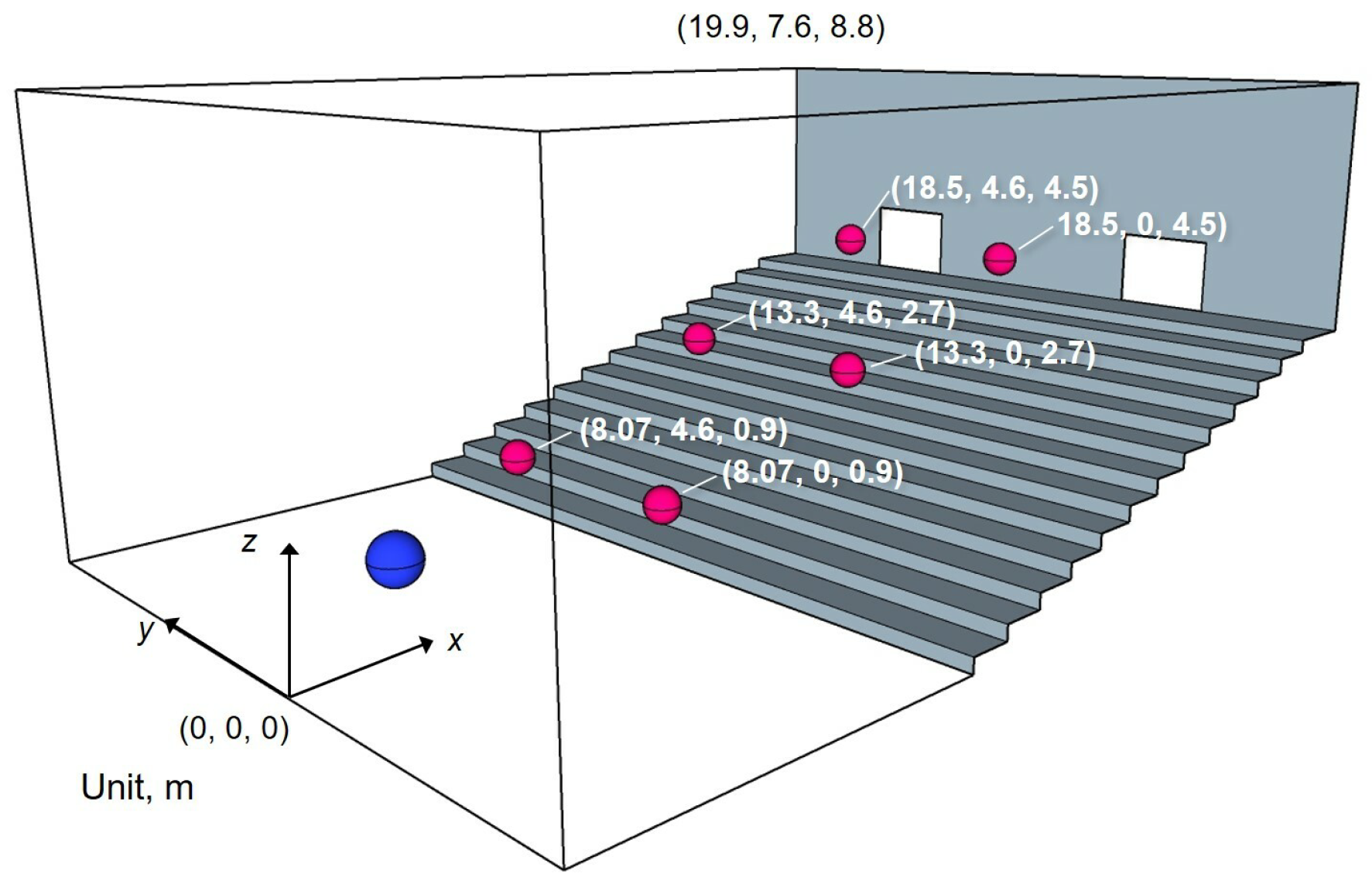
| Receiver | (x, y, z) |
|---|---|
| R1 | (8.07, 0, 0.9) |
| R2 | (8.07, 4.6, 0.9) |
| R3 | (13.3, 0, 2.7) |
| R4 | (13.3, 4.6, 2.7) |
| R5 | (18.5, 0, 4.5) |
| R6 | (18.5, 4.6, 4.5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshida, T.; Okuzono, T.; Sakagami, K. Binaural Auralization of Room Acoustics with a Highly Scalable Wave-Based Acoustics Simulation. Appl. Sci. 2023, 13, 2832. https://doi.org/10.3390/app13052832
Yoshida T, Okuzono T, Sakagami K. Binaural Auralization of Room Acoustics with a Highly Scalable Wave-Based Acoustics Simulation. Applied Sciences. 2023; 13(5):2832. https://doi.org/10.3390/app13052832
Chicago/Turabian StyleYoshida, Takumi, Takeshi Okuzono, and Kimihiro Sakagami. 2023. "Binaural Auralization of Room Acoustics with a Highly Scalable Wave-Based Acoustics Simulation" Applied Sciences 13, no. 5: 2832. https://doi.org/10.3390/app13052832
APA StyleYoshida, T., Okuzono, T., & Sakagami, K. (2023). Binaural Auralization of Room Acoustics with a Highly Scalable Wave-Based Acoustics Simulation. Applied Sciences, 13(5), 2832. https://doi.org/10.3390/app13052832








