Nodal Accuracy Improvement Technique for Linear Elements with Application to Adaptivity
Abstract
1. Introduction
2. Basic Theory
2.1. Finite Element Method
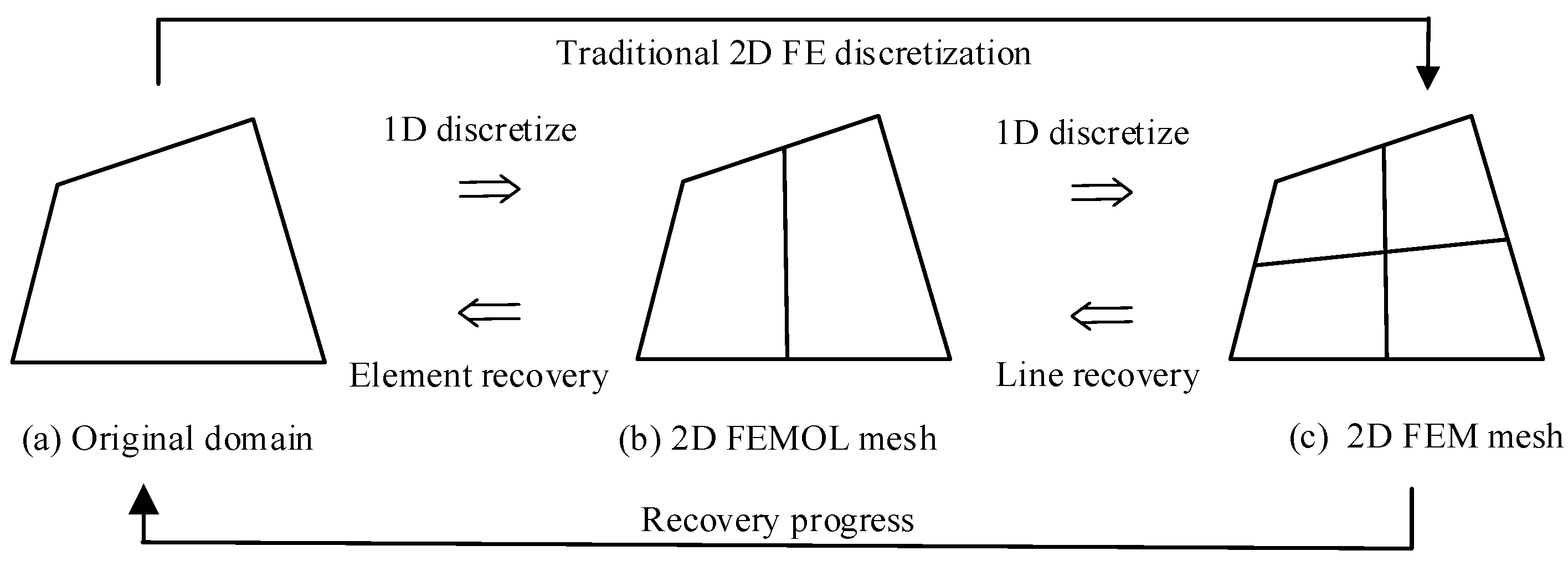
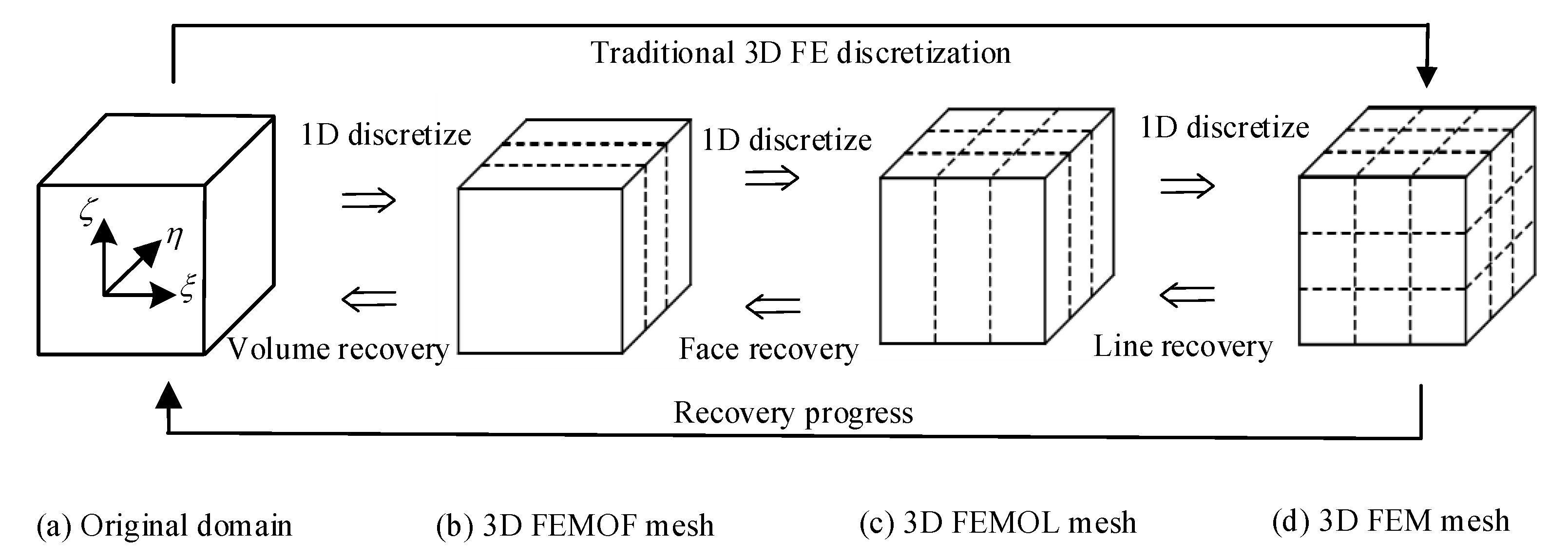
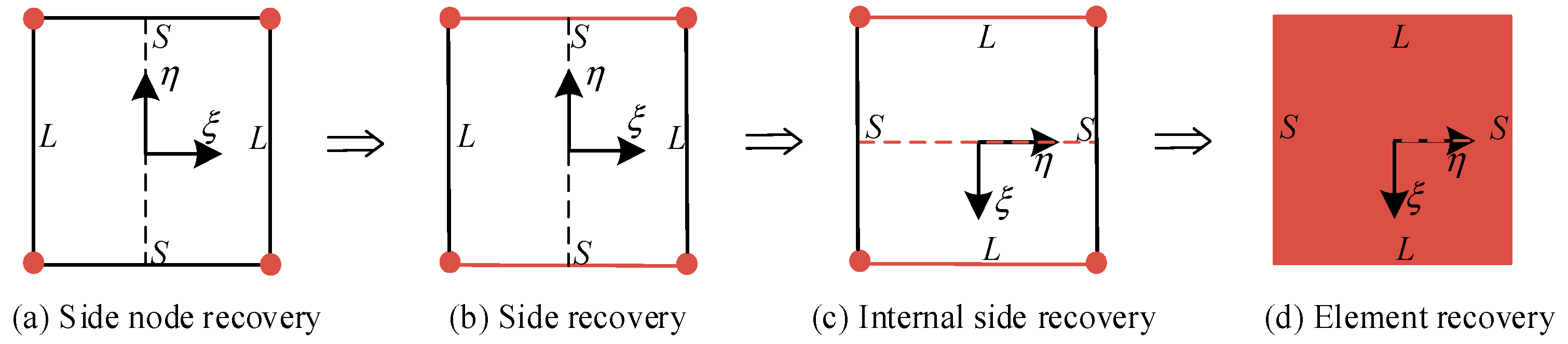
2.2. Element Energy Projection Recovery Strategy
3. Nodal Accuracy Improvement Technology for Linear Elements
3.1. Nodal Accuracy Improvement for 1D Problems
3.2. Nodal Accuracy Improvement for 2D and 3D Problems
- (i)
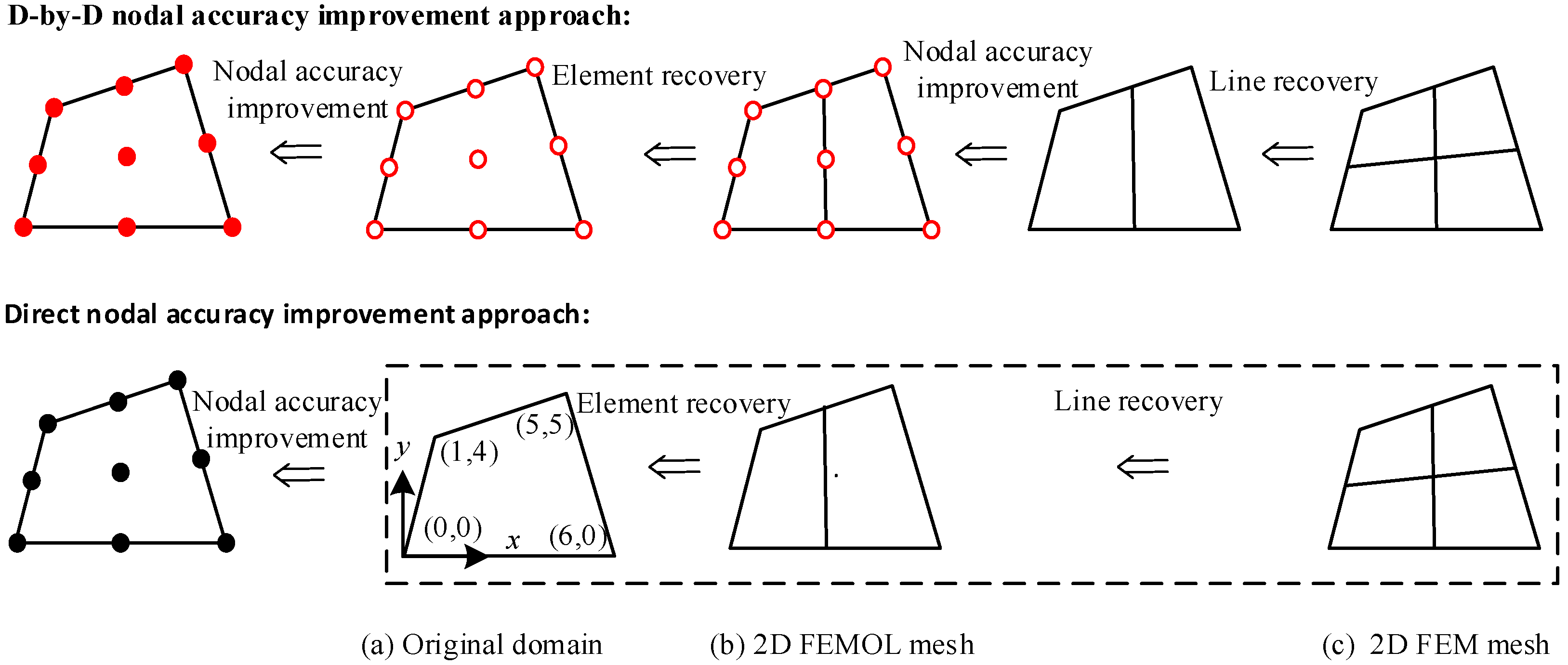
- D-by-D nodal accuracy improvement approach
- (a) After the line recovery has finished (c.f. Figure 1 and Section 2.2), and before the element recovery, a supplementary problem similar to Equation (11) can be derived for the ODEs of FEMOL (c.f. Equation (8)) and is then solved by using the same FE mesh and trial space used in solving Equation (8) for an improved nodal solution and better FE and EEP solutions on the “mesh lines”.
- (b) After element recovery has finished (c.f. Figure 1 and Section 2.2), another supplementary problem can be derived for the PDE in Equation (1). As before, this additional problem will be solved for using the same FE mesh and trial space used when solving problem (1) for an improved nodal solution for the original PDE problem (1).
- (ii)
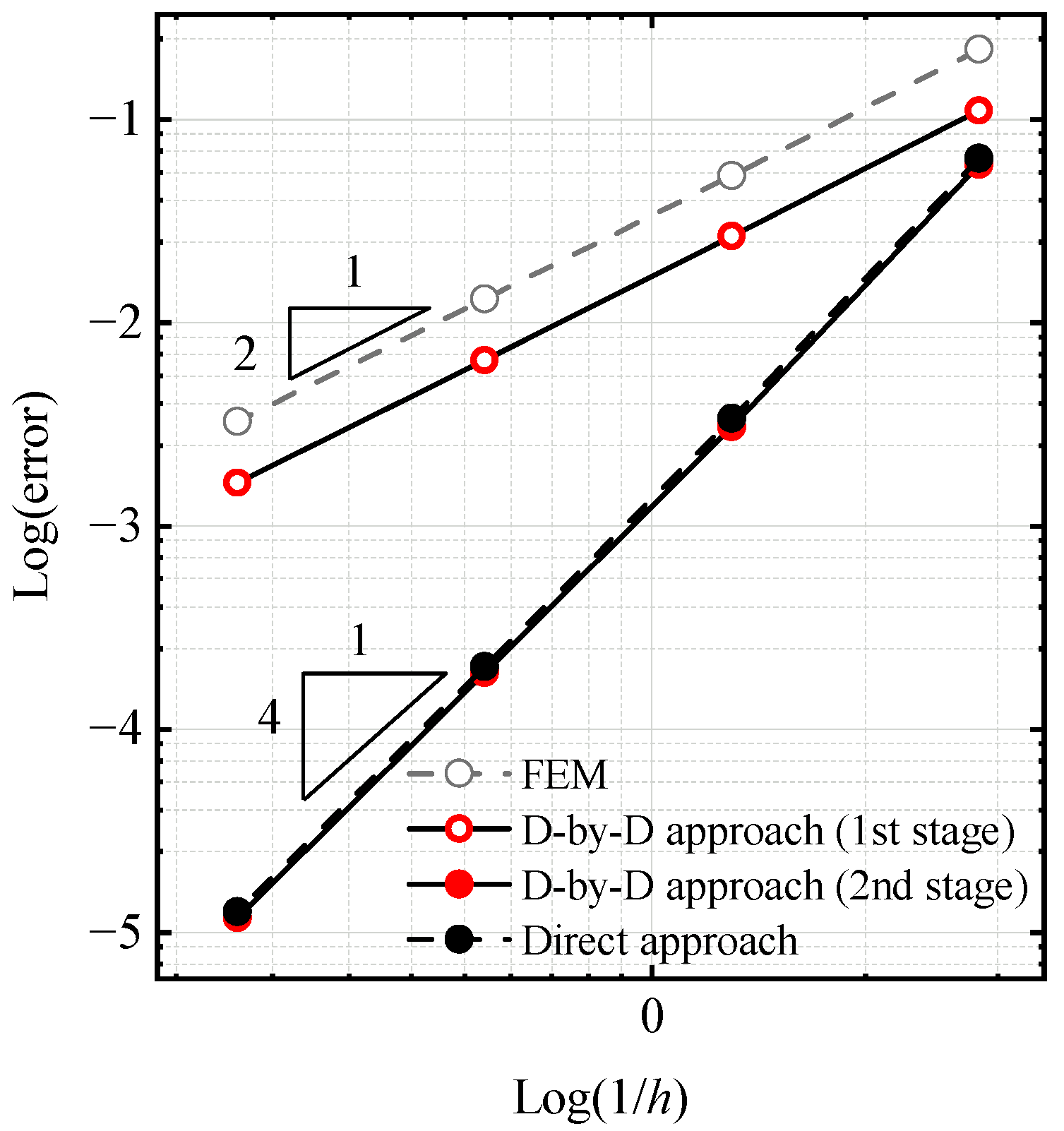
- Direct nodal accuracy improvement approach
3.3. Super-Convergent Schemes
- (i)
- For the improved FE solution , the EEP recovery strategy described in Section 2.2 is used to obtain the super-convergent solution of , which is noted by .
- (ii)
- For the improved EEP solution , it is found that itself is super-convergent over the FE solution directly.
4. Self-Adaptive Algorithm
- (1)
- Find a mesh such that the linear FE solution on satisfies
- (2)
- Further refine the mesh if necessary to find an optimal mesh , such that the linear FE solution on satisfies Equation (16).
5. Numerical Examples
5.1. Two-Point Boundary Value Problem
5.2. Elastic Plane Stress Problem
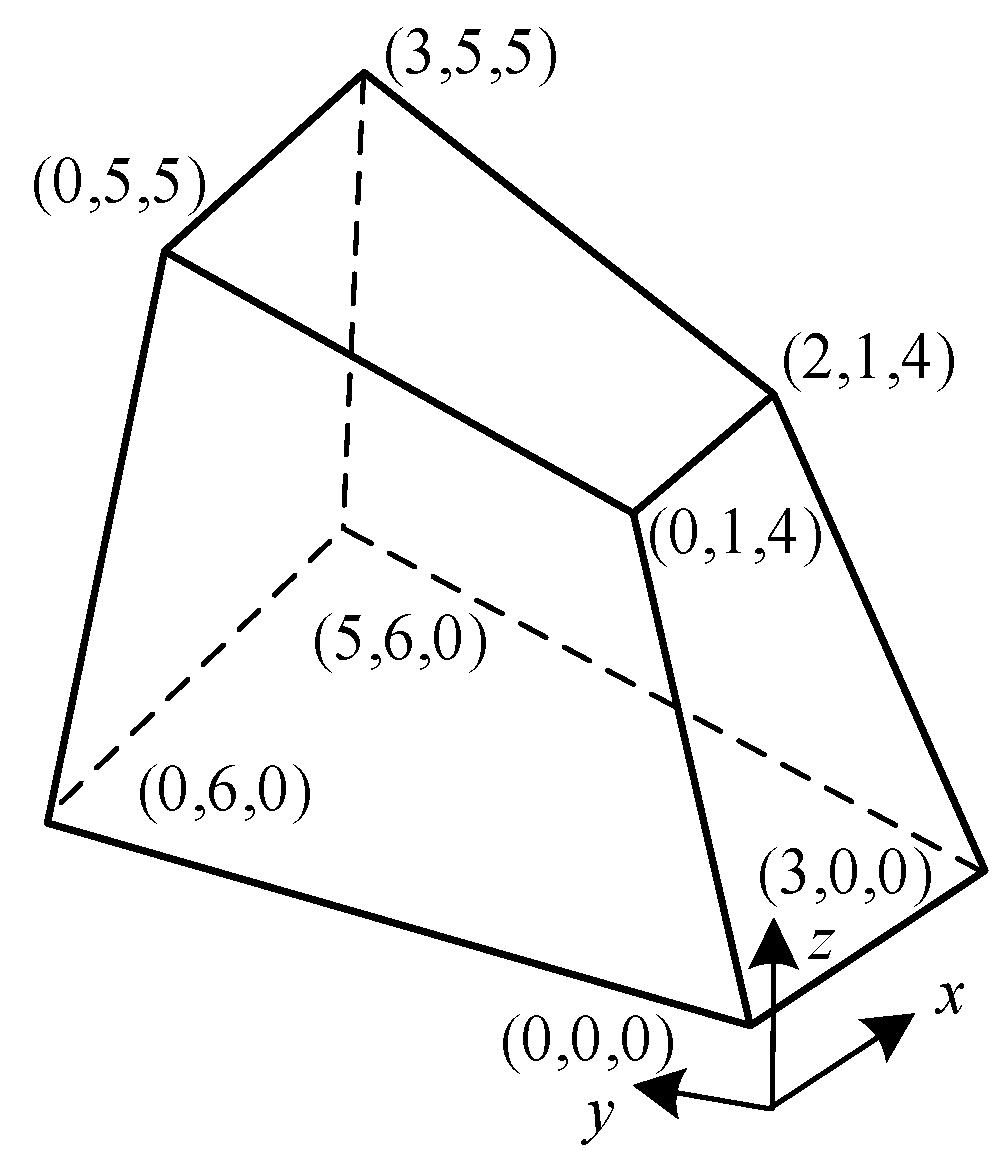
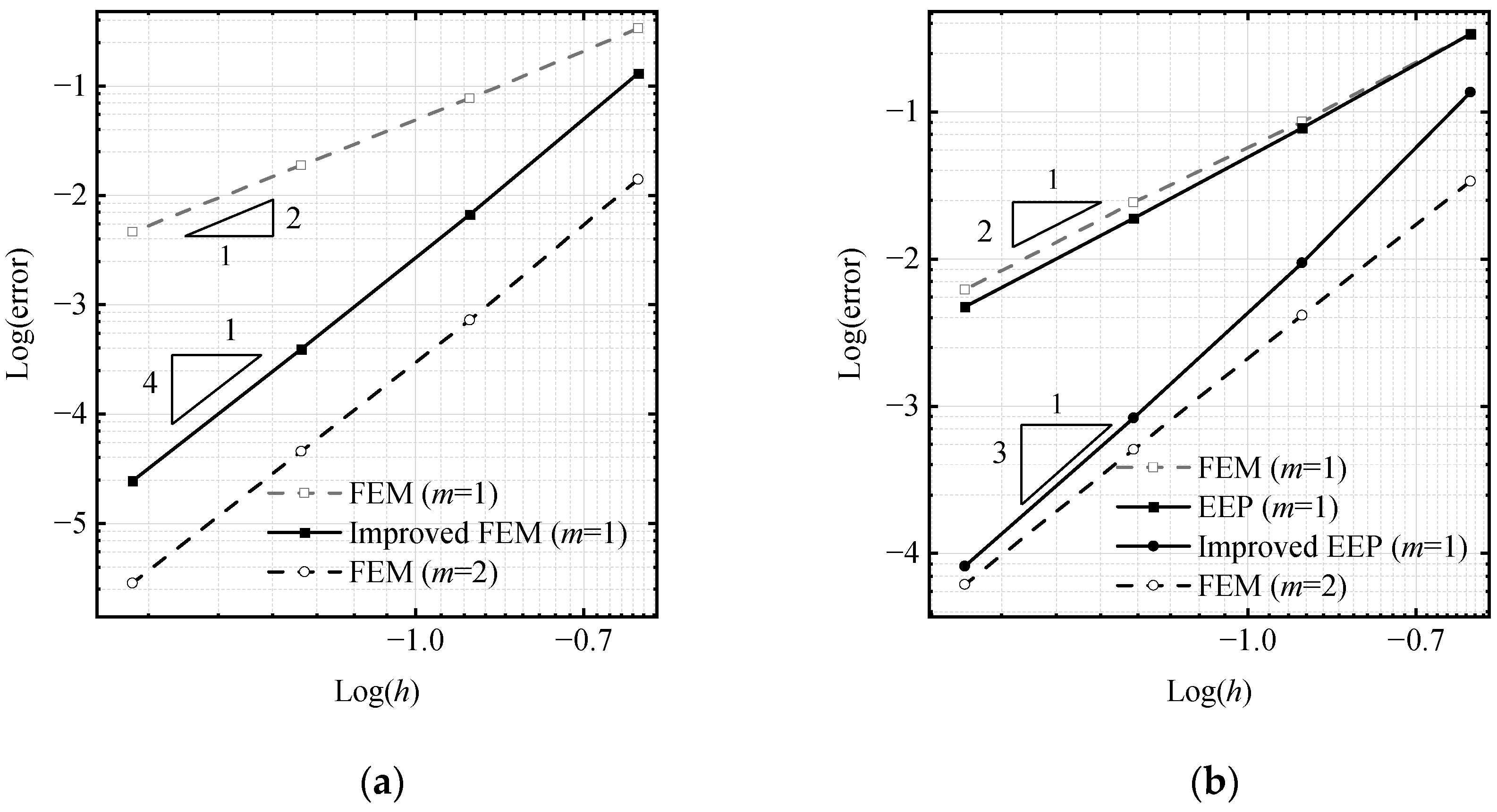
5.3. The 3D Poisson Problem
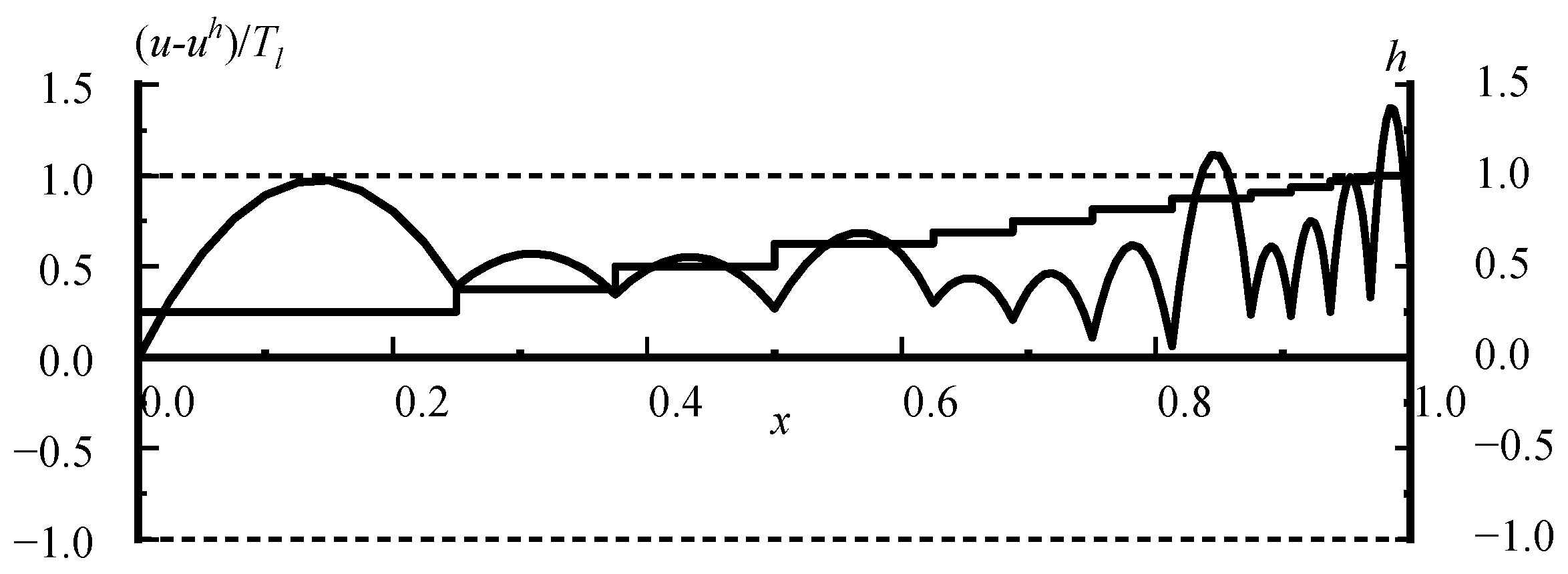
5.4. Preliminary Application of Adaptive Algorithm to 1D Problem
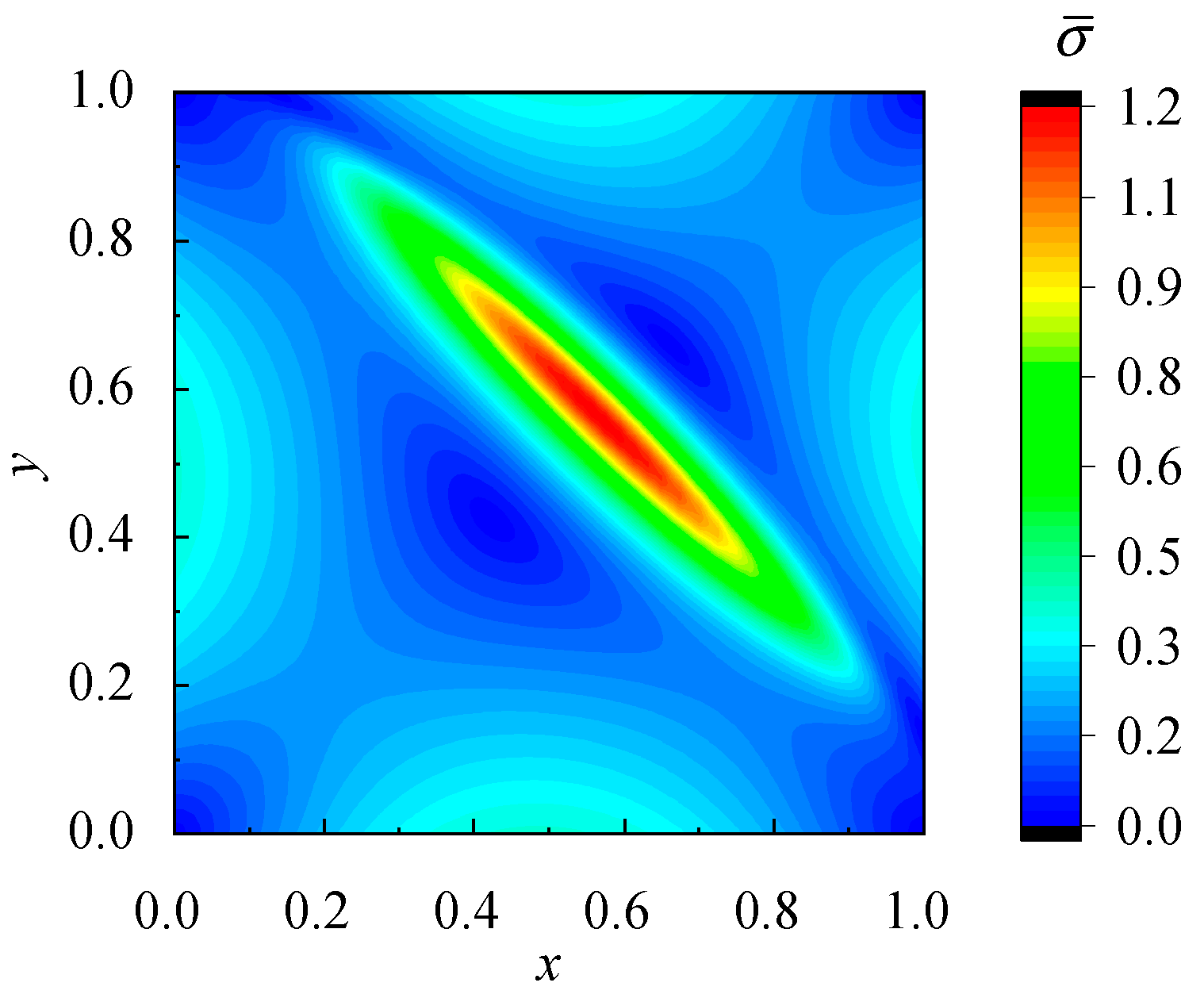
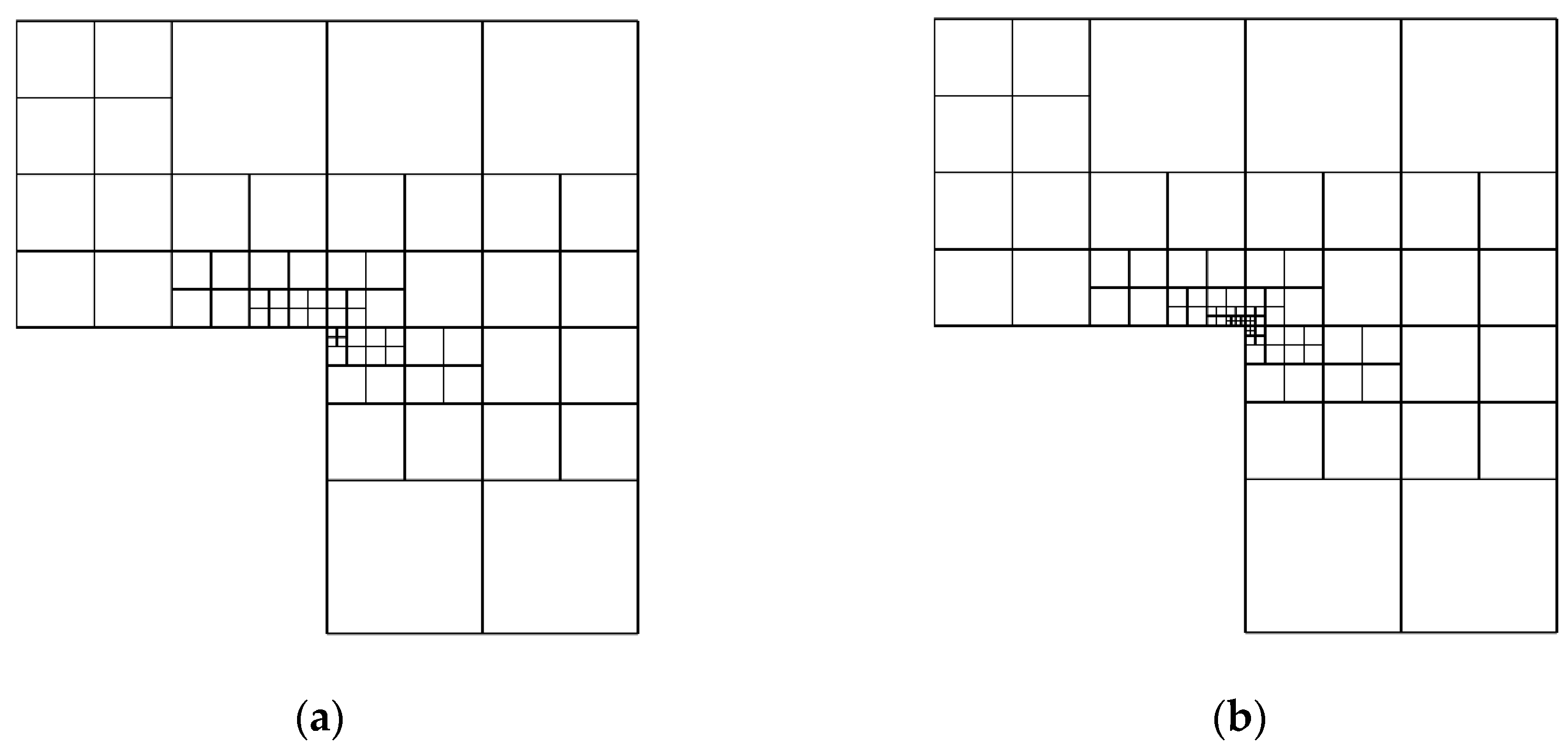
5.5. Stress Concentration Problem
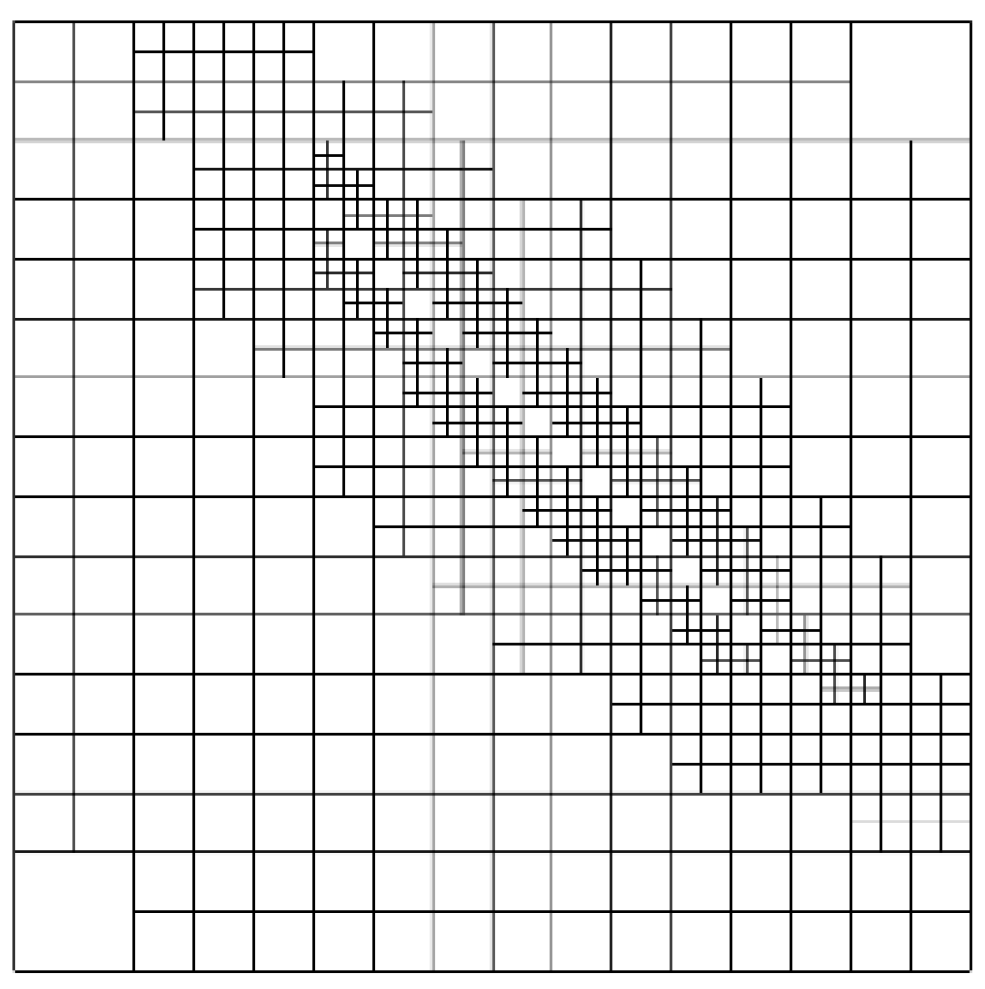
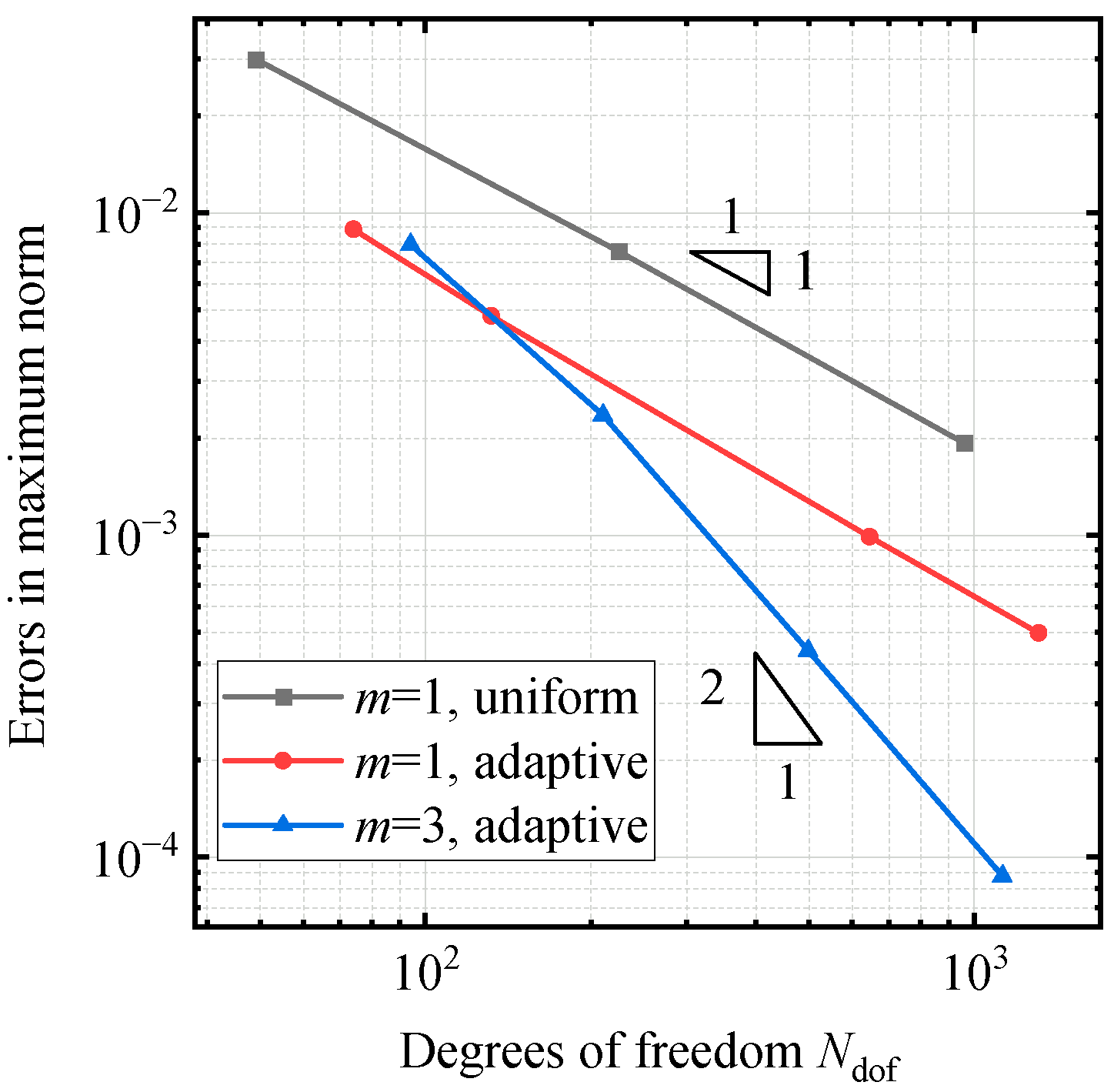
5.6. Singularity Problem
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babuška, I.; Rheinboldt, W.C. A posteriori error estimates for the finite element method. Int. J. Numer. Methods Eng. 1978, 12, 1597–1615. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier: Singapore, 2013. [Google Scholar]
- Babuska, I.M.; Strouboulis, T.; Upadhyay, C.S. A Model Study of The Quality of a Posteriori Error Estimators for Finite Element Solutions of Linear Elliptic Problems, With Particular Reference to the Behavior Near the Boundary. Int. J. Numer. Methods Eng. 1997, 40, 2521–2577. [Google Scholar] [CrossRef]
- Kelly, D.W.; Gago, D.S.R.; Zienkiewicz, O.C. A posteriori error analysis and adaptive processes in the finite element method: Part I—Error analysis. Int. J. Numer. Methods Eng. 1983, 19, 1593–1619. [Google Scholar] [CrossRef]
- Ladeveze, P.; Leguillon, D. Error Estimate Procedure in the Finite Element Method and Applications. SIAM J. Numer. Anal. 1983, 20, 485–509. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. The super-convergent patch recovery and a posteriori error estimates. Part 1: The recovery technique. Int. J. Numer. Methods Eng. 1992, 33, 1331–1364. [Google Scholar] [CrossRef]
- Naga, A.; Zhang, Z. A posteriori error estimates based on the polynomial preserving recovery. SIAM J. Numer. Anal. 2004, 42, 1780–1800. [Google Scholar] [CrossRef]
- Boroomand, B.; Zienkiewicz, O.C. Recovery by equilibrium in patches (REP). Int. J. Numer. Methods Eng. 1997, 40, 137–164. [Google Scholar] [CrossRef]
- Ubertini, F. Patch recovery based on complementary energy. Int. J. Numer. Methods Eng. 2004, 59, 1501–1538. [Google Scholar] [CrossRef]
- Benedetti, A.; Miranda, S.D.; Ubertini, F. A posteriori error estimation based on the superconvergent Recovery by Compability in Patches. Int. J. Numer. Methods Eng. 2006, 67, 108–131. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, M. An element-energy-projection method for post-computation of super-convergent solutions in one-dimensional FEM. Eng. Mech. 2004, 21, 1–9. (In Chinese) [Google Scholar]
- Payen, D.J.; Bathe, K.J. The use of nodal point forces to improve element stresses. Comput. Struct. 2011, 89, 485–495. [Google Scholar] [CrossRef]
- Payen, D.J.; Bathe, K.J. A stress improvement procedure. Comput. Struct. 2012, 112, 311–326. [Google Scholar] [CrossRef]
- Sharma, R.; Zhang, J.; Langelaar, M.; Keulen, F.V.; Aragón, A.M. An improved stress recovery technique for low order 3-D finite elements. Int. J. Numer. Methods Eng. 2018, 114, 88–103. [Google Scholar] [CrossRef]
- Babuška, I.; Rheinboldt, W.C. Adaptive approaches and reliability estimations in finite element analysis. Comput. Methods Appl. Mech. Eng. 1979, 17, 519–540. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. A simple error estimator and adaptive procedure for practical engineering analysis. Int. J. Numer. Methods Eng. 1987, 24, 337–357. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. The super-convergent patch recovery and a posteriori error estimates. Part 2: Error estimates and adaptivity. Int. J. Numer. Methods Eng. 1992, 33, 1365–1382. [Google Scholar] [CrossRef]
- Richter, T. A posteriori error estimation and anisotropy detection with dual-weighted residual method. Int. J. Numer. Methods Fluids 2010, 62, 90–118. [Google Scholar] [CrossRef]
- Cao, W.H. On the superconvergence patch recovery techniques for the linear finite element approximation on anisotropic meshes. J. Comput. Appl. Math. 2014, 265, 33–51. [Google Scholar] [CrossRef]
- Pereira, J.T.; da Silva, J. Anisotropic Mesh Refinement Considering a Recovery-Based Error Estimator and Metric Tensors. Arab. J. Sci. Eng. 2019, 44, 5613–5630. [Google Scholar] [CrossRef]
- Yuan, S.; Xing, Q.Y.; Ye, K.S. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order. Appl. Math. Mech. (Engl. Ed.) 2008, 19, 591–602. [Google Scholar] [CrossRef]
- Dong, Y.Y.; Yuan, S.; Xing, Q.Y. Adaptive finite element analysis with local mesh refinement based on a posteriori error estimate of element energy projection technique. Eng. Comput. 2019, 36, 2010–2033. [Google Scholar] [CrossRef]
- Wiberg, N.E.; Li, X.D. Super-convergent patch recovery of finite element solution and a posteriori L2 norm error estimate. Commun. Numer. Methods Eng. 1994, 10, 313–320. [Google Scholar] [CrossRef]
- Douglas, J.; Dupond, T. Galerkin approximations for the two-point boundary problem using continuous, piecewise polynomial spaces. Numer. Math. 1974, 22, 99–109. [Google Scholar] [CrossRef]
- Chen, C.M. Structure Theory of Super-Convergence of Finite Elements; Hunan Science & Technology Press: Changsha, China, 2001. (In Chinese) [Google Scholar]
- Sun, H.H.; Yuan, S. Adaptive finite element analysis of free vibration of elastic membranes via element energy projection technique. Eng. Comput. 2021, 38, 3492–3516. [Google Scholar] [CrossRef]
- Yuan, S. The Finite Element Method of Lines; Science Press: Beijing, China; New York, NJ, USA, 1993. [Google Scholar]
- Yuan, S.; Xing, Q.Y.; Yuan, Q. Calculation of errors of nodal displacements in one-dimensional finite element methods using element energy projection technique. Eng. Mech. 2020, 37, 1–7. (In Chinese) [Google Scholar]
- Castellazzi, G.; De Miranda, S.; Ubertini, F. Adaptivity based on the recovery by compatibility in patches. Finite Elem. Anal. Des. 2010, 46, 379–390. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NJ, USA, 1970. [Google Scholar]





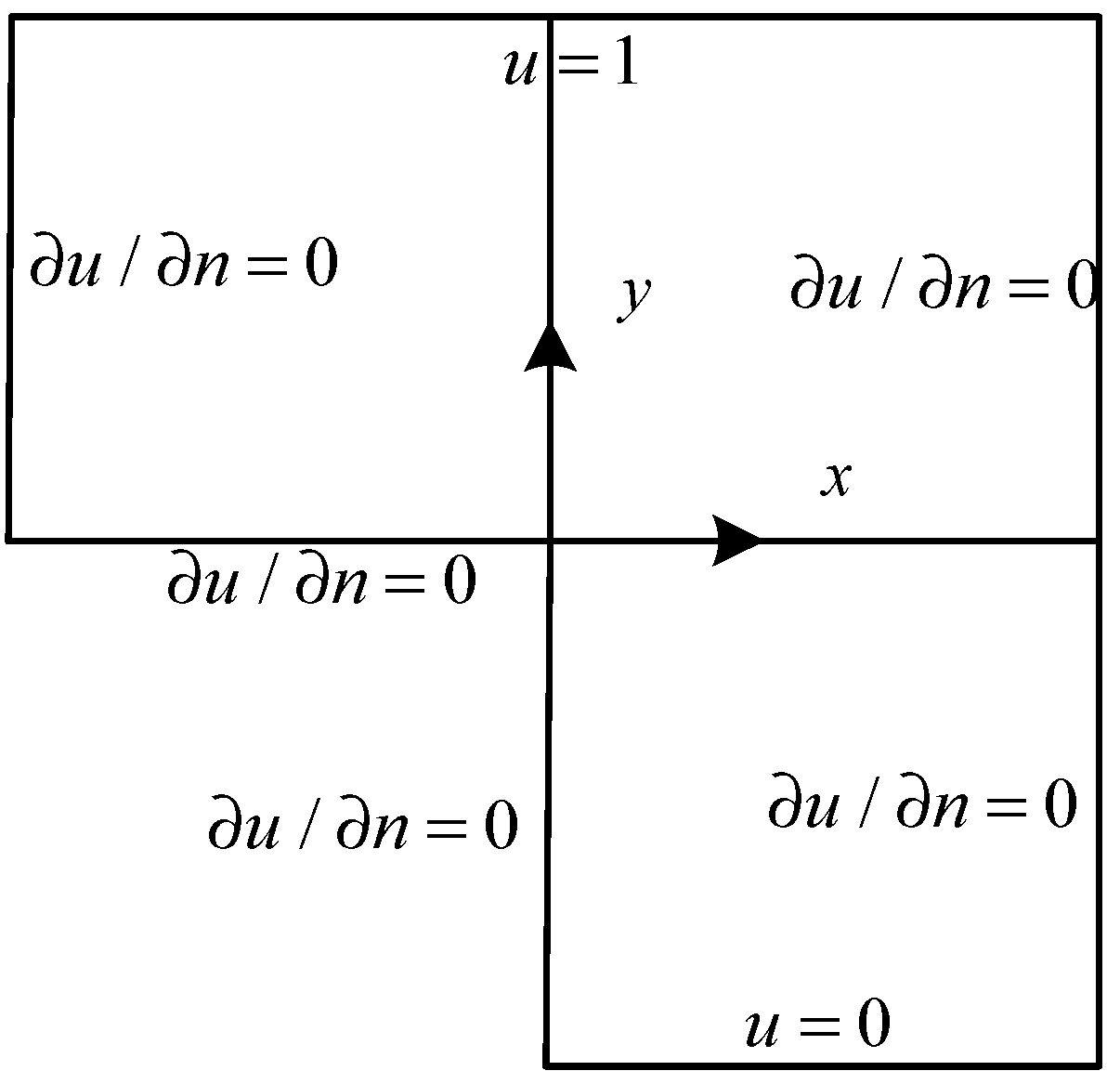

| FEM | Improved FEM | FEM | EEP | Improved EEP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 1.72 × 10−3 | - | 5.99 × 10−4 | - | 1.84 × 10−3 | - | 2.22 × 10−3 | - | 7.79 × 10−4 | - |
| 8 | 4.97 × 10−4 | 1.80 | 5.44 × 10−5 | 3.46 | 7.99 × 10−4 | 1.20 | 5.38 × 10−4 | 2.04 | 1.21 × 10−4 | 2.69 | |
| 16 | 1.08 × 10−4 | 2.21 | 3.31 × 10−6 | 4.04 | 2.84 × 10−4 | 1.49 | 1.14 × 10−4 | 2.23 | 1.80 × 10−5 | 2.74 | |
| 32 | 2.68 × 10−5 | 2.01 | 1.88 × 10−7 | 4.14 | 8.78 × 10−5 | 1.69 | 2.75 × 10−5 | 2.06 | 2.31 × 10−6 | 2.96 | |
| FEM | Improved FEM | FEM | EEP | Improved EEP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 × 8 | 9.68 × 10−2 | - | 1.12 × 10−2 | - | 2.27 × 10−1 | - | 1.30 × 10−1 | - | 4.65 × 10−2 | - |
| 16 × 16 | 2.40 × 10−2 | 2.01 | 7.20 × 10−4 | 3.96 | 6.31 × 10−2 | 1.85 | 2.62 × 10−2 | 2.31 | 2.54 × 10−3 | 4.19 | |
| 32 × 32 | 6.24 × 10−3 | 1.95 | 4.58 × 10−5 | 3.98 | 1.70 × 10−2 | 1.89 | 6.31 × 10−3 | 2.05 | 1.48 × 10−4 | 4.10 | |
| 64 × 64 | 1.55 × 10−3 | 2.01 | 2.91 × 10−6 | 3.98 | 4.32 × 10−3 | 1.97 | 1.56 × 10−3 | 2.01 | 1.27 × 10−5 | 3.54 | |
| FEM | Improved FEM | FEM | EEP | Improved EEP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 × 8 | 8.68 × 10−2 | - | 9.72 × 10−3 | - | 8.68 × 10−2 | - | 8.78 × 10−2 | - | 3.06 × 10−2 | - |
| 16 × 16 | 2.26 × 10−2 | 1.94 | 6.56 × 10−4 | 3.89 | 2.39 × 10−2 | 1.86 | 2.26 × 10−2 | 1.96 | 3.05 × 10−3 | 3.33 | |
| 32 × 32 | 5.58 × 10−3 | 2.01 | 4.84 × 10−5 | 3.76 | 6.17 × 10−3 | 1.95 | 5.58 × 10−3 | 2.01 | 3.70 × 10−4 | 3.04 | |
| 64 × 64 | 1.40 × 10−3 | 2.00 | 3.32 × 10−6 | 3.87 | 1.55 × 10−3 | 1.99 | 1.40 × 10−3 | 2.00 | 4.59 × 10−5 | 3.01 | |
| FEM | Improved FEM | FEM | EEP | Improved EEP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 × 2 × 2 | 3.37 × 10−1 | - | 1.31 × 10−1 | - | 3.37 × 10−1 | - | 3.37 × 10−1 | 2.92 | 1.36 × 10−1 | - |
| 4 × 4 × 4 | 7.71 × 10−2 | 2.13 | 6.71 × 10−3 | 4.28 | 8.53 × 10−2 | 1.98 | 7.79 × 10−2 | 2.11 | 9.44 × 10−3 | 3.84 | |
| 8 × 8 × 8 | 1.88 × 10−2 | 2.04 | 3.94 × 10−4 | 4.09 | 2.42 × 10−2 | 1.82 | 1.89 × 10−2 | 2.04 | 8.29 × 10−4 | 3.51 | |
| 16 × 16 × 16 | 4.66 × 10−3 | 2.01 | 2.45 × 10−5 | 4.01 | 6.19 × 10−3 | 1.97 | 4.71 × 10−3 | 2.01 | 8.19 × 10−5 | 3.34 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Yuan, S.; Xing, Q. Nodal Accuracy Improvement Technique for Linear Elements with Application to Adaptivity. Appl. Sci. 2023, 13, 2844. https://doi.org/10.3390/app13052844
Huang Z, Yuan S, Xing Q. Nodal Accuracy Improvement Technique for Linear Elements with Application to Adaptivity. Applied Sciences. 2023; 13(5):2844. https://doi.org/10.3390/app13052844
Chicago/Turabian StyleHuang, Zemin, Si Yuan, and Qinyan Xing. 2023. "Nodal Accuracy Improvement Technique for Linear Elements with Application to Adaptivity" Applied Sciences 13, no. 5: 2844. https://doi.org/10.3390/app13052844
APA StyleHuang, Z., Yuan, S., & Xing, Q. (2023). Nodal Accuracy Improvement Technique for Linear Elements with Application to Adaptivity. Applied Sciences, 13(5), 2844. https://doi.org/10.3390/app13052844







