Efficient Data Preprocessing with Ensemble Machine Learning Technique for the Early Detection of Chronic Kidney Disease

Abstract

It is a serious global health concern that chronic kidney disease (CKD) kills millions of people each year as a result of poor lifestyle choices and inherited factors. Effective prediction tools for prior detection are essential due to the growing number of patients with this disease. By utilizing machine learning (ML) approaches, this study aids specialists in studying precautionary measures for CKD through prior detection. The main objective of this paper is to predict and classify chronic kidney disease using ML approaches on a publicly available dataset. The dataset of CKD has been taken from the publicly available and accessible dataset Irvine ML Repository, which included 400 instances. ML methods (Support Vector Machine (SVM), K-Nearest Neighbors (KNN), random forest (RF), Logistic Regression (LR), and Decision Tree (DT) Classifier) are used as base learners and their performance has been compared with eXtreme Gradient Boosting (XGBoost). All ML algorithms are evaluated against different performance parameters: accuracy, recall, precision, and F1-measure. The results indicated that XGBoost outperformed with 98.00% accuracy as compared to other ML algorithms. For policymakers to forecast patterns of CKD in the population, the model put forth in this paper may be helpful. The model may enable careful monitoring of individuals who are at risk, early CKD detection, better resource allocation, and management that is patient-centered.

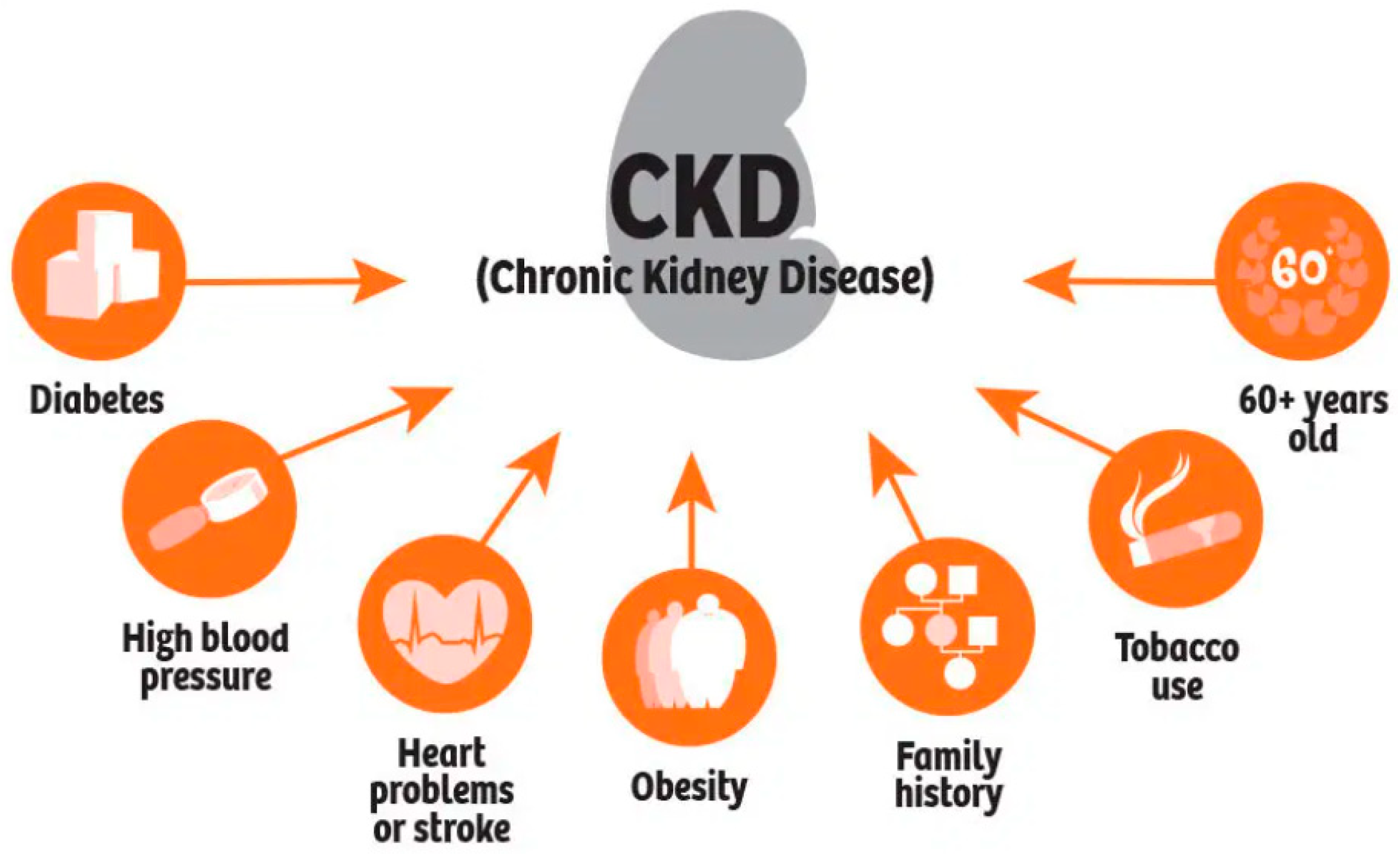
1. Introduction

The kidney is a very important organ in the human body. Excretion and osmoregulation are two of the most important functions of this organ. In layman’s terms, the kidney and excretion systems gather and dispose of all poisonous and useless material from the body. In India, 1 million instances of CKD are diagnosed each year. The patient can live for a long period with poor kidney functions if the condition is detected early on and the appropriate treatments are started [1,2]. However, it is common that the patient’s condition deteriorates over time and the number of nephrons falls rapidly. As a result, increased hazardous materials in the blood endanger the patient’s life. The final stage is referred to as “terminal kidney failure.” To keep the patient alive at this stage, one of hemodialysis, continuous peritoneal dialysis, or kidney transplantation procedures should be used. CKD, which eventually leads to renal failure, can cause a variety of issues in society, including economic, social, and medical issues. The high cost of hemodialysis might be used as an illustration of economic issues. Patients experience emotional and social problems as a result of their continued use of medicines and the consequences thereof. Furthermore, the medications utilized can interact with various organs and systems, resulting in a considerable reduction in life expectancy [3].

Chronic kidney disease is referred to as “chronic” because it develops gradually and often lasts for a long period, impairing the urinary system’s function. High blood pressure, diabetes, as well as cardiovascular disease are all risk factors for CKD patients [4]. Patients with CKD experience adverse effects, particularly in the late stages that harm the neurological and immunological systems. Patients in countries that are developing may come to the end of their lives and require dialysis. GFR is calculated using information such as the patient’s age, blood test results, gender, and other criteria [5]. The various parameters affecting CKD are shown in Figure 1.

The patient’s age, race, blood creatinine, gender, and other criteria can be used to assess chronic kidney disease. The severity of impairment caused by CKD is classified into five phases, as shown in

Table 1. Different stages present in CKD.

Stage	Description	GFR (mL/min)
I	Kidney function is normal	≥90
II	Mild increase in GFR	60–89
III	Moderate increase in GFR	30–59
IV	Severe increase in GFR	15–29
V	Kidney failure	15 or dialysis

, based on GFR [6]:

As there is a growing number of CKD patients, there is a scarcity of CKD-specialized physicians [7]. Computer-assisted diagnostics are required to assist physicians as well as radiologists in making diagnostic judgments. Machine learning (ML) as well as deep learning (DL) methods have been used in the early phases of CKD prediction as well as diagnosis. Artificial intelligence (AI) techniques have played a major role in medical and health industries [8]. CKD is one of the key issues in medical science because it involves significant criteria and complexity to effectively forecast this disease. Algorithms, such as Naive Bayes (NB), Decision Trees (DTs), K-Nearest Neighbors (KNN), and Neural Networks, are used to predict CKD risk. Each algorithm has a specialty, such as Naive Bayes’ use of probability to predict CKD, Decision Trees’ use of classification to produce a classified report for CKD, and Neural Networks’ use of opportunities to minimize CKD prediction error [9].

The contribution of this study are summarized as follows:

• Detection of chronic kidney disease in the early stages to avoid critical health issues.
• Early detection of chronic kidney disease will be helpful for low-income people so that they can take prior precautions as they cannot undergo or afford major surgery.

To provide better clarification and highlight the core theme of this research, this article is structured as follows. Section 1 briefs the essential basic concepts and significance of the proposed model with key attributes. Section 2 discusses the contributions of related research. It also summarizes different related studies, their proposed techniques, and the performance achieved. Section 3 enumerates the flow of the research process from elaborating the dataset, the preprocessing technique, the feature selection process, and classification. Section 4 discusses and exhibits the empirical observations and analysis in comparison with all other existing key methodologies. Section 5 includes the vital end notes of this study with planned future works.

2. Related Works

Many academics are consistently working on the prediction of CKD using various classification algorithms. Numerous studies have been undertaken in the last few decades to better understand and investigate CKD. Many researchers have employed various classification strategies for the early detection of CKD in the literature. Data mining (DM) is the methodology of extracting specific data from a large dataset. Medical diagnosis, facial recognition, and data filtering are just a few of the uses of these techniques.

The authors of one study [9] described an ultrasonography (USG)-based approach for diagnosing the phases of CKD. The algorithm works to detect fibrotic instances at various times. Authors of another study [10] performed a comparison of the outcomes of various models. They found and claimed that the Multiclass DT approach outperforms previous algorithms, with an accuracy of roughly 98% for a smaller dataset of 14 attributes. To decide whether the urinary system is harmless or harmful, the authors [11] suggested an expert system based on fuzzy logic. The authors [12] employed Softmax to categorize the final class after using a stacked autoencoder prototype to extract the features of CKD. In one study, the authors [13] introduced a genetic algorithm (GA) in which the GA optimized the weight vectors to train the NN. For CKD diagnosis, the system outperforms using standard neural networks.

The authors of another study [14] used multiple machine learning classification algorithms to reduce diagnosis time and enhance the accuracy of diagnosis. The planned study looks at how different phases of CKD are classified based on their severity. The RBF algorithm performs better than other classifiers, with an accuracy of 85.3%. In one study, the authors [15] examined the missing values in the CKD dataset as they greatly decreased accuracy as well as prediction.

Authors of one study [16] incorporated a unique methodology to figure out CKD using ML algorithms. The dataset consists of 400 instances with 24 dependent variables and one independent variable or class variable whose values are “ckd” or “nockd.” They used KNN, Neural Networks, and RF in order to obtain the results. Pinar Yildirim [17] performed an investigation on the impact of class imbalance. Using a sampling algorithm, a comparison study was done. In another study, the authors [18] evaluated 12 alternative categorization algorithms. They calculated the accuracy of their prediction findings by comparing their calculated results to real results. Accuracy, sensitivity, precision, and specificity were utilized as assessment criteria.

Clustering, classification, and other data mining techniques play an important role in extracting undisclosed knowledge from large databases. The technique of classification is one of the supervised learning techniques for defining subgroups ahead of time. The data attribute value must be used to identify the classes in the classification process. It establishes the classes by taking into account the quality of the data. These preconfigured specimens are used by the training algorithm to identify the set of parameters required for proper segregation [19,20,21]. In one article, the authors [22] utilized Apriori as well as k-means algorithms to construct a prediction system, and these were also employed to forecast individuals with kidney failure. The authors used machine learning algorithms to assess 42 data characteristics and used Receiver Operating Characteristic (ROC) plots to evaluate the data.

The authors of one study [23] developed a diagnosis and prediction system and also used the tool Weka to evaluate the data. The authors analyzed ROC plots using the J48 classifier, AD Trees, the K-Star method, the NB classifier, and the random forest (RF) classifier. In their research, the K-Star algorithm and the RF classifier were found to be the best approaches for the dataset. Sinha [24] suggested a method for comparing the performance of two data mining approaches. To assess accuracy and precision, the author employed KNN and also support vector machine (SVM). In terms of precision as well as accuracy performance metrics, the author found that the KNN outperformed the SVM classifier.

To extract the most critical vital characteristics, the authors of one study [25] presented an approach called LVW-FS. In another study, the author [26] tested diabetes in patients with chronic kidney illness using a model. The statistical method of chi-square was used to minimize the dimensionality of large amounts of data. The model uses parameters including glucose, age, albumin rate, and others to predict kidney health. The authors of one study [27] used two strategies to minimize the dimensionality of the dataset so as to strongly choose the attributes linked with CKD.

Table 2. Summary of recent related research on the detection of CKD.

Study and Year	ML Techniques	Performance
Ilyas, H. et al. (2019) [28]	Random forest and J48 algorithms	Random forest accuracy—78.25% and J48 accuracy—85%
Sabanayagam et al. (2020) [29]	Deep Learning Algorithm (DLA)	DLA accuracy—95%
Poonia, R.C. et al. (2022) [30]	LR model + chi-square feature selection (K > 14), where K is number of features	Accuracy—97.5%
Elhoseny, M. et al. (2019) [31]	Ant Colony-based Optimization (D-ACO) algorithm	D-ACO accuracy—95%

summarizes some of the recent related work being carried out in the detection CKD with techniques and performance.

In this study, the different ML models (KNN, SVM, RF, DT Classifier, Logistic Regression, and XGBoost) are used to diagnose CKD. In order to determine the optimal attributes, the Recursive Feature Elimination (RFE) approach is also used. For promising accuracy, all six machine learning techniques were utilized and compared among themselves, and it was observed that XGBoost exhibited the best performance.

3. Proposed Methodology

To analyze the CKD dataset, a sequence of experiments has been conducted utilizing ML methods such as SVM, KNN, DT, RF, LR, and XGBoost classifier. Figure 2 depicts the general pattern of CKD classification.

The mean approach was used to calculate missing values that are numeric, while the mode has been utilized to calculate missing values that are nominal during preprocessing. RFE, which is a Recursive Feature Elimination approach, has been utilized to select the aspects of relevance related to the attributes of high importance for the diagnosis of CKD. For disease diagnosis, these chosen features were given as inputs to the classifiers.

3.1. Dataset

The dataset of CKD has been taken from the Irvine ML Repository [6], which included 400 patients. Besides the class characteristics, namely “ckd” and “notckd,” the dataset has twenty-four features separated into eleven numeric features as well as thirteen category features. Age, specific gravity, blood pressure, albumin, red blood cells, sugar, pus cells, red blood cells, pus cell clumps, bacteria, blood glucose random, blood urea, serum creatinine, sodium, potassium, hemoglobin, packed cell volume, white blood cell count, red blood cell count, hypertension, diabetes mellitus, coronary artery disease, appetite, pedal edoema, and anaemia are some of the characteristics. Ckd and notckd are the two diagnostic classes. Figure 3 depicts count of diagnosis of kidney disease in the dataset.

3.2. Preprocessing

To ensure satisfactory accuracy, missing values must be handled in the preprocessing step depending on their distributions. Little’s MCAR (Missing Completely At Random) test was used in this study to confirm the randomization of missing values. The possibility of bias as a result of missing data is dependent on the mechanism that caused the data to be missing. The chi-square test of MCAR for multi-variate quantitative data is used to examine the analytical approaches used to correct the missingness and all the inference/computation work. In this study, the KNN Imputer method was employed to fill in the missing values.

Many classification algorithms strive to collect only pure examples for learning and to make the boundary between each class as clear as possible to improve prediction. The majority of classifiers find it significantly more difficult to learn how to classify synthetic cases that are close to the boundary than those that are far from it. Based on these results, authors of one study presented an enhanced preprocessing method (A-SMOTE) for imbalanced training sets [27]. The SMOTE method is carried out in 3 stages, as explained below.

Step A: Using Equation (1) synthetic instance is created.

$$N=2\ast \left(r-z\right)+z$$

(1)

where $r\to$majority class samples, z → minority class samples and $N$ → newly created synthetic instance.

Step B: The below-mentioned steps are carried out to remove the outlier; that is, noise.

If, $\hat{S}$ ={${\hat{S}}_1$, ${\hat{S}}_2$,${\hat{S}}_3$,….${\hat{S}}_n$} is a new instance received by Step A, then we will calculate the distance among ${\hat{S}}_i$ with original minority $S_m, Mi{n}_{Rap}({\hat{S}}_i$, ${\hat{S}}_m)$ defined using Equation (2).

$$Mi{n}_{Rap}({\hat{S}}_i, {\hat{S}}_m)={\displaystyle {{\displaystyle \sum }}_{k=1}^z}{\displaystyle {{\displaystyle \sum }}_{j=1}^M}\sqrt{{({\hat{S}}_i{}^{\left(j\right)}-S_{mk}{}^{\left(j\right)})}^2}$$

(2)

where

$Mi{n}_{Rap}({\hat{S}}_i$, ${\hat{S}}_m)\to$ samples rapprochement and as per Equation (2), L is calculated using Equation (3).

$$L={\displaystyle {{\displaystyle \sum }}_{i=1}^n}(Mi{n}_{Rap} ({\hat{S}}_i, S_m))$$

(3)

Step C: Calculate distance between ${\hat{S}}_i$, and every original majority $S_a$, $Ma{j}_{Rap}({\hat{S}}_i$,$S_a$), described using Equation (4).

$$Ma{j}_{Rap}({\hat{S}}_i,S_a)={\displaystyle {{\displaystyle \sum }}_{i=1}^r}{\displaystyle {{\displaystyle \sum }}_{j=1}^M}\sqrt{{({\hat{S}}_i{}^{\left(j\right)}-S_{al}{}^{\left(j\right)})}^2}$$

(4)

$Ma{j}_{Rap}({\hat{S}}_i$,$S_a$) → samples rapprochement and as per Equation (4), H is computed using Equation (5).

$$H={\displaystyle {{\displaystyle \sum }}_{i=1}^n}(Ma{j}_{Rap} ({\hat{S}}_i, S_a))$$

(5)

Entropy is nothing but the measure of disorder. The following Equations (6) and (7) were used by Claude E. Shannon to put this link between probability and heterogeneity.

$$H\left(X\right)=-{\displaystyle \sum }\left(p_i\ast lo{g}_2{p}_i\right)$$

(6)

$$\mathrm{Entropy} (\mathrm{p})=-{\displaystyle {{\displaystyle \sum }}_{i=1}^N}{p}_{i}lo{g}_2{p}_i$$

(7)

There are missing values in all the features except diagnostic class. In this study, the KNN Imputer method was employed to fill in the missing values. Since the dataset comprises 250 cases of the “ckd” class (62.5%) and 150 cases of “notckd” (37.5%), the dataset is uneven or unbalanced. The analysis of the features before and after application of the SMOTE technique is shown in

Table 3. SMOTE analysis.

Components		Before SMOTE	After Smote	(Mean ± SD)
		Overall (N = 400)	Overall (N = 750)
Age (Mean ± SD)		38.52 ± 16.49	38.40 ± 16.53	-
Gender, [N (%)]	Male	280 (70)	375 (50)	38.13 ± 16.51
	Female	120 (30)	375 (50)
CKD		250 (62.5)	300 (40)	38.25 ± 16.55
Non-CKD		150 (37.5)	300 (40)
Testing Samples		-	150 (20)	38.29 ± 16.49

.

3.3. Feature Selection

A heat map represents the Pearson correlation coefficient matrix. The linear correlation between two properties can be described by the Pearson correlation coefficient. Figure 4 depicts the heat map.

We observe that several of the features we developed have a stronger linear link with one another. The Pearson correlation coefficient between these two features is close to one, which supports the heat map’s message. Two features that are completely correlated with one another can be expressed by one another, which means that the information these two features carry is identical. The accuracy of the model can be increased while causing less data information loss for the two features with a high linear association by deleting one of them. Figure 4 shows that the absolute values of the heat map of attribute correlations to the class label demonstrate that age, specific gravity, and blood pressures have the highest correlations (more than 0.5). The secondary characteristics of sugar and albumin, for example, have correlations greater than 0.2.

The RFE approach is selected to choose the most prominent features by identifying those that have a high correlation with the target. DT is used as a base model for the RFE approach for feature selection. From the 24 dependent attributes included in the dataset, we chose 14 relevant features apart from class label to develop the prediction model.

Table 4. Attributes/features chosen.

Attributes/Features	Values Used
Age (A)	Discrete integer values
Blood pressure (BP)	Discrete integer values
Specific gravity (sg)	Nominal values
Albumin (Al)	Nominal values
Sugar(su)	Nominal values
Blood glucose random (bgr)	Numerical value
Blood urea (bu)	Numerical value
Serum creatinine (sc)	Numerical value
Sodium (sod)	Numerical value
Potassium (pot)	Numerical value
Haemoglobin (haem)	Numerical value
Packed cell volume	Numerical value
White blood cell count	Numerical value
Red blood cell count	Numerical value

provides the attributes that were chosen. During preprocessing, the missing values are replaced with the mean value for a few attributes, such as age, and the highest threshold was taken for a few attributes, including BP.

The nominal error rate, as determined by Little’s MCAR test on a sample of 400 records, is shown in Figure 5. Incorporating incomplete data flow factors into the inference approach is useless if they do not correlate with the result. It is a fallacious perception to integrate any attributes in the inference process only because there is a possibility that they are associated with multicollinearity in the result.

3.4. Classification

The dataset is divided into 2 subsets, each having 14 features. The training dataset consists of 75% of the total CKD dataset, i.e., 300 out of 400 records, and the testing dataset consists of the remaining 100 records out of 400 in the overall CKD dataset.

3.4.1. Regression Analysis (RA)

With a linear regression line, the dependent variable is continuous, and the independent variable is more typically continuous or discrete. For logistic regression, we use the natural logarithm, as shown in Equation (8).

$$log\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_{1}x$$

(8)

where ${\beta }_0$ is the intercept and ${\beta }_1$ is the slope. LR can be extended to situations involving outcome variables with three or more categories.

3.4.2. K-Nearest-Neighbors (k-NN)

Despite the fact that the k-NN approach has higher processing costs than other methods, it is still the best choice for applications where predictions are not demanded frequently but accuracy is critical. For distance metrics, the Euclidean metric can be used, and last, the input x gets allocated to that class that has the largest probability, as shown in Equation (9).

$$\begin{array}{cc}d\left(x,x^{|}\right)\hfill & =\mathsf{\surd }{\left(x_1-x_1^{|}\right)}^2+\dots .+{\left(x_n-x_n^{|}\right)}^2\hfill \\ & \mathrm{P}(\mathrm{y}=\mathrm{j}|\mathrm{X}=\mathrm{x})=\frac{1}{K}{\displaystyle {{\displaystyle \sum }}_{i\in A}^n}I \left(y^{\left(i\right)}=j\right)\hfill \end{array}$$

(9)

3.4.3. Decision Tree (DT) Classifier

A DT is a flowchart-like structure in which each internal node represents an attribute “test,” each branch reflects the test’s conclusion, and each leaf node represents a class label [28]. It is one of the most well-known modeling strategies because it was one of the first elite regression analysis methods individuals learned when learning predictive modeling. With a linear regression line, the dependent variable is usually continuous, while the independent variable is more commonly discrete.

3.4.4. Random Forest (RF) Classifier

A machine learning (ML) method called a random forest is employed to resolve regression and classification issues. It makes use of ensemble learning, a method for solving complicated issues by combining a number of classifiers. In a random forest algorithm, there are many different decision trees. The random forest algorithm creates a “forest” that is trained via bagging or bootstrap aggregation. Based on the decision trees’ predictions, the RF algorithm determines the result. It makes predictions by averaging or averaging out the results from different trees. The accuracy of the result grows as the number of trees increases. The decision tree algorithm’s shortcomings are eliminated with a random forest. It improves precision and lowers dataset overfitting.

3.4.5. Support Vector Classifiers (SVM)

Groups of supervised learning techniques called SVMs are employed in the identification of outliers, regression, and classification. Because they select the decision boundary that optimizes the distance from the nearest data points of all the classes, SVMs vary from other classification techniques. The maximum margin classifier or maximum margin hyper plane is the name of the decision boundary produced by SVMs.

3.4.6. XGBoost

XGBoost, an ensemble method, is used with k-fold cross-validation. The working of XGBoost and its evaluation with respect to the performance metrics is discussed in the next section.

Boosting is an ensemble modeling technique for creating a classifier that is strong from a huge number of classifiers, which are weak. It is performed by putting together a model from a series of weak models. The training data are used to develop a model to start the process. The second model is then developed, with the goal of correcting the original model’s flaws. This method is repeated until all of the training data are correctly predicted. The overall functioning of XGBoost is shown in Algorithm 1.

Algorithm 1: Overall functioning of XGBoost

A: booster: • At each iteration, choose the kind of model to run. There are two choices: ○ gradboostree: tree-based models. ○ gradboostree: linear models.

B. silent: • When this is set to 1, no running messages will be printed. • It is best to leave it at 0, as the messages may aid in comprehending the model.

C. nthread • Total cores in the system must be put here for parallel processing.

If one wishes to run on all cores, leave the value blank and the algorithm will figure it out.

Despite the fact that there are two sorts of boosters, we will only consider the tree booster because it consistently performs better than the linear booster, which is why the second one is rarely utilized.

The function y = f(x) is recovered by approximately estimating $\hat{f}$(x) while measuring how good the mapping is using a loss function $l$(y,x) and then taking the average over all the dataset points to obtain the final cost, given the dataset {(xi, yi)}i = 1…., n, where x are the features and y is the target, to solve any supervised machine learning problem.

XGBoost uses K additive trees to create the ensemble model as shown in Equation (10)

$$\hat{y}=\hat{f}\left(x\right)={{\displaystyle \sum }}_{i=0}^K\widehat{f_l} \left(x\right), \widehat{f_l}\left(x\right)\in F$$

(10)

where $F=f\left(x\right)={\mathsf{\omega }}_{q\left(x\right)}\left(q: R^m\to T, \mathsf{\omega }\in R^T\right)$.

The tree structure that transfers an input to the relevant leaf index at which it finishes up is represented by q. The number of leaves on the tree is denoted by T. Each leaf of a regression tree consists of a continuous score. The score on the i^th leaf is represented by $\mathsf{\omega }$i.

Then, minimize the following regularized objective to learn the set of functions employed in the model as shown in Equations (11) and (12).

$$l\left(\varnothing \right)={\displaystyle {{\displaystyle \sum }}_i}l\left({\hat{y}}_i,y_i\right)+{\displaystyle {{\displaystyle \sum }}_k}\mathsf{\Omega }(f_k)$$

(11)

where

$$\mathsf{\Omega }\left(f_k\right)=\gamma T+\frac{1}{2}\mathsf{\lambda }||\mathsf{\omega }{\left|k\right|}^2$$

(12)

To minimize overfitting, the additional regularization term smooths out the final learned weights. Trees with deeper depth have more leaf nodes, which can lead to overfitting on the training data, as only a few samples end up in each leaf node. As a result, we impose a penalty for the amount of leaf nodes to limit the depth and overfitting. The objective reverts to classic gradient tree boosting when the regularization parameter is set to zero.

To minimize the following objective function, as shown in Equation (13), it is necessary to add $f_t$ for the t^th iteration.

$$l^{\left(t\right)}={\displaystyle {{\displaystyle \sum }}_i}l({\hat{y}}_i{}^{t-1}+f_t\left(x_i\right),y_i)+{{\displaystyle \sum }}_t\mathsf{\Omega }\left(f_k\right)$$

(13)

The extension of a real function f(x) around a point x = a is called a one-dimensional Taylor series, and it is given by the Equation (14).

$$f\left(x\right)=f\left(a\right)+f^{|}\left(a\right)\left(x-a\right)+\frac{f^{||}}{2!}{\left(x-a\right)}^2+\dots +\frac{f^n}{n!}{\left(x-a\right)}^n+\dots ,$$

(14)

Then, the function can be approximated as shown in Equation (15) by using second order approximation while disregarding higher-order terms.

$$l^{\left(t\right)}={\displaystyle {{\displaystyle \sum }}_i^n}[ l({\hat{\mathrm{y}}}_{\mathrm{i}}{}^{t-1}, y_i)+g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_i^2\left(x_i\right)]+\mathsf{\Omega } \left(f_k\right)$$

(15)

To make the objective function simpler, delete the constant terms as depicted in Equation (16).

$$l^{\left(t\right)}={\displaystyle {{\displaystyle \sum }}_i^n}[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_i^2\left(x_i\right)]+\mathsf{\Omega } \left(f_k\right)$$

(16)

Let I_j = {i|q(x_i = j)} represent the instance collection of leaf j; that is, the collection of all the input data points that ended up in the j-th leaf node. So, for a particular tree, if one of the input data points ends up at the j-th leaf node after all of the decisions, then include it in the set I_j as shown below in Equation (17).

$$\begin{array}{cc}{l}^{\left(t\right)}=\hfill & {\displaystyle {{\displaystyle \sum }}_i^n}[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_i^2\left( x_i\right)]+\gamma T+\frac{1}{2}\mathsf{\lambda }||\mathsf{\omega }|{|}^2\hfill \\ \hfill & ={\displaystyle {{\displaystyle \sum }}_{i=1}^n}[( {{\displaystyle \sum }}_{i\in I_j}{g}_i){\mathsf{\omega }}_{\mathrm{j}}+\frac{1}{2}({{\displaystyle \sum }}_{i\in I_j}{h}_i+\mathsf{\lambda }){\displaystyle {\mathsf{\omega }}_{\mathrm{j}}^2}]+\gamma T\hfill \end{array}$$

(17)

The optimal weight ${\displaystyle {\mathsf{\omega }}_{\mathrm{j}}^{*}}$ of leaf j for a fixed tree structure q(x) can be determined by differentiating the previous equation with regard to w and equating to 0 as shown in Equation (18).

$${\displaystyle {\mathsf{\omega }}_{\mathrm{j}}^{*}}=\frac{{\displaystyle {{\displaystyle \sum }}_{i\in I_j}}{g}_i}{{\displaystyle {{\displaystyle \sum }}_{i\in I_j}}{h}_i+\mathsf{\lambda }}$$

(18)

For the time being, let us assume that we have a tree structure q for which we have determined the best weights at each leaf node. If you look at the above ${\displaystyle {\mathsf{\omega }}_{\mathrm{j}}^{*}}$ equation, you will note that the leaf nodes are missing, i.e., I_j has not been calculated yet. The following step is used to locate the best tree structure that minimizes the loss, and then we would be finished with our tree search.

Now, replace ${\displaystyle {\mathsf{\omega }}_{\mathrm{j}}^{*}}$ in the preceding equation as shown below in Equation (19) with the appropriate optimal value for the provided tree structure q.

$$l^{\left(t\right)}\left(q\right)=-\frac{1}{2}{\displaystyle {{\displaystyle \sum }}_{j=1}^T}\frac{{\left({{\displaystyle \sum }}_{i\in I_j}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_j}{h}_i+\mathsf{\lambda }}+\gamma T$$

(19)

The quality “q” of a tree structure can be measured using the above equation. The score is very much similar to that of impurity score in terms of evaluating trees, but it is calculated for a broader variety of objective functions. Generally, it is difficult to list all of the feasible tree architectures q. Instead, a greedy algorithm is used, which starts with a single leaf and later iteratively adds branches to the tree. For instance, assume that IL and IR are the left and right node instance sets after the split. If we assume I = IL$\cup$IR, the loss decrease after the split is shown in Equation (20).

$$\begin{array}{cc}{l}_{split}\hfill & =\frac{1}{2} [\frac{{\left({{\displaystyle \sum }}_{i\in I_L}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_L}{h}_i+\mathsf{\lambda }}+\frac{{\left({{\displaystyle \sum }}_{i\in I_R}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_R}{h}_i+\mathsf{\lambda }}-\frac{{\left({{\displaystyle \sum }}_{i\in I}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I}{h}_i+\mathsf{\lambda }}]-\gamma (t+1-t)\hfill \\ \hfill & =\frac{1}{2} [\frac{{\left({{\displaystyle \sum }}_{i\in I_L}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_L}{h}_i+\mathsf{\lambda }}+\frac{{\left({{\displaystyle \sum }}_{i\in I_R}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_R}{h}_i+\mathsf{\lambda }}-\frac{{\left({{\displaystyle \sum }}_{i\in I}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I}{h}_i+\mathsf{\lambda }}]-\gamma \hfill \end{array}$$

(20)

i.e., Total loss after splitting minus total loss prior to splitting.

Similar to the Gini index or entropy, this score can be used to evaluate split candidates.

XGBoost uses well-known metrics, namely Mean Squared Error (MSE), as shown in (21), and Mean Absolute Error (MAE), as shown in (22), to assess a regression model’s performance.

$$MSE=\frac{{\displaystyle {{\displaystyle \sum }}_{i=1}^n}{(y_i-y_i^p)}^2}{n}$$

(21)

$$MAE=\frac{{\displaystyle {{\displaystyle \sum }}_{i=1}^n}\left|y_i-y_i^p\right|}{n}$$

(22)

As discussed earlier, XGBoost computes the Gain of the root node by making use of Similarity Score as shown in Equations (23)–(25), respectively.

$$SimilarityScore=\frac{{(\sum {\mathrm{Residual}}_{\mathrm{i}})}^2}{\sum \left[{\mathrm{Previous} \mathrm{Probability}}_{\mathrm{i}}\ast \left(1-{\mathrm{Previous} \mathrm{Probability}}_{\mathrm{i}}\right)\right]+\mathsf{\lambda }}$$

(23)

$$Gain={\mathrm{Left}}_{\mathrm{Similarity} }+{ \mathrm{Right}}_{\mathrm{Similarity} }-{\mathrm{Root}}_{\mathrm{Similarity} }$$

(24)

$$\mathrm{Output} \mathrm{Value}=\frac{(\sum {\mathrm{Residual}}_{\mathrm{i}})}{\sum \left[{\mathrm{Previous} \mathrm{Probability}}_{\mathrm{i}}\ast \left(1-{\mathrm{Previous} \mathrm{Probability}}_{\mathrm{i}}\right)\right]+\mathsf{\lambda }}$$

(25)

4. Results and Discussion

Figure 6 displays Area under the (ROC) Curve. The LR, SVM, DT, RF, KNN, and XGBoost models are represented by lines of a different color in the figure. The black curve’s AUC value of XGBoost is somewhat higher than that of the other four curves, indicating that it has the best performance out of the five models.

Initially, the few vital steps taken in the preprocessing stages are evaluated. The essential process is to assess the estimation accuracy of mean and mode methods in identifying the missing values over 400 considered instances. Thus, Figure 7a,b depicts the resultants of the process in comparison with the randomized manual verifications.

The results precisely state that the average estimation accuracy of both mean and mode methods in identifying numerical and nominal missing values are 97.77% and 96.93%, respectively, which is 5.71% more accurate than the randomized manual verifications. The values in the confusion matrix for all ML algorithms being implemented is shown in Figure 8.

Precision indicates what amount of the total positive anticipated is genuinely positive. The ratio of true positives (TPs) to total number of TPs and true negatives are called precision (TNs). Precision is a good statistic to utilize when the cost of false positives (FNs) is high. Using Equation (26), the precision is calculated.

$$\mathrm{Precision}=\frac{\mathrm{TPs}}{\mathrm{TPs}+\mathrm{FPs}}$$

(26)

The precision values of LR, SVM, KNN, DT, RF, and XGBoost classifiers are 96.3%, 95.69%, 91.18, 91.95, 93.10%, and 98.9%, respectively.

Recall quantifies how many right positive predictions were made. The equation used to calculate the recall is (27) shown below.

$$\mathrm{Recall}=\frac{\mathrm{TPs}}{\mathrm{TPs}+\mathrm{FNs}}$$

(27)

Recall of LR, SVM, KNN, DT, RF, and XGBoost classifiers are 97.56%, 97.8%, 96.47%, 94.11%, 96.42%, and 98.9% respectively.

The F1-score considers both recall and precision. F1-score is computed using the below Equation (28).

$$\mathrm{F}1 \mathrm{Score}=2\ast \frac{\mathrm{precision}\ast \mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}$$

(28)

The F1-score of the SVM, LR, DT, KNN, RF, and XGBoost classifiers is 96.73%, 96.93%, 93.01%, 94.75%, 94.73%, and 98.9%, respectively. The performance evaluation of these ML algorithms is shown in Figure 9.

One technique to determine how often an ML classification system properly classifies a record or instance is looking at accuracy. The Equation (29) is used to compute accuracy.

$$\mathrm{Accuracy}=\frac{\mathrm{TNs}+\mathrm{TPs}}{\mathrm{TNs}+\mathrm{TPs}+\mathrm{FPs}+\mathrm{FNs}}$$

(29)

The performance of different ML Techniques for CKD classification is shown in

Table 5. Performance in classification of CKD.

ML Techniques	Accuracy	Precision	Recall	F1-Score
LR	95.00	96.30	97.56	96.93
KNN	91.00	91.18	96.47	94.75
RF	90.00	93.10	96.42	94.73
DT	88.00	91.95	94.11	93.01
SVM	94.00	95.69	97.80	96.73
XGBoost (EL Method)	98.00	98.90	98.90	98.90

in terms of percentage.

Table 6. Performance comparison with other ensemble methods.

ML Techniques	Accuracy	Precision	Recall	F1-Score
Boosting	95.44	94.22	96.66	98.01
Bagging	93.62	91.22	92.55	94.44
Voting	94.66	94.70	96.77	95.34
Rotation Forest	91.20	91.88	92.24	90.40
XGBoost (EL Method)	98.00	98.90	98.90	98.90

shows the comparison of XGBoost performance with other ensemble techniques and XGBoost again outperforms with an accuracy of 98.33%.

Figure 10 exposes the superior performance of the proposed EL method during the testing phase in the classification of CKD. Such test validation is required to monitor the development of the trained algorithm and fine-tune or maximize its performance. Therefore, the learnt logic of the EL technique is regularly evaluated on a sample size of about 100 instances, and the findings (average accuracy is 97.78%) acquired provide concise evidence that the system maintains ideal consistency and precision.

This accuracy provides the correctly classified instances of CKD. The accuracy of different ML techniques in the classification of CKD is shown in Figure 11. It is noted that XGBoost exhibits the best prediction with an accuracy of 98.93% and outperforms compared to other algorithms in classifying the instances of the records of the dataset into “ckd” and “notckd.”

All the performance measures reported in this study are statistically different compared to the other studies, as shown in

Table 7. Comparison of the outcomes of this study with other studies found in the literature.

Study and Year	Sampling Strategy	Accuracy
Ifraz et al. (2021) [32]	70–30% training-testing	97.00%
S. Y. Yashfi et al. (2020) [33]	10-fold cross-validation	97.12%
Cheng-Sheng Yu et al. (2020) [34]	10-fold cross-validation	90.40%
Kovesdy et al. (2018) [35]	70–30% training-testing	95.0%
Proposed model	75–25% training-testing	98.00%

.

5. Conclusions

This study sheds light on how CKD patients might be diagnosed and treated early on in the disease’s progression. A total of 400 patients contributed to the dataset, which included 24 distinct characteristics. After the estimation of missing values using the mean and mode methods, KNN imputation is employed to fill in the missing values. Later, the RFE process is applied to select the desirable attribute of CKD, thus enhancing the data quality in the preprocessing stages. To classify features, KNN, SVM, RF, DT, LR, and XGBoost were used. All of the classifiers’ parameters were tweaked to achieve the best classification results, and all of the algorithms produced promising results. The proposed model also demonstrated decreased entropy by showing very less impurity measure. All other algorithms were outperformed by the XGBoost technique, which achieved the best precision, recall, F1-score, and accuracy of 98.90%, 98.90%, 98.90%, and 98.00%, respectively. Future work is planned to include the deep learning method, especially to deal with raw CKD informative image datasets.