Strain Prediction Using Deep Learning during Solidification Crack Initiation and Growth in Laser Beam Welding of Thin Metal Sheets
Abstract
1. Introduction
- A video of strained welding using CTW was generated;
- Two deep neural networks called StrainNetR and StrainNetD for strain prediction were proposed;
- The two models were trained and evaluated on the real generated dataset.
2. Methods
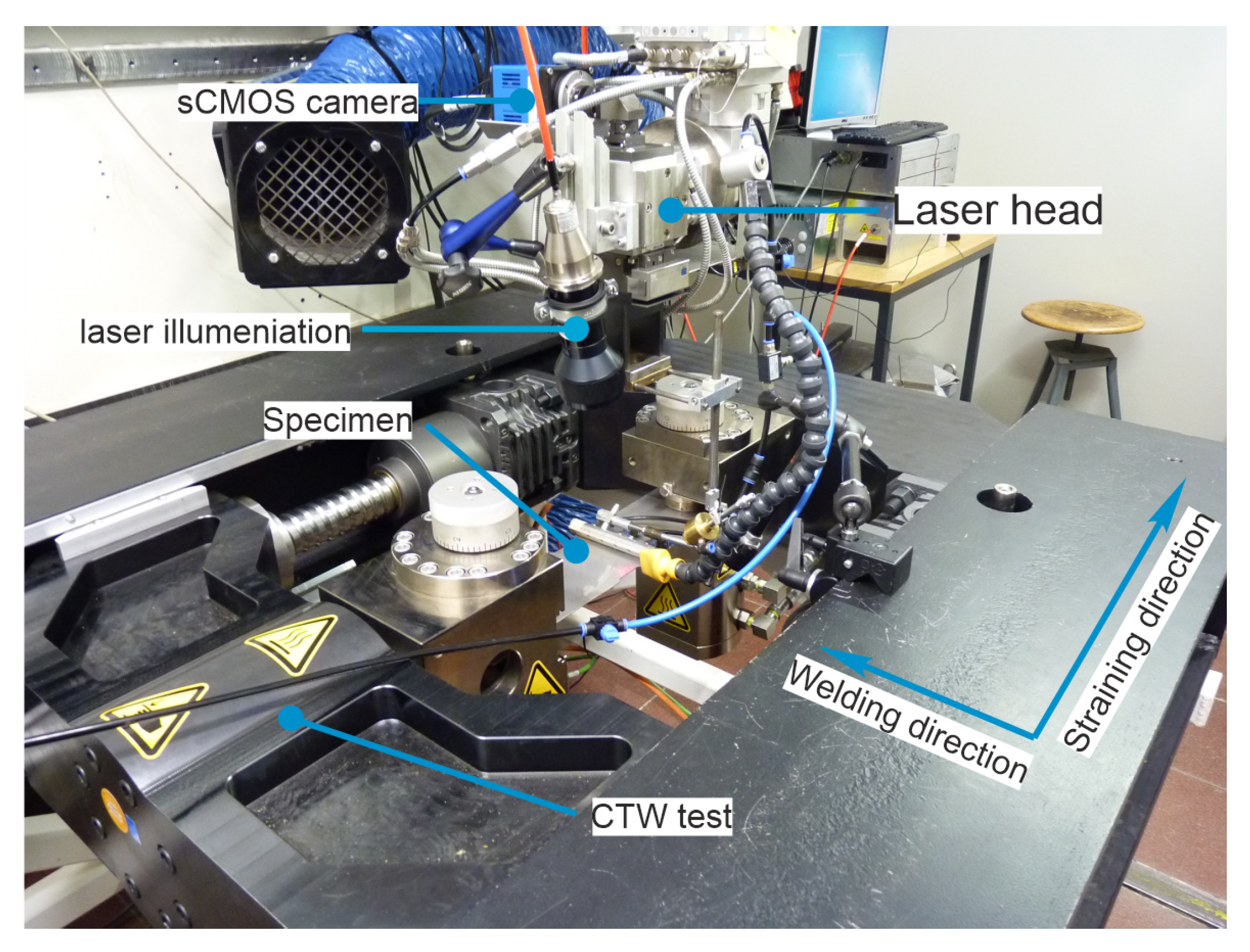
2.1. Data Collection
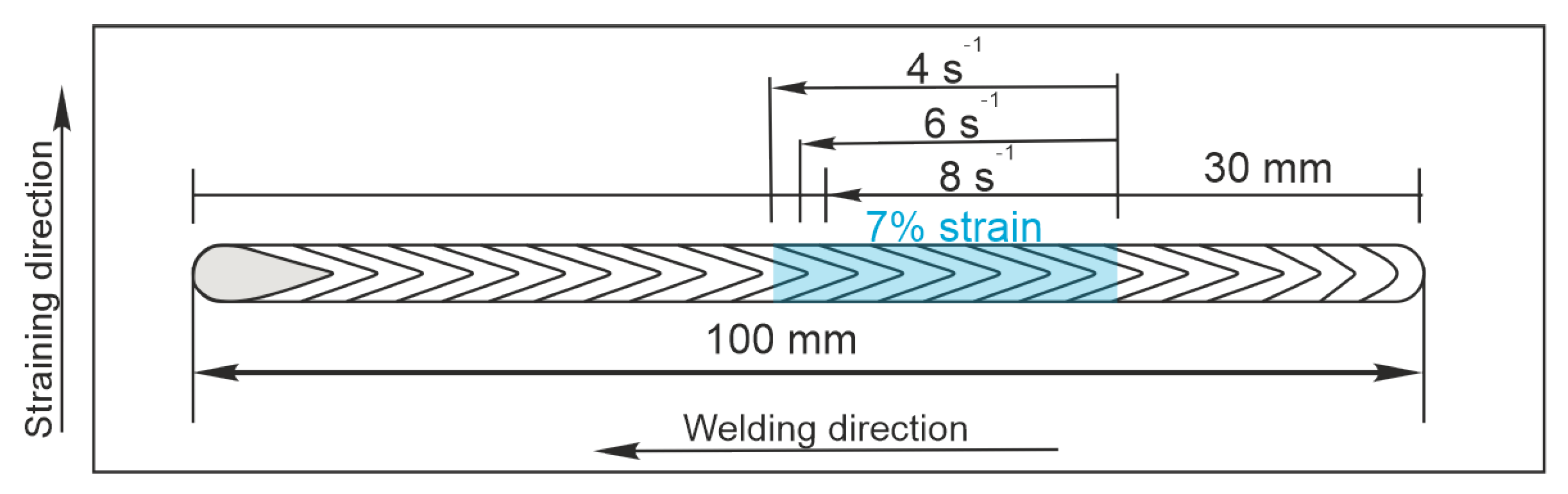
2.1.1. Welding under External Strain
2.1.2. Data Acquisition
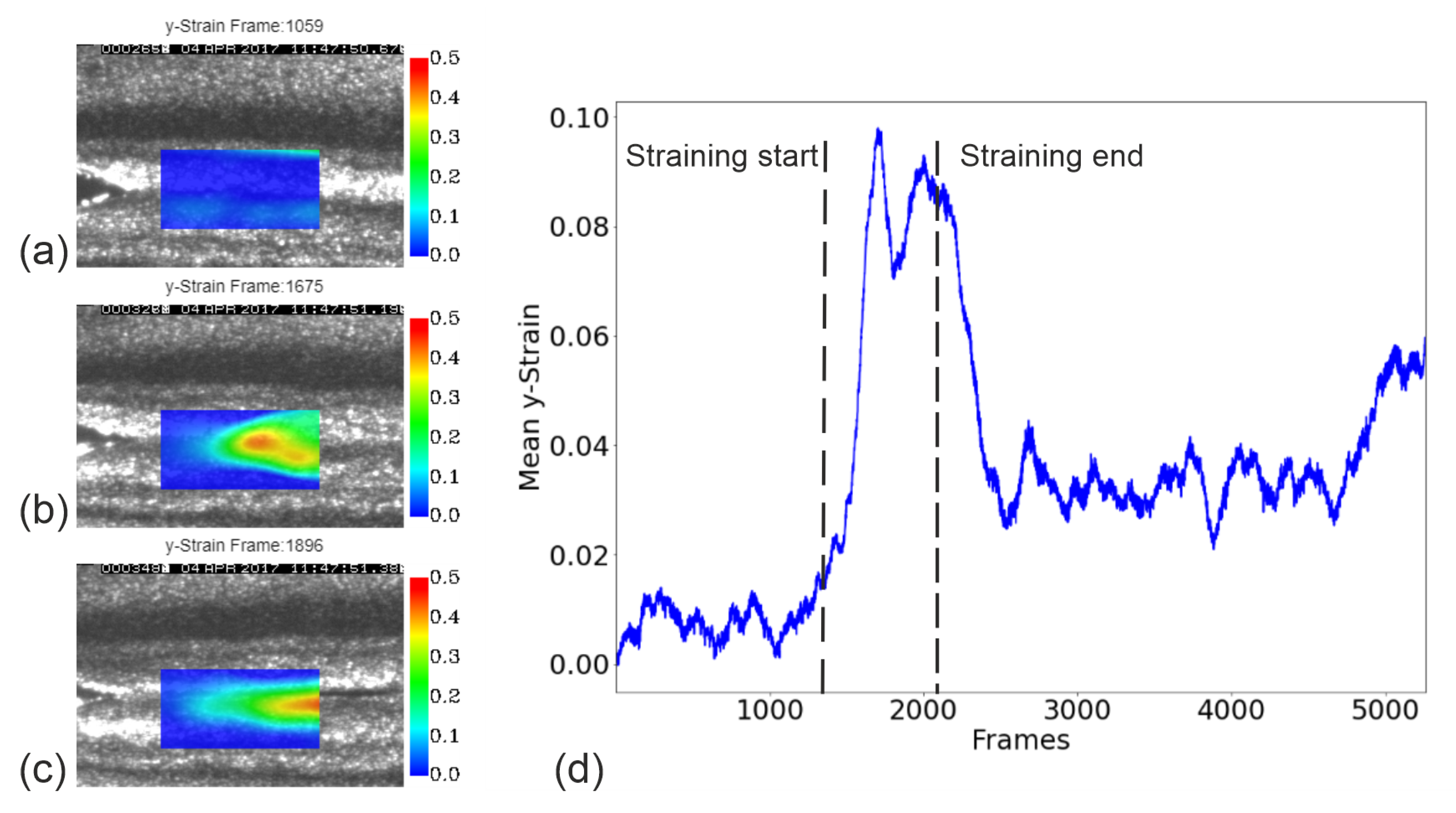
2.1.3. Strain Estimation
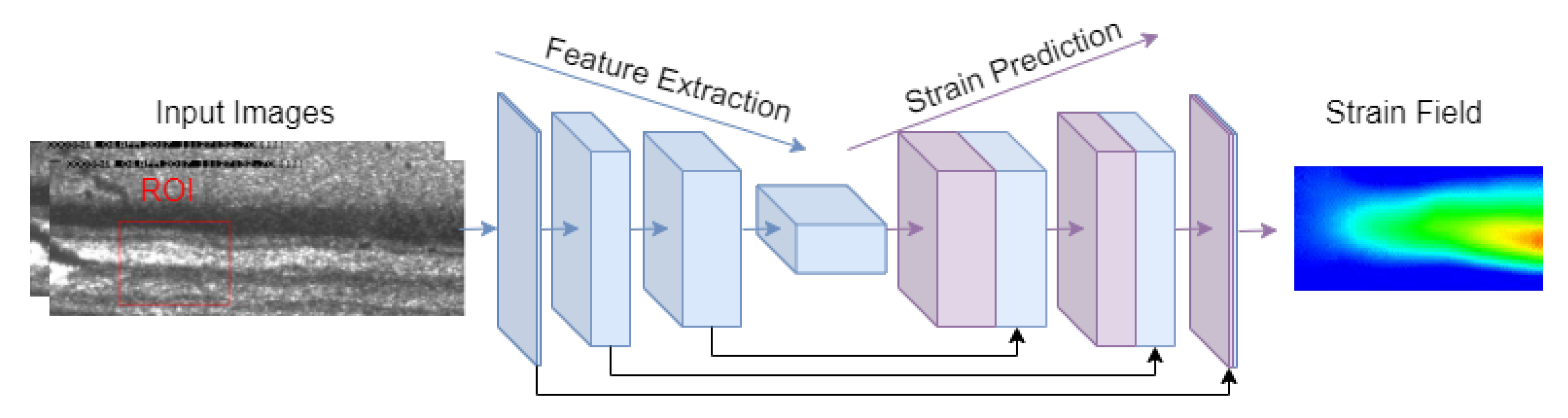
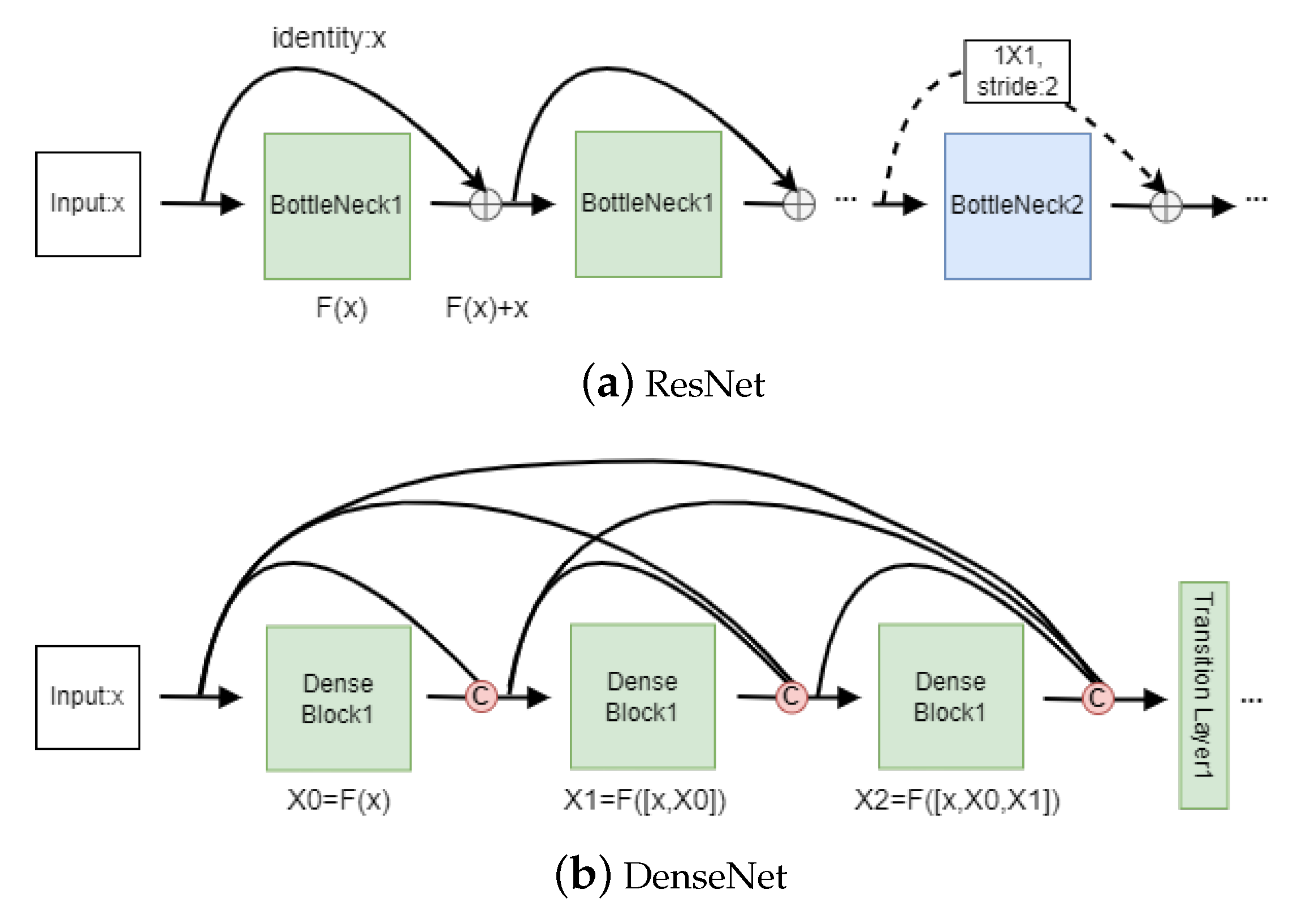
2.2. Neural Network Model Architecture
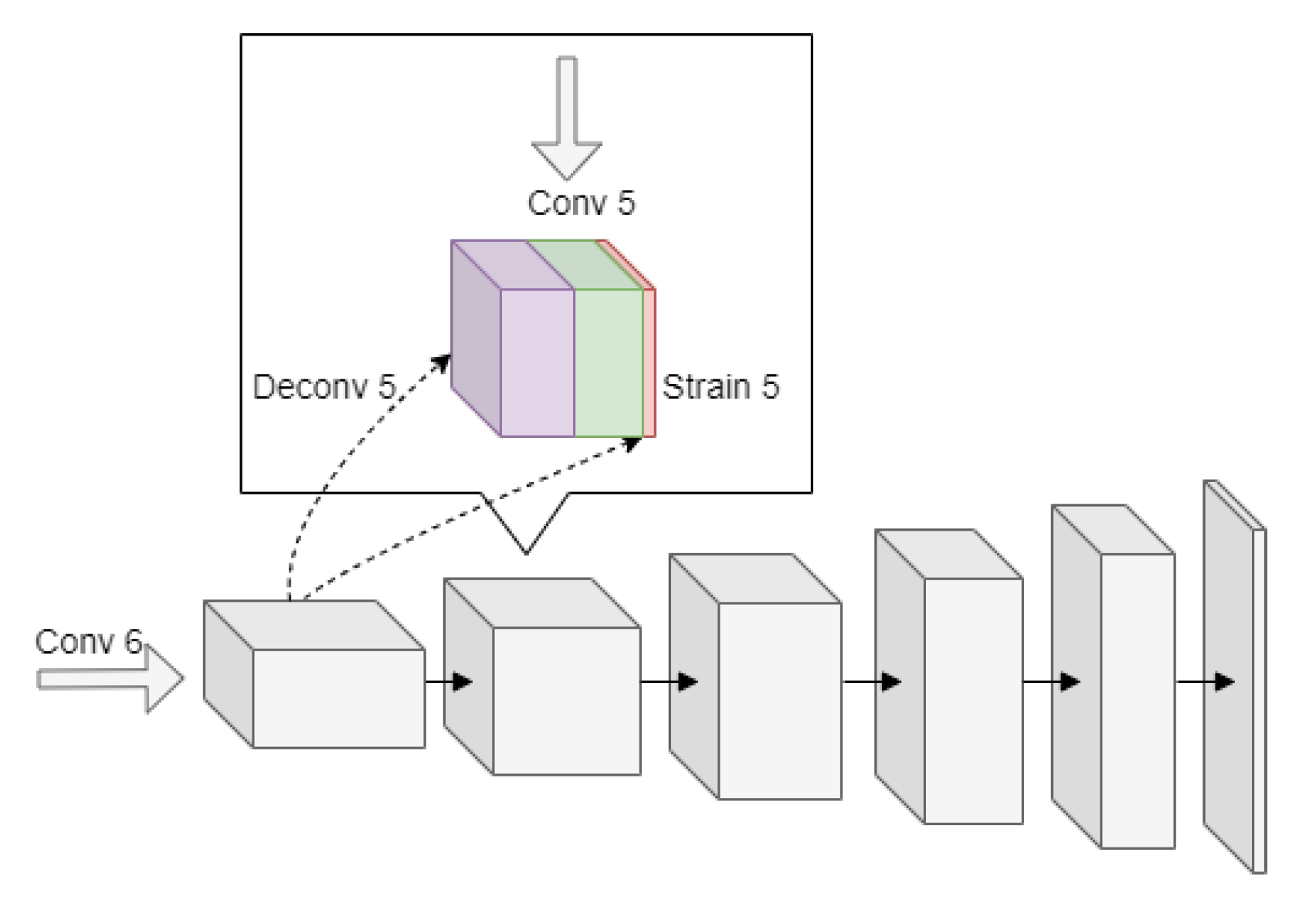
2.2.1. The Encoder
2.2.2. Decoder
3. Results of the Strain Prediction
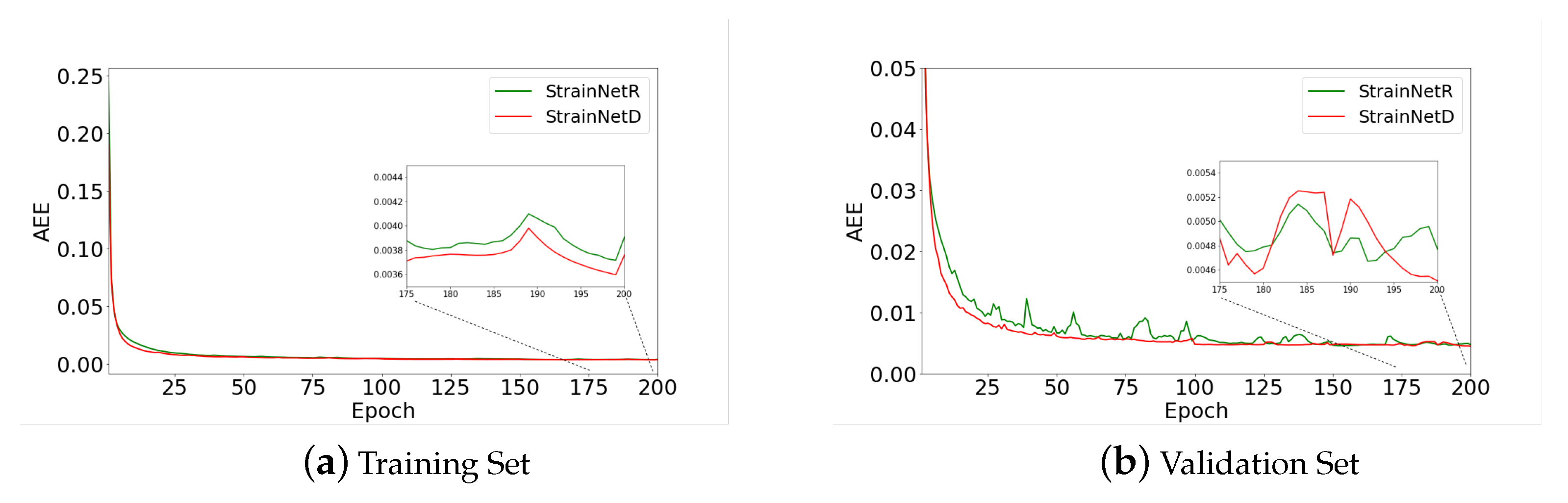
3.1. Training Details
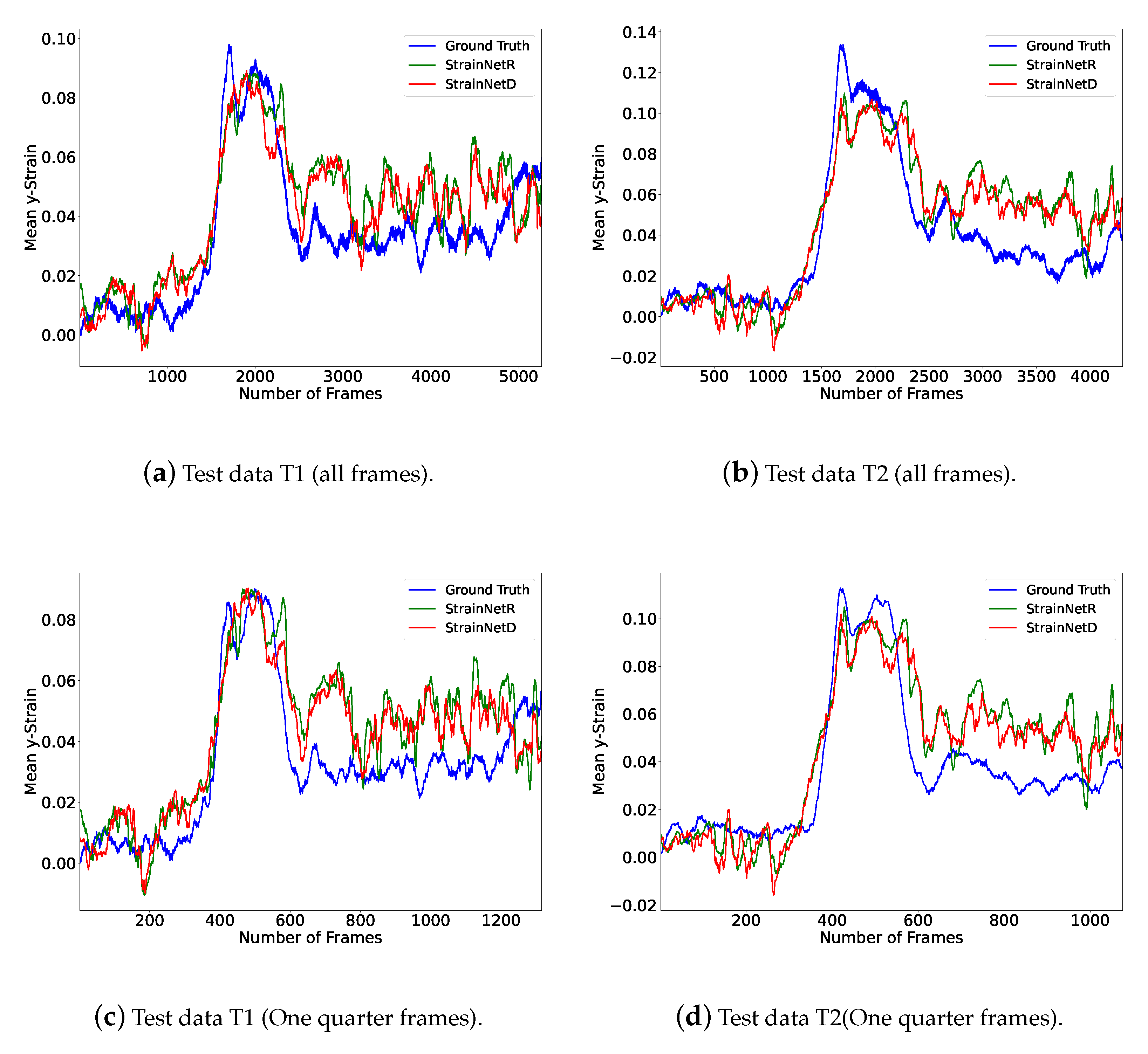
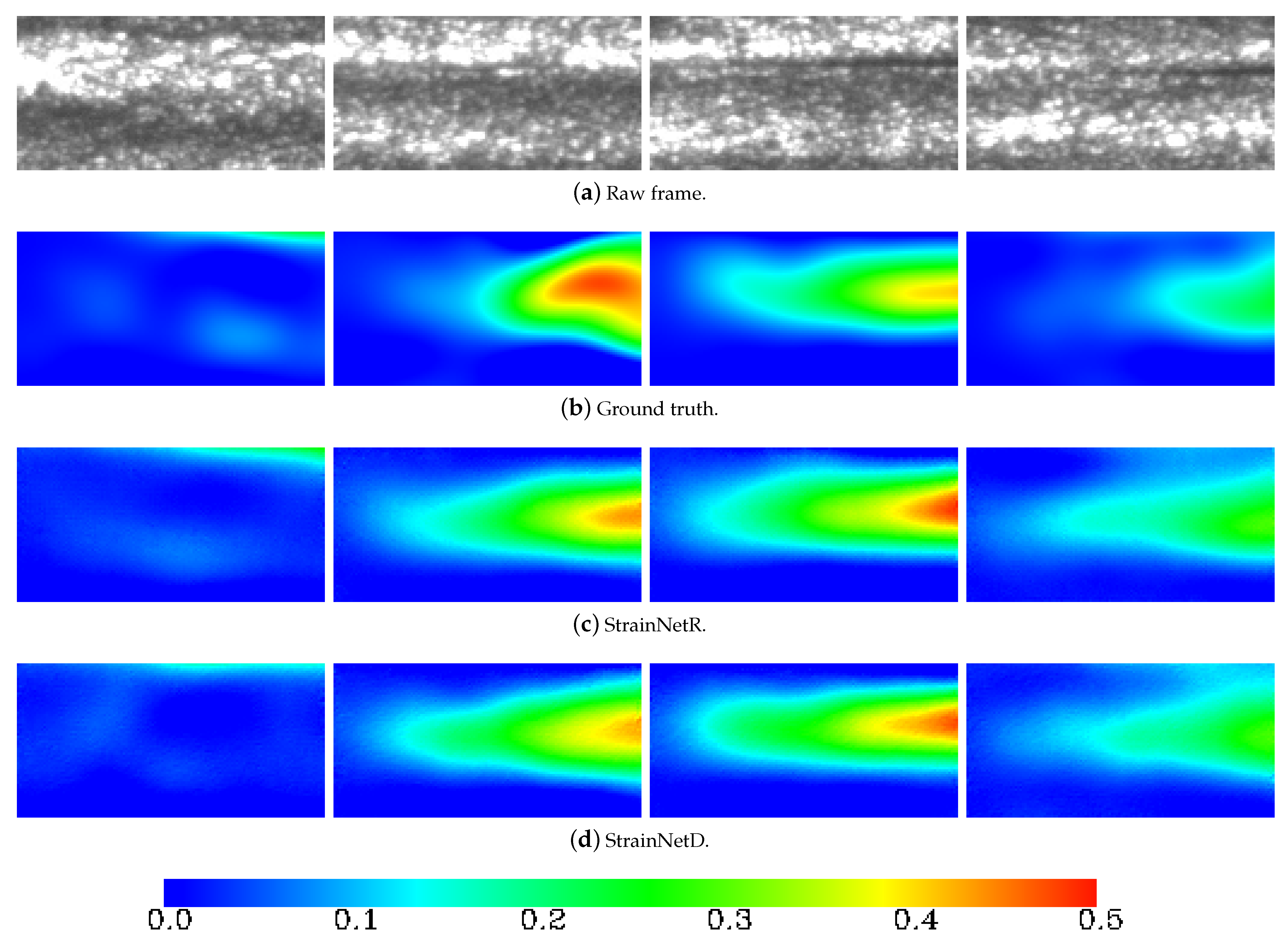
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| DIC | Digital image correlation |
| CNN | Convolutional neural network |
| CTW test | Controlled tensile weldabilit test |
| AEE | Average endpoint error |
| GT | Ground truth |
| flops | Floating point operations per second |
References
- Pellini, W.S. Strain theory of hot tearing. Foundry 1952, 80, 125–133. [Google Scholar]
- Apblett, W.; Pellini, W. Factors which influence weld hot cracking. Weld. J. 1954, 33, 83–90. [Google Scholar]
- Prokhorov, N. The problem of the strength of metals while solidifying during welding. Svarochnoe Proizv. 1956, 6, 5–11. [Google Scholar]
- Prokhorov, N. The Technological Strength of Metals While Crystallizing during Welding; Technical Report, IX-479-65; IIW-Doc, 1965. [Google Scholar]
- De Strycker, M.; Lava, P.; Van Paepegem, W.; Schueremans, L.; Debruyne, D. Measuring welding deformations with the digital image correlation technique. Weld. J. 2011, 90, 107S–112S. [Google Scholar]
- Shibahara, M.; Onda, T.; Itoh, S.; Masaoka, K. Full-field time-series measurement for three-dimensional deformation under welding. Weld. Int. 2014, 28, 856–864. [Google Scholar] [CrossRef]
- Shibahara, M.; Yamaguchi, K.; Onda, T.; Itoh, S.; Masaoka, K. Studies on in-situ full-field measurement for in-plane welding deformation using digital camera. Weld. Int. 2012, 26, 612–620. [Google Scholar] [CrossRef]
- Shibahara, M.; Kawamura, E.; Ikushima, K.; Itoh, S.; Mochizuki, M.; Masaoka, K. Development of three-dimensional welding deformation measurement based on stereo imaging technique. Weld. Int. 2012, 27, 920–928. [Google Scholar] [CrossRef]
- Chen, J.; Yu, X.; Miller, R.G.; Feng, Z. In situ strain and temperature measurement and modelling during arc welding. Sci. Technol. Weld. Join. 2015, 20, 181–188. [Google Scholar] [CrossRef]
- Chen, J.; Feng, Z. Strain and distortion monitoring during arc welding by 3D digital image correlation. Sci. Technol. Weld. Join. 2018, 23, 536–542. [Google Scholar] [CrossRef]
- Gollnow, C.; Kannengiesser, T. Hot cracking analysis using in situ digital image correlation technique. Weld. World 2013, 57, 277–284. [Google Scholar] [CrossRef]
- Gao, H.; Agarwal, G.; Amirthalingam, M.; Hermans, M.; Richardson, I. Investigation on hot cracking during laser welding by means of experimental and numerical methods. Weld. World 2018, 62, 71–78. [Google Scholar] [CrossRef]
- Hagenlocher, C.; Stritt, P.; Weber, R.; Graf, T. Strain signatures associated to the formation of hot cracks during laser beam welding of aluminum alloys. Opt. Lasers Eng. 2018, 100, 131–140. [Google Scholar] [CrossRef]
- Baker, S.; Patil, R.; Cheung, K.M.; Matthews, I. Lucas-Kanade 20 Years on: Part 5; Tech. Rep. CMU-RI-TR-04-64; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2004. [Google Scholar]
- Pełczyński, P.; Szewczyk, W.; Bieńkowska, M. Single-camera system for measuring paper deformations based on image analysis. Metrol. Meas. Syst. 2021, 28, 509–522. [Google Scholar]
- Hoffmann, H.; Vogl, C. Determination of true stress-strain-curves and normal anisotropy in tensile tests with optical strain measurement. CIRP Ann. 2003, 52, 217–220. [Google Scholar] [CrossRef]
- Gong, X.; Bansmer, S.; Strobach, C.; Unger, R.; Haupt, M. Deformation measurement of a birdlike airfoil with optical flow and numerical simulation. AIAA J. 2014, 52, 2807–2816. [Google Scholar] [CrossRef]
- Bakir, N.; Gumenyuk, A.; Rethmeier, M. Investigation of solidification cracking susceptibility during laser beam welding using an in-situ observation technique. Sci. Technol. Weld. Join. 2018, 23, 234–240. [Google Scholar] [CrossRef]
- Bakir, N.; Pavlov, V.; Zavjalov, S.; Volvenko, S.; Gumenyuk, A.; Rethmeier, M. Development of a novel optical measurement technique to investigate the hot cracking susceptibility during laser beam welding. Weld. World 2019, 63, 435–441. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Ranjan, A.; Black, M.J. Optical flow estimation using a spatial pyramid network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4161–4170. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.Y.; Kautz, J. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8934–8943. [Google Scholar]
- Hui, T.W.; Tang, X.; Loy, C.C. Liteflownet: A lightweight convolutional neural network for optical flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8981–8989. [Google Scholar]
- Hur, J.; Roth, S. Iterative residual refinement for joint optical flow and occlusion estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5754–5763. [Google Scholar]
- Yin, Z.; Darrell, T.; Yu, F. Hierarchical discrete distribution decomposition for match density estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6044–6053. [Google Scholar]
- Yang, G.; Ramanan, D. Volumetric correspondence networks for optical flow. Adv. Neural Inf. Process. Syst. 2019, 32, 794–805. [Google Scholar]
- Zhao, S.; Sheng, Y.; Dong, Y.; Chang, E.I.; Xu, Y. Maskflownet: Asymmetric feature matching with learnable occlusion mask. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6278–6287. [Google Scholar]
- Teed, Z.; Deng, J. Raft: Recurrent all-pairs field transforms for optical flow. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 402–419. [Google Scholar]
- Sui, X.; Li, S.; Geng, X.; Wu, Y.; Xu, X.; Liu, Y.; Goh, R.; Zhu, H. CRAFT: Cross-Attentional Flow Transformer for Robust Optical Flow. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2022; pp. 17602–17611. [Google Scholar]
- Xu, H.; Zhang, J.; Cai, J.; Rezatofighi, H.; Tao, D. GMFlow: Learning Optical Flow via Global Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8121–8130. [Google Scholar]
- Zhao, S.; Zhao, L.; Zhang, Z.; Zhou, E.; Metaxas, D. Global Matching with Overlapping Attention for Optical Flow Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17592–17601. [Google Scholar]
- Hu, L.; Zhao, R.; Ding, Z.; Ma, L.; Shi, B.; Xiong, R.; Huang, T. Optical Flow Estimation for Spiking Camera. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17844–17853. [Google Scholar]
- Rezaie, A.; Achanta, R.; Godio, M.; Beyer, K. Comparison of crack segmentation using digital image correlation measurements and deep learning. Constr. Build. Mater. 2020, 261, 120474. [Google Scholar] [CrossRef]
- Boukhtache, S.; Abdelouahab, K.; Berry, F.; Blaysat, B.; Grediac, M.; Sur, F. When deep learning meets digital image correlation. Opt. Lasers Eng. 2021, 136, 106308. [Google Scholar] [CrossRef]
- Yang, R.; Li, Y.; Zeng, D.; Guo, P. Deep DIC: Deep learning-based digital image correlation for end-to-end displacement and strain measurement. J. Mater. Process. Technol. 2022, 302, 117474. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J. DIC-Net: Upgrade the performance of traditional DIC with Hermite dataset and convolution neural network. Opt. Lasers Eng. 2023, 160, 107278. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Q.; Xie, H.; Li, Q.; Sun, G. Digital image correlation (DIC) based damage detection for CFRP laminates by using machine learning based image semantic segmentation. Int. J. Mech. Sci. 2022, 230, 107529. [Google Scholar] [CrossRef]
- Bakir, N.; Gumenyuk, A.; Rethmeier, M. Numerical simulation of solidification crack formation during laser beam welding of austenitic stainless steels under external load. Weld. World 2016, 60, 1001–1008. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24 August 1981; Volume 81. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]

| C | Cr | Ni | Mn | Mo | Si | P | S | N | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 0.03 | 16.95 | 10.57 | 1.36 | 2.28 | 0.39 | 0.04 | 0.004 | 0.019 | Bal. |
| Train/Validation Set | CTW Strain in % | CTW Strain Rate in s | Data Quantity (Images) |
|---|---|---|---|
| TD1 | 7 | 4 | 5030 |
| TD2 | 7 | 4 | 5080 |
| TD3 | 7 | 6 | 5000 |
| TD4 | 7 | 6 | 5000 |
| Test Set | CTW Strain in % | CTW Strain Rate in s | Data Quantity (Images) |
| T1 | 7 | 8 | 5260 |
| T2 | 7 | 8 | 4300 |
| StrainNetR | StrainNetD | ||||
|---|---|---|---|---|---|
| Layer Name | Kernel Size | Output Size | Layer Name | Kernel Size | Output Size |
| Convolution | , 32 | Convolution | , 32 | ||
| Bottleneck1 | Dense Block1 | ||||
| Transition Layer1 | |||||
| Bottleneck2 | Dense Block2 | ||||
| Transition Layer2 | |||||
| Bottleneck3 | Dense Block3 | ||||
| Transition Layer3 | |||||
| Bottleneck4 | Dense Block4 | ||||
| Pooling | |||||
| Model | Parameters (M) | Flops (G) | AEE | Time (ms) |
|---|---|---|---|---|
| StrainNetR | 1.47 | 0.88 | 0.0439 | 3.39 |
| StrainNetD | 0.57 | 1.27 | 0.0427 | 5.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, W.; Bakir, N.; Gumenyuk, A.; Rethmeier, M.; Wolter, K. Strain Prediction Using Deep Learning during Solidification Crack Initiation and Growth in Laser Beam Welding of Thin Metal Sheets. Appl. Sci. 2023, 13, 2930. https://doi.org/10.3390/app13052930
Huo W, Bakir N, Gumenyuk A, Rethmeier M, Wolter K. Strain Prediction Using Deep Learning during Solidification Crack Initiation and Growth in Laser Beam Welding of Thin Metal Sheets. Applied Sciences. 2023; 13(5):2930. https://doi.org/10.3390/app13052930
Chicago/Turabian StyleHuo, Wenjie, Nasim Bakir, Andrey Gumenyuk, Michael Rethmeier, and Katinka Wolter. 2023. "Strain Prediction Using Deep Learning during Solidification Crack Initiation and Growth in Laser Beam Welding of Thin Metal Sheets" Applied Sciences 13, no. 5: 2930. https://doi.org/10.3390/app13052930
APA StyleHuo, W., Bakir, N., Gumenyuk, A., Rethmeier, M., & Wolter, K. (2023). Strain Prediction Using Deep Learning during Solidification Crack Initiation and Growth in Laser Beam Welding of Thin Metal Sheets. Applied Sciences, 13(5), 2930. https://doi.org/10.3390/app13052930







