Sum Rate Optimization Scheme of UAV-Assisted NOMA under Hardware Impairments
Abstract
1. Introduction
1.1. Background
1.2. Related Works and Motivation
1.3. Contributions and Organization
2. System Model and Problem Formulation
Problem Formulation
3. Optimization of UAV Position and Power Allocation
3.1. Uav Position Optimization
3.2. Power Allocation Optimization
4. Proposed Algorithm and Complexity Analysis
| Algorithm 1 Iterative Algorithm for P1 |
|
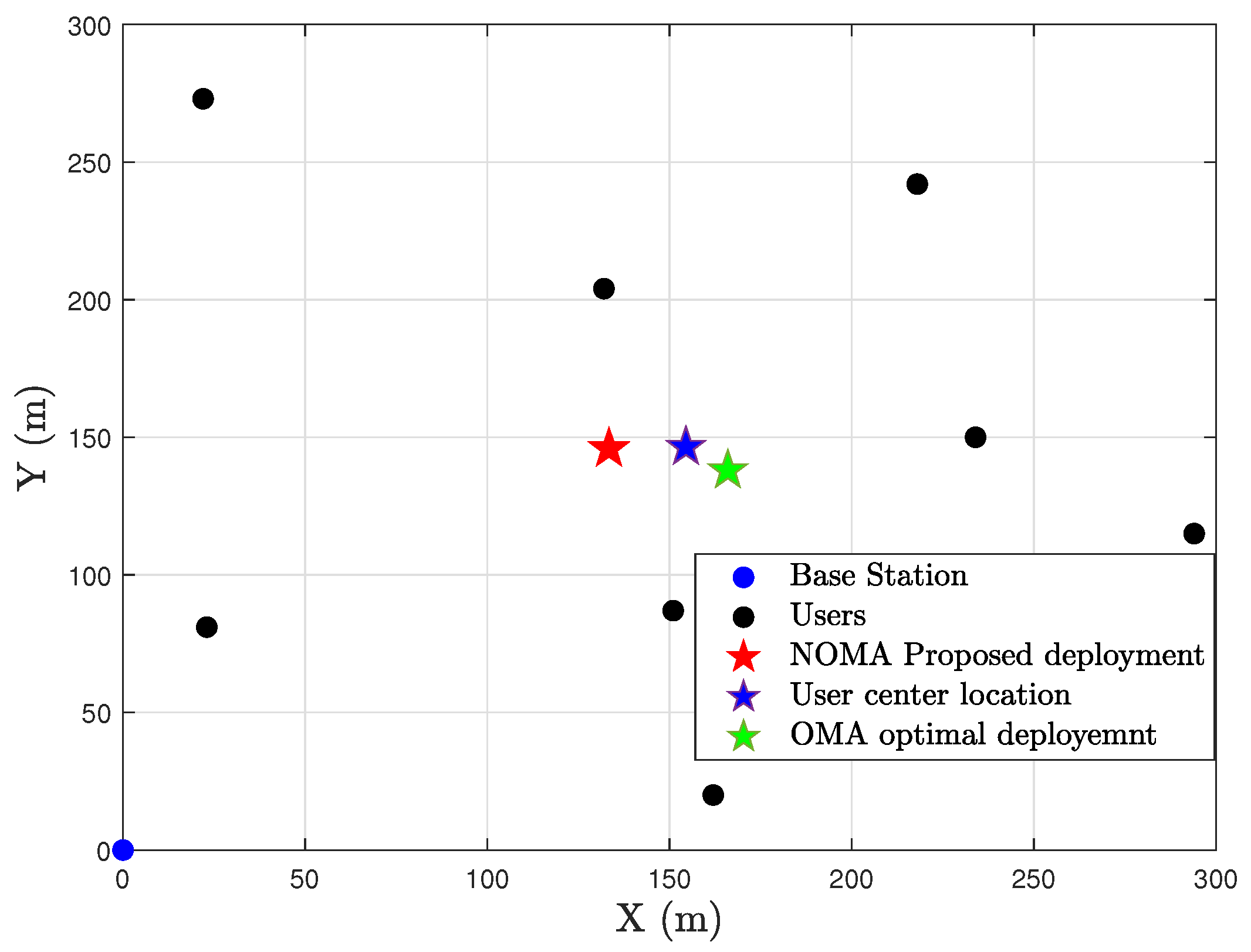
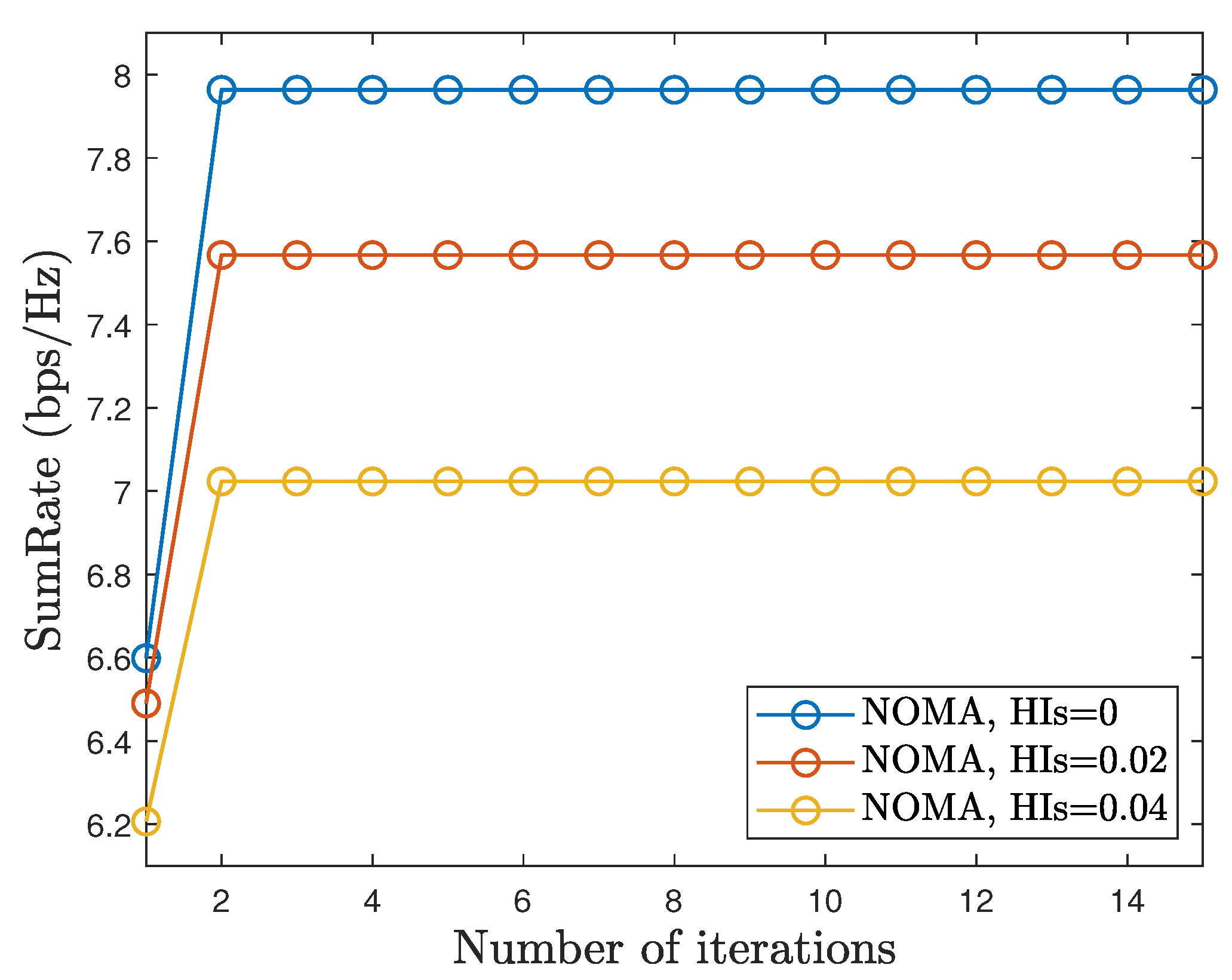
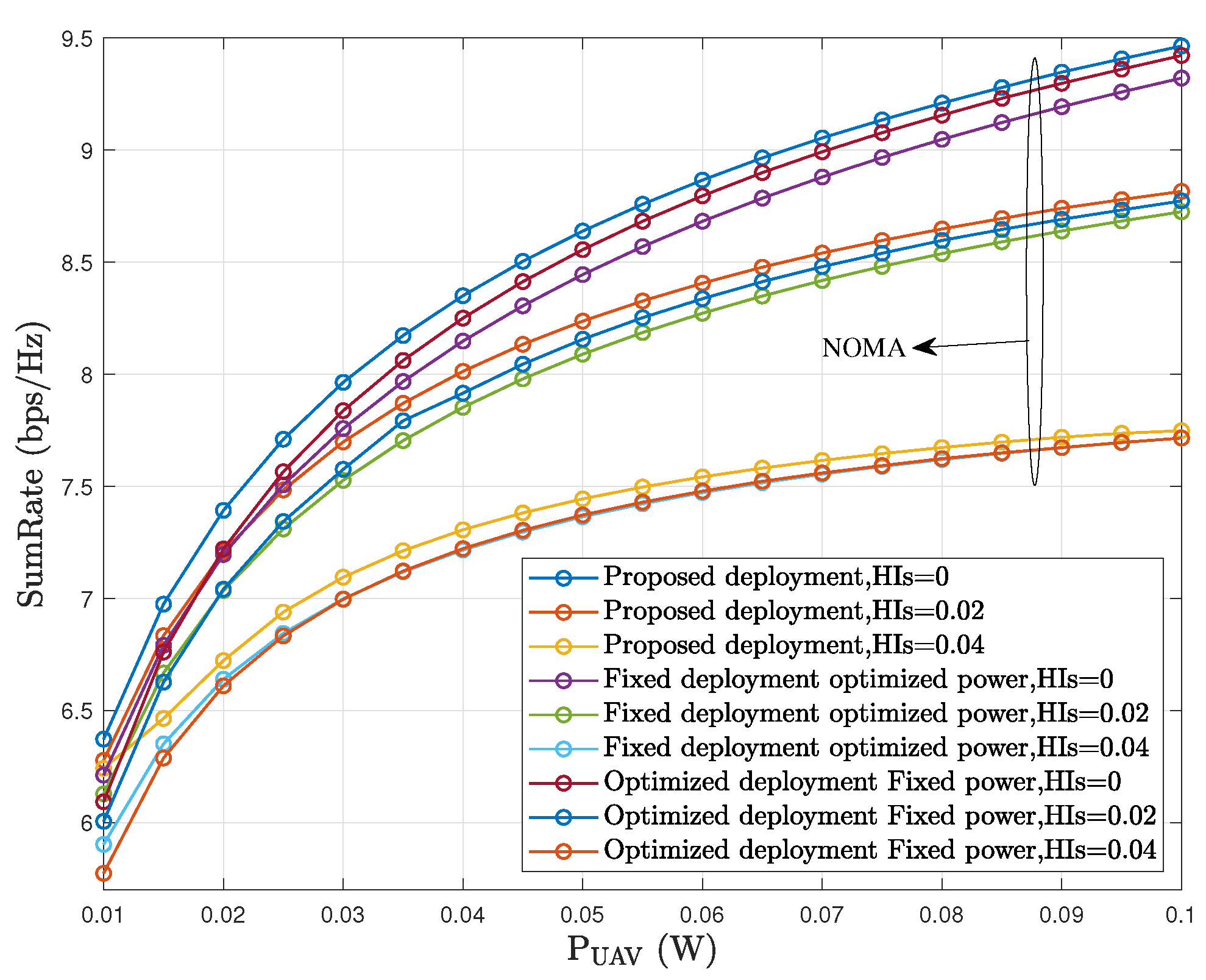
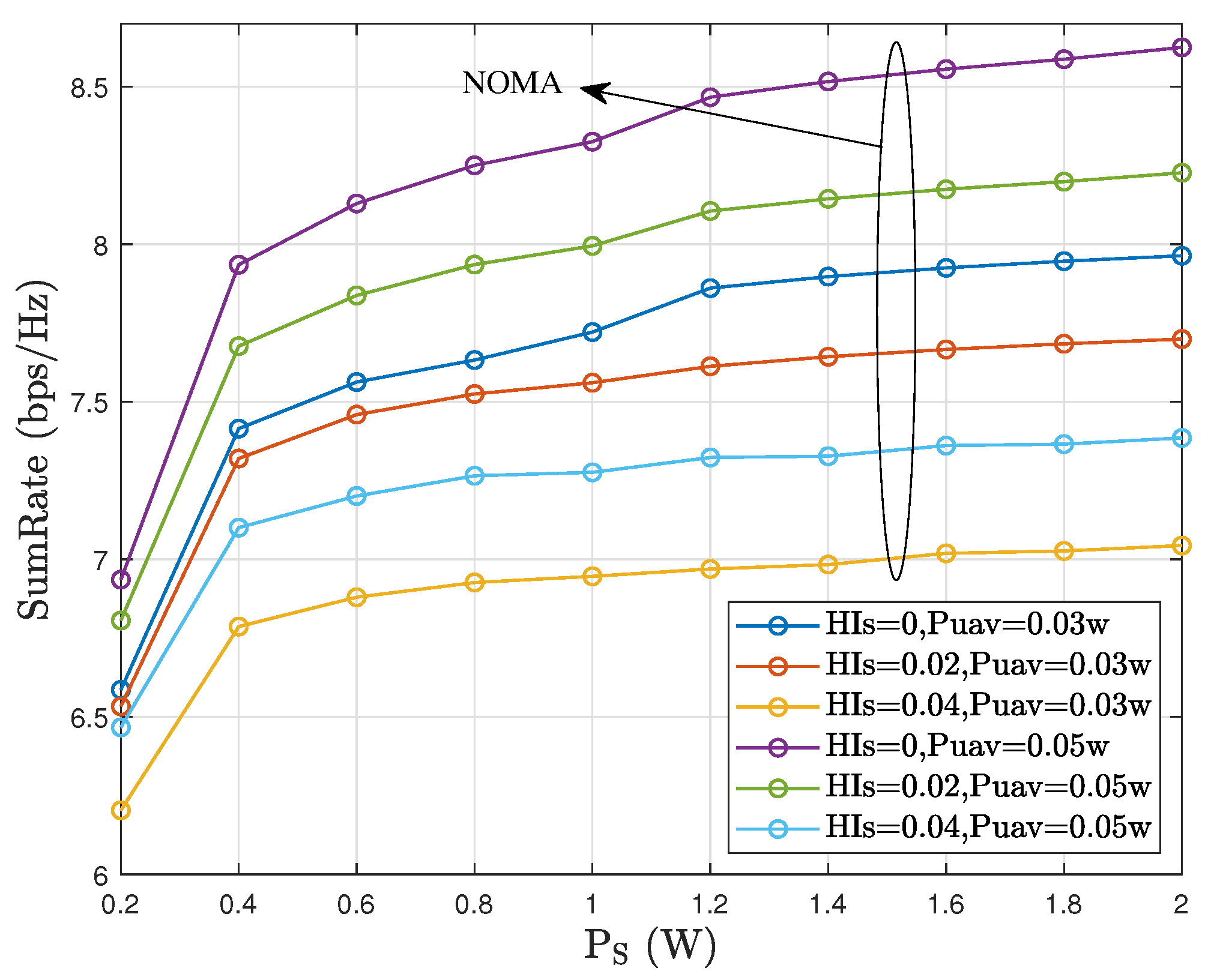
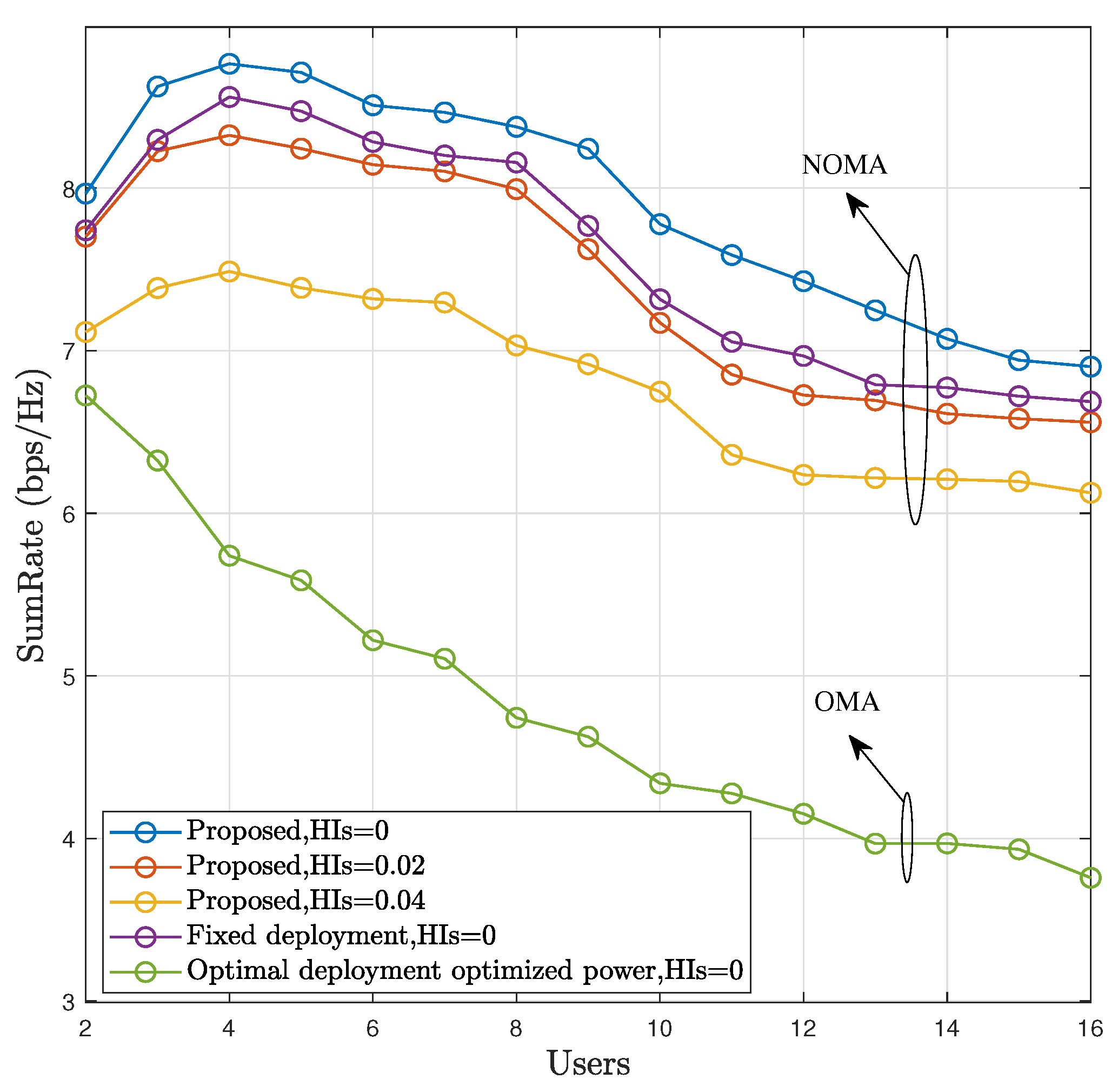
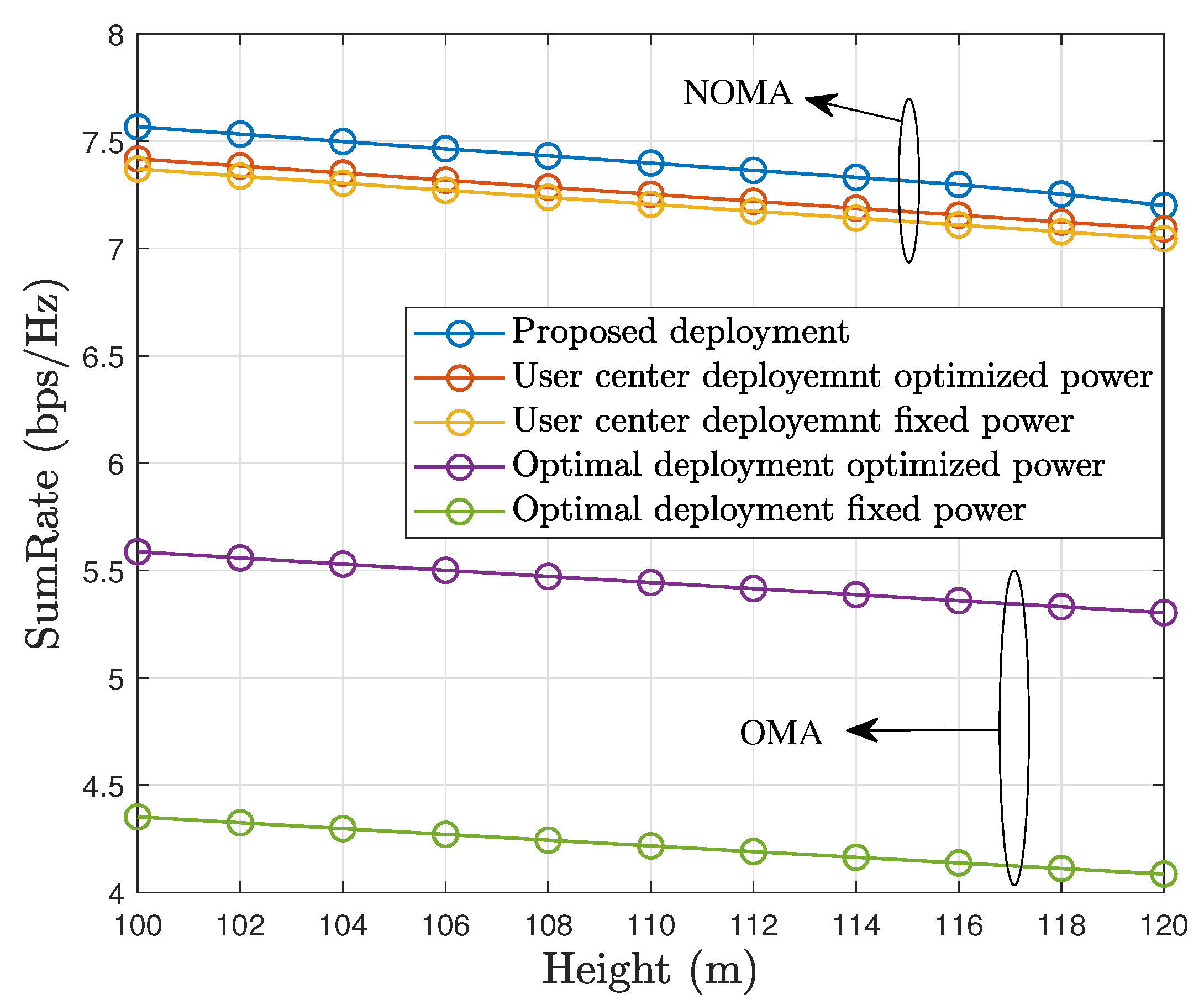
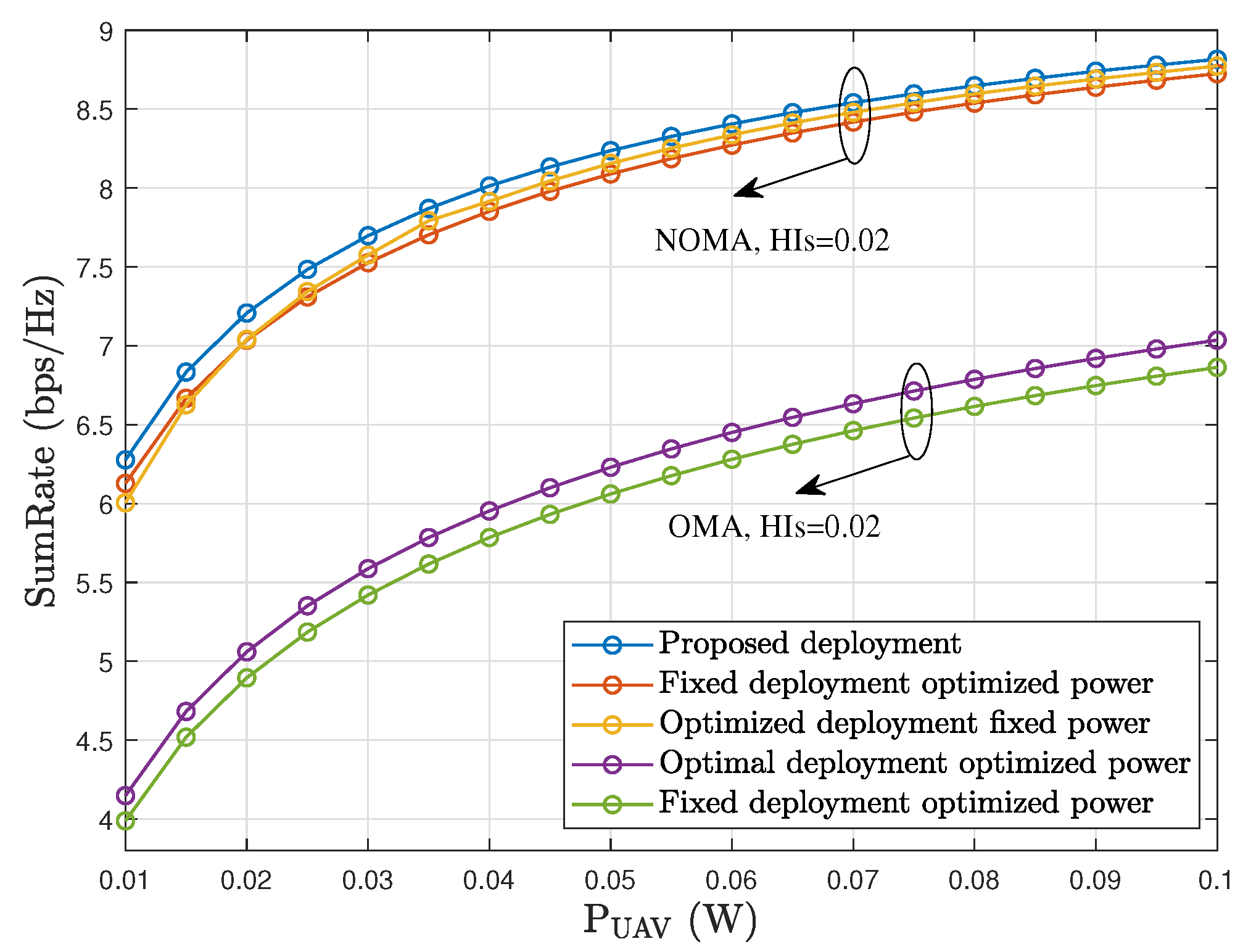
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khan, W.U.; Li, X.; Zeng, M.; Dobre, O.A. Backscatter-enabled noma for future 6G systems: A new optimization framework under imperfect SIC. IEEE Commun. Lett. 2021, 25, 1669–1672. [Google Scholar] [CrossRef]
- Wang, Z.; Wen, C.; Fan, Z.; Wan, X. A novel price-based power allocation algorithm in Non-Orthogonal Multiple Access Networks. IEEE Wirel. Commun. Lett. 2018, 7, 230–233. [Google Scholar] [CrossRef]
- Wan, X.-Y.; Chang, R.-F.; Wang, Z.-Q.; Fan, Z.-F. Sum rate maximization for Cooperative Noma with hardware impairments. IEICE Trans. Inf. Syst. 2021, E104.D, 1399–1405. [Google Scholar] [CrossRef]
- Islam, S.M.; Avazov, N.; Dobre, O.A.; Kwak, K. Power-domain Non-Orthogonal Multiple Access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef]
- Amine Ouamri, M.; Alkanhel, R.; Gueguen, C.; Abdullah Alohali, M.; Ghoneim, S.M.S. Modeling and analysis of UAV-assisted mobile network with imperfect beam alignment. Comput. Mater. Contin. 2023, 74, 453–467. [Google Scholar] [CrossRef]
- Qureshi, H.N.; Imran, A. On the tradeoffs between coverage radius, altitude, and beamwidth for practical UAV deployments. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2805–2821. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, W.; Zheng, G. Optimum placement of UAV as relays. IEEE Commun. Lett. 2018, 22, 248–251. [Google Scholar] [CrossRef]
- Lee, J.-H.; Park, K.-H.; Ko, Y.-C.; Alouini, M.-S. Throughput maximization of mixed FSO/RF UAV-aided mobile relaying with a buffer. IEEE Trans. Wirel. Commun. 2021, 20, 683–694. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, N.; Ao, S.; Tang, J.; Zhang, X.; Fu, Y.; So, D.K.; Wong, K.-K. Joint 3D trajectory and power optimization for UAV-aided mmwave MIMO-Noma Networks. IEEE Trans. Commun. 2021, 69, 2346–2358. [Google Scholar] [CrossRef]
- Luo, J.; Song, J.; Zheng, F.-C.; Gao, L.; Wang, T. User-centric UAV deployment and content placement in cache-enabled Multi-UAV networks. IEEE Trans. Veh. Technol. 2022, 71, 5656–5660. [Google Scholar] [CrossRef]
- Ji, J.; Zhu, K.; Niyato, D.; Wang, R. Joint Cache Placement, flight trajectory, and transmission power optimization for Multi-UAV Assisted Wireless Networks. IEEE Trans. Wirel. Commun. 2020, 19, 5389–5403. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Oteşteanu, M.-E.; Barb, G.; Gueguen, C. Coverage Analysis and Efficient Placement of Drone-BSs in 5G Networks. Eng. Proc. 2022, 14, 18. [Google Scholar] [CrossRef]
- Do, D.-T.; Le, A.-T.; Liu, Y.; Jamalipour, A. User grouping and energy harvesting in UAV-noma system with AF/DF relaying. IEEE Trans. Veh. Technol. 2021, 70, 11855–11868. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Zhao, N.; Chen, Y.; Zhang, S.; Ding, Z.; Yu, F.R. Placement and power allocation for Noma-UAV Networks. IEEE Wirel. Commun. Lett. 2019, 8, 965–968. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Q.; Li, Q.; Qin, J. Joint position, Decoding Order, and power allocation optimization in UAV-based Noma Downlink Communications. IEEE Syst. J. 2020, 14, 2949–2960. [Google Scholar] [CrossRef]
- Nasir, A.A.; Tuan, H.D.; Duong, T.Q.; Poor, H.V. UAV-enabled communication using noma. IEEE Trans. Commun. 2019, 67, 5126–5138. [Google Scholar] [CrossRef]
- Zhao, N.; Pang, X.; Li, Z.; Chen, Y.; Li, F.; Ding, Z.; Alouini, M.-S. Joint trajectory and precoding optimization for UAV-assisted Noma Networks. IEEE Trans. Commun. 2019, 67, 3723–3735. [Google Scholar] [CrossRef]
- Li, B.; Zhang, R.; Yang, L. Joint user grouping and power allocation for noma-based UAV relaying networks. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021. [Google Scholar] [CrossRef]
- Xu, W.; Tian, J.; Gu, L.; Tao, S. Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System. Drones 2022, 6, 304. [Google Scholar] [CrossRef]
- Jia, M.; Gao, Q.; Guo, Q.; Gu, X. Energy-Efficiency Power Allocation Design for UAV-Assisted Spatial NOMA. IEEE Internet Things J. 2021, 8, 15205–15215. [Google Scholar] [CrossRef]
- Solanki, S.; Upadhyay, P.K.; da Costa, D.B.; Bithas, P.S.; Kanatas, A.G.; Dias, U.S. Joint IMPACT OF RF hardware impairments and channel estimation errors in spectrum sharing multiple-relay networks. IEEE Trans. Commun. 2018, 66, 3809–3824. [Google Scholar] [CrossRef]
- Canbilen, A.E.; Ikki, S.S.; Basar, E.; Gultekin, S.S.; Develi, I. Impact of I/Q imbalance on amplify-and-forward relaying: Optimal Detector Design and Error Performance. IEEE Trans. Commun. 2019, 67, 3154–3166. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Liu, Y.; Tsiftsis, T.A.; Ding, Z.; Nallanathan, A. UAV-aided multi-way NOMA networks with residual hardware impairments. IEEE Wirel. Commun. Lett. 2020, 9, 1538–1542. [Google Scholar] [CrossRef]
- Guo, K.; An, K. On the performance of RIS-Assisted Integrated Satellite-UAV-terrestrial networks with hardware impairments and interference. IEEE Wirel. Commun. Lett. 2022, 11, 131–135. [Google Scholar] [CrossRef]
- Sharma, P.K.; Gupta, D. Outage performance of Multi-UAV relaying-based imperfect hardware hybrid satellite-terrestrial networks. IEEE Syst. J. 2022, 16, 2311–2314. [Google Scholar] [CrossRef]
- Arzykulov, S.; Celik, A.; Nauryzbayev, G.; Eltawil, A. UAV-Assisted Cooperative & Cognitive Noma: Deployment, clustering, and resource allocation. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 263–281. [Google Scholar] [CrossRef]
- Lin, X.; Yajnanarayana, V.; Muruganathan, S.D.; Gao, S.; Asplund, H.; Maattanen, H.-L.; Bergstrom, M.; Euler, S.; Wang, Y.-P.E. The sky is not the limit: LTE for Unmanned Aerial Vehicles. IEEE Commun. Mag. 2018, 56, 204–210. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, T.; Yang, D.; Liu, Y.; Tao, M. Joint Resource and trajectory optimization for security in UAV-assisted MEC systems. IEEE Trans. Commun. 2021, 69, 573–588. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, T.; Liu, Y.; Yang, D.; Xiao, L.; Tao, M. UAV-assisted MEC networks with aerial and ground cooperation. IEEE Trans. Wirel. Commun. 2021, 20, 7712–7727. [Google Scholar] [CrossRef]
- Lu, W.; Ding, Y.; Gao, Y.; Chen, Y.; Zhao, N.; Ding, Z.; Nallanathan, A. Secure noma-based UAV-MEC network towards a flying eavesdropper. IEEE Trans. Commun. 2022, 70, 3364–3376. [Google Scholar] [CrossRef]
- Khan, W.U.; Jameel, F.; Ristaniemi, T.; Khan, S.; Sidhu, G.A.; Liu, J. Joint Spectral and energy efficiency optimization for downlink NOMA Networks. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 645–656. [Google Scholar] [CrossRef]
- Shen, K.; Yu, W. Fractional Programming for Communication Systems—Part I: Power control and beamforming. IEEE Trans. Signal Process. 2018, 6, 2616–2630. [Google Scholar] [CrossRef]
- Nesterov, Y.; Nemirovskii, A. Interior-Point Polynomial Algorithms in Convex Programming; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Fan, Z.-F.; Cheng, Q.; Wang, Z.-Q.; Meng, X.-H.; Wan, X.-Y. Energy efficient resource allocation for downlink cooperative Non-Orthogonal Multiple Access Systems. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, E101.A, 1603–1607. [Google Scholar] [CrossRef]
- Adam, A.B.; Wan, X.; Wang, Z. Energy efficiency maximization in downlink multi-cell multi-carrier Noma Networks with hardware impairments. IEEE Access 2020, 8, 210054–210065. [Google Scholar] [CrossRef]
- Wang, Z.; Du, J.; Fan, Z.; Wan, X.; Xu, Y. Energy Efficiency Maximization for multi-carrier cooperative non-orthogonal Multiple Access Systems. Digit. Signal Process. 2022, 130, 103725. [Google Scholar] [CrossRef]
- Qureshi, H.N.; Manalastas, M.; Ijaz, A.; Imran, A.; Liu, Y.; Al Kalaa, M.O. Communication Requirements in 5G-Enabled Healthcare Applications: Review and Considerations. Healthcare 2022, 10, 293. [Google Scholar] [CrossRef] [PubMed]
- Alkama, D.; Ouamri, M.A.; Alzaidi, M.S.; Shaw, R.N.; Azni, M.; Ghoneim, S.S.M. Downlink Performance Analysis in MIMO UAV-Cellular Communication With LOS/NLOS Propagation Under 3D Beamforming. IEEE Access 2022, 10, 6650–6659. [Google Scholar] [CrossRef]


| Objective | HIs | Model | UAV Relay | Article |
|---|---|---|---|---|
| Sum Rate | × | Los | × | [9] |
| Performance Analysis | × | Rician | ✔ | [13] |
| Sum Rate | × | Los | × | [14] |
| Achievable Rate | × | LoS | × | [15] |
| Max-min Rate | × | Rician | × | [16] |
| Sum Rate | × | LoS | × | [17] |
| Total Transmit Energy | × | Los | ✔ | [19] |
| Energy Efficiency | × | LoS&NLoS | × | [20] |
| Performance Analysis | ✔ | Nakagami-m | ✔ | [23] |
| Performance Analysis | ✔ | Nakagami-m | ✔ | [25] |
| Max-min Rate | ✔ | LoS&NLoS | ✔ | [26] |
| Average Request Delay | × | LoS&NLoS | × | [10] |
| Max-min Rate | × | LoS | ✔ | [11] |
| Coverage probability | × | LoS&NLoS | × | [12] |
| Sum rate | ✔ | LoS | ✔ | This Work |
| Base station transmit maximum power | 2 W |
| UAV transmit maximum power | W |
| AWGN | W |
| The flight height | 100–120 |
| QoS | 0.5 bps/Hz |
| Channel power gain at a distance of 1 m | |
| Coverage area of UAV | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Yang, X.; Wang, Z.; Fan, Z.; Duo, B. Sum Rate Optimization Scheme of UAV-Assisted NOMA under Hardware Impairments. Appl. Sci. 2023, 13, 2971. https://doi.org/10.3390/app13052971
Wan X, Yang X, Wang Z, Fan Z, Duo B. Sum Rate Optimization Scheme of UAV-Assisted NOMA under Hardware Impairments. Applied Sciences. 2023; 13(5):2971. https://doi.org/10.3390/app13052971
Chicago/Turabian StyleWan, Xiaoyu, Xiongqing Yang, Zhengqiang Wang, Zifu Fan, and Bin Duo. 2023. "Sum Rate Optimization Scheme of UAV-Assisted NOMA under Hardware Impairments" Applied Sciences 13, no. 5: 2971. https://doi.org/10.3390/app13052971
APA StyleWan, X., Yang, X., Wang, Z., Fan, Z., & Duo, B. (2023). Sum Rate Optimization Scheme of UAV-Assisted NOMA under Hardware Impairments. Applied Sciences, 13(5), 2971. https://doi.org/10.3390/app13052971





