A Free-Space Transmission Setup for Material Parameters Estimation with Affordable and Non-Synchronized Software-Defined Radios in the 0.85–1.55 GHz Band
Abstract
:1. Introduction
2. Methodology
2.1. Experimental—Electromagnetics
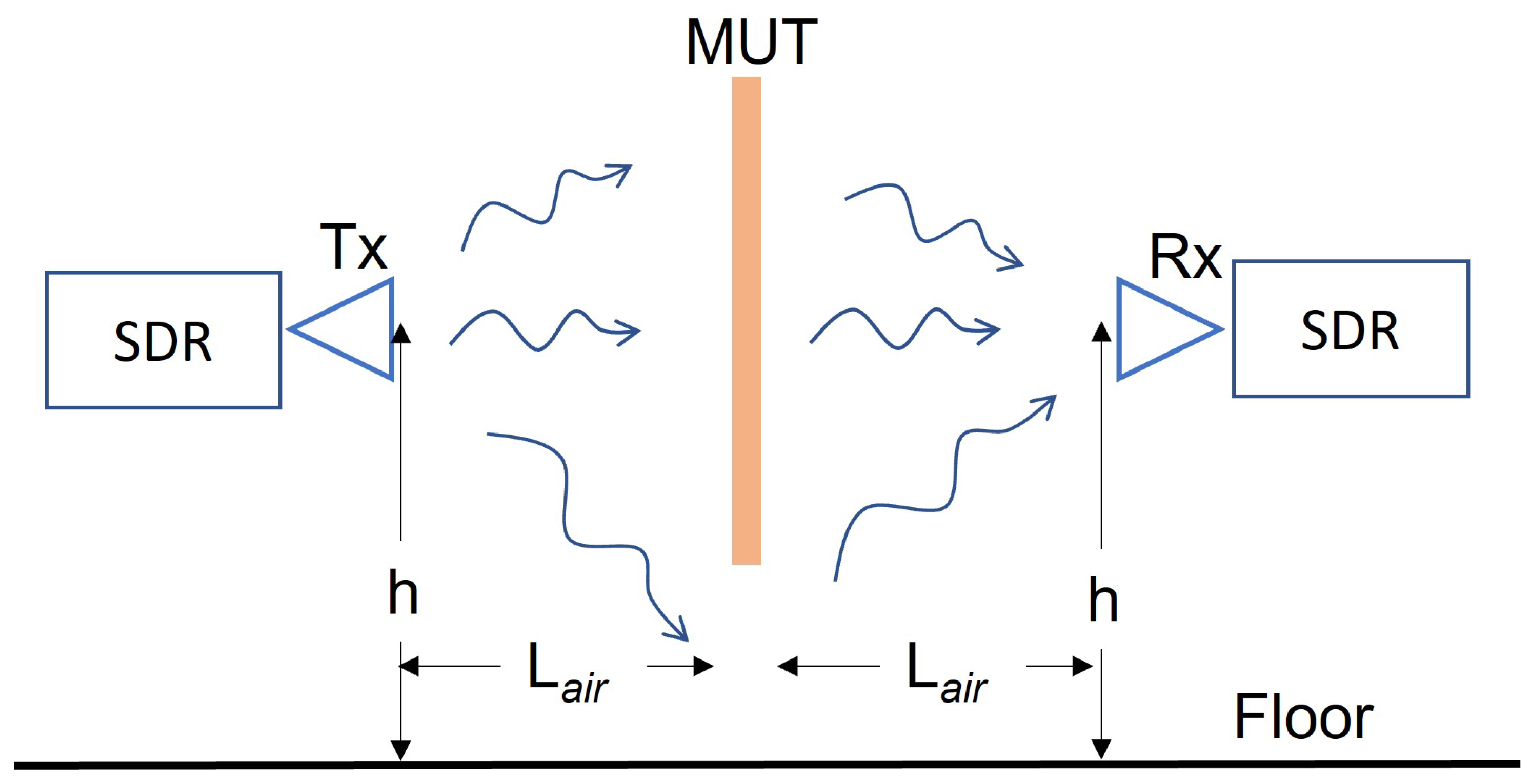
2.1.1. General Description
2.1.2. Effects on the Signals
2.2. Experimental—Configurable Hardware
2.3. Model and Simulation
2.4. Parametric Study
2.5. Optimization
2.5.1. The Path Length
2.5.2. The Error Function
3. Results and Discussion
3.1. Parametric Study
3.2. Measured Signals
3.3. Optimization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Ong, C.; Neo, C.; Varadan, V.; Varadan, V. Microwave Electronics—Measurement and Materials Characterization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Collier, R.; Skinner, D. (Eds.) Microwave Measurements, 3rd ed.; IET: London, UK, 2007. [Google Scholar]
- Liu, X.; Gan, L.; Yang, B. Millimeter-wave free-space dielectric characterization. Measurement 2021, 179, 109472. [Google Scholar] [CrossRef]
- Hasar, U.C.; Kaya, Y.; Ozturk, G.; Ertugrul, M.; Korasli, C. Broadband, Stable, and Noniterative Dielectric Constant Measurement of Low-Loss Dielectric Slabs Using a Frequency-Domain Free-Space Method. IEEE Trans. Antennas Propag. 2022, 70, 12435–12439. [Google Scholar] [CrossRef]
- Singh, V.; Bhattacharyya, S. A free space frequency-time-domain technique for electromagnetic characterization of materials using reflection-based measurement. Int. J. Microw.-Comput.-Aided Eng. 2021, 31, 1–12. [Google Scholar] [CrossRef]
- Sagnard, F.; El Zein, G. Characterization of building materials for propagation modelling: Frequency and time responses. AEU—Int. J. Electron. Commun. 2005, 59, 337–347. [Google Scholar] [CrossRef]
- Davis, B.; Grosvenor, C.; Johnk, R.; Novotny, D.; Baker-Jarvis, J.; Janezic, M. Complex Permittivity of Planar Building Materials Measured With an Ultra-Wideband Free-Field Antenna Measurement System. J. Res. Natl. Inst. Stand. Technol. 2007, 112, 67. [Google Scholar] [CrossRef]
- Pisa, S.; Pittella, E.; Piuzzi, E.; D’Atanasio, P.; Zambotti, A. Permittivity measurement on construction materials through free space method. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Torino, Italy, 22–25 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Brancaccio, A.; D’Alterio, G.; De Stefano, E.; Di Guida, L.; Feo, M.; Luce, S. A free-space method for microwave characterization of materials in aerospace application. In Proceedings of the 2014 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 29–30 May 2014; pp. 423–427. [Google Scholar] [CrossRef]
- Hiebel, M. Fundamentals of Vector Network Analysis, 5th ed.; Rohde & Schwarz: München, Germany, 2011. [Google Scholar]
- Balanis, C.A. Anntena Theory—Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Collins, T.F.; Getx, R.; Pu, D.; Wyglinski, A.M. Software-Defined Radio for Engineers, 1st ed.; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Akcelik, H.; Durna, Y.; Saraydemir, S.; Kocer, H. Measurement of a metamaterial antenna angular power reception performance utilizing Software Defined Radio. AEU—Int. J. Electron. Commun. 2017, 75, 91–97. [Google Scholar] [CrossRef]
- Debatty, T. Software defined RADAR a state of the art. In Proceedings of the 2010 2nd International Workshop on Cognitive Information Processing, Elba Island, Italy, 14–16 June 2010; pp. 253–257. [Google Scholar] [CrossRef]
- Costanzo, S.; Spadafora, F.; Massa, G.D.; Borgia, A.; Costanzo, A.; Aloi, G.; Pace, P.; Loscri, V.; Moreno, H.O. Potentialities of USRP-Based Software Defined Radar Systems. Prog. Electromagn. Res. B 2013, 53, 417–435. [Google Scholar] [CrossRef] [Green Version]
- Costanzo, S.; Spadafora, F.; Moreno, O.H.; Scarcella, F.; Massa, G.D. Multiband Software Defined Radar for Soil Discontinuities Detection. J. Electr. Comput. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cerquera, M.R.P.; Montaño, J.D.C.; Mondragón, I. UAV for Landmine Detection Using SDR-Based GPR Technology. In Robots Operating in Hazardous Environments; Canbolat, H., Ed.; IntechOpen: Rijeka, Croatia, 2017; Chapter 2; pp. 25–58. [Google Scholar] [CrossRef] [Green Version]
- Chuma, E.L.; Iano, Y.; Roger, L.L.B.; Fontgalland, G. Measuring dielectric properties by two methods using software-defined radio. IET Sci. Meas. Technol. 2019, 13, 1003–1008. [Google Scholar] [CrossRef]
- Aloi, G.; Loscrí, V.; Borgia, A.; Natalizio, E.; Costanzo, S.; Pace, P.; Di Massa, G.; Spadafora, F. Software Defined Radar: Synchronization Issues and Practical Implementation. In Proceedings of the 4th International Conference on Cognitive Radio and Advanced Spectrum Management, Barcelona Spain, 26–29 October 2011; CogART ’11; Association for Computing Machinery: New York, NY, USA, 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Bourreau, D.; Péden, A. Solid and Non-Solid Dielectric Material Characterization for Millimeter and Sub-Millimeter Wave Applications. In Proceedings of the 2020 50th European Microwave Conference (EuMC), Utrecht, The Netherlands, 12–14 January 2021; pp. 909–912. [Google Scholar] [CrossRef]
- Chung, J.Y. Broadband Characterization Techniques for RF Materials and Engineered Composites. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2010. [Google Scholar]
- Davidson, D.B. Computational Electromagnetics for RF and Microwave Engineering, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Gonçalves, F.J.F.; Pinto, A.G.; Mesquita, R.C.; Silva, E.J.; Brancaccio, A. Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms. Electronics 2018, 7, 260. [Google Scholar] [CrossRef] [Green Version]
- Baker-Jarvis, J.; Janezic, M.; Riddle, B.; Johnk, R.; Holloway, C.; Geyer, R.; Grosvenor, C. Measuring the Permittivity and Permeability of Lossy Materials: Solids, Liquids, Metals, and negative-Index Materials. Technical Note (NIST TN) 1536, National Institute of Standards and Technology, Gaithersburg, MD, USA, 2005. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote1536.pdf (accessed on 21 February 2023).
- Stewart, R.W.; Barlee, K.W.; Atkinson, D.S.W.; Crockett, L.H. Software Defined Radio Using MATLAB & Simulink and the RTL-SDR, 1st ed.; Strathclyde Academic Media: Glasgow, Scotland, UK, 2015. [Google Scholar]
- GNU Radio Project. 2022. Available online: https://www.gnuradio.org (accessed on 10 March 2022).
- Analog Devices. ADF4351 Wideband Synthesizer with Integrated VCO; Data Sheet, Rev. A.; Analog Devices: Norwood, MA, USA, 2017. [Google Scholar]
- Holdsworth, J. Pyadf43x, A Package for Automating AD4350/1 Boards. 2018. Available online: http://github.com/jhol/pyadf435x (accessed on 9 March 2022).
- Hopcraft, K.; Smith, P.R. An Introduction to Electromagnetic Inverse Scattering, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Büyüköztürk, O.; Yu, T.Y.; Ortega, J.A. A methodology for determining complex permittivity of construction materials based on transmission-only coherent, wide-bandwidth free-space measurements. Cem. Concr. Compos. 2006, 28, 349–359. [Google Scholar] [CrossRef]
- ITU. Effects of Building Materials and Structures on Radiowave Propagation Above About 100 MHz; Recommendation ITU-R P.2040-1; P Series Radiowave Propagation, Electronic Publication; International Telecommunication Union Radiocommunication Sector: Geneva, Switzerland, 2021. [Google Scholar]
- Mathworks. MATLAB Genetic Algorithm: Genetic Algorithm Solver for Mixed-Integer or Continuous-Variable Optimization, Constrained or Unconstrained. 2019. Available online: https://www.mathworks.com/help/gads/genetic-algorithm.html (accessed on 26 May 2022).
- Trabelsi, S.; Kraszewski, A.; Nelson, S. Phase-shift ambiguity in microwave dielectric properties measurements. IEEE Trans. Instrum. Meas. 2000, 49, 56–60. [Google Scholar] [CrossRef] [Green Version]












| AIR | MUT | MET | |
|---|---|---|---|
| c | 1.9213 | 1.9500 | 1.2155 |
| i | 956 | 917 | 849 |
| d | 1.1932 | 1.2025 | 1.6187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves, F.J.F.; Brancaccio, A.; Ferreira, L.A.; da Silva, E.J. A Free-Space Transmission Setup for Material Parameters Estimation with Affordable and Non-Synchronized Software-Defined Radios in the 0.85–1.55 GHz Band. Appl. Sci. 2023, 13, 3010. https://doi.org/10.3390/app13053010
Gonçalves FJF, Brancaccio A, Ferreira LA, da Silva EJ. A Free-Space Transmission Setup for Material Parameters Estimation with Affordable and Non-Synchronized Software-Defined Radios in the 0.85–1.55 GHz Band. Applied Sciences. 2023; 13(5):3010. https://doi.org/10.3390/app13053010
Chicago/Turabian StyleGonçalves, Fábio Júlio Fonseca, Adriana Brancaccio, Leonardo Augusto Ferreira, and Elson José da Silva. 2023. "A Free-Space Transmission Setup for Material Parameters Estimation with Affordable and Non-Synchronized Software-Defined Radios in the 0.85–1.55 GHz Band" Applied Sciences 13, no. 5: 3010. https://doi.org/10.3390/app13053010
APA StyleGonçalves, F. J. F., Brancaccio, A., Ferreira, L. A., & da Silva, E. J. (2023). A Free-Space Transmission Setup for Material Parameters Estimation with Affordable and Non-Synchronized Software-Defined Radios in the 0.85–1.55 GHz Band. Applied Sciences, 13(5), 3010. https://doi.org/10.3390/app13053010







