Predictive Energy Management Strategy for Hybrid Electric Air-Ground Vehicle Considering Battery Thermal Dynamics
Abstract
1. Introduction
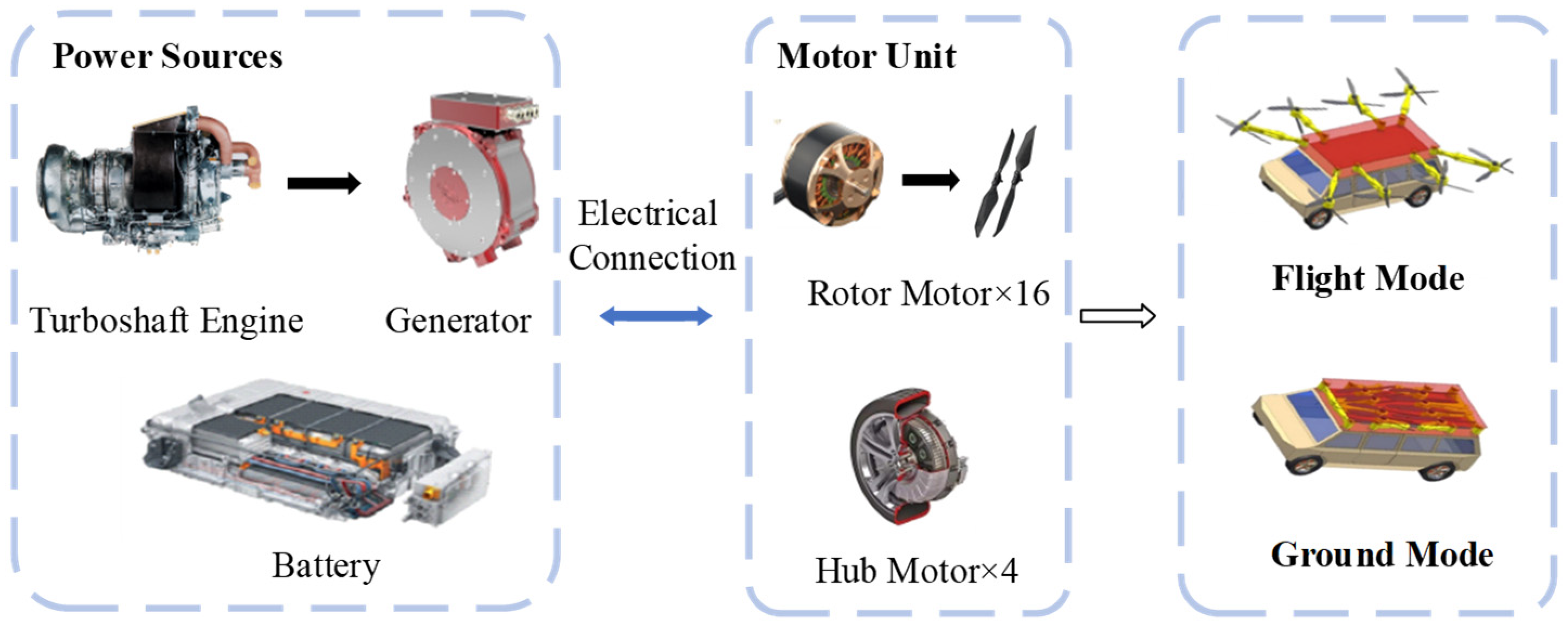
2. Descriptions of HEAGV with Series Hybrid Powertrain
2.1. Air-Ground Vehicle Model
2.2. Engine Model
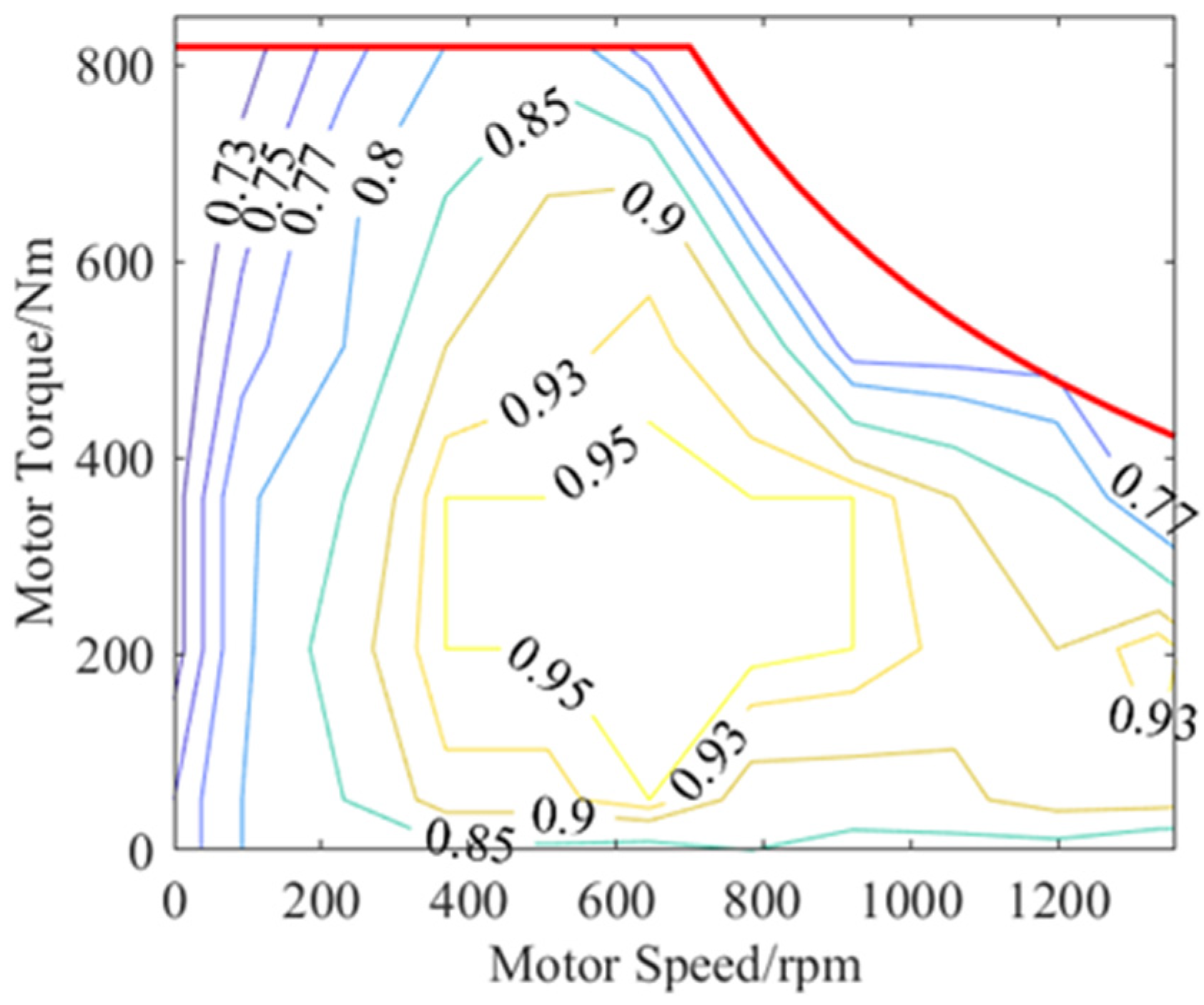
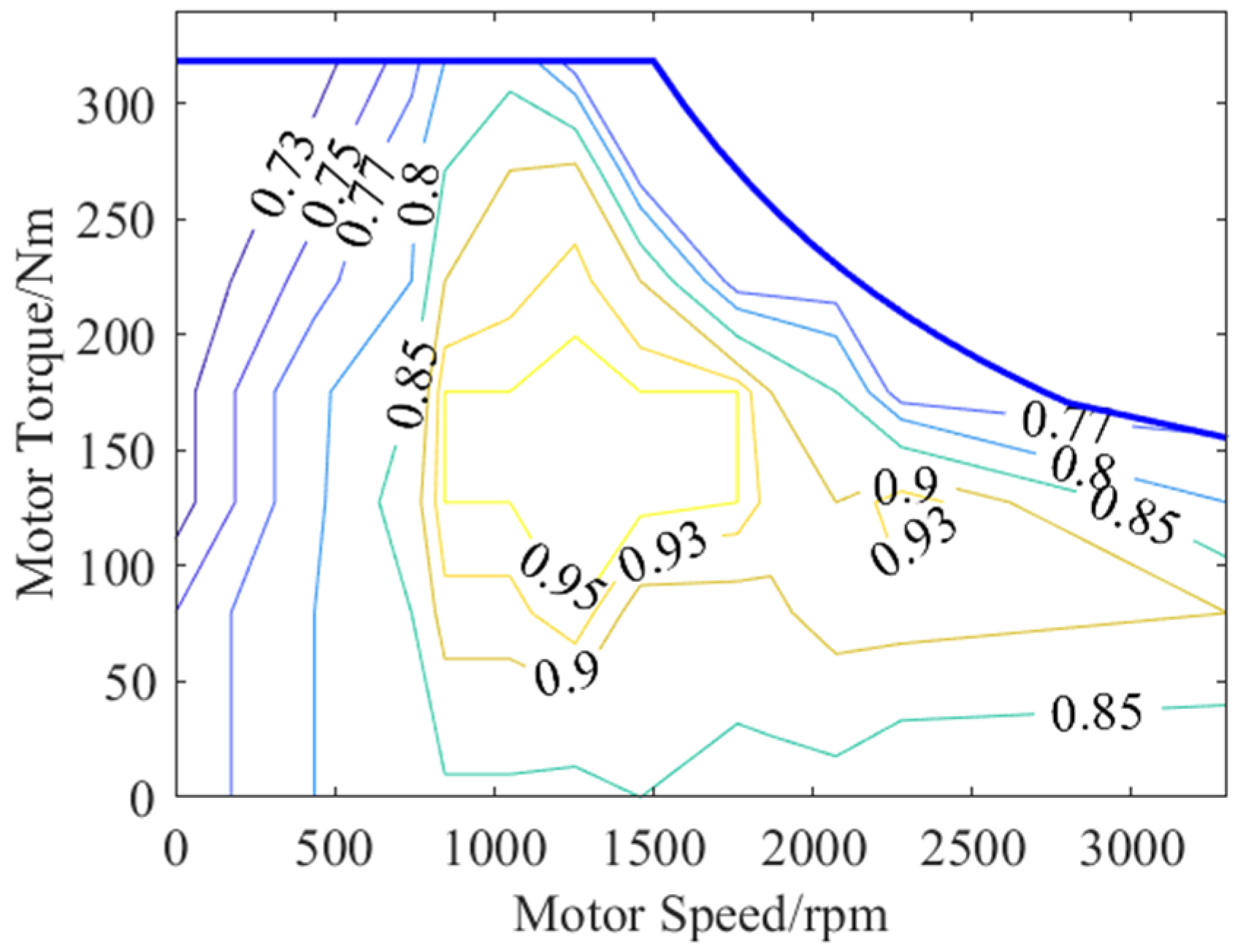
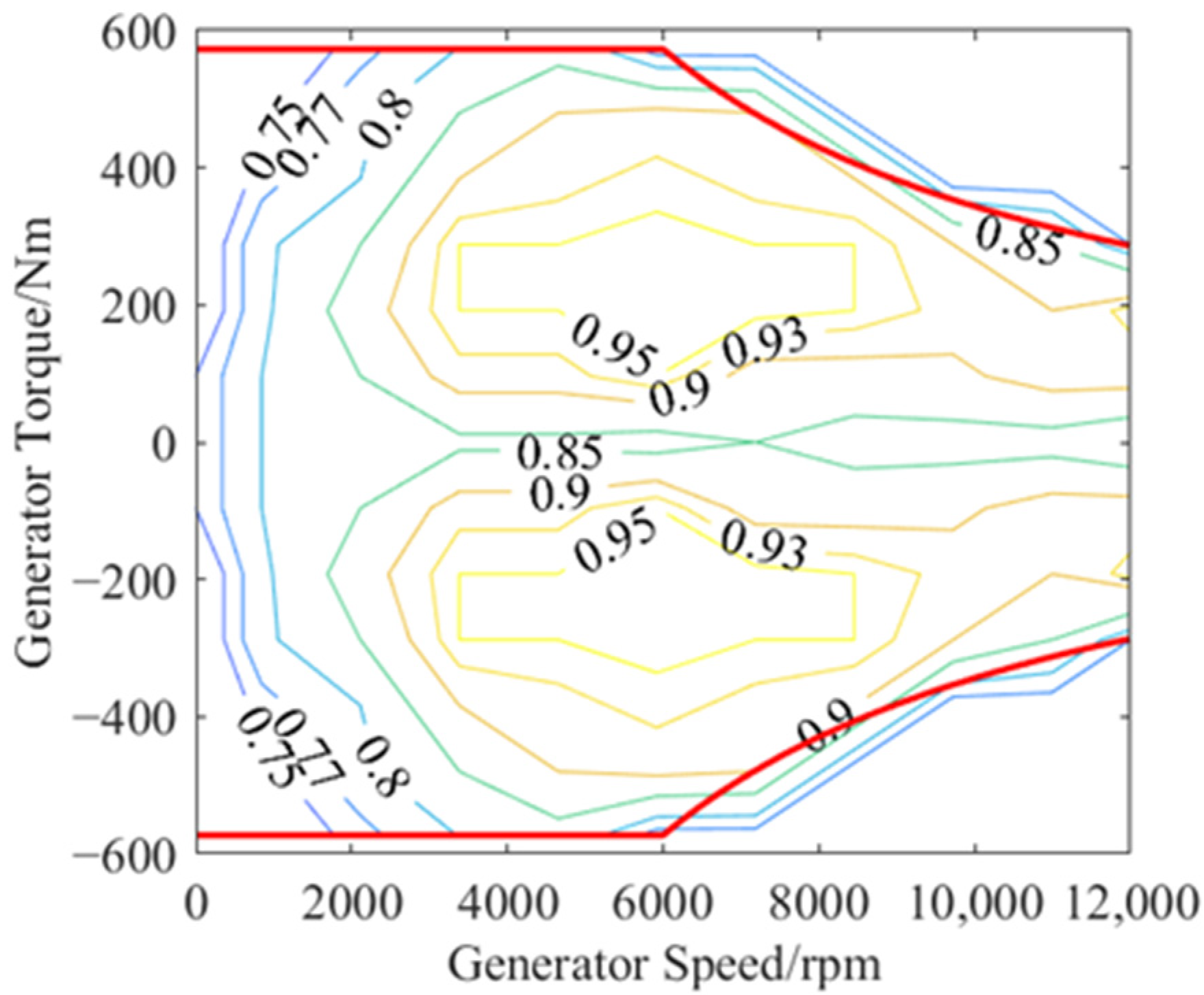
2.3. Motor/Generator Models
2.4. Battery Model
3. PMP-MPC Energy Management Strategy for HEAGV
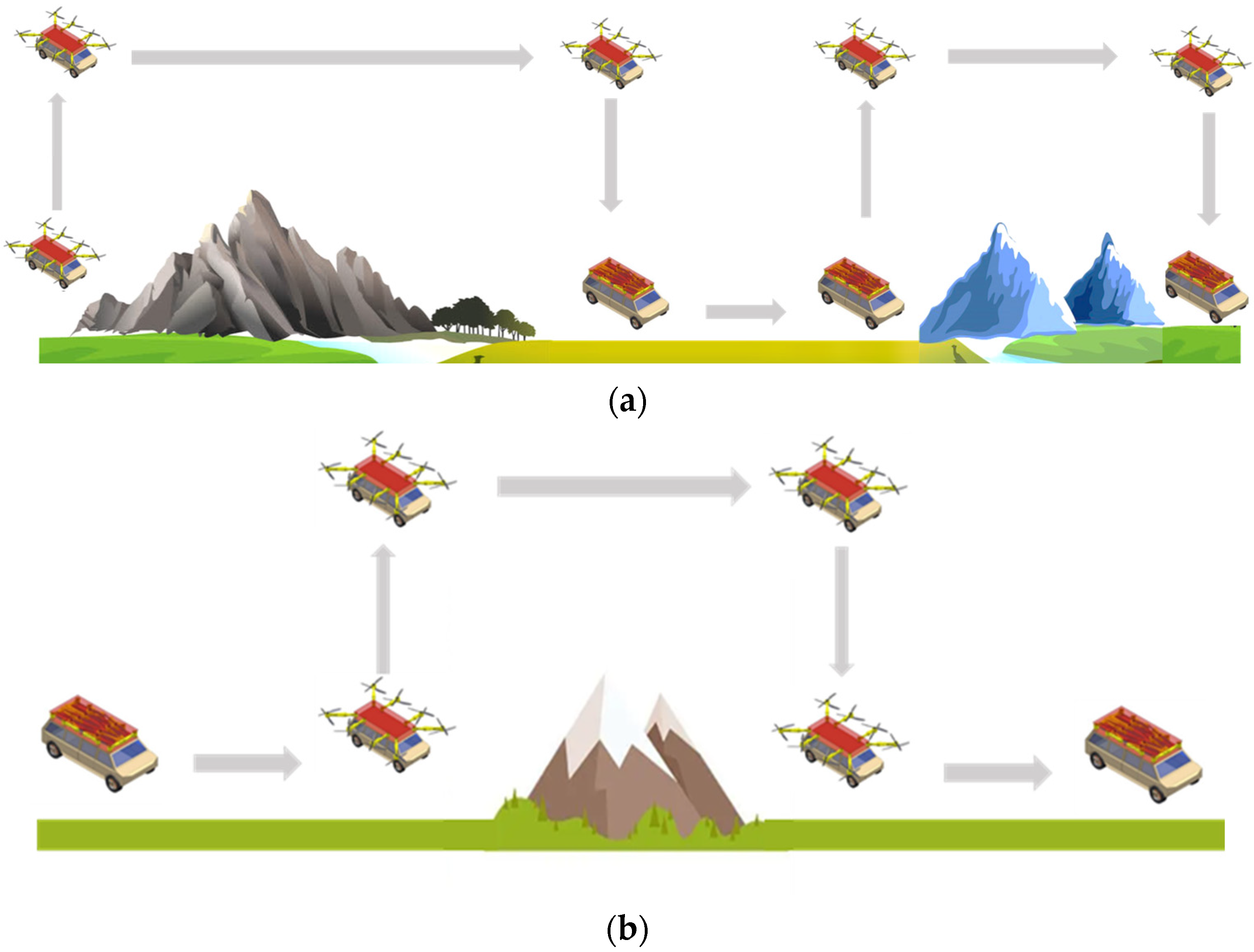
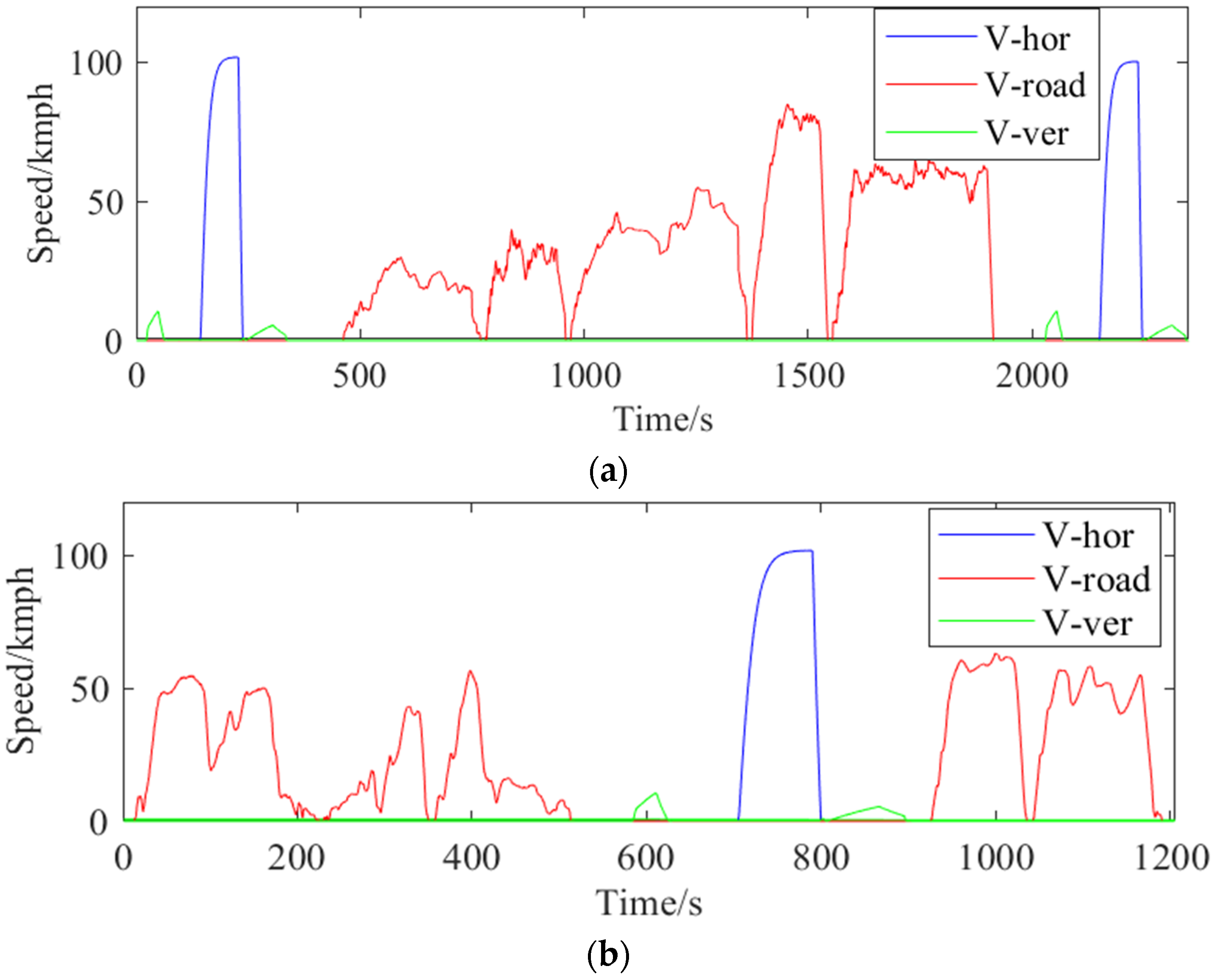
3.1. Speed Information Acquisition
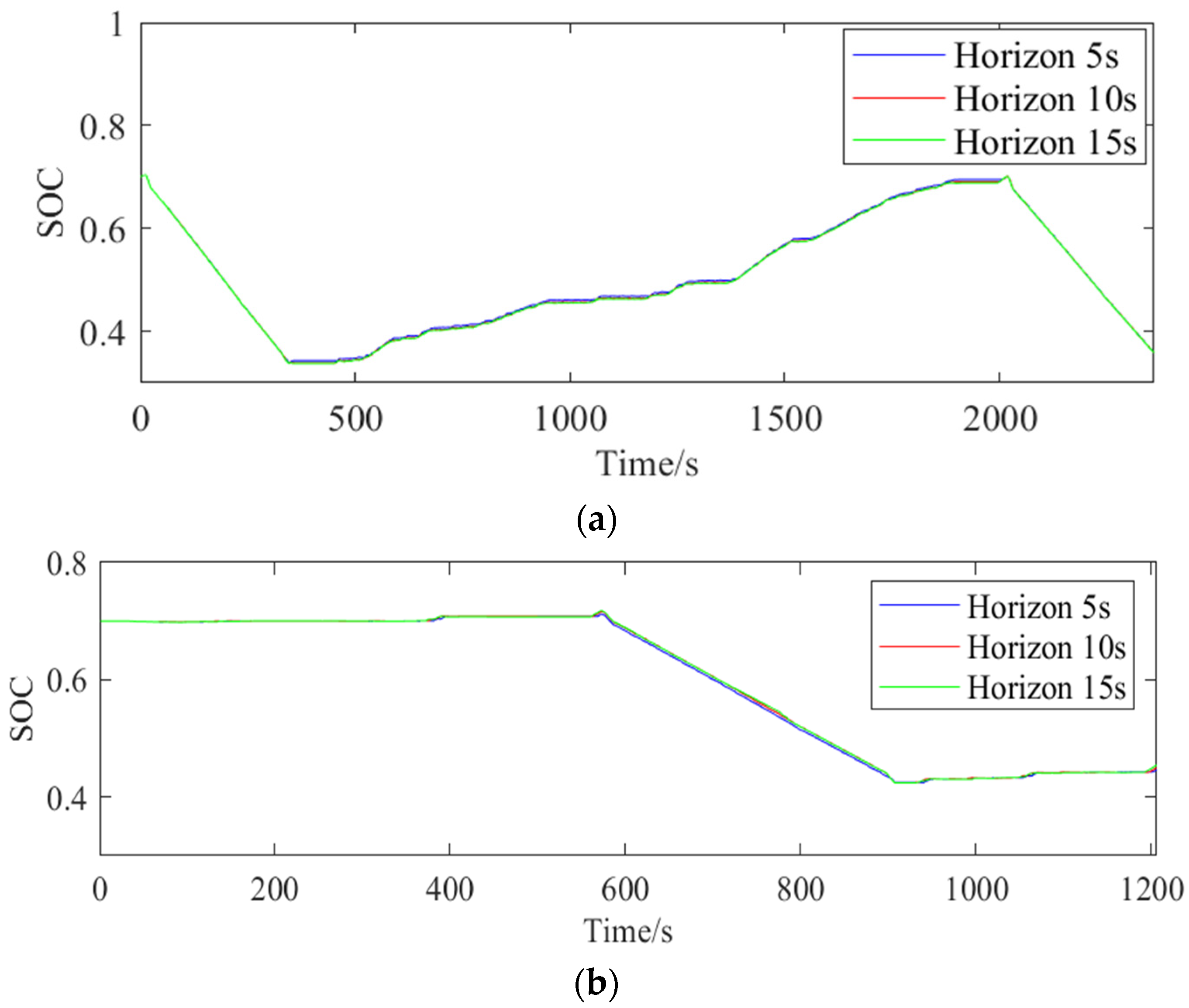
3.2. SOC Reference Trajectory Planning
3.3. PMP-MPC Framework
4. Result and Discussion
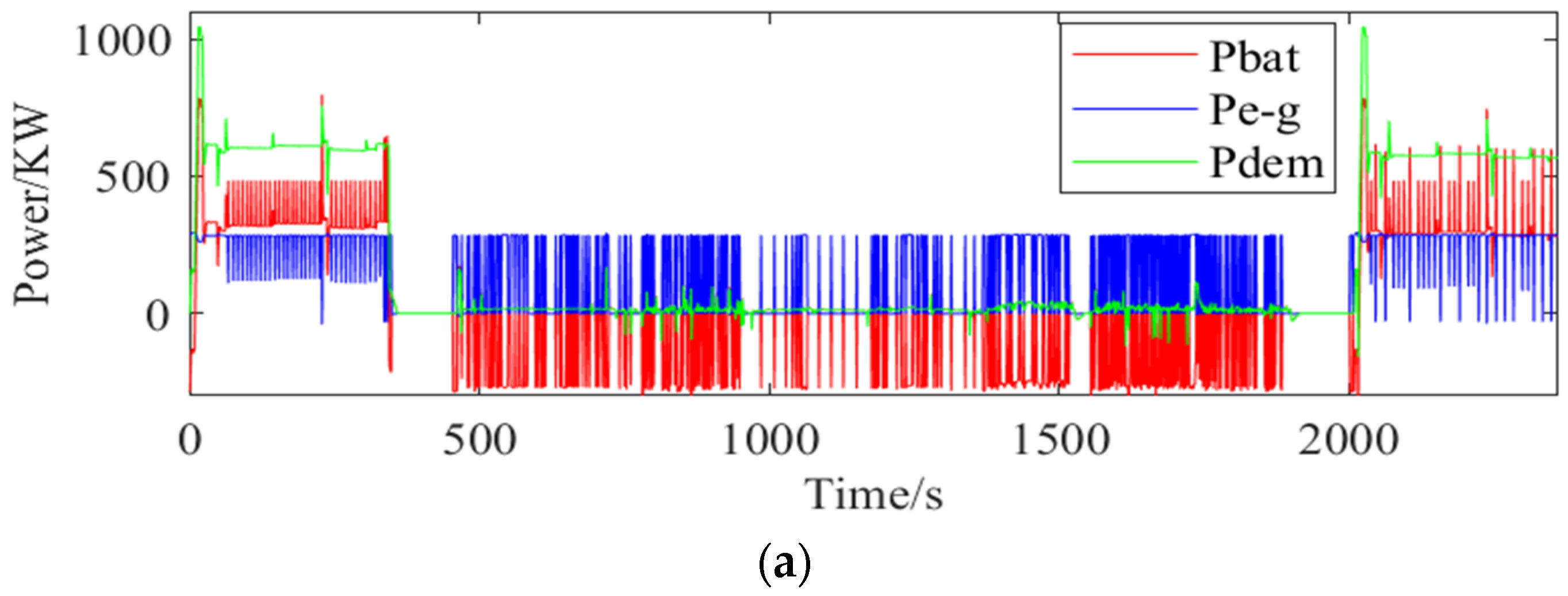
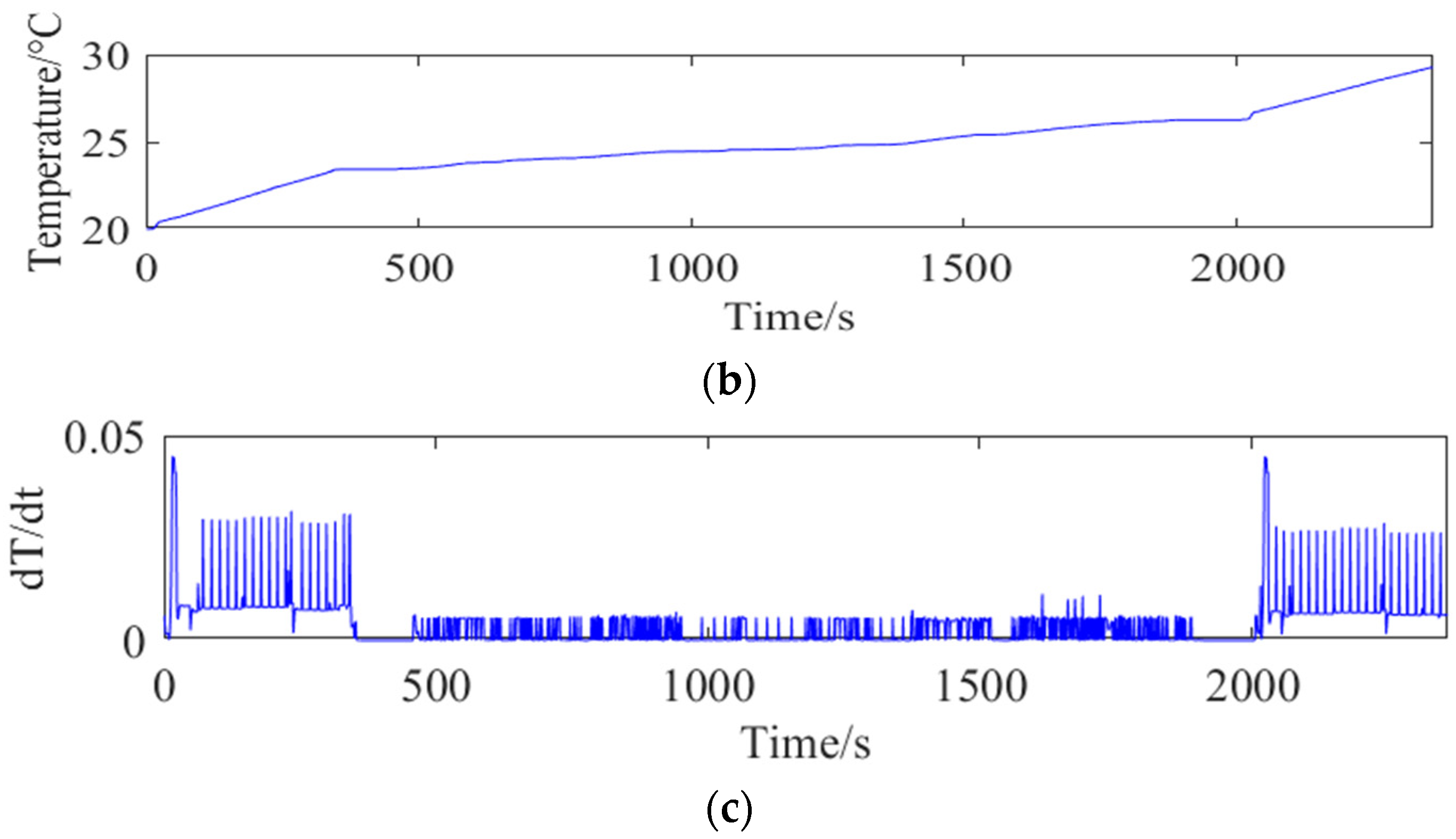
4.1. PMP-MPC Framework
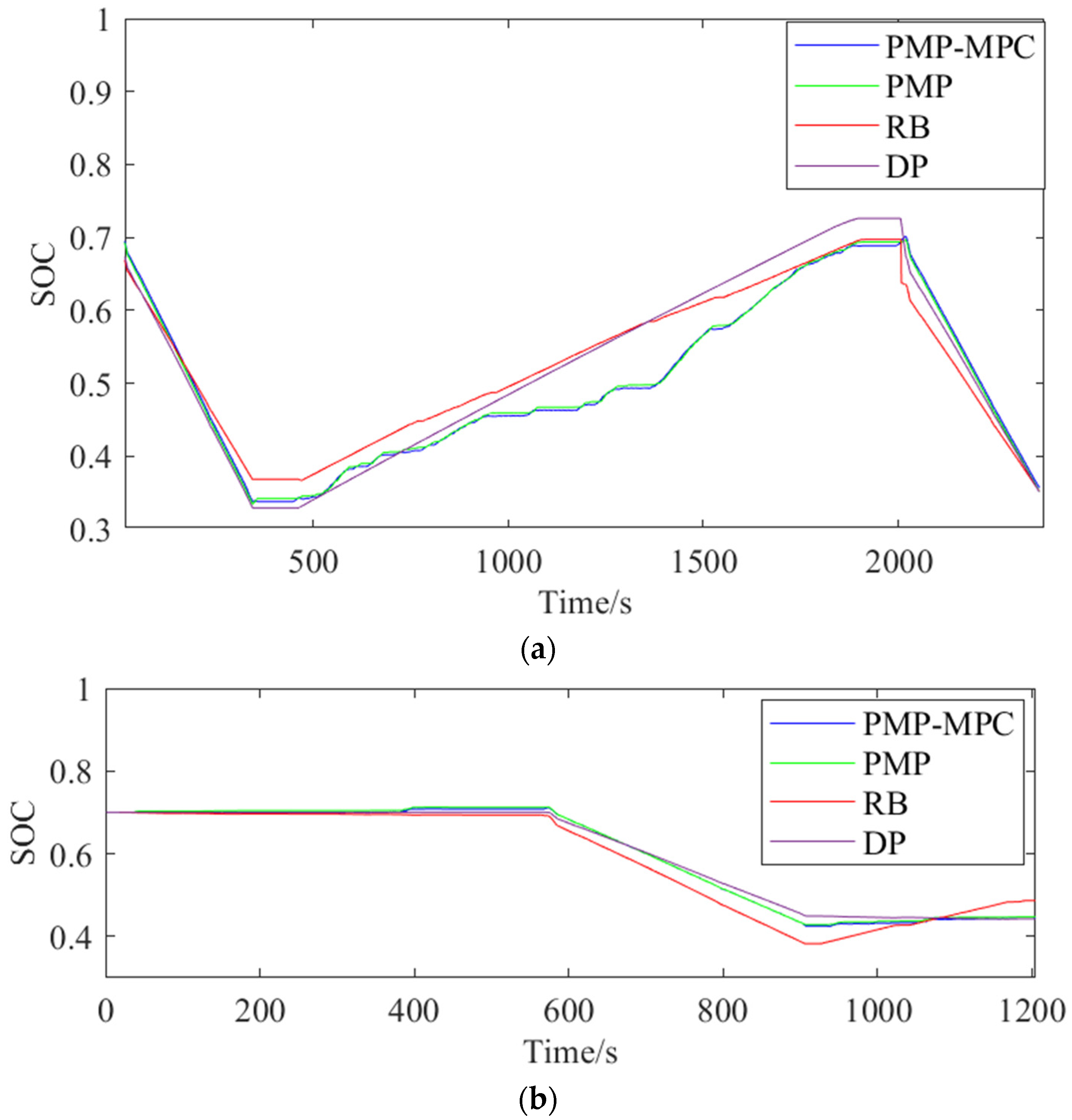
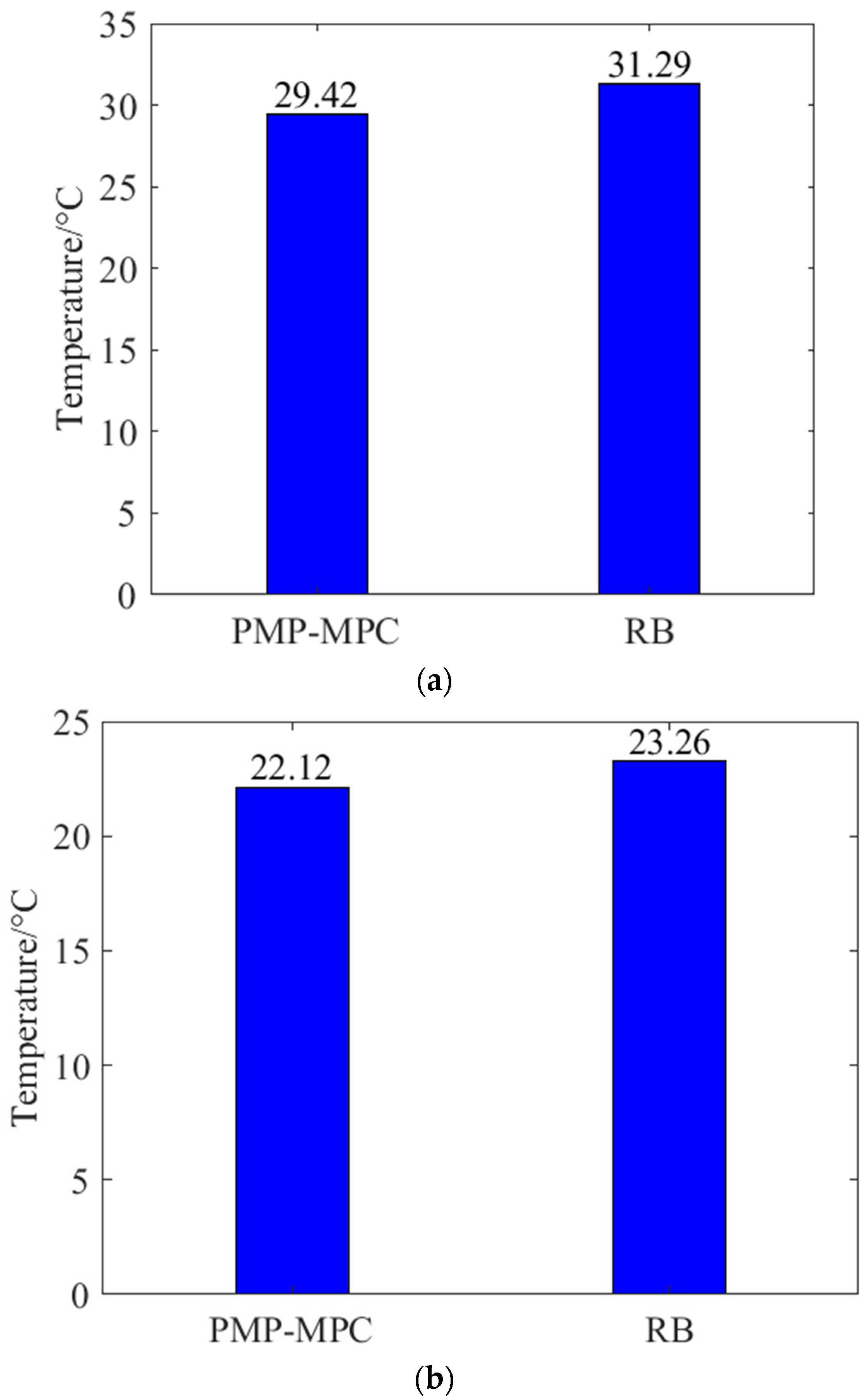
4.2. Comparison of Different Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jordi, P.; Tanja, Z.; Jovana, K. On the understanding of the current status of urban air mobility development and its future prospects: Commuting in a flying vehicle as a new paradigm. Transp. Res. Part E 2022, 166, 102868. [Google Scholar]
- Qie, T.; Wang, W.; Yang, C.; Li, Y.; Liu, W.; Xiang, C. A path planning algorithm for autonomous flying vehicles in cross-country environments with a novel TF-RRT∗ method. Green Energy Intell. Transp. 2022, 1, 100026. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, C.; Wang, W.; Xu, B.; Li, Y.; Yang, L.; Zhu, H.; Xiang, C. A game-learning-based smooth path planning strategy for intelligent air-ground vehicle considering mode switching. IEEE Trans. Transp. Electrif. 2022, 8, 3142150. [Google Scholar] [CrossRef]
- Xie, Y.; He, S.; Savvaris, A.; Tsourdos, A.; Zhang, D.; Xie, A. Convexification in energy optimization of a hybrid electric propulsion system for aerial vehicles. Aerosp. Sci. Technol. 2022, 123, 107509. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Yang, C.; Li, Y.; Xu, B.; Xiang, C. An enhanced hypotrochoid spiral optimization algorithm based intertwined optimal sizing and control strategy of a hybrid electric air-ground vehicle. Energy 2022, 257, 124749. [Google Scholar] [CrossRef]
- Huang, K.; Nguyen, M.; Chen, P. A Rule-Based Control Strategy of Driver Demand to Enhance Energy Efficiency of Hybrid Electric Vehicles. Appl. Sci. 2022, 12, 8507. [Google Scholar] [CrossRef]
- Yang, C.; Lu, Z.; Wang, W.; Li, Y.; Chen, Y.; Xu, B. Energy management of hybrid electric propulsion system: Recent progress and a flying car perspective under three-dimensional transportation networks. Green Energy Intell. Transp. 2023, 2, 100061. [Google Scholar] [CrossRef]
- Liu, K.; Jiao, X.; Yang, C.; Wang, W.; Xiang, C.; Wang, W. Event-Triggered intelligent energy management strategy for plug-in hybrid electric buses based on vehicle cloud optimization. Intell. Transp. Syst. 2020, 14, 1153–1162. [Google Scholar] [CrossRef]
- Tang, W.; Wang, Y.; Jiao, X.; Ren, L. Hierarchical energy management strategy based on adaptive dynamic programming for hybrid electric vehicles in car-following scenarios. Energy 2023, 265, 126264. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, X.; Xie, S.; Song, Z.; Hu, L.; Hou, C. Adaptively coordinated optimization of battery aging and energy management in plug-in hybrid electric buses. Appl. Energy 2019, 256, 113891. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Zhan, J.; Shang, F. Heuristic Dynamic Programming Based Online Energy Management Strategy for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 4479–4493. [Google Scholar] [CrossRef]
- Yang, C.; Du, S.; Li, L.; You, S.; Yang, Y.; Zhao, Y. Adaptive real-time optimal energy management strategy based on equivalent factors optimization for plug-in hybrid electric vehicle. Appl. Energy 2017, 203, 883–896. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R.; Sun, F. Model predictive control for power management in a plug-in hybrid electric vehicle with a hybrid energy storage system. Appl. Energy 2017, 185, 1645–1662. [Google Scholar] [CrossRef]
- Wei, Z.; Ma, Y.; Xiang, C.; Liu, D. Power Prediction-Based Model Predictive Control for Energy Management in Land and Air Vehicle with Turboshaft Engine. Complexity 2021, 2021, 2953241. [Google Scholar] [CrossRef]
- Asadi, B.; Vahidi, A. Predictive Cruise Control: Utilizing Upcoming Traffic Signal Information for Improving Fuel Economy and Reducing Trip Time. IEEE Trans. Control. Syst. Technol. A Publ. IEEE Control. Syst. Soc. 2011, 19, 707–714. [Google Scholar] [CrossRef]
- Deshpande, S.R.; Jung, D.; Bauer, L.; Canova, M. Integrated approximate dynamic programming and equivalent consumption minimization strategy for eco-driving in a connected and automated vehicle. IEEE Trans. Technol. 2021, 70, 11204–11215. [Google Scholar] [CrossRef]
- Brunelli, L.; Capancioni, A.; Gonnella, P.; Casadio, R.; Brusa, A.; Cavina, N.; Caggiano, M. A hybrid vehicle hardware-in-the-loop system with integrated connectivity for ehorizon functions validation. IEEE Trans. Veh. Technol. 2021, 70, 4340–4352. [Google Scholar] [CrossRef]
- Tang, X.; Jia, T.; Hu, X.; Huang, Y.; Deng, Z.; Pu, H. Naturalistic Data-Driven Predictive Energy Management for Plug-in Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2020, 7, 497–508. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Qu, Z.; Zhang, J.; Jin, Z. Effects of graphite microstructure evolution on the anisotropic thermal conductivity of expanded graphite/paraffin phase change materials and their thermal energy storage performance. Int. J. Heat Mass Transf. 2020, 155, 119853. [Google Scholar] [CrossRef]
- Asef, A.; Chitsaz, I.; Madani, N. Modeling and total cost optimization of battery thermal management system in a hybrid electric vehicle. J. Energy Storage 2022, 172, 104844. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Pires, R.A.; Carvalho, S.A.; Cardoso Filho, B.J.; Pires, I.A.; Huebner, R.; Maia, T.A. The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System. Batteries 2023, 9, 10. [Google Scholar] [CrossRef]
- Harrison, J.; Charles, D.; Zenker, J.; Frank, E. Using multi-physics system simulation to predict battery pack thermal performance and risk of Thermal runaway during eVTOL aircraft operations. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019. [Google Scholar]
- Zhou, W.; Chen, Y.; Zhai, H.; Zhang, W. Predictive Energy Management for a Plug-in Hybrid Electric Vehicle Using Driving Profile Segmentation and Energy-based Analytical SoC Planning. Energy 2020, 220, 119700. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, X.; Zou, Y.; Guo, N.; Li, J.; Du, G. Cost-optimal energy management strategy for plug-in hybrid electric vehicles with variable horizon speed prediction and adaptive state-of-charge reference. Energy 2021, 232, 120993. [Google Scholar] [CrossRef]
- He, H.; Huang, R.; Meng, X.; Zhao, X.; Wang, Y.; Li, M. A novel hierarchical predictive energy management strategy for plug-in hybrid electric bus combined with deep deterministic policy gradient. Energy Storage 2022, 52, 104787. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Yang, C.; Li, Y.; Xu, B.; Huang, K.; Xiang, C. An efficient optimal sizing strategy for a hybrid electric air-ground vehicle using adaptive spiral optimization algorithm. Power Sources 2022, 517, 230704. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Pawlikowski, E.M.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K.; Araki, T. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles. J. Power Sources 2006, 158, 535–542. [Google Scholar] [CrossRef]
- Wang, W.; Guo, X.; Yang, C.; Zhang, Y.; Zhao, Y.; Huang, D.; Xiang, C. A multi-objective optimization energy management strategy for power split HEV based on velocity prediction. Energy 2021, 238, 121714. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, C. A two-term energy management strategy of hybrid electric vehicles for power distribution and gear selection with intelligent state-of-charge reference. J. Energy Storage 2021, 42, 103054. [Google Scholar] [CrossRef]
- Padovani, T.M.; Debert, M.; Colin, G.; Chamaillard, Y. Optimal energy management strategy including battery health through thermal management for hybrid vehicles. IFAC Proc. Vol. 2013, 46, 384–389. [Google Scholar] [CrossRef]
- Ritter, A.; Widmer, F.; Duhr, P.; Onder, C.H. Long-term stochastic model predictive control for the energy management of hybrid electric vehicles using Pontryagin’s minimum principle and scenario-based optimization. Appl. Energy 2022, 322, 119192. [Google Scholar] [CrossRef]







| Parameter | Value | Title 3 |
|---|---|---|
| Powertrain system | Series Hybrid Electric | Air/Ground |
| Vehicle mass (kg) | 2000 | Air/Ground |
| Gravity acceleration (m/s2) | 9.81 | Air/Ground |
| Wheel radius (m) | 0.39 | Ground |
| Frontal area (m2) | 7.8 | Ground |
| Paddle radius (m) | 0.9 | Air |
| Vertical area while climbing/landing (m2) | 32 | Air |
| Equivalent frontal area in cruise (m2) | 12.4 | Air |
| Engine peak power (kW) | 110 | Air/Ground |
| Rotor-motor peak power (kW) | 50 | Air |
| Hub motor peak power (kW) | 60 | Ground |
| Battery-rated capacity (Ah) | 150 | Air/Ground |
| Battery-rated voltage (V) | 500 | Air/Ground |
| Horizon (s) | FC (L) | Temperature (°C) |
|---|---|---|
| 5 | 78.47 | 29.42 |
| 10 | 78.94 | 29.07 |
| 15 | 79.62 | 28.74 |
| Horizon (s) | FC (L) | Temperature (°C) |
|---|---|---|
| 5 | 24.79 | 22.12 |
| 10 | 25.12 | 22.27 |
| 15 | 25.63 | 23.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Jiao, X.; Zha, M.; Yang, C.; Yang, L. Predictive Energy Management Strategy for Hybrid Electric Air-Ground Vehicle Considering Battery Thermal Dynamics. Appl. Sci. 2023, 13, 3032. https://doi.org/10.3390/app13053032
Li Z, Jiao X, Zha M, Yang C, Yang L. Predictive Energy Management Strategy for Hybrid Electric Air-Ground Vehicle Considering Battery Thermal Dynamics. Applied Sciences. 2023; 13(5):3032. https://doi.org/10.3390/app13053032
Chicago/Turabian StyleLi, Zhe, Xiaohong Jiao, Mingjun Zha, Chao Yang, and Liuquan Yang. 2023. "Predictive Energy Management Strategy for Hybrid Electric Air-Ground Vehicle Considering Battery Thermal Dynamics" Applied Sciences 13, no. 5: 3032. https://doi.org/10.3390/app13053032
APA StyleLi, Z., Jiao, X., Zha, M., Yang, C., & Yang, L. (2023). Predictive Energy Management Strategy for Hybrid Electric Air-Ground Vehicle Considering Battery Thermal Dynamics. Applied Sciences, 13(5), 3032. https://doi.org/10.3390/app13053032






