An Efficient Digital Channelized Receiver for Low SNR and Wideband Chirp Signals Detection
Abstract
1. Introduction
2. Methodology
2.1. Problem Formulation
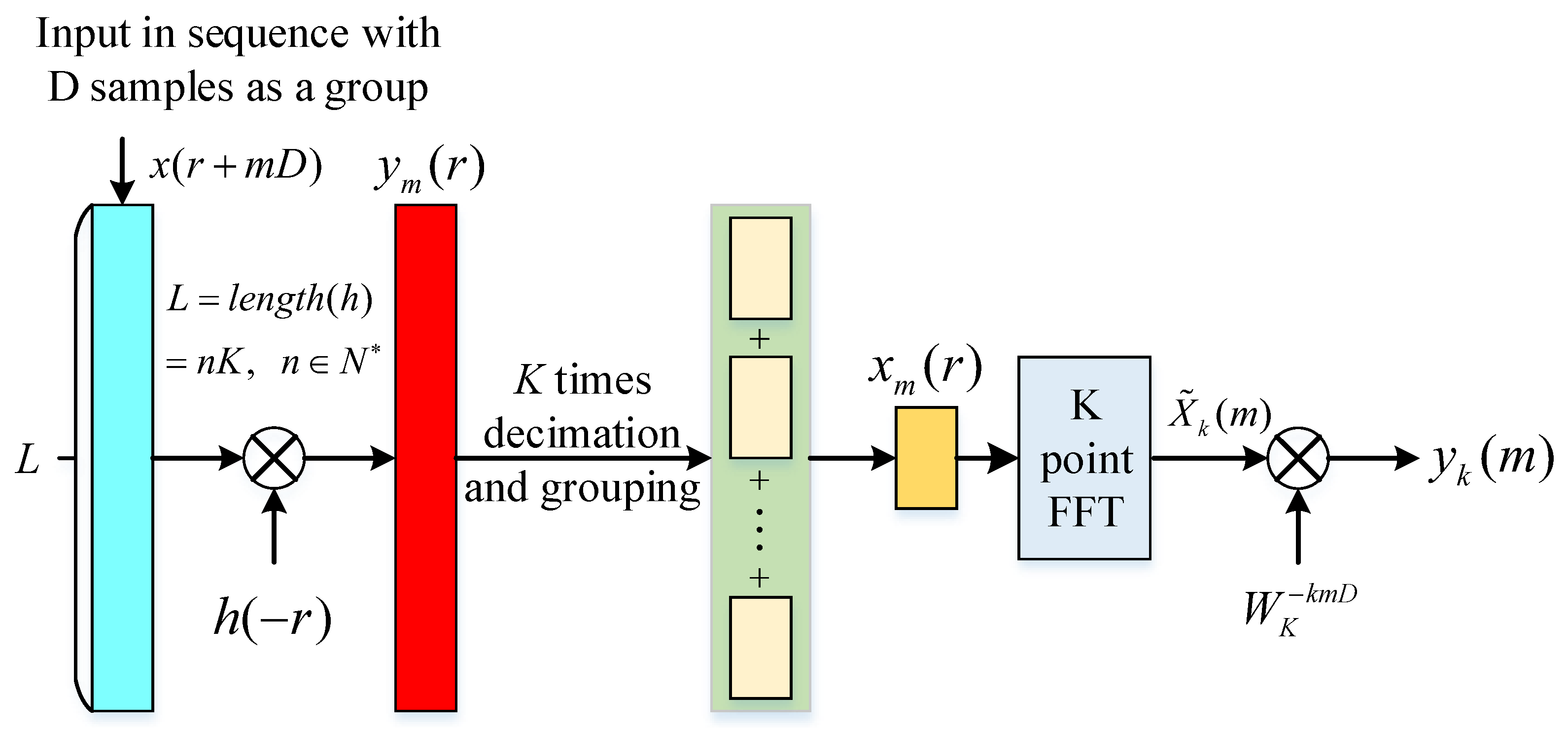
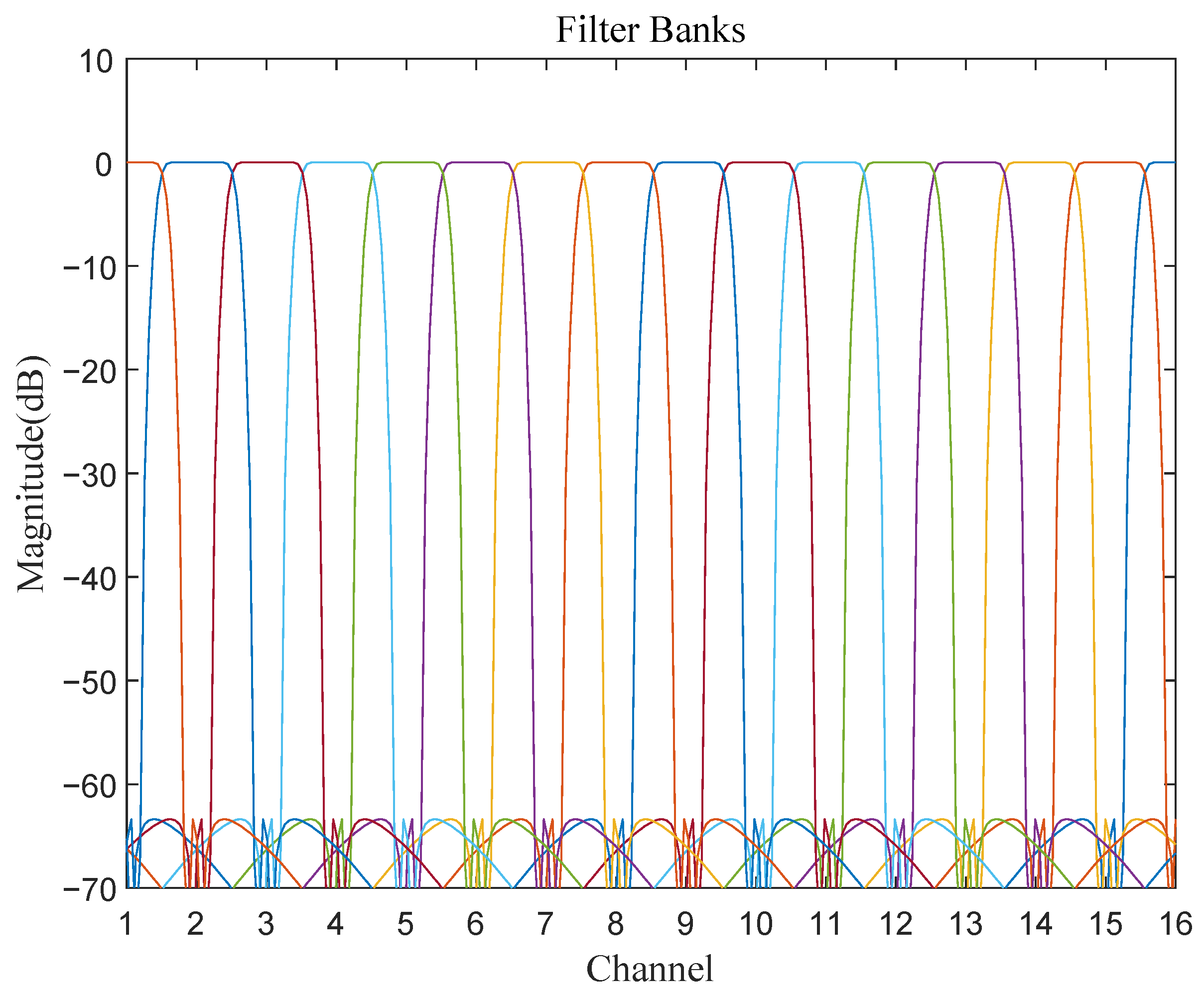
2.1.1. The Principle of Channelization
2.1.2. The Channel Division Method
2.2. Proposed Algorithm Description
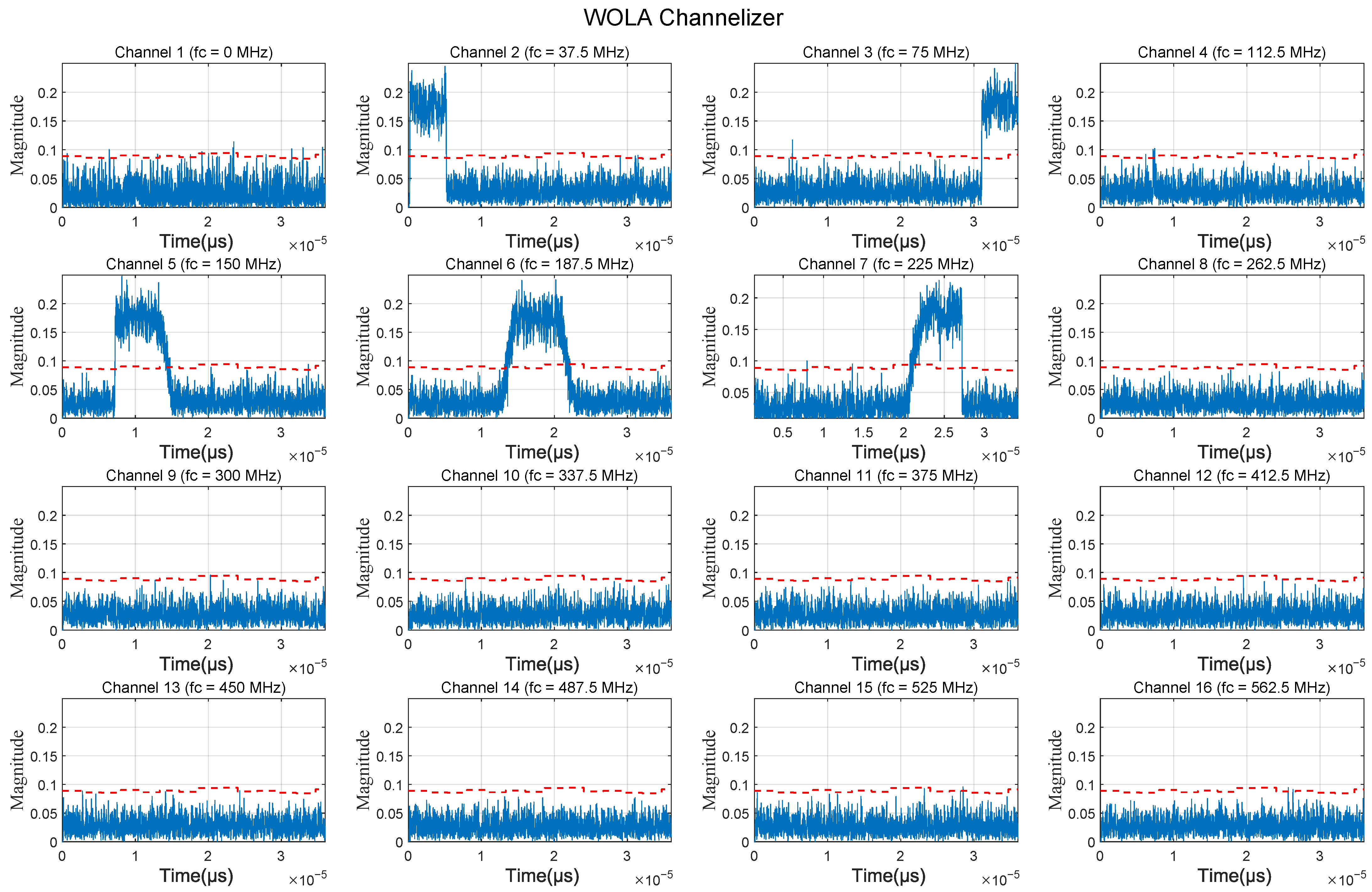
2.2.1. WOLA Channelization Structure
2.2.2. Adaptive Threshold Generation Algorithm
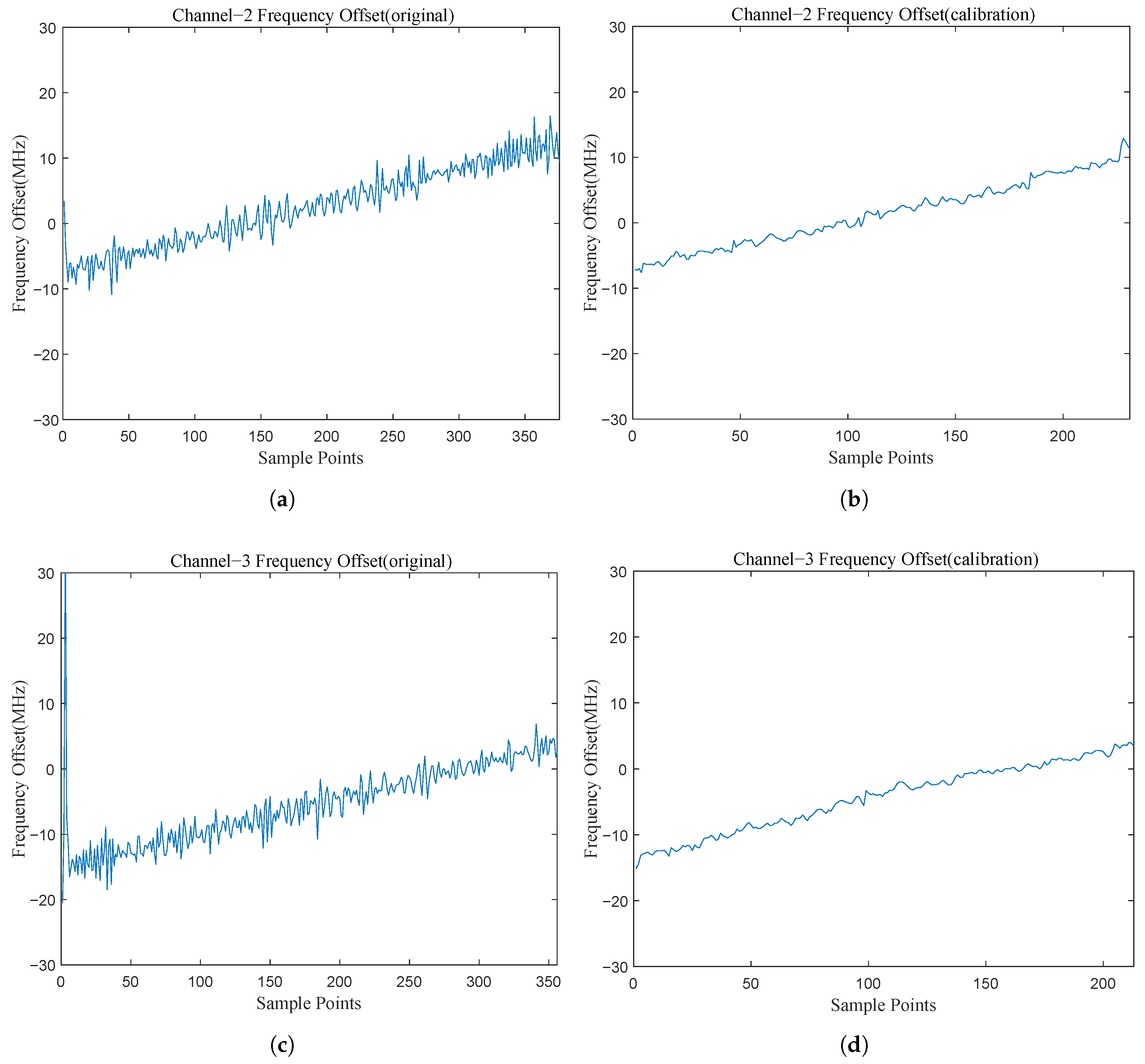
2.2.3. IFM and Channel Arbitration
3. Results and Discussion
3.1. Simulation Experiments
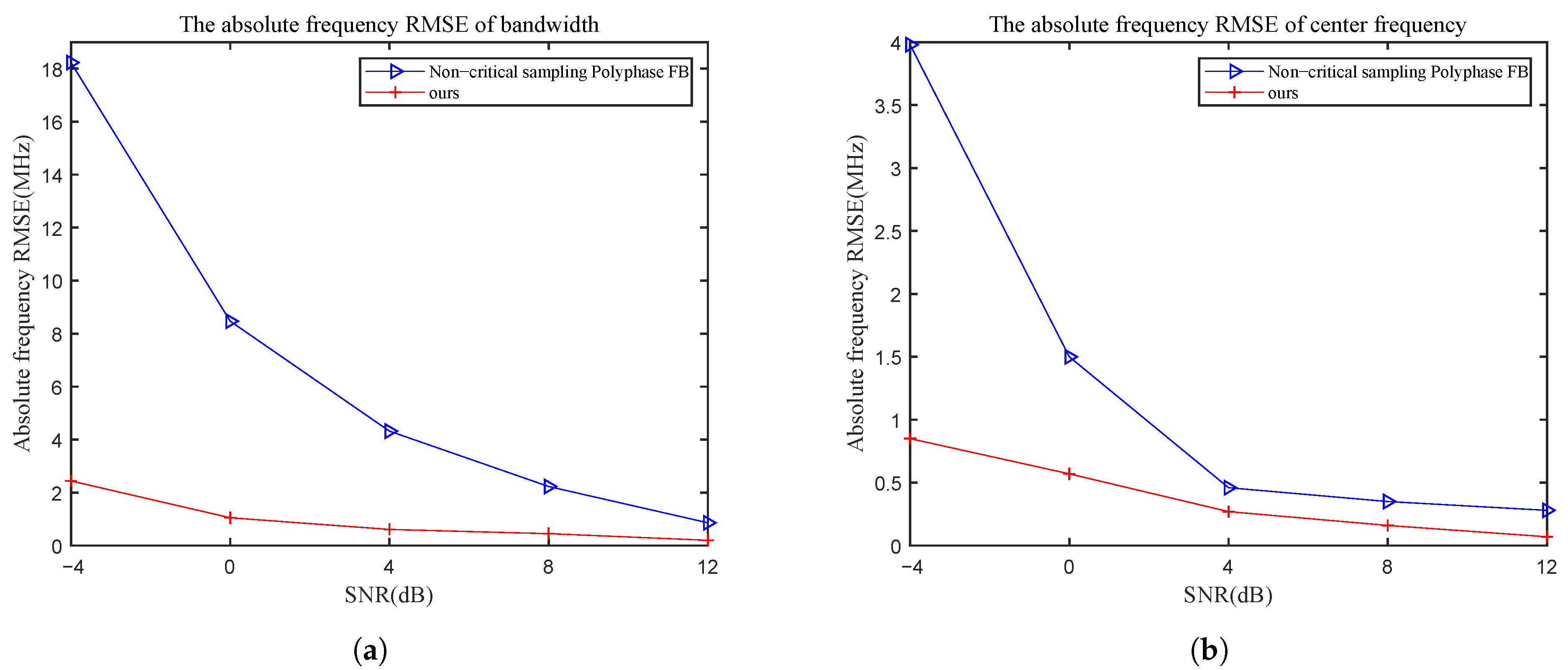
3.2. Performance Evaluation of the Proposed IFM Algorithm
3.3. Computational Costs
3.4. Discussion
4. Conclusions and Recommendation
- 1.
- A non-critical sampling digital channelized receiver architecture is proposed to detect wideband low SNR chirp signals. The proposed receiver architecture can adapt to a wide instantaneous bandwidth with high frequency estimation accuracy when the SNR is greater than 0 dB.
- 2.
- An adaptive threshold generation algorithm is proposed to detect signals without prior information.
- 3.
- A CORDIC-based instantaneous frequency measurement algorithm is also proposed, improving low SNR chirp signals’ frequency estimation accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Collins, J.; Grant, P. A review of current and future components for electronic warfare receivers. IEEE Trans. Sonics Ultrason. 1981, 28, 117–125. [Google Scholar] [CrossRef]
- Butt, F.A.; Jalil, M. An overview of electronic warfare in radar systems. In Proceedings of the 2013 The International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 213–217. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Ming, F.; Sun, X.; Hong, J. A Controllable Suppression Jamming Method against SAR Based on Active Radar Transponder. Remote Sens. 2022, 14, 3949. [Google Scholar] [CrossRef]
- Song, C.; Wang, Y.; Jin, G.; Wang, Y.; Dong, Q.; Wang, B.; Zhou, L.; Lu, P.; Wu, Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sens. 2022, 14, 5370. [Google Scholar] [CrossRef]
- Lou, M.; Yang, J.; Li, Z.; Ren, H.; An, H.; Wu, J. Joint Optimal and Adaptive 2-D Spatial Filtering Technique for FDA-MIMO SAR Deception Jamming Separation and Suppression. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5238414. [Google Scholar] [CrossRef]
- Cheng, D.; Liu, Z.; Guo, Z.; Shu, G.; Li, N. A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse. Remote Sens. 2022, 14, 4597. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Xie, J.; Yang, Y.; Tian, B.; Xu, S. Ultra-Low Sidelobe Waveforms Design for LPI Radar Based on Joint Complementary Phase-Coding and Optimized Discrete Frequency-Coding. Remote Sens. 2022, 14, 2592. [Google Scholar] [CrossRef]
- Govoni, M.A.; Li, H.; Kosinski, J.A. Range-Doppler Resolution of the Linear-FM Noise Radar Waveform. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 658–664. [Google Scholar] [CrossRef]
- Zangi, K.; Koilpillai, R. Software radio issues in cellular base stations. IEEE J. Sel. Areas Commun. 1999, 17, 561–573. [Google Scholar] [CrossRef]
- Gupta, D.; Filippov, T.V.; Kirichenko, A.F.; Kirichenko, D.E.; Vernik, I.V.; Sahu, A.; Sarwana, S.; Shevchenko, P.; Talalaevskii, A.; Mukhanov, O.A. Digital Channelizing Radio Frequency Receiver. IEEE Trans. Appl. Supercond. 2007, 17, 430–437. [Google Scholar] [CrossRef]
- Namgoong, W. A channelized digital ultrawideband receiver. IEEE Trans. Wirel. Commun. 2003, 2, 502–510. [Google Scholar] [CrossRef]
- Adame, B.O.; Salau, A. Genetic Algorithm Based Optimum Finger Selection for Adaptive Minimum Mean Square Error Rake Receivers Discrete Sequence-CDMA Ultra-Wide Band Systems. Wirel. Pers. Commun. 2022, 123, 1537–1551. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Garrido, M.; Lopez-Vallejo, M.; Grajal, J. Implementing FFT-based digital channelized receivers on FPGA platforms. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1567–1585. [Google Scholar] [CrossRef]
- Harris, F.; Dick, C.; Rice, M. Digital receivers and transmitters using polyphase filter banks for wireless communications. IEEE Trans. Microw. Theory Tech. 2003, 51, 1395–1412. [Google Scholar] [CrossRef]
- Kumar, R.; Nguyen, T.; Wang, C.; Goo, G. Signal processing techniques for wideband communications systems. In Proceedings of the MILCOM 1999—IEEE Military Communications, Conference Proceedings (Cat. No.99CH36341). Atlantic City, NJ, USA, 31 October–3 November 1999; Volume 1, pp. 452–457. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, G.; Wang, Y.; Bao, D. Wideband digital channelized receiver design. J. Xidian Univ. 2010, 37, 487–491. [Google Scholar] [CrossRef]
- Xu, Z.W.; Ming, S.F.; Tong, L.; Tao, C.; Zheng, D. Model of Non-leaking-Alarms and Non-aliasing Channelized Digital Receiver. In Proceedings of the 2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 21–23 July 2016; pp. 994–997. [Google Scholar] [CrossRef]
- Bregovic, R.; Saramaki, T. Design of two-channels FIR filterbanks with rational sampling factors using the FRM technique. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems (ISCAS), Kobe, Japan, 23–26 May 2005; Volume 2, pp. 1098–1101. [Google Scholar] [CrossRef]
- Li, F.; Hermansky, H. Effect of filter bandwidth and spectral sampling rate of analysis filterbank on automatic phoneme recognition. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 7121–7124. [Google Scholar] [CrossRef]
- Darak, S.J.; Palicot, J.; Zhang, H.; Prasad, V.A.; Moy, C. Reconfigurable Filter Bank With Complete Control Over Subband Bandwidths for Multistandard Wireless Communication Receivers. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 1772–1782. [Google Scholar] [CrossRef]
- Ling, W.; Yan, J.; Lu, J. High-Resolution Wideband Digital Channelizer with Adjustable Reconstruction Performance. In Proceedings of the 2018 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018; pp. 12–17. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, Z.; Guo, D.; Wang, X. Design of near perfect reconstruction prototype filter with FFT interpolation. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 159–163. [Google Scholar] [CrossRef]
- Cheng, Q.; Gong, K.; Zhang, M.; Liu, X. An efficient wide-band signal detection and extraction method. MATEC Web Conf. 2021, 336, 04011. [Google Scholar] [CrossRef]
- Wenxu, Z.; Limin, G. Design and simulation of wideband channelized receiver. In Proceedings of the 2010 Second IITA International Conference on Geoscience and Remote Sensing, Qingdao, China, 28–31 August 2010; Volume 2, pp. 575–578. [Google Scholar] [CrossRef]
- Yu, X.; Tian, S.; Zeng, H.; Tian, Y.; Ye, P.; Guo, L.; Zhang, S.; Wang, M. Research on Method of Instantaneous Frequency Measurement Based on CORDIC Algorithm. In Proceedings of the 2021 IEEE 15th International Conference on Electronic Measurement & Instruments (ICEMI), Nanjing, China, 29–31 October 2021; pp. 245–249. [Google Scholar] [CrossRef]
- Lu, H.Y.; Yen, M.H.; Chang, C.W.; Cheng, C.W.; Hsu, T.C.; Lin, Y.C. Efficient Hardware Implementation of CORDIC-Based Symbol Detector for GSM MIMO Systems: Algorithm and Hardware Architecture. IEEE Access 2022, 10, 114232–114241. [Google Scholar] [CrossRef]
- Ben, G.; Zheng, X.; Wang, Y.; Zhang, N.; Zhang, X. A Local Search Maximum Likelihood Parameter Estimator of Chirp Signal. Appl. Sci. 2021, 11, 673. [Google Scholar] [CrossRef]
- Swiercz, E.; Janczak, D.; Konopko, K. Detection of LFM Radar Signals and Chirp Rate Estimation Based on Time-Frequency Rate Distribution. Sensors 2021, 21, 5415. [Google Scholar] [CrossRef]
- Qu, Z.; Qu, F.; Hou, C.; Jing, F. Quadratic Frequency Modulation Signals Parameter Estimation Based on Two-Dimensional Product Modified Parameterized Chirp Rate-Quadratic Chirp Rate Distribution. Sensors 2018, 18, 1624. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, Z.; Guo, D. Research on dynamic channelization receiving technology of wideband satellite communication. In Proceedings of the 2017 First International Conference on Electronics Instrumentation & Information Systems (EIIS), Harbin, China, 3–5 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, J.; Zuo, Z.; Huang, Z.; Dong, Z. Dynamic Digital Channelizer Based on Spectrum Sensing. PLoS ONE 2015, 10, e0136349. [Google Scholar] [CrossRef] [PubMed]
- Zahirniak, D.; Sharpin, D.; Fields, T. A hardware-efficient, multirate, digital channelized receiver architecture. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 137–152. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Y.; Wang, X. Channelized Receiver with WOLA Filterbank. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–3. [Google Scholar] [CrossRef]






| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Input sampling sequence | System sampling rate | ||
| Prototype low-pass filter system function | Channel sampling rate after downsampling | ||
| The channel band-pass filter system function | K | Channel number | |
| The output sampling sequence of channel k | D | Downsampling decimation factor | |
| The center frequency of the channel | Channel overlap factor for channel division | ||
| The phase difference between the m and sampling point in channel k | The estimated angular frequency of the m sampling point in channel k |
| Parameter Type | Parameter Value | |
|---|---|---|
| System parameters | Sampling Rate () | 1200 MHz |
| Channel number | 32 | |
| Decimation number | 20 | |
| Filter parameters | Passband frequency | 19.5 MHz |
| Stopband frequency | 28.5 MHz | |
| Filter order | 256 |
| Parameter Type | Signal 1 | Signal 2 | Signal 3 |
|---|---|---|---|
| Modulation type | Chirp | Chirp | Chirp |
| SNR | 0 dB | 0 dB | 0 dB |
| Bandwidth | 20 MHz | 20 MHz | 100 MHz |
| Center frequency | 40 MHz | 70 MHz | 185 MHz |
| Pulse width | 5 μs | 5 μs | 20 μs |
| Parameter Type | Signal 1 | Signal 2 | Signal 3 |
|---|---|---|---|
| Bandwidth | 19.95 MHz | 19.68 MHz | 99.86 MHz |
| Center frequency | 40.31 MHz | 69.92 MHz | 183.33 MHz |
| Pulse width | 5 μs | 5 μs | 20 μs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Zhang, Q.; Lu, W.; Wang, H.; Liu, X. An Efficient Digital Channelized Receiver for Low SNR and Wideband Chirp Signals Detection. Appl. Sci. 2023, 13, 3080. https://doi.org/10.3390/app13053080
Cheng W, Zhang Q, Lu W, Wang H, Liu X. An Efficient Digital Channelized Receiver for Low SNR and Wideband Chirp Signals Detection. Applied Sciences. 2023; 13(5):3080. https://doi.org/10.3390/app13053080
Chicago/Turabian StyleCheng, Wenhai, Qunying Zhang, Wei Lu, Haiying Wang, and Xiaojun Liu. 2023. "An Efficient Digital Channelized Receiver for Low SNR and Wideband Chirp Signals Detection" Applied Sciences 13, no. 5: 3080. https://doi.org/10.3390/app13053080
APA StyleCheng, W., Zhang, Q., Lu, W., Wang, H., & Liu, X. (2023). An Efficient Digital Channelized Receiver for Low SNR and Wideband Chirp Signals Detection. Applied Sciences, 13(5), 3080. https://doi.org/10.3390/app13053080






