Encoding the Intensity and Phase Gradient of Light Beams with Arbitrary Shapes
Abstract
:1. Introduction
2. Materials and Methods
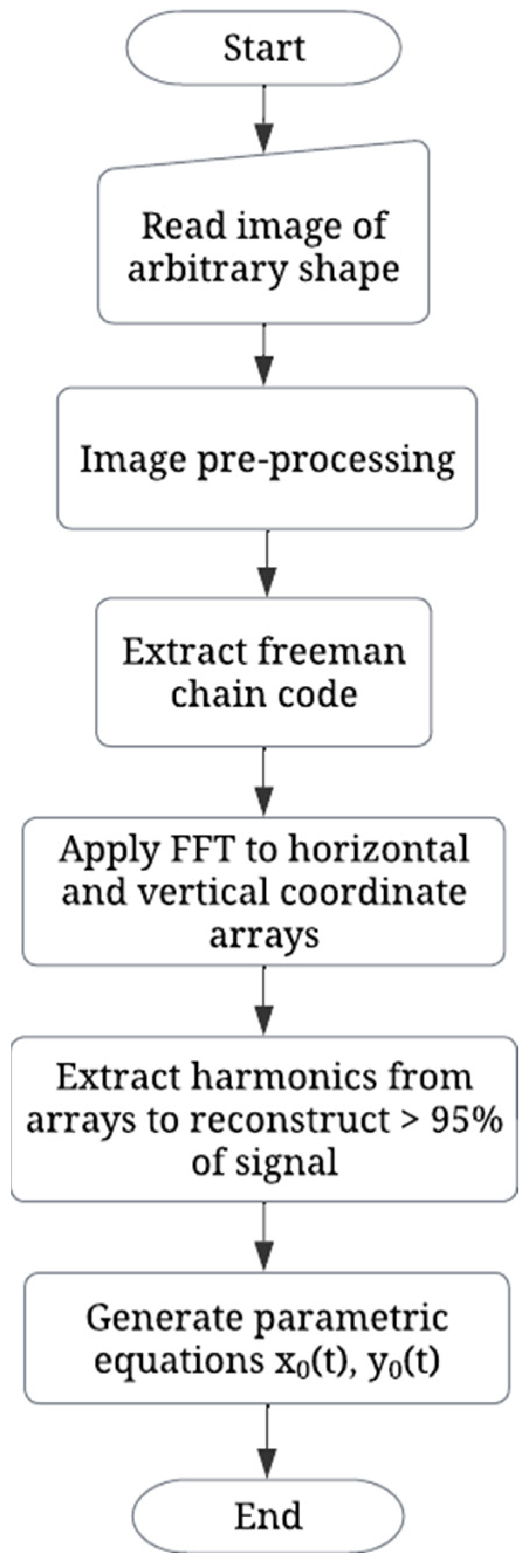
2.1. Signal Processing Algorithms
2.2. Experimental Setup
3. Results
3.1. Estimation of Parametric Equations
3.2. Testing the Intensity of the Designed Light Beams
3.3. Testing the Phase Gradient of the Designed Light Beams
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rhodes, P.W.; Shealy, D.L. Refractive Optical Systems for Irradiance Redistribution of Collimated Radiation: Their Design and Analysis. Appl. Opt. 1980, 19, 3545. [Google Scholar] [CrossRef] [PubMed]
- Veldkamp, W.B.; Kastner, C.J. Beam Profile Shaping for Laser Radars That Use Detector Arrays. Appl. Opt. 1982, 21, 345. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liang, Y. Generation and Detection of Structured Light: A Review. Front. Phys. 2021, 9, 345–356. [Google Scholar] [CrossRef]
- Serrano-Trujillo, A.; Anderson, M.E. Surface Profilometry Using Vortex Beams Generated with a Spatial Light Modulator. Opt. Commun. 2018, 427, 557–562. [Google Scholar] [CrossRef]
- Zhao, D.; Jia, C.; Ma, Y.; Yang, X.; Zhang, B.; Chu, W. High-Accuracy Surface Profile Measurement Based on the Vortex Phase-Shifting Interferometry. Int. J. Opt. 2021, 2021, 6937072. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, A.; Wang, J. Free-Space Data-Carrying Bendable Light Communications. Sci. Rep. 2019, 9, 14969. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, M.; Kozawa, Y.; Sato, S. Subtraction Imaging by the Combination of Higher-Order Vector Beams for Enhanced Spatial Resolution. Opt. Lett. 2019, 44, 883. [Google Scholar] [CrossRef] [PubMed]
- Kozawa, Y.; Matsunaga, D.; Sato, S. Superresolution Imaging via Superoscillation Focusing of a Radially Polarized Beam. Optica 2018, 5, 86. [Google Scholar] [CrossRef]
- Grier, D.G.; Roichman, Y. Holographic Optical Trapping. Appl. Opt. 2006, 45, 880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Q.; Chew, K.-H.; Huang, Y.; Liu, C.; Hu, X.; Li, Y.; Chen, R.-P. Effect of Twisting Phases on the Polarization Dynamics of a Vector Optical Field. Photonics 2022, 9, 722. [Google Scholar] [CrossRef]
- Liu, C. Vortex Beam and Its Application in Optical Tweezers. J. Phys. Conf. Ser. 2020, 1549, 032012. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castro, I. Shaping of Light Beams along Curves in Three Dimensions. Opt. Express 2013, 21, 20544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serrano-Trujillo, A.; Palafox, L.E.; Ruiz-Cortés, V. Engineering of Cylindrical Vector Fields with a Twisted Nematic Spatial Light Modulator. Appl. Opt. 2017, 56, 1310. [Google Scholar] [CrossRef]
- Mendoza-Hernández, J. Customizing Structured Light Beams with a Differential Operator. Opt. Lett. 2021, 46, 5232. [Google Scholar] [CrossRef]
- Li, J.; Hill, E.H.; Lin, L.; Zheng, Y. Optical Nanoprinting of Colloidal Particles and Functional Structures. ACS Nano 2019, 13, 3783–3795. [Google Scholar] [CrossRef]
- Levichev, N.; Herwig, P.; Wetzig, A.; Duflou, J.R. Towards Robust Dynamic Beam Shaping for Laser Cutting Applications. Procedia CIRP 2022, 111, 746–749. [Google Scholar] [CrossRef]
- Möhl, A.; Kaldun, S.; Kunz, C.; Müller, F.A.; Fuchs, U.; Gräf, S. Tailored Focal Beam Shaping and Its Application in Laser Material Processing. J. Laser Appl. 2019, 31, 042019. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Li, J.; Li, W.; Yogeesh, M.N.; Shi, J.; Peng, X.; Liu, Y.; Rajeeva, B.B.; Becker, M.F.; Liu, Y.; et al. Optothermoplasmonic Patterning: Optothermoplasmonic Nanolithography for on-Demand Patterning of 2D Materials (Adv. Funct. Mater. 41/2018). Adv. Funct. Mater. 2018, 28, 1870299. [Google Scholar] [CrossRef]
- Nan, F.; Yan, Z. Synergy of Intensity, Phase, and Polarization Enables Versatile Optical Nanomanipulation. Nano Lett. 2020, 20, 2778–2783. [Google Scholar] [CrossRef]
- Li, J.; Zheng, Y. Optothermally Assembled Nanostructures. Acc. Mater. Res. 2021, 2, 352–363. [Google Scholar] [CrossRef]
- Zannotti, A.; Denz, C.; Alonso, M.A.; Dennis, M.R. Shaping Caustics into Propagation-Invariant Light. Nat. Commun. 2020, 11, 3597. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Pearson: New York, NY, USA, 2018. [Google Scholar]
- Anderson, M.E.; Serrano, A.; Stinson, C.; Talamantes, A.; Miller, N.; Chaloupka, J.L. Spatial Manipulation of a Supercontinuum Beam for the Study of Vortex Interference Effects. Appl. Sci. 2020, 10, 1966. [Google Scholar] [CrossRef] [Green Version]
- Moreno, I.; Davis, J.A.; Womble-Dahl, T.; Cottrell, D.M. Azimuthal Multiple-Beam Interference Effects with Combinations of Vortex Beams. Opt. Lett. 2015, 40, 2341. [Google Scholar] [CrossRef]
- Turtaev, S.; Leite, I.T.; Mitchell, K.J.; Padgett, M.J.; Phillips, D.B.; Čižmár, T. Comparison of Nematic Liquid-Crystal and DMD Based Spatial Light Modulation in Complex Photonics. Opt. Express 2017, 25, 29874. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Z.; Ho, H.P. Application of Digital Micromirror Devices (DMD) in Biomedical Instruments. J. Innov. Opt. Health Sci. 2020, 13, 2030011. [Google Scholar] [CrossRef]
- Sharma, E.; Rathi, R.; Misharwal, J.; Sinhmar, B.; Kumari, S.; Dalal, J.; Kumar, A. Evolution in Lithography Techniques: Microlithography to Nanolithography. Nanomaterials 2022, 12, 2754. [Google Scholar] [CrossRef]
- Nan, F.; Yan, Z. Optical Sorting at the Single-Particle Level with Single-Nanometer Precision Using Coordinated Intensity and Phase Gradient Forces. ACS Nano 2020, 14, 7602–7609. [Google Scholar] [CrossRef]
- Chen, H.-C.; Cheng, C.-J. Holographic Optical Tweezers: Techniques and Biomedical Applications. Appl. Sci. 2022, 12, 10244. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Zheng, Y. Heat-Mediated Optical Manipulation. Chem. Rev. 2021, 122, 3122–3179. [Google Scholar] [CrossRef]





| Shape | Parametric Equation “x” | Parametric Equation “y” |
|---|---|---|
| cos(t − 3.08) | cos(t + 1.63) |
| cos(t − 3.06) + 0.11 cos(3t + 0.24) | cos(t + 1.65) + 0.10 cos(3t − 1.33) |
| −0.04 + cos(t + 3.11) + 0.05 cos(2t − 0.91) + 0.03 cos(3t − 2.43) + 0.01 cos(4t − 2.83) | 0.24 + cos(t + 1.59) + 0.04 cos(2t + 0.37) + 0.05 cos(3t − 1.25) + 0.03 cos(4t − 2.56) + 0.02 cos(5t + 2.79) + 0.02 cos(6t + 0.71) |
| cos(t − 2.69) + 0.11 cos(3t + 1.39) + 0.06 cos(5t + 2.33) + 0.02 cos(7t − 2.95) + 0.02 cos(9t − 2.12) + 0.02 cos(11t − 1.26) + 0.01 cos(13t− 0.32) | cos(t + 2.03) + 0.05 cos(3t − 0.21) |
| cos(t − 3.04) + 0.04 cos(2t − 1.42) + 0.05 cos(3t − 2.86) | −0.47 + cos(t + 1.66) + 0.23 cos(2t − 2.96) + 0.04 cos(3t + 1.82) + 0.12 cos(4t + 0.35) |
| cos(t − 3.14) + 0.31 cos(3t − 3.13) + 0.07 cos(5t − 3.13) + 0.05 cos(7t − 3.12) + 0.02 cos(9t − 3.11) + 0.01 cos(11t − 3.1) | cos(t + 1.57) + 0.32 cos(3t − 1.56) + 0.07 cos(5t + 1.59) + 0.03 cos(7t − 1.54) + 0.02 cos(9t + 1.61) + 0.01 cos(11t − 1.53) |
| −0.03 + cos(t − 2.88) + 0.13 cos(2t + 1.75) + 0.05 cos(3t − 3.04) + 0.08 cos(4t + 2.81) + 0.05 cos(5t − 1.53) + 0.08 cos(6t + 2.84) | −0.25 + cos(t + 1.83) + 0.13 (cos2t − 2.45) + 0.11 cos(3t − 0.75) + 0.03 cos(4t − 1.96) + 0.07 cos(5t + 2.8) + 0.02 cos(6t + 1.29) |
| −0.13+cos(t − 2.71) + 0.06 cos(2t + 0.9) + 0.03 cos(3t − 2.25) + 0.03 cos(4t + 2.07) | 0.2 + cos(t + 1.79) + 0.23 cos(2t − 0.92) + 0.33 cos(3t − 3.14) + 0.2 cos(4t − 2.78) + 0.02 cos(5t − 2.02) + 0.05 cos(6t + 1.68) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrano-Trujillo, A.; Ruiz-Cortés, V. Encoding the Intensity and Phase Gradient of Light Beams with Arbitrary Shapes. Appl. Sci. 2023, 13, 3192. https://doi.org/10.3390/app13053192
Serrano-Trujillo A, Ruiz-Cortés V. Encoding the Intensity and Phase Gradient of Light Beams with Arbitrary Shapes. Applied Sciences. 2023; 13(5):3192. https://doi.org/10.3390/app13053192
Chicago/Turabian StyleSerrano-Trujillo, Alejandra, and Víctor Ruiz-Cortés. 2023. "Encoding the Intensity and Phase Gradient of Light Beams with Arbitrary Shapes" Applied Sciences 13, no. 5: 3192. https://doi.org/10.3390/app13053192
APA StyleSerrano-Trujillo, A., & Ruiz-Cortés, V. (2023). Encoding the Intensity and Phase Gradient of Light Beams with Arbitrary Shapes. Applied Sciences, 13(5), 3192. https://doi.org/10.3390/app13053192





