Analytical Study of Lateral Buckling of Pipelines with Initial Imperfection Based on Fixed-Fixed Beam Model
Abstract
:1. Introduction
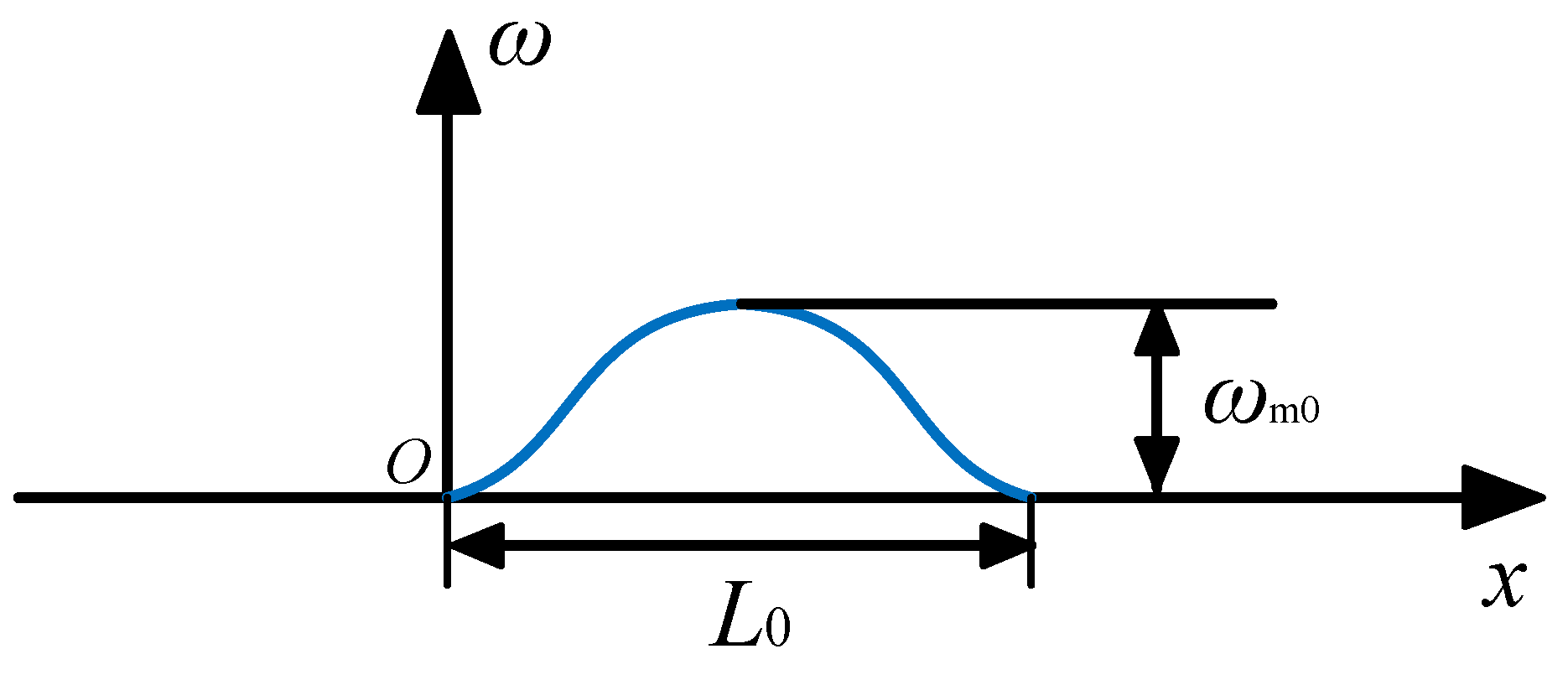
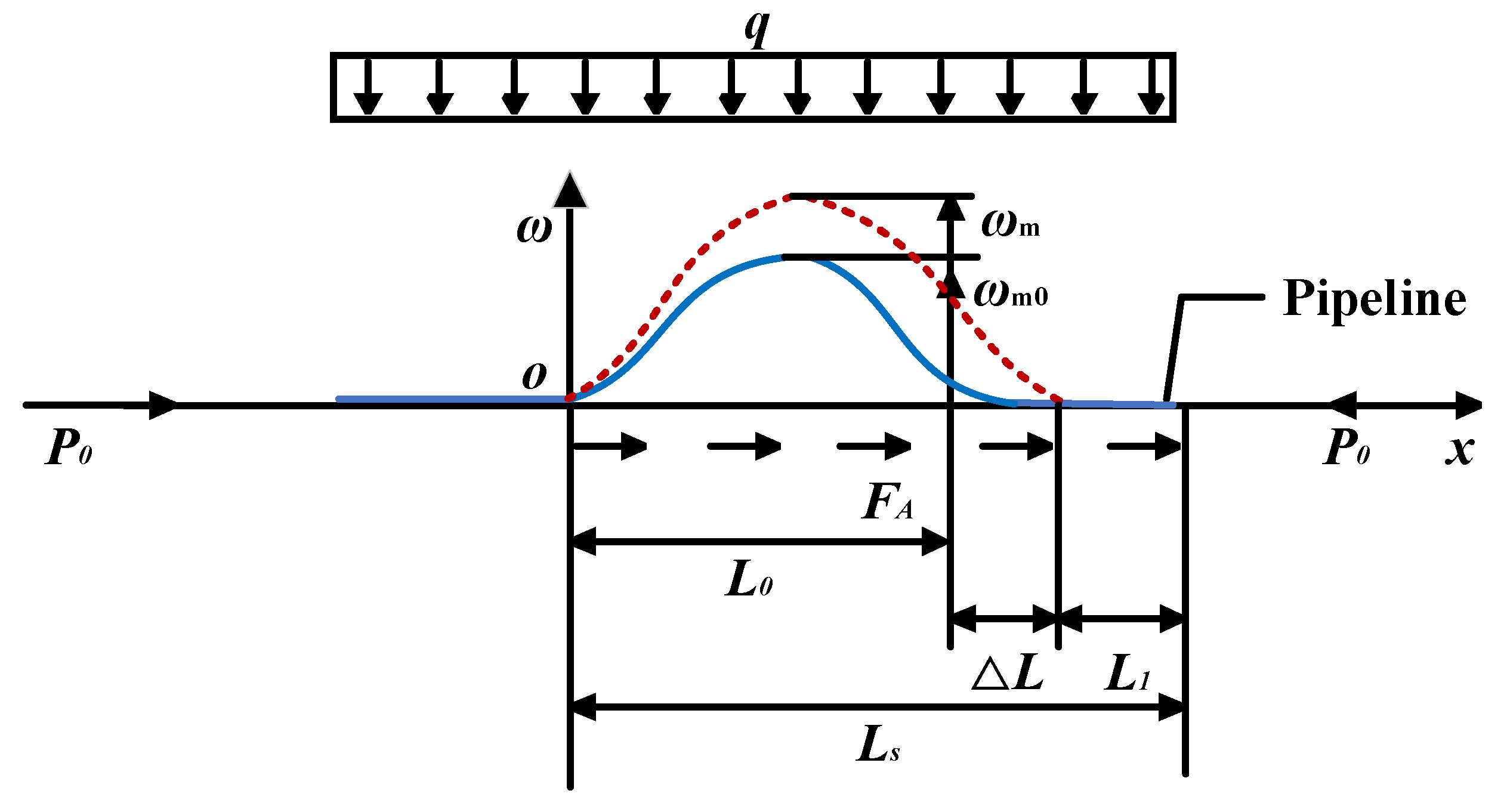
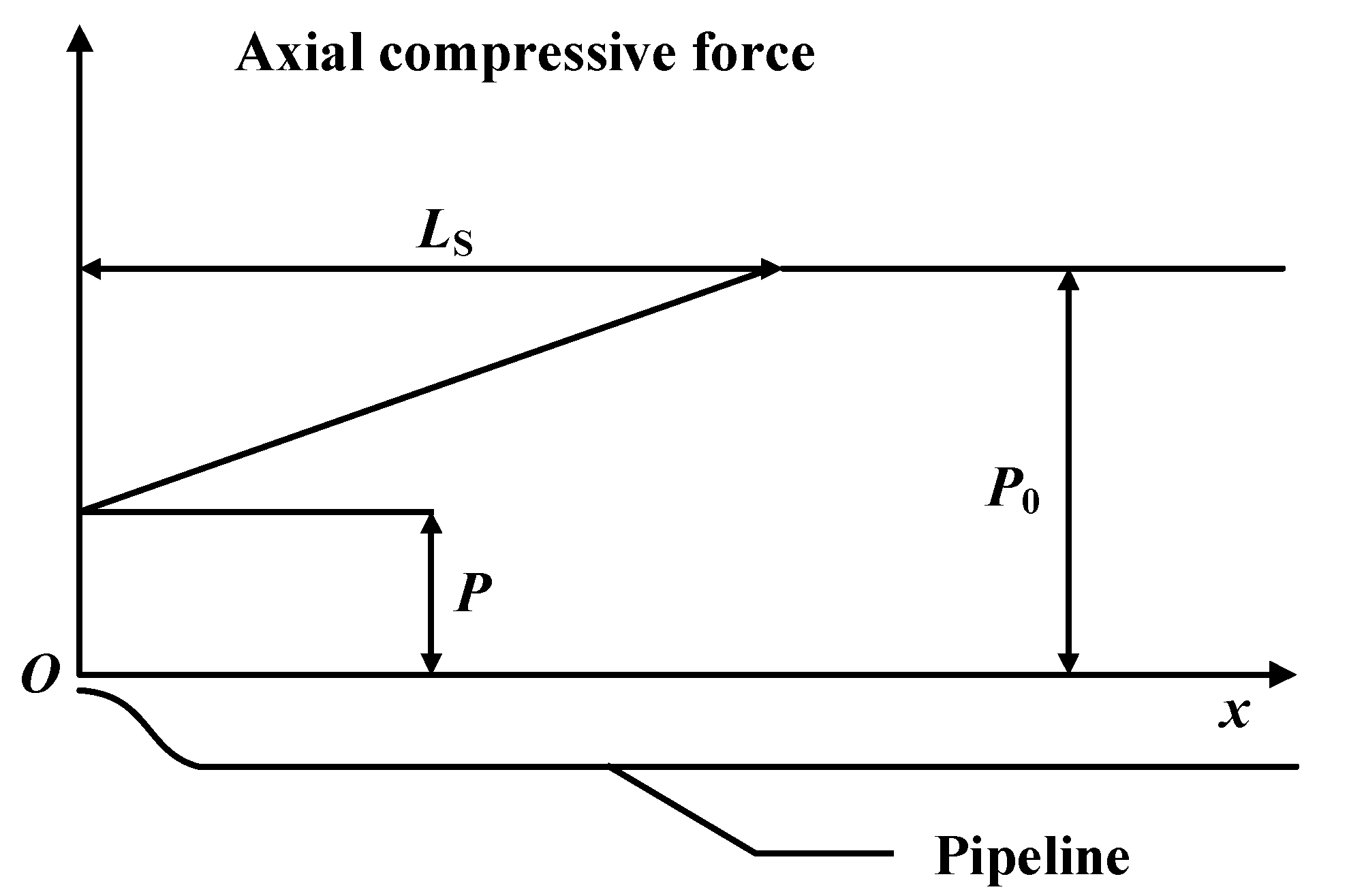
2. Mathematical Model and Assumptions
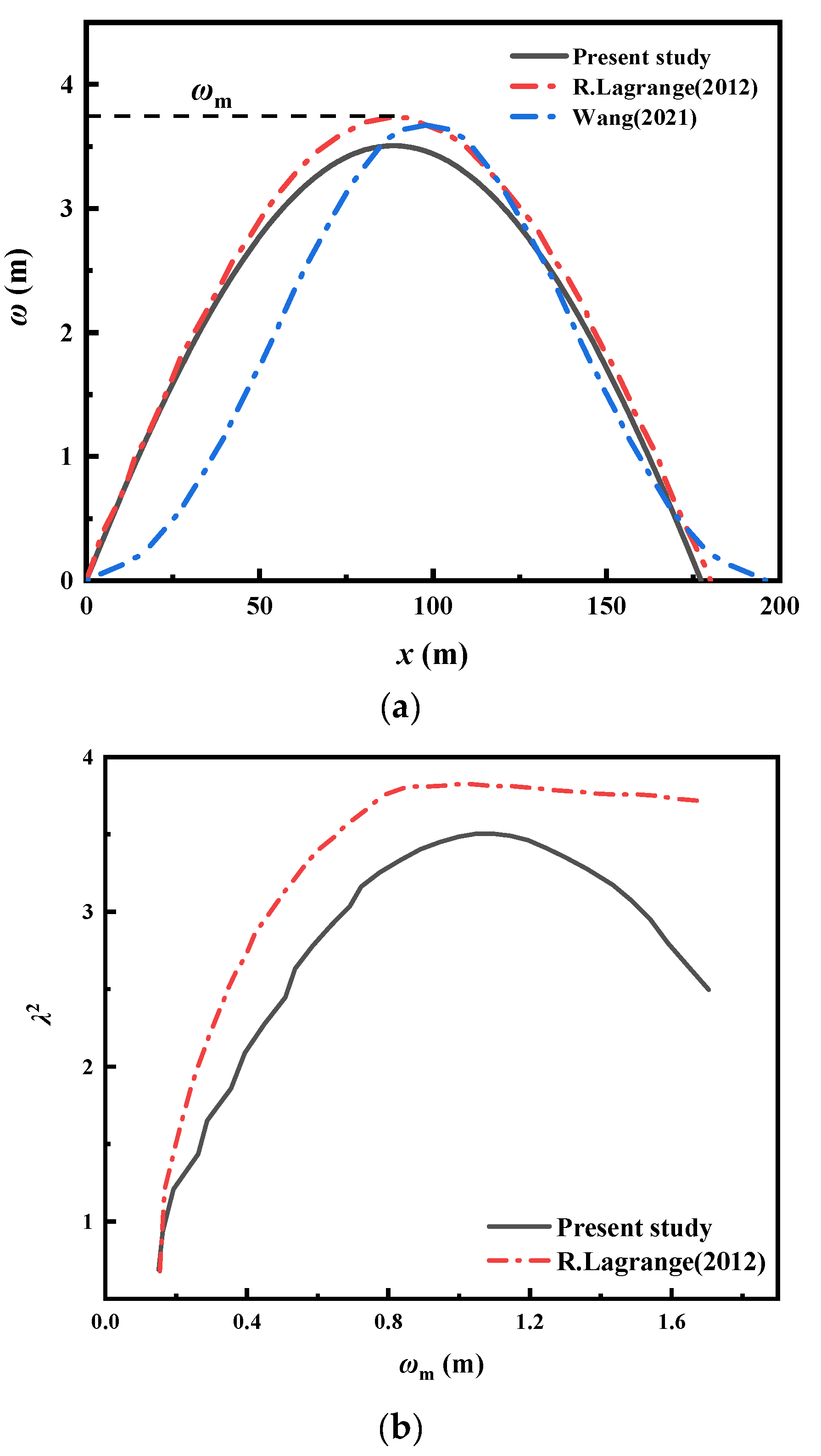
3. Comparison
4. Parametric Study
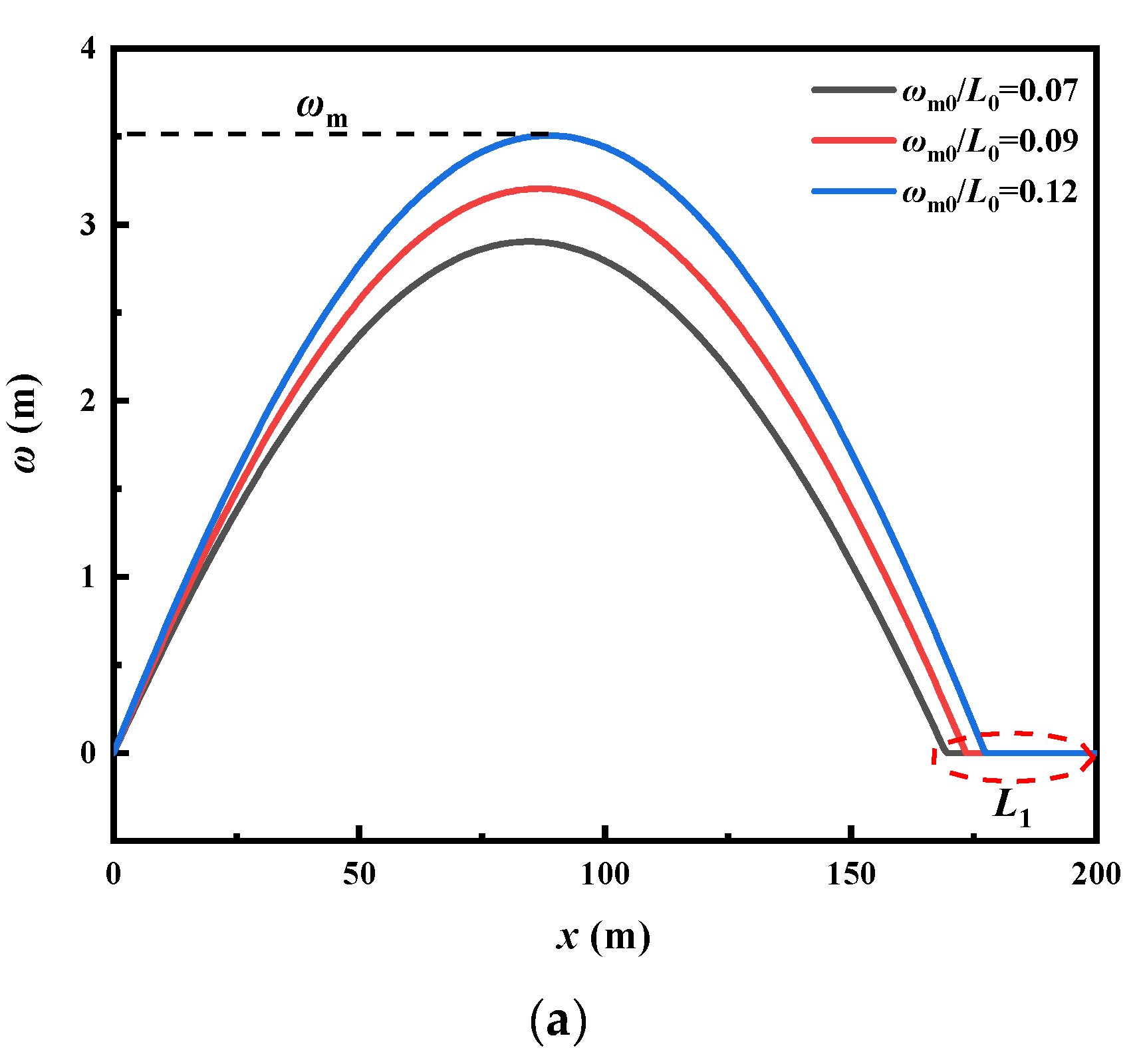
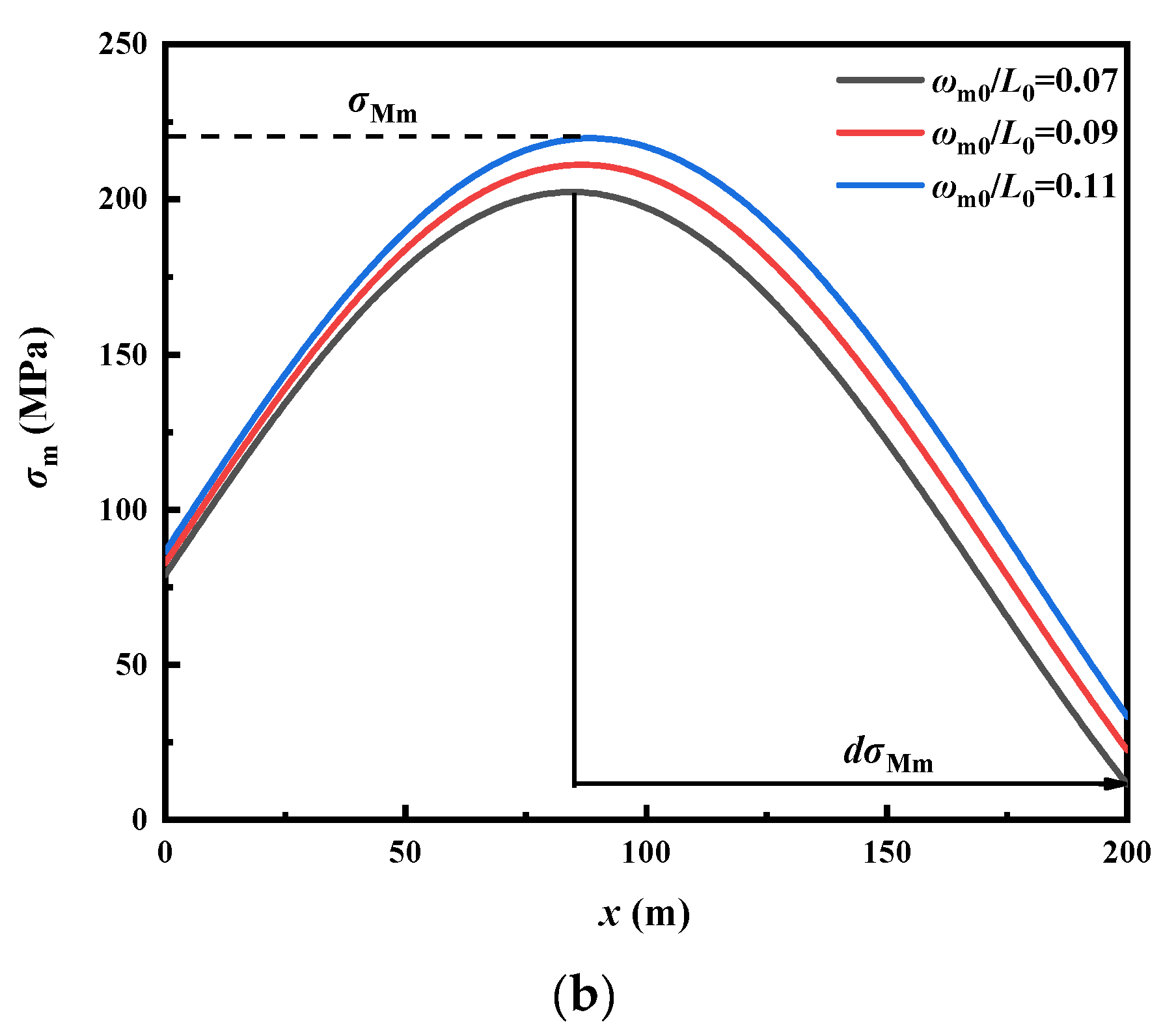
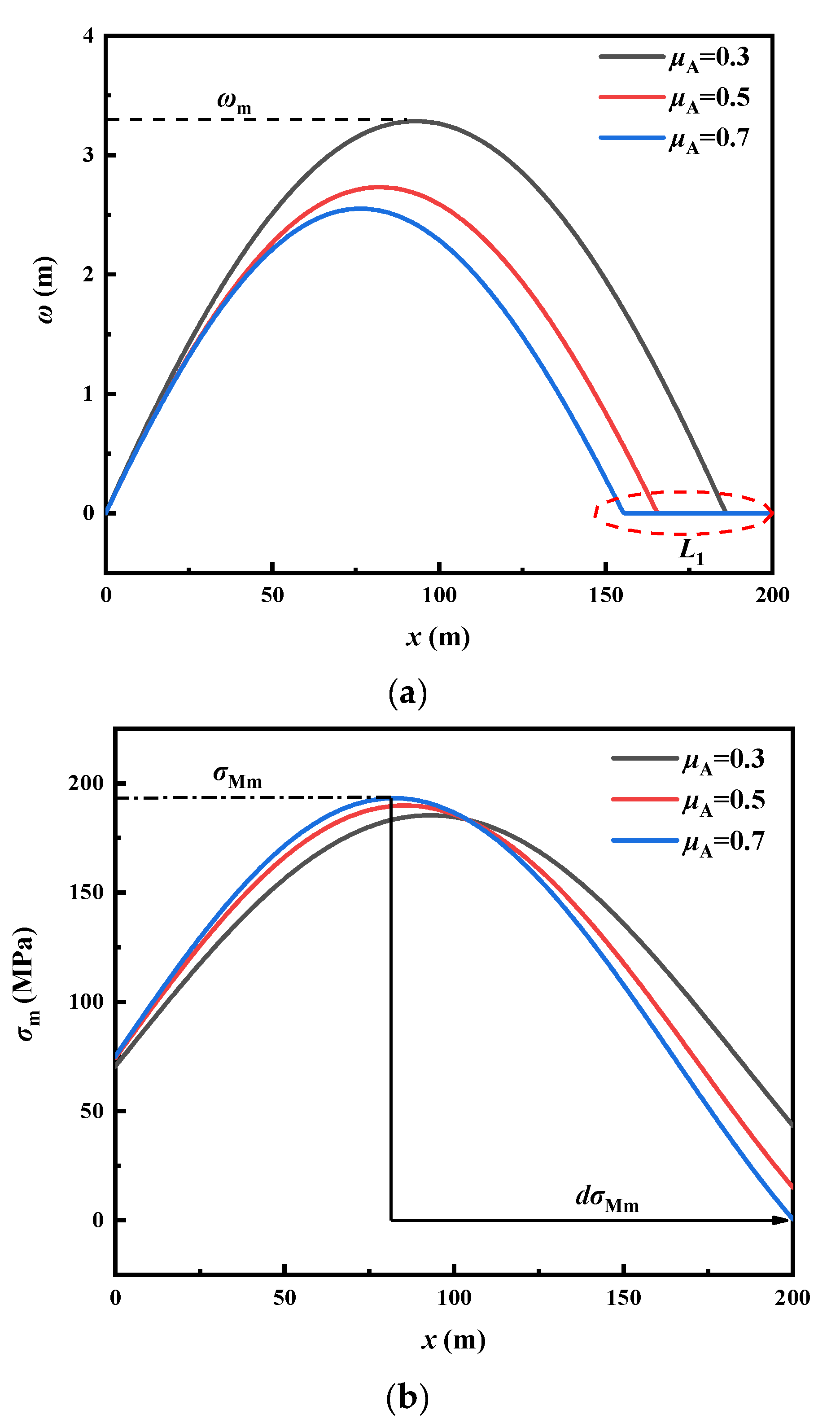
4.1. Initial Imperfection Effect
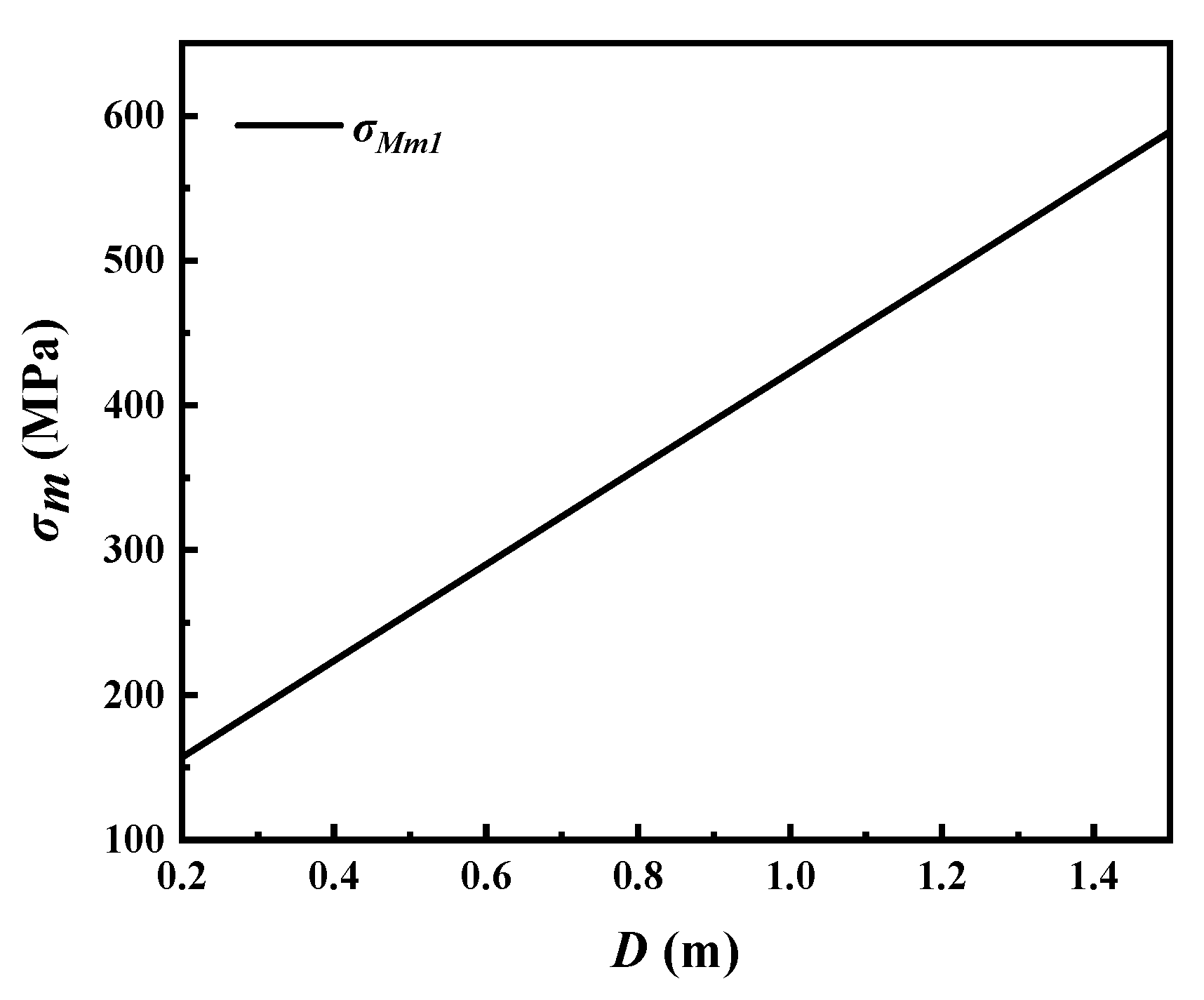
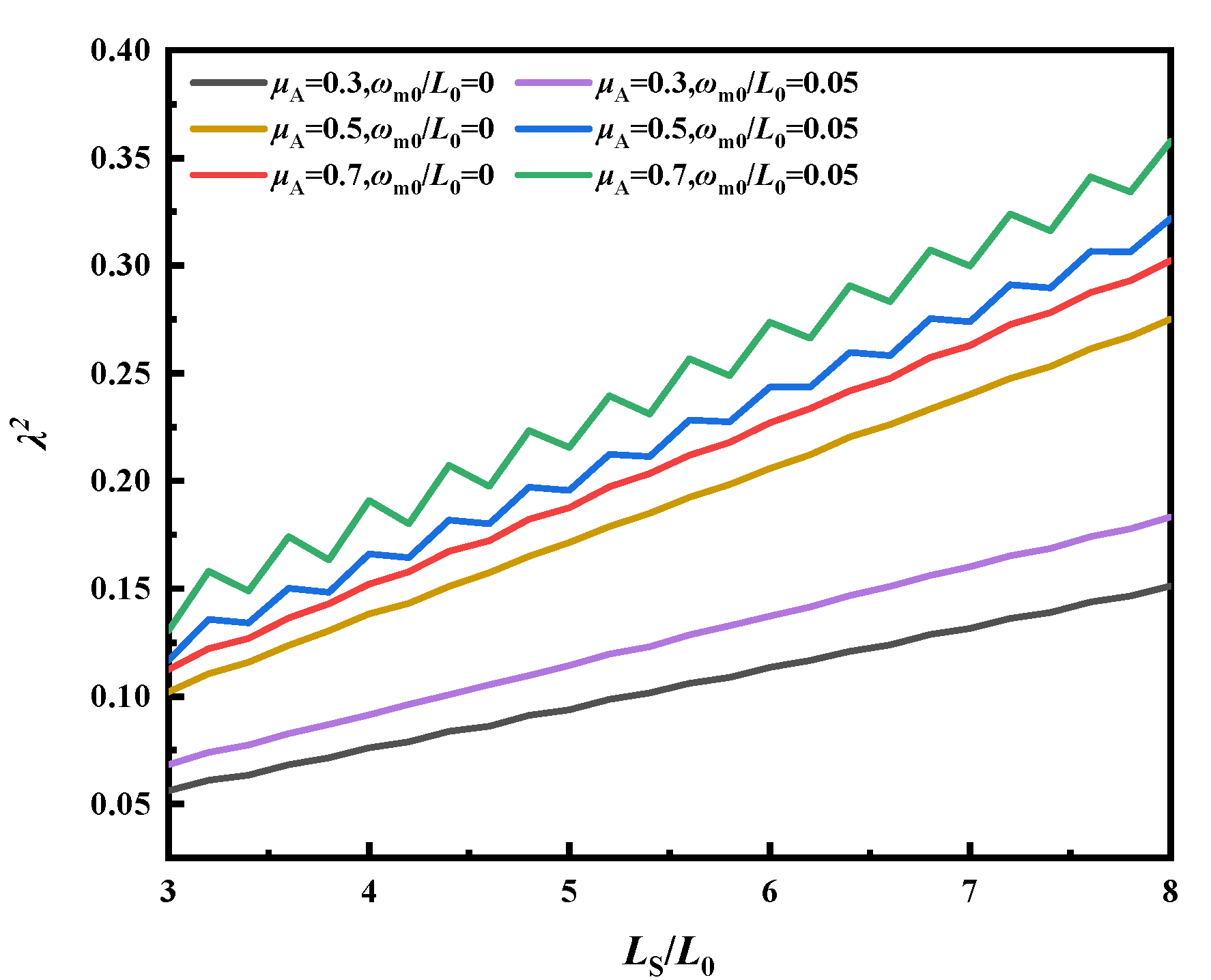
4.2. Pipeline Design Size Effect
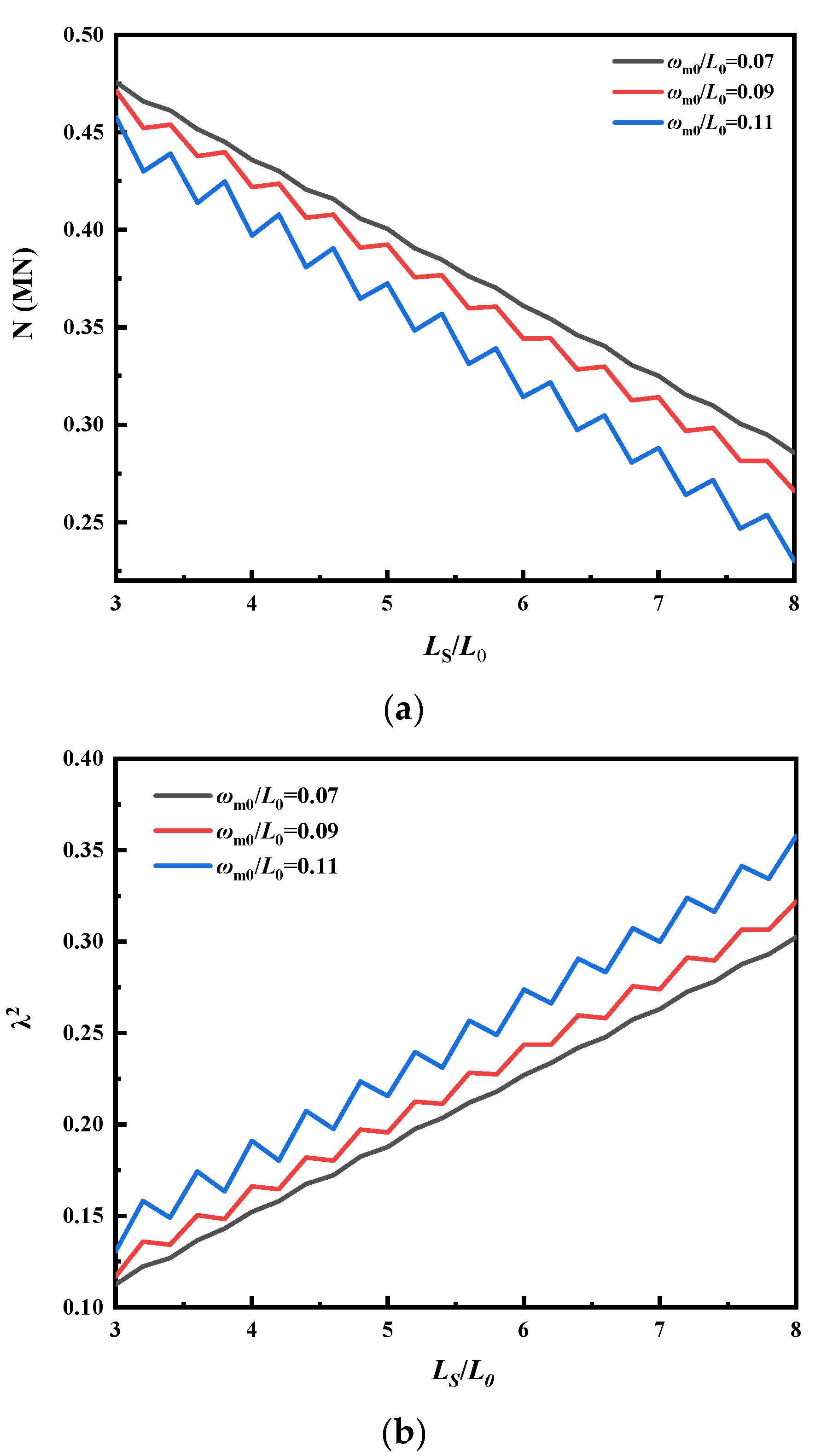
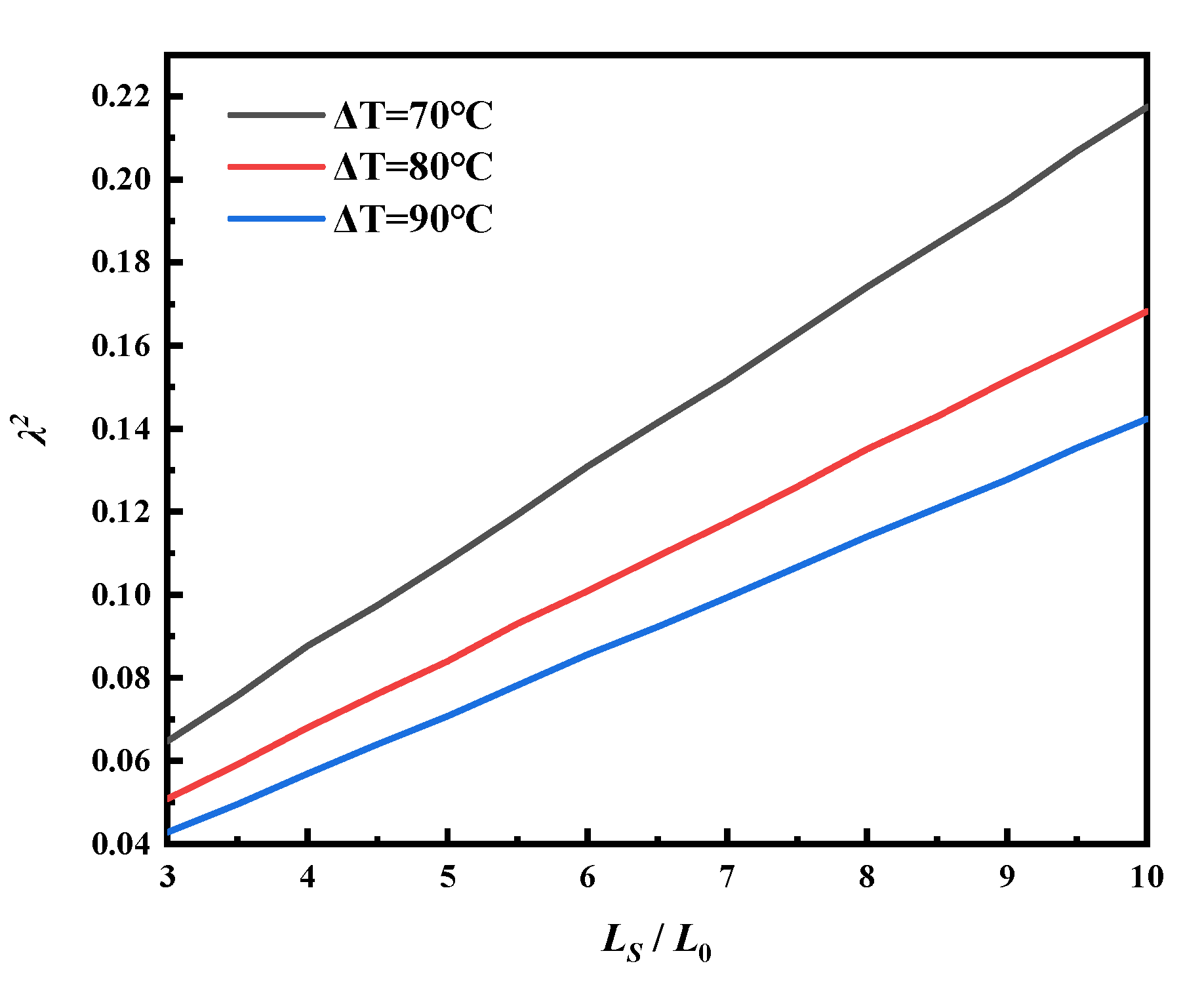
4.2.1. Virtual Anchor Segment (VAS) Length Effect
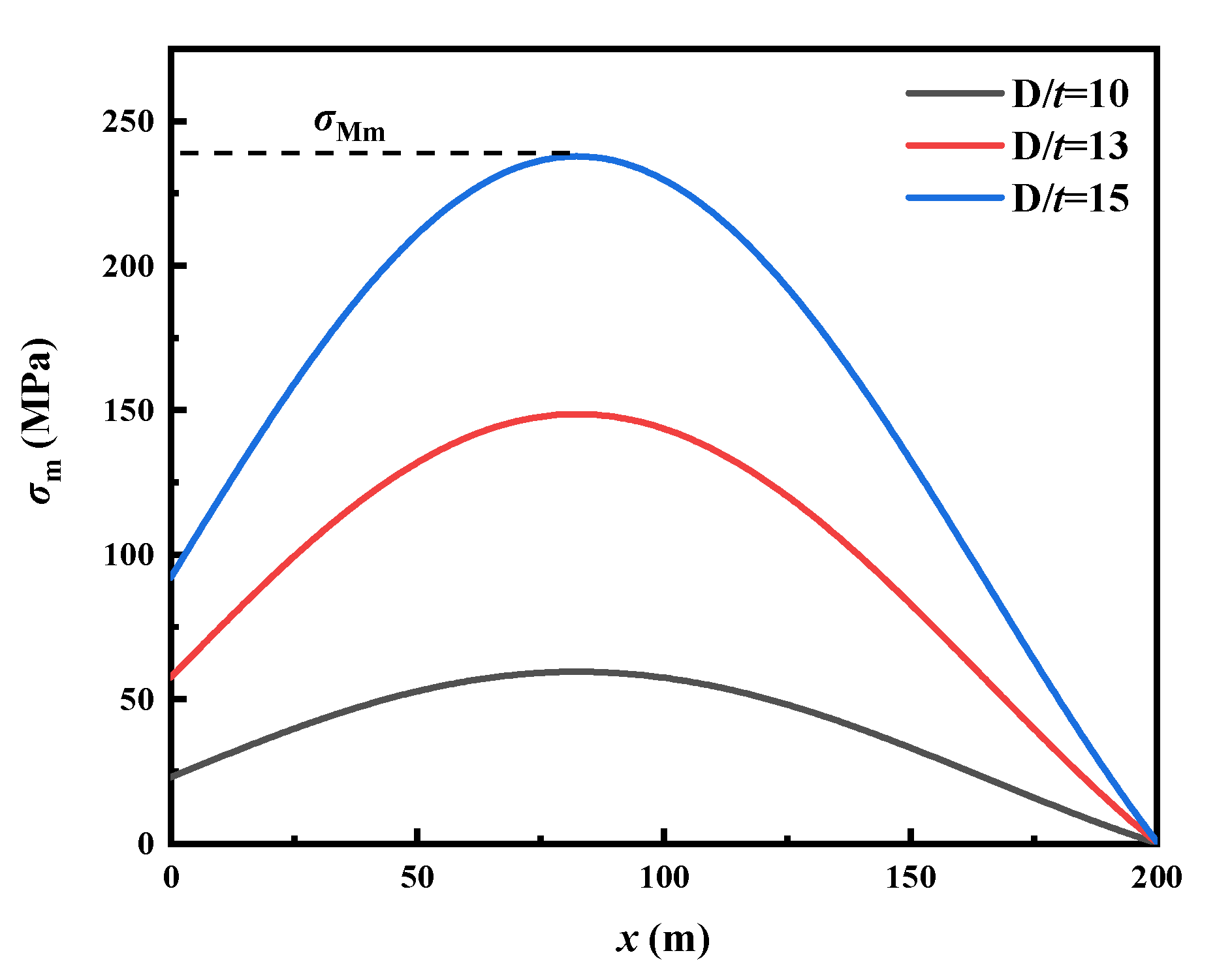
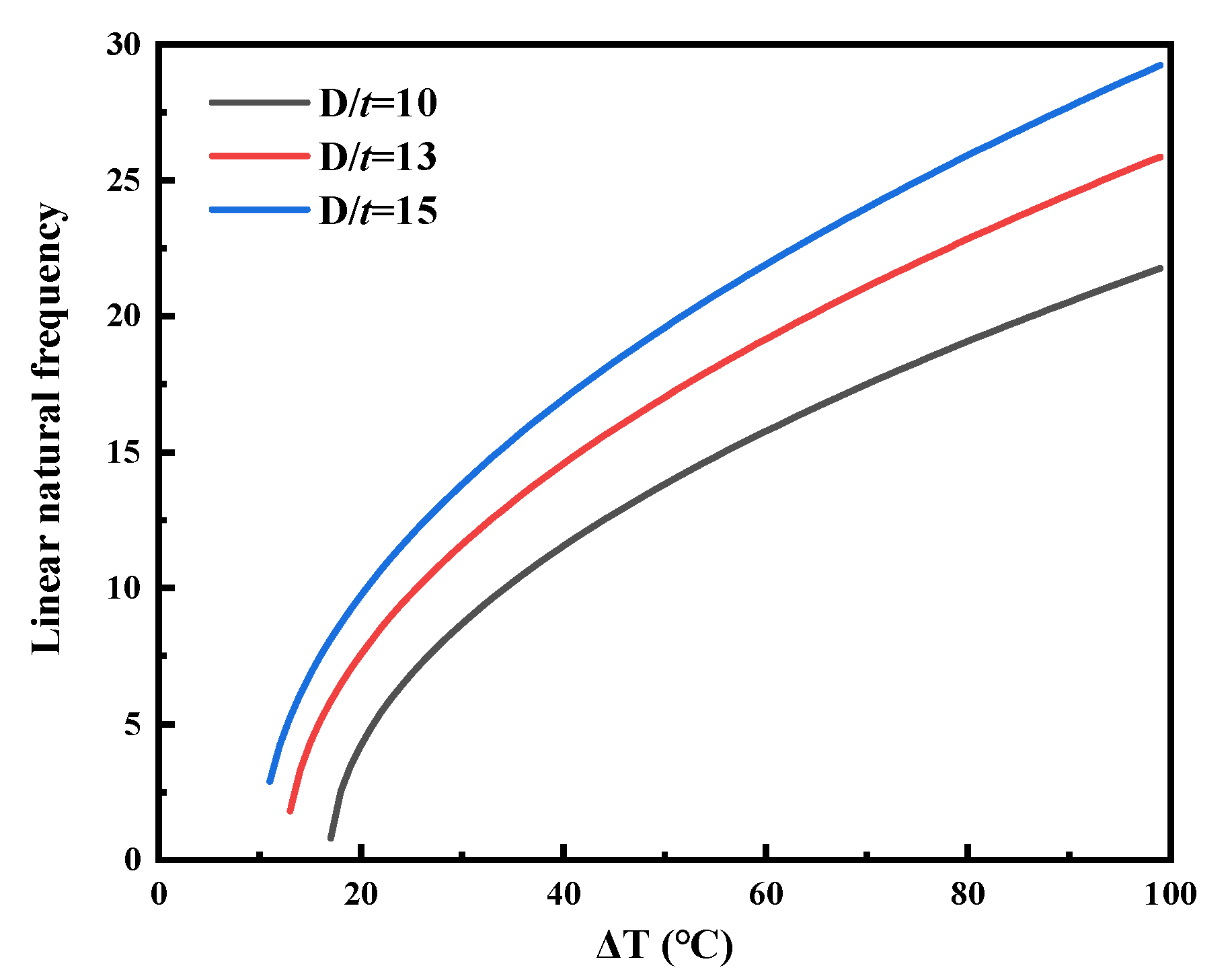
4.2.2. Diameter–Thick Ratio Effect
4.3. Temperature Effect
4.4. Soil Resistance Effect
5. Conclusions
- When the virtual anchor section divides the pipeline into multiple short sections, the thermal vibration phenomenon can be found based on the fixed-fixed beam model. The thermal vibration of the beam will cause the fatigue effect when the pipe bears the thermal load or the axial load, reducing the service life of the pipe. Therefore, when studying the lateral buckling problem of the pipeline, attention should be paid to the thermal vibration effect of the pipeline.
- With increasing initial imperfection amplitude, the displacement amplitude and bending stress of the pipe increase linearly and the maximum bending stress position moves toward the position of the imperfection. At the same time, with increasing initial imperfection, the frequency and density of the pipeline stress vibration also increases, making the stress mutation effect more obvious. Attention should be paid to the fatigue disruption caused by continuous stress mutations in the pipeline during buckling.
- Virtual anchor segment length (VAS) and diameter–thick ratio of the pipeline have an obvious influence on the behavior of lateral buckling. Increasing the diameter–thick ratio significantly increases the bending stress of the pipeline, and the anchoring effect of increasing the tensile stress on the pipeline. This is advantageous for the pipeline stability. When lateral buckling of the pipeline occurs, there is an obvious size effect. Therefore, in the pipeline design, the size effect of the pipeline must be considered.
- With increasing temperature difference, the buckling amplitude and bending stress increase linearly. In addition, the maximum bending stress point moves in the positive direction of LS, making the stress response at the pipe imperfection stronger. The corresponding tensile force also increases linearly with increasing temperature difference. Therefore, the pipeline running at high temperature is more likely to undergo lateral buckling at the initial imperfection.
- As the soil resistance increases, the buckling amplitude decreases, and the bending stress increases accordingly. The maximum bending stress point moves toward the imperfection. With increasing soil resistance, pipe buckling is less likely to occur. Therefore, it is prudent to prevent lateral buckling by increasing the effective friction coefficient, such as by digging trench lines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DNVGL-RP-F110. Global buckling of submarine pipelines structural design due to high temperature/high pressure. Oslo Det. Norske Veritas 2018. [Google Scholar]
- Hobbs, R.E. In-service buckling of heated pipelines. J. Transp. Eng. 1984, 110, 175–189. [Google Scholar] [CrossRef]
- Taylor, N.; Tran, V. Experimental and theoretical studies in subsea pipeline buckling. Mar. Struct. 1996, 9, 59–78. [Google Scholar] [CrossRef]
- Sriskandarajah, T.; Dong, S.; Sribalachandran, S. Effect of initial imperfections on the lateral buckling of subsea pipelines. In Proceedings of the 1999 9th International Offshore and Polar Engineering Conference (ISOPE-99), Brest, France, 30 May–4 June 1999; pp. 168–175. [Google Scholar]
- Zeng, X.G.; Duan, M.L.; Che, X.Y. Critical upheaval buckling forces of imperfect pipelines. Appl. Ocean Res. 2014, 45, 33–39. [Google Scholar] [CrossRef]
- Wang, Z.K.; van der Heijden, G.H.M. Mode jumping in the lateral buckling of subsea pipelines. Mar. Struct. 2021, 80, 103077. [Google Scholar] [CrossRef]
- Liu, R.; Wang, X.Y. Lateral global buckling high-order mode analysis of a submarine pipeline with imperfection. Appl. Ocean Res. 2018, 73, 107–126. [Google Scholar] [CrossRef]
- Shi, R.; Wang, L.; Guo, Z.; Yuan, F. Upheaval buckling of a pipeline with prop imperfection on a plastic soft seabed. Thin-Walled Struct. 2013, 65, 1–6. [Google Scholar] [CrossRef]
- Croll, J.G.A. A simplified model of upheaval thermal buckling of subsea pipelines. Thin-Walled Struct. 1997, 29, 59–78. [Google Scholar] [CrossRef]
- Hunt, G.W.; Bolt, H.M.; Thompson, J.M.T. Structural localization phenomena and the dynamical phase-space analogy. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 425, 175–189. [Google Scholar]
- Kiani, Y.; Eslami, M.R. Thermal buckling analysis of functionally graded material beams. Int. J. Mech. Mater. Des. 2010, 6, 229–238. [Google Scholar] [CrossRef]
- Wang, Z.K.; Tang, Y.G.; Soares, C.G. Analytical and numerical study on lateral buckling of imperfect subsea pipelines with nonlinear lateral pipe-soil interaction model. Ocean Eng. 2021, 221, 108495. [Google Scholar] [CrossRef]
- Fu, Y.M.; Zhong, J.; Shao, X.F.; Chen, Y. Thermal postbuckling analysis of functionally graded tubes based on a refined beam model. Int. J. Mech. Sci. 2015, 96–97, 58–64. [Google Scholar] [CrossRef]
- Mudhaffar, I.M.; Tounsi, A.; Chikh, A.; Al-Osta, M.A.; Al-Zahrani, M.M.; Al-Dulaijan, S.U. Hygro-thermo-mechanical bending behavior of advanced functionally graded ceramic metal plate resting on a viscoelastic foundation. Structures 2021, 33, 2177–2189. [Google Scholar] [CrossRef]
- Emam, S.; Lacarbonara, W. A review on buckling and post-buckling of thin elastic beams. Eur. J. Mech. 2022, 92, 104449. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Wang, Z.Q.; El Naggar, M.H.; Wu, W.B.; Wang, L.X.; Jiang, G.S. Three-dimensional wave propagation in a solid pile during torsional low strain integrity test. Int. J. Numer. Anal. Methods. Geomech. 2022, 46, 2398–2411. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.K.; Soares, C.G. Lateral buckling of subsea pipelines triggered by a sleeper with lateral constraint. Ocean Eng. 2021, 234, 109306. [Google Scholar] [CrossRef]
- Walker, A.C.; Chee, K.Y.; Cooper, P. Particular aspects regarding the lateral buckling analysis of flowlines. In Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 49–56. [Google Scholar]
- Haq, M.M.; Kenny, S. Lateral buckling response of subsea HTHP pipelines using finite element methods. In Proceedings of the ASME 2013 32nd International Conference on Ocean. Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; pp. 1–8. [Google Scholar]
- Liang, Z.; Lu, X.; Zhang, J. Thermal vertical buckling of surface-laid submarine pipelines on a sunken seabed. Ocean Eng. 2019, 173, 331–344. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, M. Prediction of the upheaval buckling critical force for imperfect submarine pipelines. Ocean Eng. 2015, 109, 330–343. [Google Scholar] [CrossRef]
- Zhang, X.; Guedes, S.C.; An, C.L.; Duan, M. An unified formula for the critical force of lateral buckling of imperfect submarine pipelines. Ocean Eng. 2018, 166, 324–325. [Google Scholar] [CrossRef]
- Burgreen, D. Free vibrations of a pin-ended column with constant distance between pin ends. J. Appl. Mech.-T Asme. 1951, 18, 135–139. [Google Scholar] [CrossRef]
- McDonald, P.H. Nonlinear dynamic coupling in abeam vibration. J. Appl. Mech.-T Asme. 1955, 22, 573–578. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Emam, S.A. Exact solutions and stability of the postbuckling configurations of beams. Nonlinear Dynam. 2008, 54, 395–408. [Google Scholar] [CrossRef]
- Lagrange, R.; Averbuch, D. Solution methods for the growth of a repeating imperfection in the line of a strut on a nonlinear foundation. Int. J. Mech. Sci. 2012, 63, 48–58. [Google Scholar] [CrossRef]
- Wang, Z.K.; Tang, Y.G.; Soares, C.G. Imperfection study on lateral thermal buckling of subsea pipeline triggered by a distributed buoyancy section. Mar. Struct. 2021, 76, 102916. [Google Scholar] [CrossRef]
- Bruton, D.A.S.; White, D.J.; Carr, M.; Cheuk, J.C.Y. Pipe-soil interaction during lateral buckling and pipeline walking. SAFEBUCK JIP. 2008, 2557–2576. [Google Scholar]
- Wu, W.B.; Wang, Z.Q.; Zhang, Y.P.; El Naggar, M.H.; Wu, T.; Wen, M.J. Semi-analytical solution for negative skin friction development on deep foundations in coastal reclamation areas. Int. J. Mech. Sci. 2023, 241, 107981. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Di, T.Y.; El Naggar, M.H.; Wu, W.B.; Liu, H.; Jiang, G.S. Modified Rayleigh-Love rod model for 3D dynamic analysis of large-diameter thin-walled pipe pile embedded in multilayered soils. Comput. Geotech. 2022, 149, 104853. [Google Scholar] [CrossRef]
- Wu, W.B.; Zhang, Y.P. A review of pile foundations in viscoelastic medium: Dynamic analysis and wave propagation modeling. Energies 2022, 15, 9432. [Google Scholar] [CrossRef]




| Parameter | Value | Unit |
|---|---|---|
| Elastic modulus E | 206 | GPa |
| External diameter D | 0.65 | m |
| Wall thickness t | 0.0227 | m |
| Steel density | 7850 | kg/m3 |
| Moment of inertia I | 1.509 × 10−3 | m4 |
| Coefficient of thermal expansion α | 1.1 × 10−5 | °C−1 |
| Axial friction coefficient μA | 0.5 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Li, L.; Wu, W.; Wang, T.; Liu, H. Analytical Study of Lateral Buckling of Pipelines with Initial Imperfection Based on Fixed-Fixed Beam Model. Appl. Sci. 2023, 13, 3227. https://doi.org/10.3390/app13053227
Wang S, Li L, Wu W, Wang T, Liu H. Analytical Study of Lateral Buckling of Pipelines with Initial Imperfection Based on Fixed-Fixed Beam Model. Applied Sciences. 2023; 13(5):3227. https://doi.org/10.3390/app13053227
Chicago/Turabian StyleWang, Songxian, Lichen Li, Wenbing Wu, Tianwei Wang, and Hao Liu. 2023. "Analytical Study of Lateral Buckling of Pipelines with Initial Imperfection Based on Fixed-Fixed Beam Model" Applied Sciences 13, no. 5: 3227. https://doi.org/10.3390/app13053227
APA StyleWang, S., Li, L., Wu, W., Wang, T., & Liu, H. (2023). Analytical Study of Lateral Buckling of Pipelines with Initial Imperfection Based on Fixed-Fixed Beam Model. Applied Sciences, 13(5), 3227. https://doi.org/10.3390/app13053227








