Reactor Temperature Prediction Method Based on CPSO-RBF-BP Neural Network
Abstract
:1. Introduction
2. RBF-BP Combined Neural Network Model
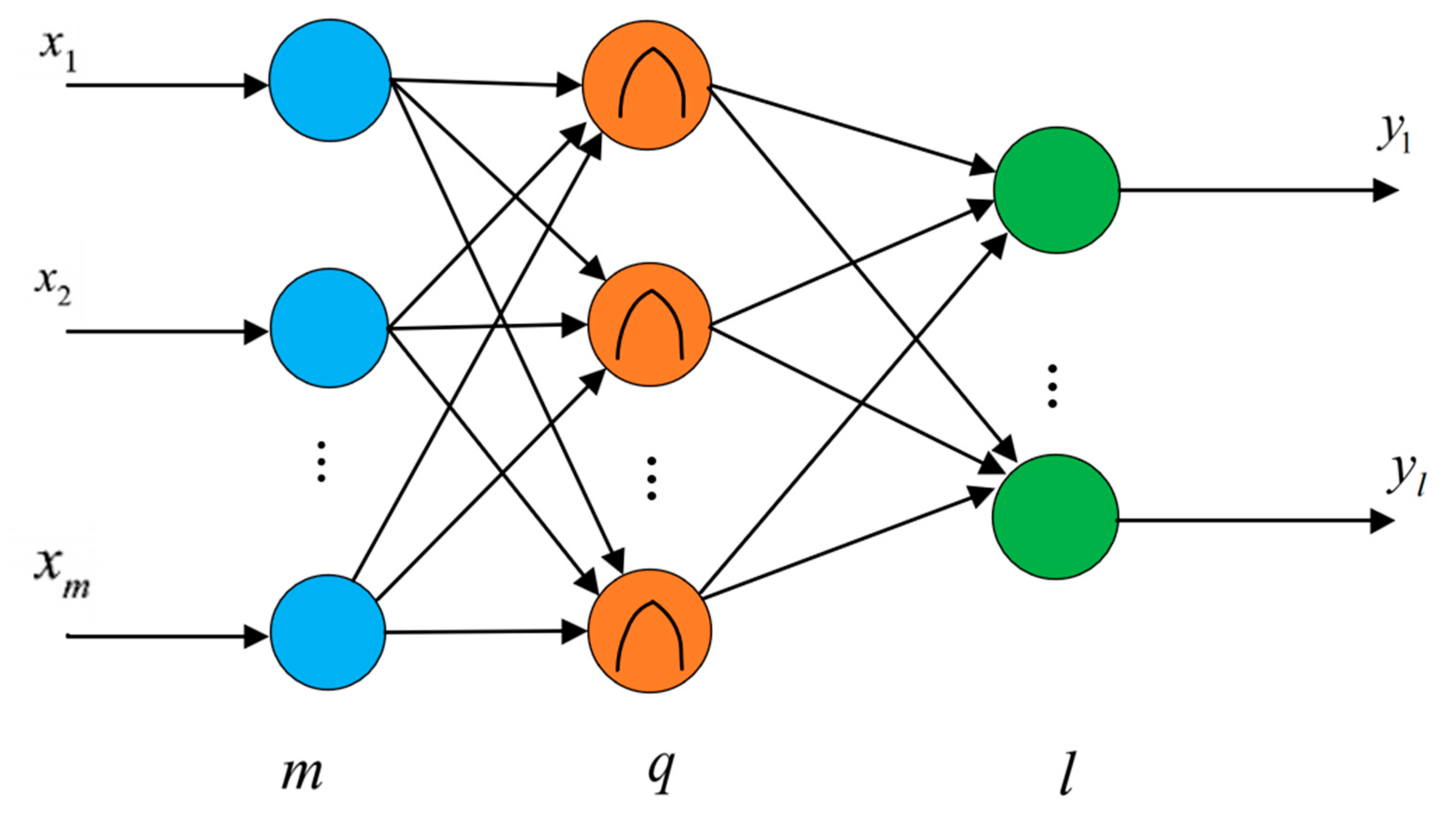
2.1. RBF Neural Network
2.2. BP Neural Network
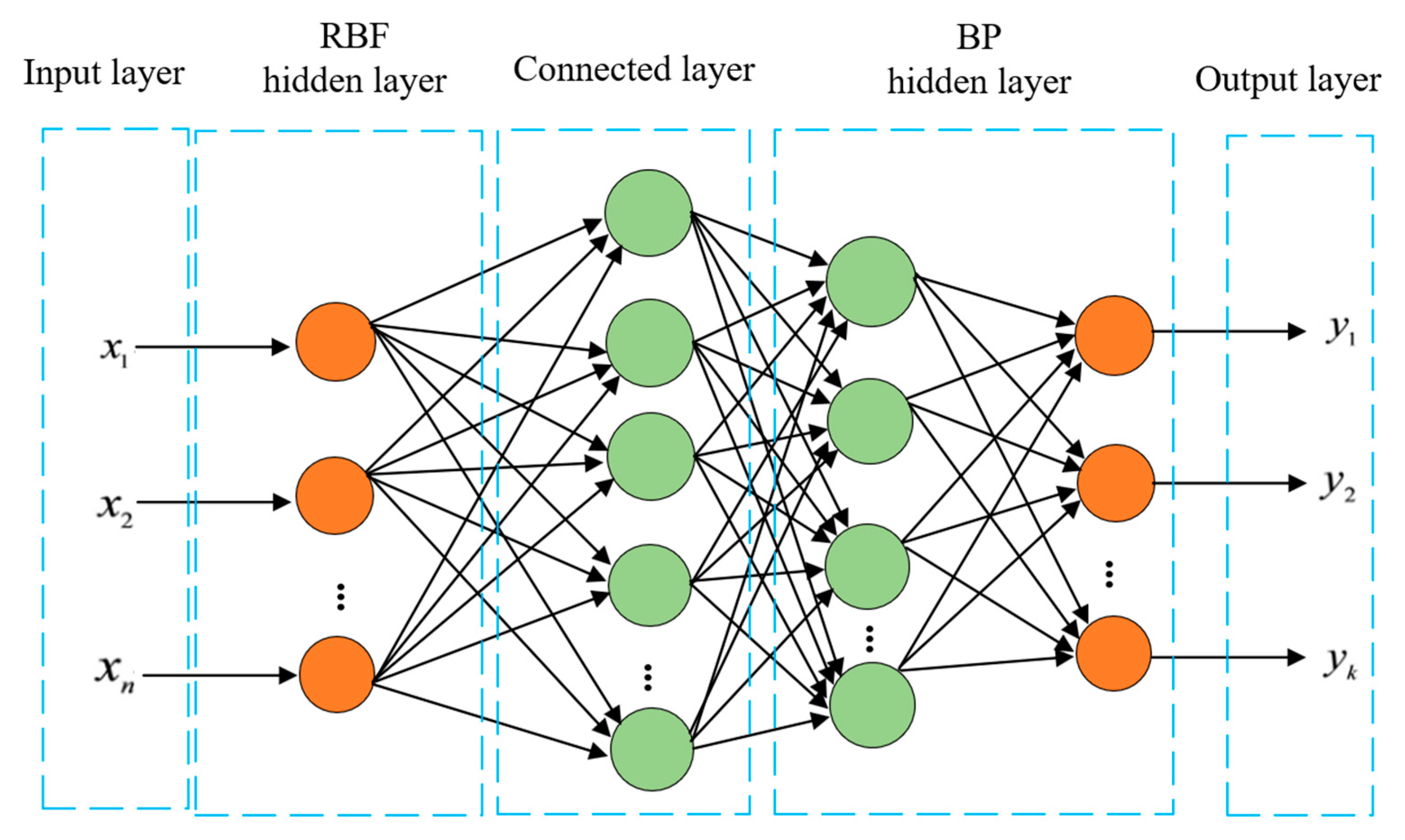
2.3. RBF-BP Neural Network
2.4. Algorithm for Chaotic Particle Swarm (CPSO)
- (1)
- Particle swarm method
- (2)
- Algorithm for chaotic particle swarm
- Chaotic initializes the particle positions in the population. Based on the chaotic motion characteristics, selecting individuals with high fitness as the initial population can improve search efficiency.
- Carry out a chaotic search on the top 20% of the population with high fitness, generate the corresponding chaotic sequence through Logistic mapping, and the search can be carried out in the field. Once there is a better individual extremum position, the local search ability of the algorithm can be improved by replacing it.
- To improve the optimization performance of the algorithm, the main parameter selection and method of the algorithm were improved. In this paper, the inertia weight was linearly decreased, which can have a strong optimization ability in the early stage and can be carefully searched locally in the later stage. The formula is as follows:
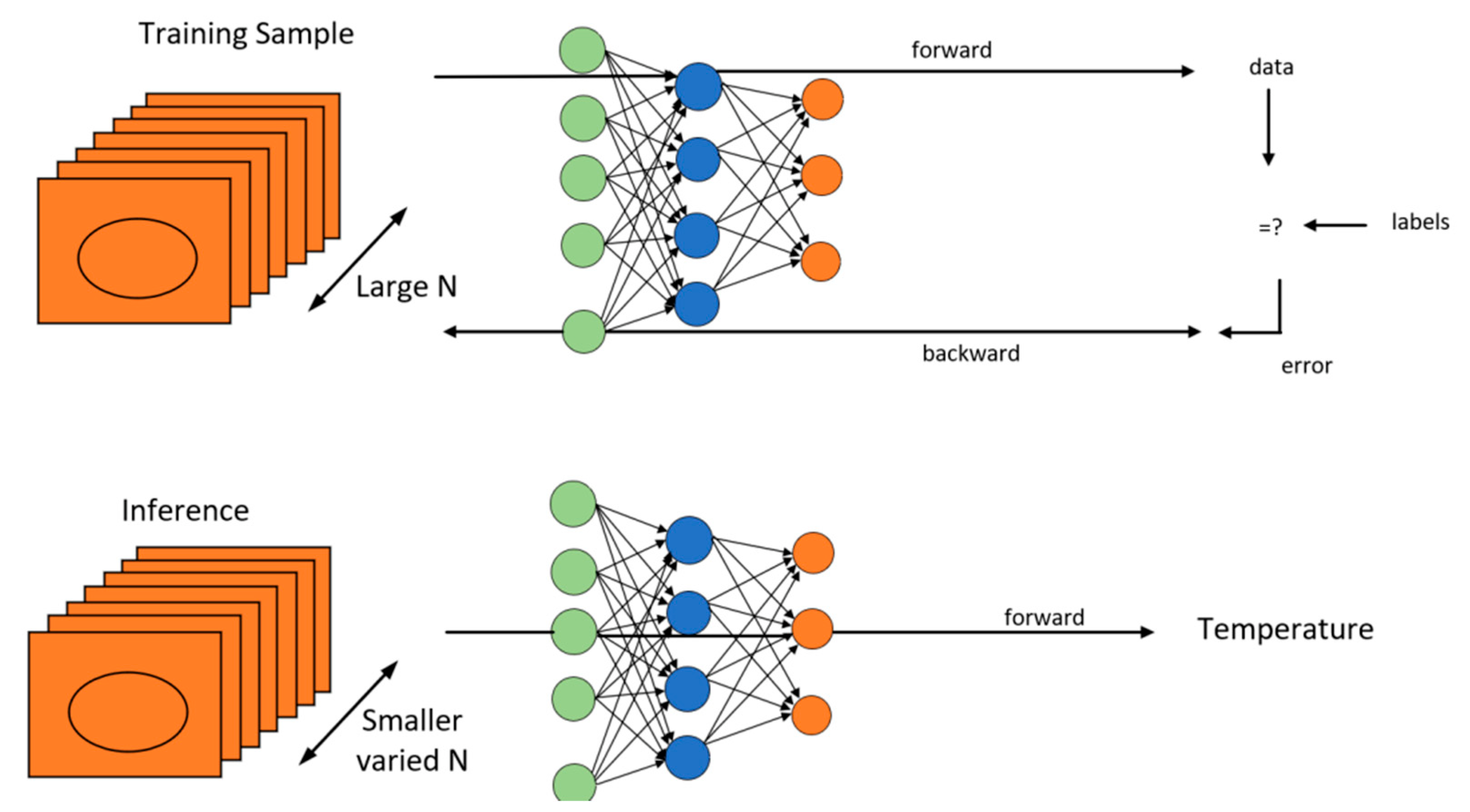
2.5. CPSO-RBF-BP Reactor Temperature Model Construction
3. Analysis of Predicted Reactor Temperature
3.1. Selection of Data
3.2. Indices for Performance Evaluation
- (1)
- MAE
- (2)
- RMSE
- (3)
4. Conclusions
- (1)
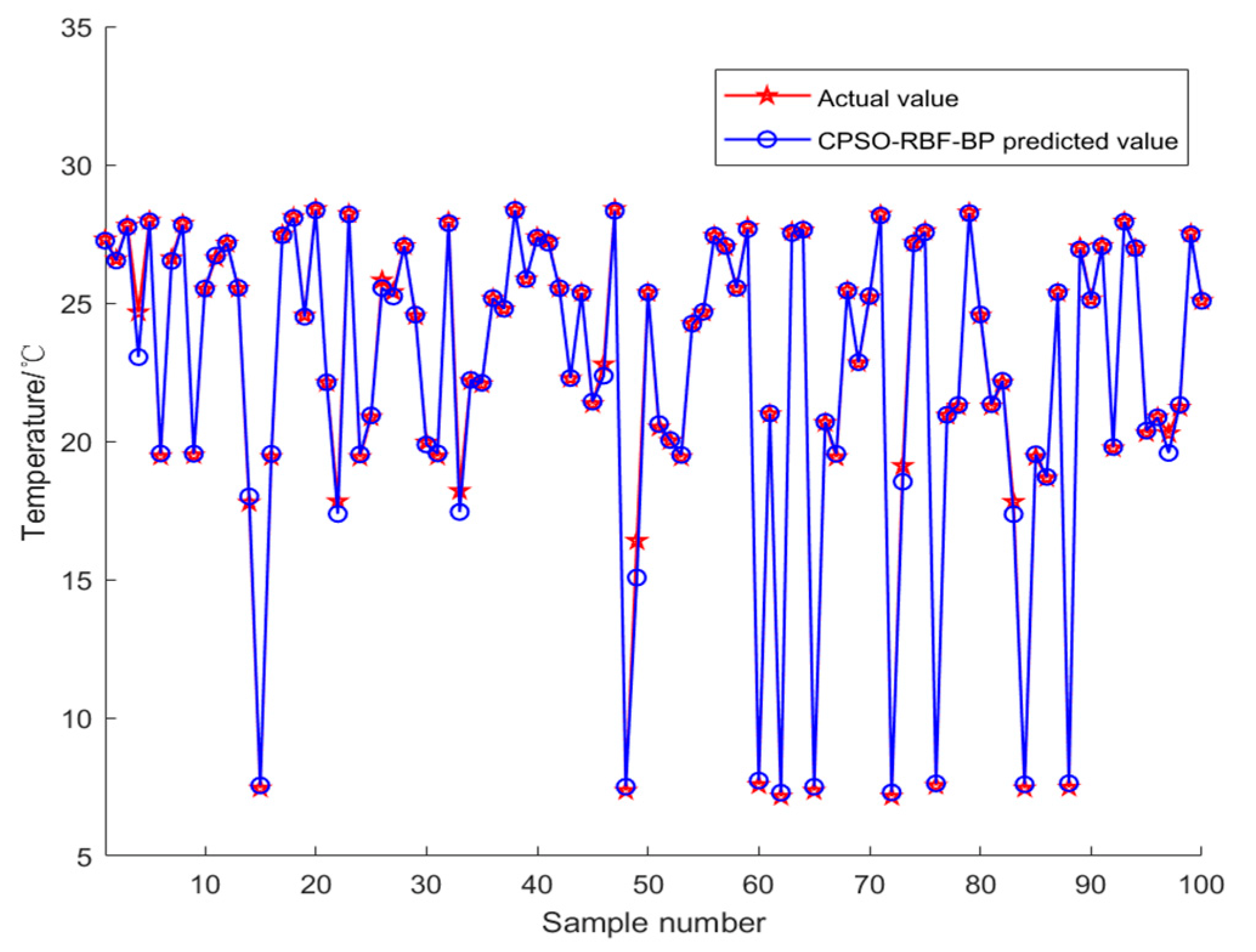
- The control object in this study was the reactor of a chemical enterprise in Hengdian, Zhejiang, China. Because reactor temperature control is inaccurate, it is always a difficult issue for businesses to overcome. A chaotic particle algorithm CPSO is suggested in this paper to optimize the RBF-BP neural network model of the reactor temperature prediction control method. In this study, the CPSO optimization algorithm was used to correct the RBF-BP model’s weights and thresholds, and the impact of initial weight and threshold uncertainties on the training efficiency of the RBF-BP combined neural network was investigated. Other prediction models were used in this study for prediction comparison at the same time. Among several prediction datasets, the CPSO-RBF-BP model outperformed the BP and RBF-BP models in terms of prediction accuracy. The CPSO-RBF-BP variant is extremely accurate.
- (2)
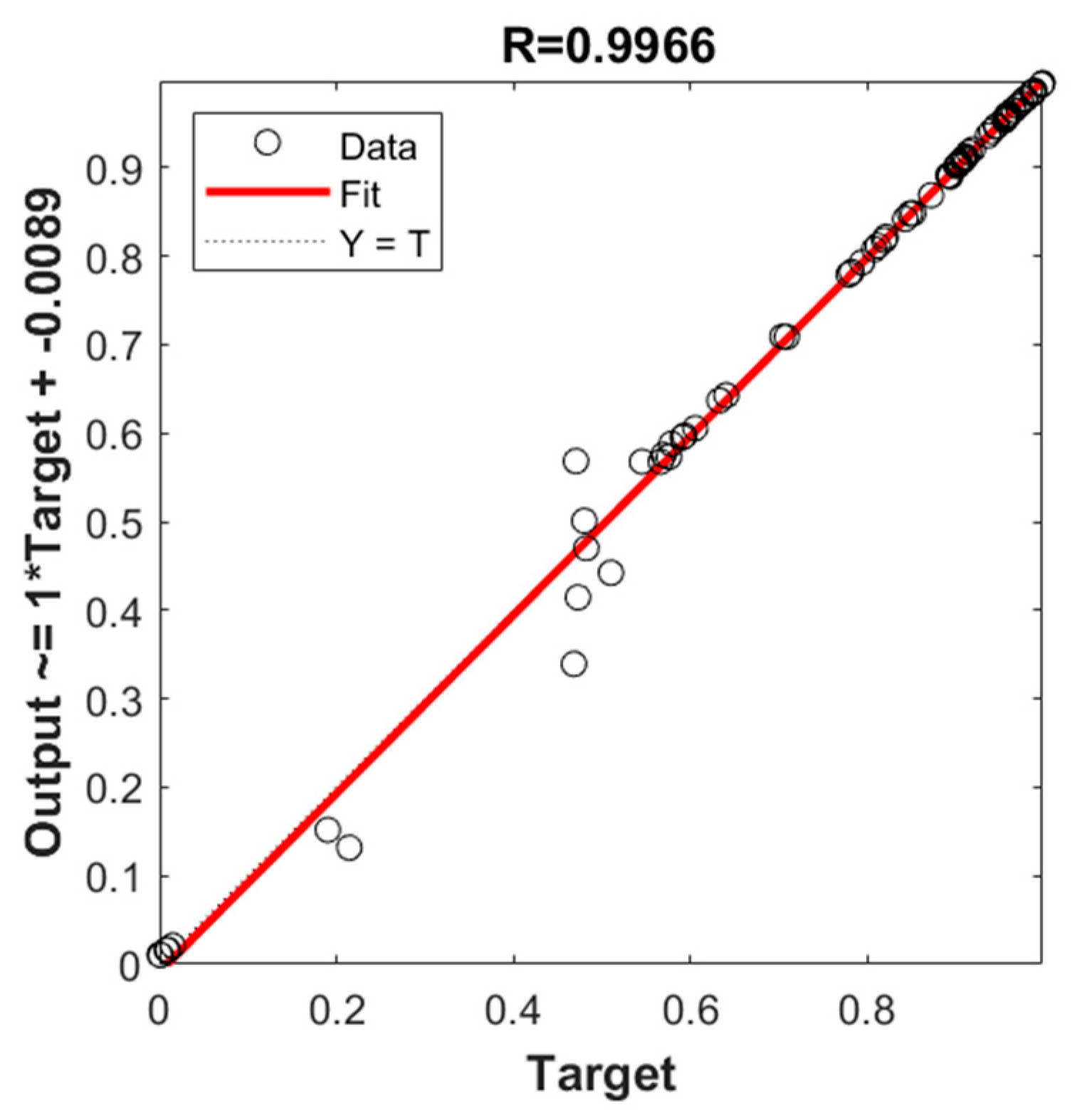
- The simulation findings indicate that the proposed prediction method outperforms the BP and RBF-BP neural network prediction models in all aspects. The CPSO-RBF-BP mixed neural network model has a root mean square error of 17.3%, an average absolute error of 11.4%, and a fitting value of 99.791%. The CPSO-RBF-BP model used in this article outperforms the BP and RBF-BP neural network models in terms of control performance. The RBF-BP neural network model used in this paper has good nonlinear mapping ability, which accounts for better control performance. The optimal and suitable control variables can be found thanks to the chaotic particle swarm optimization CPSO algorithm’s good convergence and optimization ability. The optimum control variable for the reactor temperature can be used. The simulation results demonstrate the effectiveness of the proposed predictive control technique.
- (3)
- At the moment, only a subset of the data described in this article has been collected, which is all data from normal operation, and data from various factors affecting the temperature of the reactor is missing. Later, the operation data will be supplemented, and the prediction model for various temperature factors will be constructed to make the model universal, and the model will be applied to real production at the same time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cervantes, A.L.; Agamennoni, O.E.; Figueroa, J.L. A nonlinear model predictive control system based on Wiener piecewise linear models. J. Process Control 2003, 13, 655–666. [Google Scholar] [CrossRef]
- Arefi, M.M.; Montazeria, A.; Poshtana, J.; Motlagh, M. Wiener neural identification and predictive control of a more realistic plug flow tubular reactor. Chem. Eng. J. 2007, 138, 274–282. [Google Scholar] [CrossRef]
- Venkateswarlu, C.; Rao, K.V. Dynamic recurrent radial basis model predictive control of unstable function network nonlinear process. Chem. Eng. Sci. 2005, 60, 6718–6732. [Google Scholar] [CrossRef]
- Bao, Z.; Pi, D.; Sun, Y. Nonlinear Model Predictive Control Based on Support Vector Machine with Multi-kernel. Chin. J. Chem. Eng. 2007, 15, 691–697. [Google Scholar] [CrossRef]
- Zhang, R.D.; Wang, S.Q. Support vector machine based predictive functional control design for output temperature of coking furnace. J. Process Control 2008, 18, 439–448. [Google Scholar] [CrossRef]
- Liu, C.; Ding, W.; Li, Z. Prediction of high-speed grinding temperature of titanium matrix composites using BP neural network based on PSO algorithm. Int. J. Adv. Manuf. Technol. 2016, 89, 2277–2285. [Google Scholar] [CrossRef]
- Liu, Y.; Lei, S.; Sun, C. A multivariate forecasting method for short-term load using chaotic features and RBF neural network. Eur. Trans. Electr. Power 2011, 21, 1376–1391. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Liu, S.; Fang, K. Prediction model of PM2.5 concentration Based on CPSO-BP Neural Network. J. Gansu Sci. 2019, 32, 47–50+62. [Google Scholar]
- Yang, Q. Research on Predictive Control Method Based on CPSO-RBF Neural Network Algorithm. J. Guiyang Coll. (Nat. Sci. Ed.) 2021, 3, 13–17. [Google Scholar]
- Wu, X.; Mou, L. Research on Prediction Method Based on improved RBF-BP Neural Network. Foreign Electron. Meas. Technol. 2022, 9, 105–110. [Google Scholar]
- Li, Y.; Ding, J.; Sun, B.; Guan, S. Comparison of BP and RBF neural networks for short-term prediction of sea surface temperature and salinity. Adv. Mar. Sci. 2022, 40, 220–232. [Google Scholar]
- Zulqurnain, S.; Adi, A.; Sanaullah, D.; Muhammad, A.R.; Gilder, C.A.; Soheil, S.; Sadat, R.; Mohamed, R.A. A mathematical model of coronavirus transmission by using the heuristic computing neural networks. Eng. Anal. Bound. Elem. 2023, 146, 473–482. [Google Scholar]
- Zulqurnain, S.; Sadat, R.; Mohamed, R.A.; Salem, B.S.; Muhammad, A. A numerical performance of the novel fractional water pollution model through the Levenberg-Marquardt backpropagation method. Arab. J. Chem. 2023, 16, 104493. [Google Scholar]
- Mukdasai, K.; Sabir, Z.R.; Singkibud, P.; Sadat, R.; Ali, M. A computational supervised neural network procedure for the fractional SIQ mathematical model. Eur. Phys. J. Spec. Top. 2023, 1–12. [Google Scholar] [CrossRef]
- Latif, S.; Sabir, Z.; Raja, M.A.Z.; Altamirano, G.C.; Núñez, R.A.S.; Gago, D.O.; Sadat, R.; Ali, M.R. IoT technology enabled stochastic computing paradigm for numerical simulation of heterogeneous mosquito model. Multimed. Tools Appl. 2022. [Google Scholar] [CrossRef]
- Akkilic, A.N.; Sabir, Z.; Raja, A.M.Z.; Bulut, H.; Sadat, R.; Ali, M.R. Numerical performances through artificial neural networks for solving the vector-borne disease with lifelong immunity. Comput. Methods Biomech. Biomed. Eng. 2022. [Google Scholar] [CrossRef]
- Du, H.; Xie, G.-Z. GA-BP network algorithm based on optimization of mixed gas recognition. J. Electron. Compon. Mater. 2019, 38, 69–79. [Google Scholar]
- Wang, X.M.; Xu, J.P.; He, Y. Stress and Temperature Prediction of aero-Engine Compressor Disk Based on Multi-layer Perceptron. J. Air Power 2022, 1–9. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Q.Q.; Lu, J. Short-term Load Forecasting Based on Stochastic Neural Network. Manuf. Autom. 2019, 41, 44–48. [Google Scholar]
- Panda, S.; Chakraborty, D.; Pal, S. Flank wear prediction in drilling using back propagation neural network and radial basis function network. Appl. Soft Comput. 2008, 8, 858–871. [Google Scholar] [CrossRef]
- Peng, G.; Nourani, M.; Harvey, J.; Dave, H. Feature selection using f-statistic values for EEG signal analysis. In Proceedings of the 42nd Annual International Conference of the IEEE Engineering in Biomedicine and Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 5936–5966. [Google Scholar]
- Zhang, X.L.; Li, J.H.; Li, J.X.; Wei, K.L.; Kang, X.N. Morphology defect identification based on Hybrid Optimization RBF-BP Network. Fuzzy Syst. Math. 2020, 34, 149–156. [Google Scholar]
- Yi, Z.M.; Deng, Z.D.; Qin, J.Z.; Liu, Q.; Du, D.; Zhang, D.S. Based on RBF and BP hybrid neural network of sintering flue gas NOx prediction. J. Iron Steel Res. 2020, 32, 639–646. [Google Scholar]
- Shankar, R.; Narayanan, G.; Robert, Č.; Rama, C.N.; Subham, P.; Kanak, K. Hybridized particle swarm—Gravitational search algorithm for process optimization. Processes 2022, 10, 616. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Hefny, H.A.; Azab, S.S. Chaotic particle swarm optimization. In Proceedings of the 2010 the 7th International Conference on Informatics and Systems (INFOS), Cairo, Egypt, 28–30 March 2010; pp. 1–8. [Google Scholar]
- Sheng, X.; Zhu, W. Application of particle swarm optimization in soil simulation. Sci. Technol. Inf. 2012, 15, 90–92. [Google Scholar]
- Zeng, Y.Y.; Feng, Y.X.; Zhao, W.T. Adaptive Variable Scale Chaotic Particle Swarm Optimization Algorithm Based on logistic Mapping. J. Syst. Simul. 2017, 29, 2241–2246. [Google Scholar]
- Dey, K.; Kalita, K.; Chakraborty, S. Prediction performance analysis of neural network models for an electrical discharge turning process. Int. J. Interact. Des. Manuf. (IJIDeM) 2022, 1–19. [Google Scholar] [CrossRef]
- Kumar, M.; Lenka, Č.; Raja, M.; Allam, B.; Muniyandy, E. Evaluation of the Quality of Practical Teaching of Agricultural Higher Vocational Courses Based on BP Neural Network. Appl. Sci. 2023, 13, 1180. [Google Scholar] [CrossRef]


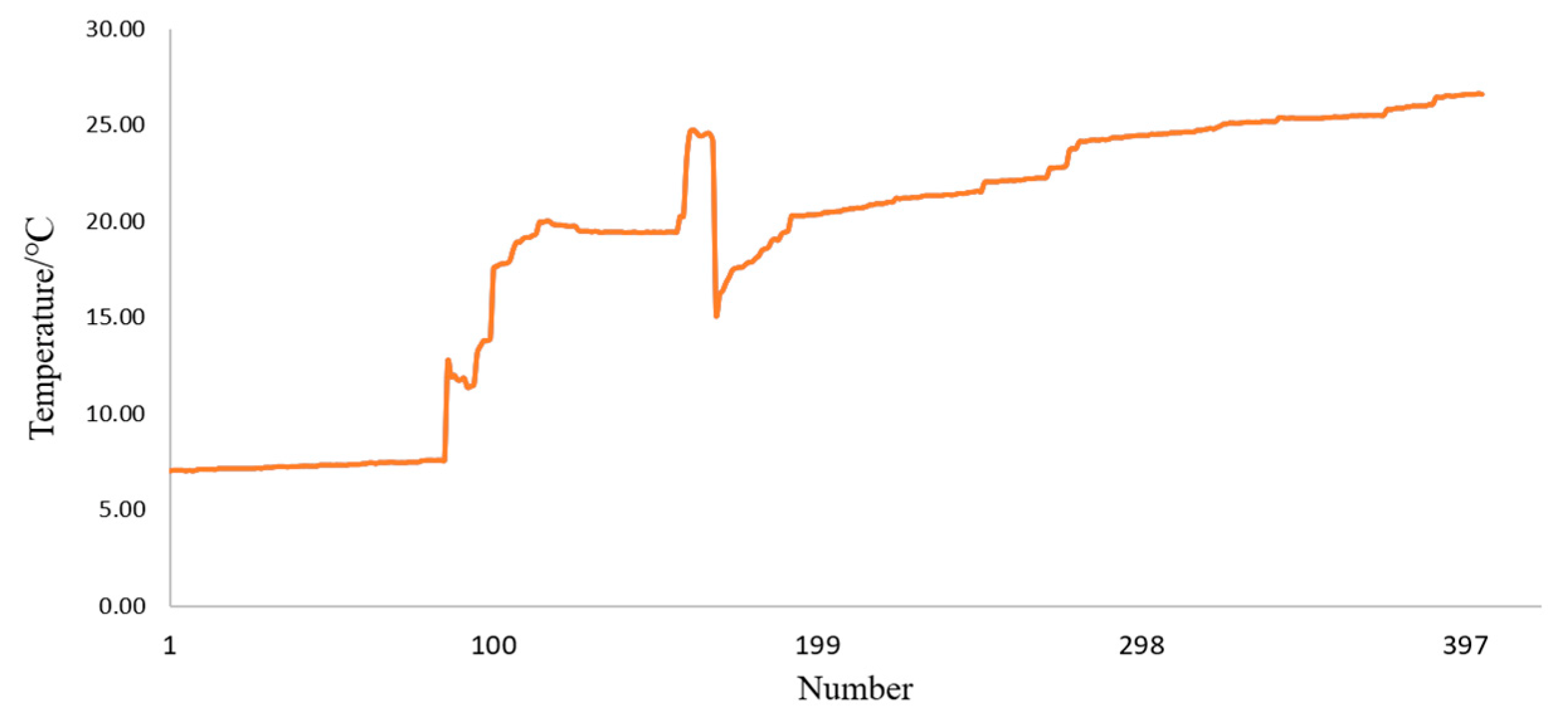





| Number | Temperature/°C | Number | Temperature/°C | Number | Temperature/°C | Number | Temperature/°C |
|---|---|---|---|---|---|---|---|
| 1 | 7.02 | 101 | 11.75 | 201 | 20.68 | 301 | 23.81 |
| 2 | 7.02 | 102 | 11.81 | 202 | 21.95 | 302 | 24.16 |
| 3 | 7.06 | 103 | 11.80 | 203 | 24.63 | 303 | 24.18 |
| 4 | 7.06 | 104 | 11.76 | 204 | 24.75 | 304 | 24.22 |
| 5 | 7.06 | 105 | 11.63 | 205 | 24.68 | 305 | 24.25 |
| 6 | 7.11 | 106 | 11.40 | 206 | 25.57 | 306 | 24.23 |
| 7 | 7.12 | 107 | 11.41 | 207 | 25.57 | 307 | 24.28 |
| … | … | … | … | … | … | … | … |
| 28 | 7.23 | 128 | 14.34 | 228 | 18.30 | 328 | 27.38 |
| 29 | 7.23 | 129 | 15.63 | 229 | 18.42 | 329 | 27.43 |
| 30 | 7.25 | 130 | 15.66 | 230 | 18.50 | 330 | 27.47 |
| 31 | 7.25 | 131 | 15.96 | 231 | 18.91 | 331 | 27.55 |
| 32 | 7.25 | 132 | 16.28 | 232 | 19.48 | 332 | 27.58 |
| 33 | 7.23 | 133 | 16.96 | 233 | 19.66 | 333 | 27.60 |
| 34 | 7.27 | 134 | 17.42 | 234 | 19.81 | 334 | 27.67 |
| 35 | 7.27 | 135 | 17.42 | 235 | 20.01 | 335 | 27.63 |
| … | … | … | … | … | … | … | … |
| 100 | 11.71 | 200 | 20.30 | 300 | 23.47 | 400 | 29.47 |
| Sample Number | BP Actual/Predicted/Error | RBF-BP Actual/Predicted/Error | CPSO-RBF-BP Actual/Predicted/Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 | 7.51 | 7.83 | 0.32 | 7.65 | 7.62 | −0.03 | 21.95 | 21.90 | 0.05 |
| 40 | 7.31 | 7.48 | 0.17 | 25.21 | 25.24 | 0.03 | 26.06 | 26.08 | 0.02 |
| 60 | 18.74 | 18.85 | 0.11 | 18.91 | 18.92 | 0.01 | 7.51 | 7.50 | 0.01 |
| 80 | 24.63 | 23.45 | −1.18 | 24.63 | 23.22 | −1.41 | 24.63 | 24.62 | 0.01 |
| 100 | 18.42 | 15.35 | −3.07 | 21.95 | 22.62 | 0.67 | 25.57 | 25.53 | 0.04 |
| Neural Network | RMSE | R2 | MAE |
|---|---|---|---|
| BP | 2.391 | 0.68779 | 0.628 |
| RBF-BP | 0.507 | 0.90245 | 0.433 |
| CPSO-RBF-BP | 0.263 | 0.99791 | 0.114 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Xu, B.; Xu, Z. Reactor Temperature Prediction Method Based on CPSO-RBF-BP Neural Network. Appl. Sci. 2023, 13, 3230. https://doi.org/10.3390/app13053230
Tang X, Xu B, Xu Z. Reactor Temperature Prediction Method Based on CPSO-RBF-BP Neural Network. Applied Sciences. 2023; 13(5):3230. https://doi.org/10.3390/app13053230
Chicago/Turabian StyleTang, Xiaowei, Bing Xu, and Zichen Xu. 2023. "Reactor Temperature Prediction Method Based on CPSO-RBF-BP Neural Network" Applied Sciences 13, no. 5: 3230. https://doi.org/10.3390/app13053230
APA StyleTang, X., Xu, B., & Xu, Z. (2023). Reactor Temperature Prediction Method Based on CPSO-RBF-BP Neural Network. Applied Sciences, 13(5), 3230. https://doi.org/10.3390/app13053230






