A Heuristic Approach to Support Route Planning for Delivery and Installation of Furniture: A Case Study
Abstract
:1. Introduction
2. Materials and Methods
- Each team has a vehicle with a specific transport capacity;
- The customers time window must be respected;
- Constraints must be respected.
2.1. Problem Characterisation
2.1.1. Product Categories
2.1.2. Time Window
2.1.3. Teams Classification
- PAX (P) type, serving customers whose contract includes items of the PAX type;
- Assembly (M) type, serving customers whose contract comprises all kinds of items;
- Mixed (S) type, only serving customers whose contract includes less complex items.
- In total, the company has 29 teams:
- M and S-type teams, representing a total of 26 teams, are divided into the first, second, and third categories. Customers should be assigned to teams considering their type and category. As such, customers are first allocated by teams within the first category, then by those within the second category, and finally, by those within the third category.
- There are three P-type teams in total, and thus, they are not divided into categories, and each one has a maximum limit on the number of linear meters of PAX to serve per route.
2.1.4. Travel and Service Time
2.2. Data Collection
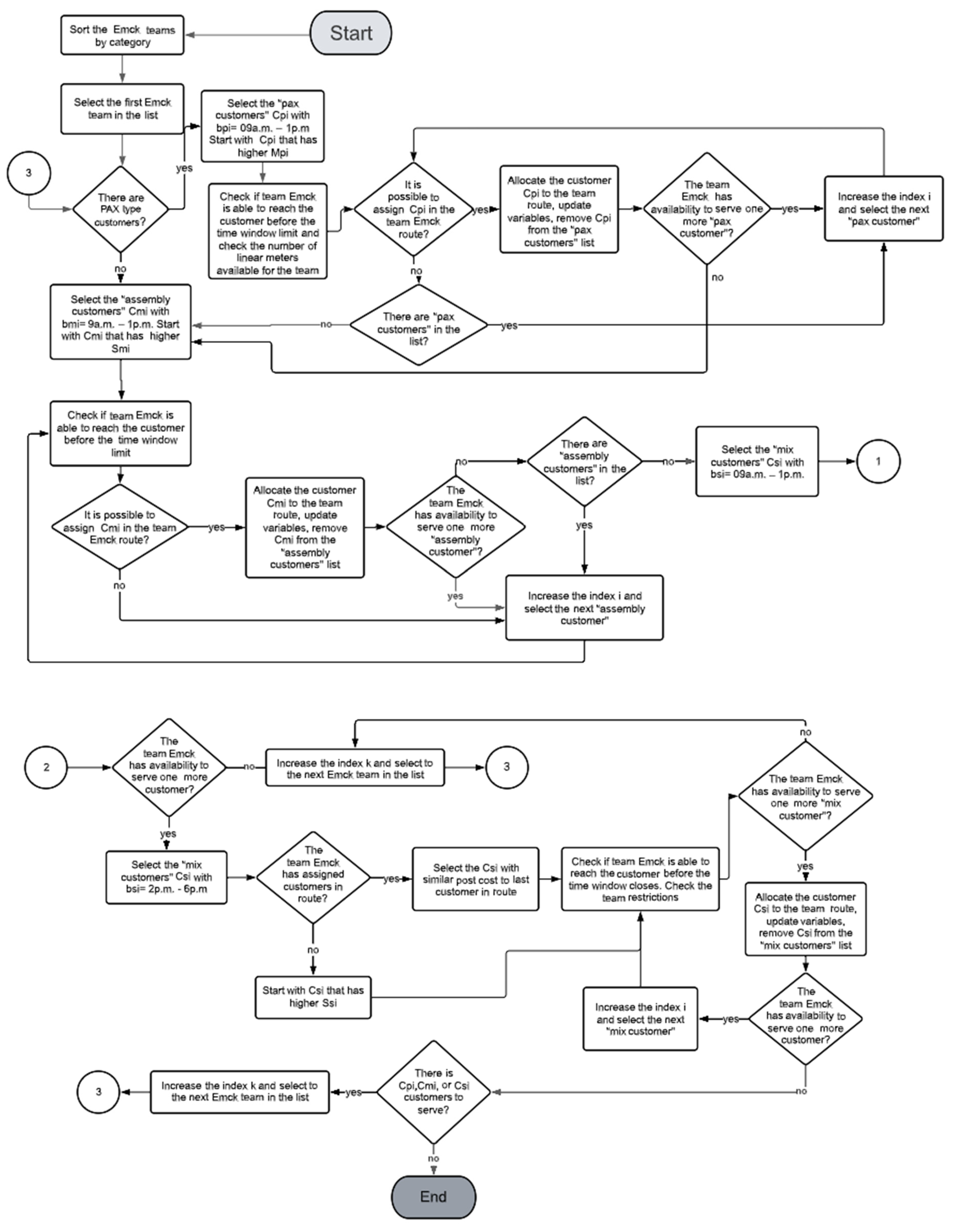
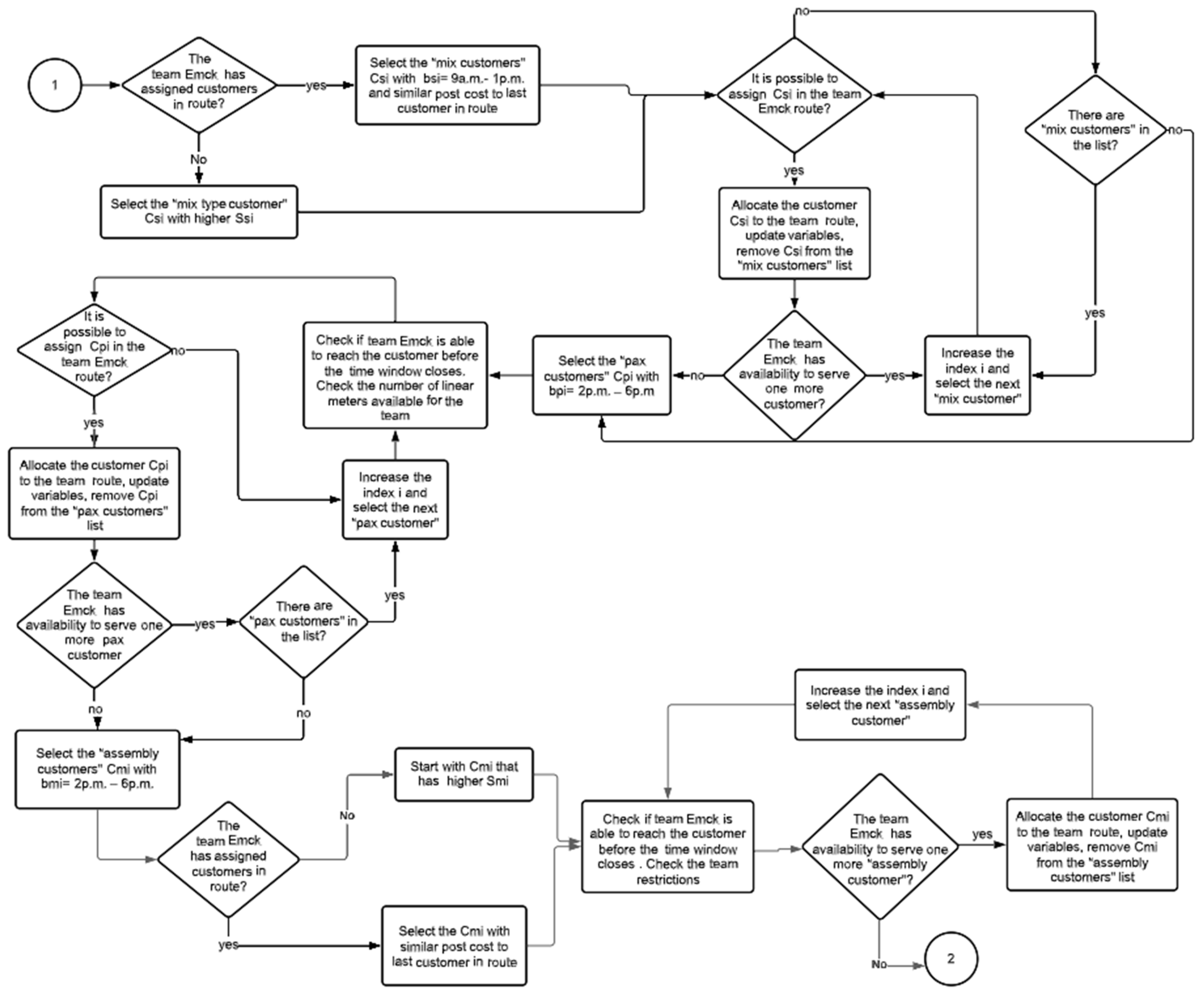
2.3. Proposed Heuristic
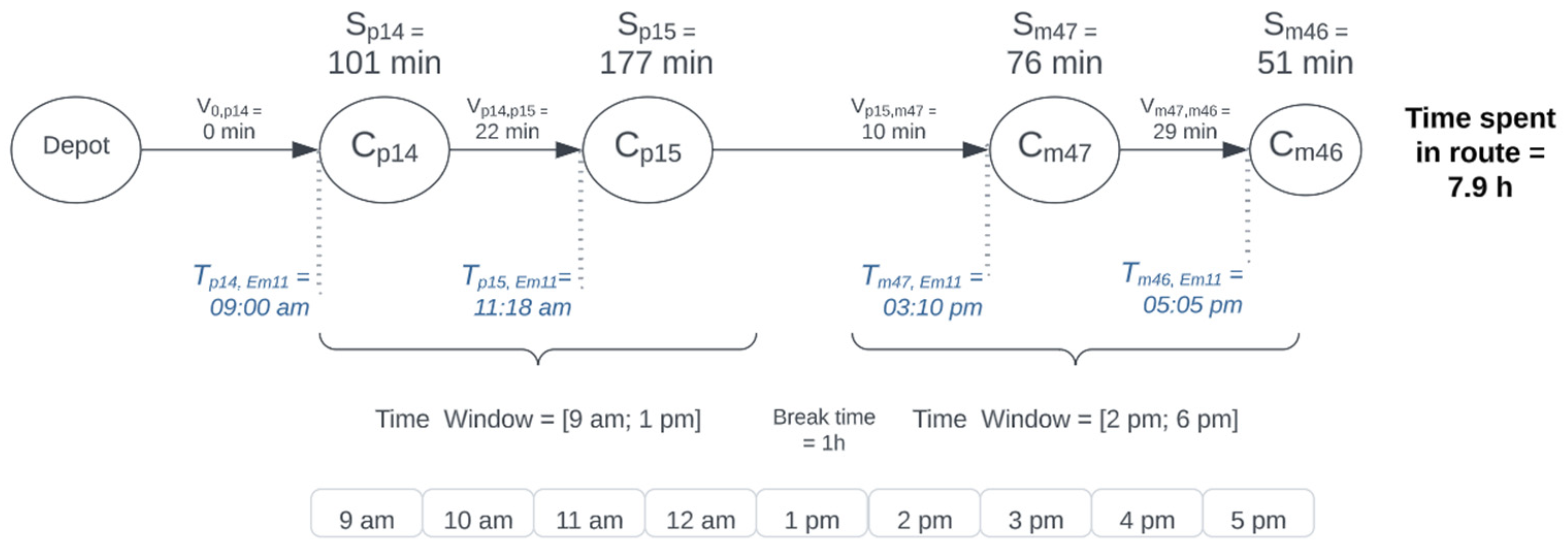
2.4. Illustrative Example—M-Type Teams Heuristic in Pseudocode
3. Results
3.1. Results and Assessment of the Proposed Heuristic
3.2. Discussion and Insights
- –
- It allows affecting customers to teams without compromising the competence of the team to serve the affected customer;
- –
- All routes obtained through the heuristic are possible and achievable;
- –
- It allowed affecting all customers to teams, without leaving any customer left to serve;
- –
- All teams’ constraints have been respected;
- –
- The use of zip codes as the criteria for selecting the next customer to include in the route may not be the best criteria to improve the distances traveled between customers. Regardless, these criteria can be used;
- –
- All time windows were respected, and this should have resulted in no reschedules of teams;
- –
- The number of clients each team served was consistently affected, thus resulting in routes that did not serve a high number of customers nor a low number of customers. Only three teams have a higher number of clients to serve when compared to the others.
- It is critical to understand how routes are developed since this process allows to define the predominant criteria used to create routes;
- There is a need to monitor the planning process to create routes. In this way, it is possible to understand how the workers responsible for this task operate and how they organize and affect different customers into teams;
- There is a need to carefully define the main objectives to achieve the proposed heuristic and to define decision variables and restrictions, as it is crucial to understand how to make decisions and the boundaries of the problem;
- General rules, as priority rules, are important to be defined, and all rules need to be clearly defined. Additionally, rules for unpredictable situations need to be defined;
- Finally, it is important to test the proposed heuristic through performance indicators to understand if it is adequate for the problem.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Algorithm A1
| Algorithm A1 |
| For all Emck in List of Teams If (List of PAX-type customers <> 0) For all Cpi in List of PAX-type customers For all Cpi with (bpi = 09 a.m. – 1 p.m.) i = i from the Cpi with higher Mpi If (Mpi + MEmck ≤ METROSEmck) Insert Cpi in Emck route Remove Cpi from List of PAX-type customers MEmck = MEmck + Mpi VAEmck = VAEmck + VApi PEmck = PEmck + Ppi VOLEmck = VOLEmck + VOLpi TTEmck = TTEmck + Spi + Vp(i-1), pi + Dpi If (MEmck < METROSEmck AND PEmck < PESOEmck AND TTEmck < 240) Go to the next Cpi with a zip code similar the last inserted customer and so on Else Go to the next type of customers, Cmi End if Else if Go to the next PAX-type customer, with higher Mpi and so on End if End for End for For all Cmi in List of Assembly-type customers For all Cmi with (bpi = 09 a.m. – 1 p.m.) If (Emck route <> {}) i = i of Cpi with zip code similar to the last inserted customer If (TTEmck + Vti, mi ≤ 240) Insert Cmi in Emck route Remove Cmi from List of Assembly-type customers VAEmck = VAEmck + VAmi PEmck = PEmck + Pmi VOLEmck = VOLEmck + VOLmi TTEmck = TTEmck + Vti, mi + Smi + Dmi If (PEmck < PESOEmck and TTEmck < 240) Go to the next Cmi with zip code similar to the last inserted customer and so on Else Go to the PAX-type customers with the next-time window End if Else Go to the next type of customers, Csi End if Else i = i of Cmi with higher Smi If (TTEmck + Vm(i-1), mi ≤ 240) Insert Cmi in Emck route Remove Cmi from List of Assembly-type customers VAEmck = VAEmck + VAmi PEmck = PEmck + Pmi VOLEmck = VOLEmck + VOLmi TTEmck = TTEmck + Vti, mi + Smi + Dmi If (PEmck < PESOEmck and TTEmck < 240) Go to the next Cmi with zip code similar to the last inserted customer and so on Else Go to the PAX-type customers with the next time window End if End if End if End for For all Csi in List of Mixed-type customers For all Csi with (bpi = 09 a.m. – 1 p.m.) If (Emck route <> {}) i = i of Csi with zip code similar to the last inserted customer If (TTEmck + Vti, mi ≤ 240) Insert Csi in Emck route Remove Csi from List of Mixed-type customers VAEmck = VAEmck + VAsi PEmck = PEmck + Psi VOLEmck = VOLEmck + VOLsi TTEmck = TTEmck + Vti, mi + Ssi + Dsi If (PEmck < PESOEmck and TTEmck < 240) Go to the next Csi with zip code similar to the last inserted customer and so on Else Go to the PAX-type customers with the next time window End if End if End if End for End for End for End for |
Appendix B
| Team ID | Start Time | Finish Time * | Route | Time Spent in Route [h] |
|---|---|---|---|---|
| Em11 | 09 a.m. | 5.52 p.m. | 0→Cp14→Cp15→Cm47→Cm46 | 7.88 |
| Em12 | 09 a.m. | 6.58 p.m. | 0→Cp11→Cp12→Cm44 | 8.97 |
| Em13 | 09 a.m. | 7.24 p.m. | 0→Cp5→Cp2→Cp1→Cm29→Cm30→Cm31 | 9.41 |
| Em14 | 09 a.m. | 10.14 p.m. | 0→Cp16→Cp13→Cp27→Cm45 | 13.43 |
| Em15 | 09 a.m. | 8.19 p.m. | 0→Cm10→Cp21 | 10.32 |
| Em16 | 09 a.m. | 6.15 p.m. | 0→Cm14→Cm15→Cm40→Cm41 | 8.25 |
| Em17 | 09 a.m. | 8.22 p.m. | 0→Cm26→Cm25→Cm43→Cs50 | 10.38 |
| Em18 | 09 a.m. | 7.57 p.m. | 0→Cm27→Cm28→Cm49 | 9.96 |
| Em19 | 09 a.m. | 8.57 p.m. | 0→Cm7→Cm8→Cm9→Cp19→Cp20 | 10.95 |
| Em110 | 09 a.m. | 7.58 p.m. | 0→Cm20→Cm21→Cm22→Cm42 | 9.97 |
| Em111 | 09 a.m. | 8.02 p.m. | 0→Cm16→Cm17→Cm18→Cm39 | 10.04 |
| Em21 | 09 a.m. | 6.00 p.m. | 0→Cm6→Cm5→Cm4→Cm32 | 7.99 |
| Em22 | 09 a.m. | 7.24 p.m. | 0→Cm11→Cm12→Cm13→Cm38 | 9.40 |
| Em23 | 09 a.m. | 6.02 p.m. | 0→Cm2→Cm3→Cm1→Cm19→Cm36→Cm35 | 8.04 |
| Em24 | 09 a.m. | 7.01 p.m. | 0→Cm24→Cm23→Cs22→Cs23→Cp22 | 9.02 |
| Em25 | 09 a.m. | 5.44 p.m. | 0→Cs18→Cs19→Cs17→Cs16→Cm37→Cm48 | 7.73 |
| Em26 | 09 a.m. | 5.08 p.m. | 0→Cs13→Cs12→Cs11→Cs10→Cs9→Cs8→→Cs7→Cs28→Cs29→Cs30 | 7.13 |
| Em27 | 09a.m. | 4.25 p.m. | 0→Cs2→Cs3→Cs4→Cs5→Cs6→Cs14→Cs31→Cs32 | 6.43 |
| Em29 | 09 a.m. | 7.06 p.m. | 0→Cs27→Cs1→Cm33 | 6.84 |
| Em211 | 2 p.m. | 5.56 p.m. | 0→Cs36→Cs37→Cs38→Cs39 | 3.94 |
References
- Mangiaracina, R.; Perego, A.; Seghezzi, A.; Tumino, A. Innovative solutions to increase last-mile delivery efficiency in B2C e-commerce: A literature review. Int. J. Phys. Distrib. Logist. Manag. 2019, 49, 901–920. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jung, H. Robot Routing Problem of Last-Mile Delivery in Indoor Environments. Appl. Sci. 2022, 12, 9111. [Google Scholar] [CrossRef]
- Silvestri, P.; Zoppi, M.; Molfino, R. Dynamic investigation on a new robotized vehicle for urban freight transport. Simul. Model. Pract. Theory 2019, 96, 101938. [Google Scholar] [CrossRef]
- Rose, W.J.; A Mollenkopf, D.; Autry, C.W.; Bell, J.E. Exploring urban institutional pressures on logistics service providers. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 153–176. [Google Scholar] [CrossRef]
- Ali, O.; Côté, J.-F.; Coelho, L.C. Models and algorithms for the delivery and installation routing problem. Eur. J. Oper. Res. 2020, 291, 162–177. [Google Scholar] [CrossRef]
- Amonde, T.M.; Ajagunna, I.; Iyare, N.F. Last mile logistics and tourist destinations in the Caribbean. Worldw. Hosp. Tour. Themes 2017, 9, 17–30. [Google Scholar] [CrossRef]
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. OR Spectr. 2020, 43, 1–58. [Google Scholar] [CrossRef]
- Galkin, A.; Obolentseva, L.; Balandina, I.; Kush, E.; Karpenko, V.; Bajdor, P. Last-Mile Delivery for Consumer Driven Logistics. Transp. Res. Procedia 2019, 39, 74–83. [Google Scholar] [CrossRef]
- Chen, P.; Chankov, S.M. Crowdsourced Delivery for Last-mile Distribution: An Agent-based Modelling and Simulation Approach. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 1271–1275. [Google Scholar] [CrossRef]
- Ghiani, G.; Laporte, G.; Musmanno, R. Introduction to Logistics Systems Management; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Lummus, R.R.; Krumwiede, D.W.; Vokurka, R.J. The relationship of logistics to supply chain management: Developing a common industry definition. Ind. Manag. Data Syst. 2001, 101, 426–432. [Google Scholar] [CrossRef]
- Lin, I.-C.; Lin, T.-H.; Chang, S.-H. A Decision System for Routing Problems and Rescheduling Issues Using Unmanned Aerial Vehicles. Appl. Sci. 2022, 12, 6140. [Google Scholar] [CrossRef]
- He, P.; Wen, J.; Ye, S.; Li, Z. Logistics service sharing and competition in a dual-channel e-commerce supply chain. Comput. Ind. Eng. 2020, 149, 106849. [Google Scholar] [CrossRef]
- Konstantakopoulos, G.D.; Gayialis, S.P.; Kechagias, E.P. Vehicle routing problem and related algorithms for logistics distribution: A literature review and classification. Oper. Res. 2020, 22, 2033–2062. [Google Scholar] [CrossRef]
- Hosny, M. Heuristic Techniques for the Vehicle Routing Problem with Time Windows. Int. Proc. Comput. Sci. Inf. 2011, 13, 19–23. [Google Scholar]
- Sluijk, N.; Florio, A.M.; Kinable, J.; Dellaert, N.; Van Woensel, T. Two-echelon vehicle routing problems: A literature review. Eur. J. Oper. Res. 2023, 304, 865–886. [Google Scholar] [CrossRef]
- Cook, T.M.; Russell, R.A. A simulation and statistical analysis of stochastic vehicle routing with timing constraints. Decis. Sci. 1978, 9, 673–687. [Google Scholar] [CrossRef]
- Kumar, S.N.; Panneerselvam, R. A Survey on the Vehicle Routing Problem and Its Variants. Intell. Inf. Manag. 2012, 04, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Vidal, T.; Laporte, G.; Matl, P. A concise guide to existing and emerging vehicle routing problem variants. Eur. J. Oper. Res. 2020, 286, 401–416. [Google Scholar] [CrossRef] [Green Version]
- Ammouriova, M.; Herrera, E.M.; Neroni, M.; Juan, A.A.; Faulin, J. Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization. Appl. Sci. 2023, 13, 101. [Google Scholar] [CrossRef]
- Tan, S.-Y.; Yeh, W.-C. The Vehicle Routing Problem: State-of-the-Art Classification and Review. Appl. Sci. 2021, 11, 10295. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Toth, P.; Vido, D. (Eds.) The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar] [CrossRef]
- Arnold, F.; Sörensen, K. What makes a VRP solution good? The generation of problem-specific knowledge for heuristics. Comput. Oper. Res. 2019, 106, 280–288. [Google Scholar] [CrossRef]
- Gutierrez, A.; Dieulle, L.; Labadie, N.; Velasco, N. A multi-population algorithm to solve the VRP with stochastic service and travel times. Comput. Ind. Eng. 2018, 125, 144–156. [Google Scholar] [CrossRef]
- Agárdi, A.; Kovács, L.; Bányai, T. Ontology Support for Vehicle Routing Problem. Appl. Sci. 2022, 12, 12299. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Laporte, G.; Savelsbergh, M.W.; Vigo, D. Chapter 6 Vehicle Routing. In Handbooks in Operations Research and Management Science; Barnhart, C., Laporte, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 14, pp. 367–428. [Google Scholar] [CrossRef]
- Leclerc, F.; Potvin, J.-Y. Genetic Algorithms for Vehicle Dispatching. Int. Trans. Oper. Res. 1997, 4, 391–400. [Google Scholar] [CrossRef]
- Dale, S. Heuristics and biases: The science of decision-making. Bus. Inf. Rev. 2015, 32, 93–99. [Google Scholar] [CrossRef]
- Shi, Y.; Lv, L.; Hu, F.; Han, Q. A Heuristic Solution Method for Multi-Depot Vehicle Routing-Based Waste Collection Problems. Appl. Sci. 2020, 10, 2403. [Google Scholar] [CrossRef] [Green Version]
- Irnich, S.; Toth, P.; Vigo, D. Chapter 1: The Family of Vehicle Routing Problems. In Vehicle Routing; SIAM: Philadelphia, PA, USA, 2014; pp. 1–33. [Google Scholar] [CrossRef]
- Errico, F.; Desaulniers, G.; Gendreau, M.; Rei, W.; Rousseau, L.-M. A priori optimization with recourse for the vehicle routing problem with hard time windows and stochastic service times. Eur. J. Oper. Res. 2016, 249, 55–66. [Google Scholar] [CrossRef]
- Miranda, D.M.; Conceição, S.V. The vehicle routing problem with hard time windows and stochastic travel and service time. Expert Syst. Appl. 2016, 64, 104–116. [Google Scholar] [CrossRef]
- Kenyon, A.S.; Morton, D.P. Stochastic Vehicle Routing with Random Travel Times. Transp. Sci. 2003, 37, 69–82. [Google Scholar] [CrossRef] [Green Version]
- Laporte, G.; Louveaux, F.; Mercure, H. The Vehicle Routing Problem with Stochastic Travel Times. Transp. Sci. 1992, 26, 161–170. [Google Scholar] [CrossRef]
- Baradaran, V.; Shafaei, A.; Hosseinian, A.H. Stochastic vehicle routing problem with heterogeneous vehicles and multiple prioritized time windows: Mathematical modeling and solution approach. Comput. Ind. Eng. 2019, 131, 187–199. [Google Scholar] [CrossRef]
- Baranwal, M.; Parekh, P.M.; Marla, L.; Salapaka, S.M.; Beck, C.L. Vehicle Routing Problem with Time Windows: A De-terministic Annealing approach. arXiv 2016, arXiv:1604.03590. [Google Scholar]
- Cortés, C.E.; Gendreau, M.; Rousseau, L.M.; Souyris, S.; Weintraub, A. Branch-and-price and constraint programming for solving a real-life technician dispatching problem. Eur. J. Oper. Res. 2014, 238, 300–312. [Google Scholar] [CrossRef]
- Pang, K.-W. An adaptive parallel route construction heuristic for the vehicle routing problem with time windows constraints. Expert Syst. Appl. 2011, 38, 11939–11946. [Google Scholar] [CrossRef]
- Nagata, Y.; Bräysy, O. A powerful route minimization heuristic for the vehicle routing problem with time windows. Oper. Res. Lett. 2009, 37, 333–338. [Google Scholar] [CrossRef]
- Belfiore, P.; Yoshizaki, H. Scatter search for a real-life heterogeneous fleet vehicle routing problem with time windows and split deliveries in Brazil. Eur. J. Oper. Res. 2009, 199, 750–758. [Google Scholar] [CrossRef]
- Chen, H.-K.; Hsueh, C.-F.; Chang, M.-S. The real-time time-dependent vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2006, 42, 383–408. [Google Scholar] [CrossRef]
- Liu, B.; Guo, X.; Yu, Y.; Zhou, Q. Minimizing the total completion time of an urban delivery problem with uncertain assembly time. Transp. Res. Part E Logist. Transp. Rev. 2019, 132, 163–182. [Google Scholar] [CrossRef]
- Savsar, M.; Nadoom, A.; Al-Muraished, D.; Ibrahim, R.; Al-Debasi, M. Analysis of Delivery and Assembly Operations in a Furniture Company Using Discrete Event Simulation. 2013. Available online: https://www.semanticscholar.org/paper/Analysis-of-Delivery-and-Assembly-Operations-in-a-Savsar-Nadoom/4cb1803aa5b41d5602082cabeb2def3e846f5e3f (accessed on 26 December 2022).
- Wicaksono, T.; Pathomsiri, S. Time Series Analysis for Home Furniture Delivery and Assembly Service in Indonesia a December nd Thailand. In Proceedings of the 5th International Conference on Urban Planning, Transport and Construction Engineering (ICUPTCE’17), Pattaya, Thailand, 2–3 May 2017; pp. 1–9. [Google Scholar] [CrossRef]
- Tunyaplin, S.; Chanpuypetch, W. Development of a performance measurement system for a home furniture delivery and assembly logistics provider in Thailand. Int. J. Bus. Process. Integr. Manag. 2019, 9, 292. [Google Scholar] [CrossRef]
- Tunyaplin, S.; Chanpuypetch, W. A SCOR-based performance evaluation framework for last-mile delivery of DIY home furniture products. Int. J. Logist. Syst. Manag. 2021, 38, 277. [Google Scholar] [CrossRef]
- Yin, R.K. Case Study Research: Design and Methods; Sage Publications: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Hyett, N.; Kenny, A.; Dickson-Swift, V. Methodology or method? A critical review of qualitative case study reports. Int. J. Qual. Stud. Heal. Well-Being 2014, 9, 23606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voss, C.; Tsikriktsis, N.; Frohlich, M. Case research in operations management. Int. J. Oper. Prod. Manag. 2002, 22, 195–219. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, I.A.; Oliveira, J.; Antonissen, J.; Carvalho, H. Assessing the impact of fusion-based additive manufacturing technologies on green supply chain management performance. J. Manuf. Technol. Manag. 2022, 34, 187–211. [Google Scholar] [CrossRef]
- Naghshineh, B.; Carvalho, H. Exploring the interrelations between additive manufacturing adoption barriers and supply chain vulnerabilities: The case of an original equipment manufacturer. J. Manuf. Technol. Manag. 2022, 33, 1473–1489. [Google Scholar] [CrossRef]
- Desaulniers, G.; Madsen, O.B.; Ropke, S. Chapter 5: The Vehicle Routing Problem with Time Windows. In Vehicle Routing; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 119–159. [Google Scholar] [CrossRef]
- Gendreau, M.; Ghiani, G.; Guerriero, E. Time-dependent routing problems: A review. Comput. Oper. Res. 2015, 64, 189–197. [Google Scholar] [CrossRef]
- Saksuriya, P.; Likasiri, C. Hybrid Heuristic for Vehicle Routing Problem with Time Windows and Compatibility Constraints in Home Healthcare System. Appl. Sci. 2022, 12, 6486. [Google Scholar] [CrossRef]

| Paper ID | Description | Problem Characteristics | Methods | Observations |
|---|---|---|---|---|
| [5] | Exploratory case Investigates a distribution strategy where two fleets of deliverymen and installers are used to deliver and install home appliances and furniture | - Delivery and installation routing problem - VRP with multiple synchronization constraints - VRP with time windows and driver-specific times | Mixed-integer linear programming model and tailored adaptive large neighborhood search heuristics | Results show that even though flexibility is included in a model, it generates better costs but also has more potential for computational burden. With the developed algorithms several issues related to VRP with multiple synchronization constraints and VRP with time windows and driver-specific times are solved optimally in shorter times and new lower bunds and some best-known solutions are observed |
| [37] | Exploratory case Investigates a Deterministic–Annealing-based approach to solve VRPTW and to model constraints related to shipments and heterogeneous vehicles | - VRPTW with aspects of routes and schedules and VRPTW with heterogeneous fleet - Assignment of priorities to customers - Scheduling and route planning restrictions | Deterministic Annealing Heuristic | - Unlimited scheduling resulted in between 15% to 20% of shipments not being collected - Capacity-constrained scheduling resulted in 30% of shipments not being collected - Scheduling with multiple restrictions resulted in 29% of shipments not being collected - Planning routes with time window resulted in 18% of shipments not being collected |
| [38] | Study case Investigates a company that provides repair services for office machines and that has 20 technicians that must do around 70 repairs daily, located in Chile | - VRPTW - Priority restrictions assigned to customers | Constrained programming based on column generation through an algorithm of Branch-and-Price. | Results show that the developed model allowed to improve performance, with improvements obtained between 15% and 45% in terms of total travel time and total time-window violation |
| [39] | Exploratory case Investigates a parallel route construction heuristic to deal with VRPTW | VRPTW | Route construction heuristic with an adaptive parallel scheme | - The algorithm allowed to have larger vehicle capacity and longer scheduling horizon - The average total travel distances were shorter with the algorithm - The proposed heuristic was confirmed to be effective and efficient for routes construction |
| [40] | Exploratory case Investigates an efficient heuristic method to reduce the number of routes in VRPTW | VRPTW | Heuristic-based on the powerful insertion, ejection pol and guided local search strategies | The proposed method performed the best heuristic that has been applied to Gehring and Homberger’s benchmark in terms of the number of routes |
| [41] | Study case Investigates a real distribution problem, related to a company that supplies goods for several supermarkets distributed in Brazil | Heterogeneous fleet VRPTW and split deliveries | Two constructive heuristics to generate the initial solution of scatter search | - The approach allowed decreasing the number of trucks used - The algorithm shows that it could offer a better solution in terms of costs distribution |
| [22] | Exploratory case Investigates a cohesive heuristic that can solve five different variants of the VRP | Five variants of the VRP: CVRP; VRPTW; the multi-depot vehicle routing problem; the side-dependent vehicle routing problem; and the open vehicle routing problem | Adaptive large neighbourhood search heuristic for the pick-up and delivery problem with time window | - The algorithm was able to improve 183 best-known solutions out of 486 benchmark tests - The heuristic has shown promising results for a large group of VRP with backhauls |
| [42] | Study case Investigates professional logistics company located in Taiwan | Real-time time-dependent VRPTW | Anytime algorithm comprising route construction and improvement | - All customers could be served by six vehicles with seven routes - The total travelled time is shorter than the result of manual planning - The total waiting time for services was zero - Contrary to the traditional VRP, the model developed does not require a vehicle to the customer’s location as soon as the service ends |
| Product Category | Item Type | ||
|---|---|---|---|
| PAX | Assembly | Mixed | |
| Accessories | X | X | |
| Sideboard/Showcase | X | ||
| Dressers | X | X | |
| Banks | X | X | |
| Hanger | X | X | |
| Chairs | X | X | |
| Beds | X | X | |
| Beds/Bunk Beds | X | ||
| Add-ons | X | X | |
| Hinges | X | X | X |
| Bookcases | X | X | |
| Structures | X | X | |
| Drawers | X | X | X |
| General | X | X | |
| Lighting | X | X | X |
| Knobs/Handles/Feet/Legs | X | X | X |
| Tables | X | X | |
| Extending tables | X | ||
| Tables + Chairs | X | X | |
| Panels | X | X | |
| Doors | X | X | X |
| Shelves | X | X | X |
| Closets | X | X | |
| Closets + | X | ||
| Sofas | X | X | |
| Type of Team | Team ID | Category | Nº of Teams | Commodity Value (€) | Weight (kg) | Nº of Linear Meters PAX (m/Route) | Type of Customers |
|---|---|---|---|---|---|---|---|
| PAX | Epi | N/A | 1 | N/A (a) | N/A (b) | 14 | PAX, Assembly and Mixed |
| N/A | 1 | N/A (a) | N/A (b) | 10 | PAX, Assembly and Mixed | ||
| N/A | 1 | N/A (a) | N/A (b) | 7 | PAX, Assembly and Mixed | ||
| Assembly | Em1i | 1st | 11 | ≥1500 | 1200 | 3 to 4 | PAX, Assembly and Mixed |
| Em2i | 2nd | 11 | ≥1500 | 1200 | 2 to 3 | PAX, Assembly and Mixed | |
| Mixed | Es1i | 1st | 2 | >500 | 1000 | N/A (c) | Mixed |
| Es2i | 2nd | 1 | >500 | 1000 | N/A (c) | Mixed | |
| Es3i | 3rd | 1 | >500 | 1000 | N/A (c) | Mixed |
| Type of Data | Data Designation | Collection Method | Time Horizon |
|---|---|---|---|
| Primary Data | Team Operating Modus | Observation of how the team execute operations and organises the daily work | Duration: 2 weeks |
| Loading Time | Collected using the timing technique while monitoring the team at the customer’s house | ||
| Assembly Time | While monitoring the team, some products’ assembly times were collected using the timing technique. Other products’ assembly times were estimated | ||
| Problem Restrictions | Observed and discussed while observing the worker creating the routes manually | Duration: 1 week | |
| Secondary Data | List of products delivered and assembled in 2019 | Obtained through the database, available in the company’s software Imoovit | Duration: 4 weeks |
| Information about IKEA products | IKEA website | ||
| Team Classification | Company internal document | ||
| Team Restrictions | Company internal document | ||
| Travel Time | Obtained through Google Maps | ||
| Planned routes by the collaborator | Software Imoovit query for the following fields: customer in route; team’s name assigned to the route; weight to carry; volume; commodity value; number of linear meters PAX. These were copied to an Excel worksheet |
| Notation | Designation |
|---|---|
| Cti | Set of Customers For PAX-type Customers: t = p i = 1, 2, 3, …, N, sequential index that runs through all PAX-type customers For Assembly-type Customers: t = m i = 1, 2, 3, …, N, sequential index that runs through all Assembly-type customers For Mixed-type Customers: t = s i = 1, 2, 3, …, N, sequential index that runs through all Mixed-type customers |
| Etck | Set of Teams For Assembly-type Teams: t = m k = 1, 2, 3, …, N, sequential index that runs through all Assembly-type teams c = 1, 2 and 3 for 1st, 2nd, and 3rd categories for Assembly-type Teams For Mixed-type Teams: t = s k = 1, 2, 3, …, N, sequential index that runs through all Mixed-type teams c = 1, 2 and 3 for 1st, 2nd, and 3rd categories for Mixed-type Teams |
| Epk | Set of PAX-type Teams k = 1, 2, 3, …, N, sequential index that runs through all PAX-type teams |
| bti | Time window upper limit for customer i of type t |
| PEtck | Weight to carry, in kilos, for a team k of type t (i.e., m or s type) with category c |
| PEpk | Weight to carry, in kilos, for a team k of PAX-type |
| PESOEtck | Weight to carry upper limit, in kilos, for a team k of type t with category c |
| VAti | Commodity value, in euros, transported to a customer i of type t |
| VAEtck | Commodity value, in euros, transported by a team k of type t with category c. |
| VAEpk | Commodity value, in euros, transported by a team k of PAX-type. |
| VOLti | Volume, in m3, occupied by orders of a customer i of type t |
| VOLEtck | Volume, in m3, transported by a team k of type t with category c |
| VOLEpk | Volume, in m3, transported by a team k of PAX-type |
| Vti, ti+1 | Travel time, in minutes, between a customer i+1 of type t and a customer i of type t Travel time from the depot to a customer i of type t, V0, ti, is 0 min, given that it was assumed that the team arrives at the first customer at the beginning of the time window, so the travel occurs before the time window starts. Therefore, the travel time for the first customer is not included in the total travel time of the route. |
| Sti | Total estimated service time, in minutes, for a customer i of type t |
| Dti | Loading time of products to a customer i of type t If t = p, PAX-type customer For Mpi between 0 to 3 linear meters—then Dpi = 15 min; For Mpi between 3 to 6 linear meters—then Dpi = 30 min For Mpi ≥ 6 linear meters—then Dpi = 40 min. For the other types of customers, a fixed time of 10 min was considered. |
| Tti, tck | Arrival time at a customer i of type t, for a team k of type t with category c |
| TTEtck | Total estimated route time, in minutes, for a team k of type t with category c |
| Mpi | Number of linear meters, in meters, to be assembled at a customer i of PAX-type |
| MEtck | Number of linear meters, in meters, to assemble for a team k of type t with category c |
| MEpk | Number of linear meters, in meters, to assemble for a team k of PAX-type |
| METROSEtck | Number of linear meters upper limit, for a team k of type t with category c |
| METROSEpk | Number of linear meters upper limit, in meters, for a team k of PAX-type |
| Type of Team | Team Selection | 1st Customer to Insert | Next Customer to Insert | After the Allocation of All Teams |
|---|---|---|---|---|
| Pax Team (P-type) | Criteria:“Highest PAX linear meter capacity” First the team with highest capacity | Start with the first time window: Select the “PAX customer” with the highest number of PAX linear meters to be assembled. After the customer selection, calculate the number of linear meters available for the team. Once the first PAX team’s capacity reaches 0 or there are no more “PAX customers” to serve in the first time window, go to the second time window. | If the first team has capacity available, select the “PAX customer” with the zip code more similar the last customer inserted. | If there are still “PAX customers” to allocate, once the teams have all been used, add the “PAX customers” to the route with the lowest ratio between the allocated number of linear meters and the maximum number of linear meters available for the team. |
| Assembly Team (M-type) | Criteria: “Team category” First the first category teams | Start with the 1st time window: If there are “PAX customers” to allocate, start with them. Select the “PAX customer” with the highest number of linear meters to assemble. After that, calculate the number of linear meters available for the team, the weight to carry, and the commodity value. If there are no “PAX customers” to allocate, start with the “Assembly customers”. Select the “Assembly customer” with the higher estimated service time, weight to carry, and commodity value. After that, calculate the time available in the time window. If there are no “Assembly customers”, start with the “Mixed customers”. Select the “Mixed customer” with the highest estimated service time. After that, calculate the time available in the time window, weight to carry and commodity value. Once the team reaches the weight to carry limit, the number of linear meters to assemble limit or cannot get to the next customer inside the time window interval, or there are no more customers to serve in the first time window, go to the second time window. | If there are still “PAX customers” to allocate and the team has capacity available in linear meters, select the “PAX customer” with the zip code more similar to the last customer inserted. If there’s still a “PAX customer” to allocate, but the team does not have enough capacity in linear meters and has time available in the time window, select the “Assembly customer” with the zip code more similar to the last customer inserted. If the team still has time available in the time window and there is still “Assembly customers” to allocate, select the “Assembly customer” with the zip code more similar to the last customer inserted. If the team still has time available in the time window and there are no “Assembly customers” to allocate, select the “Mixed customer” with the zip code more similar to the last customer inserted. | If there are still “Assembly customers” to allocate, once the teams have all been used, add the “Assembly customers” to the route with the lowest estimated total time to be completed. |
| Mixed-type Team (S-type) | Criteria: “Team category” First the first category teams | Start with the first time window: Select the “Mixed customer” with the highest estimated service time. After that, calculate the time available in the time window, the weight to carry and the commodity value. Once the team cannot get to the next “Mixed customer” inside the time window interval, or there are no more customers to serve in the first time window, or the team reaches its limit of weight to carry, go to the second time window. | If the team has time available in the time window and if there is still a ”Mixed customer” to allocate, select the Mixed customer with the zip code more similar to the last customer inserted. | If there are still “Mixed customers” to allocate, once the teams have all been used, add the “Mixed customers” to the route with the lowest estimated total time to be completed. |
| Team ID | Ratio of the Commodity Value to Be Transported in Relation to the Minimum Value | Vehicle Occupancy Rate by Weight | Vehicle Occupancy Rate by Volume | Ratio of Linear Meters to Be Transported in Relation to the Maximum Value | Average Travel Time between Customers (min) | Rate of Customers Visited within the Time Window | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Current State | Future State | Current State | Future State | Current State | Future State | Current State | Future State | Current State | Future State | Current State | Future State | |
| Ep1 | N/A | N/A | N/A | N/A | N/A | N/A | 0.57 | 0.96 | 12 | 21 | N/A | N/A |
| Ep2 | N/A | N/A | N/A | N/A | N/A | N/A | 0.68 | 0.93 | 7 | 15 | N/A | N/A |
| Ep3 | N/A | N/A | N/A | N/A | N/A | N/A | 1.54 | 1.00 | 11 | 9 | N/A | N/A |
| Em11 | 4.78 | 1.61 | 91% | 28% | 95% | 20% | 0.00 | 0.88 | 8 | 15 | 100% | 100% |
| Em12 | 3.24 | 1.25 | 86% | 35% | 49% | 10% | 0.00 | 0.88 | 4 | 11 | 100% | 100% |
| Em13 | 3.28 | 1.86 | 93% | 48% | 81% | 27% | 0.00 | 0.95 | 12 | 10 | 100% | 100% |
| Em14 | 2.85 | 2.09 | 99% | 71% | 36% | 19% | 0.25 | 1.00 | 5 | 15 | 57% | 100% |
| Em15 | 2.56 | 1.69 | 89% | 84% | 34% | 23% | 0.00 | 0.50 | 5 | 3 | 75% | 100% |
| Em16 | 1.24 | 2.37 | 46% | 55% | 11% | 38% | 0.38 | 0.00 | 10 | 11 | 100% | 100% |
| Em17 | 3.99 | 2.78 | 112% | 68% | 31% | 34% | 1.25 | 0.00 | 7 | 21 | 20% | 100% |
| Em18 | 3.23 | 93% | 42% | 0.00 | 13 | 100% | ||||||
| Em19 | 3.31 | 1.61 | 96% | 47% | 41% | 12% | 1.32 | 0.75 | 15 | 4 | 33% | 100% |
| Em110 | 5.10 | 3.15 | 141% | 82% | 59% | 44% | 0.00 | 0.00 | 10 | 13 | 47% | 100% |
| Em111 | 2.79 | 97% | 35% | 0.00 | 12 | 100% | ||||||
| Em21 | 3.01 | 93% | 52% | 0.00 | 10 | 100% | ||||||
| Em22 | 2.08 | 1.75 | 81% | 50% | 33% | 14% | 0.56 | 0.00 | 6 | 16 | 100% | 100% |
| Em23 | 2.72 | 71% | 23% | 0.00 | 26 | 100% | ||||||
| Em24 | 1.48 | 1.74 | 37% | 57% | 7% | 33% | 0.00 | 0.75 | 7 | 18 | 50% | 100% |
| Em25 | 1.74 | 58% | 28% | 0.00 | 16 | 100% | ||||||
| Em26 | 2.19 | 1.16 | 116% | 29% | 37% | 15% | 0.00 | 0.00 | 7 | 11 | 75% | 100% |
| Em27 | 1.36 | 28% | 15% | 0.00 | 19 | 100% | ||||||
| Em28 | 1.31 | 1.34 | 40% | 30% | 9% | 28% | 0.38 | 0.00 | 14 | 15 | 67% | 100% |
| Em29 | 1.87 | 0.80 | 66% | 32% | 25% | 14% | 0.00 | 0.00 | 9 | 17 | 67% | 100% |
| Em210 | 1.04 | 0.69 | 22% | 13% | 4% | 8% | 0.38 | 0.00 | 8 | 13 | 60% | 100% |
| Em211 | 3.68 | 0.56 | 87% | 26% | 51% | 6% | 1.50 | 0.00 | 2 | 10 | 67% | 100% |
| Es11 | 0.50 | 15% | 4% | N/A | N/A | 9 | 100% | |||||
| Es12 | 0.33 | 5% | 8% | N/A | N/A | 0 | 100% | |||||
| Es21 | 0.00 | 0% | N/A | N/A | ||||||||
| Es31 | 1.91 | 0.00 | 40% | 0% | 23% | N/A | N/A | 3 | 100% | |||
| Item | Current Scenario | Future Scenario |
|---|---|---|
| Number of teams | 22 teams | 28 teams |
| Time window requirements | 12 routes with the shortest estimated travel time | Although the routes have a higher estimated travel time, the routes comply with the established time window |
| Commodity Value/team | The commodity value reaches higher values in 15 routes | The routes have higher commodity value than the minimum limit |
| Weight to carry/team | 3 teams have weight to carry higher than the maximum limit | The weight to carry is lower than the maximum limit |
| Number of linear meters PAX/team | 4 teams have number of PAX linear meters to assemble above the maximum limit | The number of PAX linear meters respects the upper limit, being used in full for some teams |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, I.A.; Bento, C.; Mascarenhas, L.; Pimentel, C.; Carvalho, H. A Heuristic Approach to Support Route Planning for Delivery and Installation of Furniture: A Case Study. Appl. Sci. 2023, 13, 3285. https://doi.org/10.3390/app13053285
Ferreira IA, Bento C, Mascarenhas L, Pimentel C, Carvalho H. A Heuristic Approach to Support Route Planning for Delivery and Installation of Furniture: A Case Study. Applied Sciences. 2023; 13(5):3285. https://doi.org/10.3390/app13053285
Chicago/Turabian StyleFerreira, Inês A., Catarina Bento, Luís Mascarenhas, Carina Pimentel, and Helena Carvalho. 2023. "A Heuristic Approach to Support Route Planning for Delivery and Installation of Furniture: A Case Study" Applied Sciences 13, no. 5: 3285. https://doi.org/10.3390/app13053285
APA StyleFerreira, I. A., Bento, C., Mascarenhas, L., Pimentel, C., & Carvalho, H. (2023). A Heuristic Approach to Support Route Planning for Delivery and Installation of Furniture: A Case Study. Applied Sciences, 13(5), 3285. https://doi.org/10.3390/app13053285







