Active Disturbance Rejection Optimization Control for SOFCs in Offshore Wind Power
Abstract
:1. Introduction
- An improved firefly algorithm is proposed to optimize the parameters of an LADRC controller;
- The firefly algorithm is improved by introducing stepped inertia weights and using a random generation method to replace 30% of individuals with low luminescence degrees to optimize LADRC parameters;
- The LADRC controller is applied to suppress the influence of disturbance and uncertainty on SOFC systems using offshore wind power hydrogen.
2. Solid Oxide Fuel Cell Control Method
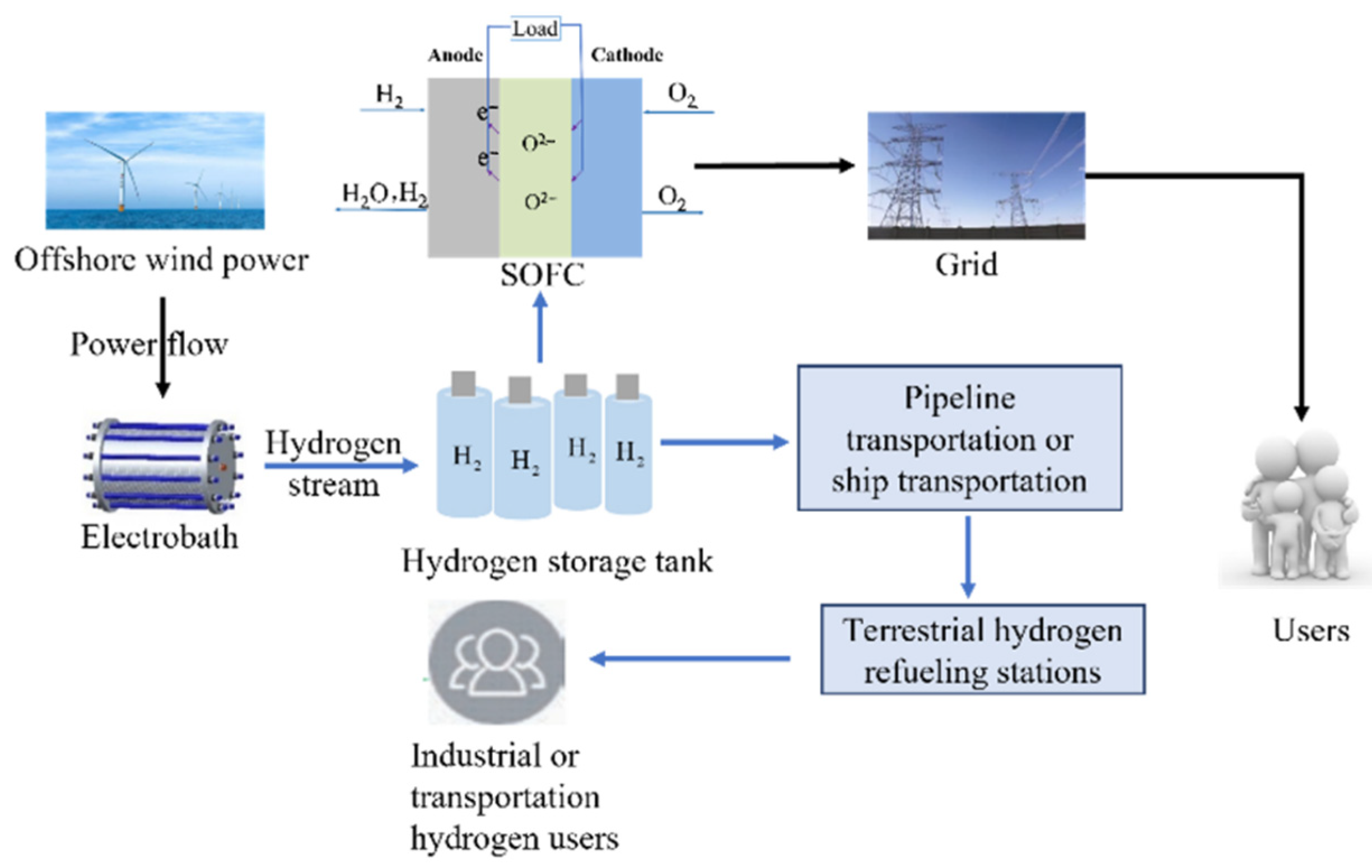
2.1. Offshore Wind Power SOFC System Structure Analysis
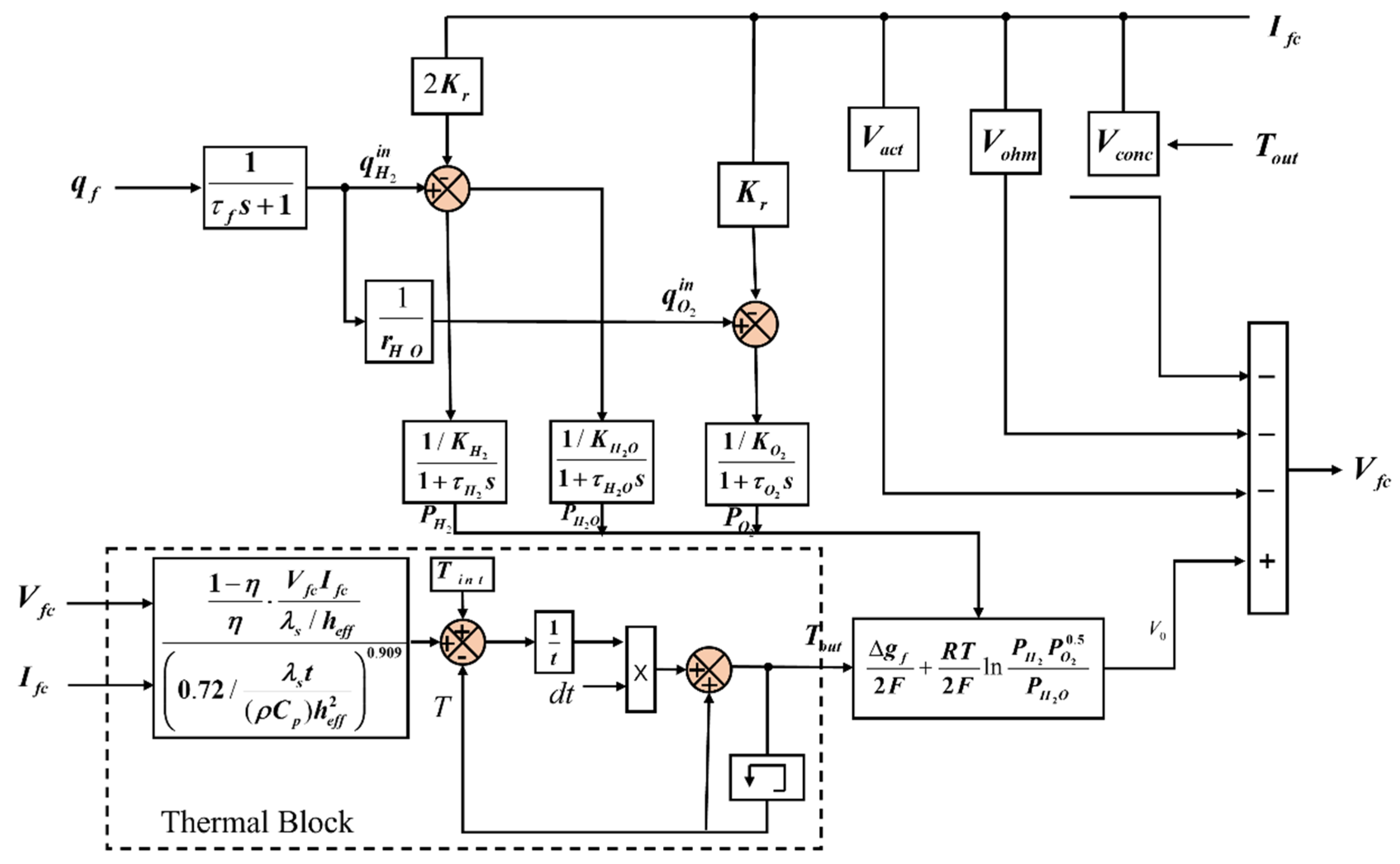
2.2. SOFC Working Principle
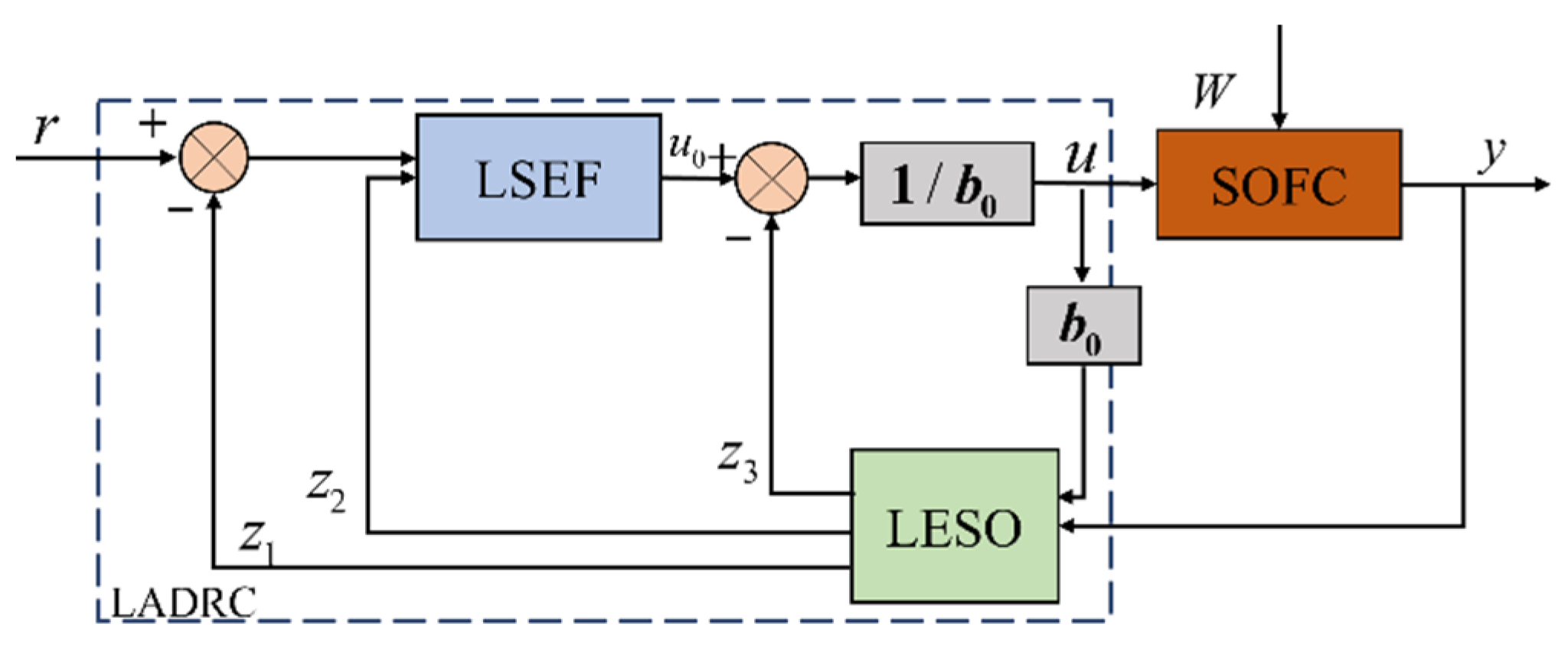
2.3. LADRC
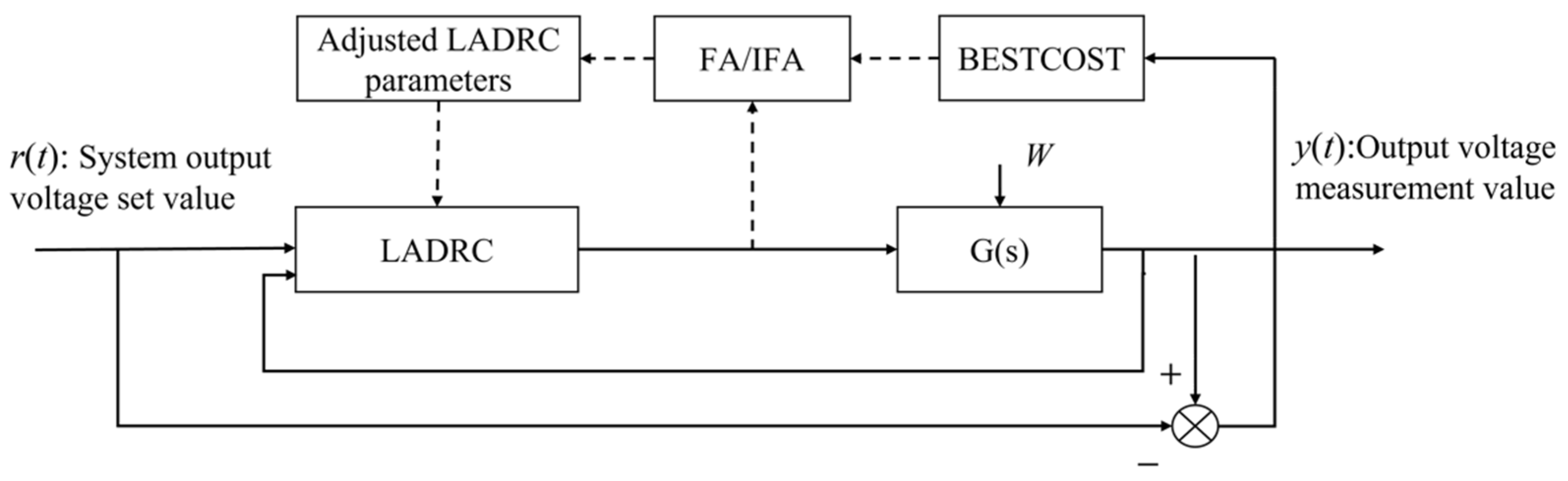
3. IFA-LADRC Control Scheme
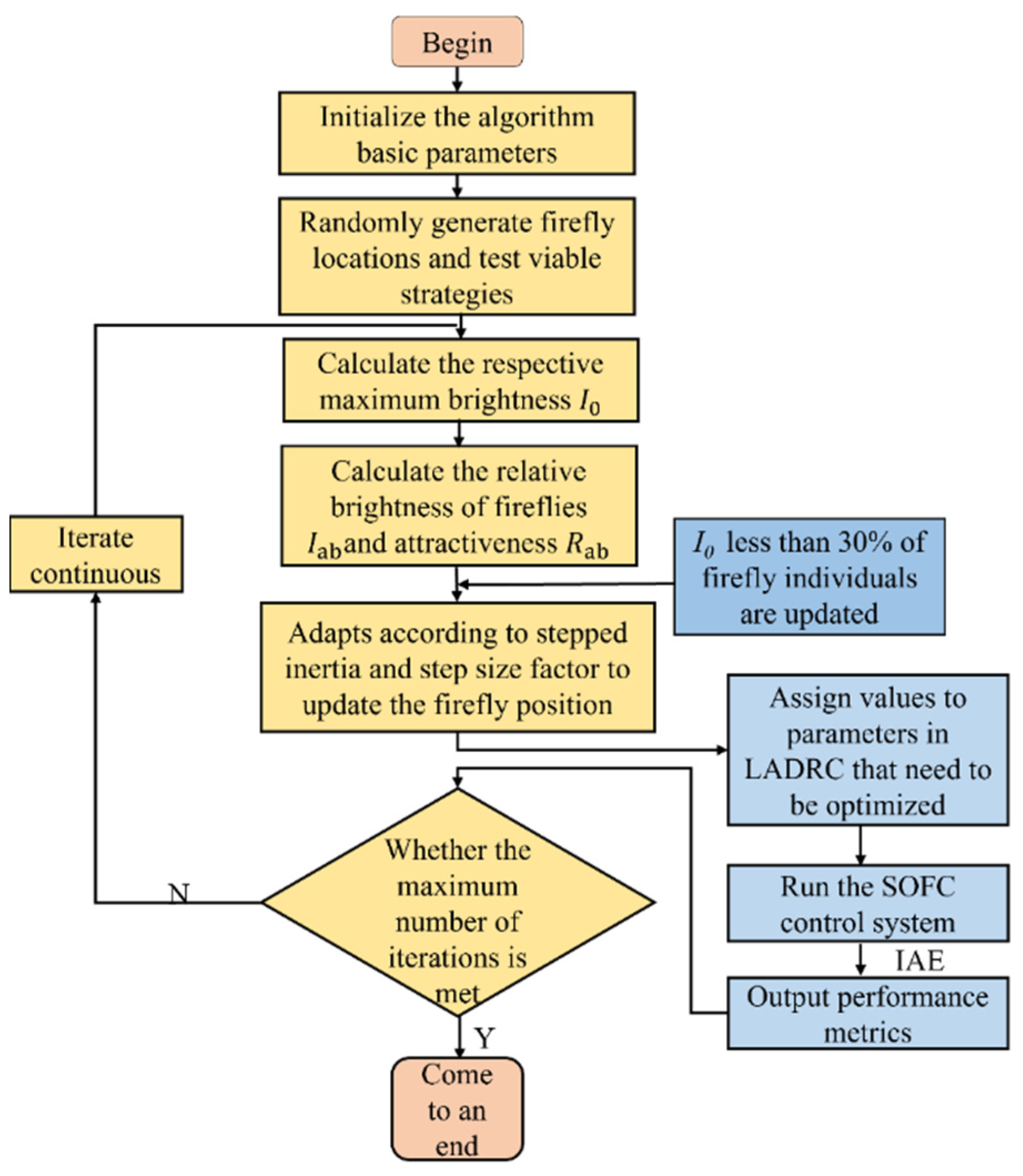
3.1. Improved Firefly Algorithm Based on Inertia Weights
- Step 1: Initialize the FA, such as the total number of fireflies, the step size factor, and the number of iterations.
- Step 2: Randomly generate the location of the fireflies.
- Step 3: The respective maximum brightness of the fireflies can be calculated from Equation (24).
- Step 4: Calculate its attraction and relative brightness according to Equation (25), and then update the position of the firefly.
- Step 5: Recalculate the brightness and attraction and move again, iterating until the maximum number of iterations, and then arrive at the global optimal solution.
3.2. IFA-LADRC Control Scheme Flow
- (1)
- Assign the parameters to be optimized to the LADRC controller using the IFA based on inertia weights described in the previous subsection.
- (2)
- The deviation performance index (IAE) is used to evaluate the performance of the LADRC, and the system performance index is output after running the whole SOFC simulation system.
- (3)
- If the control performance requirement is not satisfied, continue iterations until the maximum number of iterations is met to achieve the optimal control of the system.
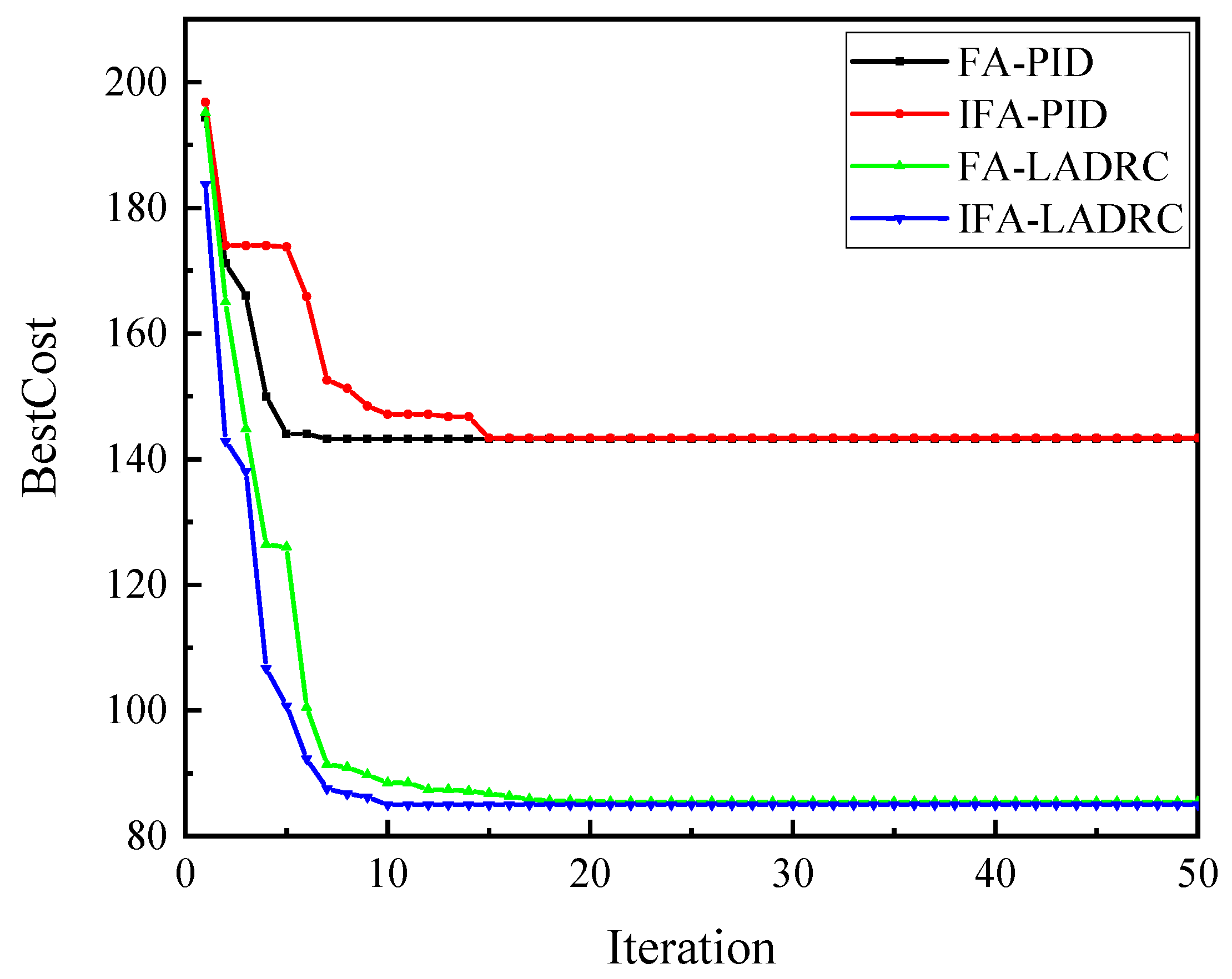
4. Simulation Analysis
4.1. System Parameters
- (1)
- Objective function: To quantify the performance of the control system, the deviation performance index IAE is used to evaluate the performance of the LADRC. That is, it is used as the fitness function of the algorithm, and the expression of the minimum objective function to be optimized iswhere is the SOFC control error. The smaller the value of the expression , the better the control effect.
- (2)
- Constraints: The parameters of the firefly algorithm are set as follows: The number of firefly populations nPop is 5, and the number of dimensions nVar is 3, where the three variables to be optimized are ω0, ωC, and b0, and the range of decision variables Var is empirically set asThe initial value of step length is 0.2, the initial attraction value is 2, and the light absorption coefficient is 1.
- (3)
- Termination criterion: To make the parameters close to the optimal values, the maximum number of update iterations of the firefly algorithm is set to 50.
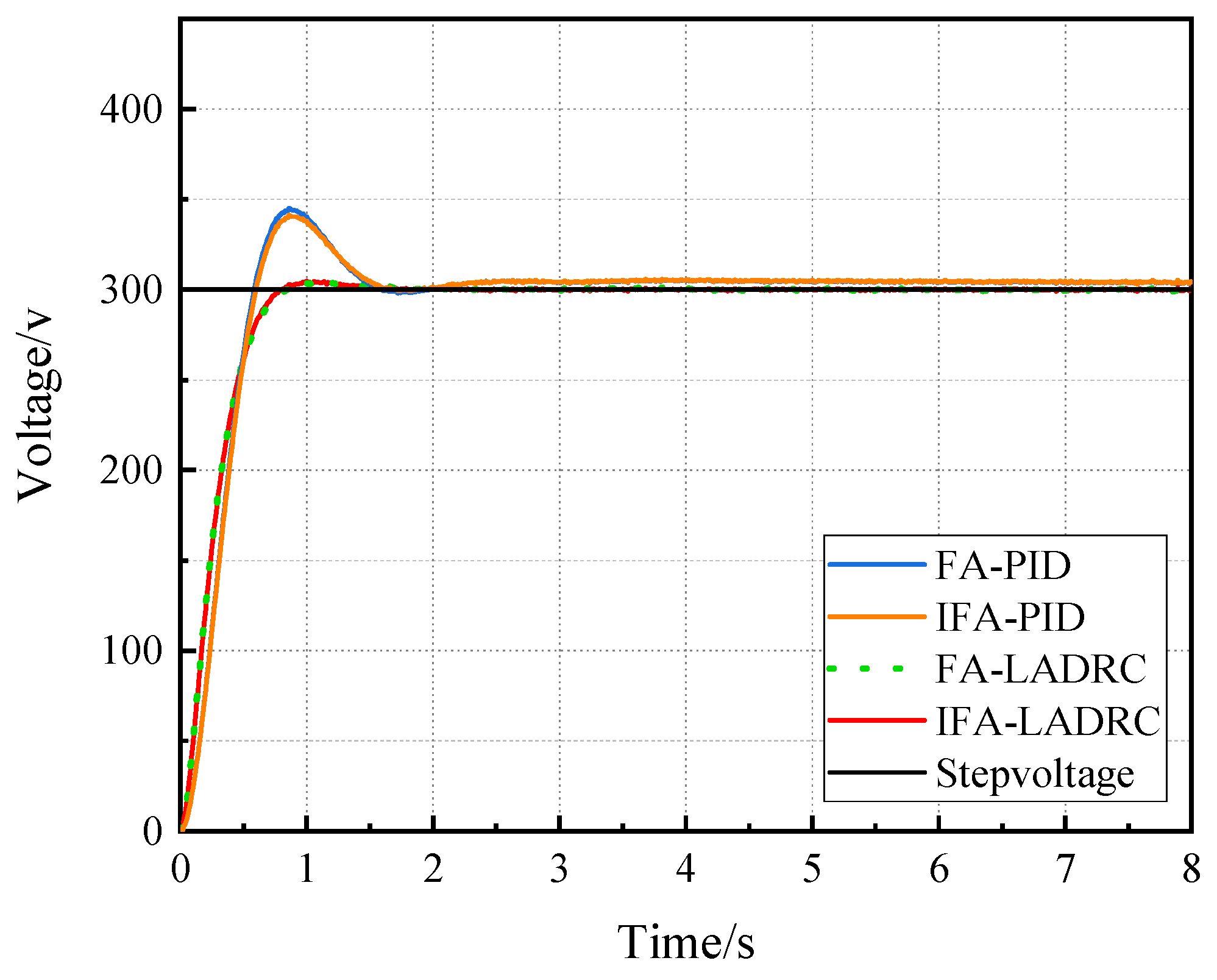
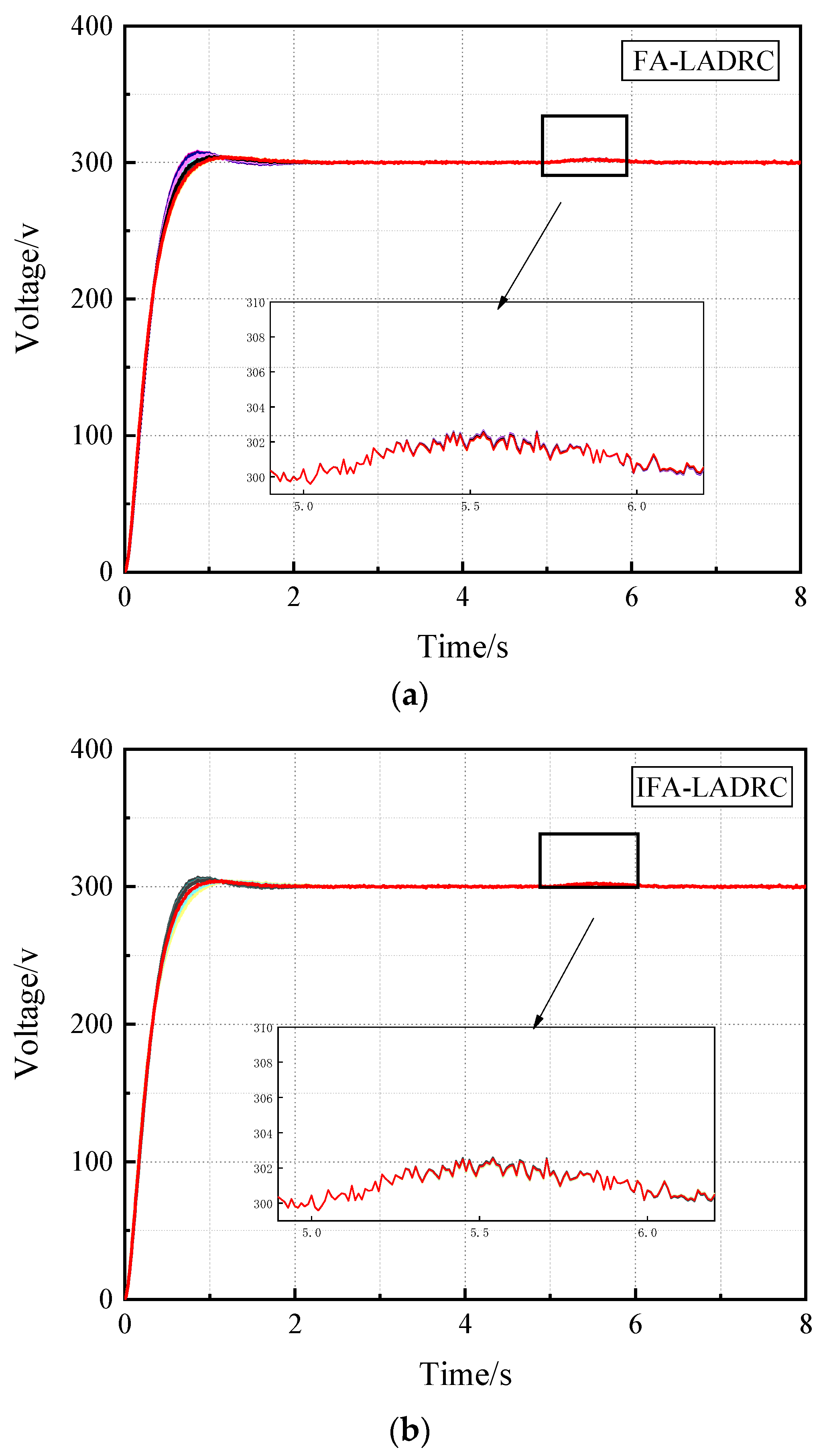
4.2. Voltage Tracking Experiment
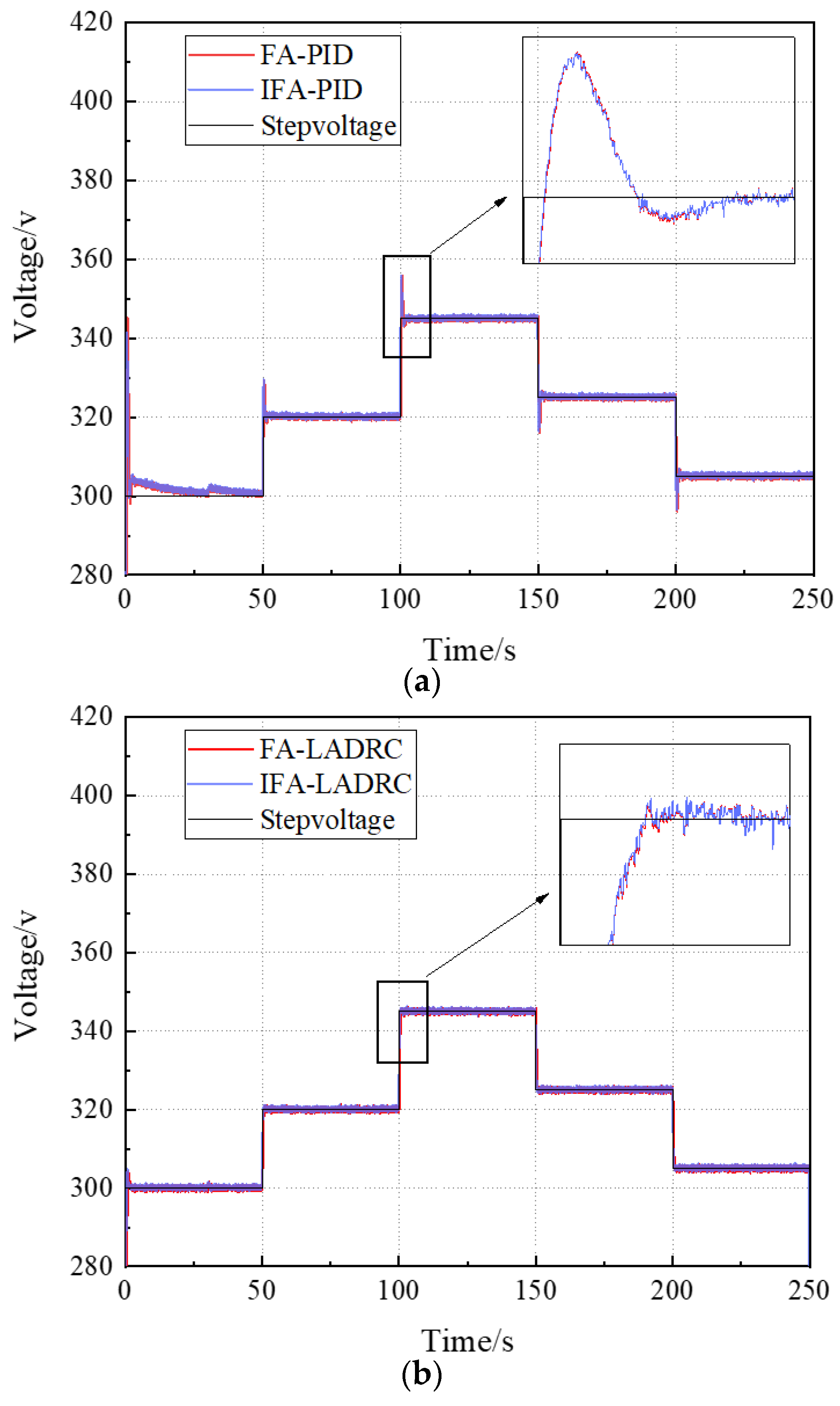
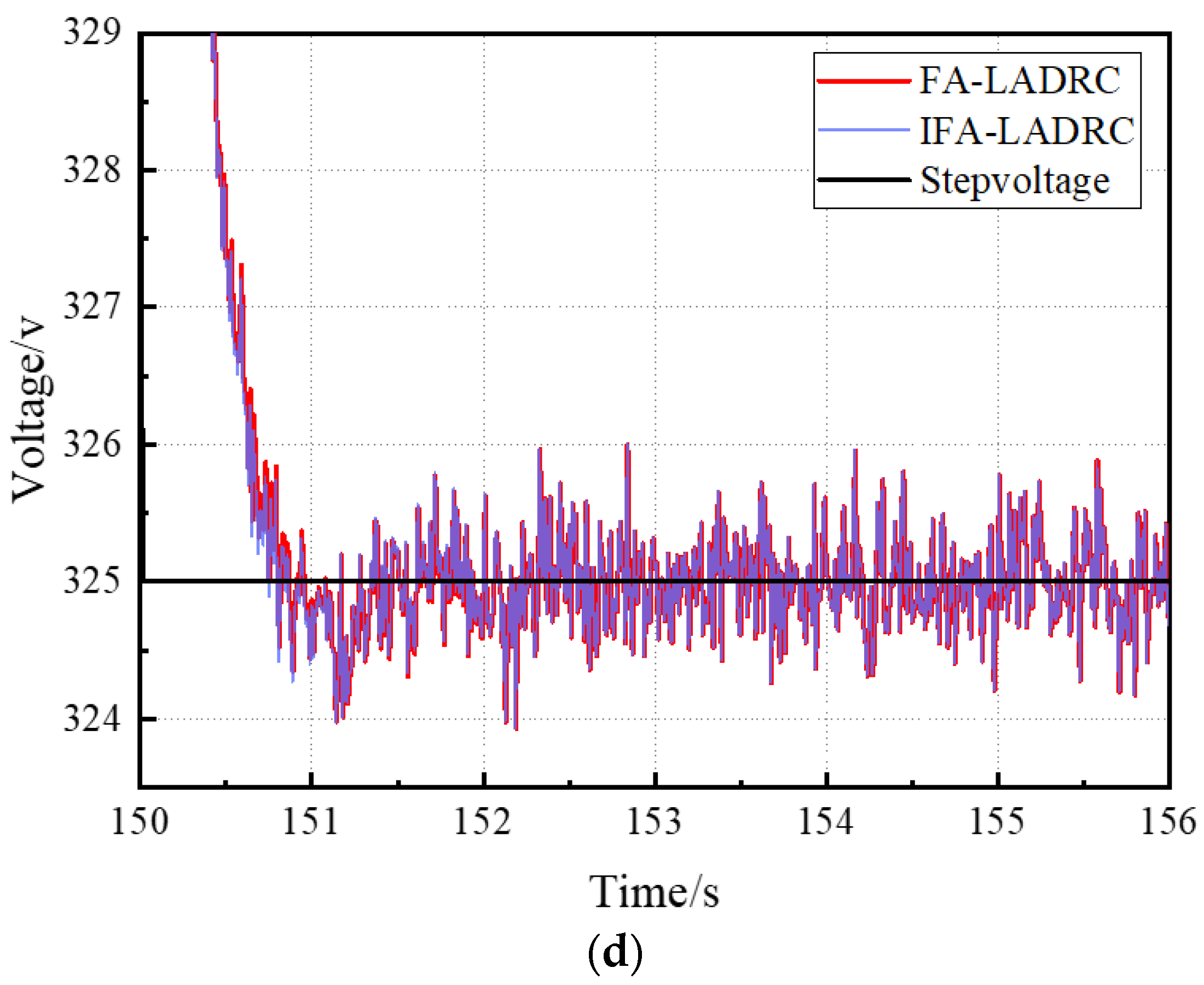
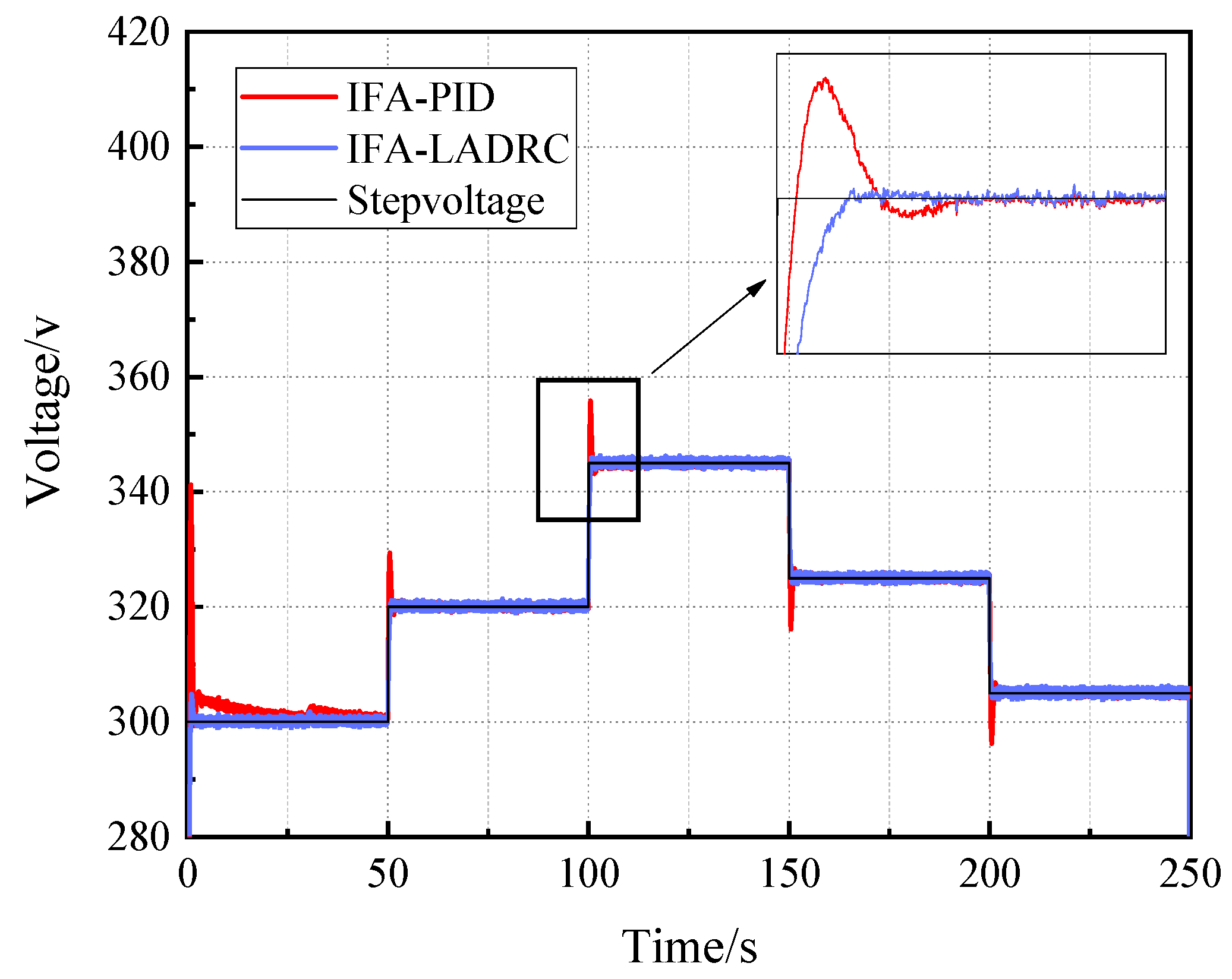
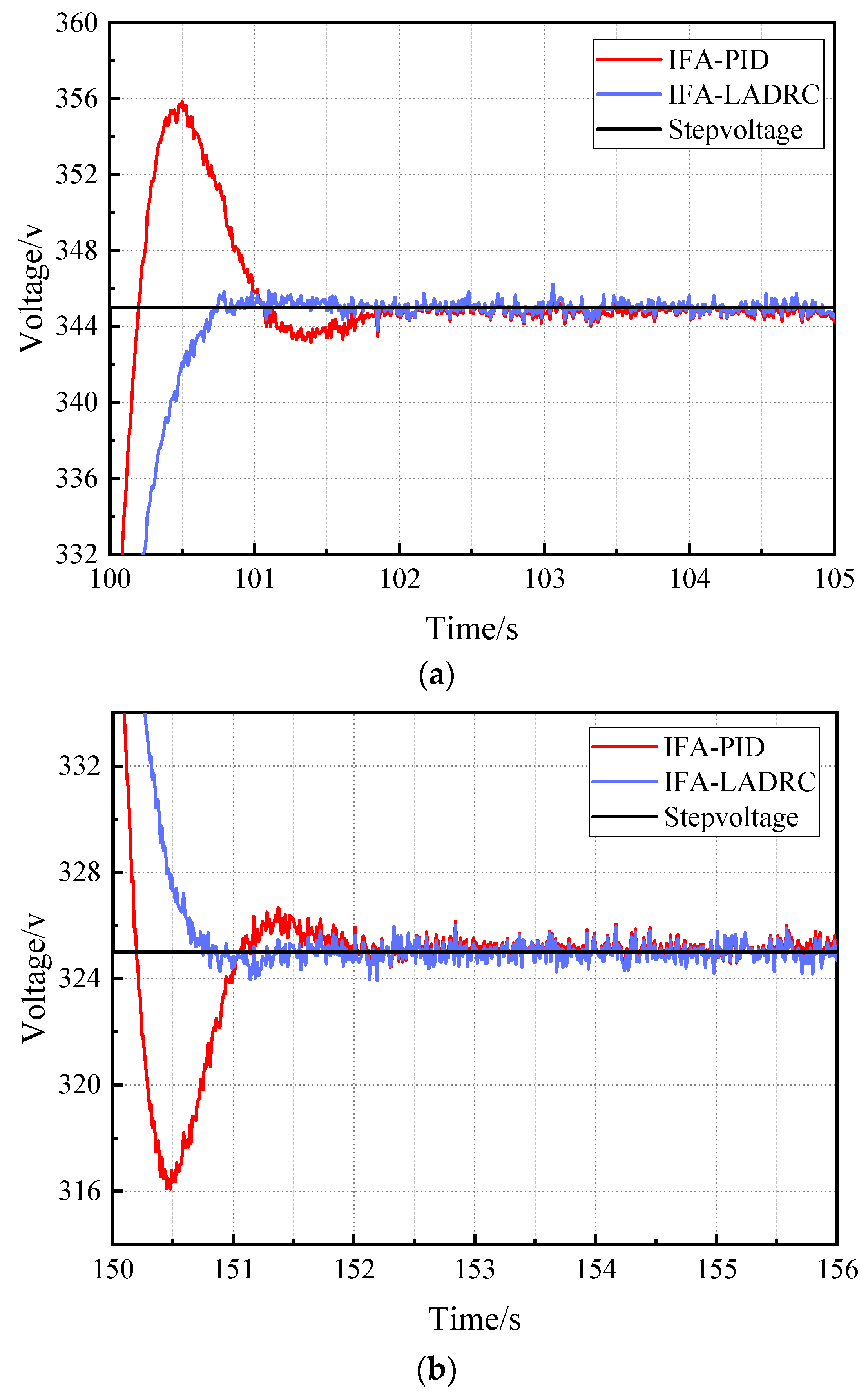
4.3. Voltage Disturbance Experiment
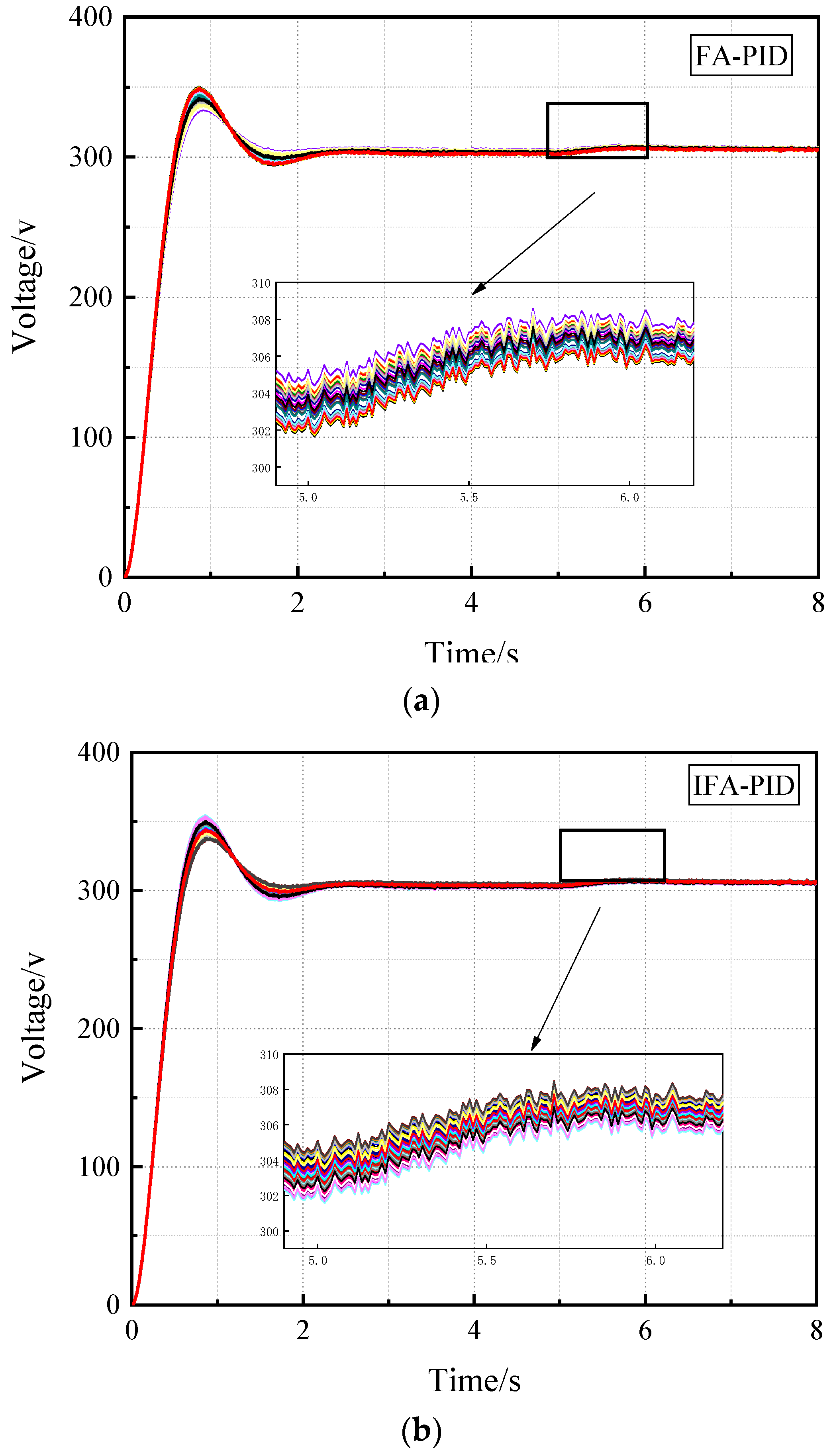
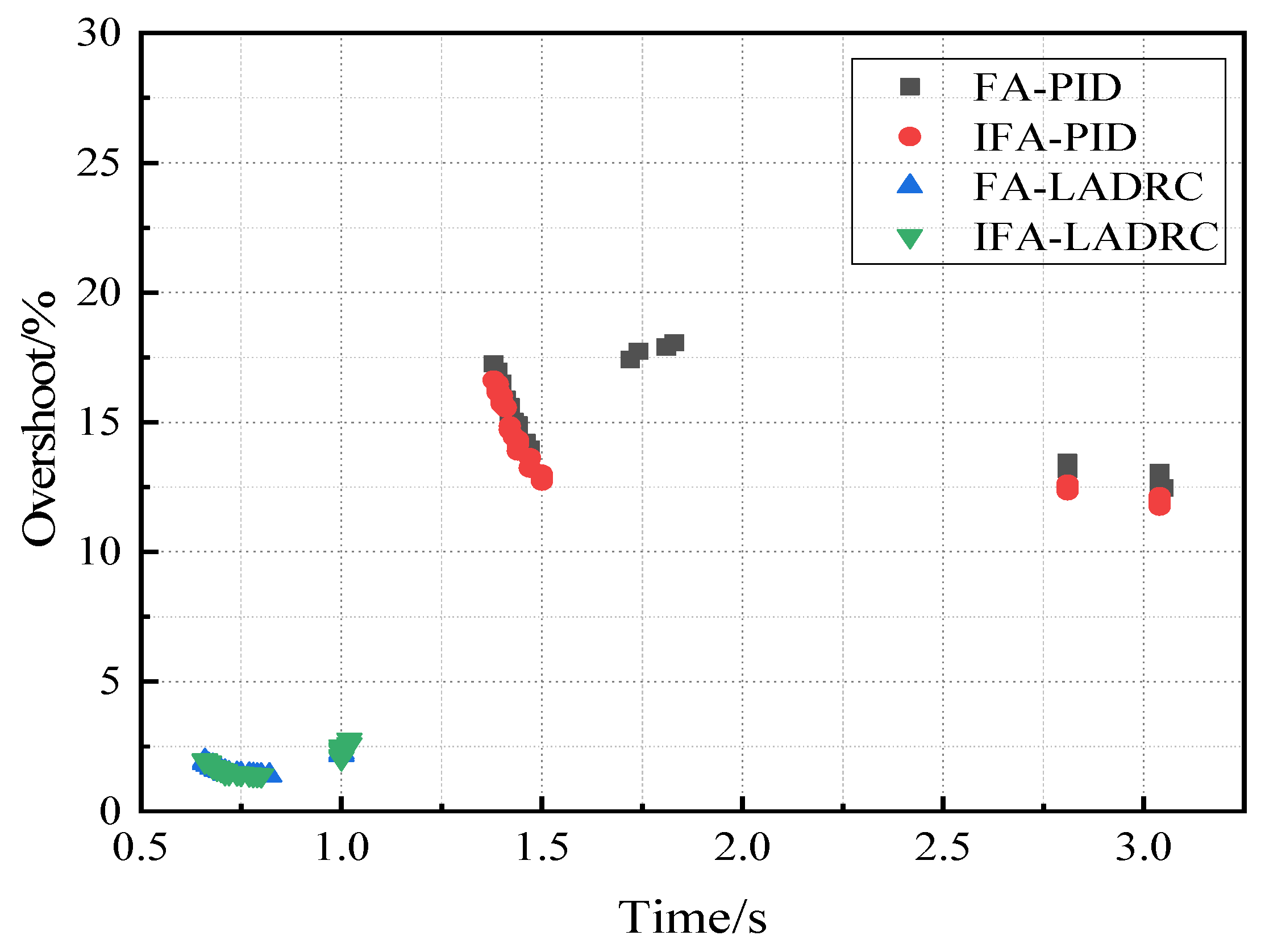
4.4. Monte Carlo Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, Y.; Zhang, H.; Long, Y.; Wang, Y.-F.; Liang, Y.-T.; Song, X.; James, J. Multi-objective design optimization of combined cooling, heating and power system for cruise ship application. J. Clean. Prod. 2019, 233, 264–279. [Google Scholar] [CrossRef]
- Lucas, T.R.; Ferreira, A.F.; Pereira, R.B.S.; Alves, M. Hydrogen production from the Wind Float Atlantic offshore wind farm: A techno-economic analysis. Appl. Energy 2022, 310, 118481. [Google Scholar] [CrossRef]
- Kaiser, S.; Siems, F.; Mostert, C.; Bringezu, S. Environmental and Economic Performance of CO2-Based Methanol Production Using Long-Distance Transport for H2 in Combination with CO2 Point Sources: A Case Study for Germany. Energies 2022, 15, 2507. [Google Scholar] [CrossRef]
- Lin, H.; Wu, Q.; Chen, X.; Yang, X.; Guo, X.; Lv, J.; Lu, T.; Song, S.; McElroy, M. Economic and technological feasibility of using power-to-hydrogen technology under higher wind penetration in China. Renew. Energy 2021, 173, 569–580. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, X.; Wen, H.; Pei, A. Hydrogen production from offshore wind power in South China. Int. J. Hydrog. Energy 2022, 47, 24558–24568. [Google Scholar] [CrossRef]
- Kuterbekov, K.A.; Nikonov, A.V.; Bekmyrza, K.Z.; Pavzderin, N.B.; Kabyshev, A.M.; Kubenova, M.M.; Kabdrakhimova, G.D.; Aidarbekov, N. Classification of Solid Oxide Fuel Cells. Nanomaterials 2022, 12, 1059. [Google Scholar] [CrossRef]
- Singh, M.; Zappa, D.; Comini, E. Solid oxide fuel cell: Decade of progress, future perspectives and challenges. Int. J. Hydrog. 2021, 46, 27643–27674. [Google Scholar] [CrossRef]
- Beigzadeh, M.; Pourfayaz, F.; Ghazvini, M.; Ahmadi, M. Energy and exergy analyses of solid oxide fuel cell-gas turbine hybrid systems fed by different renewable biofuels: A comparative study. J. Clean. Prod. 2021, 280, 124383. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Peng, L.; Ye, X.-C.; Xu, S.-C.; Zhang, T. Feedforward-decoupled closed-loop fuzzy proportion-integral-derivative control of air supply system of proton exchange membrane fuel cell. Energy 2022, 240, 122490. [Google Scholar] [CrossRef]
- Tyczka, M.; Skarka, W. Optimisation of operational parameters based on simulation numerical model of hydrogen fuel cell stack used for electric car drive. In Transdisciplinary Engineering: Crossing Boundaries; IOS Press: Amsterdam, The Netherlands, 2016; pp. 622–631. [Google Scholar]
- Malik, F.R.; Tieqing, Z.; Kim, Y.B. Temperature and hydrogen flow rate controls of diesel autothermal reformer for 3.6 kW PEM fuel cell system with autoignition delay time analysis. Int. J. Hydrog. 2020, 45, 29345–29355. [Google Scholar] [CrossRef]
- Wu, X.; Wang, J.; Hao, J.; Li, X.I. Control of a solid oxide fuel cell stack based on unmodeled dynamic compensations. Int. J. Hydrog. 2018, 43, 22500–22510. [Google Scholar] [CrossRef]
- Li, H.; Chen, H.; Gao, N.; T-Ahmed, N.A.; Charpentier, J.F.; Benbouzid, M. Ship Dynamic Positioning Control Based on Active Disturbance Rejection Control. J. Mar. Sci. Eng. 2022, 10, 865. [Google Scholar] [CrossRef]
- Song, J.; Su, J.; Hu, Y.; Zhao, M.; Gao, K. Stability and performance comparison analysis for linear active disturbance rejection control–based system. T. I. Meas. Control 2022, 44, 2037–2048. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, G.; Li, D.; Liu, Y.; Chen, Y. Active disturbance rejection control design for high-order integral systems. ISA Trans. 2022, 125, 560–570. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Liu, Q.; Chen, Y.; Wang, X.-D.; Li, W.-B.; Ding, Y.-J.; Wan, Z.-M. Active disturbance rejection control strategy applied to cathode humidity control in PEMFC system. Energy Convers. Manag. 2020, 224, 113389. [Google Scholar] [CrossRef]
- Zhuo, S.; Xu, L.; Huang, F.-Y.; Gaillard, A.; Paire, D.; Gao, F. Robust adaptive control of interleaved boost converter for fuel cell application. IEEE T Ind. Appl. 2021, 57, 6603–6610. [Google Scholar] [CrossRef]
- Dos-Santos-Coelho, L.; Mariani, V.-C. Improved firefly algorithm approach applied to chiller loading for energy conservation. Energy Build. 2013, 59, 273–278. [Google Scholar] [CrossRef]
- Hao, X.; Salhi, I.; Laghrouche, S.; Ait-Amirat, Y.; Djerdir, A. Backstepping Supertwisting Control of Four-Phase Interleaved Boost Converter for PEM Fuel Cell. IEEE Trans. Power Electron. 2022, 37, 7858–7870. [Google Scholar] [CrossRef]
- Kumar, R.; Talukdar, F.A.; Rajan, A.; Devi, A.; Raja, R. Parameter optimization of 5.5 GHz low noise amplifier using multi-objective Firefly Algorithm. Microsyst. Technol. 2020, 26, 3289–3297. [Google Scholar] [CrossRef]
- Eyni, E.; Stanko, M.; Schümann, H.; Qureshi, A.H. Dynamic Process Modeling of Topside Systems for Evaluating Power Consumption and Possibilities of Using Wind Power. Energies 2022, 15, 9482. [Google Scholar] [CrossRef]
- Jang, D.; Kim, K.; Kim, K.H.; Kang, S. Techno-economic analysis and Monte Carlo simulation for green hydrogen production using offshore wind power plant. Energy Convers. Manag. 2022, 263, 115695. [Google Scholar] [CrossRef]
- Yang, B.; Li, Y.; Li, J.; Shu, H.; Zhao, X.; Ren, Y.; Li, Q. Comprehensive summary of solid oxide fuel cell control: A state-of-the-art review. Prot. Control Mod. Power Syst. 2022, 7, 36. [Google Scholar] [CrossRef]
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Energy 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Qin, X.; Cao, J.; Geng, G.; Li, Y.; Zheng, Y.; Zhang, W.; Yu, B. Solid oxide fuel cell system for automobiles. Int. J. Green Energy 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, W.; Wang, F.; Xie, C.; Zhou, W.; Xie, H. Optimization and Control for Solid Oxide Fuel Cell System Hybrid DC Microgrids From the Perspective of High Efficiency, Thermal Safety, and Transient Response. Front. Energy Res. 2023, 16648714, 953082. [Google Scholar] [CrossRef]
- Padulles, J.; Ault, G.W.; McDonald, J.R. An integrated SOFC plant dynamic model for power systems simulation. J. Power Sources 2000, 86, 495–500. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Parametric study of solid oxide fuel cell performance. Energy Convers. Manag. 2007, 48, 1525–1535. [Google Scholar]
- Kumar PG, A.; Jeyanthy, P.A.; Devaraj, D. Hybrid multi-objective method based on ant colony optimization and firefly algorithm for renewable energy sources. Sustain. Comput. Infor. 2022, 36, 100810. [Google Scholar] [CrossRef]
- Flori, A.; Oulhadj, H.; Siarry, P. QUAntum Particle Swarm Optimization: An auto-adaptive PSO for local and global optimization. Comput. Optim. Appl. 2022, 82, 525–559. [Google Scholar] [CrossRef]
- Behera, M.; Sarangi, A.; Mishra, D.; Mallick, P.K.; Shafi, J.; Srinivasu, P.N.; Ljaz, M.F. Automatic Data Clustering by Hybrid Enhanced Firefly and Particle Swarm Optimization Algorithms. Mathematics 2022, 10, 3532. [Google Scholar] [CrossRef]
- Qin, Y.; Sun, L.; Hua, Q.; Liu, P. A fuzzy adaptive PID controller design for fuel cell power plant. Sustainability 2018, 10, 2438. [Google Scholar] [CrossRef] [Green Version]

| Symbol | Parameter |
|---|---|
| Valve molar constant for hydrogen | |
| Valve molar constant for steam | |
| Valve molar constant for oxygen | |
| Reaction constant | |
| Response time for steam flow | |
| Response time for oxygen flow | |
| Response time for hydrogen flow | |
| Fuel processor response time | |
| Initial temperature | |
| Constant temperature | |
| Thermal conductivity | |
| Thickness |
| Symbol | Value |
|---|---|
| 0.843 mol/(s atm) | |
| 0.281 mol/(s atm) | |
| 2.52 mol/(s atm) | |
| 0.993 × 10−3 mol/(s A) | |
| 78.3 s | |
| 2.91 s | |
| 26.1 s | |
| 5 s | |
| 1273 K | |
| 973 K | |
| 2 W/(m K) | |
| 10−3 m |
| Kp | Ki | Kd | BestCost | |
|---|---|---|---|---|
| IFA-PID | 7.500 | 0.500 | 1.8154 | 143.3511 |
| FA-PID | 7.500 | 0.500 | 1.7522 | 143.2294 |
| ω0 | ωc | b0 | BestCost | |
|---|---|---|---|---|
| IFA-ADRC | 7.500 | 7.500 | 2.5788 | 85.0153 |
| FA-ADRC | 7.4986 | 7.4906 | 2.5221 | 85.4307 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Liu, J.; Liu, J.; Ning, X.; Qin, Z.; He, L. Active Disturbance Rejection Optimization Control for SOFCs in Offshore Wind Power. Appl. Sci. 2023, 13, 3364. https://doi.org/10.3390/app13053364
Pan Z, Liu J, Liu J, Ning X, Qin Z, He L. Active Disturbance Rejection Optimization Control for SOFCs in Offshore Wind Power. Applied Sciences. 2023; 13(5):3364. https://doi.org/10.3390/app13053364
Chicago/Turabian StylePan, Zhixuan, Jia Liu, Jing Liu, Xiaoge Ning, Zheng Qin, and Lulu He. 2023. "Active Disturbance Rejection Optimization Control for SOFCs in Offshore Wind Power" Applied Sciences 13, no. 5: 3364. https://doi.org/10.3390/app13053364





