Reinforcement Learning-Based Path Following Control with Dynamics Randomization for Parametric Uncertainties in Autonomous Driving
Abstract
1. Introduction
1.1. Contribution of This Paper
1.2. Paper Overview
1.3. Notation
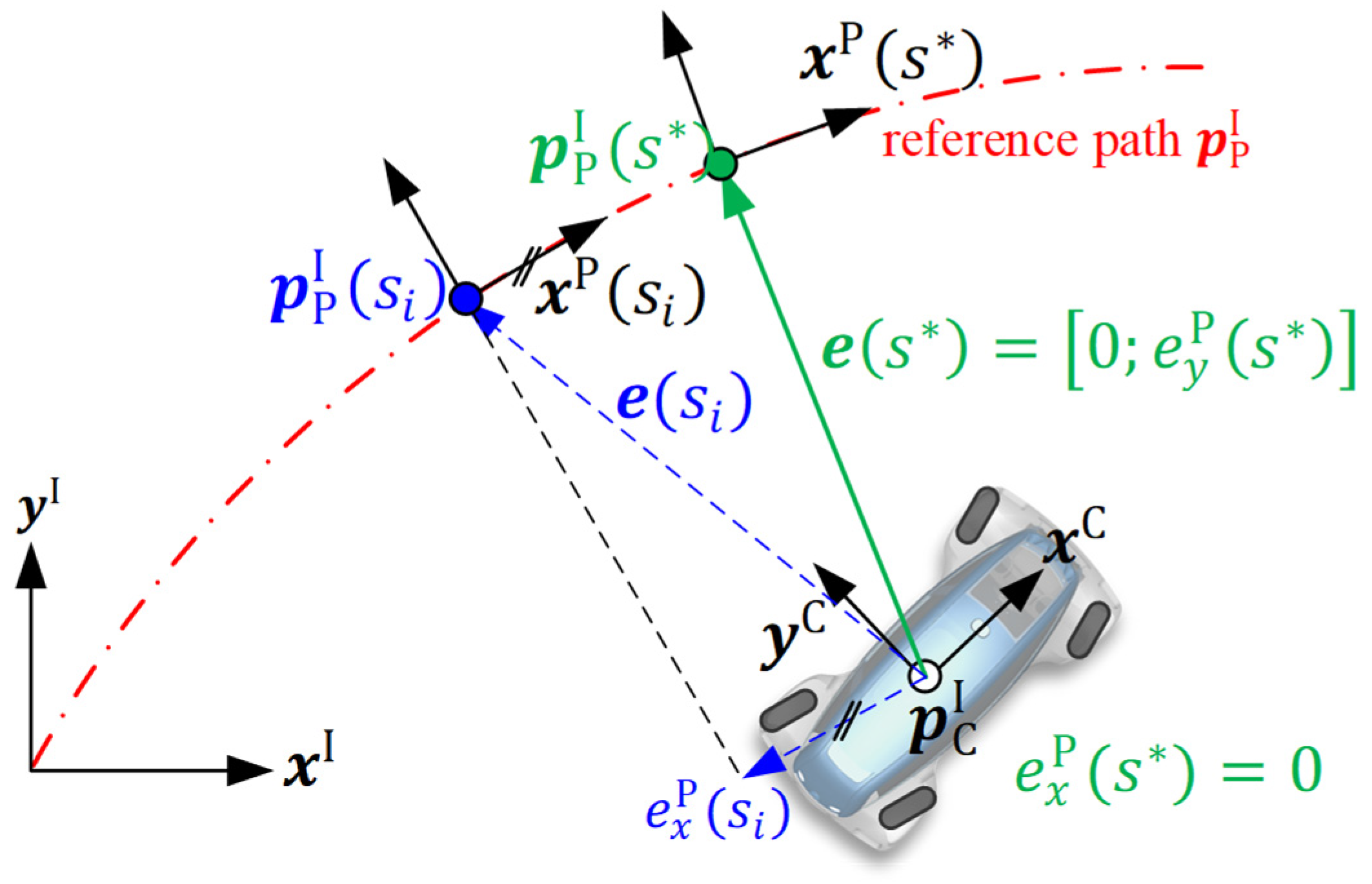
2. Problem Statement
3. Learning-Based Path following Control with Parametric Uncertainties
3.1. Oberservation Space of the Path following Control Environment
3.2. Action Space of the Agents
3.3. Design of the Reward Function
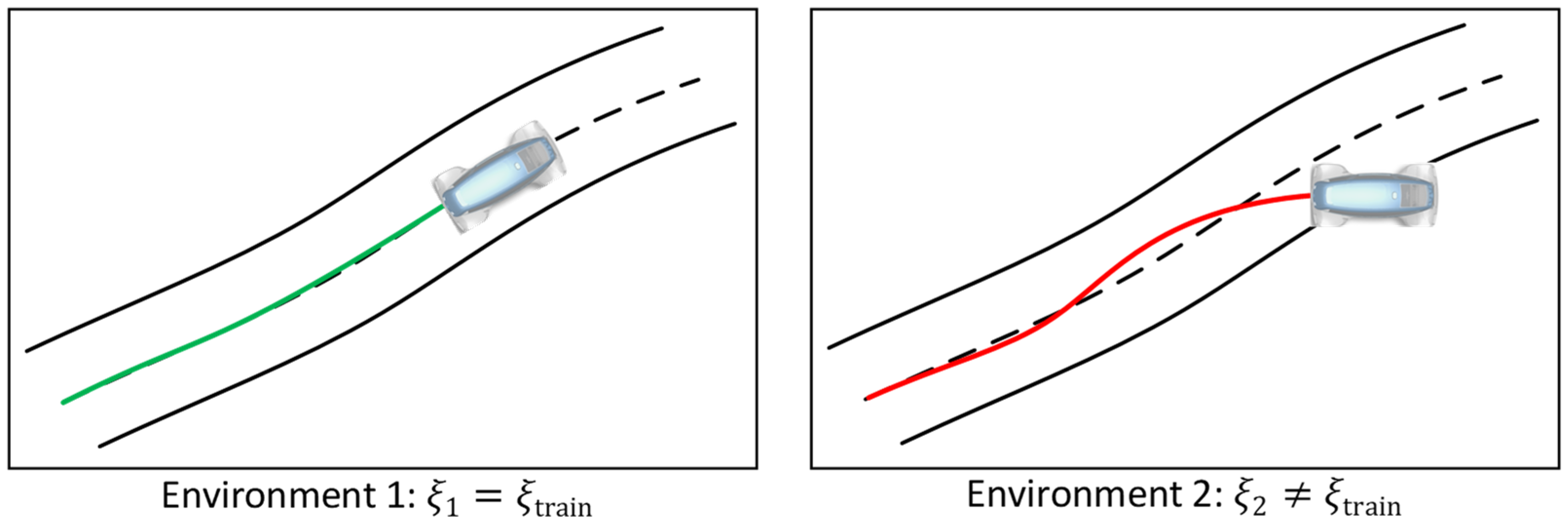
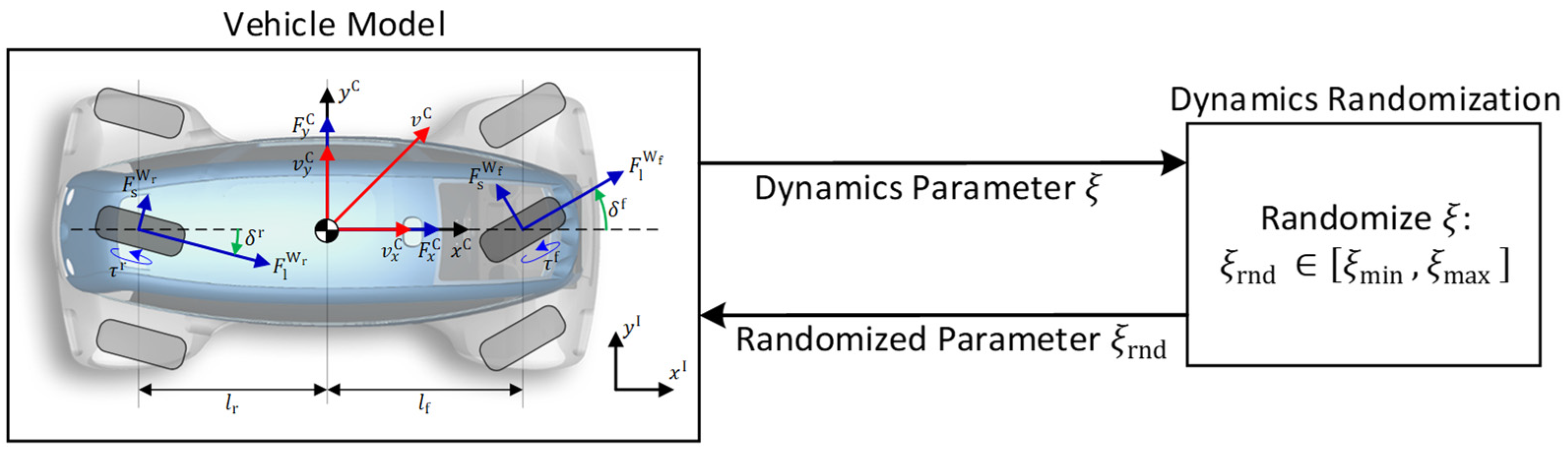
3.4. Learning with Dynamics Randomization
3.4.1. Mass Randomization
3.4.2. Inertia Randomization
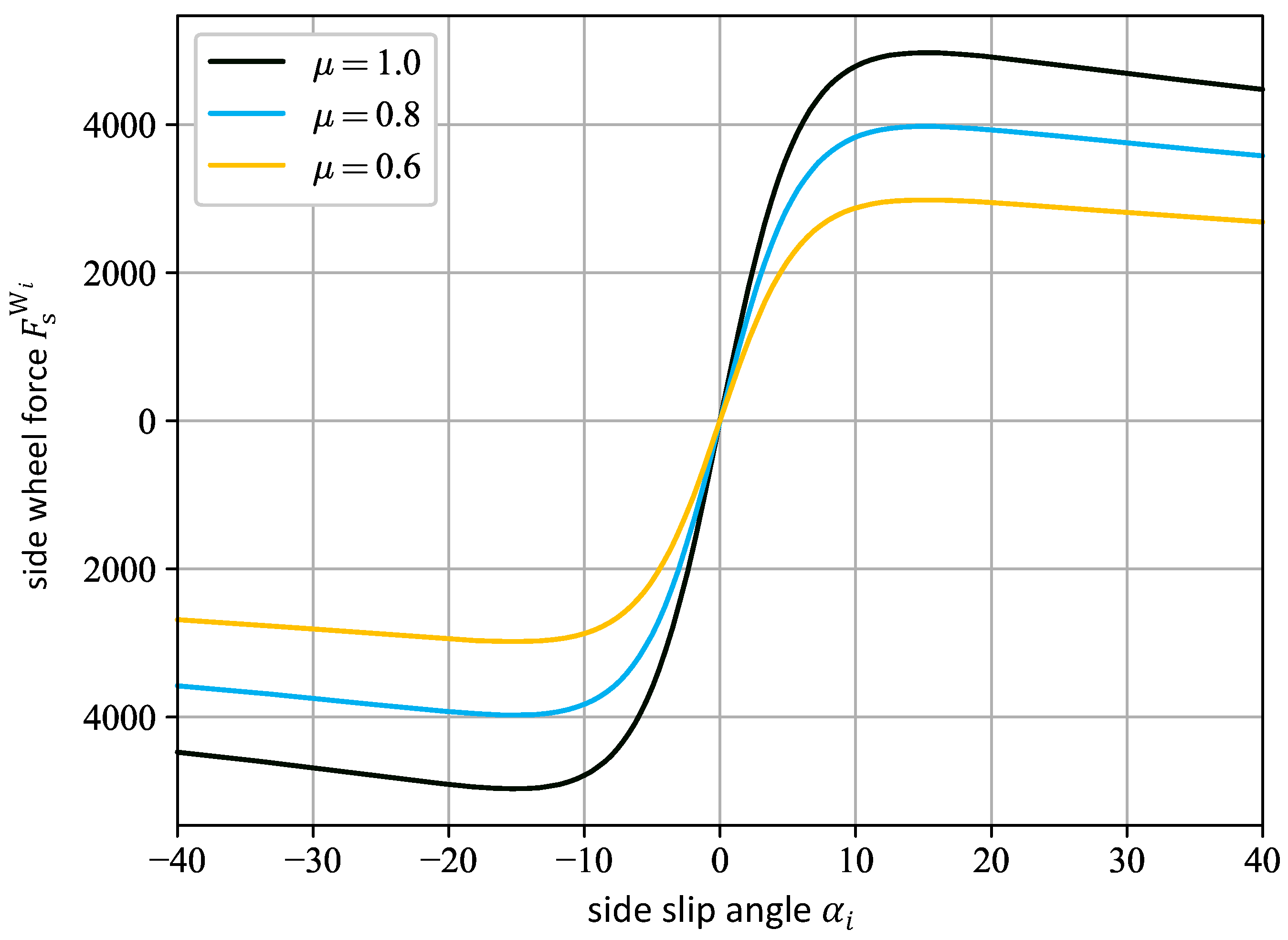
3.4.3. Friction Randomization
4. Training Setup
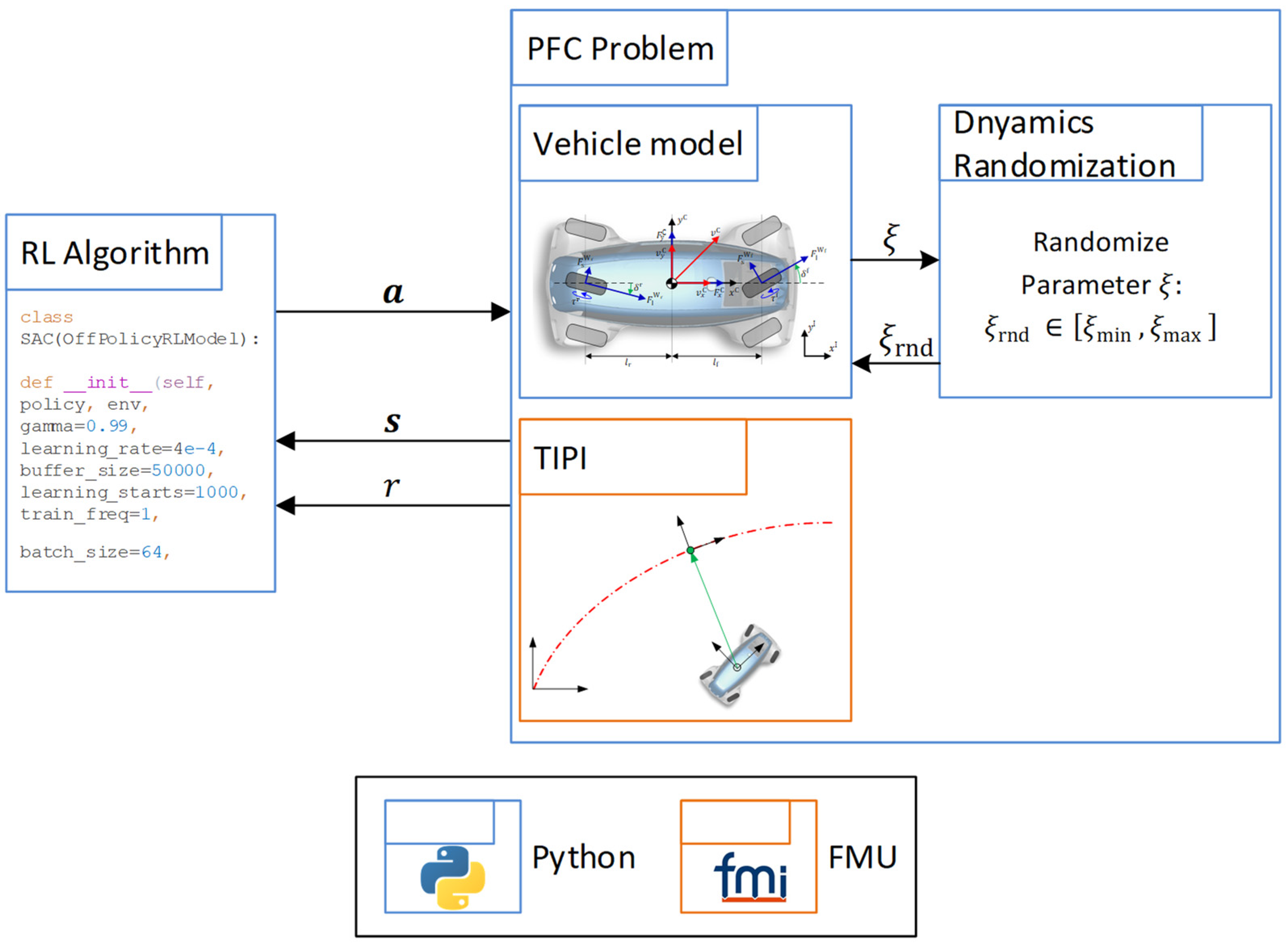
4.1. Simulation Framework
4.2. Training Procedure
5. Tests and Performance Comparison
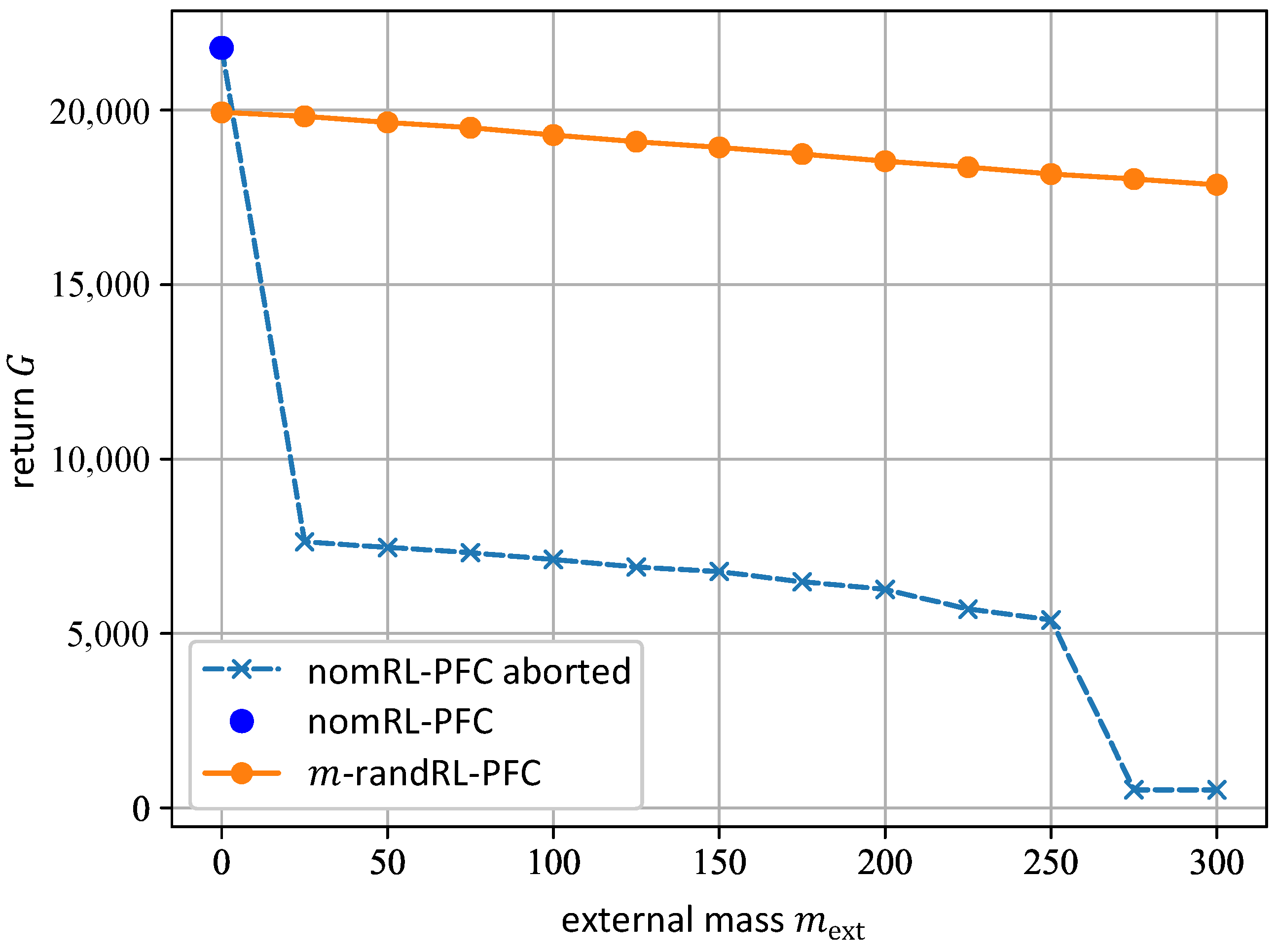
5.1. Tests and Comparison of the nomRL-PFC and the -randRL-PFC
5.2. Tests and Comparison of the nomRL-PFC and the 𝐽-randRL-PFC
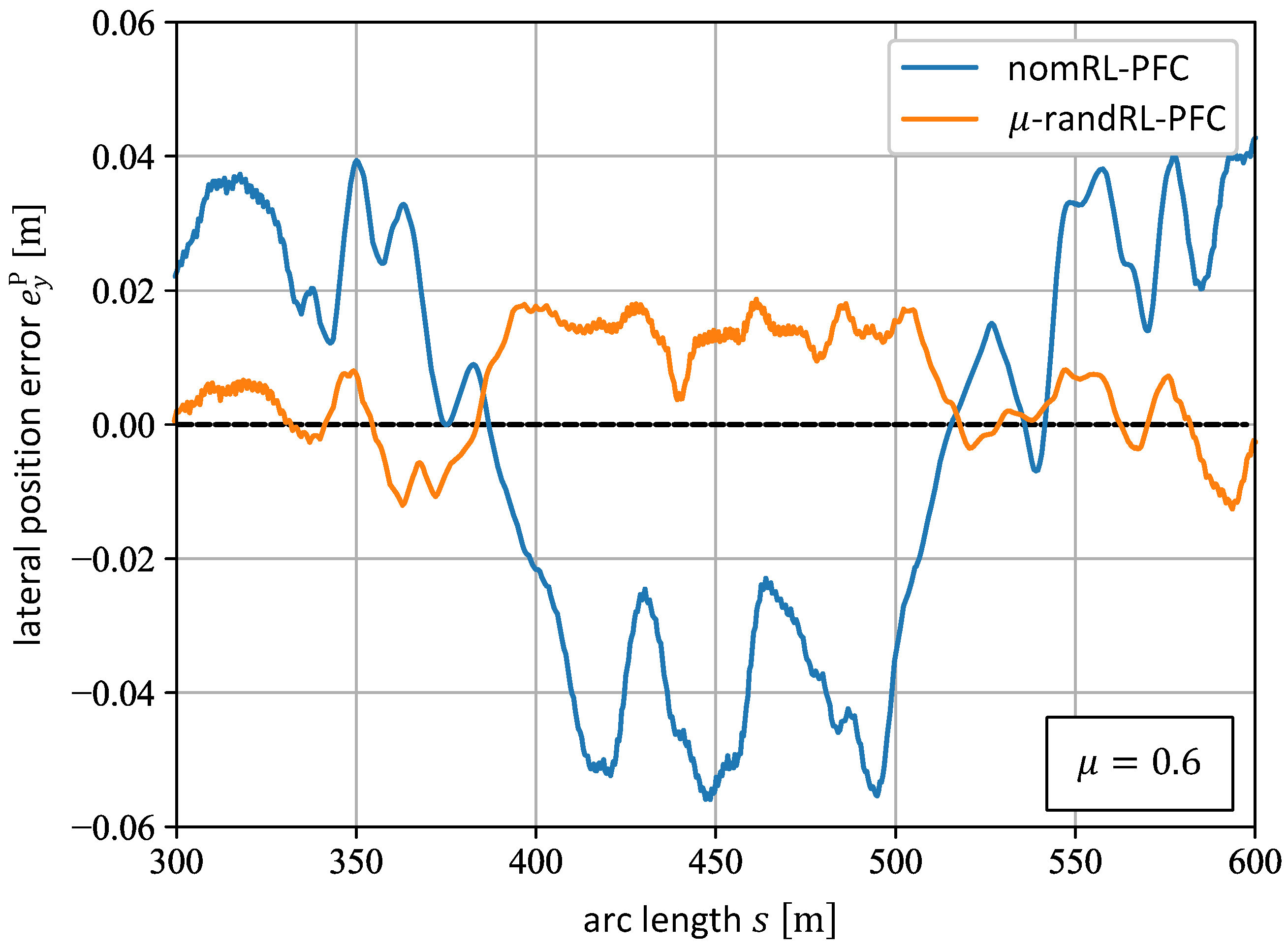
5.3. Tests and Comparison of the nomRL-PFC and the -randRL-PFC
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
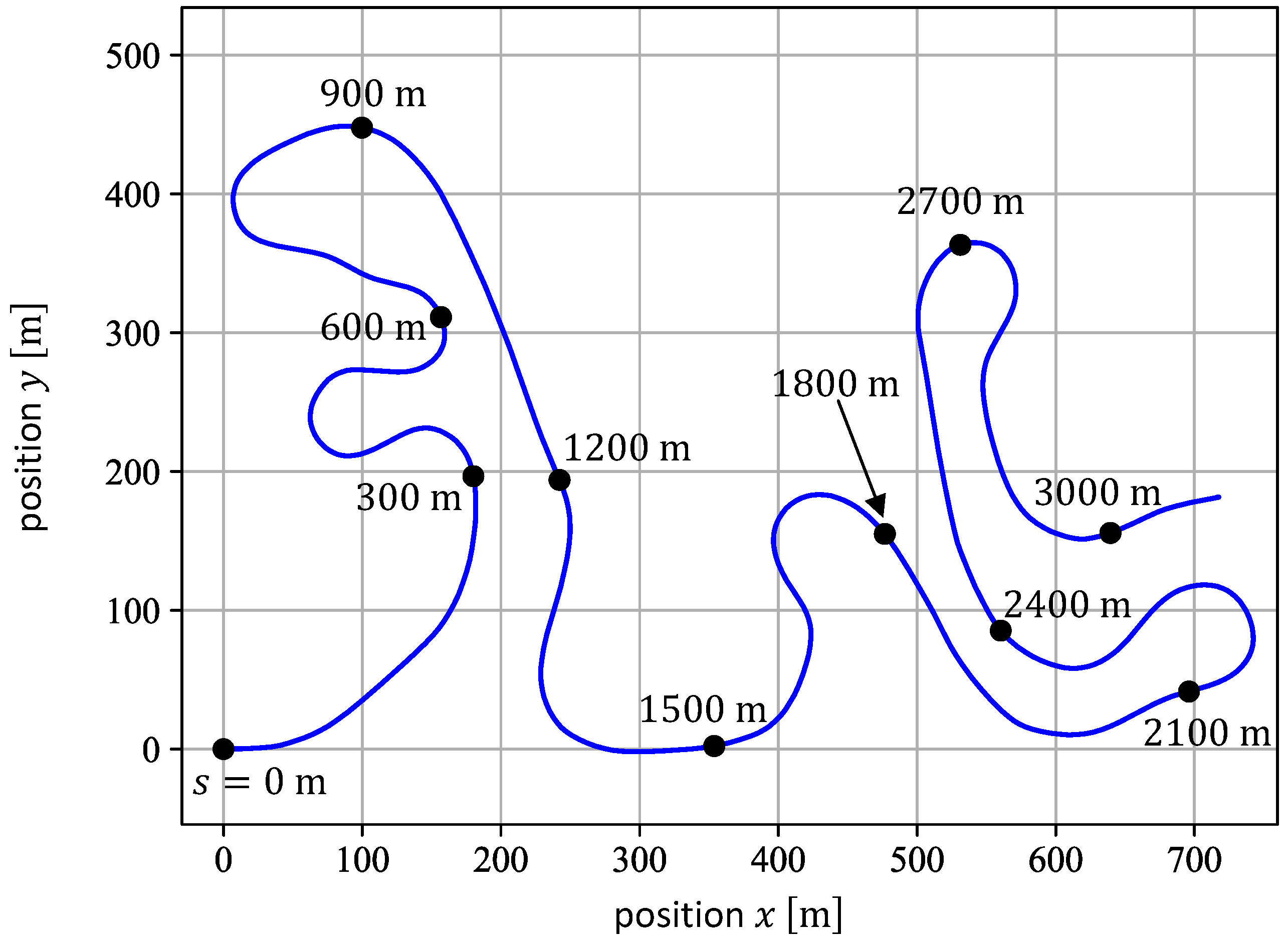
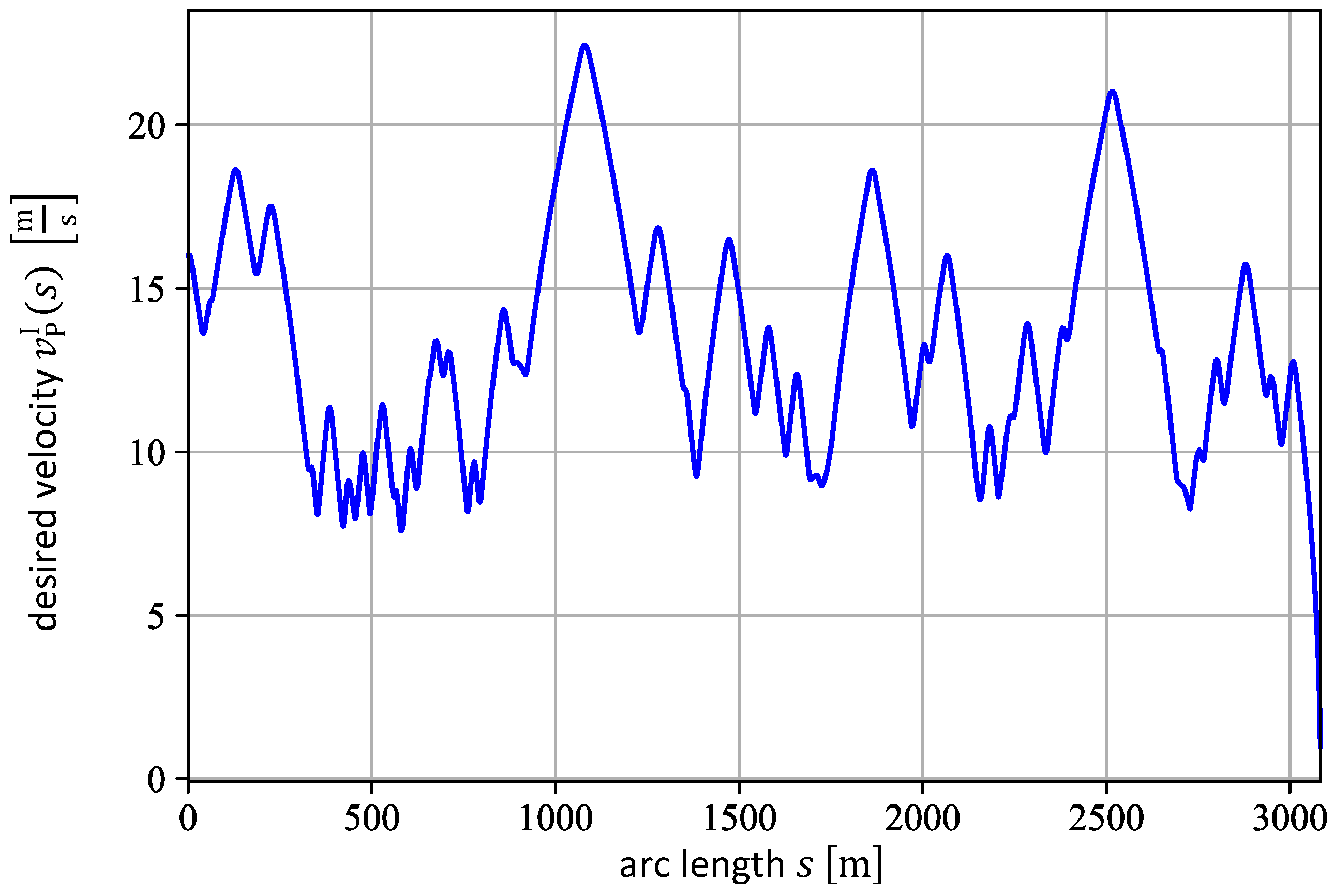
Appendix A. Path Representation

Appendix B. Vehicle Dynamics of the ROboMObil

Appendix C. Deep Reinforcement Learning Fundamentals

Appendix D. Hyperparameters of the Training Algorithm
| Hyperparameter | Value |
|---|---|
| Discount rate | |
| Learning rate | |
| Entropy coefficient | auto |
| Buffer size | |
| Batch size | |
| Policy network | |
| Policy network activation function | ReLU |
References
- Arnold, E.; Al-Jarrah, O.Y.; Dianati, M.; Fallah, S.; Oxtoby, D.; Mouzakitis, A. A Survey on 3D Object Detection Methods for Autonomous Driving Applications. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3782–3795. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A Survey of Autonomous Driving: Common Practices and Emerging Technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Krasowski, H.; Wang, X.; Althoff, M. Safe Reinforcement Learning for Autonomous Lane Changing Using Set-Based Prediction. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020. [Google Scholar] [CrossRef]
- Wang, X.; Krasowski, H.; Althoff, M. CommonRoad-RL: A Configurable Reinforcement Learning Environment for Motion Planning of Autonomous Vehicles. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021. [Google Scholar] [CrossRef]
- Di, X.; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103008. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Al Sallab, A.A.; Yogamani, S.; Perez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Pérez-Gil, Ó.; Barea, R.; López-Guillén, E.; Bergasa, L.M.; Gómez-Huélamo, C.; Gutiérrez, R.; Díaz-Díaz, A. Deep reinforcement learning based control for Autonomous Vehicles in CARLA. Multimed. Tools Appl. 2022, 81, 3553–3576. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, T.; Coumans, E.; Iscen, A.; Bai, Y.; Hafner, D.; Bohez, S.; Vanhoucke, V. Sim-to-Real: Learning Agile Locomotion for Quadruped Robots. In Proceedings of the Robotics: Science and Systems XIV Conference, Pennsylvania, PA, USA, 26–30 June 2018; p. 10. [Google Scholar] [CrossRef]
- Bin Peng, X.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-Real Transfer of Robotic Control with Dynamics Randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Antonova, R.; Cruciani, S.; Smith, C.; Kragic, D. Reinforcement Learning for Pivoting Task. arXiv 2017, arXiv:1703.00472. [Google Scholar] [CrossRef]
- Osinski, B.; Jakubowski, A.; Ziecina, P.; Milos, P.; Galias, C.; Homoceanu, S.; Michalewski, H. Simulation-Based Reinforcement Learning for Real-World Autonomous Driving. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar] [CrossRef]
- Brembeck, J. Model Based Energy Management and State Estimation for the Robotic Electric Vehicle ROboMObil. Dissertation Thesis, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Brembeck, J.; Ho, L.; Schaub, A.; Satzger, C.; Tobolar, J.; Bals, J.; Hirzinger, G. ROMO—The Robotic Electric Vehicle. In Proceedings of the 22nd IAVSD International Symposium on Dynamics of Vehicle on Roads and Tracks, Manchester, UK, 11–14 August 2011. [Google Scholar]
- Ultsch, J.; Brembeck, J.; De Castro, R. Learning-Based Path Following Control for an Over-Actuated Robotic Vehicle. In Autoreg 2019; VDI Verlag: Düsseldorf, Germany, 2019; pp. 25–46. [Google Scholar] [CrossRef]
- Winter, C.; Ritzer, P.; Brembeck, J. Experimental investigation of online path planning for electric vehicles. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016. [Google Scholar] [CrossRef]
- Brembeck, J. Nonlinear Constrained Moving Horizon Estimation Applied to Vehicle Position Estimation. Sensors 2019, 19, 2276. [Google Scholar] [CrossRef] [PubMed]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Brembeck, J.; Winter, C. Real-time capable path planning for energy management systems in future vehicle architectures. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. Available online: https://github.com/hill-a/stable-baselines (accessed on 15 December 2022).
- Virtanen, P.; Gommers, R.; Oliphant, T.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0 Contributors. SciPy 1.0 Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Ritzer, P.; Winter, C.; Brembeck, J. Advanced path following control of an overactuated robotic vehicle. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015. [Google Scholar] [CrossRef]
- Modelica Association. Modelica—A Unified Object-Oriented Language for Systems Modeling. Available online: https://modelica.org/documents/MLS.pdf (accessed on 13 January 2023).
- Modelica Association. Functional Mock-Up Interface. Available online: https://fmi-standard.org/ (accessed on 4 January 2023).
- Bünte, T.; Chrisofakis, E. A Driver Model for Virtual Drivetrain Endurance Testing. In Proceedings of the 8th International Modelica Conference, Dresden, Germany, 20–22 March 2011. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- Ziebart, B. Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy. Dissertation Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. [Google Scholar]

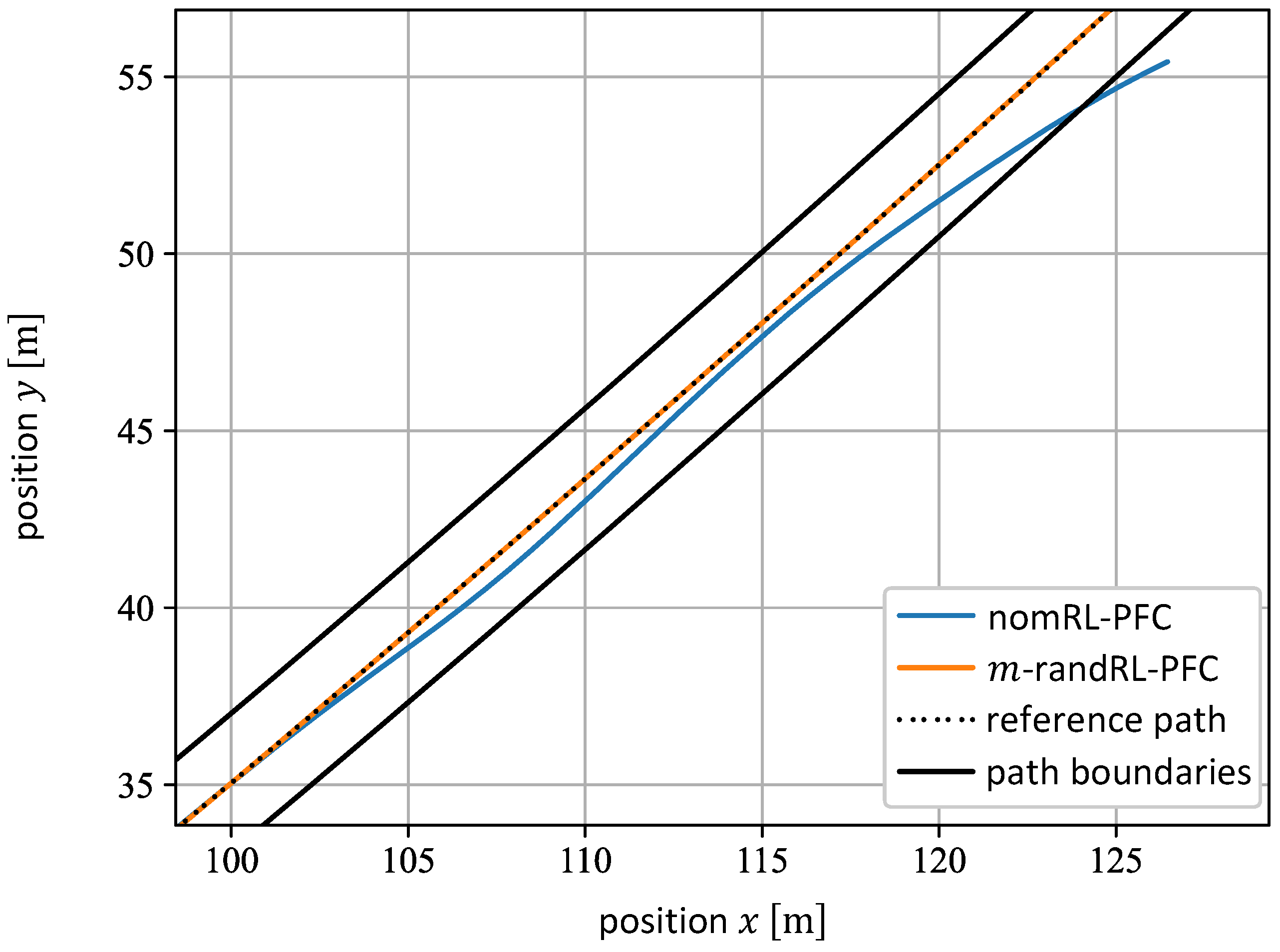
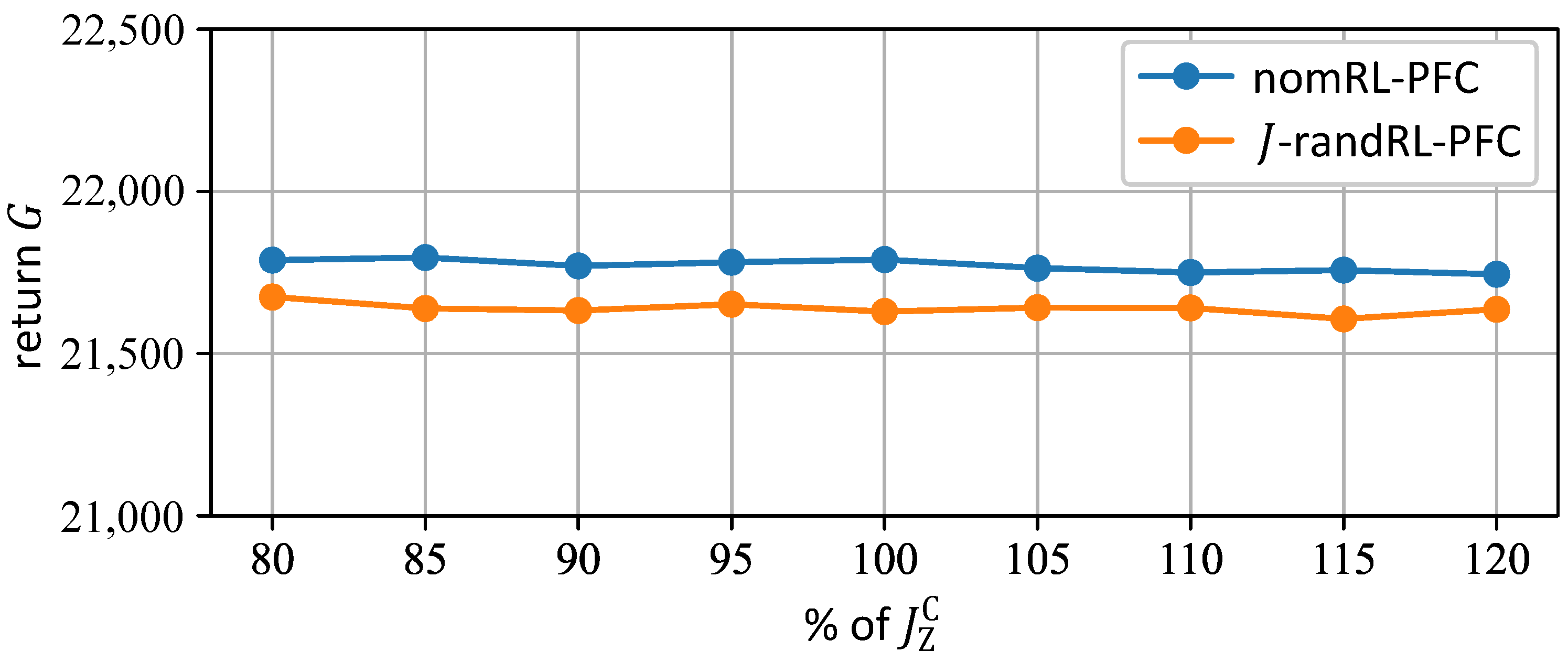
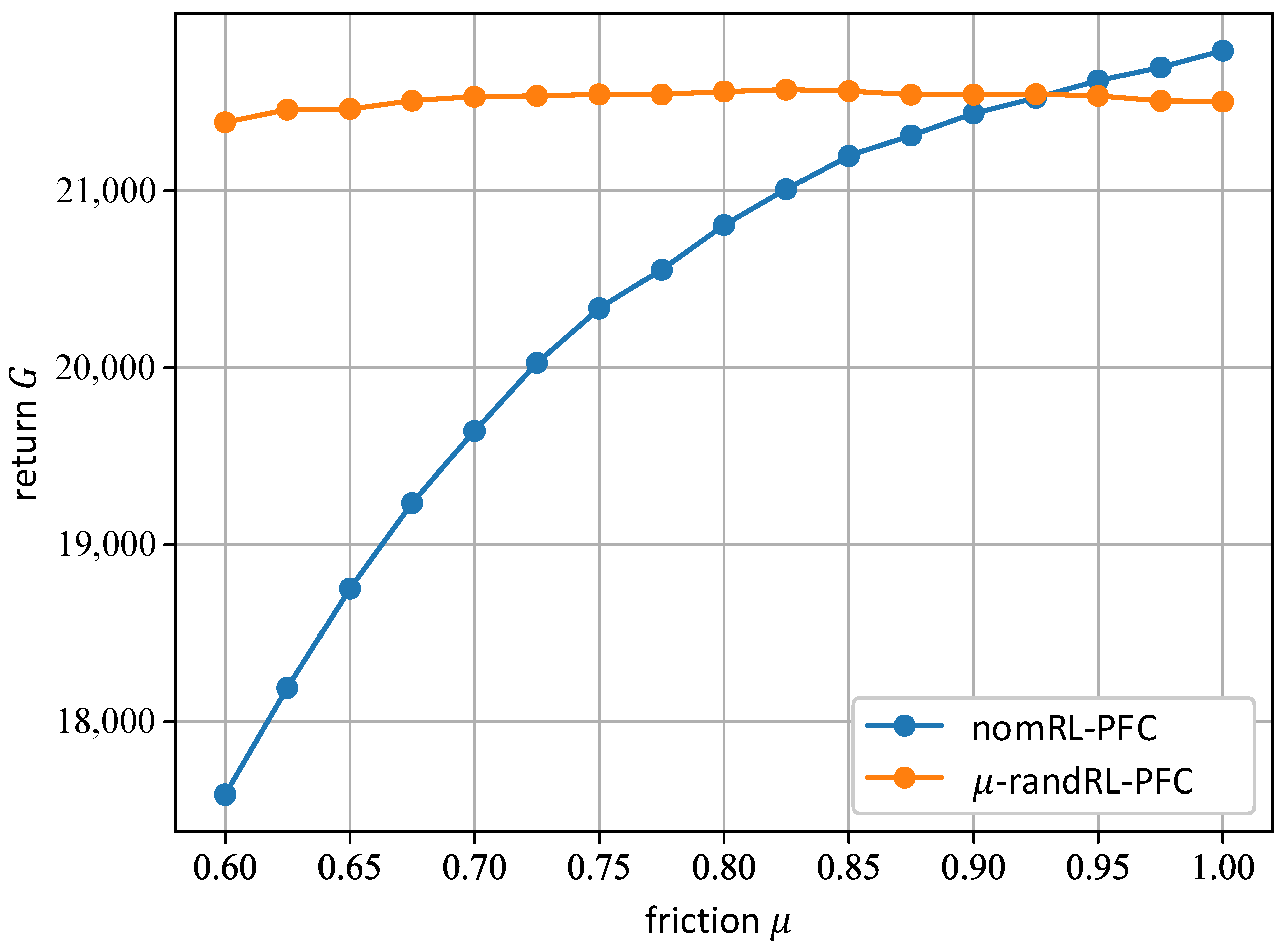
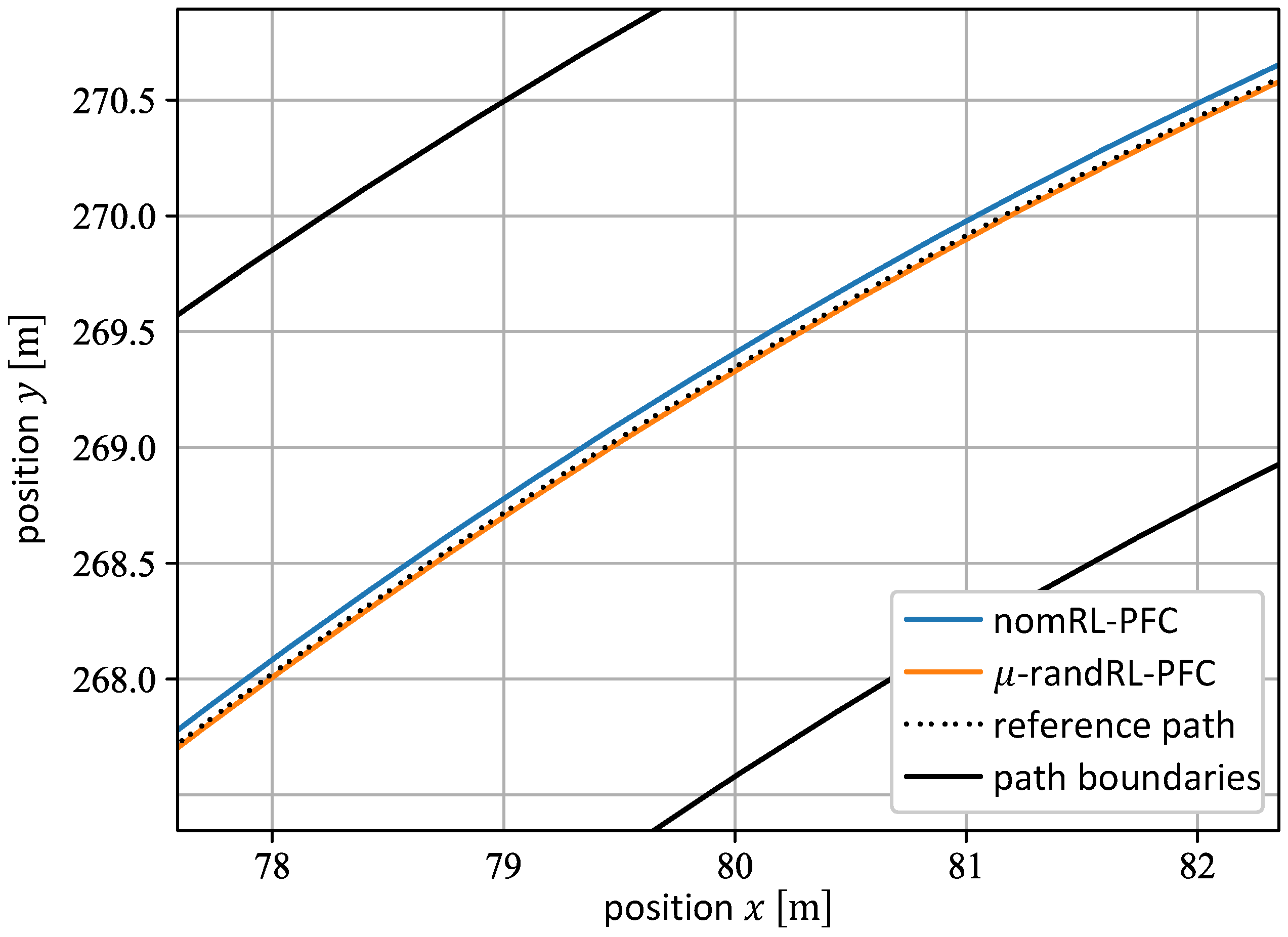

| External Mass | ||||
|---|---|---|---|---|
| Agent | nomRL-PFC | -randRL-PFC | nomRL-PFC | -randRL-PFC |
| (RMS) | 0.013 | 0.009 | - | 0.013 |
| (RMS) | 0.106 | 0.149 | - | 0.594 |
| (RMS) | 0.020 | 0.032 | - | 0.033 |
| Agent | nomRL-PFC | -randRL-PFC | ||||
|---|---|---|---|---|---|---|
| (RMS) | 0.013 | 0.013 | 0.013 | 0.010 | 0.010 | 0.010 |
| (RMS) | 0.106 | 0.106 | 0.106 | 0.144 | 0.144 | 0.144 |
| (RMS) | 0.020 | 0.020 | 0.020 | 0.013 | 0.014 | 0.014 |
| Friction Value | ||||
|---|---|---|---|---|
| Agent | nomRL-PFC | -randRL-PFC | nomRL-PFC | -randRL-PFC |
| (RMS) | 0.033 | 0.011 | 0.013 | 0.013 |
| (RMS) | 0.114 | 0.171 | 0.106 | 0.150 |
| (RMS) | 0.022 | 0.020 | 0.020 | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmic, K.; Ultsch, J.; Brembeck, J.; Winter, C. Reinforcement Learning-Based Path Following Control with Dynamics Randomization for Parametric Uncertainties in Autonomous Driving. Appl. Sci. 2023, 13, 3456. https://doi.org/10.3390/app13063456
Ahmic K, Ultsch J, Brembeck J, Winter C. Reinforcement Learning-Based Path Following Control with Dynamics Randomization for Parametric Uncertainties in Autonomous Driving. Applied Sciences. 2023; 13(6):3456. https://doi.org/10.3390/app13063456
Chicago/Turabian StyleAhmic, Kenan, Johannes Ultsch, Jonathan Brembeck, and Christoph Winter. 2023. "Reinforcement Learning-Based Path Following Control with Dynamics Randomization for Parametric Uncertainties in Autonomous Driving" Applied Sciences 13, no. 6: 3456. https://doi.org/10.3390/app13063456
APA StyleAhmic, K., Ultsch, J., Brembeck, J., & Winter, C. (2023). Reinforcement Learning-Based Path Following Control with Dynamics Randomization for Parametric Uncertainties in Autonomous Driving. Applied Sciences, 13(6), 3456. https://doi.org/10.3390/app13063456







