Energy Hub Optimal Scheduling and Management in the Day-Ahead Market Considering Renewable Energy Sources, CHP, Electric Vehicles, and Storage Systems Using Improved Fick’s Law Algorithm
Abstract
1. Introduction
- Coordinated energy scheduling and management strategy in the energy hub considering the economic optimal performance based on profit maximization.
- Investigation of the load levels and forced output rate of renewable energy resources and CHP equipment on the energy hub economic performance.
- Use of a new meta-heuristic algorithm named the improved Fick’s law algorithm (IFLA) algorithm based on Rosenbrock’s direct rotational method to solve EH scheduling.
- Evaluating the superiority of the proposed EH scheduling framework compared with conventional FLA, PSO, and MRFO.
2. Problem Formulation
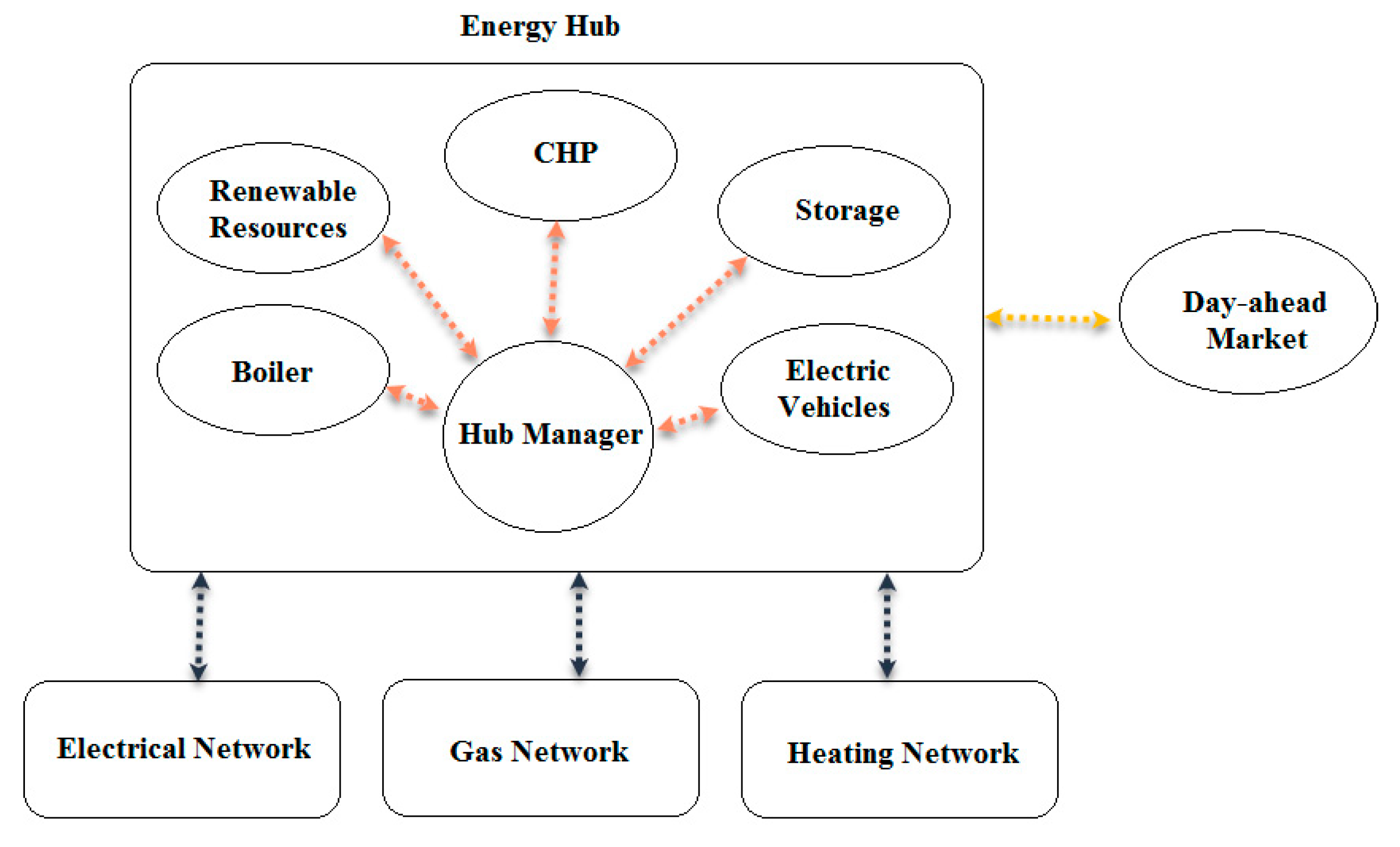
2.1. EH System
2.2. Objective Function
2.3. Constraints of the Problem
2.3.1. Power Flow Constraint
- The active and reactive power balance in different buses
- Active and reactive power flow of lines
- Voltage angle in the base bus
- Balance of gas power and flow
- The heating power balance in buses
- Heat power flow
2.3.2. Network Operation Constraints
- Voltage range of buses
- Allowed capacity of lines and stations
- Bus pressure limit
- The capacity of gas pipes and station
- The thermal limit of buses
- The capacity of the station and heating pipeline
2.3.3. EH Constraints
3. Proposed Optimization Method
3.1. Overview of the FLA
3.1.1. Inspiration
3.1.2. Formulation of FLA
- Step 1: Initialization. In the FLA, optimization starts based on several preferred solutions, shown by X, according to Equation (41). The generation of solutions is random and in each iteration, the best solution is selected as the best current almost optimal solution [29].where N represents the number of solutions (population size), D represents the dimension of the problem (number of variables), and j refers to the jth decision variable.
- Step 2: Clustering. In this step, the population of the algorithm is divided into two equal groups, N1 and N2.
- Step 3: Transfer function (TF). The efficiency of any algorithm is highly dependent on the transition from discovery to exploitation, and vice versa. In the FLA, a nonlinear transfer function (TF) is provided for this problem. TF function is defined as Equation (42) [29].
- Step 4: Update the molecule position: In this step, three phases based on transfer operators, namely DO, EO, and SSO, are presented. The transition process between the three phases is based on the following equation [31]:
3.1.3. DO Operator (Discovery Phase)
3.1.4. EO Operator (Transition Stage from Exploration to Exploitation)
3.1.5. Steady State Operator (SSO) (Exploitation Phase)
3.1.6. Balancing the Exploration and Exploitation Phases
3.1.7. FLA Pseudo Code
| Algorithm 1. Steps of implementation of the FLA |
| 1: Initialization; |
| 2: Insert parameters of D, C1, C2, C3, C4, C5; |
| 3: Initiate the population Xi (i = 1, 2, … N) as random; |
| 4: Clustering: Dividing the population into two groups N1, and N2; |
| 5: for s = 1:2 do |
| 6: Calculate the fitness of each group molecule Ns; |
| 7: Determining the best molecule is the best fitness value; |
| 8: end for |
| 9: while FES ≤ MAXFES do |
| 10: if If TF is greater than 0.9 then: (SSO) |
| 11: for op = 1: nop do |
| 12: Compute the rate of diffusion via Equation (65) |
| 13: Compute the step of motion factor via Equation (66) |
| 14: Update the position of the population via Equation (63) |
| 15: end for |
| 16: else if TF is fewer than rand then (EO) |
| 17: for op = 1: nop do |
| 18: Compute rate of diffusion via Equation (56) |
| 19: Compute quantity of group relative via Equation (55) |
| 20: Update position of the population via Equation (54) |
| 21: end for |
| 22: else (EO) |
| 23: Compute flow direction via Equation (48) |
| 24: calculate molecules number tending to move to region via Equation (46) |
| 25: Update position of the population via Equation (47) |
| 26: Update remained molecules in the region i via Equation (52) |
| 27: Update the region j molecules via Equation (53) |
| 28: Update FES ← FES + NP |
| 29: end while |
| 30: Return best solution. |
3.2. Overview of the IFLA
4. Simulation Results and Discussion
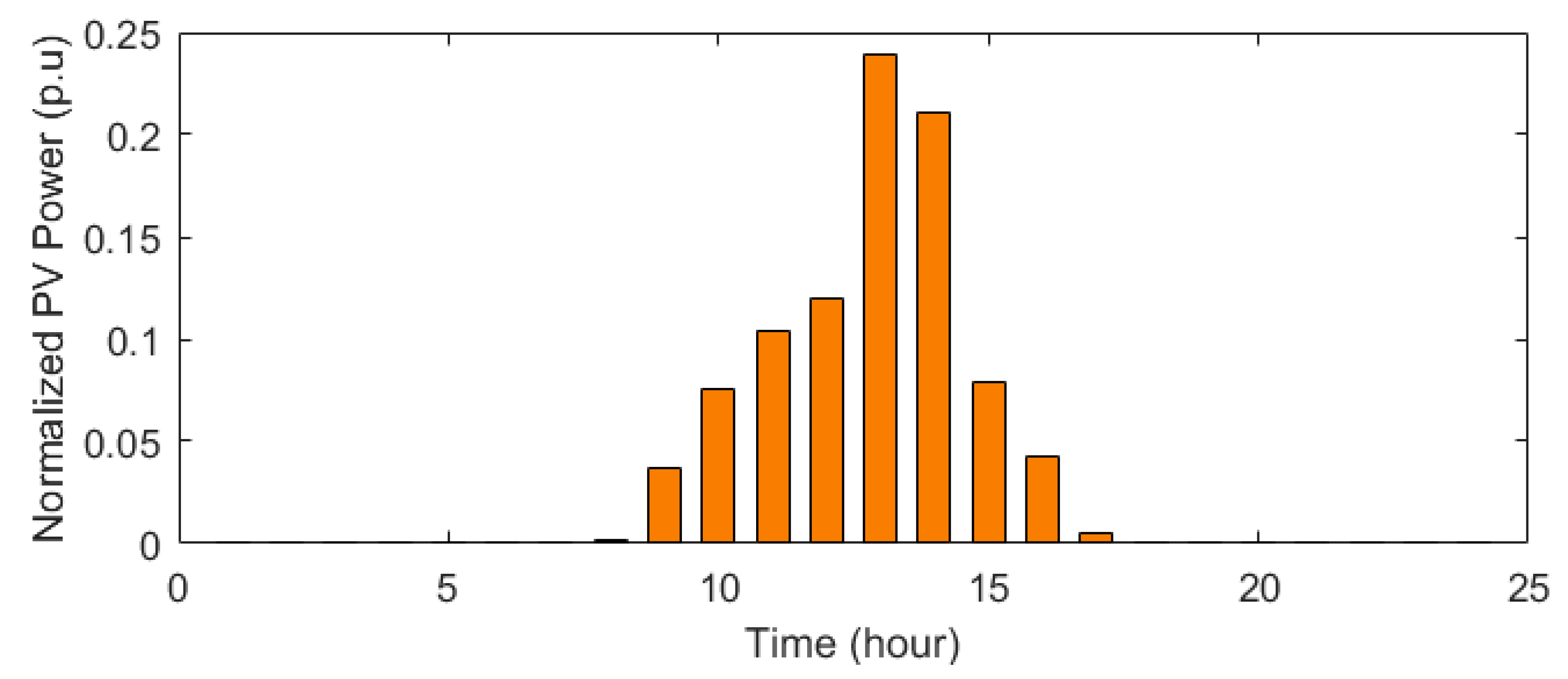
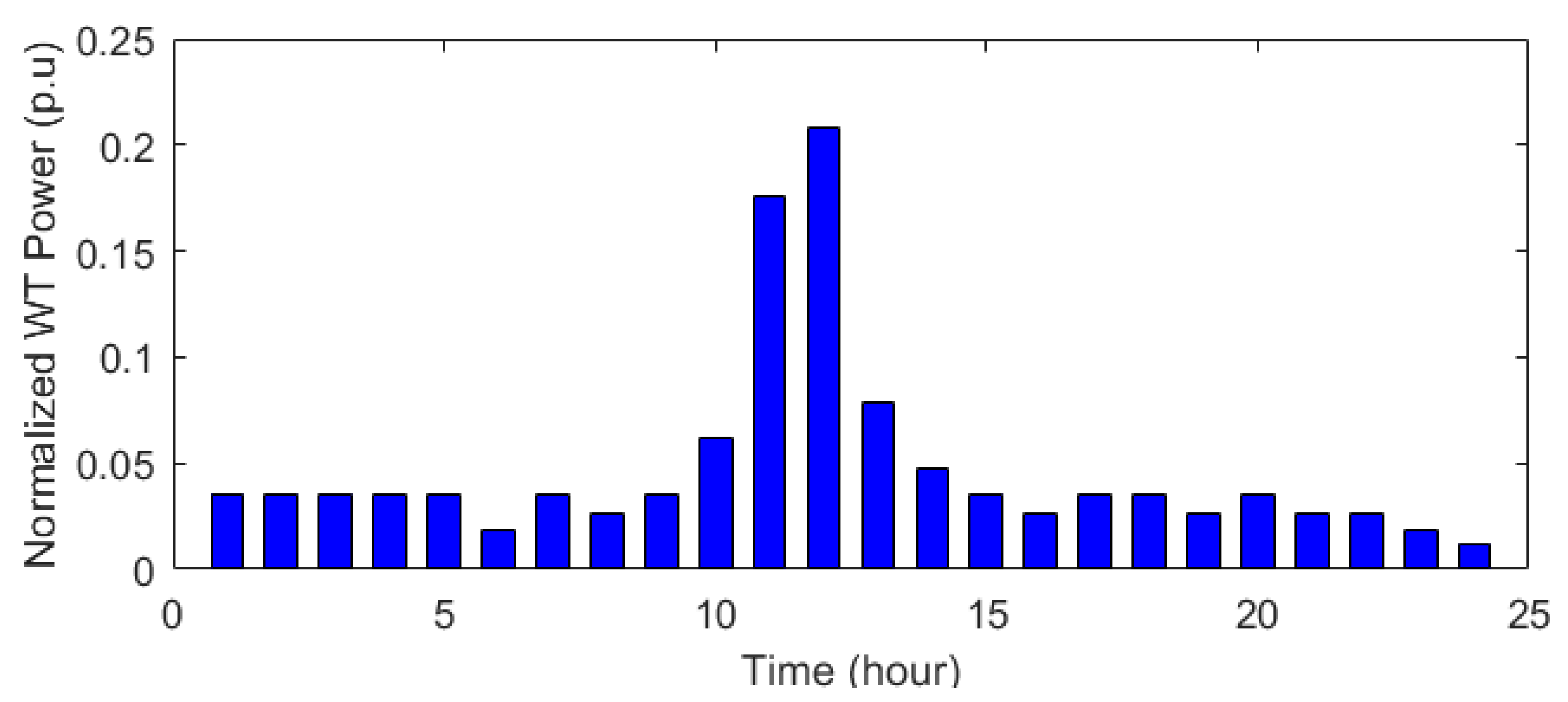
4.1. System under Study and Data
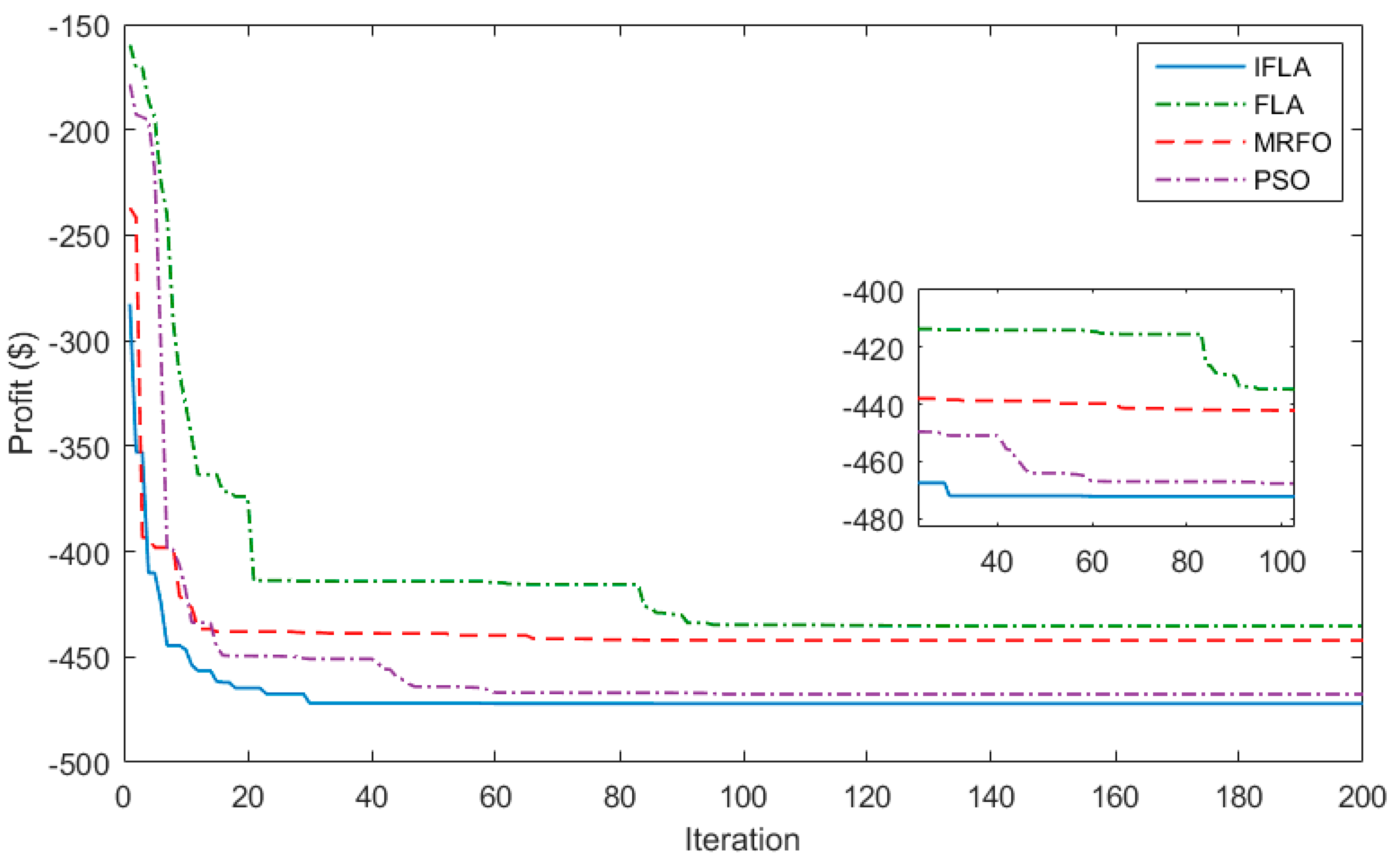
4.2. Superior Optimization Method
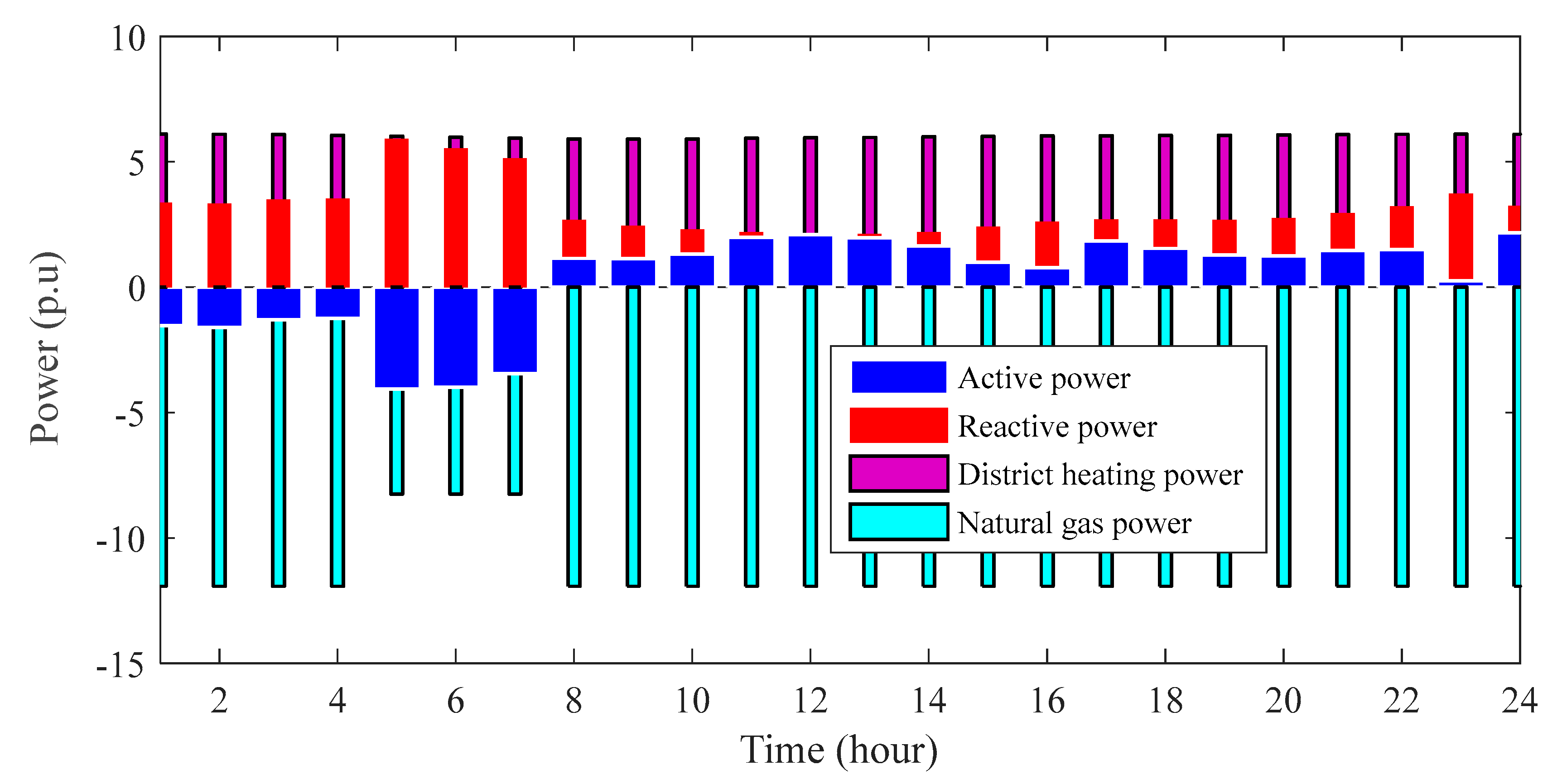
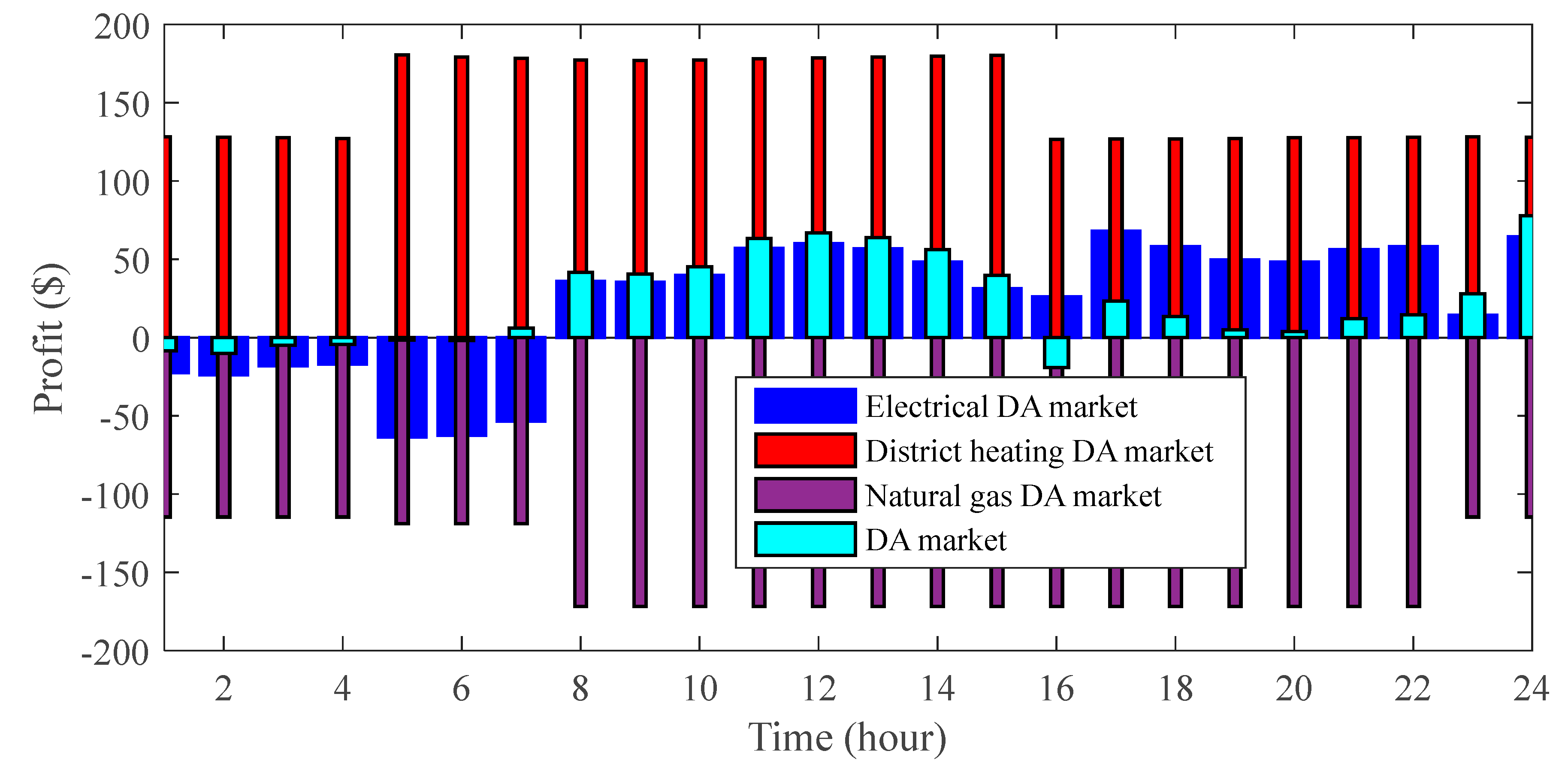
4.2.1. System Power and Profit
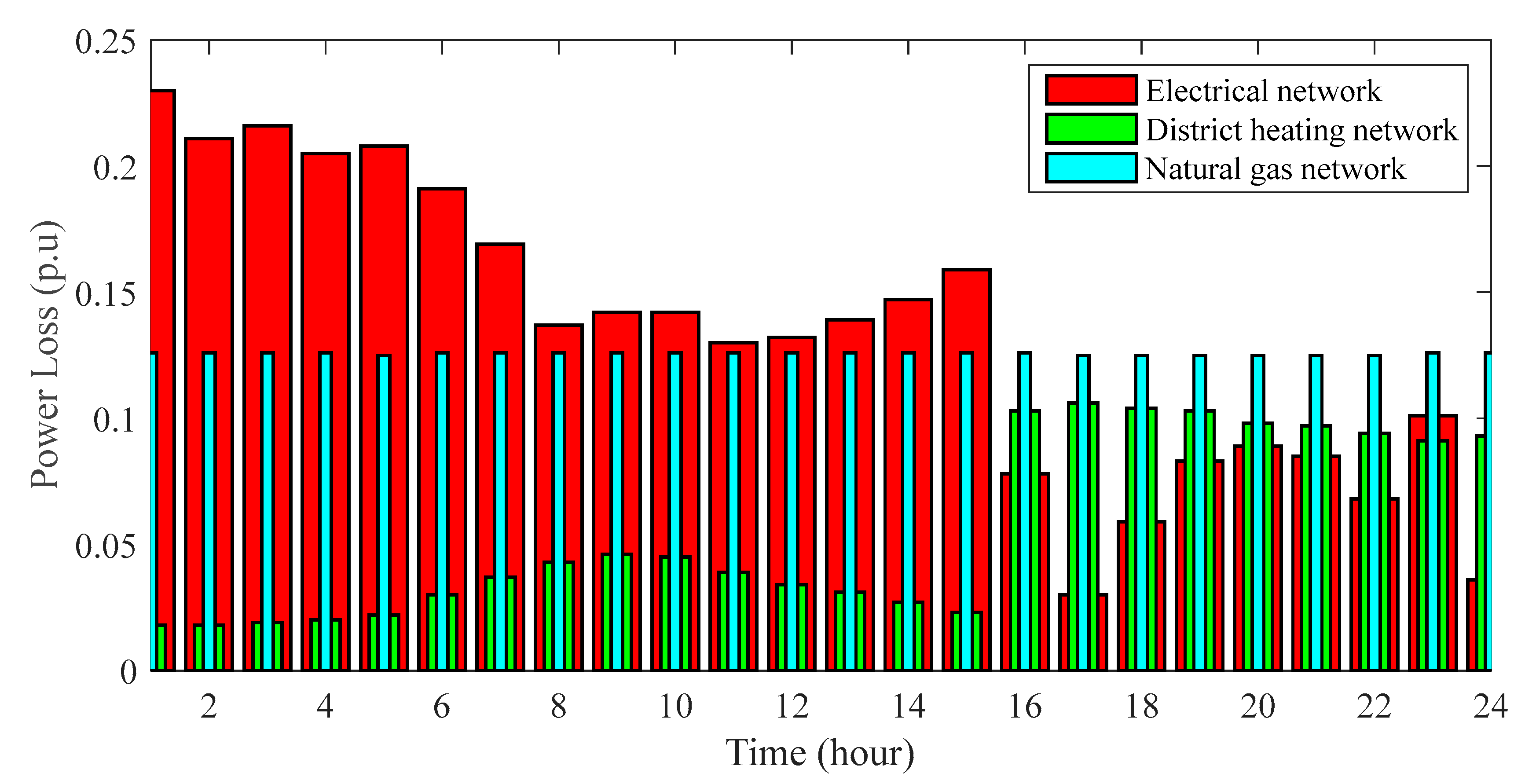
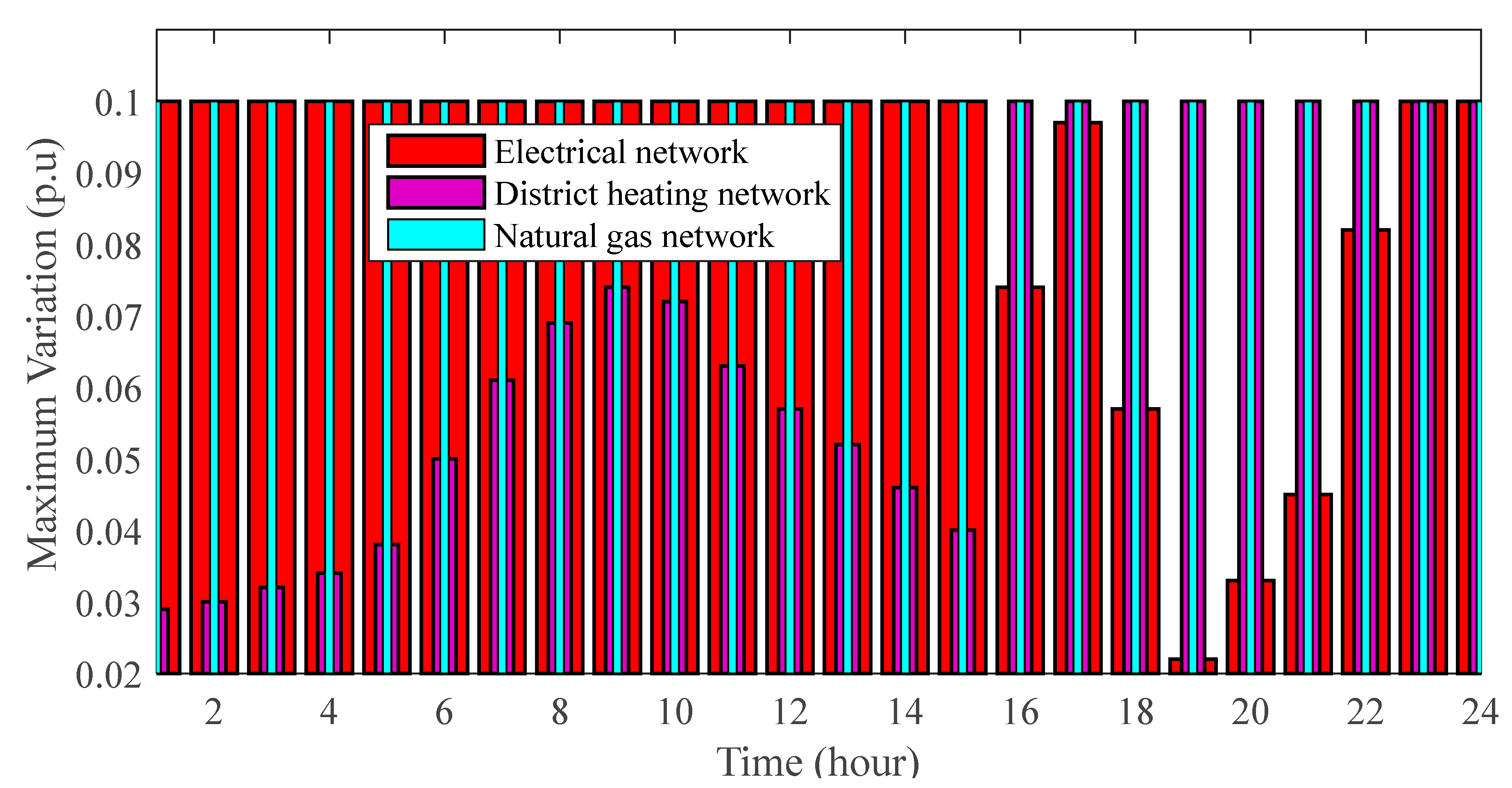
4.2.2. Network Loss and Deviations
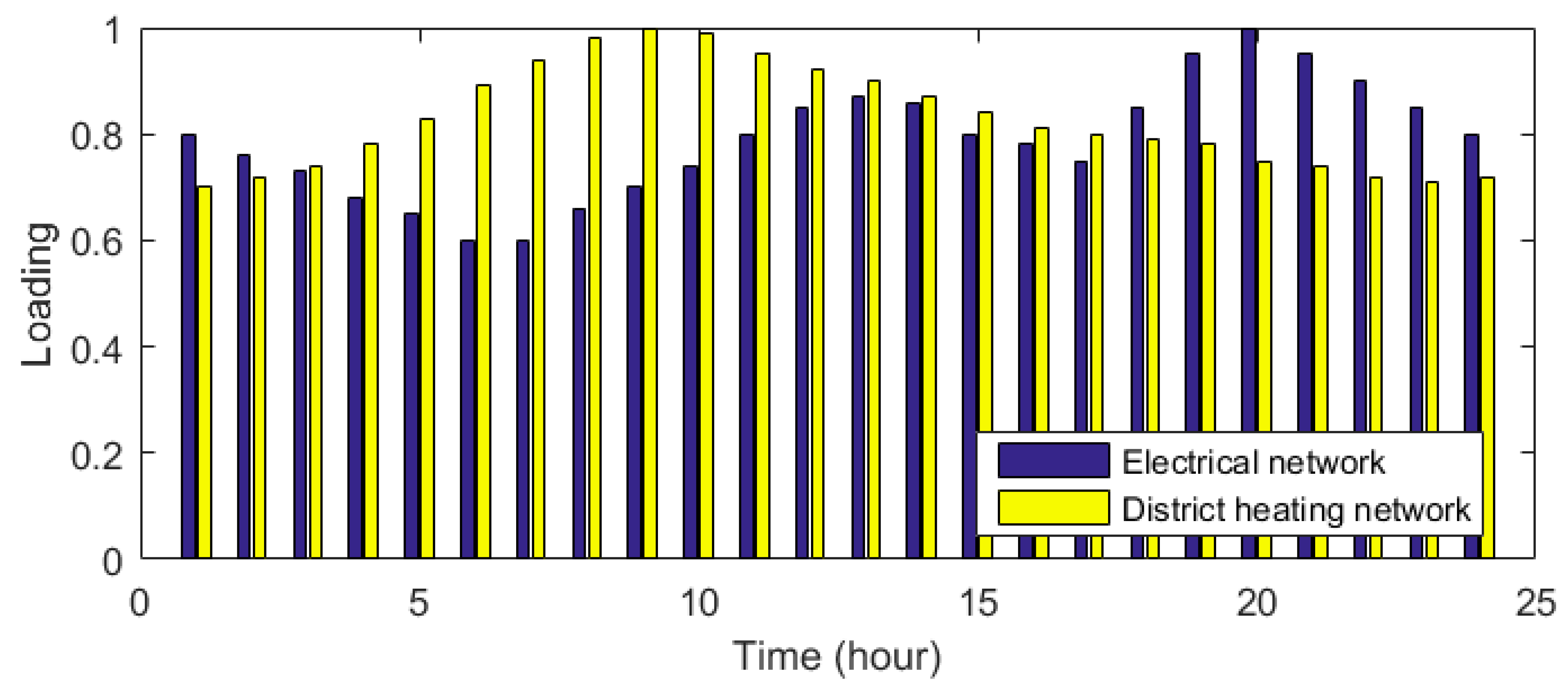
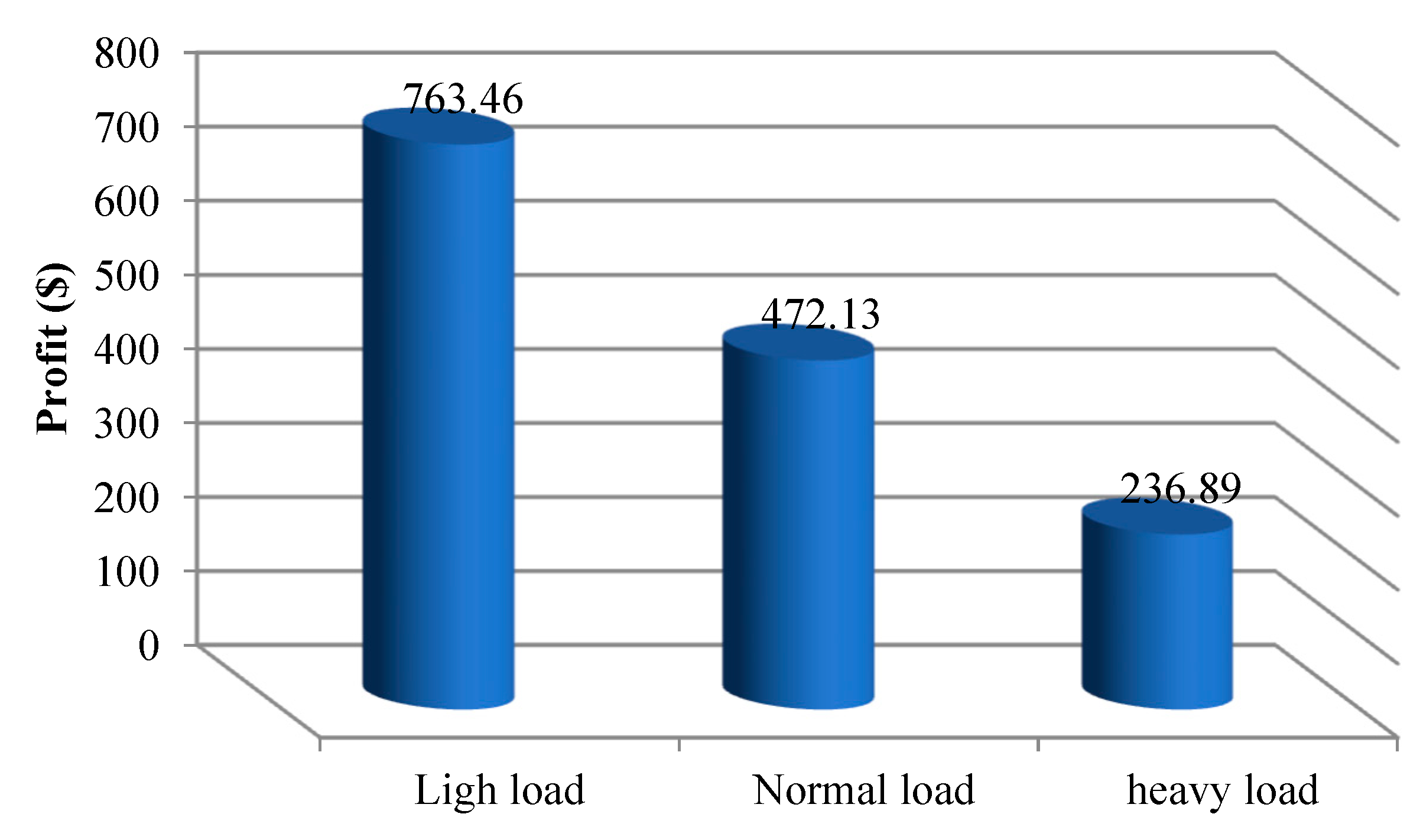
4.2.3. Impact of Different Loading Conditions
4.2.4. Impact of Forced Outage Rate
5. Conclusions
- The results showed that the IFLA, FLA, PSO, and MRFO methods obtained energy profits of $472.13, $435.34, $442.17, and $467.62, respectively, in the day-ahead market, which indicates the better performance of the proposed framework based on IFLA in achieving more energy profit.
- The system’s profit is significantly affected by the price of electricity, natural gas, and heating energy. The profit of the heating market of the day-ahead is negative in the hours of electric energy storage and positive in the rest of the hours. Furthermore, the profit of the day-ahead gas market in the day-ahead heating market is negative compared to the day-ahead gas.
- With a 20% increase in load demand compared to the base state, the profit decreases from $472.13 to $236.89, and with a 20% decrease in load demand, it increases to $763.46. Therefore, the increase (decrease) in load demand causes a decrease (increase) in the profitability of the EH.
- With the increase (decrease) in the FOR of renewable energy sources and CHP, the system profit decreases (increases). The system profit in the base state (FOR = 0%) decreases from $472.13 to $379.46 for FOR = 5%, and also declines to $297.09 for FOR = 10%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ae | Bus and line incidence matrix for electrical network |
| Ag | Bus and line incidence matrix for natural gas network |
| Ah | Bus and line incidence matrix for district heating network |
| AHe | Bus and hub incidence matrix for electrical network |
| AHg | Bus and hub incidence matrix for natural gas network |
| AHh | Bus and hub incidence matrix for district heating network |
| B | Susceptance of a line (p.u) |
| BOmax | The maximum capacity of boiler (p.u) |
| CHPg | Gas of CHP (p.u) |
| CHPh | Heating power of CHP (p.u) |
| CHPP | The active power of CHP (p.u) |
| CHPq | The reactive power of CHP (p.u) |
| CHPe,max | The maximum CHP capacity in electrical part (p.u) |
| DSp | The active power of electrical station (p.u) |
| DSq | The reactive power of electrical station (p.u) |
| Eini | Initial energy in the storage system (p.u) |
| Emin | Minimum energy of storage system (p.u) |
| Emax | Maximum energy of storage system (p.u) |
| EVp,ch | Charging active power of EVs batteries in the parking lot (p.u) |
| EVp,dch | Discharging active power of EVs batteries in the parking lot (p.u) |
| Fp | Active power flow from a line (p.u) |
| Fq | Reactive power flow from a line (p.u) |
| Fg | The gas power flow from a pipeline (p.u) |
| Fh | The heating power flow from a pipeline (p.u) |
| GS | The gas station power (p.u) |
| GSmax | Maximum capacity of gas station (p.u) |
| HDp | Active demand power in the hub (p.u) |
| CHh,max | The maximum CHP capacity in heating part (p.u) |
| HDh | Heating demand power in the hub (p.u) |
| HDg | Gas demand power in the hub (p.u) |
| HDq | Reactive demand power in the hub (p.u) |
| HS | The heating station power (p.u) |
| HSmax | Maximum capacity heating station (p.u) |
| LP, Lq | Active and reactive load power (p.u) |
| Lg, Lh | Gas and heating load power (p.u) |
| M | Indice of hub |
| STp,ch, STp,dch | Charging and discharging active power of storage system (p.u) |
| STq | Reactive power of storage system (p.u) |
| T | Temperature (p.u) |
| Tmin, Tmax | Minimum and maximum allowed temperature (p.u) |
| Vmin, Vmax | Minimum and maximum acceptable voltage magnitude (p.u) |
| ηEV, ch, ηEV, dch | EVs charging and discharging efficiency |
| ηST, ch, ηST, dch | Storage system charging and discharging efficiency |
| λe, λg, λh | DA market price for electrical, gas and heating energies ($/MWh) |
| πmin, πmax | Minimum and maximum allowed gas pressure magnitude (p.u) |
| Ωe, Ωg, Ωh | Sets of electrical bus, gas node, heating node |
References
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept–A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Naderipour, A.; Kamyab, H.; Klemeš, J.J.; Ebrahimi, R.; Chelliapan, S.; Nowdeh, S.A.; Abdullah, A.; Marzbali, M.H. Optimal design of hybrid grid-connected photovoltaic/wind/battery sustainable energy system improving reliability, cost and emission. Energy 2022, 257, 124679. [Google Scholar] [CrossRef]
- Davatgaran, V.; Saniei, M.; Mortazavi, S.S. Optimal bidding strategy for an energy hub in energy market. Energy 2018, 148, 482–493. [Google Scholar] [CrossRef]
- Zhang, G.; Ge, Y.; Ye, Z.; Al-Bahrani, M. Multi-objective planning of energy hub on economic aspects and resources with heat and power sources, energizable, electric vehicle and hydrogen storage system due to uncertainties and demand response. J. Energy Storage. 2023, 57, 106160. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Arabi Nowdeh, S.; Gandoman, F.H.; Hadidian Moghaddam, M.J. A multi-objective optimization problem for optimal site selection of wind turbines for reduce losses and improve voltage profile of distribution grids. Energies 2019, 12, 2621. [Google Scholar] [CrossRef]
- Lu, X.; Li, H.; Zhou, K.; Yang, S. Optimal load dispatch of energy hub considering uncertainties of renewable energy and demand response. Energy 2023, 262, 125564. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Nowdeh, S.A.; Ramachandaramurthy, V.K.; Kalam, A.; Guerrero, J.M. Optimal allocation for combined heat and power system with respect to maximum allowable capacity for reduced losses and improved voltage profile and reliability of microgrids considering loading condition. Energy 2020, 196, 117124. [Google Scholar] [CrossRef]
- Wen, P.; Xie, Y.; Huo, L.; Tohidi, A. Optimal and stochastic performance of an energy hub-based microgrid consisting of a solar-powered compressed-air energy storage system and cooling storage system by modified grasshopper optimization algorithm. Int. J. Hydrog. Energy 2022, 47, 13351–13370. [Google Scholar] [CrossRef]
- Bahmani, R.; Karimi, H.; Jadid, S. Cooperative energy management of multi-energy hub systems considering demand response programs and ice storage. Int. J. Electr. Power Energy Syst. 2021, 130, 106904. [Google Scholar] [CrossRef]
- Rahmatian, M.R.; Shamim, A.G.; Bahramara, S. Optimal operation of the energy hubs in the islanded multi-carrier energy system using Cournot model. Appl. Therm. Eng. 2021, 191, 116837. [Google Scholar] [CrossRef]
- Ghanbari, A.; Karimi, H.; Jadid, S. Optimal planning and operation of multi-carrier networked microgrids considering multi-energy hubs in distribution networks. Energy 2020, 204, 117936. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Liu, C.; Liu, J. Coordinating energy management for multiple energy hubs: From a transaction perspective. Int. J. Electr. Power Energy Syst. 2020, 121, 106060. [Google Scholar] [CrossRef]
- Mirzapour-Kamanaj, A.; Majidi, M.; Zare, K.; Kazemzadeh, R. Optimal strategic coordination of distribution networks and interconnected energy hubs: A linear multi-follower bi-level optimization model. Int. J. Electr. Power Energy Syst. 2020, 119, 105925. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, D.; Wu, T. Standardised modelling and optimisation of a system of interconnected energy hubs considering multiple energies—Electricity, gas, heating, and cooling. Energy Convers. Manag. 2020, 205, 112410. [Google Scholar] [CrossRef]
- Khorasany, M.; Najafi-Ghalelou, A.; Razzaghi, R.; Mohammadi-Ivatloo, B. Transactive energy framework for optimal energy management of multi-carrier energy hubs under local electrical, thermal, and cooling market constraints. Int. J. Electr. Power Energy Syst. 2021, 129, 106803. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-ivatloo, B.; Hosseinzadeh, M.; Yousefi, H.; Khorasani, S.T. Optimal management of energy hubs and smart energy hubs—A review. Renew. Sustain. Energy Rev. 2018, 89, 33–50. [Google Scholar] [CrossRef]
- Huo, D.; Le Blond, S.; Gu, C.; Wei, W.; Yu, D. Optimal operation of interconnected energy hubs by using decomposed hybrid particle swarm and interior-point approach. Int. J. Electr. Power Energy Syst. 2018, 95, 36–46. [Google Scholar] [CrossRef]
- Bostan, A.; Nazar, M.S.; Shafie-Khah, M.; Catalão, J.P. Optimal scheduling of distribution systems considering multiple downward energy hubs and demand response programs. Energy 2020, 190, 116349. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Y.; Liu, J.; Liu, X. Energy scheduling for a three-level integrated energy system based on energy hub models: A hierarchical Stackelberg game approach. Sustain. Cities Soc. 2020, 52, 101814. [Google Scholar] [CrossRef]
- Zhang, X.; Che, L.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. Reliability-based optimal planning of electricity and natural gas interconnections for multiple energy hubs. IEEE Trans. Smart Grid 2015, 8, 1658–1667. [Google Scholar] [CrossRef]
- Ghorab, M. Energy hubs optimization for smart energy network system to minimize economic and environmental impact at Canadian community. Appl. Therm. Eng. 2019, 151, 214–230. [Google Scholar] [CrossRef]
- Gholinejad, H.R.; Loni, A.; Adabi, J.; Marzband, M. A hierarchical energy management system for multiple home energy hubs in neighborhood grids. J. Build. Eng. 2020, 28, 101028. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, X.; Huang, H.; Zhang, D.; Ghadimi, N. Optimal economic scheduling of microgrids considering renewable energy sources based on energy hub model using demand response and improved water wave optimization algorithm. J. Energy Storage 2022, 55, 105311. [Google Scholar] [CrossRef]
- Shahrabi, E.; Hakimi, S.M.; Hasankhani, A.; Derakhshan, G.; Abdi, B. Developing optimal energy management of energy hub in the presence of stochastic renewable energy resources. Sustain. Energy Grids Netw. 2021, 26, 100428. [Google Scholar] [CrossRef]
- Enayati, M.; Derakhshan, G.; mehdi Hakimi, S. Optimal energy scheduling of storage-based residential energy hub considering smart participation of demand side. J. Energy Storage 2022, 49, 104062. [Google Scholar] [CrossRef]
- Lu, Q.; Zeng, W.; Guo, Q.; Lü, S. Optimal operation scheduling of household energy hub: A multi-objective optimization model considering integrated demand response. Energy Rep. 2022, 8, 15173–15188. [Google Scholar] [CrossRef]
- AkbaiZadeh, M.; Niknam, T.; Kavousi-Fard, A. Adaptive robust optimization for the energy management of the grid-connected energy hubs based on hybrid meta-heuristic algorithm. Energy 2021, 235, 121171. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Hashim, F.A.; Mostafa, R.R.; Hussien, A.G.; Mirjalili, S.; Sallam, K.M. Fick’s Law Algorithm: A physical law-based algorithm for numerical optimization. Knowl.-Based Syst. 2023, 260, 110146. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Zitar, R.A. Orthogonal Learning Rosenbrock’s Direct Rotation with the Gazelle Optimization Algorithm for Global Optimization. Mathematics 2022, 10, 4509. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 2015, 101, 579–591. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Name of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Kohansal, O.; Zadehbagheri, M.; Kiani, M.J.; Nejatian, S. Participation of Grid-Connected Energy Hubs and Energy Distribution Companies in the Day-Ahead Energy Wholesale and Retail Markets Constrained to Network Operation Indices. Int. Trans. Electr. Energy Syst. 2022, 2022, 2463003. [Google Scholar] [CrossRef]
| Algorithm | Parameter | Value |
|---|---|---|
| FLA [29] | C | 0.1 |
| PSO [32] | C1 | 2 |
| C2 | 2 | |
| Inertia weight | Linearly reduction from 0.9 to 0.1 | |
| MRFO [33] | S | 2 |
| Electrical Network | Natural Gas Network | District Heating Network | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Line | R | X | Fe,max | Pipeline | sign | Fg,max | Pipeline | Fh,max | ||
| 1-2 | 0.02 | 0.06 | 0.90 | 1-2 | 3 | 1 | 1.1 | 1-2 | 15 | 1.00 |
| 1-5 | 0.05 | 0.12 | 0.50 | 1-3 | 3.5 | 1 | 3.0 | 1-3 | 18.5 | 1.30 |
| 2-3 | 0.05 | 0.12 | 0.65 | 1-4 | 4 | 1 | 1.2 | 2-3 | 17.5 | 0.20 |
| 2-4 | 0.06 | 0.08 | 0.75 | 2-3 | 4.5 | -1 | 0.6 | 2-7 | 18.5 | 0.50 |
| 2-5 | 0.06 | 0.11 | 0.80 | 3-4 | 4.5 | 1 | 0.8 | 3-4 | 19.5 | 0.65 |
| 3-4 | 0.07 | 0.11 | 1.20 | 3-6 | 19 | 0.20 | ||||
| 4-5 | 0.01 | 0.04 | 0.65 | 4-5 | 15 | 0.35 | ||||
| 4-7 | 0.01 | 0.03 | 0.90 | 5-6 | 19 | 0.10 | ||||
| 5-6 | 0.02 | 0.05 | 1.10 | 6-7 | 19.5 | 0.20 | ||||
| 6-9 | 0.10 | 0.09 | 0.30 | |||||||
| 7-8 | 0.02 | 0.07 | 1.30 | |||||||
| 8-9 | 0.08 | 0.12 | 0.35 | |||||||
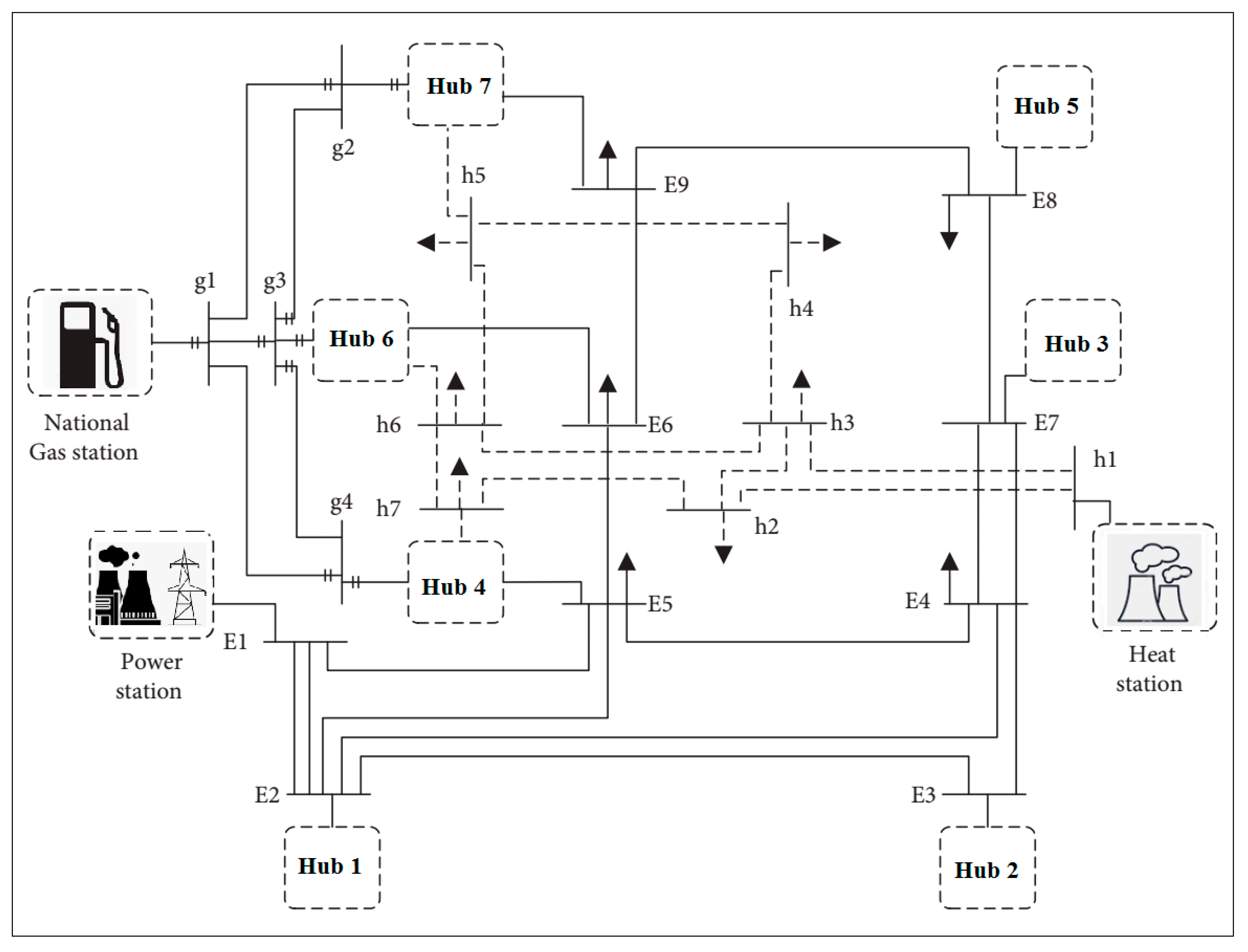
| System | Location * | RES | Storage | EVs | CHP | Boiler | Load + (p.u) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | G | h | HD P | HD q | HD h | HD g | ||||||
| Hub 1 | 2 | - | - | √ | √ | √ | 0.8 | 0.4 | 0 | 0 | ||
| Hub 2 | 3 | - | - | √ | √ | √ | 0.5 | 0.3 | 0 | 0 | ||
| Hub 3 | 7 | - | - | √ | √ | √ | 0.6 | 0.4 | 0 | 0 | ||
| Hub 4 | 5 | 4 | 7 | √ | √ | 0.2 | 0.1 | 0.3 | 0 | |||
| Hub 5 | 8 | - | - | √ | √ | √ | 0.4 | 0.2 | 0 | 0 | ||
| Hub 6 | 6 | 3 | 6 | √ | √ | √ | √ | √ | 0.4 | 0.2 | 0.2 | 0 |
| Hub 7 | 9 | 2 | 5 | √ | √ | √ | √ | √ | 0.4 | 0.2 | 0.2 | 0 |
| Algorithm/Item | Convergence Iteration | Profit ($) | Algorithm Status | CPU Time (S) |
|---|---|---|---|---|
| IFLA | 30 | 472.13 | Globally optimal | 155 |
| FLA | 91 | 435.34 | Locally optimal | 186 |
| MRFO | 66 | 442.17 | Locally optimal | 178 |
| PSO | 59 | 467.62 | Locally optimal | 167 |
| Algorithm/Index | Best ($) | Worst ($) | Mean ($) | Std ($) |
|---|---|---|---|---|
| IFLA | 472.13 | 461.78 | 469.24 | 46.37 |
| FLA | 435.34 | 419.65 | 428.03 | 94.46 |
| MRFO | 442.17 | 425.22 | 432.93 | 76.21 |
| PSO | 467.62 | 458.50 | 462.74 | 63.54 |
| FOR | Profit ($) |
|---|---|
| 0% | 472.13 |
| 1% | 445.43 |
| 2% | 428.92 |
| 3% | 412.43 |
| 4% | 395.94 |
| 5% | 379.46 |
| 6% | 362.98 |
| 7% | 346.51 |
| 8% | 330.03 |
| 9% | 313.56 |
| 10% | 297.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.S.; Alanazi, M.; Alanazi, A.; Qasaymeh, Y.; Zubair, M.; Awan, A.B.; Ashiq, M.G.B. Energy Hub Optimal Scheduling and Management in the Day-Ahead Market Considering Renewable Energy Sources, CHP, Electric Vehicles, and Storage Systems Using Improved Fick’s Law Algorithm. Appl. Sci. 2023, 13, 3526. https://doi.org/10.3390/app13063526
Alghamdi AS, Alanazi M, Alanazi A, Qasaymeh Y, Zubair M, Awan AB, Ashiq MGB. Energy Hub Optimal Scheduling and Management in the Day-Ahead Market Considering Renewable Energy Sources, CHP, Electric Vehicles, and Storage Systems Using Improved Fick’s Law Algorithm. Applied Sciences. 2023; 13(6):3526. https://doi.org/10.3390/app13063526
Chicago/Turabian StyleAlghamdi, Ali S., Mohana Alanazi, Abdulaziz Alanazi, Yazeed Qasaymeh, Muhammad Zubair, Ahmed Bilal Awan, and Muhammad Gul Bahar Ashiq. 2023. "Energy Hub Optimal Scheduling and Management in the Day-Ahead Market Considering Renewable Energy Sources, CHP, Electric Vehicles, and Storage Systems Using Improved Fick’s Law Algorithm" Applied Sciences 13, no. 6: 3526. https://doi.org/10.3390/app13063526
APA StyleAlghamdi, A. S., Alanazi, M., Alanazi, A., Qasaymeh, Y., Zubair, M., Awan, A. B., & Ashiq, M. G. B. (2023). Energy Hub Optimal Scheduling and Management in the Day-Ahead Market Considering Renewable Energy Sources, CHP, Electric Vehicles, and Storage Systems Using Improved Fick’s Law Algorithm. Applied Sciences, 13(6), 3526. https://doi.org/10.3390/app13063526











