A Helmholtz Free Energy Equation of State of CO2-CH4-N2 Fluid Mixtures (ZMS EOS) and Its Applications
Abstract
:1. Introduction
2. The ZMS EOS
2.1. The Binary CH4-N2 Mixture
2.2. The Ternary CO2-CH4-N2 Mixture
3. The Applications of the ZMS EOS
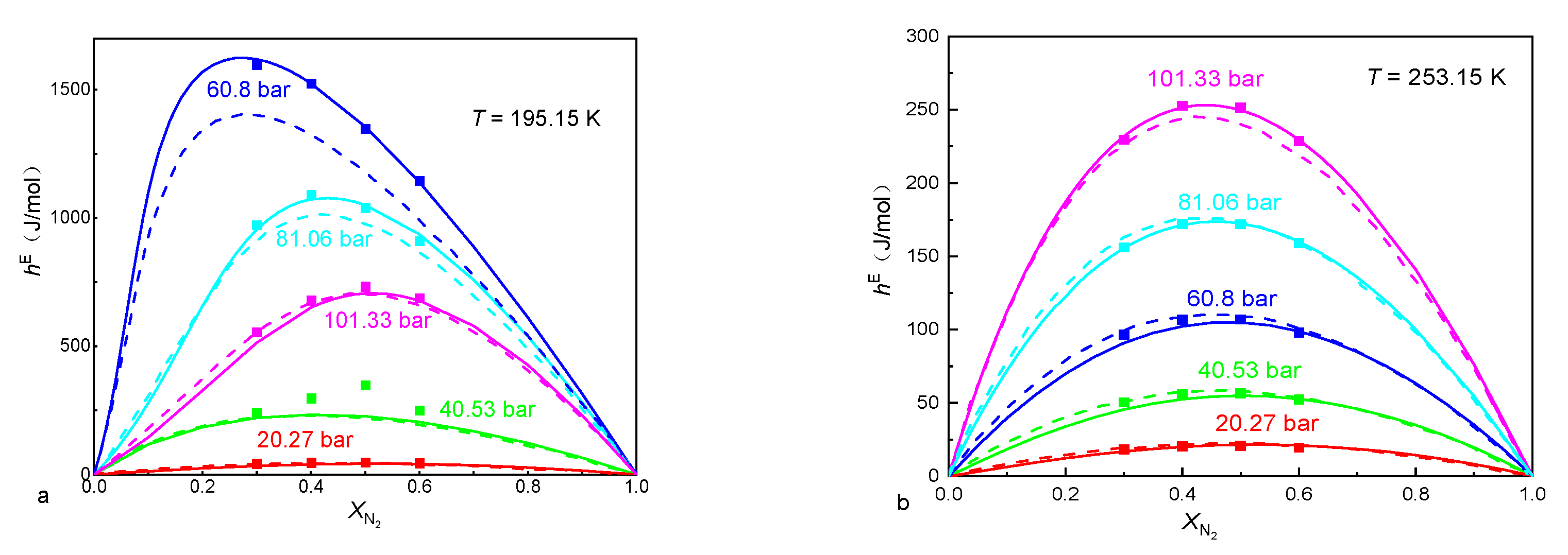
3.1. Calculating Excess Enthalpies
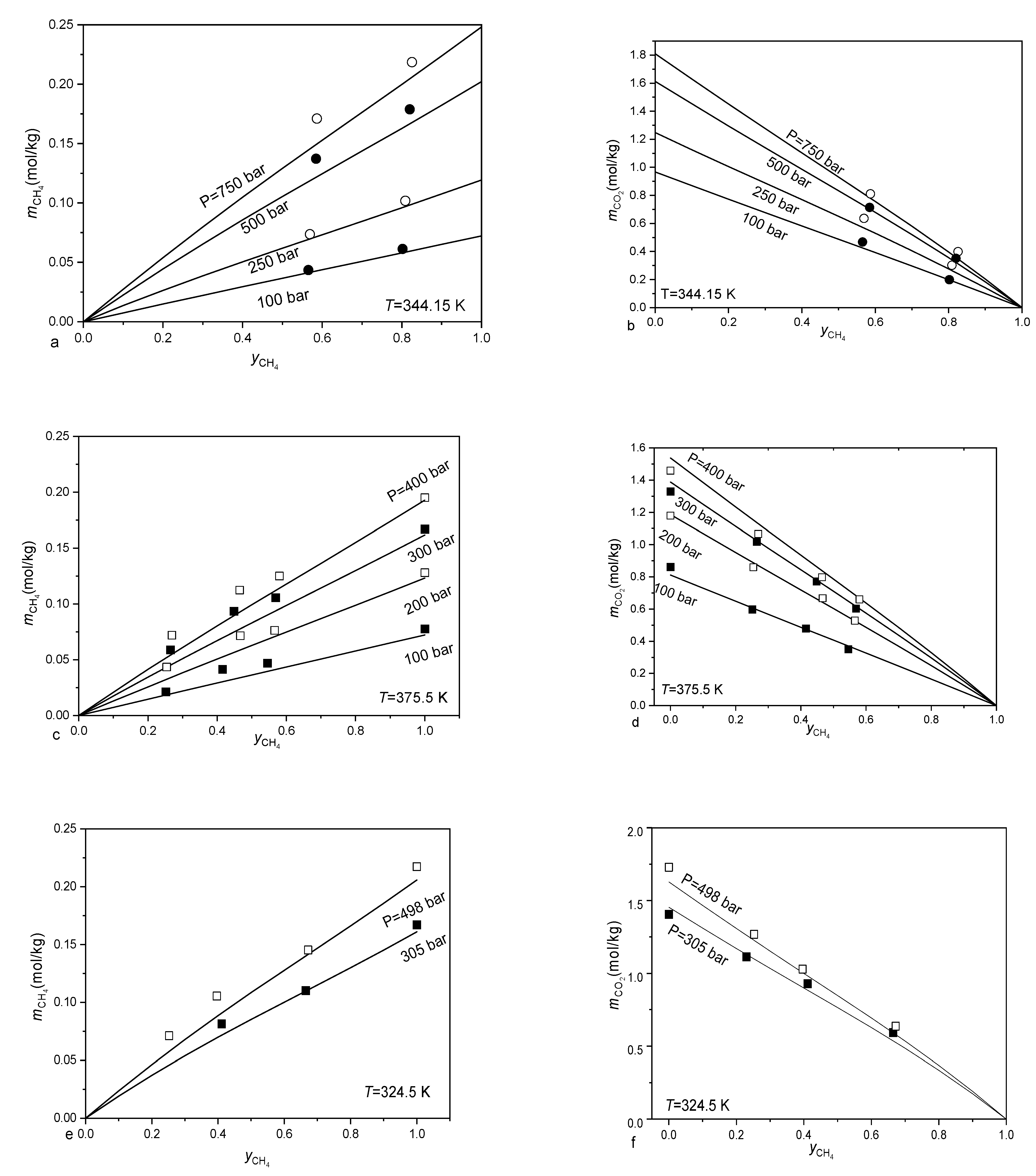
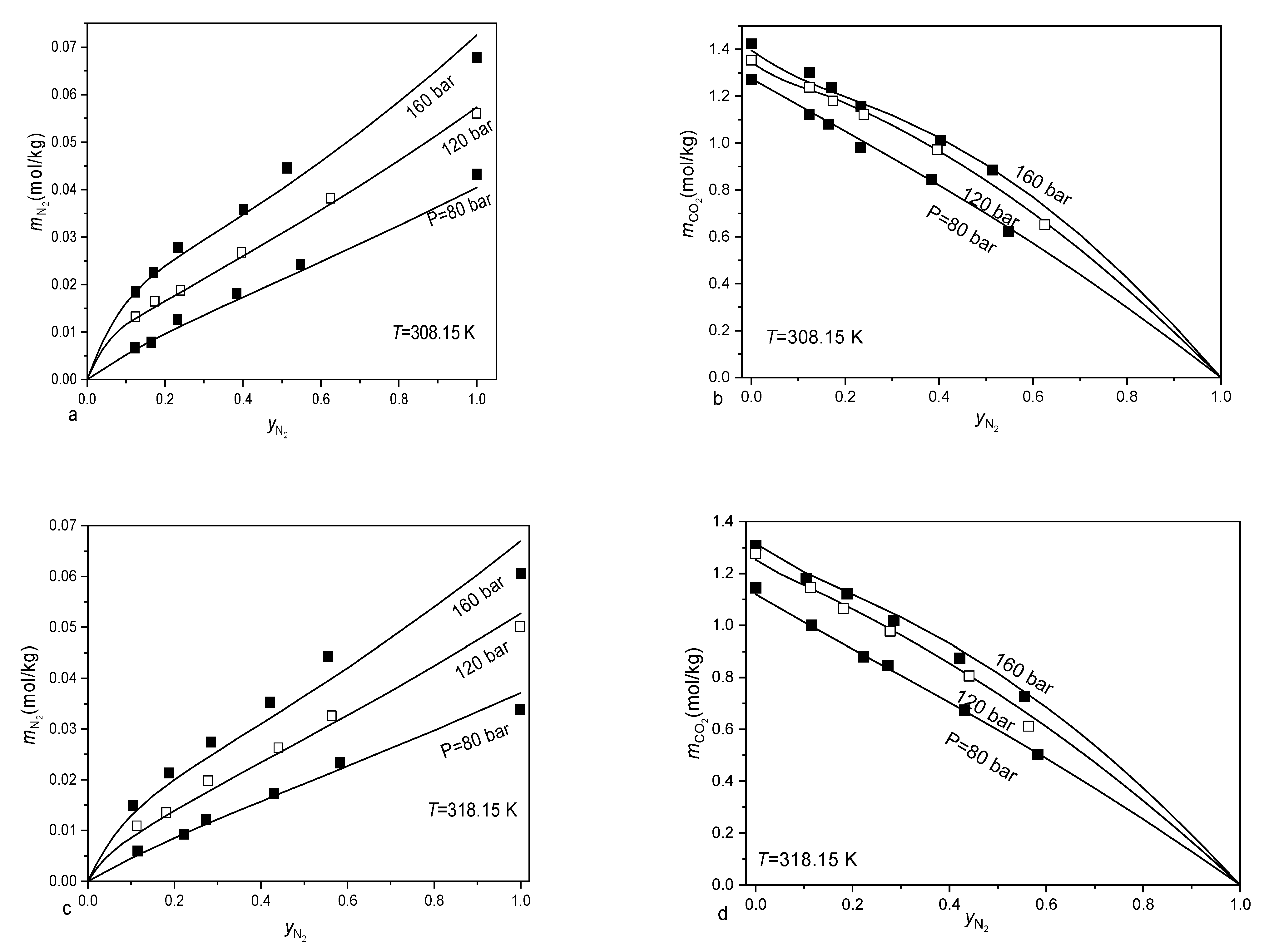
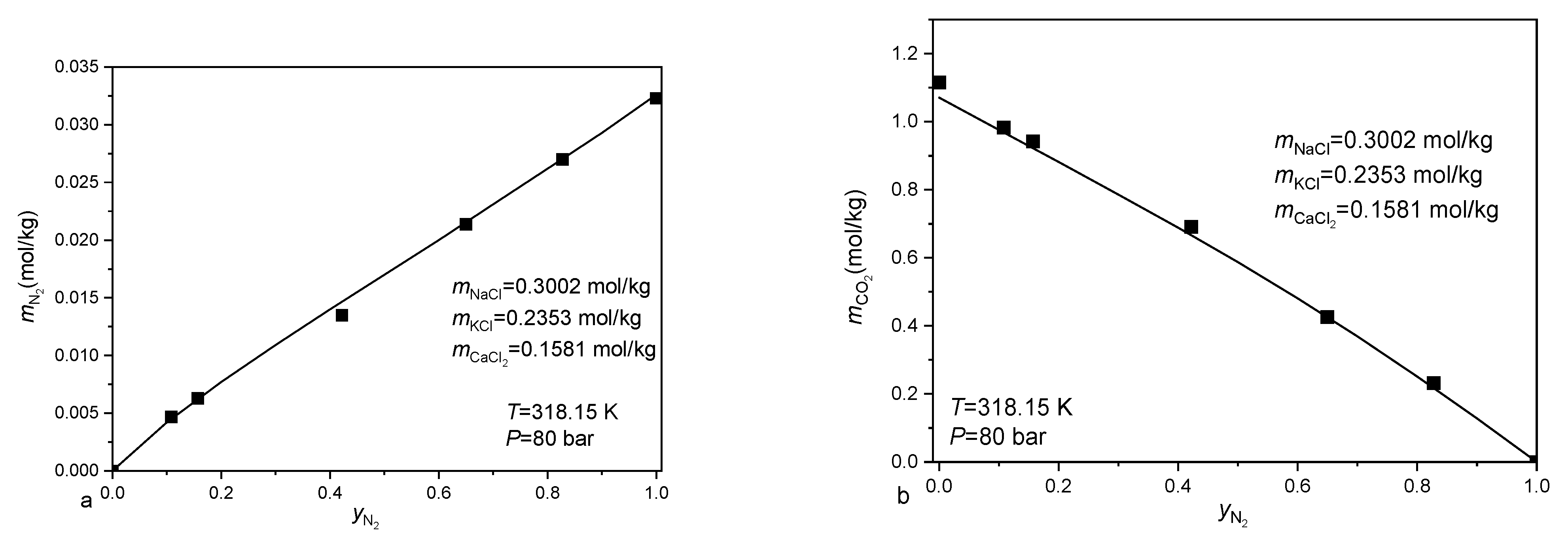
3.2. Calculating the Solubility of CO2-CH4-N2 Mixtures in Aqueous Electrolyte Solution
3.3. The Impact of Impurities (CH4 and N2) on the CO2 Storage Capacity
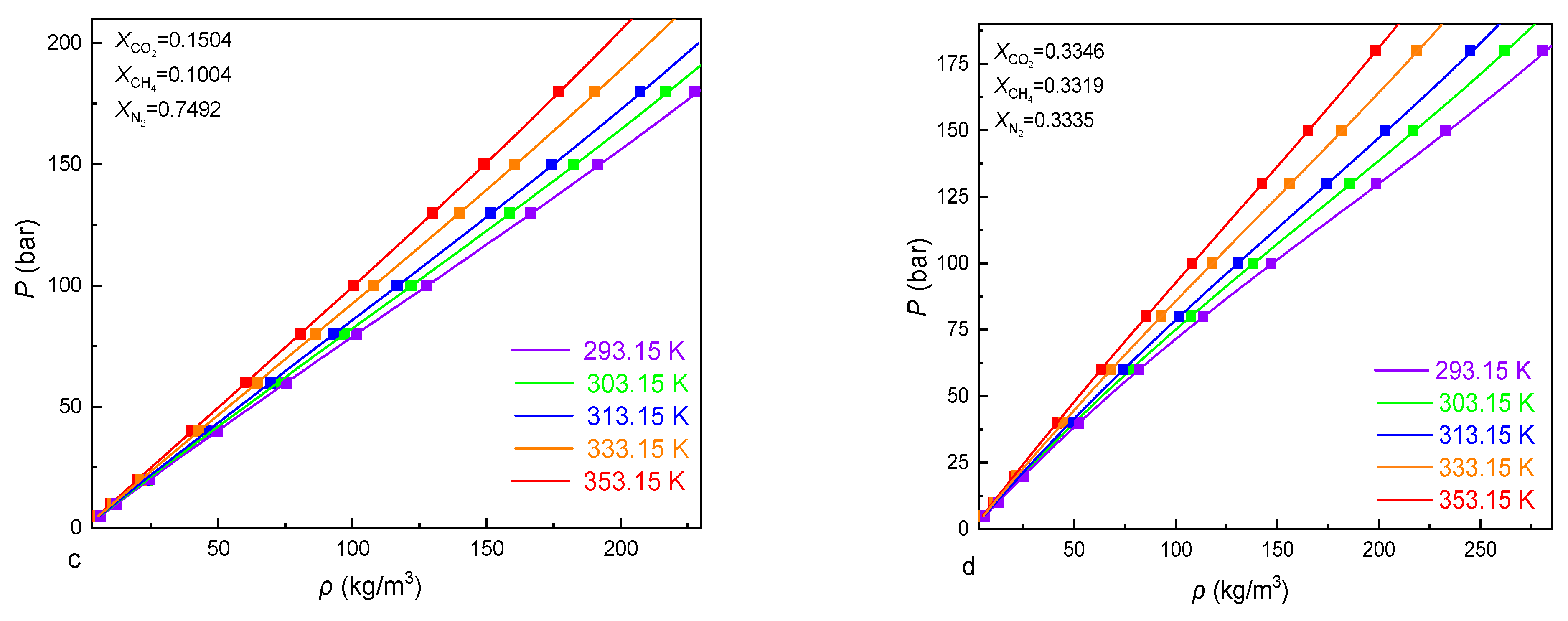
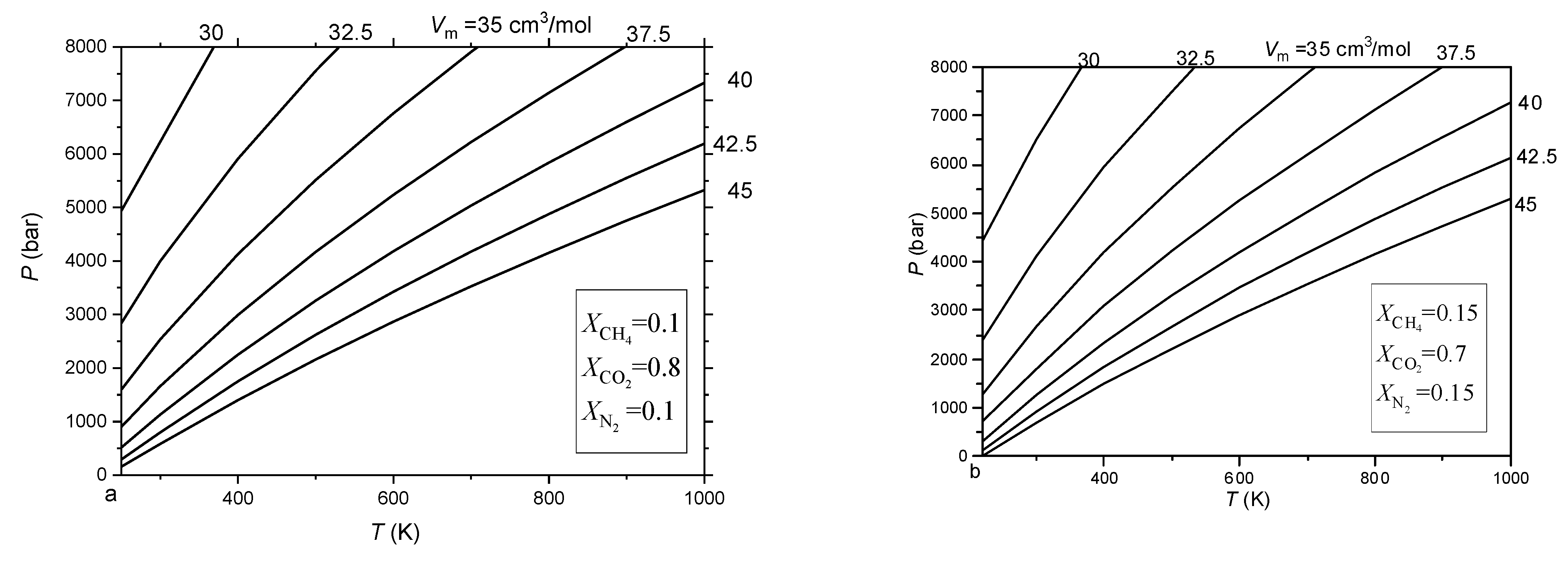
3.4. Isochores of the CO2-CH4-N2 fluid Inclusions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Le, V.H.; Caumon, M.C.; Tarantola, A.; Randi, A.; Robert, P.; Mullis, J. Calibration data for simultaneous determination of PVX properties of binary and ternary CO2-CH4-N2 gas mixtures by Raman spectroscopy over 5–600 bar: Application to natural fluid inclusions. Chem. Geol. 2020, 552, 119783. [Google Scholar] [CrossRef]
- Caumon, M.C.; Tarantola, A.; Wang, W. Raman spectra of gas mixtures in fluid inclusions: Effect of quartz birefringence on composition measurement. J. Raman Spectrosc. 2020, 51, 1868–1873. [Google Scholar] [CrossRef]
- Lüders, V.; Plessen, B.; di Primio, R. Stable carbon isotopic ratios of CH4–CO2-bearing fluid inclusions in fracture-fill mineralization from the Lower Saxony Basin (Germany)–A tool for tracing gas sources and maturity. Mar. Pet. Geol. 2012, 30, 174–183. [Google Scholar] [CrossRef]
- Gaurina-Međimurec, N.; Mavar, K.N. Carbon capture and storage (CCS): Geological sequestration of CO2. In CO2 Sequestration; IntechOpen: London, UK, 2019; pp. 1–21. [Google Scholar] [CrossRef] [Green Version]
- Pires, J.; Martins, F.; Alvim-Ferraz, M.; Simões, M. Recent developments on carbon capture and storage: An overview. Chem. Eng. Res. Des. 2011, 89, 1446–1460. [Google Scholar] [CrossRef]
- Bui, M.; Adjiman, C.S.; Bardow, A.; Anthony, E.J.; Boston, A.; Brown, S.; Fennell, P.S.; Fuss, S.; Galindo, A.; Hackett, L.A. Carbon capture and storage (CCS): The way forward. Energy Environ. Sci. 2018, 11, 1062–1176. [Google Scholar] [CrossRef] [Green Version]
- Chapoy, A.; Burgass, R.; Tohidi, B.; Austell, J.M.; Eickhoff, C. Effect of common impurities on the phase behavior of carbon-dioxide-rich systems: Minimizing the risk of hydrate formation and two-phase flow. SPE J. 2011, 16, 921–930. [Google Scholar] [CrossRef]
- Thoutam, P.; Rezaei Gomari, S.; Chapoy, A.; Ahmad, F.; Islam, M. Study on CO2 hydrate formation kinetics in saline water in the presence of low concentrations of CH4. ACS Omega 2019, 4, 18210–18218. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Ryan, D.; Anthony, E.J.; Wildgust, N.; Aiken, T. Effects of impurities on CO2 transport, injection and storage. Energy Procedia 2011, 4, 3071–3078. [Google Scholar] [CrossRef] [Green Version]
- Wetenhall, B.; Aghajani, H.; Chalmers, H.; Benson, S.; Ferrari, M.; Li, J.; Race, J.; Singh, P.; Davison, J. Impact of CO2 impurity on CO2 compression, liquefaction and transportation. Energy Procedia 2014, 63, 2764–2778. [Google Scholar] [CrossRef] [Green Version]
- Blanco, S.T.; Rivas, C.; Fernández, J.; Artal, M.; Velasco, I. Influence of methane in CO2 transport and storage for CCS technology. Environ. Sci. Technol. 2012, 46, 13016–13023. [Google Scholar] [CrossRef]
- Li, H.; Yan, J. Impact of impurities in CO2-fluids on CO2 transport process. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Barcelona, Spain, 2006; pp. 367–375. [Google Scholar]
- Li, H.; Yan, J. Impacts of equations of state (EOS) and impurities on the volume calculation of CO2 mixtures in the applications of CO2 capture and storage (CCS) processes. Appl. Energy 2009, 86, 2760–2770. [Google Scholar] [CrossRef]
- Tenorio, M.J.; Parrott, A.J.; Calladine, J.A.; Sanchez Vicente, Y.; Cresswell, A.J.; Graham, R.S.; Drage, T.C.; Poliakoff, M.; Ke, J.; George, M.W. Measurement of the vapour–liquid equilibrium of binary and ternary mixtures of CO2, N2 and H2, systems which are of relevance to CCS technology. Int. J. Greenh. Gas Control 2015, 41, 68–81. [Google Scholar] [CrossRef]
- Shi, G.U.; Tropper, P.; Cui, W.; Tan, J.; Wang, C. Methane (CH4)-bearing fluid inclusions in the Myanmar jadeitite. Geochem. J. 2005, 39, 503–516. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Van der Waals, J. On the Continuity of the Gas and Liquid State; Leiden University: Leiden, The Netherlands, 1873. [Google Scholar]
- Lasala, S.; Chiesa, P.; Privat, R.; Jaubert, J.N. Measurement and prediction of multi-property data of CO2-N2-O2-CH4 mixtures with the “Peng-Robinson+ residual Helmholtz energy-based” model. Fluid Phase Equilibria 2017, 437, 166–180. [Google Scholar] [CrossRef]
- Xu, X.; Lasala, S.; Privat, R.; Jaubert, J.N. E-PPR78: A proper cubic EOS for modelling fluids involved in the design and operation of carbon dioxide capture and storage (CCS) processes. Int. J. Greenh. Gas Control 2017, 56, 126–154. [Google Scholar] [CrossRef]
- Heyen, G. An equation of state with extended range of application. In Proceedings of the Second World Congress of Chemical Engineering, Montreal, QC, Canada, 4–9 October 1981. [Google Scholar]
- Heyen, G.; Ramboz, C.; Dubessy, J. Modelling of phase equilibria in the system CO2–CH4 below 50 °C and 100 bar. Appl. Incl. Fluids Fr. Comptes Rendus Acad. Sci. Paris 1982, 294, 203–206. [Google Scholar]
- Darimont, A.; Heyen, G. Simulation des équilibres de phases dans le système CO2-N2. Application aux inclusions fluides. Bull. Minéralogie 1988, 111, 179–182. [Google Scholar] [CrossRef]
- Thiery, R.; Vidal, J.; Dubessy, J. Phase equilibria modelling applied to fluid inclusions: Liquid-vapour equilibria and calculation of the molar volume in the CO2-CH4N2 system. Geochim. Cosmochim. Acta 1994, 58, 1073–1082. [Google Scholar] [CrossRef]
- Thiéry, R.; Van Den Kerkhof, A.M.; Dubessy, J. vX properties of CH4-CO2 and CO2-N2 fluid inclusions: Modelling for T < 31 °C and P < 400 bars. Eur. J. Miner. 1994, 6, 753–771. [Google Scholar]
- Thiéry, R.; Dubessy, J. Improved modelling of vapour-liquid equilibria up to the critical region. Application to the CO2-CH4- N2 system. Fluid Phase Equilibria 1996, 121, 111–123. [Google Scholar] [CrossRef]
- Lee, B.I.; Kesler, M.G. A generalized thermodynamic correlation based on three-parameter corresponding states. AIChE J. 1975, 21, 510–527. [Google Scholar] [CrossRef]
- Bakker, R.; Diamond, L.W. Determination of the composition and molar volume of H2O-CO2 fluid inclusions by microthermometry. Geochim. Cosmochim. Acta 2000, 64, 1753–1764. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. New reference equation of state for associating liquids. Ind. Eng. Chem. Res. 1990, 29, 1709–1721. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Kouskoumvekaki, I.A.; von Solms, N.; Michelsen, M.L.; Kontogeorgis, G.M. Application of the perturbed chain SAFT equation of state to complex polymer systems using simplified mixing rules. Fluid Phase Equilibria 2004, 215, 71–78. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; Galindo, A.; Whitehead, P.J.; Mills, S.J.; Jackson, G.; Burgess, A.N. Statistical associating fluid theory for chain molecules with attractive potentials of variable. J. Chem. Phys. 1997, 106, 4168–4186. [Google Scholar] [CrossRef]
- Kraska, T.; Gubbins, K.E. Phase Equilibria Calculations with a Modified SAFT Equation of State. 2. Binary Mixtures of n-Alkanes, 1-Alkanols, and Water. Ind. Eng. Chem. Res. 1996, 35, 4738–4746. [Google Scholar] [CrossRef]
- Zhang, J.; Mao, S.; Peng, Q. An improved equation of state of binary CO2–N2 fluid mixture and its application in the studies of fluid inclusions. Fluid Phase Equilibria 2020, 513, 112554. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Jacobsen, R. A generalized model for the thermodynamic properties of mixtures. Int. J. Thermophys. 1999, 20, 825–835. [Google Scholar] [CrossRef]
- Gernert, J.; Span, R. EOS-CG: A Helmholtz energy mixture model for humid gases and CCS mixtures. J. Chem. Thermodyn. 2016, 93, 274–293. [Google Scholar] [CrossRef]
- Kunz, O.; Klimeck, R.; Wagner, W.; Jaeschke, M. The GERG-2004 Wide-Range Reference Equation of State for Natural Gases and Other Mixtures; GERG Technical Monographs 15; GERG: Düsseldorf, Germany, 2007. [Google Scholar]
- Mao, S.; Lü, M.; Shi, Z. Prediction of the PVTx and VLE properties of natural gases with a general Helmholtz equation of state. Part I: Application to the CH4-C2H6-C 3H8 -CO2 -N2 system. Geochim. Cosmochim. Acta 2017, 219, 74–95. [Google Scholar] [CrossRef]
- Herrig, S. New Helmholtz-Energy Equations of State for Pure Fluids and CCS Relevant Mixtures; Ruhr-Universität Bochum: Bochum, Germany, 2018. [Google Scholar]
- Mao, S.; Shi, L.; Peng, Q.; Lü, M. Thermodynamic modeling of binary CH4–CO2 fluid inclusions. Appl. Geochem. 2016, 66, 65–72. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef] [Green Version]
- Setzmann, U.; Wagner, W. A new equation of state and tables of thermodynamic properties for methane covering the range from the melting line to 625 K at pressures up to 1000 MPa. J. Phys. Chem. Ref. Data 1991, 20, 1061–1155. [Google Scholar] [CrossRef] [Green Version]
- Span, R.; Lemmon, E.W.; Jacobsen, R.T.; Wagner, W.; Yokozeki, A. A reference equation of state for the thermodynamic properties of nitrogen for temperatures from 63.151 to 1000 K and pressures to 2200 MPa. J. Phys. Chem. Ref. Data 2000, 29, 1361–1433. [Google Scholar] [CrossRef] [Green Version]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties–REFPROP. NIST Stand. Ref. Database 2002, 23, v7. [Google Scholar]
- Liu, Y.P.; Miller, R. Temperature dependence of excess volumes for simple liquid mixtures: Ar+ CH4, N2+ CH4. J. Chem. Thermodyn. 1972, 4, 85–98. [Google Scholar] [CrossRef]
- Rodosevich, J.B.; Miller, R.C. Experimental liquid mixture densities for testing and improving correlations for liquefied natural gas. AIChE J. 1973, 19, 729–735. [Google Scholar] [CrossRef]
- Pan, W.; Mady, M.; Miller, R. Dielectric constants and Clausius-Mossotti functions for simple liquid mixtures: Systems containing nitrogen, argon and light hydrocarbons. AIChE J. 1975, 21, 283–289. [Google Scholar] [CrossRef]
- Hiza, M.; Haynes, W.; Parrish, W. Orthobaric liquid densities and excess volumes for binary mixtures of low molarmass alkanes and nitrogen between 105 and 140 K. J. Chem. Thermodyn. 1977, 9, 873–896. [Google Scholar] [CrossRef]
- Da Ponte, M.N.; Streett, W.; Staveley, L. An experimental study of the equation of state of liquid mixtures of nitrogen and methane, and the effect of pressure on their excess thermodynamic functions. J. Chem. Thermodyn. 1978, 10, 151–168. [Google Scholar] [CrossRef]
- Ababio, B.; McElroy, P.; Williamson, C. Second and third virial coefficients for (methane+ nitrogen). J. Chem. Thermodyn. 2001, 33, 413–421. [Google Scholar] [CrossRef]
- Brandt, L.W.; Stroud, L. Phase Equilibria in Natural Gas Systems. Apparatus with Windowed Cell for 800 PSIG and Temperatures to 320° F. Ind. Eng. Chem. 1958, 50, 849–852. [Google Scholar] [CrossRef]
- Chamorro, C.; Segovia, J.; Martín, M.; Villamañán, M.; Estela Uribe, J.; Trusler, J. Measurement of the (pressure, density, temperature) relation of two (methane+ nitrogen) gas mixtures at temperatures between 240 and 400 K and pressures up to 20 MPa using an accurate single-sinker densimeter. J. Chem. Thermodyn. 2006, 38, 916–922. [Google Scholar] [CrossRef]
- Cheung, H.; Wang, D.I.J. Solubility of volatile gases in hydrocarbon solvents at cryogenic temperatures. Ind. Eng. Chem. Fundam. 1964, 3, 355–361. [Google Scholar] [CrossRef]
- Gomez-Osorio, M.A.; Browne, R.A.; Carvajal Diaz, M.; Hall, K.R.; Holste, J.C. Density measurements for ethane, carbon dioxide, and methane+ nitrogen mixtures from 300 to 470 K up to 137 MPa using a vibrating tube densimeter. J. Chem. Eng. Data 2016, 61, 2791–2798. [Google Scholar] [CrossRef]
- Han, X.H.; Zhang, Y.J.; Gao, Z.J.; Xu, Y.J.; Wang, Q.; Chen, G.M. Vapor–liquid equilibrium for the mixture nitrogen (N2) + methane (CH4) in the temperature range of (110 to 125) K. J. Chem. Eng. Data 2012, 57, 1621–1626. [Google Scholar] [CrossRef]
- Haynes, W.; McCarty, R. Low-density isochoric (P, V, T) measurements on (nitrogen+ methane). J. Chem. Thermodyn. 1983, 15, 815–819. [Google Scholar] [CrossRef]
- Janisch, J.; Raabe, G.; Köhler, J. Vapor− liquid equilibria and saturated liquid densities in binary mixtures of nitrogen, methane, and ethane and their correlation using the VTPR and PSRK GCEOS. J. Chem. Eng. Data 2007, 52, 1897–1903. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, K.; Sheng, W. Vapor-liquid equilibrium in binary and ternary mixtures of nitrogen, argon, and methane. J. Chem. Eng. Data 1993, 38, 353–355. [Google Scholar] [CrossRef]
- Kidnay, A.; Miller, R.; Parrish, W.; Hiza, M. Liquid-vapor phase equilibria in the N2+CH4 system from 130 to 180 K. Cryogenics 1975, 15, 531–540. [Google Scholar] [CrossRef]
- Li, H.; Gong, M.; Guo, H.; Dong, X.; Wu, J. Measurement of the (pressure, density, temperature) relation of a (methane + nitrogen) gaseous mixture using an accurate single-sinker densimeter. J. Chem. Thermodyn. 2013, 59, 233–238. [Google Scholar] [CrossRef]
- McClure, D.; Lewis, K.; Miller, R.; Staveley, L. Excess enthalpies and Gibbs free energies for nitrogen+ methane at temperatures below the critical point of nitrogen. J. Chem. Thermodyn. 1976, 8, 785–792. [Google Scholar] [CrossRef]
- Miller, R.; Kidnay, A.; Hiza, M. Liquid-vapor equilibria at 112.00 K for systems containing nitrogen, argon, and methane. AIChE J. 1973, 19, 145–151. [Google Scholar] [CrossRef]
- Seitz, J.C.; Blencoe, J.G. Volumetric properties for {(1–x) CO2+ xCH4},{(1−x) CO2+ xN2}, and {(1−x) CH4+ xN2} at the pressures (19.94, 29.94, 39.94, 59.93, 79.93, and 99.93) MPa and the temperature 673.15 K. J. Chem. Thermodyn. 1996, 28, 1207–1213. [Google Scholar] [CrossRef]
- Seitz, J.C.; Blencoe, J.G.; Bodnar, R.J. Volumetric properties for {(1−x) CO2+ xCH4},{(1−x) CO2+ xN2}, and {(1−x) CH4+ xN2} at the pressures (9.94, 19.94, 29.94, 39.94, 59.93, 79.93, and 99.93) MPa and temperatures (323.15, 373.15, 473.15, and 573.15) K. J. Chem. Thermodyn. 1996, 28, 521–538. [Google Scholar] [CrossRef] [Green Version]
- Straty, G.; Diller, D. (p, V, T) of compressed and liquefied (nitrogen+ methane). J. Chem. Thermodyn. 1980, 12, 937–953. [Google Scholar] [CrossRef]
- Parrish, W.R.; Hiza, M.J. Liquid-Vapor Equilibria in the Nitrogen-Methane System between 95 and 120 K. In Advances in Cryogenic Engineering; Timmerhaus, K.D., Ed.; Springer: Boston, MA, USA, 1995; pp. 300–308. [Google Scholar]
- Perez, A.G.; Coquelet, C.; Paricaud, P.; Chapoy, A. Comparative study of vapour-liquid equilibrium and density modelling of mixtures related to carbon capture and storage with the SRK, PR, PC-SAFT and SAFT-VR Mie equations of state for industrial uses. Fluid Phase Equilibria 2017, 440, 19–35. [Google Scholar] [CrossRef]
- Jaeschke, M.; Hinze, H. Determination of the Real Gas Behaviour of Methane and Nitrogen and Their Mixtures in the Temperature Range from 270 K to 353 K and at Pressures Up To 30 MPa; Fortschritt-Berichte VDI, Verlag R. 6 Nr; VDI-Verlag: Düsseldorf, Germany, 1991; Volume 262. [Google Scholar]
- McElroy, P.; Battino, R.; Dowd, M. Compression-factor measurements on methane, carbon dioxide, and (methane+ carbon dioxide) using a weighing method. J. Chem. Thermodyn. 1989, 21, 1287–1300. [Google Scholar] [CrossRef]
- Seitz, J.C.; Blencoe, J.G.; Joyce, D.B.; Bodnar, R.J. Volumetric properties of CO2+CH4+N2 fluids at 200° C and 1000 bars: A comparison of equations of state and experimental data. Geochim. Cosmochim. Acta 1994, 58, 1065–1071. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, B.; Zhao, C.; Zhang, J.; Chen, K.; Xu, Y. Density Characteristics of a Multicomponent CO2/N2/CH4 Ternary Mixture at Temperature of 293.15–353.15 K and Pressure of 0.5–18 MPa. J. Chem. Eng. Data 2022, 67, 908–918. [Google Scholar] [CrossRef]
- Al-Sahhaf, T.A. Vapor—Liquid equilibria for the ternary system N2+ CO2+ CH4 at 230 and 250 K. Fluid Phase Equilibria 1990, 55, 159–172. [Google Scholar] [CrossRef]
- Al-Sahhaf, T.A.; Kidnay, A.J.; Sloan, E.D. Liquid+ vapor equilibriums in the nitrogen+ carbon dioxide+ methane system. Ind. Eng. Chem. Fundam. 1983, 22, 372–380. [Google Scholar] [CrossRef]
- Somait, F.A.; Kidnay, A.J. Liquid-vapor equilibriums at 270.00 K for systems containing nitrogen, methane, and carbon dioxide. J. Chem. Eng. Data 1978, 23, 301–305. [Google Scholar] [CrossRef]
- Lee, J.; Mather, A. The excess enthalpy of gaseous mixtures of carbon dioxide with methane. Can. J. Chem. Eng. 1972, 50, 95–100. [Google Scholar] [CrossRef]
- Lee, J.; Mather, A. The excess enthalpy of gaseous mixtures of nitrogen and carbon dioxide. J. Chem. Thermodyn. 1970, 2, 881–895. [Google Scholar] [CrossRef]
- Klein, R.; Bennett, C.; Dodgge, B. Experimental heats of mixing for gaseous nitrogen and methane. AIChE J. 1971, 17, 958–965. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef] [Green Version]
- Akinfiev, N.N.; Diamond, L.W. Thermodynamic model of aqueous CO2–H2O–NaCl solutions from− 22 to 100 °C and from 0.1 to 100 MPa. Fluid Phase Equilibria 2010, 295, 104–124. [Google Scholar] [CrossRef]
- Chapoy, A.; Mohammadi, A.; Chareton, A.; Tohidi, B.; Richon, D. Measurement and modeling of gas solubility and literature review of the properties for the carbon dioxide− water system. Ind. Eng. Chem. Res. 2004, 43, 1794–1802. [Google Scholar] [CrossRef]
- Chapoy, A.; Mohammadi, A.H.; Richon, D.; Tohidi, B. Gas solubility measurement and modeling for methane–water and methane–ethane–n-butane–water systems at low temperature conditions. Fluid Phase Equilibria 2004, 220, 113–121. [Google Scholar] [CrossRef]
- Darwish, N.; Hilal, N. A simple model for the prediction of CO2 solubility in H2O–NaCl system at geological sequestration conditions. Desalination 2010, 260, 114–118. [Google Scholar] [CrossRef]
- Duan, Z.; Mao, S. A thermodynamic model for calculating methane solubility, density and gas phase composition of methane-bearing aqueous fluids from 273 to 523 K and from 1 to 2000 bar. Geochim. Cosmochim. Acta 2006, 70, 3369–3386. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Dubessy, J.; Tarantola, A.; Sterpenich, J. Modelling of liquid-vapour equilibria in the H2O-CO2-NaCl and H2O-H2S-NaCl systems to 270 C. Oil Gas Sci. Technol. 2005, 60, 339–355. [Google Scholar] [CrossRef] [Green Version]
- Mao, S.; Duan, Z. A thermodynamic model for calculating nitrogen solubility, gas phase composition and density of the N2–H2O–NaCl system. Fluid Phase Equilibria 2006, 248, 103–114. [Google Scholar] [CrossRef]
- Portier, S.; Rochelle, C. Modelling CO2 solubility in pure water and NaCl-type waters from 0 to 300 °C and from 1 to 300 bar: Application to the Utsira Formation at Sleipner. Chem. Geol. 2005, 217, 187–199. [Google Scholar] [CrossRef]
- Shi, X.; Mao, S. An improved model for CO2 solubility in aqueous electrolyte solution containing Na+, K+, Mg2+, Ca2+, Cl− and SO42− under conditions of CO2 capture and sequestration. Chem. Geol. 2017, 463, 12–28. [Google Scholar] [CrossRef]
- Søreide, I.; Whitson, C.H. Peng-Robinson predictions for hydrocarbons, CO2, N2, and H2S with pure water and NaCI brine. Fluid Phase Equilibria 1992, 77, 217–240. [Google Scholar] [CrossRef]
- Spivey, J.P.; McCain, W.D.; North, R. Estimating density, formation volume factor, compressibility, methane solubility, and viscosity for oilfield brines at temperatures from 0 to 275 °C, pressures to 200 MPa, and salinities to 5.7 mole/kg. J. Can. Pet. Technol. 2004, 43. [Google Scholar] [CrossRef]
- Mao, S.; Zhang, D.; Li, Y.; Liu, N. An improved model for calculating CO2 solubility in aqueous NaCl solutions and the application to CO2–H2O–NaCl fluid inclusions. Chem. Geol. 2013, 347, 43–58. [Google Scholar] [CrossRef]
- Dhima, A.; de Hemptinne, J.-C.; Jose, J. Solubility of hydrocarbons and CO2 mixtures in water under high pressure. Ind. Eng. Chem. Res. 1999, 38, 3144–3161. [Google Scholar] [CrossRef]
- Qin, J.; Rosenbauer, R.J.; Duan, Z. Experimental measurements of vapor–liquid equilibria of the H2O+ CO2+ CH4 ternary system. J. Chem. Eng. Data 2008, 53, 1246–1249. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, M.; Ning, H.; Yang, D.; Yang, G.; Han, B. Phase equilibria of CO2+ N2+ H2O and N2+ CO2+ H2O+ NaCl+ KCl+ CaCl2 systems at different temperatures and pressures. J. Chem. Eng. Data 2012, 57, 1928–1932. [Google Scholar] [CrossRef]
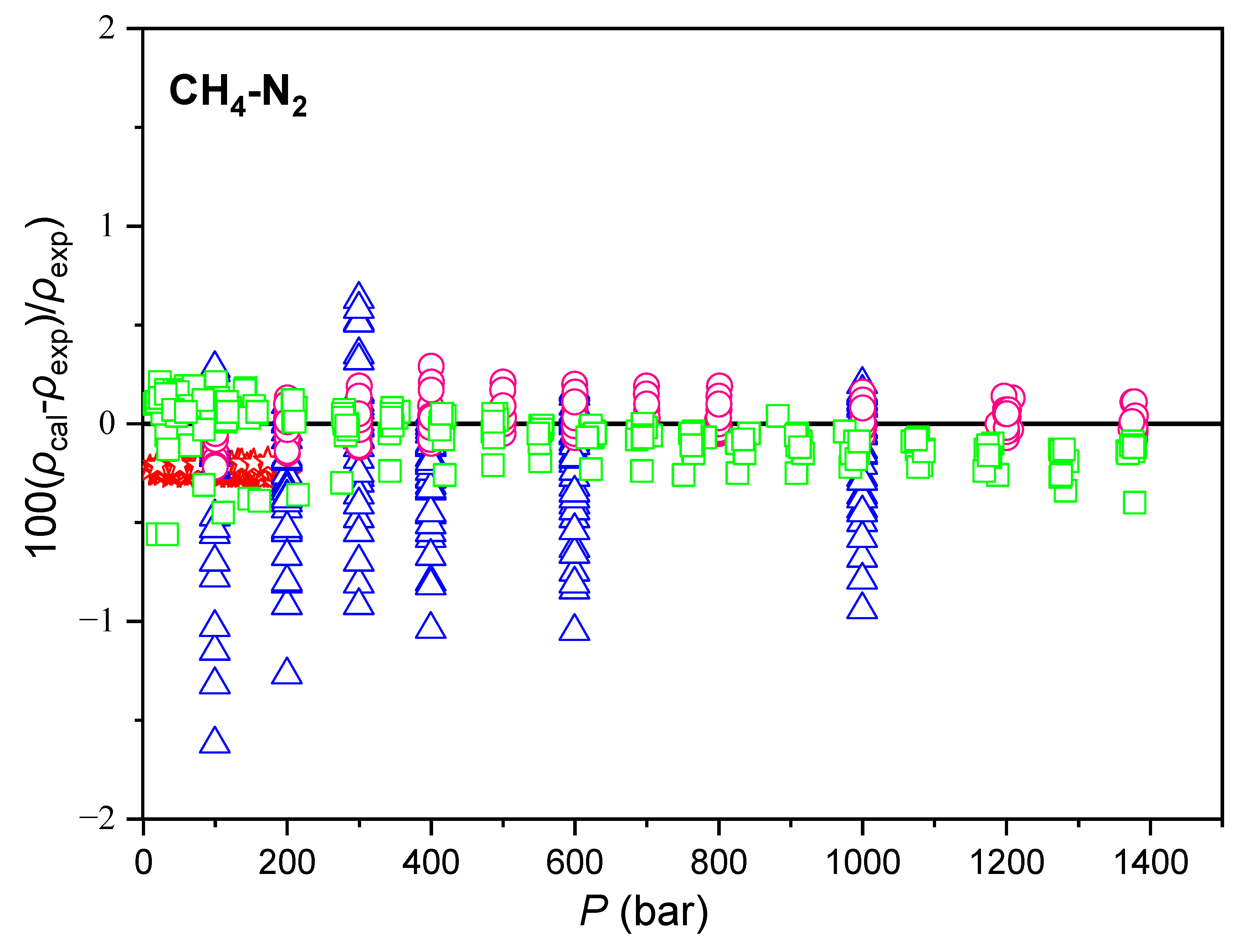
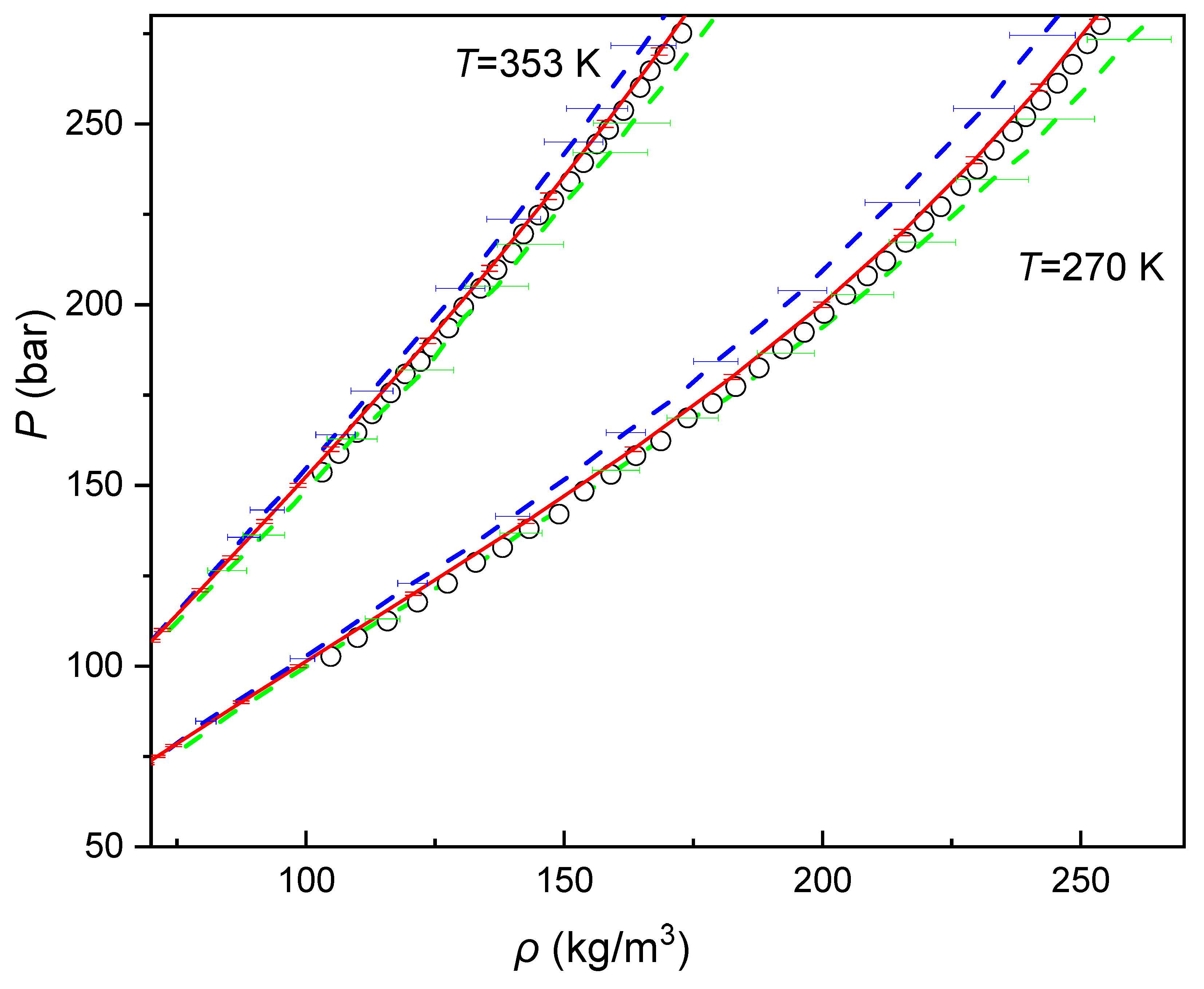
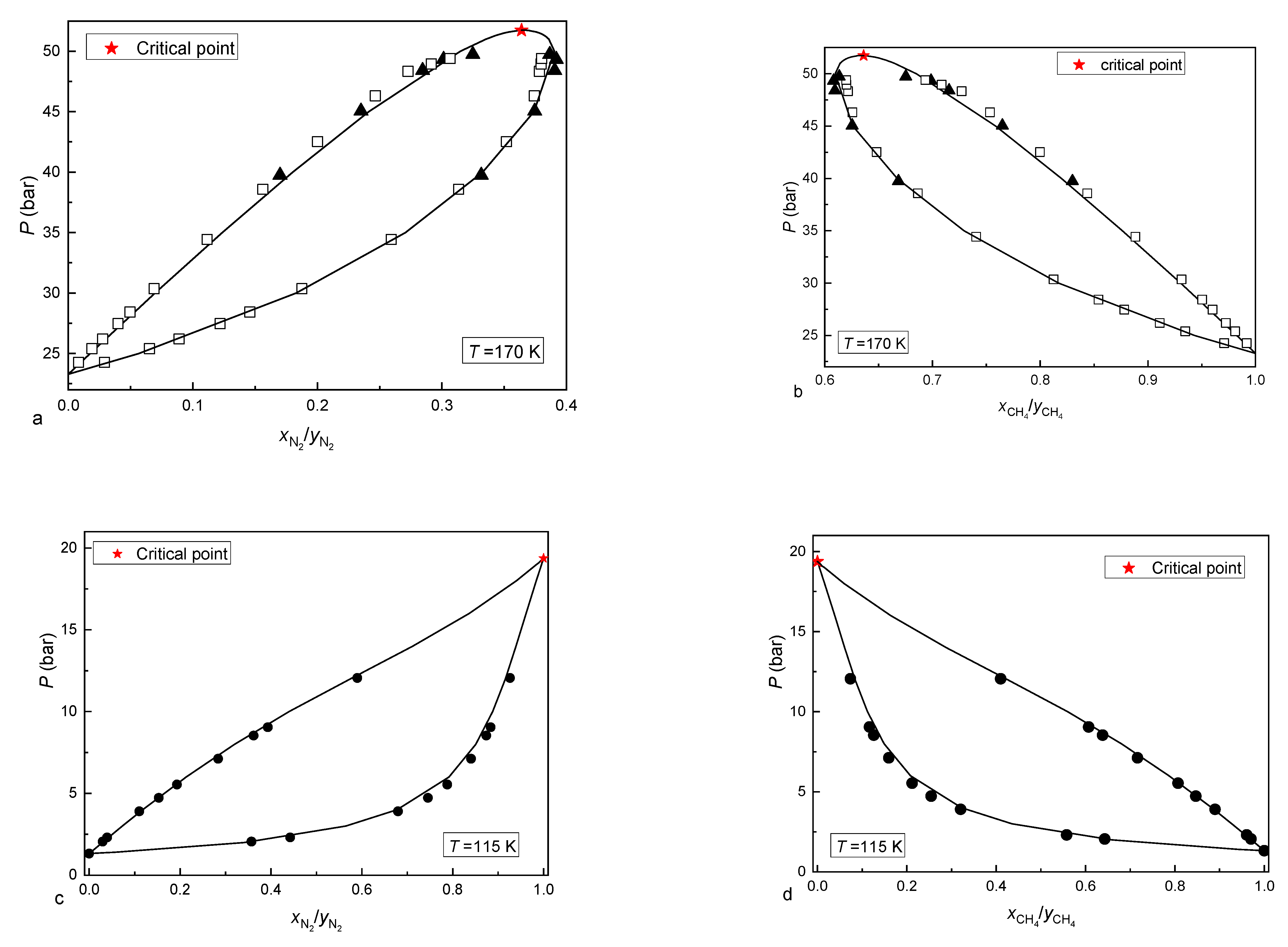

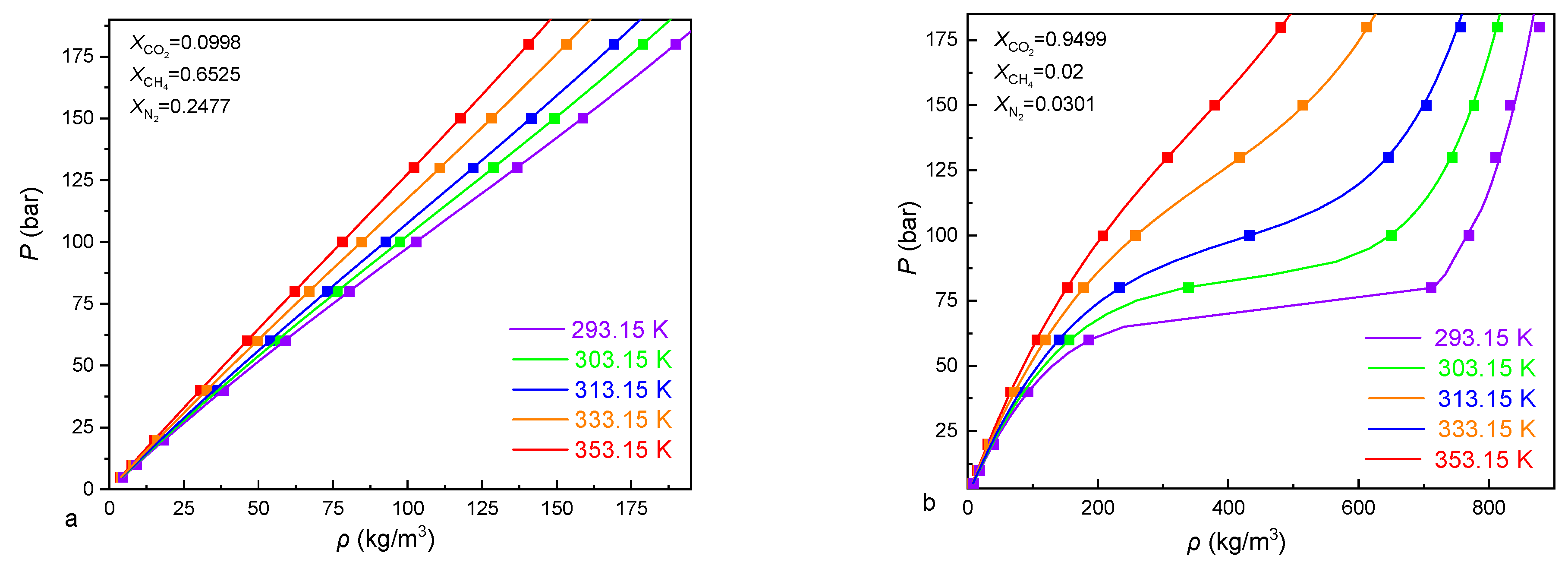





| Component i | References | ||
|---|---|---|---|
| CH4 | 90.6941 | 10.139 | Setzmann and Wagner [42] |
| CO2 | 216.592 | 10.625 | Span and Wagner [41] |
| N2 | 63.151 | 11.184 | Span et al. [43] |
| References | Binary Mixtures | ||||
|---|---|---|---|---|---|
| Mao et al. [40] | CH4-CO2 | 0.12844025 × 10 | 0.35751245 × 10−2 | −0.43720344 × 102 | 0.10358865 × 10 |
| Zhang et al. [34] | CO2-N2 | 0.16671494 × 10 | 0.58411078 × 10−2 | −0.22952094 × 102 | 0.16878787 × 10 |
| This work | CH4-N2 | 0.63739997 | 0.3812517 × 10−2 | −0.17790001 × 102 | 0.1009001 × 10 |
| References | Number of Data Points | T-P-x Range for xCH4-(1-x) N2 | AAD% | |||
|---|---|---|---|---|---|---|
| Styles | Total (Used) | T (K) | P (bar) | x | ||
| Liu and Miller [45] | PVTx | 7 (0) | 91–115 | 3–12 | 0.5 | 0.57 |
| Rodosevich and Miller [46] | PVTx | 8 (0) | 91–115 | 43–454 | 0.8–0.95 | 3.83 |
| Pan et al. [47] | PVTx | 7 (0) | 91–115 | 1–11 | 0.5–0.86 | 0.11 |
| Hiza et al. [48] | PVTx | 21 (0) | 95–140 | 1–21 | 0.5–0.95 | 0.10 |
| Da Ponte et al. [49] | PVTx | 182 (50) | 110–120 | 15–1380 | 0.3–0.68 | 0.12 |
| Straty and Diller [65] | PVTx | 578 (0) | 82–320 | 6–356 | 0.32–0.7 | 0.24 |
| Haynes and McCarty [56] | PVTx | 85 (85) | 140–320 | 10–164 | 0.3–0.71 | 0.09 |
| Seitz et al. [64] | PVTx | 190 (90) | 323–573 | 99–999 | 0.1–0.9 | 0.28 |
| Seitz and Blencoe [63] | PVTx | 43 (0) | 673.15 | 199–999 | 0.1–0.9 | 5.36 |
| Ababio et al. [50] | PVTx | 83 (83) | 308–333 | 9–120 | 0.5–0.78 | 0.12 |
| Chamorro et al. [52] | PVTx | 242 (56) | 230–400 | 9–192 | 0.8–0.9 | 0.23 |
| Janisch et al. [57] | PVTx | 17 (0) | 129–180 | 15–50 | 0.4–0.9 | 2.10 |
| Li et al. [60] | PVTx | 27 (27) | 17–270 | 1–16 | 0.9 | 0.06 |
| Gomez-Osorio et al. [54] | PVTx | 142 (42) | 304–470 | 100–1379 | 0.25–0.75 | 0.07 |
| Brandt and Stroud [51] | VLE | 23 (0) | 128–179 | 34 | 0.05–0.98 | 1.48 |
| Cheung and Wang [53] | VLE | 20 (0) | 92–124 | 0.2–6 | 0.85–1.0 | 5.02 |
| Pan et al. [47] | VLE | 60 (60) | 95–120 | 0.2–25 | 0.05–1 | 5.05 |
| Miller et al. [62] | VLE | 11 (0) | 112 | 2–13 | 0.2–0.97 | 3.30 |
| Kidnay et al. [59] | VLE | 83 (83) | 112–180 | 2–49 | 0.1–0.99 | 1.31 |
| McClure et al. [61] | VLE | 8 (8) | 91 | 1–3 | 0.1–0.8 | 5.60 |
| Jin et al. [58] | VLE | 10 (10) | 123 | 4–26 | 0.1–0.95 | 2.96 |
| Parrish and Hiza [66] | VLE | 48 (43) | 95–120 | 2–20 | 0.1–0.9 | 3.14 |
| Janisch et al. [57] | VLE | 16 (6) | 130–180 | 0.5–5 | 0.4–0.96 | 1.14 |
| Han et al. [55] | VLE | 77 (60) | 110–123 | 4–13 | 0.7–1.0 | 2.49 |
| References | N | T-P-x Range for xCO2-yCH4-(1-x-y) N2 | AAD% | |||
|---|---|---|---|---|---|---|
| T (K) | P (bar) | x | y | |||
| McElroy et al. [59] | 242 | 303–333 | 6–126 | 0–0.9998 | 0–0.999 | 0.45 |
| Seitz et al. [60] | 42 | 474.15 | 1000 | 0.0–1.0 | 0.0–1.0 | 0.28 |
| Seitz et al. [55] | 271 | 323–573 | 199–999 | 0.1–0.8 | 0.1–0.8 | 0.28 |
| Zhang et al. [61] | 200 | 293.15–353.25 | 5–180 | 0.098–0.9949 | 0.02–0.6525 | 0.52 |
| Le et al. [1] | 84 | 305.15 | 5–600 | 0.499–0.899 | 0.0505–0.331 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Mao, S.; Shi, Z. A Helmholtz Free Energy Equation of State of CO2-CH4-N2 Fluid Mixtures (ZMS EOS) and Its Applications. Appl. Sci. 2023, 13, 3659. https://doi.org/10.3390/app13063659
Zhang J, Mao S, Shi Z. A Helmholtz Free Energy Equation of State of CO2-CH4-N2 Fluid Mixtures (ZMS EOS) and Its Applications. Applied Sciences. 2023; 13(6):3659. https://doi.org/10.3390/app13063659
Chicago/Turabian StyleZhang, Jia, Shide Mao, and Zeming Shi. 2023. "A Helmholtz Free Energy Equation of State of CO2-CH4-N2 Fluid Mixtures (ZMS EOS) and Its Applications" Applied Sciences 13, no. 6: 3659. https://doi.org/10.3390/app13063659
APA StyleZhang, J., Mao, S., & Shi, Z. (2023). A Helmholtz Free Energy Equation of State of CO2-CH4-N2 Fluid Mixtures (ZMS EOS) and Its Applications. Applied Sciences, 13(6), 3659. https://doi.org/10.3390/app13063659







