H∞ Optimization of a Novel Maxwell Dynamic Vibration Absorber with Lever, Inerter, and Grounded Stiffness
Abstract
1. Introduction
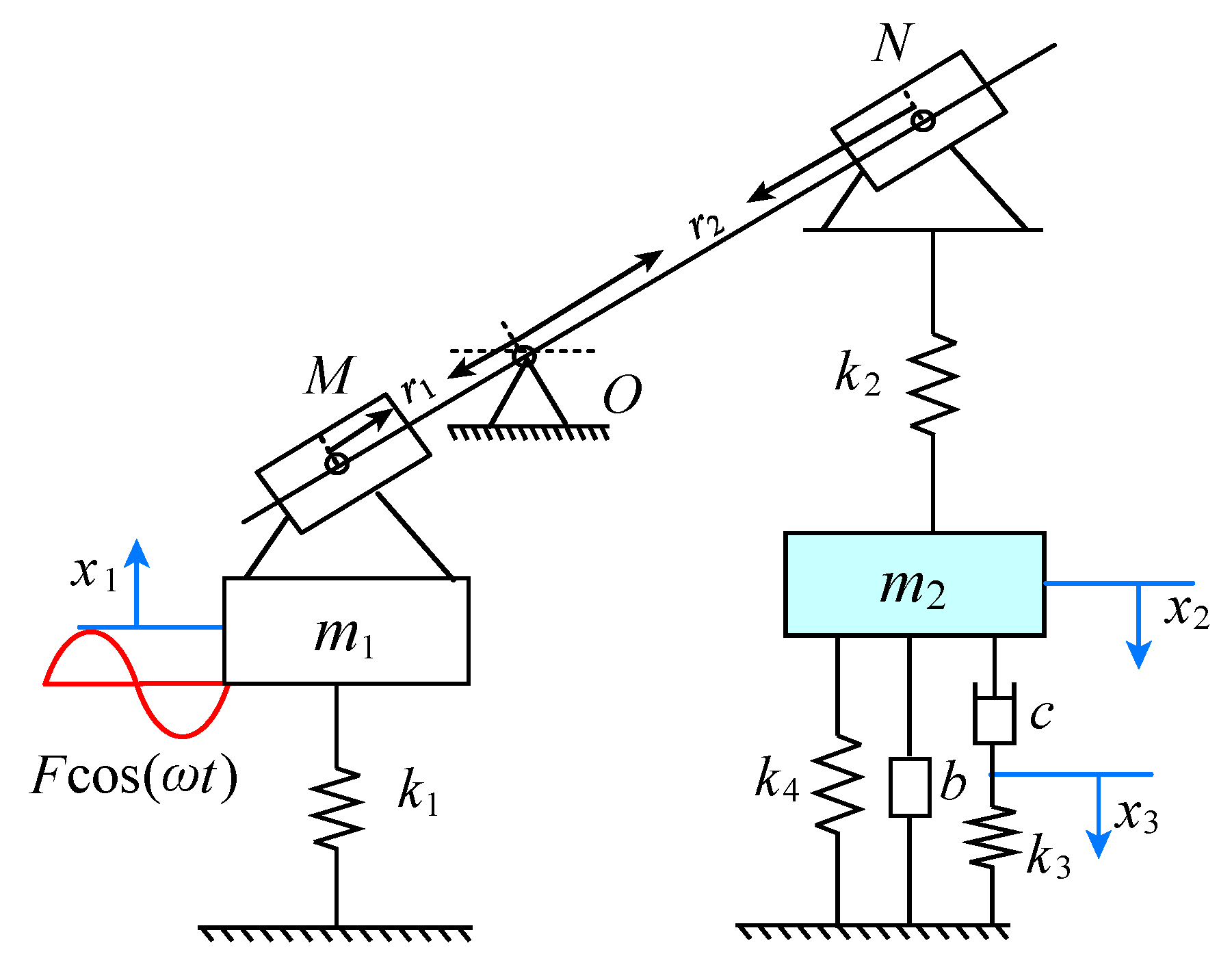
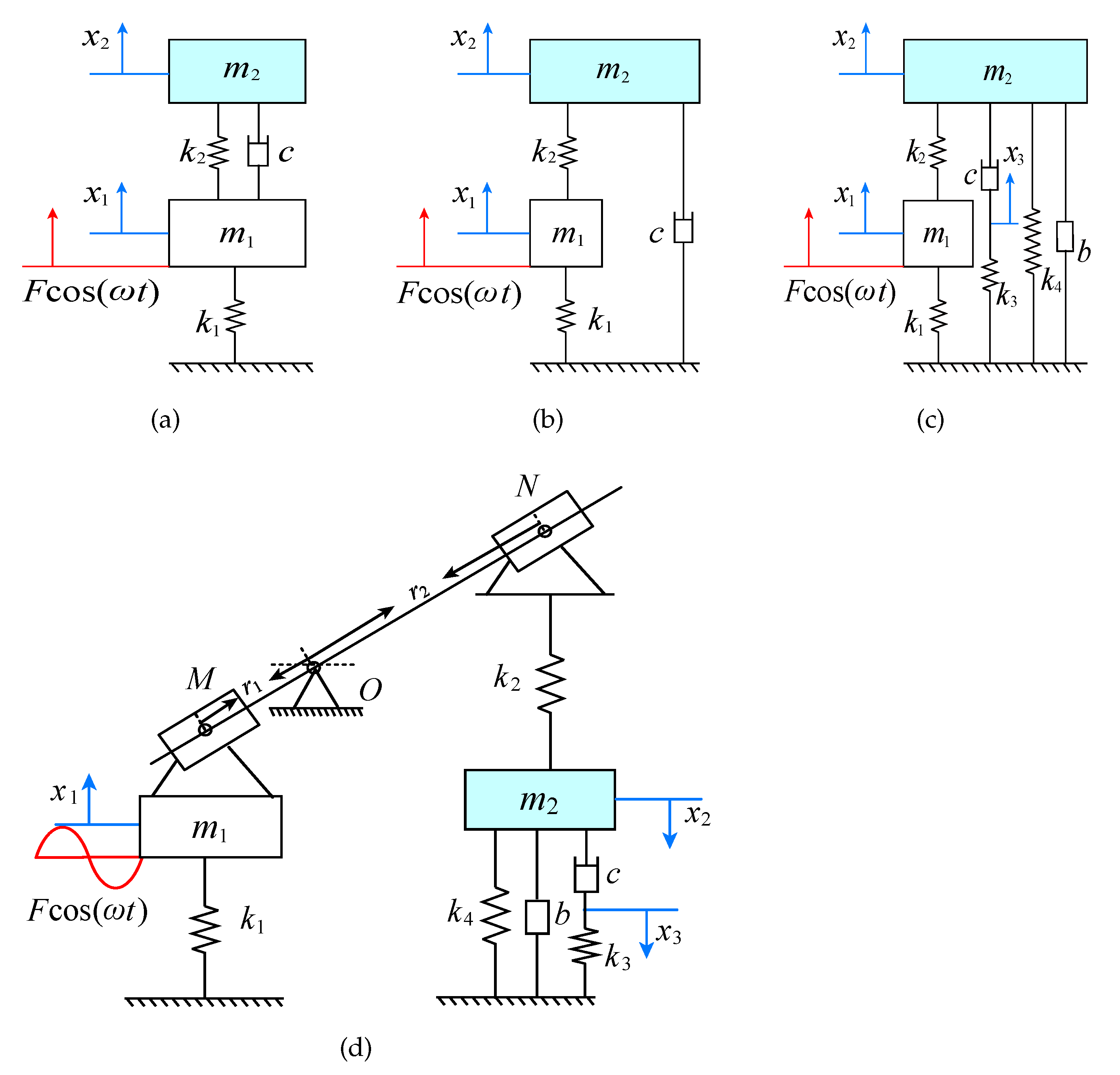
2. Dynamic Model and Parameters Optimization
2.1. The Analytical Solution
2.2. Parameters Optimization
3. Analysis of the Working Ranges of Inerter in Different Conditions
3.1. The Working Range of Inerter
3.2. Response Characteristics of Primary System for Different Cases
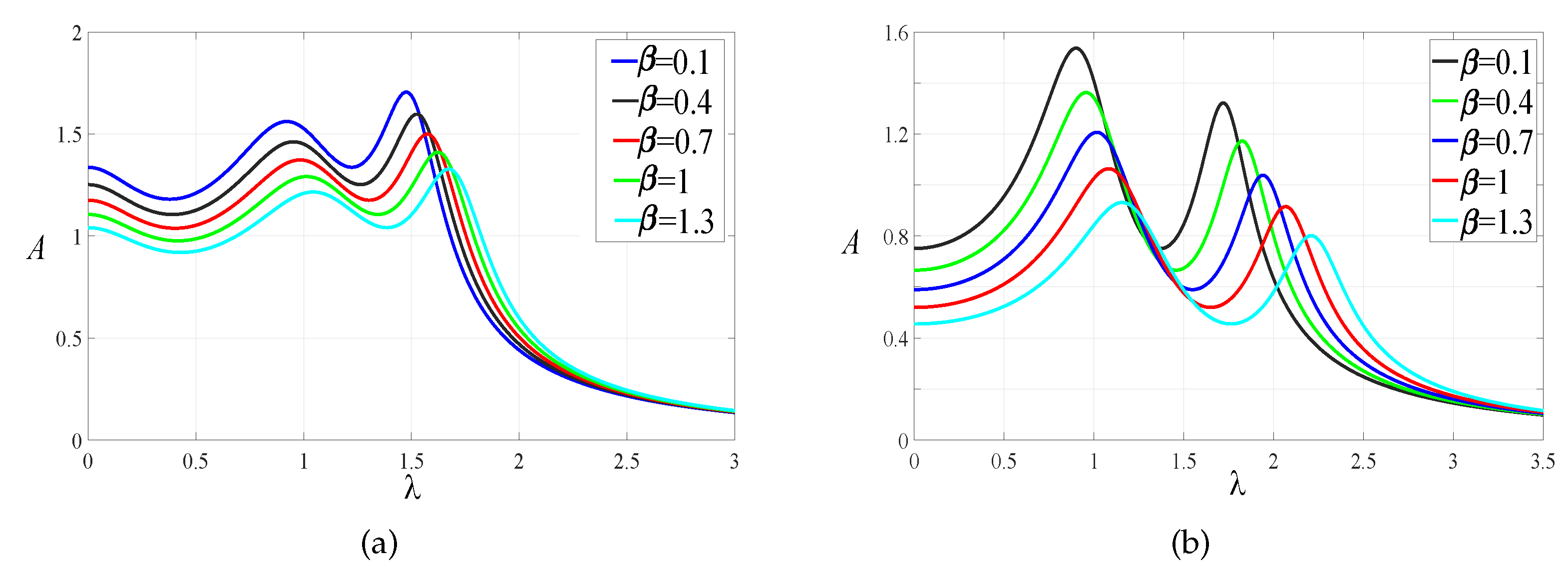
4. The Influence of System Parameters on Response Characteristics
4.1. The Relationship between System Parameters and Optimal Parameters
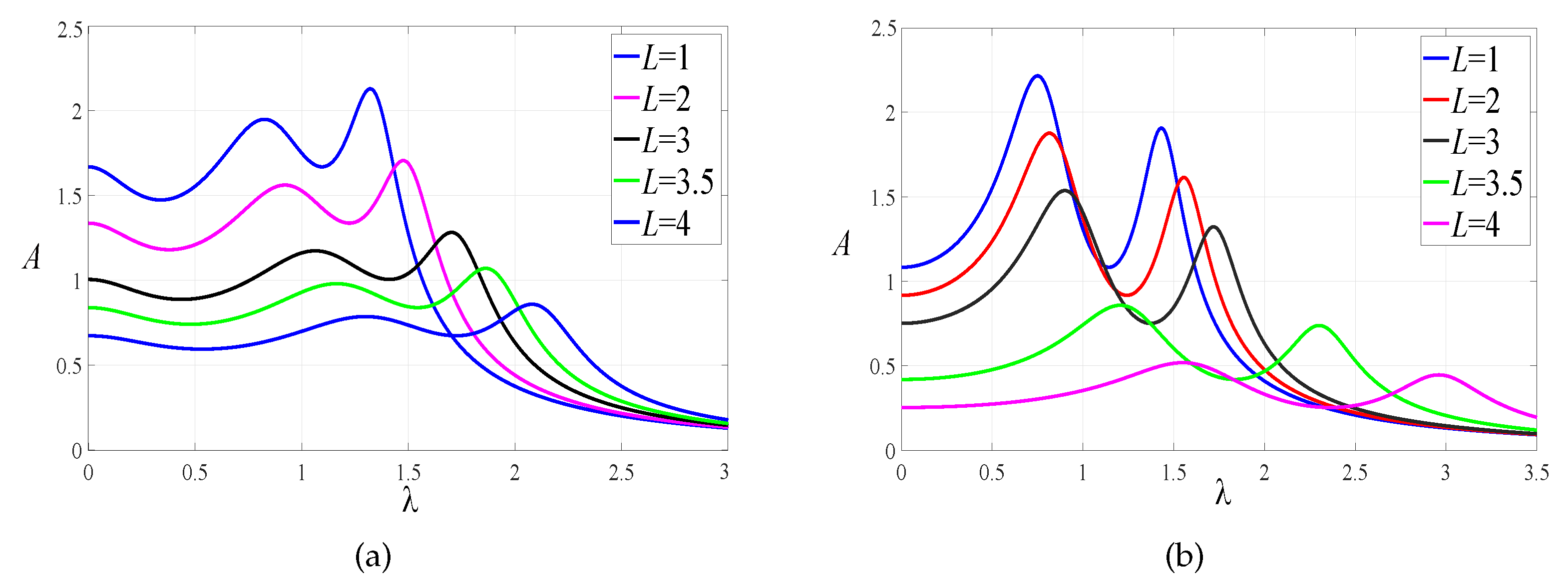
4.2. The Effect of Lever Mechanism on the Amplitude of Primary System
4.3. The Effect of Inerter–Mass Ratio on the Amplitude of the Primary System
5. Comparisons of the Control Performances
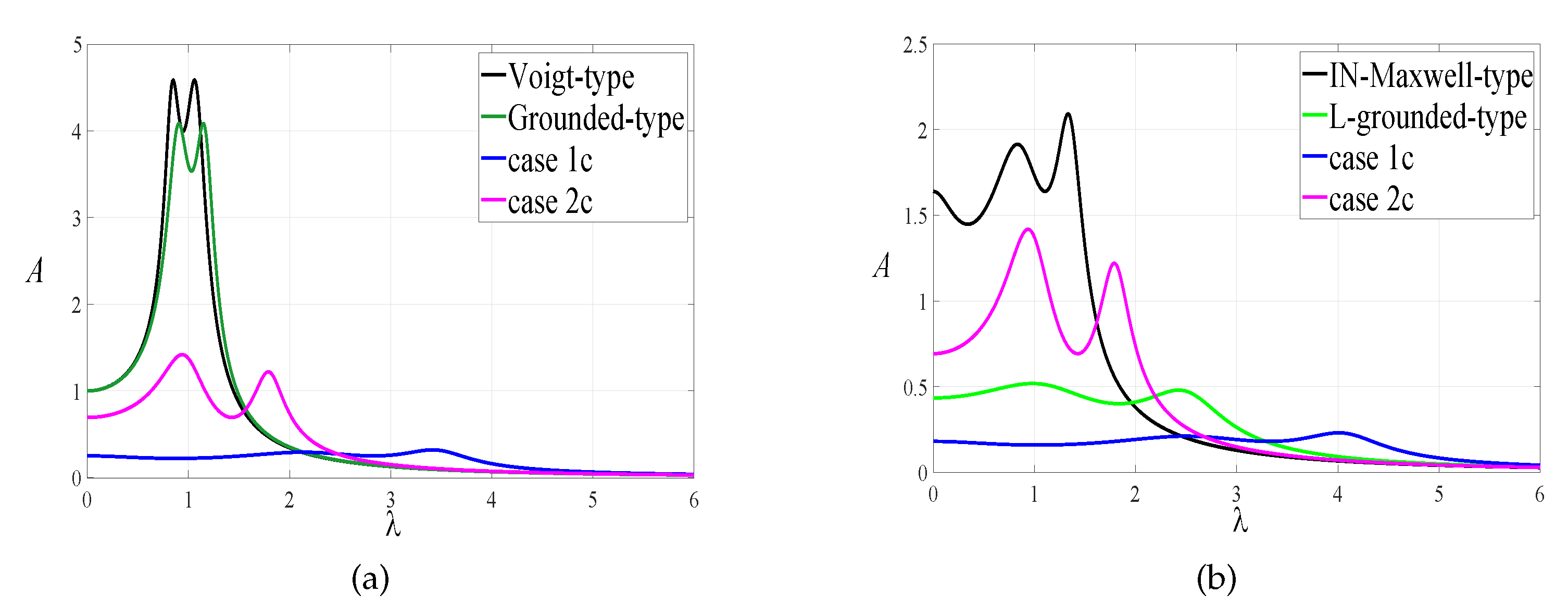
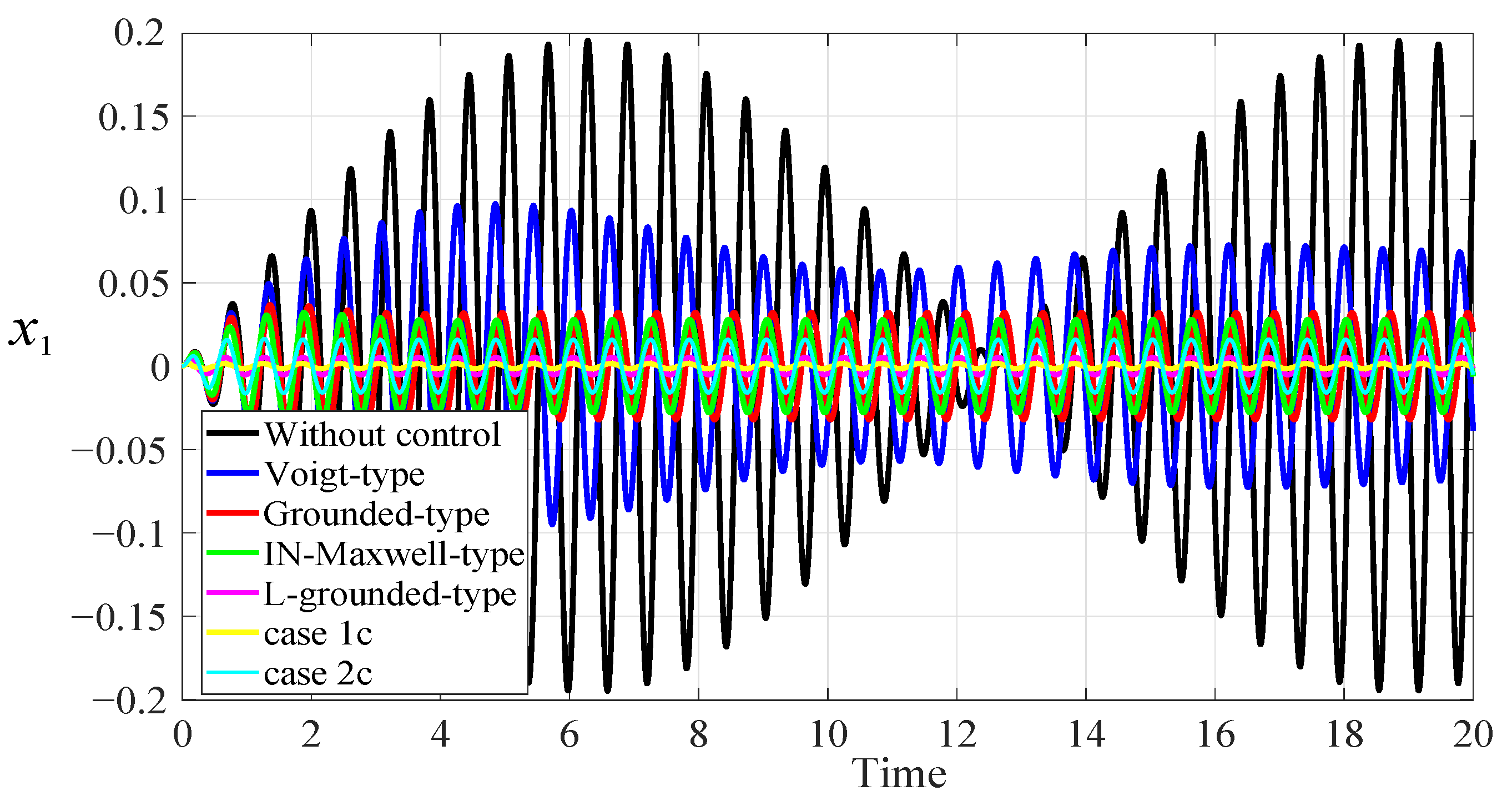
5.1. Comparison with Other DVAs under Harmonic Excitation
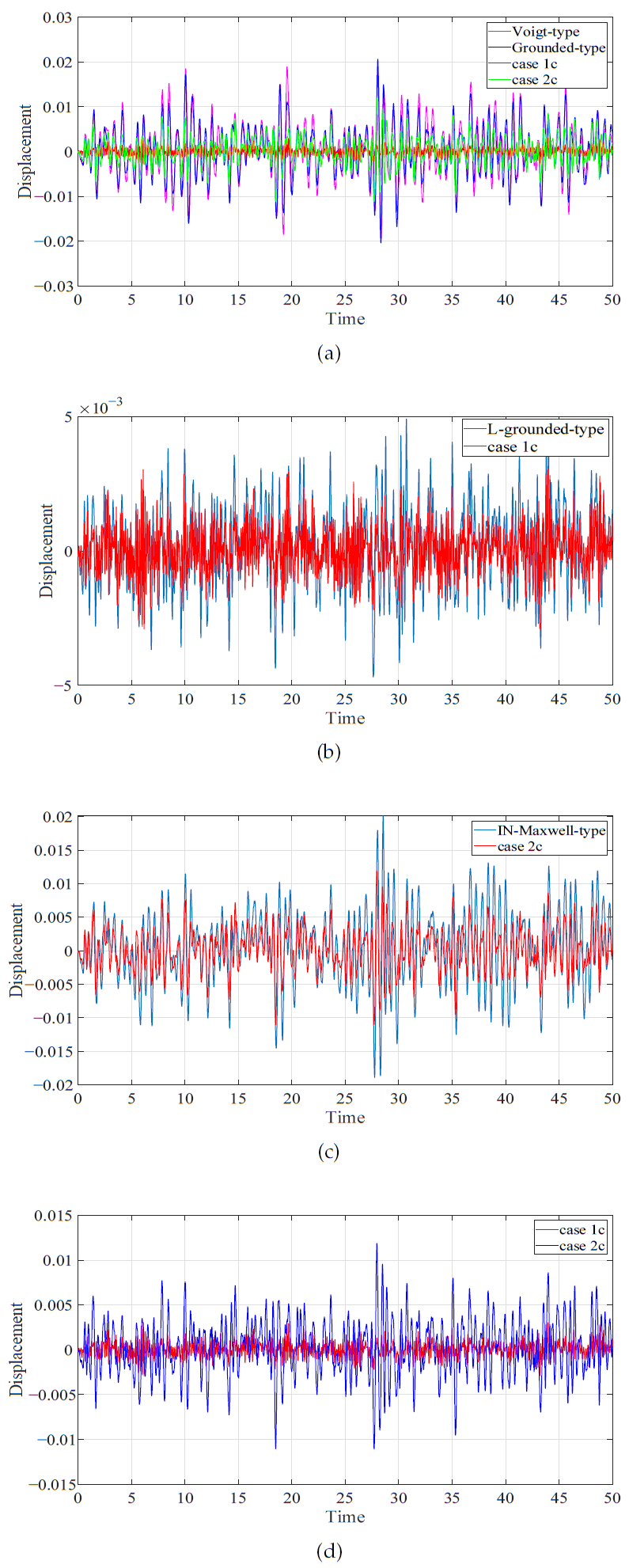
5.2. The Comparison with Other DVAs under Random Excitation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hermann, F. Device for Damping Vibrations of Bodies. U.S. Patent 0,989,958, 30 October 1909. [Google Scholar]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. J. Appl Mech. 1928, 50, 9–22. [Google Scholar]
- Asami, T.; Nishihara, O. Analytical and experimental evaluation of an air damped dynamic vibration absorber: Design optimizations of the three-element type model. J. Vib. Acoust. 1999, 121, 334–342. [Google Scholar] [CrossRef]
- Ren, M.Z. A variant design of the dynamic vibration absorber. J. Sound Vib. 2001, 245, 762–770. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hall Book Company: New York, NY, USA, 1947. [Google Scholar]
- Wong, W.O.; Fan, R.P.; Cheng, F. Design optimization of a viscoelastic dynamic vibration absorber using a modified fixed-points theory. J. Acoust Soc. Am. 2018, 143, 1064. [Google Scholar] [CrossRef] [PubMed]
- Batou, A.; Adhikari, S. Optimal parameters of viscoelastic tuned-mass dampers. J. Sound Vib. 2019, 445, 17–28. [Google Scholar] [CrossRef]
- Chang, T.L.; Lee, C.L. Numerical simulation of generalised Maxwell-type viscous dampers with an efficient iterative algorithm. Mech. Syst. Signal Process. 2022, 170, 108795. [Google Scholar] [CrossRef]
- Dai, J.; Xu, Z.D.; Gai, P.P.; Hu, Z.W. Optimal design of tuned mass damper inerter with a Maxwell element for mitigating the vortex-induced vibration in bridges. Mech. Syst. Signal Process. 2021, 148, 107180. [Google Scholar] [CrossRef]
- Shen, Y.J.; Peng, H.B.; Li, X.H.; Yang, S.P. Analytically optimal parameters of dynamic vibration absorber with negative stifness. Mech. Syst. Signal Process. 2017, 85, 192–203. [Google Scholar] [CrossRef]
- Wang, X.R.; He, T.; Shen, Y.J.; Shan, Y.C.; Liu, X.D. Parameters optimization and performance evaluation for the novel inerter-based dynamic vibration absorbers with negative stiffness. J. Sound Vib. 2019, 463, 114941. [Google Scholar] [CrossRef]
- Yao, H.L.; Cao, Y.B.; Wang, Y.W.; Wen, B.C. A tri-stable nonlinear energy sink with piecewise stiffness. J. Sound Vib. 2019, 463, 114971. [Google Scholar] [CrossRef]
- Salvatore, A.; Carboni, B.; Lacarbonara, W. Nonlinear dynamic response of an isolation system with superelastic hysteresis and negative stiffness. Nonlinear Dyn. 2021, 107, 1765–1790. [Google Scholar] [CrossRef]
- Chang, Y.P.; Zhou, J.X.; Wang, K.; Xu, D.L. A quasi-zero-stiffness dynamic vibration absorber. J. Sound Vib. 2021, 494, 115859. [Google Scholar] [CrossRef]
- Baduidana, M.; Kenfack-Jiotsa, A. Parameters optimization and performance evaluation for the novel tuned inertial damper. Eng. Struct. 2022, 250, 113396. [Google Scholar] [CrossRef]
- Zhang, M.J.; Xu, F. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind Eng. Ind. Aerod. 2021, 220, 104836. [Google Scholar] [CrossRef]
- Zhang, M.J.; Song, Y.; Abdelkefi, A.; Yu, H.Y.; Wang, J.L. Vortex-induced vibration of a circular cylinder with nonlinear stiffness: Prediction using forced vibration data. Nonlinear Dyn. 2022, 108, 1867–1884. [Google Scholar] [CrossRef]
- He, M.X.; Tang, Y.; Ding, Q. Dynamic analysis and optimization of a cantilevered beam with both the acoustic black hole and the nonlinear energy sink. J. Int. Mat. Syst. Str. 2022, 33, 70–83. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter. J. Struct. Eng. 2018, 144, 08217004. [Google Scholar] [CrossRef]
- Chen, Q.J.; Zhao, Z.P.; Xia, Y.Y.; Pan, C.; Luo, H.; Zhang, R.F. Comfort based floor design employing tuned inerter mass system. J. Sound Vib. 2019, 458, 143–157. [Google Scholar] [CrossRef]
- Xu, K.; Bi, K.M.; Han, Q.; Li, X.P.; Du, X.L. Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: Analytical study. Eng. Struct. 2019, 182, 101–111. [Google Scholar] [CrossRef]
- Wang, X.R.; Liu, X.D.; Shan, Y.C.; Shen, Y.J.; He, T. Analysis and optimization of the novel inerter-based dynamic vibration absorbers. IEEE Access. 2018, 6, 33169–33182. [Google Scholar] [CrossRef]
- Yu, H.Y.; Zhang, M.J.; Hu, G. Effect of inerter locations on the vibration control performance of nonlinear energy sink inerter. Eng. Struct. 2022, 273, 115121. [Google Scholar] [CrossRef]
- Brzeski, P.; Kapitaniak, T.; Perlikowski, P. Novel type of tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 2015, 349, 56–66. [Google Scholar] [CrossRef]
- Javidialesaadi, A.; Wierschem, N.E. Three-element vibration absorber-inerter for passive control of single-degree-of-freedom structures. J. Vib. Acoust. 2018, 140, 061007. [Google Scholar] [CrossRef]
- Li, J.; Gu, X.Q.; Zhu, S.T.; Yu, C.L.; Yang, X.D. Parameter optimization for a novel inerter-based dynamic vibration absorber with negative stiffness. J. Nonlinear Math. Phy. 2022, 29, 280–295. [Google Scholar] [CrossRef]
- Baduidana, M.; Wang, X.R.; Kenfack-Jiotsa, A. Parameters optimization of series-parallel inerter system with negative stiffness in controlling a single-degree-of-freedom system under base excitation. J. Vib. Control 2021, 28, 864–881. [Google Scholar] [CrossRef]
- Kun, Y.; Nyangi, P. H∞ optimization of tuned inerter damper with negative stiffness device subjected to support excitation. Shock Vib. 2020, 7608078. [Google Scholar]
- Alotta, G.; Failla, G. Improved inerter-based vibration absorbers. Int. J. Mech. Sci. 2020, 192, 106087. [Google Scholar] [CrossRef]
- Weber, F.; Borchsenius, F.; Distl, J.; Braun, C. Performance of numerically optimized tuned mass damper with inerter. Appl. Sci. 2022, 12, 6204. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Z.Q.; Ding, H.; Chen, L.Q. An inertial nonlinear energy sink. J. Sound Vib. 2019, 450, 199–213. [Google Scholar] [CrossRef]
- Flannelly, W.G. Dynamic Antiresonant Vibration Isolator. U.S. Patent 3,322,379, 29 April 1967. [Google Scholar]
- Li, C.X.; Li, Q.S. Evaluation of the lever-type multiple tuned mass dampers for mitigating harmonically forced vibration. Int. J. Struct. Stab. Dyn. 2004, 5, 641–664. [Google Scholar] [CrossRef]
- Liu, C.C.; Jing, X.J.; Chen, Z.B. Band stop vibration suppression using a passive X-shape structured lever-type isolation system. Mech. Syst. Signal Process. 2016, 68–69, 342–353. [Google Scholar] [CrossRef]
- Zang, J.; Yuan, T.C.; Lu, Z.Q.; Zhang, Y.W.; Ding, H.; Chen, L.Q. A lever-type nonlinear energy sink. J. Sound Vib. 2018, 437, 119–134. [Google Scholar] [CrossRef]
- Cao, R.Q.; Wang, Z.J.; Zang, J.; Zhang, Y.W. Resonance response of fluid-conveying pipe with asymmetric elastic supports coupled to lever-type nonlinear energy sink. Appl. Math. Mech. 2023, 43, 1873–1886. [Google Scholar] [CrossRef]
- Yan, B.; Wang, Z.H.; Ma, H.Y.; Bao, H.H.; Wang, K.; Wu, C.Y. A novel lever-type vibration isolator with eddy current damping. J. Sound Vib. 2021, 494, 115862. [Google Scholar] [CrossRef]
- Shen, Y.J.; Xing, Z.Y.; Yang, S.P.; Sun, J.Q. Parameters optimization for a novel dynamic vibration absorber. Mech. Syst. Signal Process. 2019, 133, 106282. [Google Scholar] [CrossRef]
- Sui, P.; Shen, Y.J.; Yang, S.P.; Wang, J.F. Parameters optimization of dynamic vibration absorber based on grounded stiffness, inerter, and amplifying mechanism. J. Vib. Control 2021, 28, 3767–3779. [Google Scholar] [CrossRef]
- Shi, A.M.; Shen, Y.J.; Wang, J.F. Parameter optimization of a grounded dynamic vibration absorber with lever and inerter. J. Low Freq. Noise, Vib. Act. Control 2022, 41, 784–798. [Google Scholar] [CrossRef]
- Churchill, C.B.; Shahan, D.W.; Smith, S.P.; Keefe, A.C.; McKnight, G.P. Dynamically variable negative stiffness structures. Sci. Adv. 2016, 2, e1500778. [Google Scholar] [CrossRef] [PubMed]
- Qu, S.C.; Gao, N.; Tinel, A.; Morvan, B.; Romero-García, V.; Jean-Philippe, G.; Sheng, P. Underwater metamaterial absorber with impedance-matched composite. Sci. Adv. 2022, 8, eabm4206. [Google Scholar] [CrossRef]
- Basta, E.; Ghommem, M.; Emam, S. Flutter control and mitigation of limit cycle oscillations in aircraft wings using distributed vibration absorbers. Nonlinear Dyn. 2021, 106, 1975–2003. [Google Scholar] [CrossRef]
- Du, Y.; Zou, T.D.; Pang, F.Z.; Hu, C.; Ma, Y.; Li, H.C. Design method for distributed dynamic vibration absorbers of stiffened plate under different constraints. Thin-Walled Struct. 2023, 185, 110494. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.N.; Wang, D. Unique normal form of a class of 3 dimensional vector fields with symmetries. J. Differ. Equations 2014, 257, 2341–2359. [Google Scholar] [CrossRef]

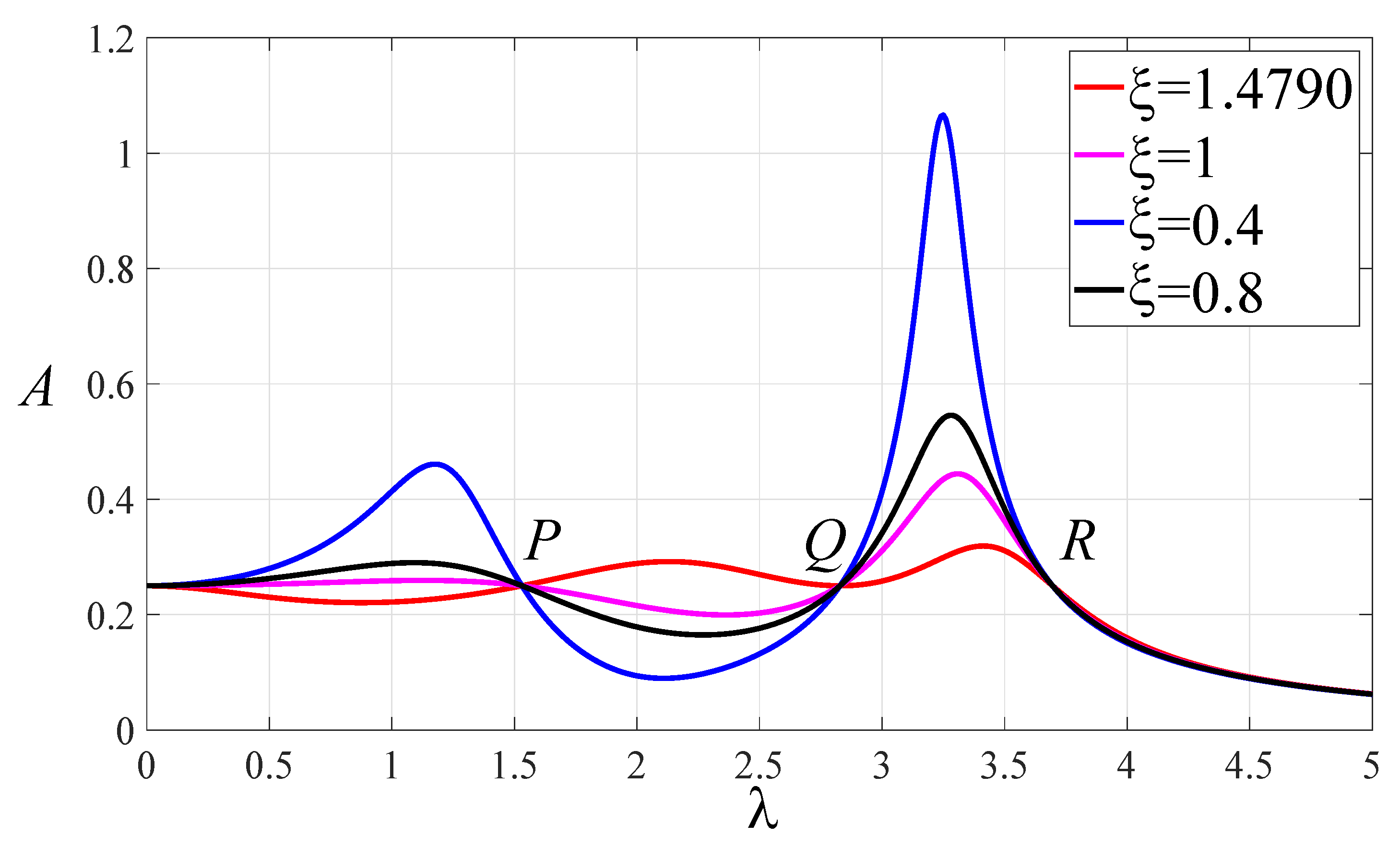

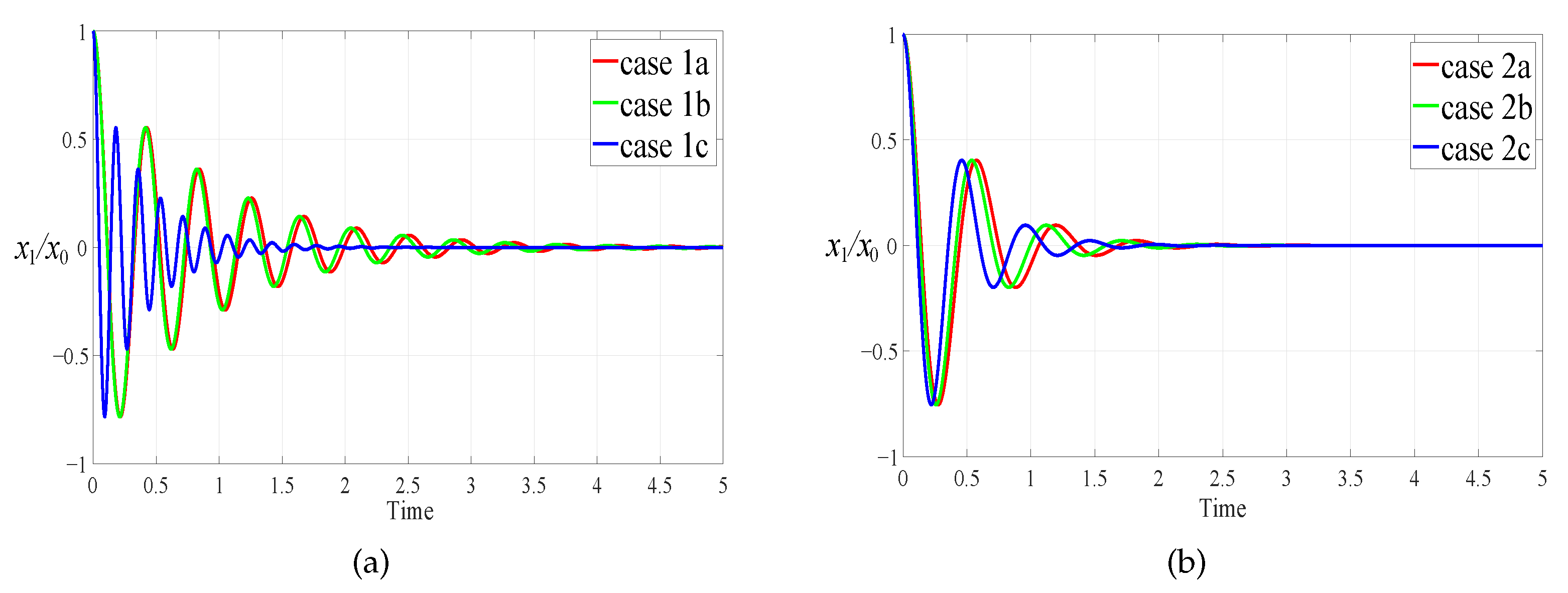

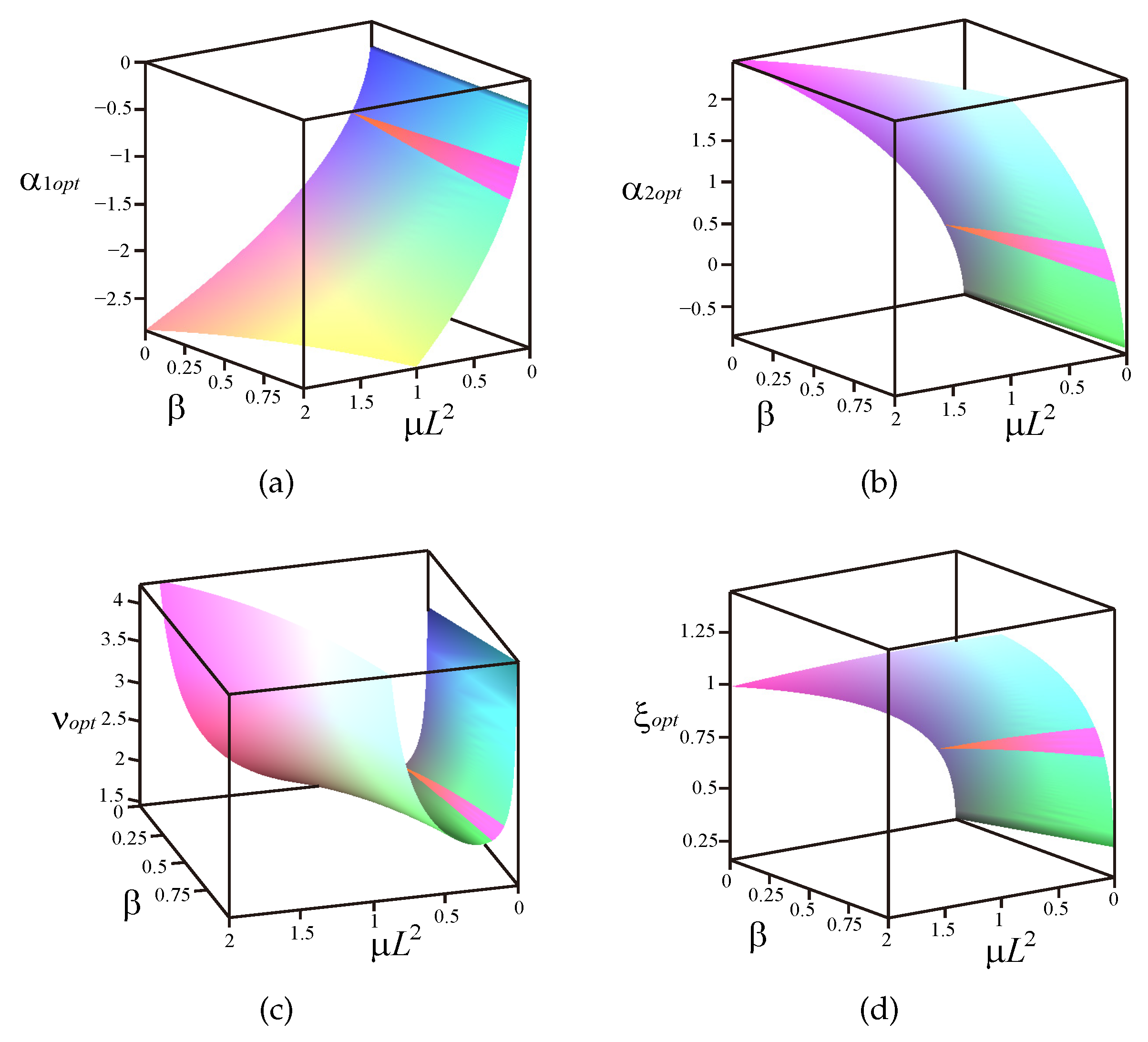
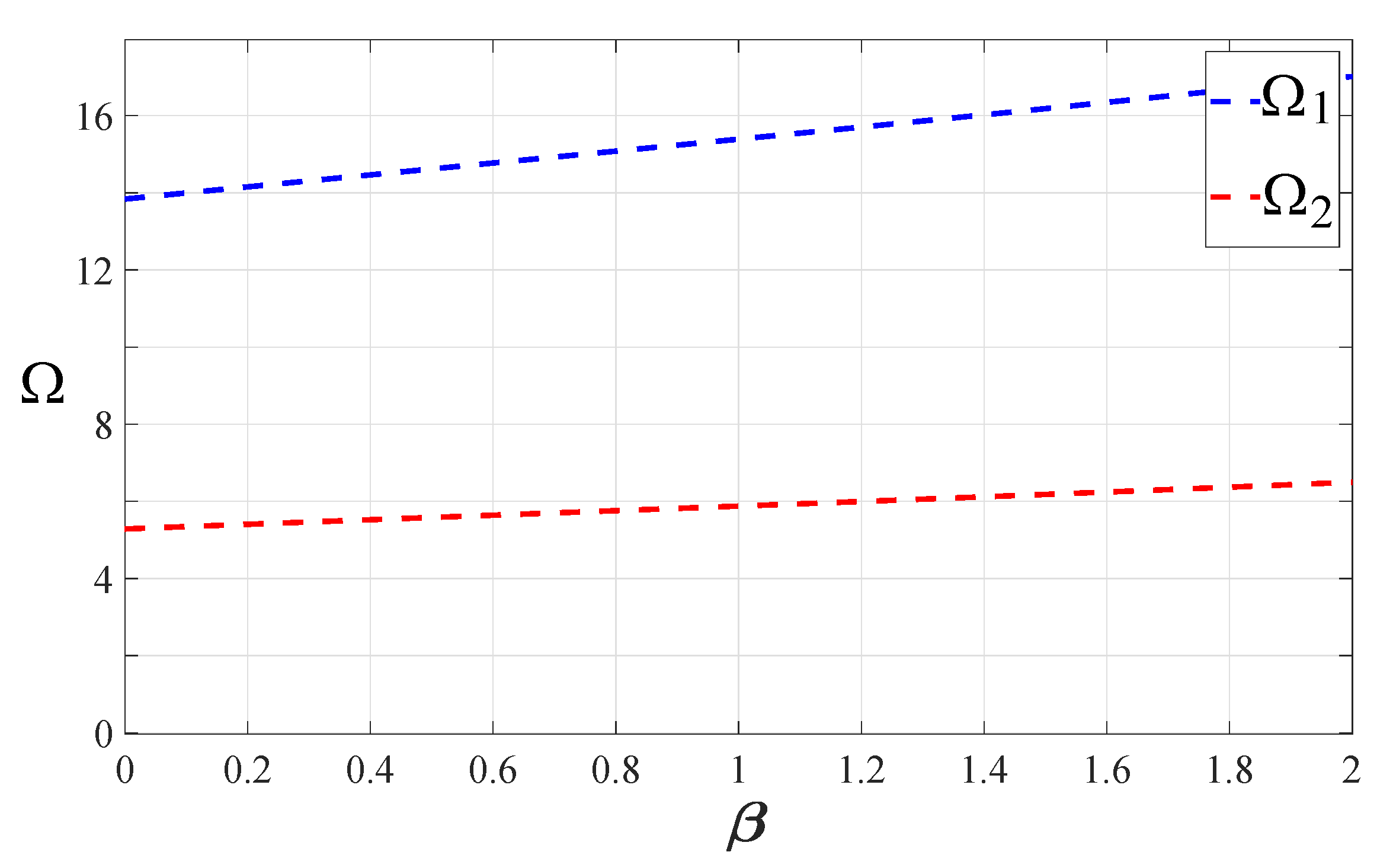
| Different Cases | The Sign of | The Sign of | Ranges of | Ranges of |
| case 1a | ||||
| case 1b | ||||
| case 1c | ||||
| case 2a | ||||
| case 2b | ||||
| case 2c |
| Different Cases | L | v | |||||
| case 1a | 0.1 | 3 | 0.1 | 1.0488 | 0.7397 | 1.9899 | −0.0050 |
| case 1b | 0.1 | 3 | 0.2 | 1.0963 | 0.7896 | 2.0785 | 0.0392 |
| case 1c | 0.1 | 3.5 | 1.7 | 2.8612 | 1.5669 | 3.6373 | 0.8186 |
| case 2a | 0.1 | 1 | 0.1 | 1.7503 | 0.5079 | −0.6633 | −0.1992 |
| case 2b | 0.1 | 1.2 | 0.5 | 1.8437 | 0.7021 | −0.9295 | 0.1220 |
| case 2c | 0.1 | 2 | 0.3 | 1.6128 | 0.8142 | −1.4422 | 0.7409 |
| The Model of DVAs | |||
| Voigt-type [2] | − | ||
| Grounded-type [4] | − | ||
| IN-Maxwell-type [11] | |||
| L-grounded-type [38] | |||
| case 1 | |||
| case 2 |
| Model of DVA | Variances | Decrease Ratios (%) |
|---|---|---|
| Without DVA | 2.8464 × 10 | |
| Voigt-type DVA | 3.7631 × 10 | 86.78 |
| Grounded-type DVA | 3.0478 × 10 | 89.29 |
| IN-Maxwell-type DVA | 2.7244 × 10 | 90.43 |
| L-grounded-type DVA | 2.2196 × 10 | 99.22 |
| DVA of case 1c | 7.5018 × 10 | 99.74 |
| DVA of case 2c | 1.0018 × 10 | 96.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Gao, T.; Zhu, S.; Yang, X. H∞ Optimization of a Novel Maxwell Dynamic Vibration Absorber with Lever, Inerter, and Grounded Stiffness. Appl. Sci. 2023, 13, 3697. https://doi.org/10.3390/app13063697
Li J, Gao T, Zhu S, Yang X. H∞ Optimization of a Novel Maxwell Dynamic Vibration Absorber with Lever, Inerter, and Grounded Stiffness. Applied Sciences. 2023; 13(6):3697. https://doi.org/10.3390/app13063697
Chicago/Turabian StyleLi, Jing, Ting Gao, Shaotao Zhu, and Xiaodong Yang. 2023. "H∞ Optimization of a Novel Maxwell Dynamic Vibration Absorber with Lever, Inerter, and Grounded Stiffness" Applied Sciences 13, no. 6: 3697. https://doi.org/10.3390/app13063697
APA StyleLi, J., Gao, T., Zhu, S., & Yang, X. (2023). H∞ Optimization of a Novel Maxwell Dynamic Vibration Absorber with Lever, Inerter, and Grounded Stiffness. Applied Sciences, 13(6), 3697. https://doi.org/10.3390/app13063697





