Diffraction by a Semi-Infinite Parallel-Plate Waveguide with Five-Layer Material Loading: The Case of H-Polarization
Abstract
:1. Introduction
2. Formulation of the Problem
3. Exact and Approximate Solutions
4. Scattered Field
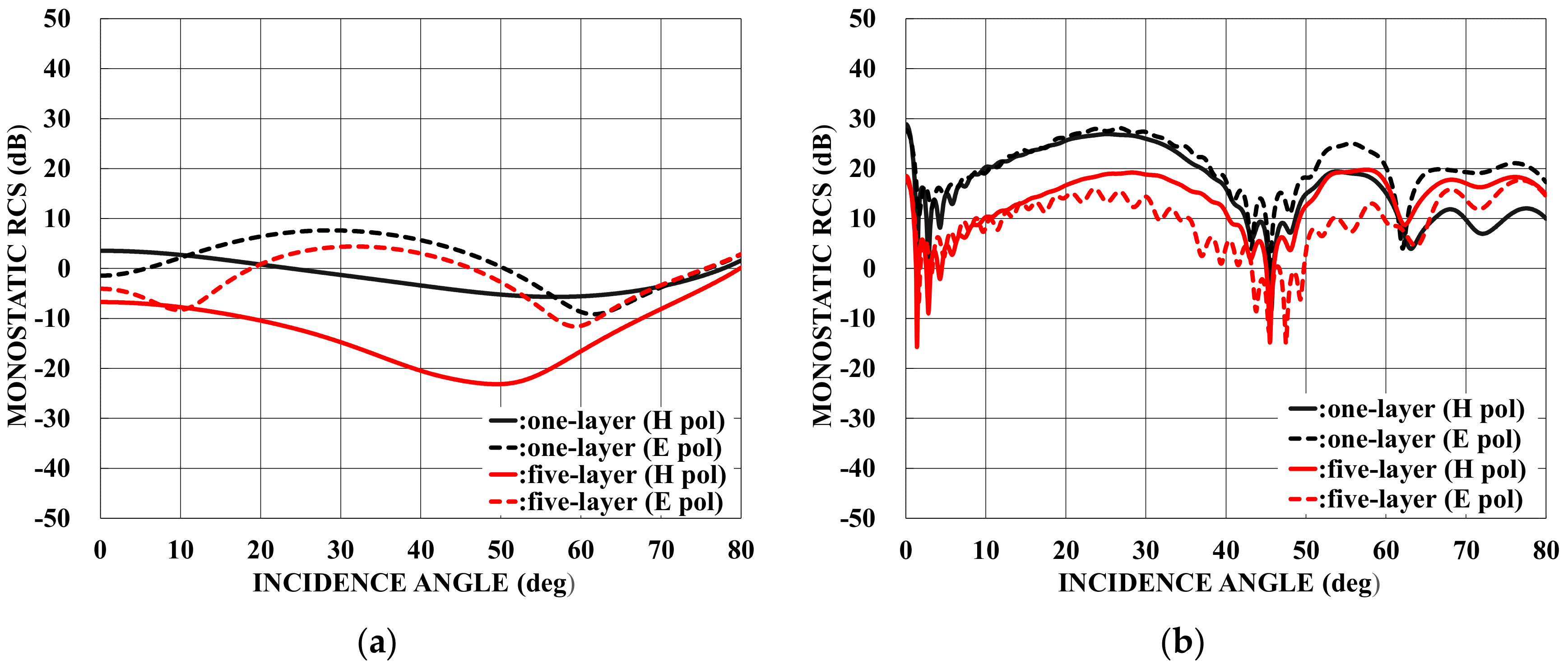
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Some Properties of the Fourier Coefficients
References
- Knott, E.F.; Shaeffer, J.; Tuley, M. Radar Cross Section, 2nd ed.; SciTech: Raleigh, NC, USA, 2004; pp. 269–367. [Google Scholar]
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; Wiley: New York, NY, USA, 2012; pp. 351–543. [Google Scholar]
- Stone, W.R. (Ed.) Radar Cross Sections of Complex Objects; IEEE Press: New York, NY, USA, 1990. [Google Scholar]
- Bhattacharyya, A.K.; Sengupta, D.L. Radar Cross Section Analysis and Control; Artech House: Boston, MA, USA, 1991. [Google Scholar]
- Bernard, J.M.L.; Pelosi, G.; Ufimtsev, P.Y. Special issue on radar cross section of complex objects. Ann. Telecommun. 1995, 50, 471–598. [Google Scholar]
- Michielssen, E.; Sajer, J.M.; Ranjithan, S.; Mittra, R. Design of lightweight, broad-band microwave absorbers using genetic algorithms. IEEE Trans. Microw. Theory Tech. 1993, 41, 1024–1031. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, X.; Du, Z. Analysis and design of multilayered broadband radar absorbing metamaterial using the 3-D printing technology-based method. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 133–136. [Google Scholar] [CrossRef]
- Toktas, A.; Ustun, D.; Tekbas, M. Multi-objective design of multilayer radar absorber using surrogate-based optimization. IEEE Trans. Microw. Theory Tech. 2019, 67, 3318–3329. [Google Scholar] [CrossRef]
- Pathak, P.H.; Bukholder, R.J. Electromagnetic Radiation, Scattering, and Diffraction; Wiley: New York, NY, USA, 2021; pp. 314–451. [Google Scholar]
- Lee, C.S.; Lee, S.-W. RCS of a coated circular waveguide terminated by a perfect conductor. IEEE Trans. Antennas Propag. 1987, 35, 391–398. [Google Scholar]
- Altintaș, A.; Pathak, P.H.; Liang, M.C. A selective modal scheme for the analysis of EM coupling into or radiation from large open-ended waveguides. IEEE Trans. Antennas Propag. 1988, 36, 84–96. [Google Scholar] [CrossRef]
- Ling, H.; Chou, R.-C.; Lee, S.-W. Shooting and bouncing rays: Calculating the RCS of an arbitrary shaped cavity. IEEE Trans. Antennas Propag. 1989, 37, 194–205. [Google Scholar] [CrossRef]
- Pathak, P.H.; Burkholder, R.J. Modal, ray, and beam techniques for analyzing the EM scattering by open-ended waveguide cavities. IEEE Trans. Antennas Propag. 1989, 37, 635–647. [Google Scholar] [CrossRef]
- Pathak, P.H.; Burkholder, R.J. A reciprocity formulation for the EM scattering by an obstacle within a large open cavity. IEEE Trans. Microw. Theory Tech. 1993, 41, 702–707. [Google Scholar] [CrossRef]
- Lee, R.; Chia, T.-T. Analysis of electromagnetic scattering from a cavity with a complex termination by means of a hybrid ray-FDTD method. IEEE Trans. Antennas Propag. 1993, 41, 1560–1569. [Google Scholar] [CrossRef] [Green Version]
- Ohnuki, S.; Hinata, T. Radar cross section of an open-ended rectangular cylinder with an iris inside the cavity. IEICE Trans. Electron. 1998, E81-C, 1875–1880. [Google Scholar]
- Kim, D.Y.; Lim, H.; Han, J.H.; Song, W.Y.; Myung, N.H. RCS reduction of open-ended circular waveguide cavity with corrugations using mode matching and scattering matrix analysis. Prog. Electromagn. Res. 2014, 146, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.; Xiao, G.; Mao, J. A generalized transition matrix model for open-ended cavity with complex internal structures. IEEE Trans. Antennas Propag. 2016, 64, 3920–3930. [Google Scholar] [CrossRef]
- Zhou, Y.; Yan, Y.; Xie, J.; Chen, H.; Zhang, G.; Li, F.; Zhang, L.; Wang, X.; Weng, X.; Zhou, P.; et al. Broadband RCS reduction for electrically-large open-ended cavity using random coding metasurfaces. J. Phys. D Appl. Phys. 2019, 52, 315303. [Google Scholar] [CrossRef]
- Serizawa, H.; Hongo, K. Radiation from a flanged rectangular waveguide. IEEE Trans. Antennas Propag. 2005, 53, 3953–3962. [Google Scholar] [CrossRef] [Green Version]
- Büyükaksoy, A.; Birbir, F.; Erdoǧan, E. Scattering characteristics of a rectangular groove in a reactive surface. IEEE Trans. Antennas Propag. 1995, 43, 1450–1458. [Google Scholar] [CrossRef]
- Cetiner, B.A.; Büyükaksoy, A.; Güneș, F. Diffraction of electromagnetic waves by an open-ended parallel plate waveguide cavity with impedance walls. Prog. Electromagn. Res. 2000, 26, 165–197. [Google Scholar] [CrossRef]
- Noble, B. Methods Based on the Wiener-Hopf Technique for the Solution of Partial Differential Equations; Pergamon: London, UK, 1958. [Google Scholar]
- Mittra, R.; Lee, S.-W. Analytical Techniques in the Theory of Guided Waves; Macmillan: New York, NY, USA, 1971; pp. 4–12. [Google Scholar]
- Kobayashi, K. Wiener-Hopf and modified residue calculus techniques. In Analysis Methods for Electromagnetic Wave Problems; Yamashita, E., Ed.; Artech House: Boston, MA, USA, 1990; pp. 245–302. [Google Scholar]
- Daniele, V.G.; Lombardi, G. Scattering and Diffraction by Wedges 1, the Wiener-Hopf Solution—Theory; Wiley-ISTE: Hoboken, NJ, USA, 2020. [Google Scholar]
- Daniele, V.G.; Lombardi, G. Scattering and Diffraction by Wedges 2, the Wiener-Hopf Solution—Advanced Applications; Wiley-ISTE: Hoboken, NJ, USA, 2020. [Google Scholar]
- Mittra, R.; Lee, S.-W. Diffraction by thick conducting haft-plane and a dielectric-loaded waveguide. IEEE Trans. Antennas Propag. 1968, 16, 454–461. [Google Scholar]
- Çinar, G.; Büyükaksoy, A. Diffraction by a Thick Impedance Half-Plane with a Different End Face Impedance. Electromagnetics 2002, 22, 565–580. [Google Scholar] [CrossRef]
- Ricoy, M.A.; Volakis, J.L. E-Polarization Diffraction by a Thick Metal-Dielectric Join. J. Electromagn. Waves Appl. 1989, 3, 383–407. [Google Scholar] [CrossRef]
- Daniele, V.G.; Lombardi, G.; Zich, R.S. Radiation and Scattering of an Arbitrarily Flanged Dielectric-Loaded Waveguide. IEEE Trans. Antennas Propag. 2019, 67, 7569–7584. [Google Scholar] [CrossRef]
- Daniele, V.G.; Lombardi, G.; Zich, R.S. The scattering of electromagnetic waves by two opposite staggered perfectly electrically conducting half-planes. Wave Motion 2018, 83, 241–263. [Google Scholar] [CrossRef]
- Rawlins, A.D.; McIver, P. Diffraction by a thick half–plane with an absorbent end face. Proc. R. Soc. Lond. A 1998, 454, 3167–3182. [Google Scholar] [CrossRef]
- Akbar, M.; Ahmed, S. Thickness effect on scattering by a dielectric slab for normal incidence. J. Quant. Spectrosc. Radiat. Transf. 2021, 271, 107720. [Google Scholar] [CrossRef]
- Turctken, B.; Alkumru, A. Plane wave diffraction by a dielectric loaded open parallel thick plate waveguide. Turk. J. Elec. Eng. 2002, 10, 439–448. [Google Scholar]
- Daniele, V.G.; Lombardi, G.; Zich, R.S. Physical and Spectral Analysis of a Semi-infinite Grounded Slab Illuminated by Plane Waves. IEEE Trans. Antennas Propag. 2022, 70, 12104–12119. [Google Scholar] [CrossRef]
- Tayyar, H.; Buyukaksoy, A. Plane wave diffraction by the junction of a thick impedance half-plane and a thick dielectric slab. IEE Proc. Sci. Meas. Technol. 2002, 150, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, K.; Sawai, A. Plane wave diffraction by an open-ended parallel plate waveguide cavity. J. Electromagn. Waves Appl. 1992, 6, 475–512. [Google Scholar] [CrossRef]
- Kobayashi, K.; Koshikawa, S.; Sawai, A. Diffraction by a parallel-plate waveguide cavity with dielectric/ferrite loading: Part I —The case of E polarization. Prog. Electromagn. Res. 1994, 8, 377–426. [Google Scholar] [CrossRef]
- Koshikawa, S.; Kobayashi, K. Diffraction by a parallel-plate waveguide cavity with dielectric/ferrite loading: Part II—the case of H polarization. Prog. Electromagn. Res. 1994, 8, 427–458. [Google Scholar] [CrossRef]
- Zheng, J.P.; Kobayashi, K. Plane wave diffraction by a finite parallel-plate waveguide with four-layer material loading: Part I—the case of E polarization. Prog. Electromagn. Res. B 2008, 6, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Shang, E.H.; Kobayashi, K. Plane wave diffraction by a finite parallel-plate waveguide with four-layer material loading: Part II—The case of H polarization. Prog. Electromagn. Res. B 2008, 6, 267–294. [Google Scholar] [CrossRef] [Green Version]
- Koshikawa, S.; Colak, D.; Altintas, A.; Kobayashi, K.; Nosich, A.I. A comparative study of RCS predictions of canonical rectangular and circular cavities with double-layer material loading. IEICE Trans. Electron. 1997, E80-C, 1457–1466. [Google Scholar]
- Koshikawa, S.; Kobayashi, K. Diffraction by a terminated, semi-infinite parallel-plate waveguide with three-layer material loading. IEEE Trans. Antennas Propag. 1997, 45, 949–959. [Google Scholar] [CrossRef]
- Koshikawa, S.; Kobayashi, K. Diffraction by a terminated, semi-infinite parallel-plate waveguide with three-layer material loading: The case of H polarization. Electromagn. Waves Electron. Syst. 2000, 5, 13–23. [Google Scholar] [CrossRef]
- He, K.W.; Kobayashi, K. Diffraction by a Semi-Infinite Parallel-Plate Waveguide with Five-Layer Material Loading: Rigorous Wiener-Hopf Analysis. Prog. Electromagn. Res. B 2023, 98, 125–145. [Google Scholar] [CrossRef]
- Shang, E.H.; Kobayashi, K. Diffraction by a terminated, semi-infinite parallel-plate waveguide with four-layer material loading. Prog. Electromagn. Res. B 2009, 12, 139–162. [Google Scholar] [CrossRef] [Green Version]
- Meixner, J. The behavior of electromagnetic field at edges. IEEE Trans. Antennas Propag. 1972, AP-20, 442–446. [Google Scholar] [CrossRef]
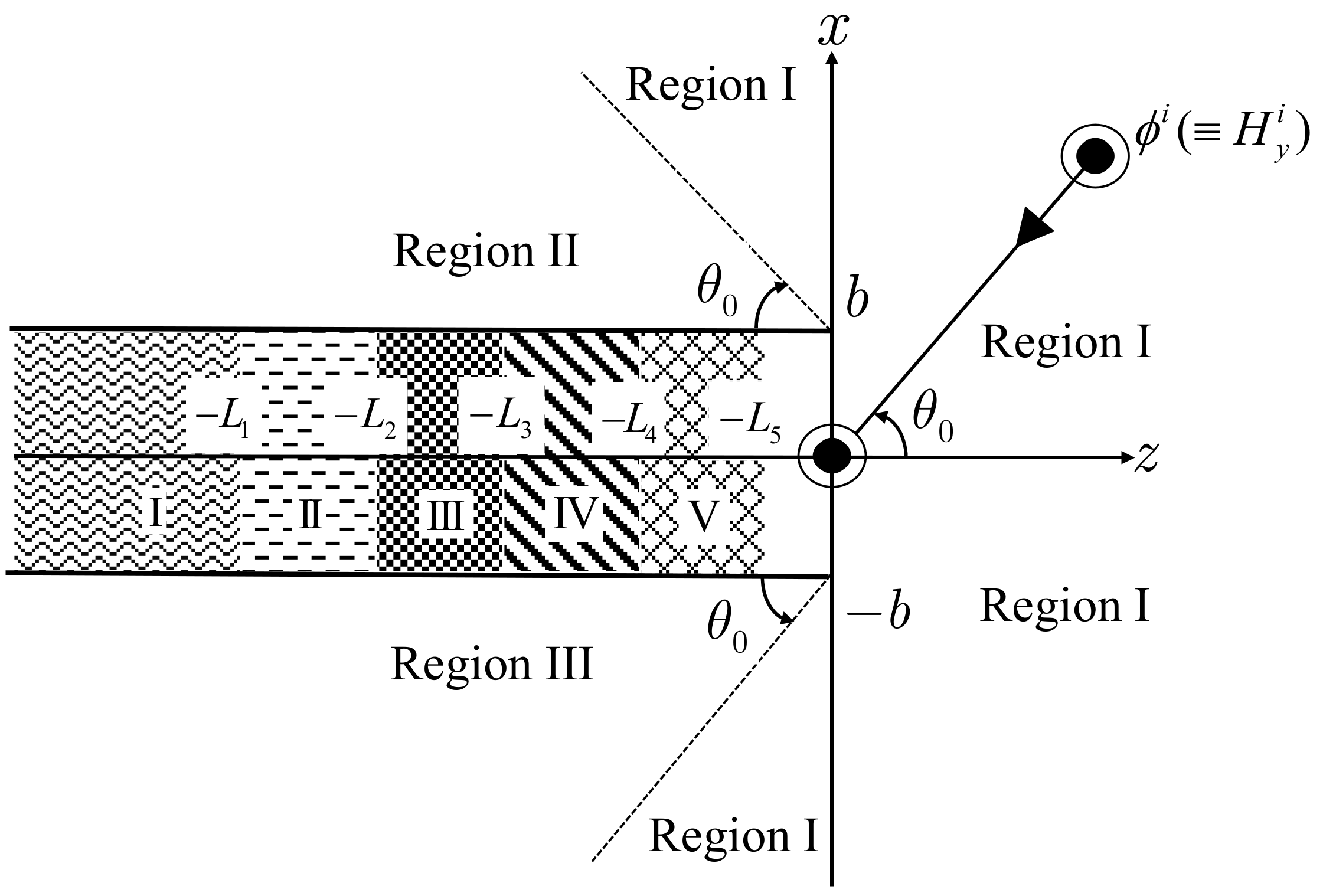
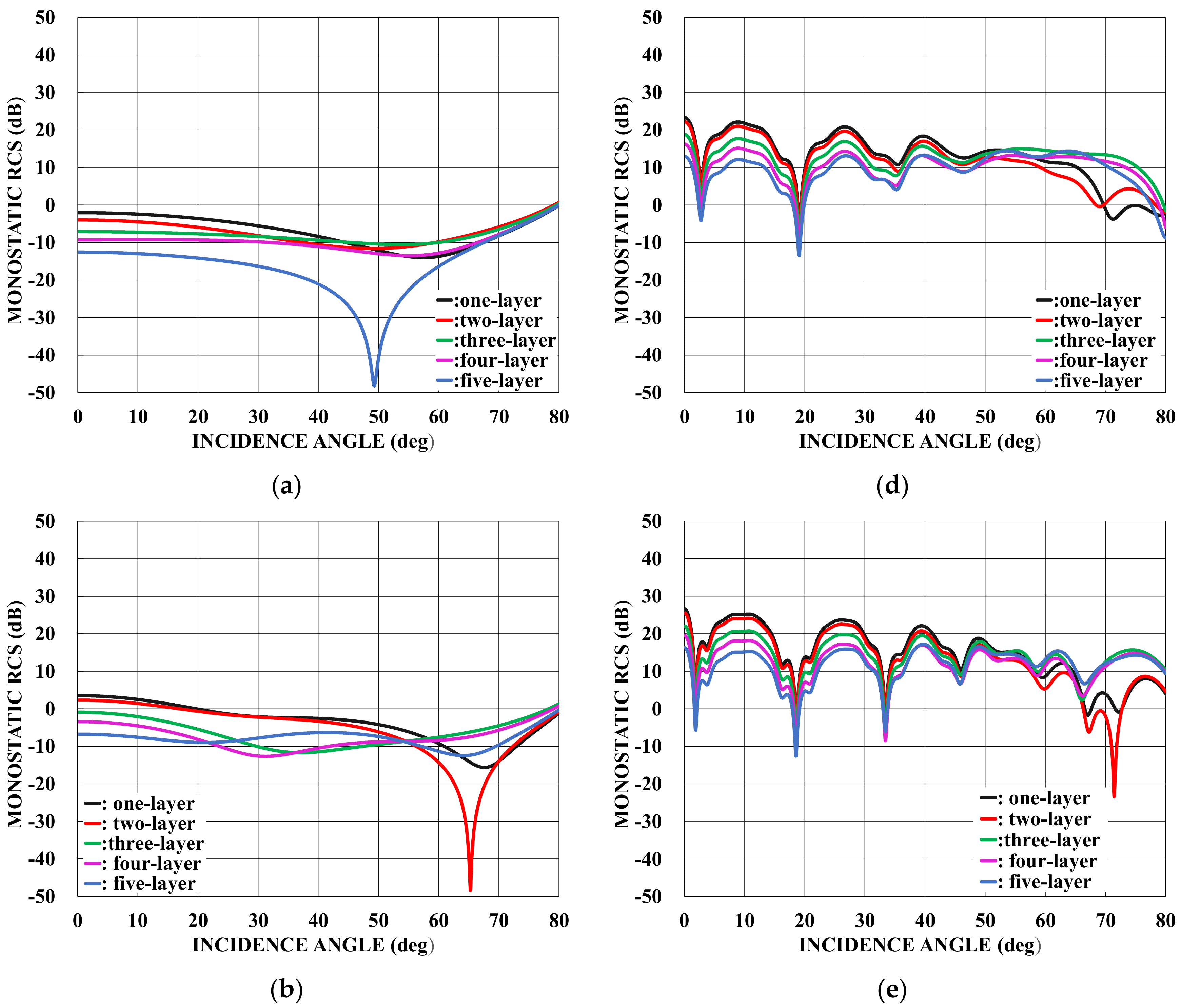
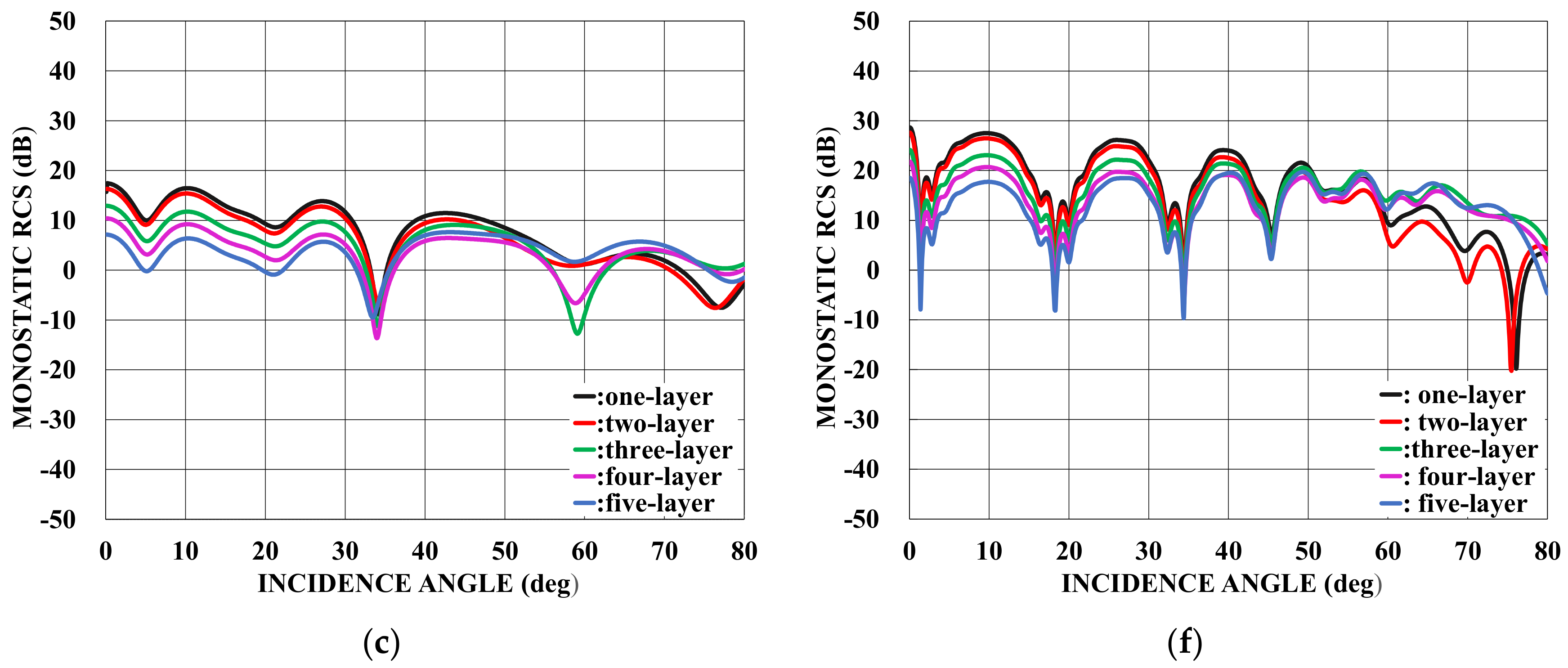
 : one-layer material loading (regions II−V: vacuum).
: one-layer material loading (regions II−V: vacuum).  : two−layer material loading (regions III−V: vacuum).
: two−layer material loading (regions III−V: vacuum).  : three−layer material loading (regions IV−V: vacuum).
: three−layer material loading (regions IV−V: vacuum).  : four−layer material loading (region V: vacuum).
: four−layer material loading (region V: vacuum).  : five−layer material loading. (a) . (b) . (c) . (d) . (e) . (f) .
: five−layer material loading. (a) . (b) . (c) . (d) . (e) . (f) .
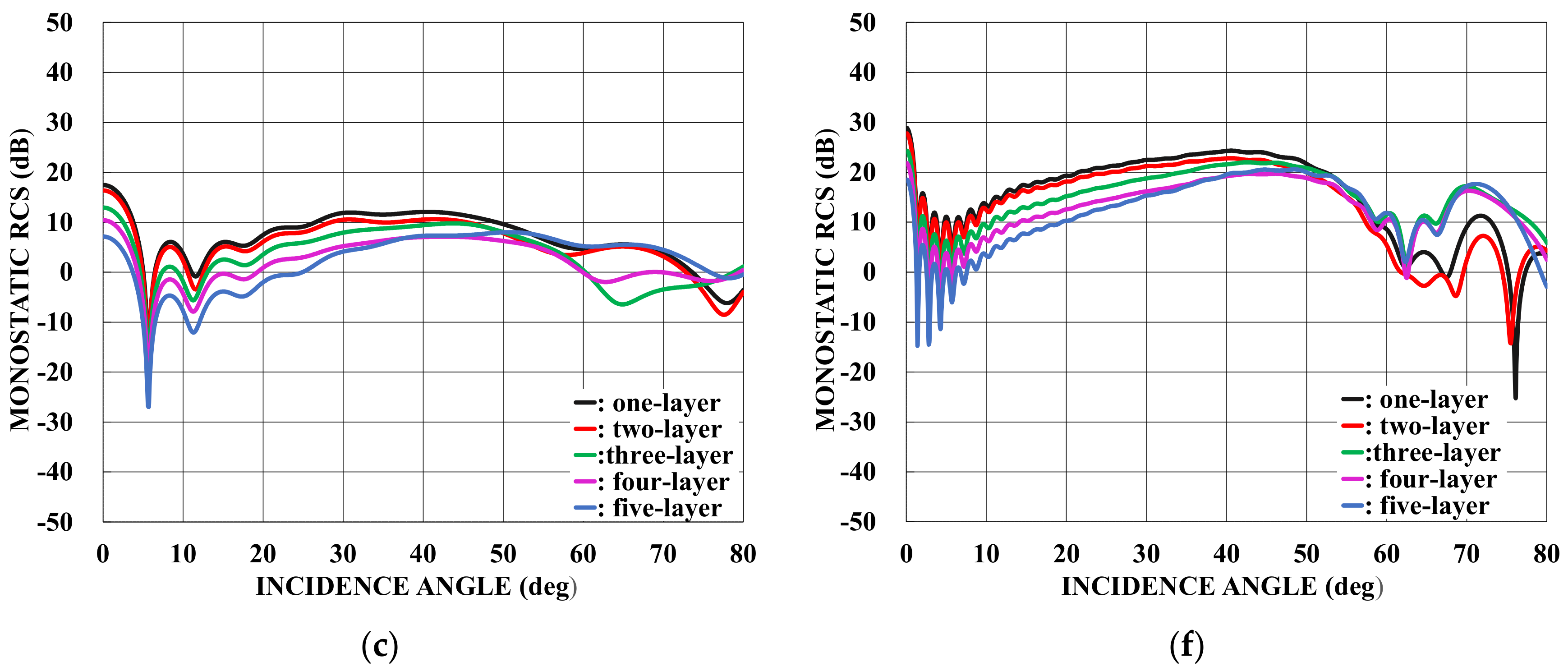
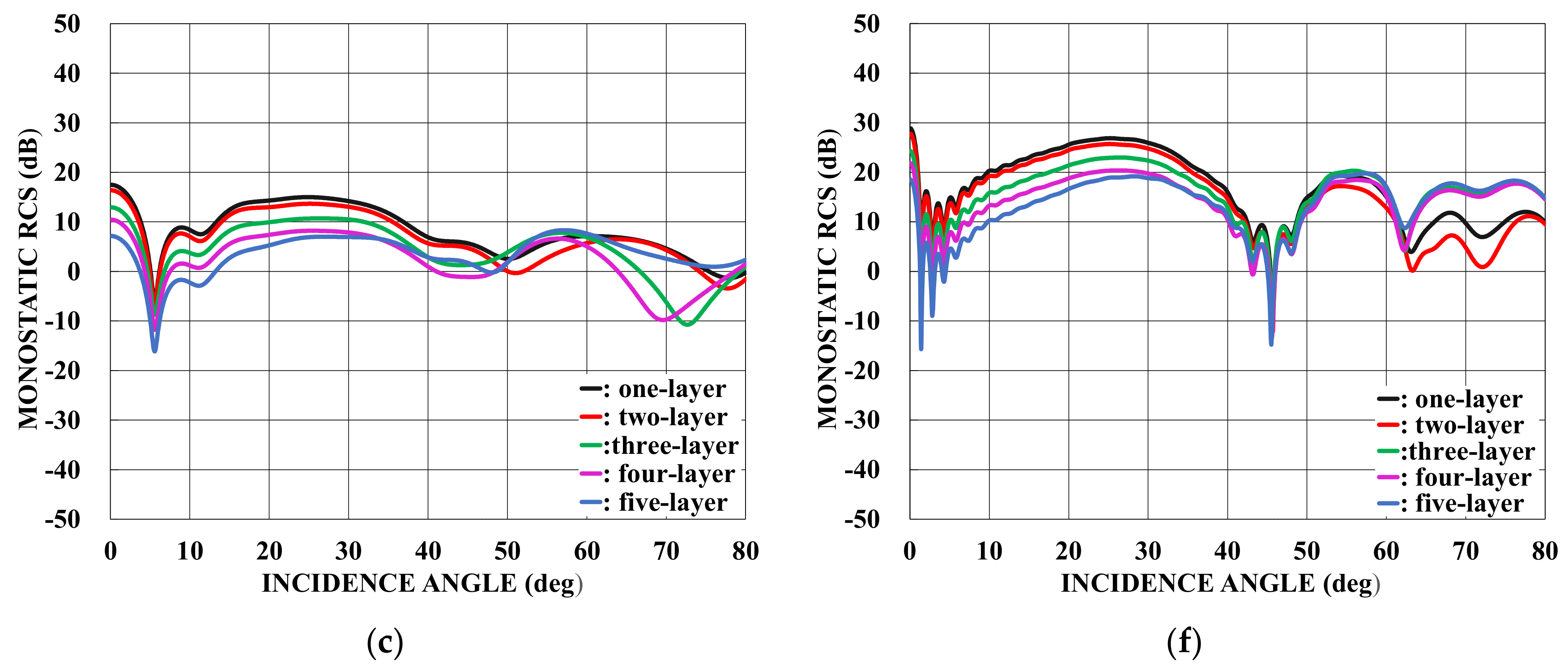
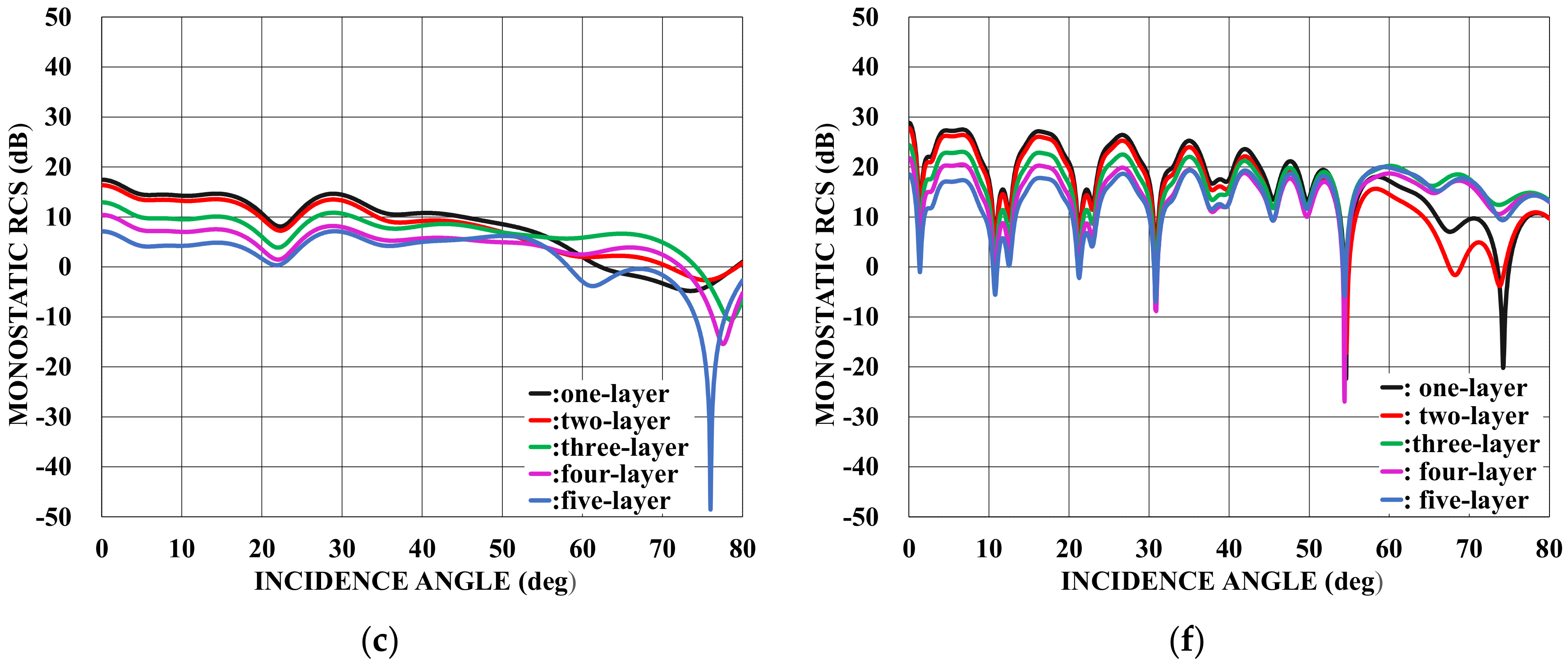
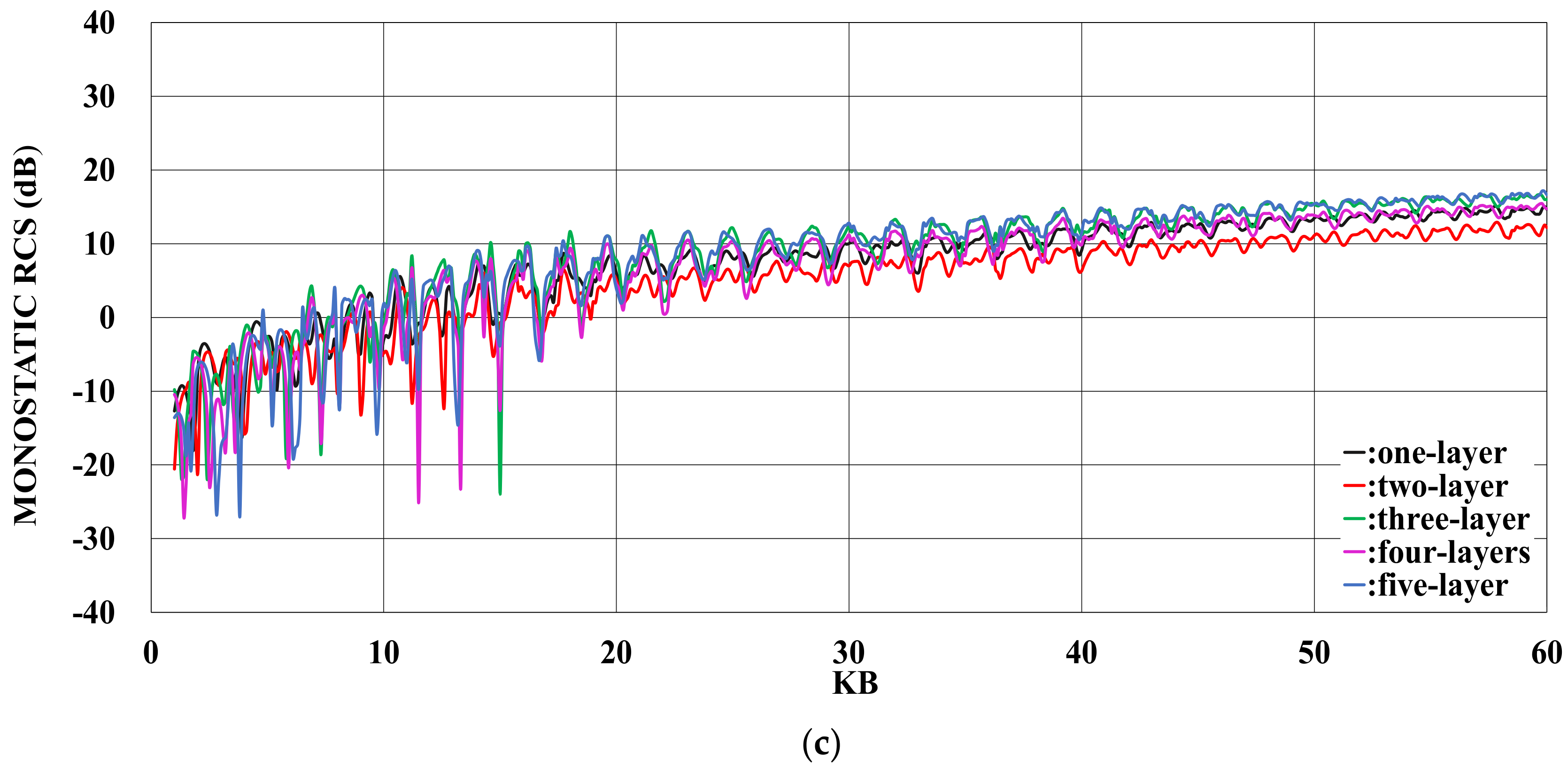
 : one-layer material loading (regions II−V: vacuum).
: one-layer material loading (regions II−V: vacuum).  : two−layer material loading (regions III−V: vacuum).
: two−layer material loading (regions III−V: vacuum).  : three−layer material loading (regions IV−V: vacuum).
: three−layer material loading (regions IV−V: vacuum).  : four−layer material loading (region V: vacuum).
: four−layer material loading (region V: vacuum).  : five−layer material loading. (a) . (b) . (c) . (d) . (e) . (f) .
: five−layer material loading. (a) . (b) . (c) . (d) . (e) . (f) .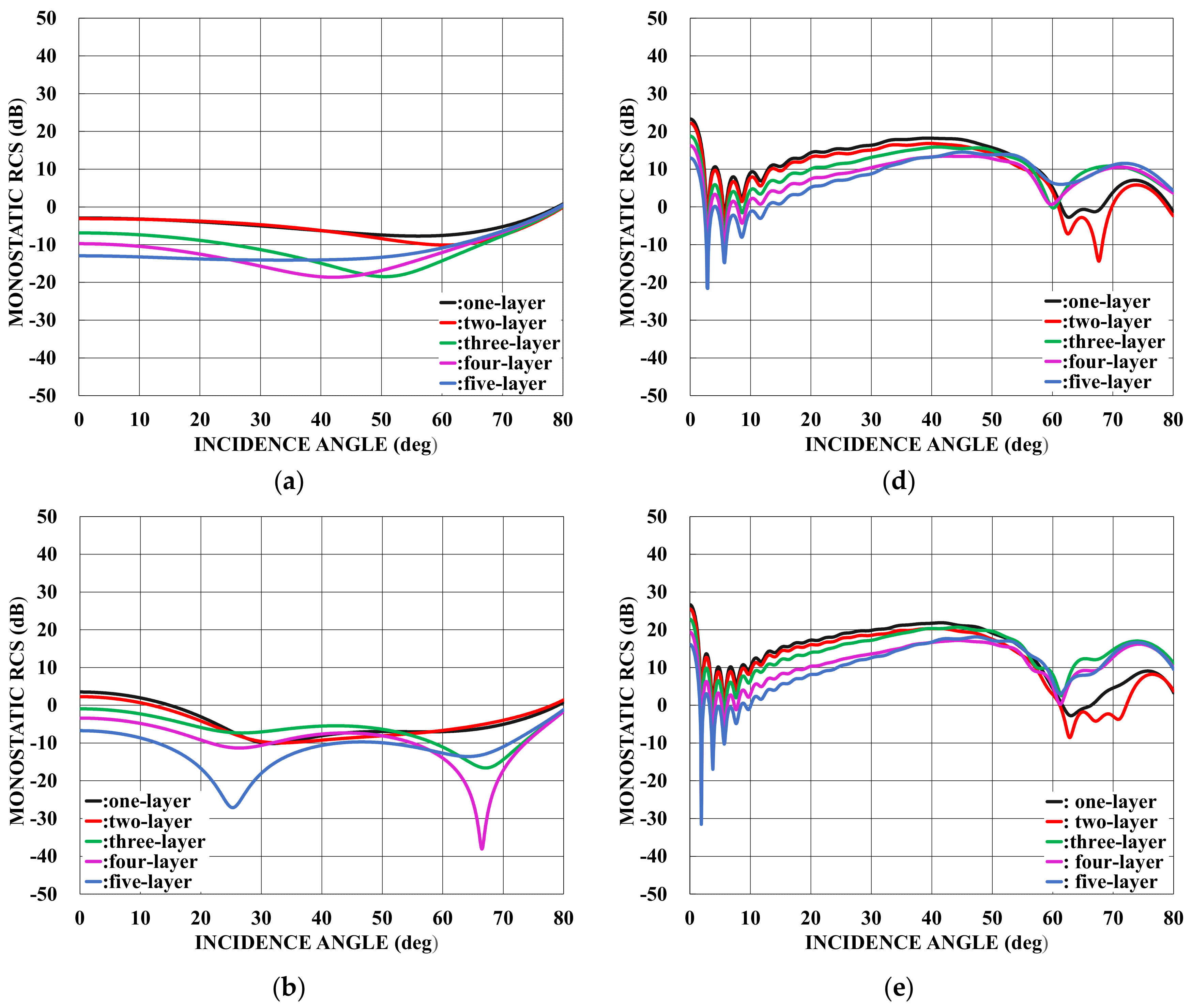




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, K.; Kobayashi, K. Diffraction by a Semi-Infinite Parallel-Plate Waveguide with Five-Layer Material Loading: The Case of H-Polarization. Appl. Sci. 2023, 13, 3715. https://doi.org/10.3390/app13063715
He K, Kobayashi K. Diffraction by a Semi-Infinite Parallel-Plate Waveguide with Five-Layer Material Loading: The Case of H-Polarization. Applied Sciences. 2023; 13(6):3715. https://doi.org/10.3390/app13063715
Chicago/Turabian StyleHe, Kewen, and Kazuya Kobayashi. 2023. "Diffraction by a Semi-Infinite Parallel-Plate Waveguide with Five-Layer Material Loading: The Case of H-Polarization" Applied Sciences 13, no. 6: 3715. https://doi.org/10.3390/app13063715




