A Methodology for Continuous Monitoring of Rail Corrugation on Subway Lines Based on Axlebox Acceleration Measurements
Abstract
:1. Introduction
2. Description of the Measurement System
3. Transfer Function of the Measurement System
3.1. Wheel Dynamics
- The axle is modelled using 2D Euler–Bernoulli beam elements;
- The wheels are considered as rigid bodies; due to the frequency range of interest for corrugation problems, the flexibility of the wheels does not have a strong influence on the different formation mechanisms [5];
- The wheels and the brake disks are modelled as concentrated masses in their centre, accounting also for their moment of inertia;
- The axleboxes are represented by concentrate masses placed in correspondence to their centre of gravity, while their rotational inertia is neglected;
- A unit vertical contact force is considered varying harmonically and it is applied to the wheel centre, also accounting for the transport moments;
- The displacement vector of the wheel centre is defined by
- The first three elements of the displacement vector are linear displacements along longitudinal, lateral and vertical axes, respectively, while the others are the rotations around the same axes. Thanks to the modal model this vector can be computed;
- The linearised displacements of the contact point can be derived from the wheel centre ones by assuming rigid motion as
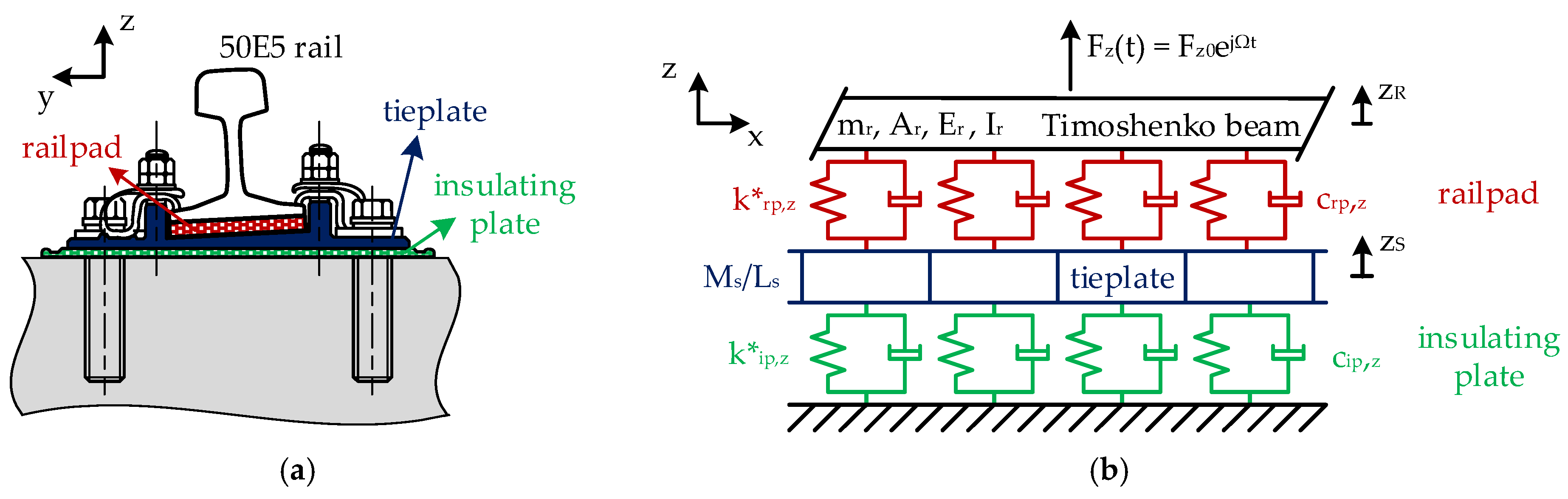
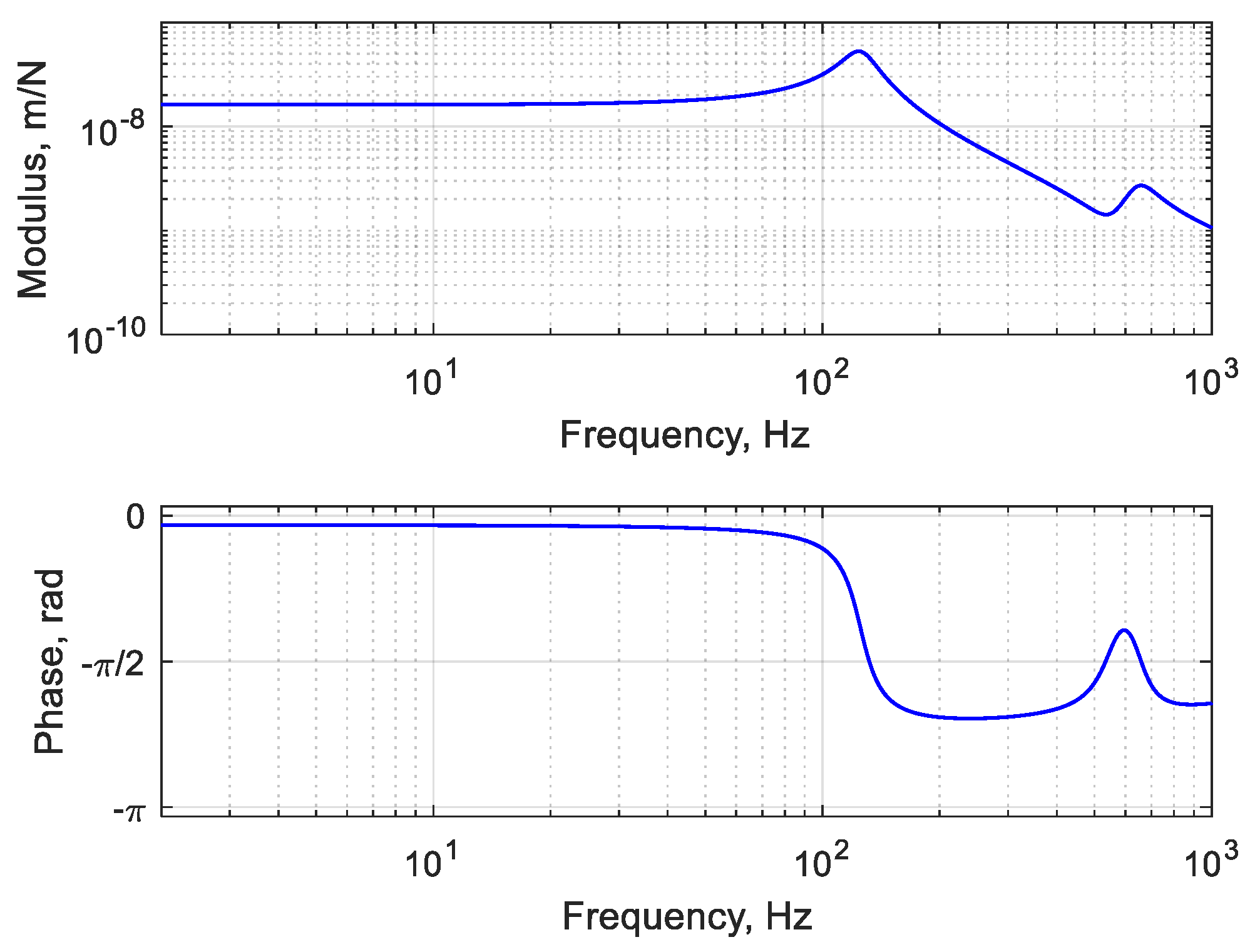
3.2. Track Dynamics
- Displacements are infinitesimally small, to ensure the linearity;
- The centroid of the beam cross-sections lays on the x-axis, while y- and z-axes are the principal axes of the beam cross-section;
- The two rails are considered dynamically decoupled;
- The load applied on the rail is considered fixed in space at x = 0, since the effect of a moving load on the beam dynamics is negligible [21], especially considering the low maximum speeds reached on metro lines;
- The inclination of the rail is neglected. The load is considered applied in correspondence to the rail neutral axis. This hypothesis allows to decouple the lateral and vertical track dynamics. This is a strong simplification, since the coupling effect increases as the distance along y-axis of the load’s point of application from the neutral axis increases due to the rotation of the rail cross-section.
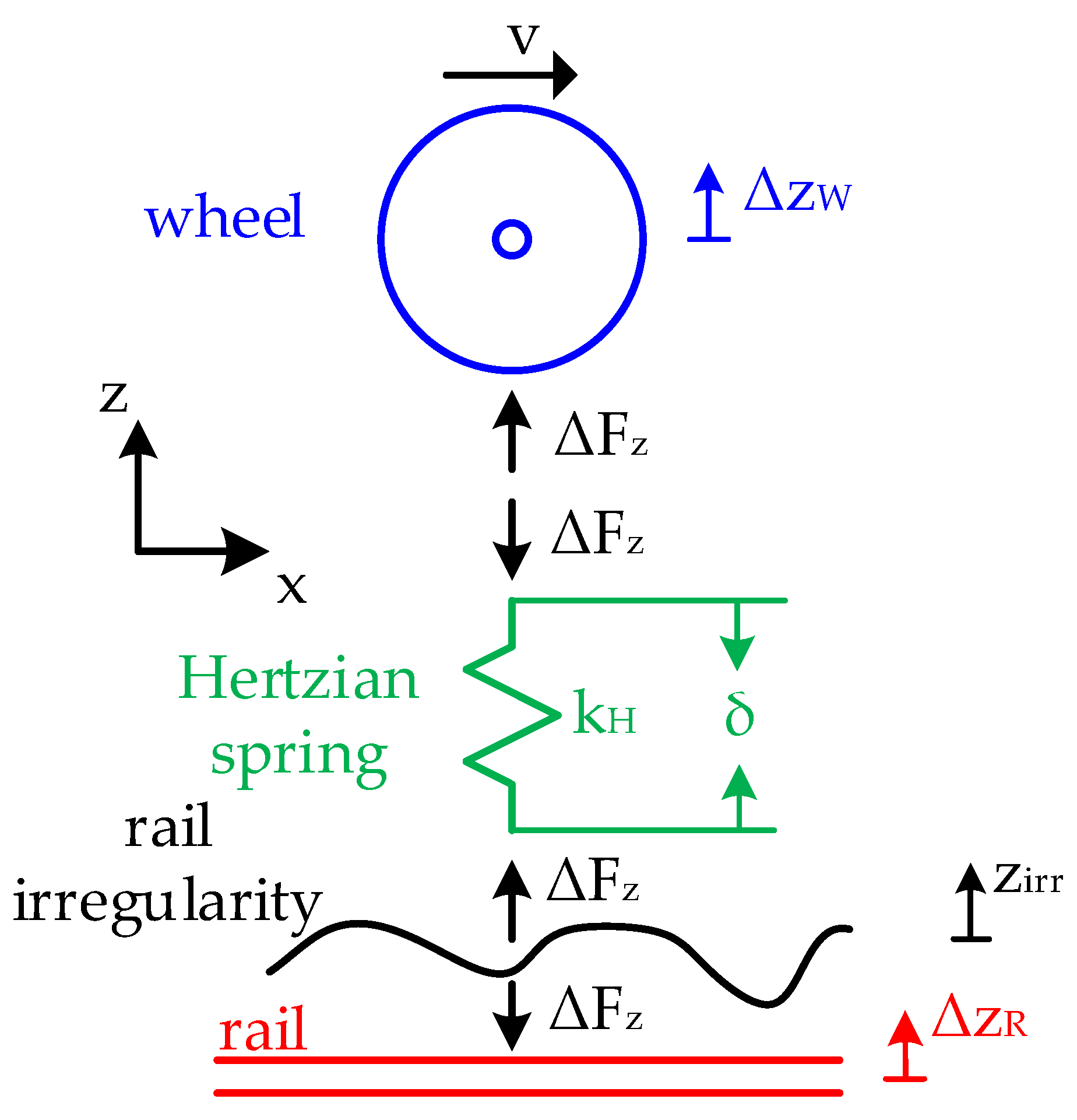
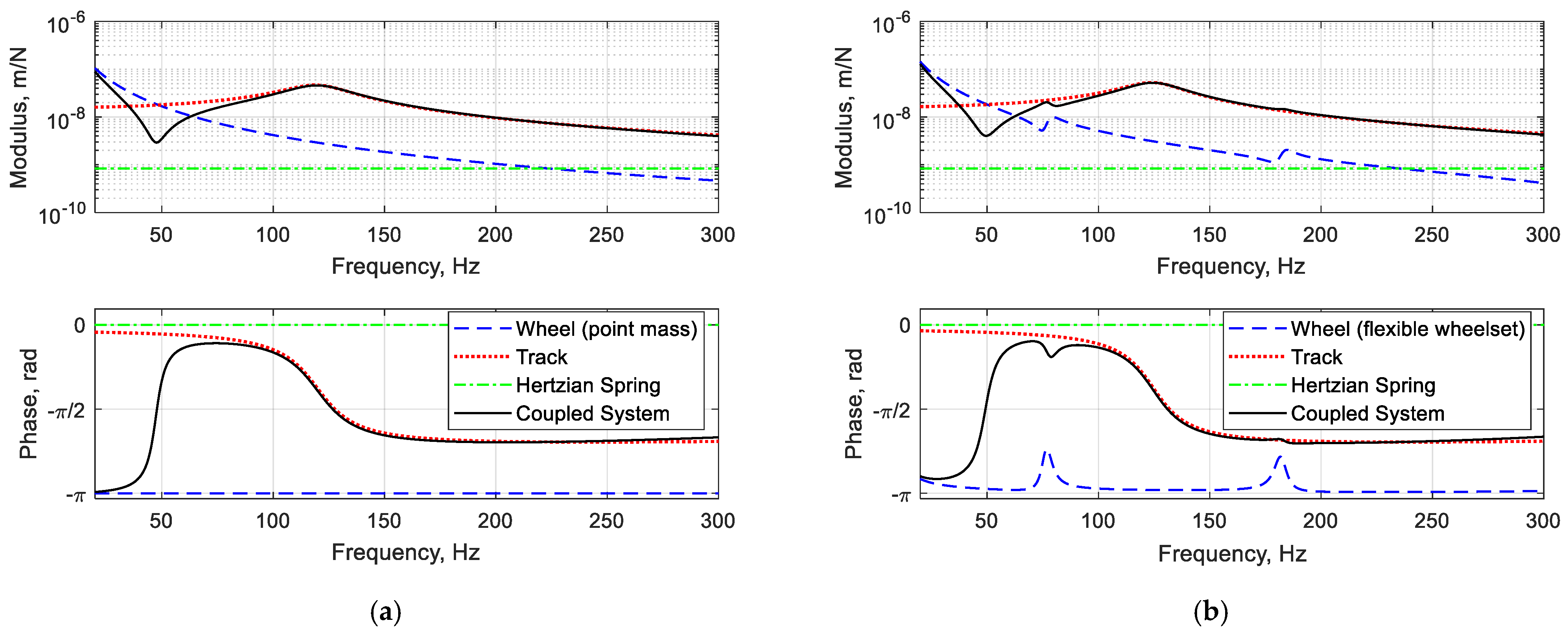
3.3. Dynamics of the Wheel–Rail Coupled System
4. Algorithm for Rail Irregularity Estimation
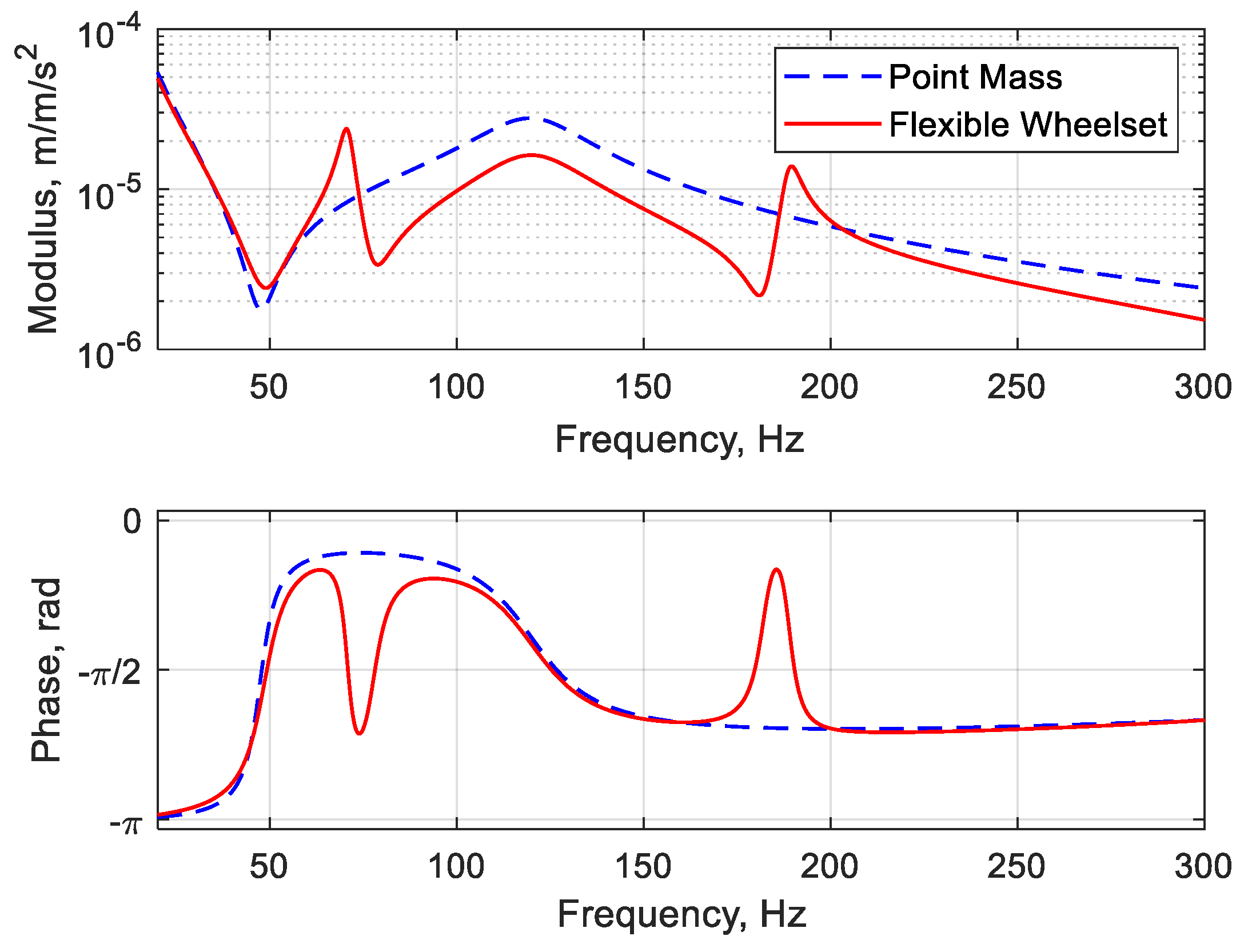
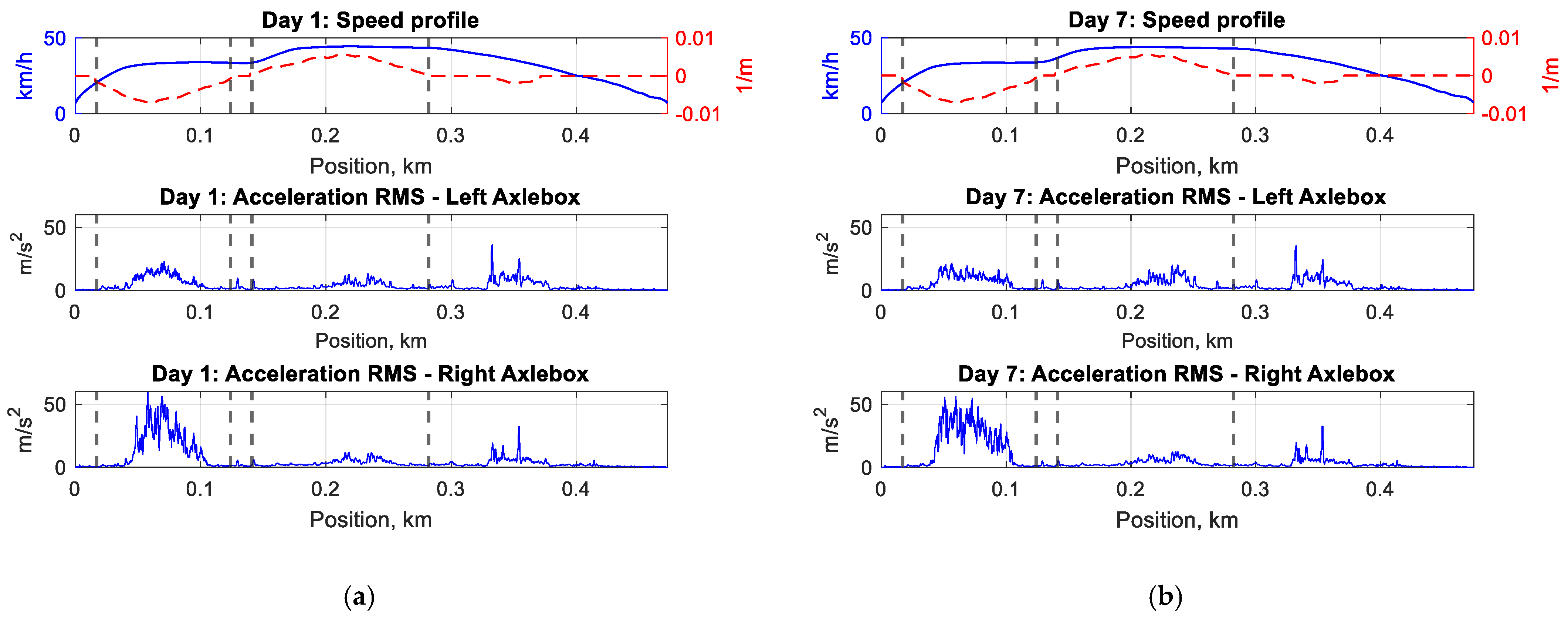
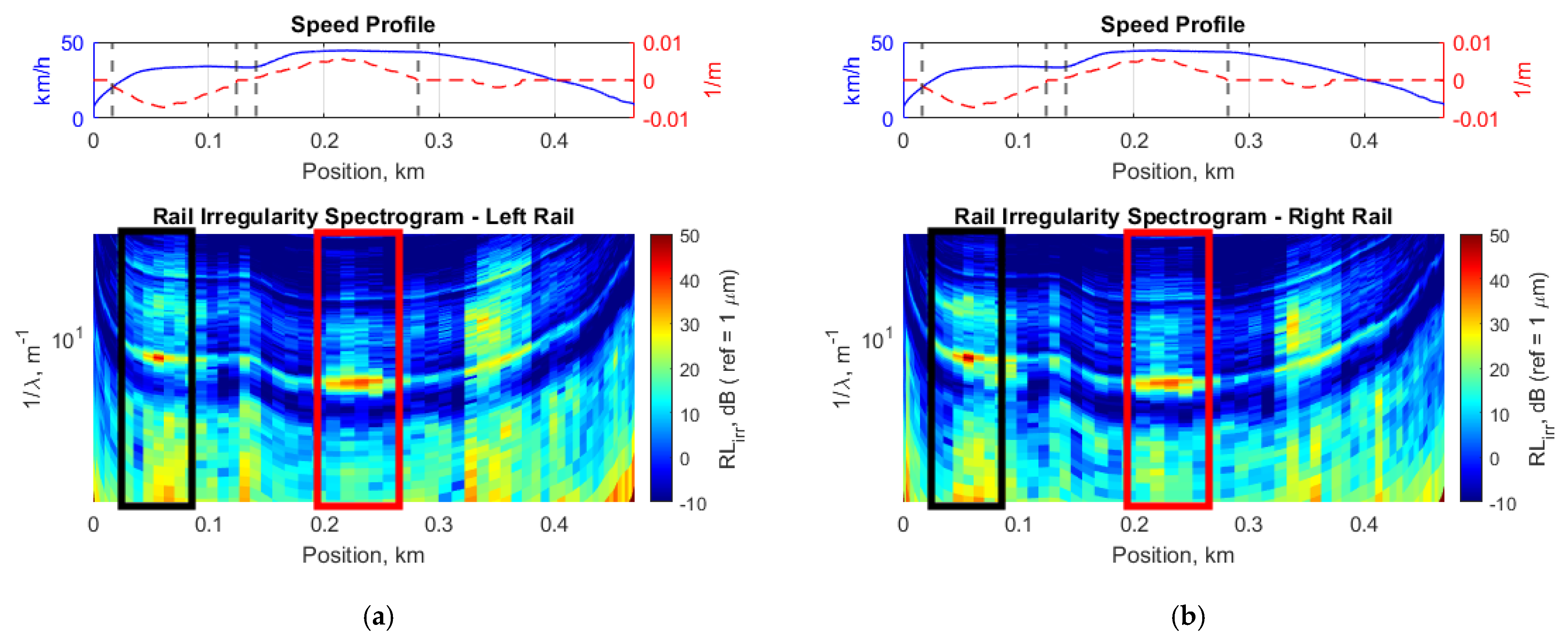
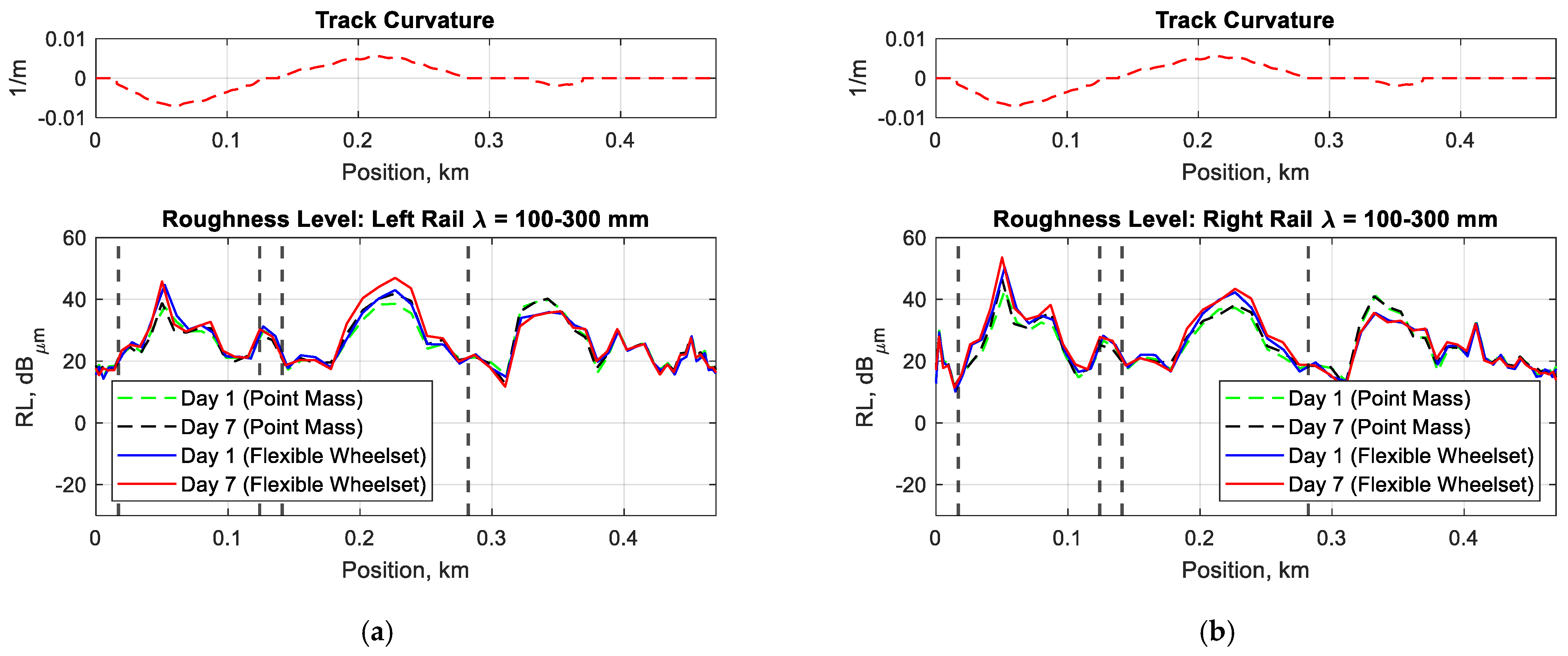
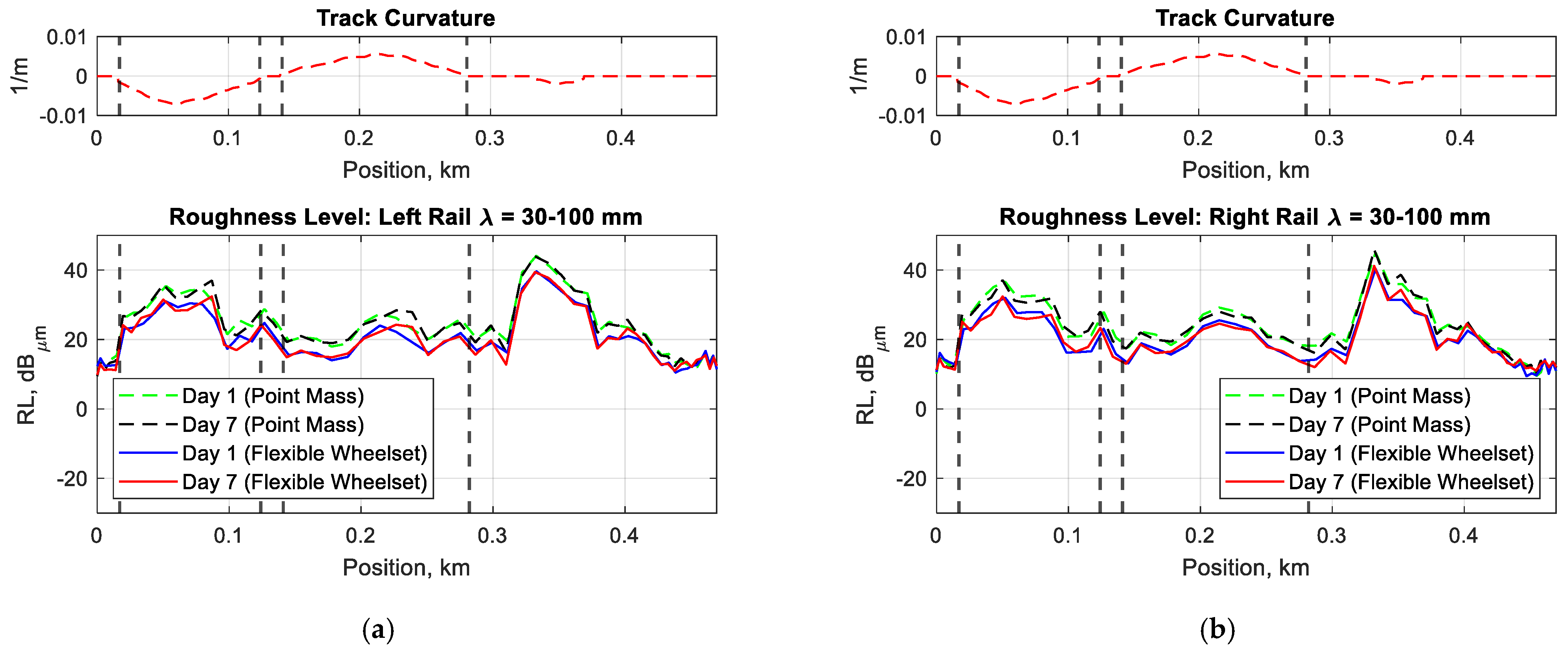
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grassie, S.L. Corrugation on Australian National: Cause, Measurement and Rectification. In Proceedings of the 4th International Heavy Haul Railway Conference, Brisbane, Australia, 1 January 1989; pp. 188–192. [Google Scholar]
- Tassilly, E.; Vincent, N. Rail Corrugations: Analytical Model and Field Tests. Wear 1991, 144, 163–178. [Google Scholar] [CrossRef]
- Grassie, S.L. The Corrugation of Railway Rails: 1. Introduction and Mitigation Measures. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2022, 2022, 095440972211256. [Google Scholar] [CrossRef]
- Grassie, S.L.; Kalousek, J. Rail Corrugation: Characteristics, Causes and Treatments. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 1993, 207, 57–68. [Google Scholar] [CrossRef]
- Grassie, S.L. Rail Corrugation: Characteristics, Causes, and Treatments. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2009, 223, 581–596. [Google Scholar] [CrossRef]
- Grassie, S.L. The Corrugation of Railway Rails: 2. Monitoring and Conclusions. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2022, 2022, 09544097221122011. [Google Scholar] [CrossRef]
- Grassie, S.L. Measurement of Railhead Longitudinal Profiles: A Comparison of Different Techniques. Wear 1996, 191, 245–251. [Google Scholar] [CrossRef]
- Mauz, F.; Wigger, R.; Wahl, T.; Kuffa, M.; Wegener, K. Acoustic Roughness Measurement of Railway Tracks: Implementation of a Chord-Based Optical Measurement System on a Train. Appl. Sci. 2022, 12, 11988. [Google Scholar] [CrossRef]
- Tufano, A.R.; Chiello, O.; Pallas, M.A.; Faure, B.; Chaufour, C.; Reynaud, E.; Vincent, N. Numerical and Experimental Analysis of Transfer Functions for On-Board Indirect Measurements of Rail Acoustic Roughness. Notes Numer. Fluid. Mech. Multidiscip. Des. 2021, 150, 295–302. [Google Scholar] [CrossRef]
- Pieringer, A.; Kropp, W. Model-Based Estimation of Rail Roughness from Axle Box Acceleration. Appl. Acoust. 2022, 193, 108760. [Google Scholar] [CrossRef]
- Grassie, S.L. Measurement of Longitudinal Irregularities on Rails Using an Axlebox Accelerometer System. Notes Numer. Fluid. Mech. Multidiscip. Des. 2021, 150, 320–328. [Google Scholar] [CrossRef]
- Frederick, C.O. A Rail Corrugation Theory. In Contact Mechanics and Wear of Rail/Wheel. Systems II; University of Waterloo Press: Waterloo, ON, Canada, 1986; Volume 2, pp. 181–211. [Google Scholar]
- Tassilly, E.; Vincent, N. A Linear Model for the Corrugation of Rails. J. Sound. Vib. 1991, 150, 25–45. [Google Scholar] [CrossRef]
- Hempelmann, K.; Knothe, K. An Extended Linear Model for the Prediction of Short Pitch Corrugation. Wear 1996, 191, 161–169. [Google Scholar] [CrossRef]
- Muller, S. A Linear Wheel-Rail Model to Investigate Stability and Corrugation on Straight Track. Wear 2000, 243, 122–132. [Google Scholar] [CrossRef]
- Knothe, K. Non-Steady State Rolling Contact and Corrugations. In Rolling Contact Phenomena; Springer: Wien, Austria, 2000; pp. 203–276. [Google Scholar]
- Baeza, L.; Fayos, J.; Roda, A.; Insa, R. High Frequency Railway Vehicle-Track Dynamics through Flexible Rotating Wheelsets. Veh. Syst. Dyn. 2008, 46, 647–659. [Google Scholar] [CrossRef]
- Martínez-Casas, J.; Di Gialleonardo, E.; Bruni, S.; Baeza, L. A Comprehensive Model of the Railway Wheelset-Track Interaction in Curves. J. Sound. Vib. 2014, 333, 4152–4169. [Google Scholar] [CrossRef] [Green Version]
- EN 13674-1:2011; Railway Applications-Track-Rail Part. 1: Vignole Railway Rails 46 Kg/m and above. British Standard Institution: London, UK, 2011.
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control, 1st ed.; Elsevier Ltd.: Oxford, UK, 2009; ISBN 9780080451473. [Google Scholar]
- Grassie, S.L.; Gregory, R.W.; Harrison, D.; Johnson, K.L. Dynamic Response of Railway Track to High Frequency Vertical Excitation. J. Mech. Eng. Sci. 1982, 24, 77–90. [Google Scholar] [CrossRef]
- Remington, P.; Webb, J. Estimation of Wheel/Rail Interaction Forces in the Contact Area Due to Roughness. J. Sound. Vib. 1996, 193, 83–102. [Google Scholar] [CrossRef]
- Bellette, P.A.; Meehan, P.A.; Daniel, W.J.T. Contact Induced Wear Filtering and Its Influence on Corrugation Growth. Wear 2010, 268, 1320–1328. [Google Scholar] [CrossRef]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- EN ISO 3095:2013; Acoustics-Railway Applications-Measurement of Noise Emitted by Railbound Vehicles. British Standard Institution: London, UK, 2013.
- EN 13231-3:2012; Railway Applications-Track-Acceptance of Works-Part. 3: Acceptance of Reprofiling Rails in Track. British Standard Institution: London, UK, 2012.




| Parameter | Symbol | Value |
|---|---|---|
| Wheelset mass | 1054 | |
| Axle mass | 283 | |
| Axlebox mass | 78 | |
| Wheel mass | 251 | |
| Brake disk mass | 135 | |
| Primary suspension stiffness (vertical) | 2 × 0.5 | |
| Primary suspension stiffness (lateral) | 2 × 2.1 | |
| Primary suspension stiffness (longitudinal) | 2 × 4.15 | |
| Primary suspension damping (vertical) | 11 | |
| Primary suspension damping (lateral) | 50 | |
| Primary suspension damping (longitudinal) | 85 | |
| Wheel nominal radius | 0.41 | |
| Point mass | 605 |
| Parameter | Symbol | Value |
|---|---|---|
| Rail mass (unit length) | 49.9 | |
| Rail cross-section | 63.62 | |
| Rail moment of inertia (y-y) | 1844 | |
| Rail Young Modulus | 2.06 × 105 | |
| Poisson ratio | 0.28 | |
| Rail shear factor | 0.34 | |
| Rail loss factor | 0.02 | |
| Support spacing | 0.75 m | |
| Railpad stiffness | 150 | |
| Railpad loss factor | 0.13 | |
| Railpad viscous damping | 1.5 | |
| Tieplate mass | 15 | |
| Ins. plate stiffness | 30 | |
| Ins. plate loss factor | 0.20 | |
| Ins. plate viscous damping | 2.8 |
| Parameter | Symbol | Value (s) |
|---|---|---|
| Time bin duration | ||
| Sub-window duration | ||
| Overlapping time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faccini, L.; Karaki, J.; Di Gialleonardo, E.; Somaschini, C.; Bocciolone, M.; Collina, A. A Methodology for Continuous Monitoring of Rail Corrugation on Subway Lines Based on Axlebox Acceleration Measurements. Appl. Sci. 2023, 13, 3773. https://doi.org/10.3390/app13063773
Faccini L, Karaki J, Di Gialleonardo E, Somaschini C, Bocciolone M, Collina A. A Methodology for Continuous Monitoring of Rail Corrugation on Subway Lines Based on Axlebox Acceleration Measurements. Applied Sciences. 2023; 13(6):3773. https://doi.org/10.3390/app13063773
Chicago/Turabian StyleFaccini, Leonardo, Jihad Karaki, Egidio Di Gialleonardo, Claudio Somaschini, Marco Bocciolone, and Andrea Collina. 2023. "A Methodology for Continuous Monitoring of Rail Corrugation on Subway Lines Based on Axlebox Acceleration Measurements" Applied Sciences 13, no. 6: 3773. https://doi.org/10.3390/app13063773
APA StyleFaccini, L., Karaki, J., Di Gialleonardo, E., Somaschini, C., Bocciolone, M., & Collina, A. (2023). A Methodology for Continuous Monitoring of Rail Corrugation on Subway Lines Based on Axlebox Acceleration Measurements. Applied Sciences, 13(6), 3773. https://doi.org/10.3390/app13063773






