A Model for Oxygen Transport from Blood in Microvessels to Tissue
Abstract
:1. Introduction
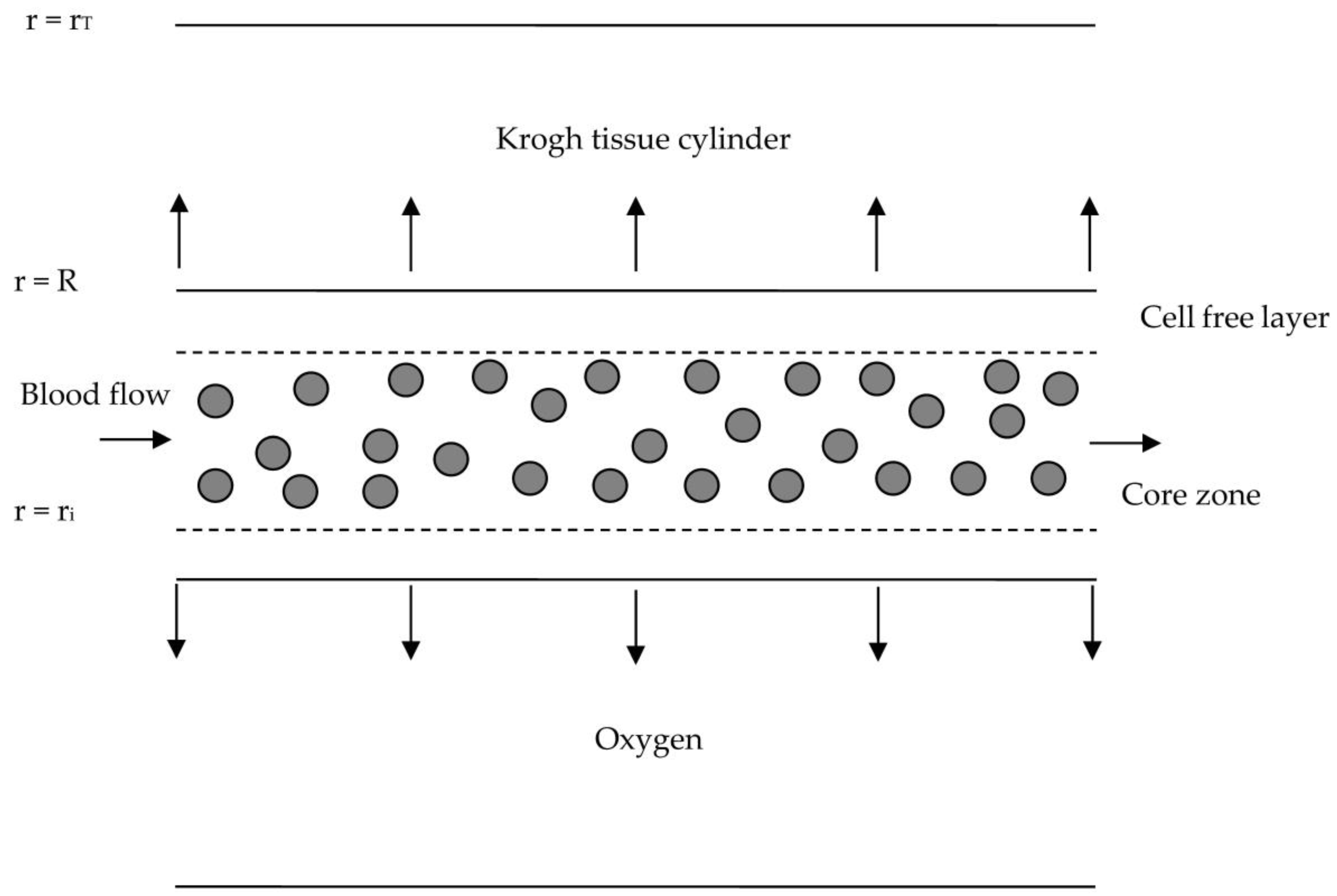
2. Governing Equations
2.1. Blood Flow Model
2.2. Mass Transfer Model
3. Solution
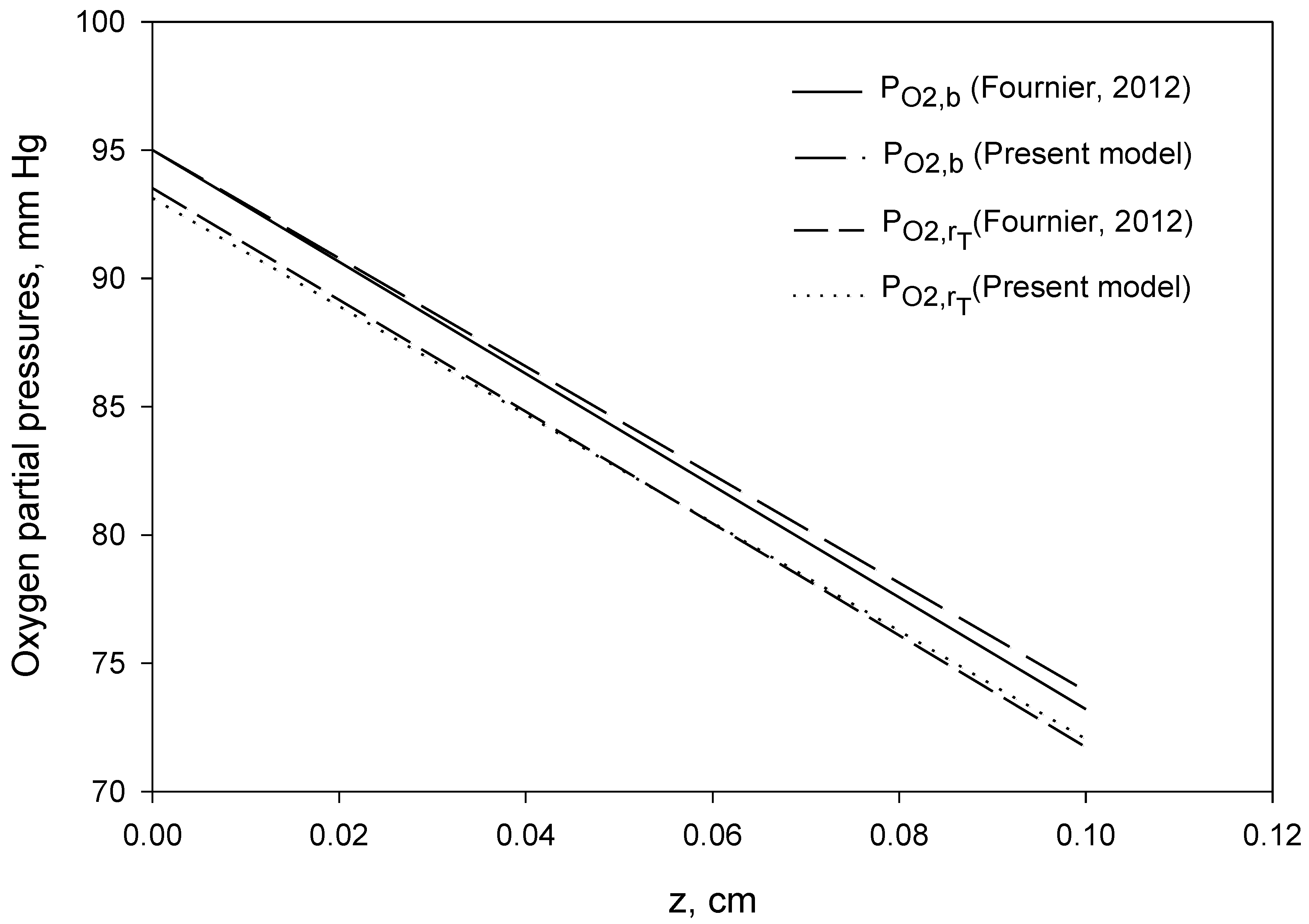
4. Computational Procedure and Results
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Fåhraeus, R. The suspension stability of blood. Physiol. Rev. 1929, 9, 241–274. [Google Scholar] [CrossRef]
- Fåhraeus, R.; Lindqvist, T. The viscosity of the blood in narrow capillary tubes. Am. J. Physiol. 1931, 96, 562–568. [Google Scholar] [CrossRef]
- Fournier, R.L. Basic Transport Phenomena in Biomedical Engineering; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Goldsmith, H.L.; Cokelet, G.R.; Gaehtgens, P.; Fåhræus, R. Evolution of his concepts in cardiovascular physiology. Am. J. Physiol. Heart Circ. Physiol. 1989, 257, H1005–H1015. [Google Scholar] [CrossRef] [PubMed]
- Toksvang, L.N.; Berg, R.M.G. Using a classic paper by Robin Fåhraeus and Torsten Lindqvist to teach basic hemorheology. Adv. Physiol. Educ. 2013, 37, 129–133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Secomb, T.W.; Pries, A.R. Blood viscosity in microvessels: Experiment and theory. Comptes Rendus Phys. 2013, 14, 470–478. [Google Scholar] [CrossRef] [Green Version]
- Haynes, R.F. Physical basis of the dependence of blood viscosity on tube radius. Am. J. Physiol. 1960, 198, 1193–1200. [Google Scholar] [CrossRef]
- Pries, A.R.; Neuhaus, D.; Gaehtgens, P. Blood viscosity in tube flow: Dependence on diameter and hematocrit. Am. J. Physiol. Heart Circul. Phys. 1992, 263, H1770–H1778. [Google Scholar] [CrossRef] [Green Version]
- Sharan, M.; Popel, A.S. A two-phase model for flow of blood in narrow tubes with increased effective viscosity near the wall. Biorheology 2001, 38, 415–428. [Google Scholar]
- Sriram, K.; Intaglietta, M.; Tartakovsky, D.M. Non-Newtonian flow of blood in arterioles: Consequences for wall shear stress measurements. Microcirculation 2014, 21, 628–639. [Google Scholar] [CrossRef] [Green Version]
- Chebbi, R. Dynamics of blood flow: Modeling of the Fåhræus–Lindqvist effect. J. Biol. Phys. 2015, 41, 313–326. [Google Scholar] [CrossRef] [Green Version]
- Weert, K.V. Numerical and Experimental Analysis of Shear-Induced Migration in Suspension Flow. Master’s Thesis, Eindhoven University, Eindhoven, The Netherlands, 2005. [Google Scholar]
- Mansour, M.H.; Bressloff, N.W.; Shearman, C.P. Red blood cell migration in Microvessels. Biorheology 2010, 47, 73–93. [Google Scholar] [CrossRef] [PubMed]
- Chebbi, R. Dynamics of blood flow: Modeling of Fåhraeus and Fåhraeus-Lindqvist effects using a shear-induced red blood cell migration model. J. Biol. Phys. 2018, 44, 591–603. [Google Scholar] [CrossRef] [PubMed]
- Chebbi, R. A two-zone shear-induced red blood cell migration model for blood flow in microvessels. Front. Phys. 2019, 7, 206. [Google Scholar] [CrossRef] [Green Version]
- Leighton, D.T.; Acrivos, A. The shear-induced migration of particles in concentrated suspension. J. Fluid Mech. 1987, 181, 415–439. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Moyers-Gonzalez, M.; Owens, R.G.; Fang, J. A non-homogeneous constitutive model for human blood. Part 1. Model derivation and steady flow. J. Fluid Mech. 2008, 617, 327–354. [Google Scholar] [CrossRef] [Green Version]
- Moyers-Gonzalez, M.A.; Owens, R.G. Mathematical modelling of the cell-depleted peripheral layer in the steady flow of blood in a tube. Biorheology 2010, 47, 39–71. [Google Scholar] [CrossRef]
- Dimakopoulos, Y.; Kelesidis, G.; Tsouka, S.; Georgiou, G.C.; Tsamopoulos, J. Hemodynamics in stenotic vessels of small diameter under steady state conditions: Effect of viscoelasticity and migration of red blood cells. Biorheology 2015, 52, 183–210. [Google Scholar] [CrossRef] [Green Version]
- Mavrantzas, V.G.; Beris, A.N. Modelling the rheology and the flow-induced concentration changes in polymer solutions. Phys. Rev. Lett. 1993, 69, 273–276, Erratum in Phys. Rev. Lett. 1993, 70, 2659. [Google Scholar] [CrossRef]
- Tsouka, S.; Dimakopoulos, Y.; Mavrantzas, V.; Tsamopoulos, J. Stress-gradient induced migration of polymers in corrugated channels. J. Rheol. 2014, 58, 911–947. [Google Scholar] [CrossRef]
- Arciero, J.C.; Causin, P.; Malgaroli, F. Mathematical methods for modeling the microcirculation. AIMS Biophys. 2017, 4, 362–399. [Google Scholar] [CrossRef]
- Bessonov, N.; Sequeira, A.; Simakov, S.; Vassilevski Yu Volpert, V. Methods of blood flow modelling. Math. Model. Nat. Phenom. 2016, 11, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Krogh, A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J. Physiol. 1919, 52, 409–415. [Google Scholar] [CrossRef]
- Popel, A.S. Theory of oxygen transport to tissue. Crit. Rev. Biomed. Eng. 1989, 17, 257–321. [Google Scholar]
- Goldman, D. Theoretical models of microvascular oxygen transport to tissue. Microcirculation 2008, 15, 795–811. [Google Scholar] [CrossRef] [Green Version]
- Truskey, G.A.; Yuan, F.; Katz, D.F. Transport Phenomena in Biological Systems; Pearson: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Hellums, J.D. The resistance to oxygen transport in the capillaries relative to that in the surrounding tissue. Microvasc. Res. 1977, 13, 131–136. [Google Scholar] [CrossRef]
- Federspiel, W.J.; Popel, A.S. A theoretical analysis of the effect of the particulate nature of blood on oxygen release in capillaries. Microvasc. Res. 1986, 32, 164–189. [Google Scholar] [CrossRef]
- Eggleton, C.D.; Vadapalli, A.; Roy, T.K.; Popel, A.S. Calculations of intracapillary oxygen tension distributions in muscle. Math. Biosci. 2000, 167, 123–143. [Google Scholar] [CrossRef]
- Vadapalli, A.; Goldman, D.; Popel, A.S. Calculations of oxygen transport by red blood cells and hemoglobin solutions in capillaries. Artif. Cells Blood Substit. Immobil. Biotechnol. 2002, 30, 157–188. [Google Scholar] [CrossRef]
- Lucker, A.; Weber, B.; Jenny, P.A. Dynamic model of oxygen transport from capillaries to tissue with moving red blood cells. Am. J. Physiol. Heart Circ. Physiol. 2015, 308, H206–H216. [Google Scholar] [CrossRef] [Green Version]
- Lücker, A.; Secomb, T.W.; Weber, B.; Jenny, P. The relative influence of hematocrit and red blood cell velocity on oxygen transport from capillaries to tissue. Microcirculation 2017, 24, e12337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Possenti, L.; Cicchetti, A.; Rosati, R.; Cerroni, D.; Costantino, M.L.; Rancati, T.; Zunino, P. A mesoscale computational model for microvascular oxygen transfer. Ann. Biomed. Eng. 2021, 49, 3356–3373. [Google Scholar] [CrossRef] [PubMed]
- Celaya-Alcala, J.T.; Lee, G.V.; Smith, A.F.; Li, B.; Sakadzi, S.; Boas, D.A.; Secomb, T.W. Simulation of oxygen transport and estimation of tissue perfusion in extensive microvascular networks: Application to cerebral cortex. J. Cereb. Blood Flow Metab. 2021, 41, 656–669. [Google Scholar] [CrossRef] [PubMed]
- Chebbi, R. An analytical model for solute transport from blood to tissue. Open Phys. 2022, 20, 249–258. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: New York, NY, USA, 2007. [Google Scholar]
| Property | Symbol | Value | Reference |
|---|---|---|---|
| Da | Diffusion coefficient in plasma | 2.18 × 10−5 cm2/s | [33] |
| DRBC | Diffusion coefficient in RBCs | 9.5 × 10−6 cm2/s | [33] |
| DT | Diffusion coefficient in tissue | 2.41 × 10−5 cm2/s | [33] |
| 2 R | Capillary diameter | 10 μm | Table 5.1 [3] |
| L | Length | 1000 μm | Table 5.1 [3] |
| Γ | Rate of oxygen consumption in tissue | 20 μM/s | Chapter 6 [3] |
| Average oxygen partial pressure in blood at z = 0 | 95 mm Hg | Chapter 6 [3] | |
| Q | Volume flow rate of blood | 7 nL/min | Chapter 6 [3] |
| αa | Oxygen solubility in plasma | 1.110 μM O2/mm Hg (2.82 × 10−5 mL O2/cm3 mm Hg) | [33] |
| αT | Oxygen solubility in tissue | 1.516 μM O2/mm Hg (3.85 × 10−5 mL O2/cm3 mm Hg) | [33] |
| Symbol | Value |
|---|---|
| v* | 0.149 cm/s |
| rT | 24 μm |
| AcR2 | −0.224 cm/s |
| AaR2 | −0.436 cm/s |
| vi | 0.0829 cm/s |
| va | 0.0415 cm/s |
| b | 210.88 mm Hg/cm |
| K | −2.013 mmHg |
| Dc | 1.60 × 10−5 cm2/s |
| bAaR4/Da | −1.06 mm Hg |
| bAcR4/Dc | −0.740 mm Hg |
| ΓR2/(αaDa) | 0.207 mm Hg |
| ΓR2/(αTDT) | 0.137 mm Hg |
| φi | 0.0840 mm Hg |
| φa at R | −0.1555 mm Hg |
| φT at rT | −1.875 mm Hg |
| pO2,b at z = L | 73.91 mm Hg |
| mav | 12.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chebbi, R. A Model for Oxygen Transport from Blood in Microvessels to Tissue. Appl. Sci. 2023, 13, 3805. https://doi.org/10.3390/app13063805
Chebbi R. A Model for Oxygen Transport from Blood in Microvessels to Tissue. Applied Sciences. 2023; 13(6):3805. https://doi.org/10.3390/app13063805
Chicago/Turabian StyleChebbi, Rachid. 2023. "A Model for Oxygen Transport from Blood in Microvessels to Tissue" Applied Sciences 13, no. 6: 3805. https://doi.org/10.3390/app13063805





