Use of Sample Entropy to Assess Sub-Maximal Physical Load for Avoiding Exercise-Induced Cardiac Fatigue
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
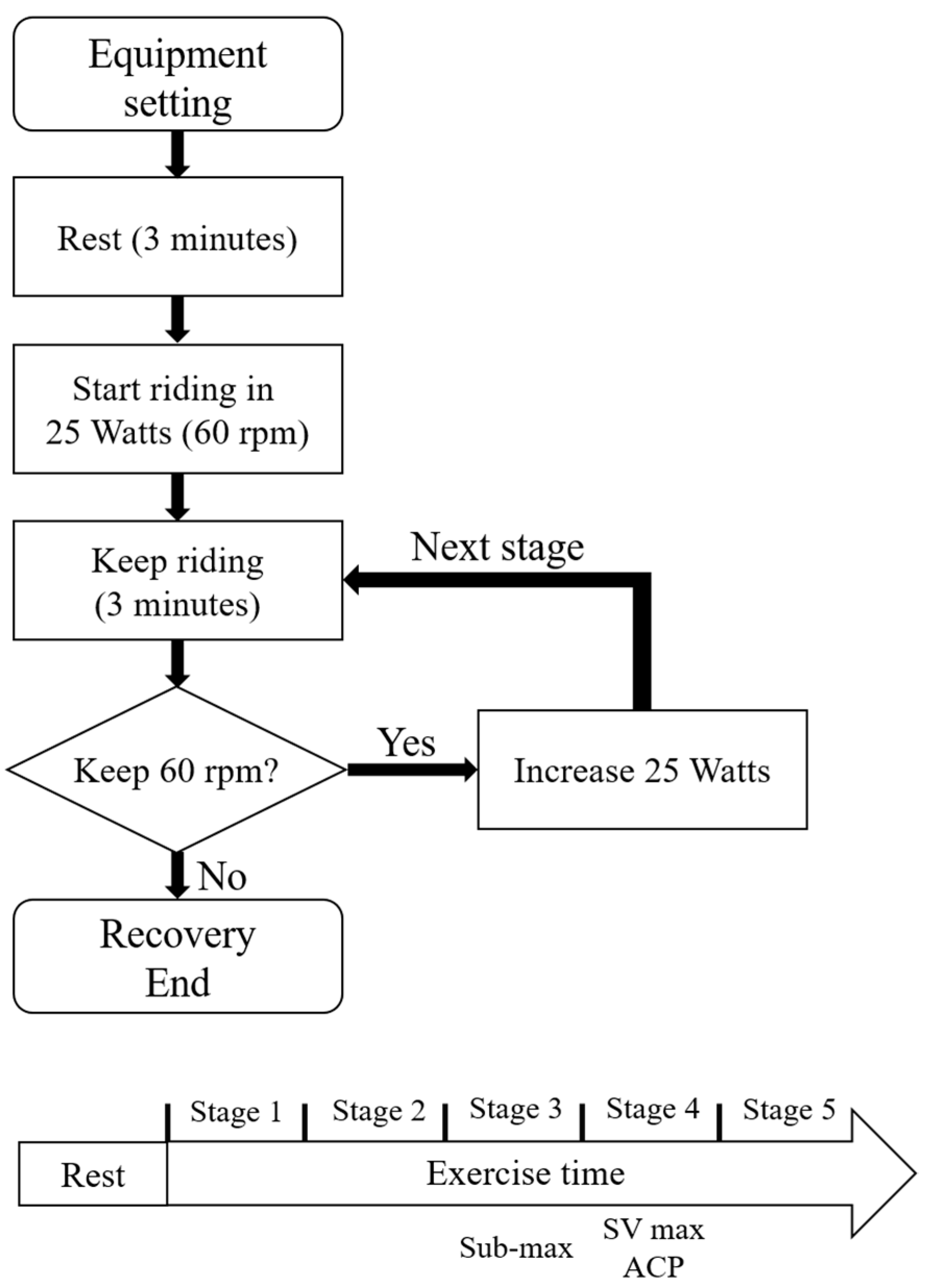
2.2. Protocol
- Survey patients about their exercise habits.
- Rest at 0 watts. At each stage, the difficulty of each stage increases by 25 W.
- The experiment continues until the patients are unable to maintain 60 rpm or are exhausted.
- The patient is in recovery the experiment ends.
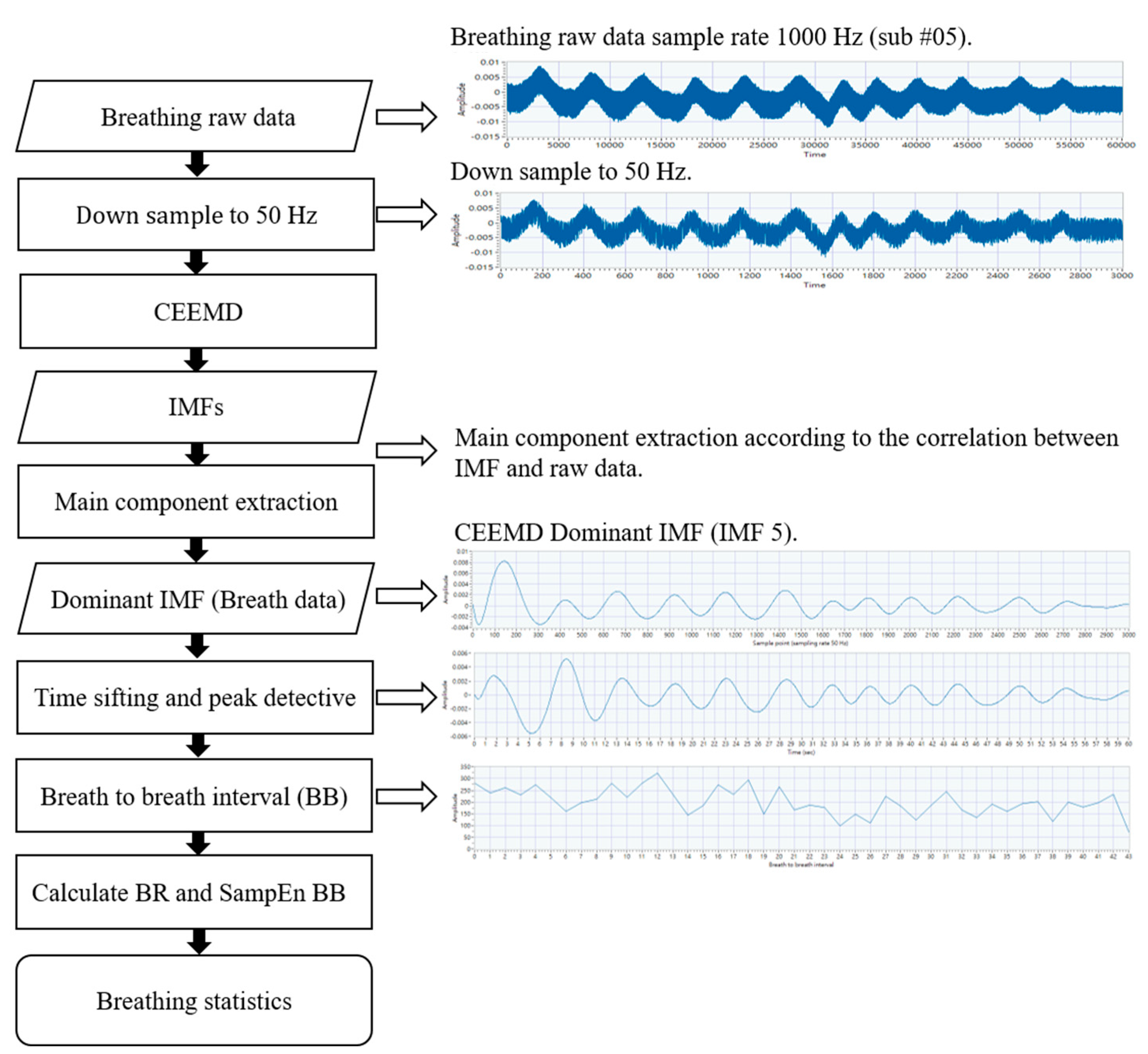
2.3. Measurement and Signal Processing
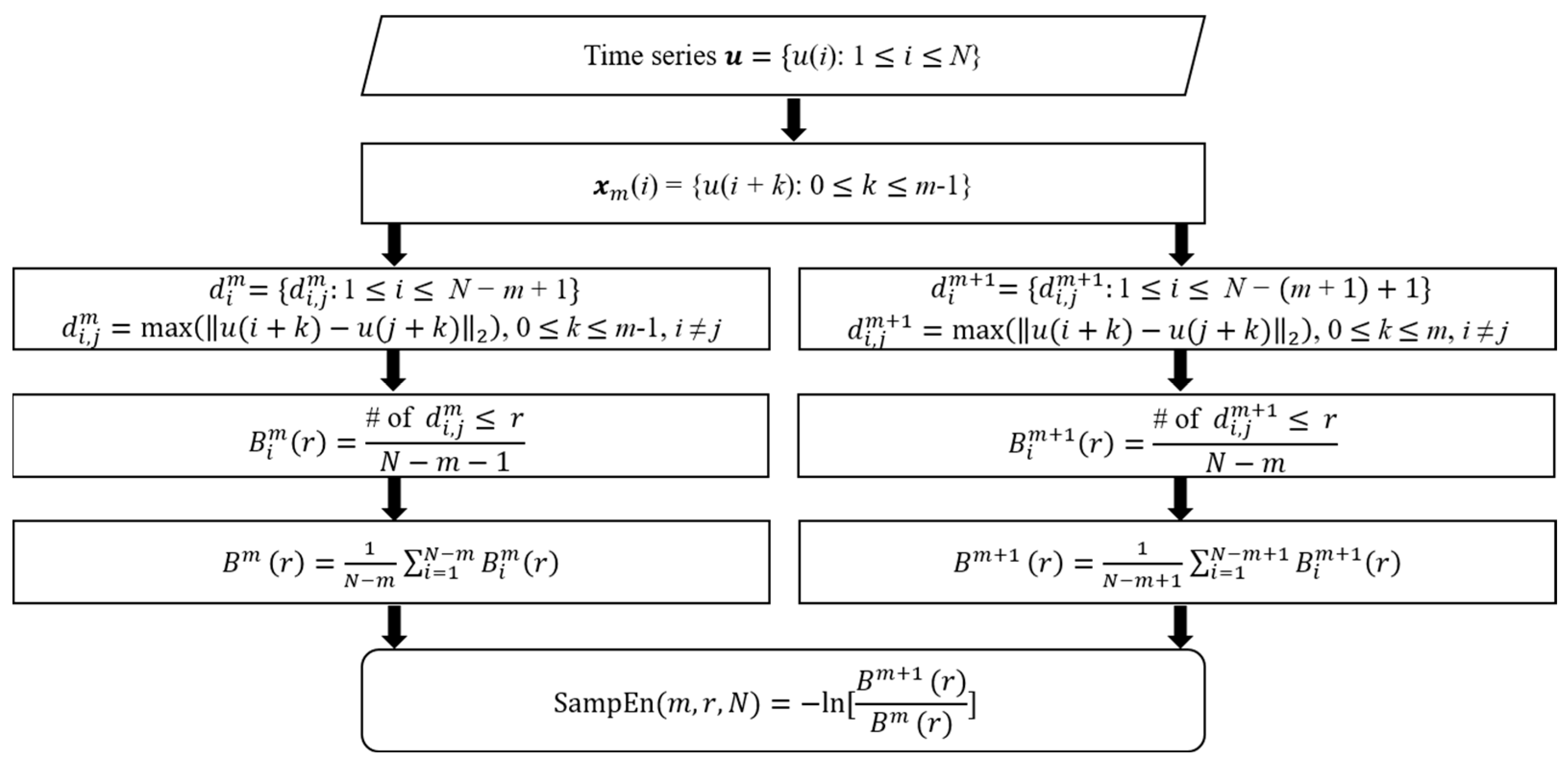
2.4. Sample Entropy Analysis
- Input a time-domain signal u with length N.
- Define the sequence xm, which is a vector with length m.
- Define the distance between xm(i) and xm(j) as the largest difference between these elements for all elements i and j.
- Count the number of less than a given threshold r as .
- The average value of these counts for all i is calculated as .
- Similarly, calculate these values for m + 1.
- .
2.5. Statistical Analysis
3. Results
3.1. Cardiovascular Response Results
3.2. Breathing Results
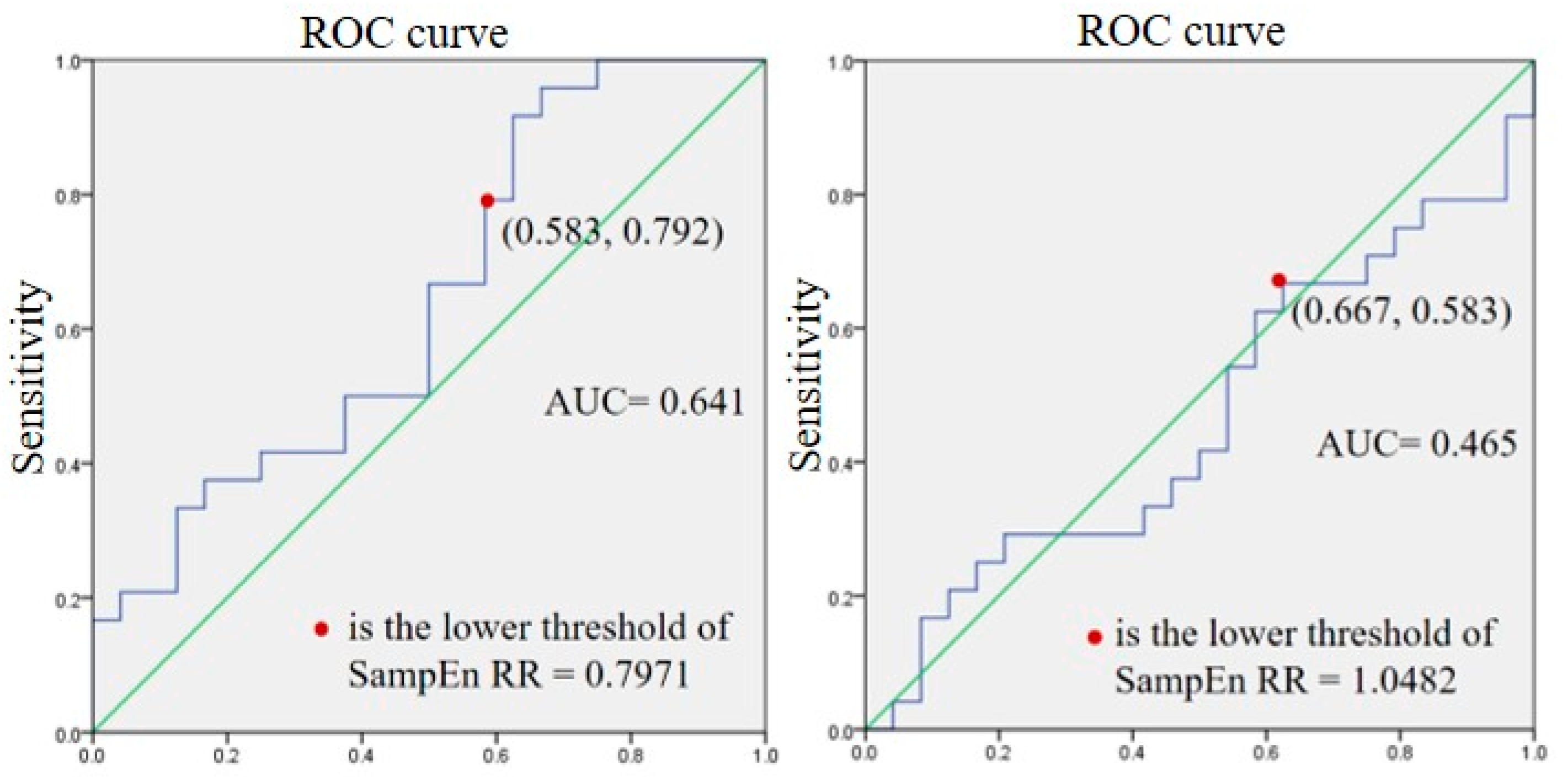
3.3. Sub-Group Results
4. Discussion
4.1. SampEn Parameters
4.2. SampEn RR at Rest and during Exercise
4.3. Loss of Complexity in Physiological Systems
4.4. Sub-Max Physical Load
4.5. Sub-Groups
5. Limitations
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goolaerts Suffered heart Attack before Crash: Autopsy. AFP. April 2018. Available online: https://www.france24.com/en/20180411-goolaerts-suffered-heart-attack-before-crash-autopsy (accessed on 1 January 2022).
- Marijon, E.; Tafflet, M.; Celermajer, D.S.; Dumas, F.; Perier, M.-C.; Mustafic, H.; Toussaint, J.-F.; Desnos, M.; Rieu, M.; Benameur, N.; et al. Sports-related sudden death in the general population. Circulation 2011, 124, 672–681. [Google Scholar] [CrossRef] [PubMed]
- Claessen, G.; La Gerche, A. Exercise-induced cardiac fatigue: The need for speed. J. Physiol. 2016, 594, 2781. [Google Scholar] [CrossRef] [PubMed]
- Leischik, R. Sports cardiology: Lessons from the past and perspectives for the future. F1000Research 2015, 4, 94. [Google Scholar] [CrossRef] [PubMed]
- Ganong, W.F. Review of medical physiology. Rev. Med. Physiol. 1975, 26, 599. [Google Scholar]
- Lai, W.-C.; Huang, P.-H.; Hsiao, T.C. Relationship between breath regulation and stroke volume with exercise intensity: A pilot study. In Proceedings of the 12th International Conference on eHealth, Telemedicine, and Social Medicine (eTELEMED 2020), Valencia, Spain, 21–25 November 2020. [Google Scholar]
- Stöhr, E.J.; González-Alonso, J.; Shave, R. Left ventricular mechanical limitations to stroke volume in healthy humans during incremental exercise. Am. J. Physiol.-Heart Circ. Physiol. 2011, 301, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Leischik, R.; Spelsberg, N. Endurance sport and “cardiac injury: A prospective study of recreational ironman athletes. Int. J. Environ. Res. Public Health 2014, 11, 9082–9100. [Google Scholar] [CrossRef] [PubMed]
- James, H.O.; Patil, H.R.; Lavie, C.J.; Magalski, A.; Vogel, R.A.; McCullough, P.A. Potential adverse cardiovascular effects from excessive endurance exercise. Mayo Clin. Proc. 2012, 87, 736–740. [Google Scholar]
- George, K.P.; Wolfe, L.A.; Burggraf, G.W. The ‘athletic heart syndrome’. Sport. Med. 1991, 11, 300–331. [Google Scholar] [CrossRef]
- La Gerche, A.; Burns, A.T.; Mooney, D.J.; Inder, W.J.; Taylor, A.J.; Bogaert, J.; MacIsaac, A.I.; Heidbüchel, H.; Prior, D.L. Exercise-induced right ventricular dysfunction and structural remodelling in endurance athletes. Eur. Heart J. 2012, 33, 998–1006. [Google Scholar] [CrossRef]
- Leischik, R. Endurance sport and cardiac injury. Kardiol. Pol. Pol. Heart J. 2014, 72, 587–597. [Google Scholar] [CrossRef]
- Denniston, J.C.; Maher, J.T.; Reeves, J.T.; Cruz, J.C.; Cymerman, A.; Grover, R.F. Measurement of cardiac output by electrical impedance at rest and during exercise. J. Appl. Physiol. 1976, 40, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Northridge, D.B.; Findlay, I.N.; Wilson, J.; Henderson, E.; Dargie, H.J. Non-invasie determination of cardiac output by Doppler echocardiography and electrical bioimpedance. Heart 1990, 63, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Mead, J. Volume displacement body plethysmograph for respiratory measurements in human subjects. J. Appl. Physiol. 1960, 15, 736–740. [Google Scholar] [CrossRef]
- Heyde, C.; Leutheuser, H.; Eskofier, B.; Roecker, K.; Gollhofer, A. Respiratory inductance plethysmography-a rationale for validity during exercise. Med. Sci. Sport. Exerc. 2014, 46, 488–495. [Google Scholar] [CrossRef]
- Swain, D.P.; Abernathy, K.S.; Smith, C.S.; Lee, S.J.; A Bunn, S. Target heart rates for the development of cardiorespiratory fitness. Med. Sci. Sport. Exerc. 1994, 26, 112–116. [Google Scholar] [CrossRef]
- Mador, M.J.; Acevedo, F.A. Effect of respiratory muscle fatigue on breathing pattern during incremental exercise. Am. Rev. Respir. Dis. 1991, 143, 462–468. [Google Scholar] [CrossRef]
- Kaikkonen, P.; Hynynen, E.; Mann, T.; Rusko, H.; Nummela, A. Can HRV be used to evaluate training load in constant load exercises? Eur. J. Appl. Physiol. 2010, 108, 435–442. [Google Scholar] [CrossRef]
- Lai, Y.-H.; Lai, W.-C.; Huang, P.-H.; Hsiao, T.-C. Time- and frequency-domain analysis of stroke volume variability using indoor cycling to evaluate physical load of body. Information 2022, 13, 148. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Pethick, J.; Winter, S.L.; Burnley, M. Fatigue reduces the complexity of knee extensor torque fluctuations during maximal and submaximal intermittent isometric contractions in man. J. Physiol. 2015, 593, 2085–2096. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Peng, C.-K.; A Lipsitz, L. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Lipsitz, L.A.; Goldberger, A.L. Loss of ‘complexity’ and aging: Potential applications of fractals and chaos theory to senescence. JAMA 1992, 267, 1806–1809. [Google Scholar] [CrossRef] [PubMed]
- Cropper, W.H. Rudolf Clausius and the road to entropy. Am. J. Phys. 1986, 54, 1068–1074. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On tables of random numbers. Sankhyā: Indian J. Stat. Ser. A 1963, 25, 369–376. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Delgado-Bonal, A.; Marshak, A. Approximate entropy and sample entropy: A comprehensive tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Lewis, M.J.; Short, A.L. Sample entropy of electrocardiographic RR and QT time-series data during rest and exercise. Physiol. Meas. 2007, 28, 731. [Google Scholar] [CrossRef]
- Naranjo-Orellana, J.; Nieto-Jiménez, C.; Ruso-Álvarez, J. Non-linear heart rate dynamics during and after three controlled exercise intensities in healthy men. Physiol. Int. 2021, 107, 501–512. [Google Scholar] [CrossRef]
- Bandara, K.; Wijesiriwardana, R. Sample entropy analysis of cardiac and respiratory responses during four limbs exercise. In Proceedings of the 3rd International Conference on Electrical Engineering (EECon) 2021, Colombo, Sri Lanka, 24 September 2021; pp. 106–111. [Google Scholar]
- Schmidt, C.; Theilmeier, G.; Van Aken, H.; Korsmeier, P.; Wirtz, S.P.; Berendes, E.; Hoffmeier, A.; Meissner, A. Comparison of electrical velocimetry and transoesophageal Doppler echocardiography for measuring stroke volume and cardiac output. Br. J. Anaesth. 2005, 95, 603–610. [Google Scholar] [CrossRef] [PubMed]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Wang, B.; Yu, M. Sample Entropy analysis of heart rate variability during rest and exercise in hypoxia. Int. J. Control Autom. 2014, 7, 1–8. [Google Scholar] [CrossRef]
- Weippert, M.; Behrens, M.; Rieger, A.; Behrens, K. Sample entropy and traditional measures of heart rate dynamics reveal different modes of cardiovascular control during low intensity exercise. Entropy 2014, 16, 5698–5711. [Google Scholar] [CrossRef]
- Platiša, M.; Mazic, S.; Nestorovic, Z.; Gal, V. Complexity of heartbeat interval series in young healthy trained and untrained men. Physiol. Meas. 2008, 29, 439. [Google Scholar] [CrossRef]
- NBerry, N.T.; Bechke, E.; Shriver, L.H.; Calkins, S.D.; Keane, S.P.; Shanahan, L.; Wideman, L. Heart rate dynamics during acute recovery from maximal aerobic exercise in young adults. Front. Physiol. 2021, 12, 627320. [Google Scholar]
- Hsu, C.F.; Wei, S.-Y.; Huang, H.-P.; Hsu, L.; Chi, S.; Peng, C.-K. Entropy of entropy: Measurement of dynamical complexity for biological systems. Entropy 2017, 19, 550. [Google Scholar] [CrossRef]
- Huang, P.-H.; Hsiao, T.-C. Intrinsic Entropy: A Novel Adaptive Method for Measuring the Instantaneous Complexity of Time Series. IEEE Signal Process. Lett. 2023, 2023, 3244508. [Google Scholar] [CrossRef]
- Lipsitz, L.A. Dynamics of stability: The physiologic basis of functional health and frailty. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2002, 57, B115–B125. [Google Scholar] [CrossRef] [PubMed]
- Vanegas, E.; Igual, R.; Plaza, I. Sensing systems for respiration monitoring: A technical systematic review. Sensors 2020, 20, 5446. [Google Scholar] [CrossRef] [PubMed]
- Bull, F.C.; Al-Ansari, S.S.; Biddle, S.; Borodulin, K.; Buman, M.P.; Cardon, G. World Health Organization 2020 guidelines on physical activity and sedentary behavior. Br. J. Sport. Med. 2020, 54, 1451–1462. [Google Scholar] [CrossRef] [PubMed]


| S (Sedentary) | N (Normal) | E (Exercise) | |
|---|---|---|---|
| Exercise time/week (hour) | 0.6 ± 0.52 * | 3.00 ± 1.00 * | 11.64 ± 8.37 |
| Gender (male/female) | 4/6 | 4/5 | 9/2 |
| Body mass index | 22.52 ± 3.57 | 22.14 ± 2.71 | 23.59 ± 2.25 |
| Riding time (min) | 20.50 ± 4.88 | 21.67 ± 3.61 | 22.91 ± 2.43 |
| ACP stage | 2.6 ± 1.17 | 2.00 ± 0.71 * | 4.45 ± 2.58 |
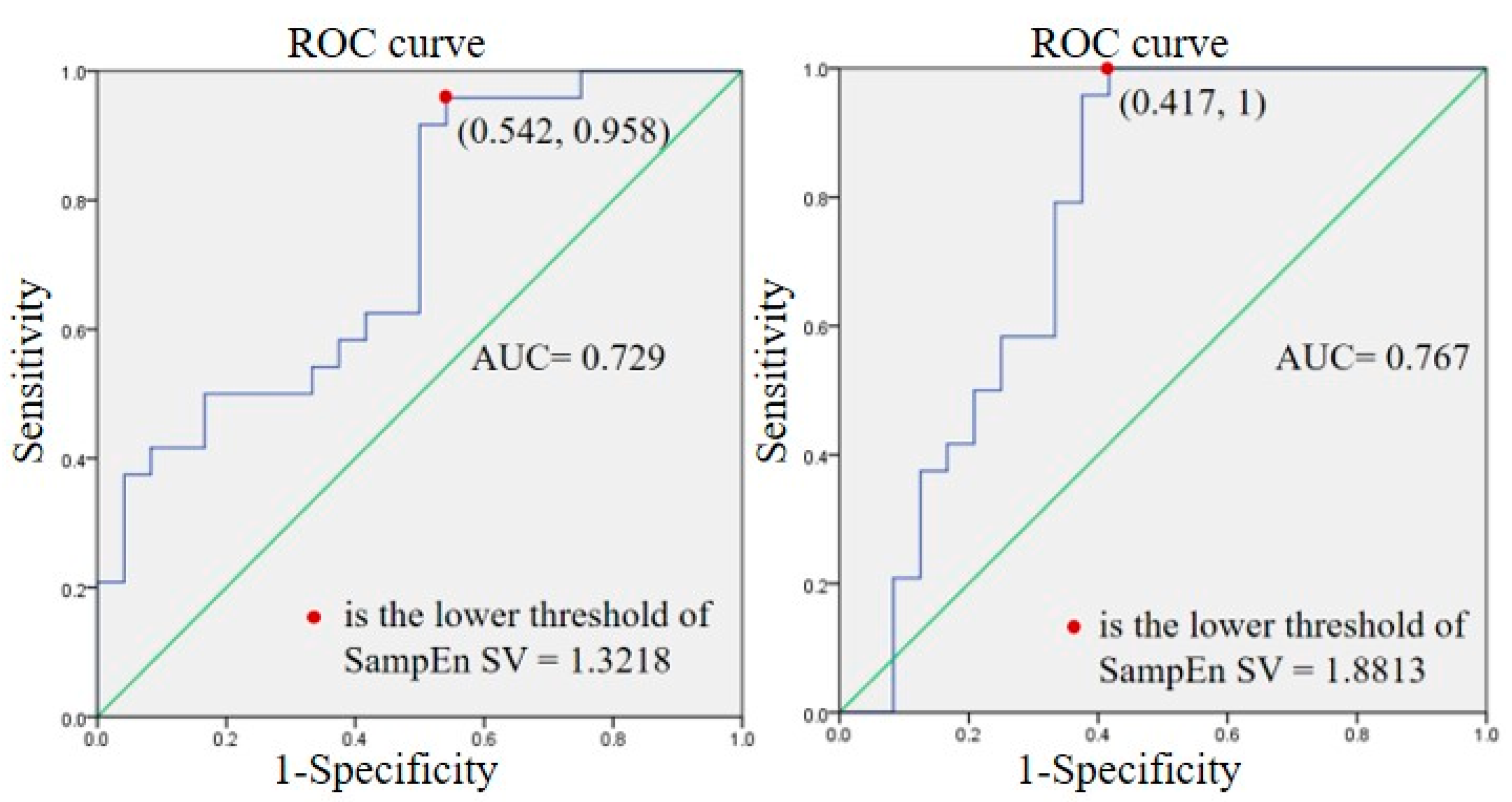
| SampEn RR | SampEn SV | SampEn CO | ||
|---|---|---|---|---|
| Rest (N = 24) | mean ± SD | 1.01 ± 0.48 | 1.44 ± 0.39 | 1.33 ± 0.41 |
| median | 1.24 | 1.43 | 1.38 | |
| Sub-max (N = 24) | mean ± SD | 1.26 ± 0.44 | 1.78 ± 0.37 | 1.86 ± 0.29 |
| median | 1.22 * | 1.77 **,## | 1.82 **,## | |
| ACP stage (N = 24) | mean ± SD | 1.31 ± 0.46 | 2.14 ± 0.09 | 2.18 ± 0.13 |
| median | 1.35 * | 2.15 ** | 2.18 ** | |
| Rest | Sub-Max Stage | ACP Stage | |
|---|---|---|---|
| RR | 0.51 ** | −0.01 | 0.17 |
| HRV nHF | 0.19 | 0.36 * | 0.11 |
| HRV nLF | −0.19 | −0.36 * | −0.11 |
| SV | 0.30 | 0.13 | −0.05 |
| SVV nHF | 0.46 * | −0.02 | 0.16 |
| SVV nLF | −0.46 * | 0.02 | −0.16 |
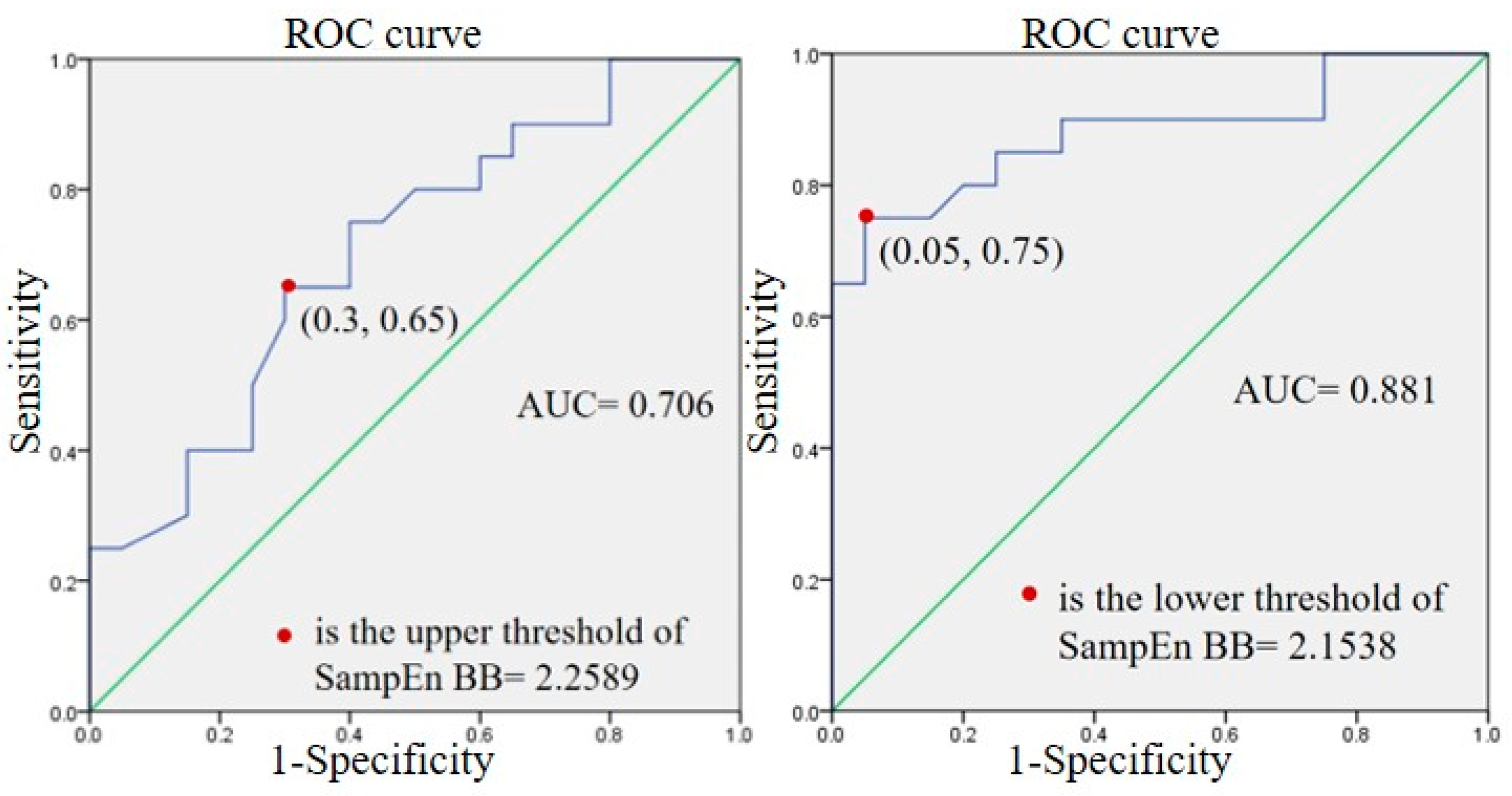
| BR | SampEn BB | ||
|---|---|---|---|
| Rest (N = 20) | Mean ± SD | 16.62 ± 3.93 | 1.98 ± 0.44 |
| median | 15.58 | 2.06 | |
| Sub-max (N = 20) | Mean ± SD | 20.08 ± 4.25 | 2.34 ± 0.44 |
| median | 18.83 ** | 2.32 *,## | |
| ACP stage (N = 20) | Mean ± SD | 21.48 ± 6.50 | 1.71 ± 0.36 |
| median | 19.17 ** | 1.77 * | |
| Rest | Sub-Max | ACP | |||||
|---|---|---|---|---|---|---|---|
| Mean ± SD | Median | Mean ± SD | Median | Mean ± SD | Median | ||
| SampEn RR | S (N = 8) | 1.04 ± 0.45 | 1.11 | 1.11 ± 0.44 | 1.02 | 1.41 ± 0.57 | 1.51 |
| N (N = 8) | 1.26 ± 0.42 | 1.31 ^ | 1.29 ± 0.51 | 1.23 | 1.36 ± 0.44 | 1.38 | |
| E (N = 8) | 0.73 ± 0.45 | 0.67 | 1.36 ± 0.44 | 1.38 * | 1.16 ± 0.38 | 1.07 * | |
| SampEn SV | S (N = 8) | 1.01 ± 0.48 | 1.24 | 1.26 ± 0.44 | 1.22 * | 1.31 ± 0.46 | 1.35 * |
| N (N = 8) | 1.18 ± 0.33 | 1.15 | 1.65 ± 0.39 | 1.54 *,# | 2.13 ± 0.12 | 2.15 * | |
| E (N = 8) | 1.39 ± 0.35 | 1.42 † | 1.68 ± 0.28 | 1.64 * | 2.13 ± 0.10 | 2.13 * | |
| SampEn CO | S (N = 8) | 1.76 ± 0.27 | 1.77 †† | 2.01 ± 0.35 † | 2.13 | 2.16 ± 0.08 | 2.16 * |
| N (N = 8) | 1.44 ± 0.39 | 1.43 | 1.78 ± 0.37 | 1.77 **,## | 2.14 ± 0.09 | 2.15 ** | |
| E (N = 8) | 1.37 ± 0.35 | 1.40 | 1.76 ± 0.27 | 1.80 ##,† | 2.17 ± 0.11 | 2.18 ** | |
| SampEn BB | S (N = 5) | 1.88 ± 0.43 | 1.98 | 2.34 ± 0.35 | 2.30 # | 1.87 ± 0.23 | 1.91 |
| N (N = 8) | 1.99 ± 0.48 | 2.15 † | 2.29 ± 0.78 | 2.47 | 1.80 ± 0.39 | 1.83 | |
| E (N = 7) | 2.10 ± 0.45 | 2.25 | 2.38 ± 0.25 | 2.35 # | 1.47 ± 0.38 | 1.51 *,† | |
| BR | S (N = 5) | 15.79 ± 2.8 | 16.50 | 17.65 ± 1.79 | 18.17 ^ | 17.15 ± 4.85 | 15.75 ^ |
| N (N = 8) | 16.47 ± 4.4 | 15.33 | 20.87 ± 5.09 | 20.67 * | 22.50 ± 6.06 | 21.50 * | |
| E (N = 7) | 17.69 ± 4.9 | 15.67 | 22.29 ± 4.69 | 24.00 | 25.69 ± 5.95 | 26.33 * | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.-H.; Huang, P.-H.; Hsiao, T.-C. Use of Sample Entropy to Assess Sub-Maximal Physical Load for Avoiding Exercise-Induced Cardiac Fatigue. Appl. Sci. 2023, 13, 3813. https://doi.org/10.3390/app13063813
Lai Y-H, Huang P-H, Hsiao T-C. Use of Sample Entropy to Assess Sub-Maximal Physical Load for Avoiding Exercise-Induced Cardiac Fatigue. Applied Sciences. 2023; 13(6):3813. https://doi.org/10.3390/app13063813
Chicago/Turabian StyleLai, Yu-Han, Po-Hsun Huang, and Tzu-Chien Hsiao. 2023. "Use of Sample Entropy to Assess Sub-Maximal Physical Load for Avoiding Exercise-Induced Cardiac Fatigue" Applied Sciences 13, no. 6: 3813. https://doi.org/10.3390/app13063813
APA StyleLai, Y.-H., Huang, P.-H., & Hsiao, T.-C. (2023). Use of Sample Entropy to Assess Sub-Maximal Physical Load for Avoiding Exercise-Induced Cardiac Fatigue. Applied Sciences, 13(6), 3813. https://doi.org/10.3390/app13063813






