1. Introduction
Many civilian applications of small unmanned aircraft systems (sUASs) have been envisioned to be operated in congested urban airspace for various purposes such as the delivery of medical supplies and the delivery of packages to rural areas [
1,
2,
3,
4,
5,
6,
7]. Such applications are expected to significantly increase the quality of these services. However, there is no infrastructure to enable and safely manage the use of urban airspace and sUAS operations yet. Learning from the history of the air traffic management (ATM) systems, numerous organisations have investigated concepts, functional designs, and prototypes of unmanned aircraft system (UAS) traffic management (UTM) systems to support safe and efficient sUAS operations for many applications in urban airspace [
8,
9,
10,
11,
12,
13,
14].
One of the most fundamental tasks facing the stakeholders of the UTM system over the world involves defining, measuring, and predicting of the capacity of urban airspace [
2,
15]. The capacity can be viewed from various perspectives such as safety, performance efficiency, conflicts, noise, communication spectrum, etc. The difficulty of the task is due to the numerous factors that affect the urban airspace capacity. In the ATM system most similar to the UTM system, the general notion of the airspace capacity is the number of flights that can be accommodated in a given airspace within a given time. In [
16,
17,
18,
19,
20], the authors proposed capacity estimation approaches, which are evaluated from the human workload of air traffic controllers and pilots. These approaches are highly dependent on the subjective assessment or judgment of the air traffic controllers. However, such human-dependent airspace capacity estimation approaches are evaded and unsuitable for the UTM system which is expected to operate a large number of sUASs by a small number of people or by itself.
In [
21], authors presented a method to calculate air traffic conflict probabilities. The method is more scalable and robust than the previous approaches. Furthermore, the method can be applied for any arbitrary stochastic distribution under the condition that the method requires constant communication between the vehicles and cooperative operations. In [
22], the authors showed that the threshold-based mathematical definition to estimate the capacity for free flight-based low-altitude airspace. The authors used two metrics to estimate the capacity: safety (total loss of flight per flight hour) and performance (percentage extension of travel distance). In [
23], the authors investigated new deconfliction schemes for unmanned aerial vehicles in high-density very low-level (VLL) uncontrolled airspace, and assessed single-layered and multi-layered airspace designs. Their aim was to provide a framework for choosing resolution strategies for regulators and policymakers for the UTM system. In [
13], the authors determined the situation-appropriate route network for unmanned aircraft in urban airspace. The authors suggested three different types of route networks (AirMatrix, Over Buildings, Over Roads), and showed the results of the capacity and throughput for each route network. The results were obtained by generating five two-way routes for aerial delivery missions from the supply point to five service points where the routing problem was solved with an assumption that once a sUAS occupies a segment, then any other sUASs cannot traverse the route.
However, the approach caused very conservative analysis results and might disturb the optimality of solutions for the following problems: scheduling and separation management, although these have a computational advantage. As presented in the literature [
11,
12,
22,
23,
24], on the development of advanced technology, the free flight-based operation in congested urban airspace can be an option for the UTM system. One of the few options is route network-based operations as described in [
13,
25]. Additionally, in the ATM context, opinions on the types of airspace operations diverge into two groups, a reduction in the constraints research [
26,
27] and more structured operations-preferred research [
28,
29].
Inspired by [
13,
25,
30,
31], we investigate strategies for analysing high-density VLL structured and controlled urban airspace capacity, with the aim to support airspace designers, regulators, and policymakers for determining tailored strategies in the consideration of regional characteristics and environment. The benchmark scenarios considered to perform capacity analysis are four different drone delivery operation types (1-to-
,
-to-1,
-to-
, and
-to-
, where
is a number of arrival or departure points and
) in a route network over the roads in a given urban airspace. To overcome the disadvantages of the five two-way route planning used in [
13] and perform quantitative capacity analysis, we develop a flight planning algorithm which is an extended version of our previous algorithm [
32,
33].
The proposed algorithm that iteratively solves multiple sUASs’ flight planning problems consists of an inner loop algorithm and an outer loop algorithm. At each iteration, the inner loop algorithm generates each sUAS’ flight route and speed profile by solving the shortest path problem, and the outer loop algorithm determines the departure and arrival sequences. To suggest an arrival and departure algorithm for each operation type, we utilise two different outer loop algorithms, which are the first-come-first-served (FCFS) algorithm and the last-come-first-served (LCFS) algorithm, for allocating the sequences. We utilise the obtained flight plans to analyse the urban airspace by defining four metrics as follows: total flight time; mission completion time; total flight distance; and normalised number of conflicts. For each operation type, we conduct 100 Monte Carlo simulations for both the FCFS algorithm and the LCFS algorithm. From the results, we can either find an appropriate outer loop algorithm for regional characteristics and the cases or reconfigure route networks as is required. We expect that the simulation results and its analysis could provide insight for policymakers, urban airspace designers, and regulators from the perspective of safety, capacity, etc.
The structure of this paper is as follows. We first focus on a design of the route network over roads in
Section 2. In the following section, we provide details of the flight planning algorithms for the different cases, and describe the metrics to analyse the urban airspace capacity. Note that, in order to avoid extraneous examples to explain the flight planning algorithm in
Section 3, we adopt one simulation case in
Section 4 to explain it. In
Section 4, we perform numerical simulations for each operation type and analyse the results. Finally, the conclusion and discussion are presented in
Section 5.
2. Urban Airspace Concept: Route Network over Roads
Many studies have focused on the sUAS path planning problem [
24,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46]. The majority of them solve the problem with the unstructured airspace assumption. For urban airspace users in high-density VLL urban airspaces, however, many difficulties are expected with sUAS studies, which are based on free routing and free flight operations, such as the risk of unforeseen crashes, the invasion of privacy, etc. On the other hand, structured and controlled airspace can predict crashes more easily than the unstructured airspace, and privacy can be considered in the airspace structural design stage.
In this section, we suggest a route network-based urban airspace structure, which can be a potential candidate for the high-density VLL airspace structure. The proposed urban airspace structure concept resembles the airspace structure used in en-route phases of the ATM system today that can be considered as a combination of the Layers and Tubes concepts amongst four concepts Full Mix, Layers, Zones, and Tubes presented in [
31]. The characteristics of the suggested airspace structure concept are as follows: consist of waypoints (nodes) and segments (edges) connecting some pair of waypoints; flight direction is strictly defined for all segments; at least two layers are stacked; separate traffic based on a time-based separation concept within each layer. As shown in
Figure 1, for example, there is an eastbound layer and a westbound layer, and each layer consists of parallel-aligned northbound segments and southbound segments. Such a route network over roads with directions in urban airspace will increase the predictability of traffic by using flight plans. In this concept, the urban airspace structure can be thought of as a directed graph (or digraph)
, called an airspace graph to highlight the aerospace context. In the airspace graph
, node
is a point in Euclidean space of dimension two or three representing a waypoint candidate to be traversed. Edge
, corresponding to a rectifiable curve, is a segment between some pair of waypoints in the airspace graph
.
The main assumptions we make for the route network-based operations in this study are as follows: each flight route is composed of a series of linear segments as shown in
Figure 2; each sUAS flies along each segment at a constant speed while it changes speed in between segments; each sUAS is able to exactly follow the flight route without deviation; a time-based separation concept is utilised for collision avoidance; uncertainties produced by external sources are neglected such as adverse weather (i.e., true airspeed is considered); a control tower exists (i.e., flight plans are shared between sUASs and a control tower); the hovering and vertical manoeuvres are not considered; sUASs have limited payload and flight range; we only consider flights within each layer (e.g., no transitions between layers), but the transitions could be adopted by establishing the vertical segments in reality; homogeneous sUASs.
3. Flight Planning Algorithm
In this section, we describe the flight planning algorithm that is used to analyse the route network-based urban airspace. The algorithm that solves multiple sUASs flight planning problems consists of the inner loop algorithm and the outer loop algorithm. The inner loop algorithm optimises each flight plan of an sUAS that minimises the flight time while satisfying the time-based minimum separation requirement from other planned sUASs. Then, the outer loop algorithm allocates arrival and departure sequences of the sUASs.
Definition 1. We define the flight planning problem as the following: (a) the flight route of each sUAS, (b) its separation-compliant speed profile including arrival times at each waypoint, and (c) the arrival and departure sequences (if it is a multiple sUASs flight planning problem).
This section consists of five parts: (a) a description of the time-based separation concept; (b) flight planning problem formulation for each sUAS (inner loop); (c) the entire flight planning algorithm with two different outer loop algorithms (FCFS and LCFS); (d) a flight planning example using the proposed algorithm for a last-mile delivery case (1-to-); and (e) a description of four metrics to quantitatively analyse the urban airspace capacity.
3.1. Separation Concept in Route Network-Based Unban Airspace
Conflict detection is activated when the separation of two sUASs is less than the minimum separation criterion. In this study, time-based separation is applied instead of the widely used distance-based separation to stabilise the spacing between all the sUASs. In this concept, a sUAS will occupy a waypoint when the sUAS passes the waypoint for a predetermined time interval. Within this time interval, no sUAS is allowed to traverse through the waypoint to satisfy the separation requirement. For each waypoint, a time interval list is maintained to keep track of the times at which the waypoint is expected to be occupied. These lists, called the flight schedule in this study, are shared between all sUASs during operation. By satisfying the separation assurance flight time at each waypoint rather than adjusting a distance between the sUASs, we can obtain results that satisfy the minimum separation along routes as well as at waypoints at all times. Note that, even if we consider homogeneous sUASs in this study, the separation concept can be applied to both heterogeneous and homogeneous cases.
The separation concept allows time-based separation to be satisfied at merging points and crossing points as shown in
Figure 3 and
Figure 4, respectively. At the time
of
Figure 3, sUAS
and sUAS
fly towards the
through the same merging point
at speeds
and
, respectively. The time
is stored at each start point
and
, and no sUAS can pass through both of the waypoints for separation time
seconds and
seconds before and after
, respectively. Note that, where
is dependent on the types of
and
. The time
of
Figure 3, when
just passes through
, is stored at the merging point
, and no sUAS can pass through this waypoint for
seconds before or after
. The time
of
Figure 3 is stored in
in the same way. Then,
and
traverse towards
at speeds of
and
, respectively. If
and
fly from
to
at speeds of
and
, respectively, the separation between the two sUASs will always meet the separation requirement or be greater than that on the segment between
and
. At the time
of
Figure 3,
and
fly at the same speed while maintaining the minimum separation. The flight schedule from
to
at each waypoint is as follows:
If no sUAS has passed waypoint , then . Such a flight schedule at each waypoint is used to formulate a flight planning problem that will be described in the following section. Note that, in this study we assume that all sUASs are of the same type to analyse the capacity with less decision parameters.
3.2. Inner Loop: Single sUAS Flight Planning Problem
In this section, our focus is on flight planning a finite set of sUASs in a given route network-based urban airspace.
Definition 2. Let be a finite set of sUASs. The set is partitioned into two sets: a set of sUASs to be planned , and a set of planned sUASs such that , .
In the urban airspace, each sUAS flies from its origin to its destination. A feasible flight route for each sUAS in the urban airspace is defined as follows:
Definition 3. Is given in the airspace graph , sUAS to be routed in , the initial waypoint and the final waypoint to construct a flight route denoted by in defined by a sequence of waypoints.
Thus, in the airspace graph
, there can be an abundance of flight route candidates denoted by
that satisfy the conditions as described in Definition 3. Through Definition 3, each flight route candidate
can be given a corresponding flight route (a set of waypoints) as follows:
where
is the number of waypoints sUAS
traverses as shown in
Figure 2. For each sUAS’ flight route as given in above equation, there is a set of segments connecting the waypoints, which is as follows:
For each flight route candidate, it is assumed that a performance index for a set of segments
can be quantified as a set of positive numeric weighting values, as follows:
Then, the airspace graph
is transformed into a weighted directed graph
by assigning a weight to each segment for all flight routes. In the airspace graph
, each flight route can be estimated by summing all weights of
, as follows:
Based on the airspace graph, , the routing problem that optimises the performance index can be defined as follows:
Definition 4. Given an airspace graph and corresponding flight route candidates , the routing problem is defined as finding a flight route (or a sequence of waypoints) such that The optimal flight route
can be found by using the well-known shortest path algorithms such as Dijkstra’s algorithm, A
* algorithm or exhaustive search algorithm [
47]. Although the optimal flight route
can be obtained according to Definition 4, if the airspace users want to manage the separation between each sUAS in sequential approaches, the optimality of the obtained flight route might be disturbed in the following separation management stages. One possible option is to solve the multiple sUASs flight planning problem using numerical trajectory optimisation approaches, which is not scalable although the approaches provide high-fidelity flight plans to each sUAS. Such approaches can also require additional processes for managing separation, which might cause optimality or scalability issues.
Our objective of formulating the flight planning problem is to find a flight route and speed profile that minimises the flight time of each sUAS while satisfying the separation requirement. The main idea for achieving the objective is to assign a weight to each segment (edge) of the airspace graph where the weight is expressed as a flight time. Then, each sUAS’ speed profile also can be obtained by finding its flight route in the airspace graph as defined in Definition 4. We set a flight time of each sUAS as weight
to each segment
of the airspace graph
. Note that, a flight time and speed of each sUAS are mutually interchangeable using geographic data included in the airspace graph. Where each speed profile of sUAS is determined within a feasible speed range of each sUAS. Another issue we have pursued is to satisfy the separation requirement between every pair of sUASs. To assign a flight time that satisfies the separation requirement to each edge of
, we need the flight schedule of the set of planned sUASs including the arrival times of each sUAS at each waypoint as discussed in
Section 3.1. The flight schedule
T will be included in the airspace graph
, and used to calculate the weights of the airspace graph. By finding a solution of the airspace graph
, then, we can obtain a flight route and speed profile of the sUASs while satisfying the separation requirement simultaneously. Each sUAS has different weights
because of different specifications such as the feasible speed range or the separation requirement depending on nearby sUASs. Therefore, sUAS
has its own airspace graph
, as shown in
Figure 5.
Flight Time Weights on
We propose a weighting scheme to be applied to the airspace graphs
to fulfil separation-compliant speed profiles. First of all, we introduce a set of constant speeds for each sUAS as follows:
where each element of the set
must be within a feasible speed range [
],
. Furthermore, we define a set of flight distances using geographical data allowing to compute the set
Let
, and
, we formulate a linear programming problem and solve the problem to obtain the flight time weight
as follows:
where
is the minimum time-based separation requirement between preceding sUAS
and following sUAS
at waypoints as shown in
Figure 3 and
Figure 4. The objective function of Equation (3) is to minimise the sum of flight time of each segment. The constraints of Equations (4)–(7) are for satisfying the minimum separation requirement at each waypoint. In
Figure 2, for example, if
consists of
segments for sUAS
, each segment requires a flight time that satisfies the separation requirement. The left-hand side of each constraint of Equations (4)–(7) is the flight time for the segment of each constraint, which must be greater than and equal to the time that satisfies the separation requirement. For the constraints, flight distances between waypoints and the flight schedule are required. The flight schedule is stored in
T for each waypoint
, and
T is updated every time a sUAS is allocated and shared with
.
A is the number of elements in
. Then, the formulated optimisation problem can be solved by any well-known linear programming algorithm. In this study, we utilise the interior-point algorithm. In Equation (8), decision variables,
, are constant speeds for the flight segment, which are transformed into flight times, and assigned into weights
for each flight route candidate of sUAS
.
Therefore, a solution to the airspace graph can simultaneously provide a flight route and its speed profile for sUAS while satisfying minimum separation at all times.
We also construct flight distance weights
on
to utilise the flight distance
d as a second criterion. The weights
are the same for all sUASs, which are necessary to prioritise for the multiple sUASs’ flight planning problem when two or more sUASs arrive at the same destination at the same time, more details about the priority are discussed in
Section 3.3. The single sUAS flight planning problem that motivated this study can be formulated as follows:
Problem 1. Given an unique airspace graph , sUAS in , and its origin and destination reachable from the origin, construct a flight route and a speed profile , such that
the separation requirement is satisfied from the planned sUAS ;
the speed profile of each sUAS must be within its feasible speed range;
and the airspace graphs are updated every time when a sUAS is planned.
In this study, we solve Problem 1 using Dijkstra’s algorithm [
47].
3.3. Outer Loop: Multiple sUASs Flight Planning
The main idea of this study is that the single sUAS flight planning problem can be formulated by assigning the separation-satisfied flight time weights in the airspace graph as described in
Section 3.2. By doing so, the problem is able to not only manage separation between every pair of sUASs, but also consider operational factors such as the feasible speed ranges, available routes, the separation requirements. However, the separation of each sUAS only satisfies the separation requirement from a set of allocated sUASs. In this section, we address the multiple sUASs flight planning problem by solving each single sUAS flight planning problem in an iterative way. At each iteration, each sUAS finds the optimal flight route including its speed profile by solving Problem 1 (inner loop), and one of the sUASs is allocated using a criterion-based algorithm (outer loop). In this study, we utilise the FCFS and LCFS algorithms for the outer loop algorithm.
Once inputs of the multiple sUASs flight planning problem are given, Algorithm 1 starts the flight planning process until
is empty (Line 3). The algorithm first generates airspace graphs
(Line 2). Assigning separation-satisfied flight time weights to all possible flight paths in the airspace graph is a time-consuming task. In order to reduce the complexity of the problem caused by the high degree of the airspace graphs, we select the
h-shortest routes for
by using Yen’s algorithm, and generate
only considering the
h-shortest routes (Line 4–5) [
48]. Then, each sUAS has its unique airspace graph that contains flight time weights
determining the optimal flight route with its speed profile. The optimal flight route
and its speed profile
are obtained by using Dijkstra’s algorithm,
(Line 6) [
49]. sUAS
that arrives first to its destination is obtained by using the FCFS algorithm (Line 7), and allocated (Line 15). The flight plan of sUAS
is transferred from
to
(Line 12). Note that, in this study,
refers to a flight as well as a sUAS. In the case that more than two sUASs arrive at the same destination at the same time (Line 8), the flight distance weights
are utilised to allocate sUAS
amongst them (Line 9–13). In either case, a sUAS is allocated and its flight schedule is shared with sUAS
,
. Based on the flight schedule each airspace graph
is updated,
(Line 20). Note that, to change the outer loop algorithm to other criterion-based algorithms, such as the LCFS algorithm, users are only required to change the outer loop algorithm Line 7 and Line 10 to what the users want.
| Algorithm 1: The multiple sUASs flight planning algorithm |
![Applsci 13 03833 i001]() |
We illustrate an example in
Figure 6 for a better understanding of Algorithm 1 with an case that
A sUASs fly in the urban airspace. In the first iteration, each sUAS generates its airspace graph
,
. Through the inner loop algorithm, each sUAS’s
is determined,
, and the most flight-time-efficient sUAS, which is
, is allocated using the FCFS algorithm. In the second iteration, sUAS
is allocated through the same process. In the (
A − 1)th iteration, sUAS
is allocated, and sUAS
is allocated last.
3.4. Flight Planning Example for 1-to- Case (Last-Mile Delivery with a Single Retail Point)
We used a simulation case in
Section 4 to explain the flight planning algorithm and did not include extraneous examples to avoid confusion. We appreciate the readers’ understanding in this matter. This example is a sample of the Monte Carlo simulations for the 1-to-
case, and its simulation settings are described at the beginning of
Section 4. Put briefly, thirty sUASs traverse from the retail point (E68) to each predetermined sUAS’ service points (E1∼E67) in Figure 8. We apply both the FCFS and LCFS algorithms to this example, and thirty flight plans for each case are shown in
Table 1 and
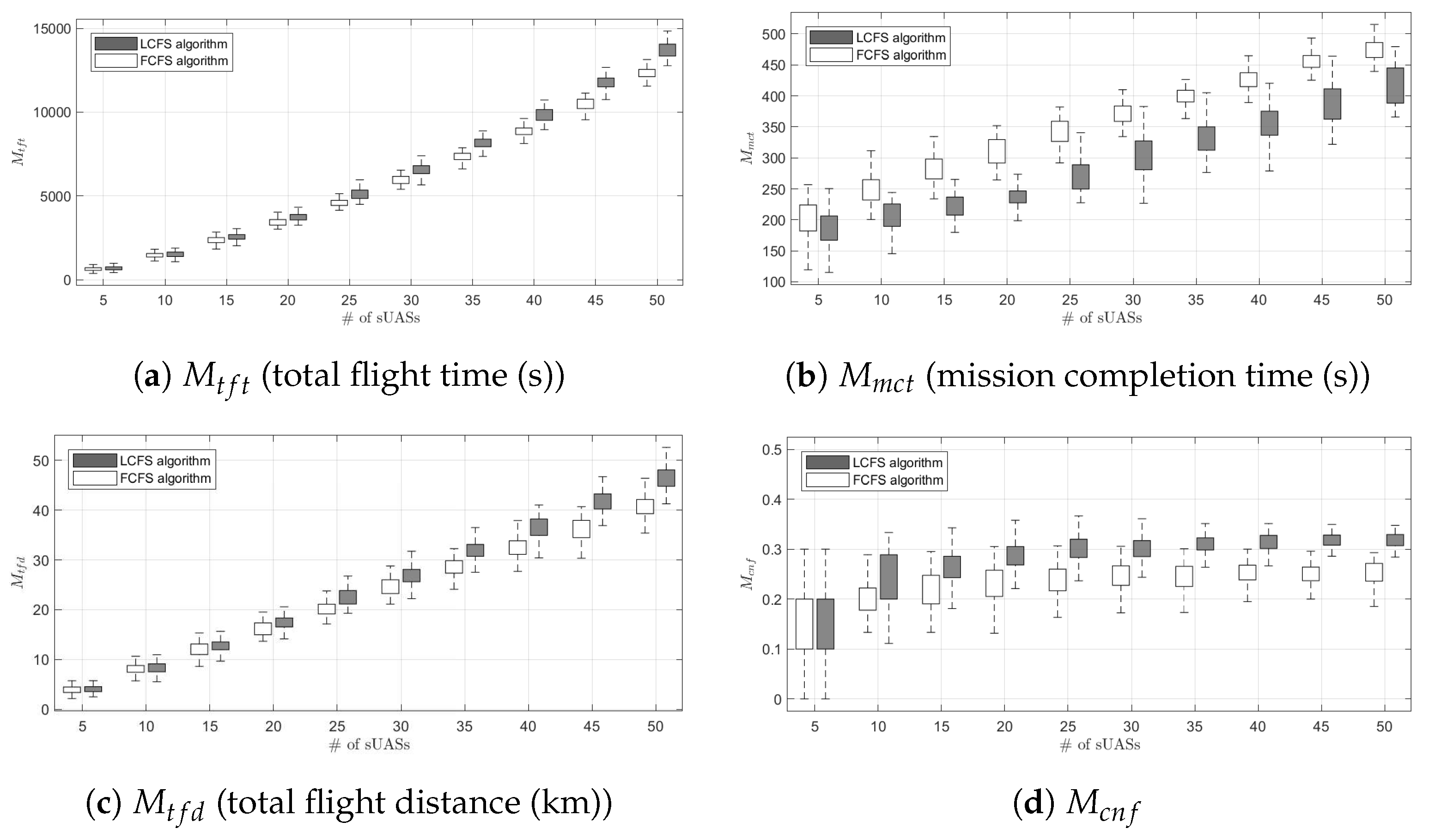
Table 2, respectively. The results show each sUAS’ separation requirement-satisfied flight route and speed profiles for each outer loop algorithm. Due to a 5 s departure separation, 5 s horizontal separation as well as the single retail point of this case, all sUASs find their flight routes with the maximum speed without any conflicts for both cases. For the same reasons, most of the flight routes are the same as the shortest path of each sUAS.
Table 3 shows a comparison of the results between the FCFS and LCFS algorithms for this example. The total flight time and the total flight distance of thirty sUASs for the FCFS algorithm case is almost same as the LCFS algorithm case. However, the mission completion time for the LCFS algorithm case is 34.5% more efficient than the FCFS algorithm case. Therefore, although the total flight time and the total flight distance are very similar for both cases, the LCFS algorithm case is more efficient with regard to the urban airspace operating time. Both airspace users and airspace service providers prefer to operate as many sUASs as possible in a given time within a given urban airspace. However, if there are more than two urban airspace users with more than two retail points, the urban airspace usage priority will be an essential factor to be considered for the flight planning problems, which is a similar situation reported for today’s airspace for commercial aircraft.
Advantages of the proposed algorithm are as follows: able to adopt different sequencing algorithms; providing separation-compliant speed profiles that satisfy each sUAS’s performance; applicable to various types of route networks; enlarge a solution-searching space by finding a flight route and speed profile of each sUAS simultaneously; and fast computational time. Therefore, we expect that the advantages of Algorithm 1, which provides not only the flight route but also the detailed schedule, will be appropriate to analyse the capacity of the high-density VLL urban airspace populated by many sUASs with short flight times, and many service providers.
3.5. Four Metrics for the Capacity Estimation
In the ATM system, typically, the airspace capacity is defined as the maximum number of aircraft that can be accommodated by the air traffic controllers in a given airspace at any point of time, while throughput is defined as the number of aircraft that land at an airport over a specific time window. In the sUASs’ flights in high-density VLL urban airspace, however, it is expected that it might be difficult to construct and negotiate multiple sUASs’ flight plans a few days in advance, such as the flight plans in the ATM system, and it might be complicated to conduct separation management through conventional human air traffic controllers due to the large number of sUASs. In addition, compared with commercial aircraft, very short flight times, many landing points, many flights, and fewer operators are expected. Thus, we can expect that one option is to analyse the urban airspace capacity based on the detailed flight plans with regard to the flight time to complete the given mission, the total flight time, the total flight distance, and the number of conflicts. We utilise such detailed flight plans to define four metrics to analyse the urban airspace capacity.
3.5.1. Total Flight Time ()
Intuitively, one metric to analyse the urban airspace capacity is the total flight time for a given mission. The total flight time can be calculated as follows:
where
A is the number of sUASs to be planned.
can also be utilised as a metric to measure the operating costs for the sUAS operators.
3.5.2. Mission
Completion Time ()
Once missions are given to a set of sUASs, each sUAS generates its separation-compliant flight plan. Then, the mission completion time is the latest arrival time at a service point or a retail point of the last sUAS, which can be found as follows:
The meaning of this metric can be used as an indicator to determine which algorithms are effective to operate the route network-based urban airspace under the same conditions. This will be one of the most important metrics for the urban airspace operators.
3.5.3. Total Flight Distance ()
The flight distance is a commonly used as a criterion for analysing the flight performance to find the optimal path in the urban airspace. Each sUAS’ flight distance, which is used for the second criterion in Algorithm 1, can be obtained from the geometry information. The total flight distance can be calculated as follows:
3.5.4. Normalised Number of Conflicts ()
Algorithm 1 generates a flight plan that only fulfils the destination separation requirement within the permissible speed range when the algorithm could not find a flight route that satisfies the separation requirement during the whole flight as well as the destination separation requirement and the permissible speed range. Namely, the sUAS could conflict with other sUASs during the flight based on the obtained flight plans. Although this paper does not provide overtaking manoeuvres, it is assumed that overtaking manoeuvres via vertical manoeuvring is sufficiently possible using current CD and R (conflict detection and resolution) technologies. Then, the number of conflicts is counted whenever a sUAS overtakes a preceding sUAS. Naturally, the number of conflicts increases with the number of sUASs in the urban airspace. We divide the number of conflicts by the total number of possible conflicts to normalise, and use it as a metric:
where
is the total number of possible conflicts, which is
, and
is the number of conflicts.
4. Monte Carlo Simulations
In this section, we conduct Monte Carlo (MC) simulations with two different outer loop algorithms (the FCFS and LCFS algorithms) that are based on the proposed flight planning algorithm for four drone delivery operation types. We investigate how the different operation types’ performance and safety behave with regard to the different flight planning algorithms and the number of sUASs in the high-density VLL urban airspace using the suggested four metrics. It aims to provide an approach for choosing between resolution strategies for urban airspace management by regulators, policymakers, and urban airspace designers.
The representative operation being considered in this study is drone delivery, especially last-mile delivery and first-mile delivery. Last-mile delivery is defined as the movement of items from transportation hubs (which are retailers in this study) to final delivery destinations, typically personal residences. First-mile delivery refers to the movement of goods from sellers to courier services who will take these goods to their final users.
A scenario for the simulations is based on the town ‘Oldbrook’, which is one of the well-planned towns in Milton Keynes in the United Kingdom. Two-dimensional infrastructure data of the town is obtained from Google Earth Pro. The scenario has an area size of 0.98 km
2 as shown in
Figure 7. Similar to the en-route airspace for commercial aircraft, in this route network, we construct two layers of nodes that are set above the roads at heights of 15 m and 25 m as shown in
Figure 8 and
Figure 9 for eastbound and westbound routes, respectively. We assume that each layer consists of 70 points (3 retail points (red pins) and 67 service points (green pins)) and 107 directed routes as shown in
Figure 8 and
Figure 9. All sUASs are of the same type as shown in
Table 4. The sUAS type can be later changed and varied based on the missions and operators. For the separation between sUASs, it is assumed that the time-based minimum vertical and horizontal separation requirement during the flight is 5 s. No hovering manoeuvres are allowed for any sUASs.
We conduct 100 MC simulations for each outer loop algorithm (FCFS and LCFS algorithms) by increasing the number of sUASs from 5 to 50 with 5 s interval for the four drone delivery operation types (1-to-
,
-to-1,
-to-
,
-to-
) as shown in
Table 5. At each simulation a service point and a retail point for each sUAS are randomly chosen except for the 1-to-
and
-to-1 cases in which there is the single retail point E68 and W68, respectively. Once the route network and each sUAS’ retail point and service point are given, which are the input of Algorithm 1, the algorithm generates each sUAS’ flight plan as described in
Section 3. From the output of the algorithm, we obtain
(total flight time),
(mission completion time),
(total flight distance), and
(normalised number of conflicts).
Both the FCFS and LCFS algorithm results quantify the route network-based urban airspace based on the four metrics. For each operation type, we analyse both results, and suggest one of the two outer loop algorithms that is more appropriate for the operation type.
4.1. 1-to- Last-Mile Delivery Case (Eastbound)
In the 1-to-
operation type, each sUAS traverses with an item from the single retail point (E68) to each sUAS’ predetermined service point between E1 and E67 in
Figure 8, where we disregard two retail points (E69 and E70) and two routes (E69→E17 and E70→E43).
In both of the outer loop algorithms, multiple sUASs traverse at maximum speed due to the five second time interval between each sUAS departure at the single retail point (E68). Thus, there is no significant difference between the two algorithms in
and
, as shown in
Figure 10a,c, respectively. Furthermore, the interval allows them to satisfy the separation requirement at all times, so there is no conflict between any pair of sUASs. However,
Figure 10b shows that the LCFS algorithm results in more efficient mission completion times compared to the FCFS algorithm, which means the LCFS algorithm allows more sUASs to fly at a given time within the urban airspace. Therefore, in the operation type of 1-to-
, the LCFS algorithm is more efficient than the FCFS algorithm in terms of total flight distance
.
4.2. -to-1 First-Mile Delivery Case (Westbound)
In the
-to-1 operation type, multiple sUASs fly from their predetermined service points between W1 and W67 to the single retail point (W68) in
Figure 9, where we ignore two retail points (W69 and W70) and two routes (W17→W69 and W43→W70). We assume that all sUASs depart from each sUAS’ service point at the same time to consider the worst case scenario.
Figure 11c shows that
of the LCFS algorithm is slightly higher than the FCFS algorithm, and
Figure 11a shows that
is rapidly raised as the number of sUASs increases compared to
. As a result, it is seen that the LCFS algorithm causes not only detours but also low flight speeds. These results are inextricably linked to
shown in
Figure 11d, resulting in inefficient and unpredictable results for
. In all respects, therefore, the FCFS algorithm is better than the LCFS algorithm for the
-to-1 operation type for the urban airspace.
4.3. -to- Last-Mile Delivery Case (Eastbound)
In the
-to-
operation type, each sUAS traverses with an item from the predetermined retail points (E68, E69, and E70) to the each sUAS’ predetermined service point from E1 to E67 in
Figure 8. It is assumed that each retail point has five second departure intervals.
From the safety and flight performance perspective, the FCFS algorithm results in more efficient results for
,
, and
, as shown in
Figure 12. However,
shows that the LCFS algorithm can allow to accommodate more sUASs in the given space within a given time. Therefore, in the case of
-to-
for the urban airspace, the algorithm is dependent on the situation as shown in
Figure 12. For example, it is appropriate to use the LCFS algorithm when a large number of items must be delivered in the given urban airspace, while the FCFS algorithm could be used for safety and individual performance when there is more room in the given urban airspace.
4.4. -to- First-Mile Delivery Case (Westbound)
In the
-to-
operation type, each sUAS traverses with an item from each sUAS’ predetermined service point between W1∼W67 to the predetermined retail points (W68, W69, W70) in
Figure 9. We assume that all sUASs depart from each sUAS’ service points at the same time to consider the worst case scenario.
Figure 13 shows that the results of
,
, and
are very similar to the results of the
-to-1 operation type. Namely, the FCFS algorithm is appropriate for this case with regard to the three metrics. However, the
result of the LCFS algorithm approaches to 0.05, while in the FCFS algorithm results steadily increases. This is because of the overtaking manoeuvres caused by the outer loop algorithm. The FCFS algorithm finds flight plans while satisfying the minimum separation requirement when there are a small number of sUASs. However, as the number of sUASs increases,
is increasing because of a bottleneck phenomenon around the retail points. In the case of the LCFS algorithm, even when a small number of sUASs are flying, the
always shows a similar tendency because the following sUASs may outstrip the preceding sUASs. Because of the same reason, when there are a small number of sUASs in the urban airspace, the variation is large as shown in
Figure 13d. Due to the tendency, the result of the FCFS algorithm shows a higher
than the LCFS algorithm’s one from when the number of sUASs is 45. From this result, we suggest applying either the FCFS algorithm or LCFS algorithm to the airspace users according to the number of sUASs in the urban airspace.
4.5. The Improvement in and between the FCFS and LCFS Algorithms
The metric, , is the cause of increasing and . Namely, and , which also indicate sUASs’ performance, are directly related to . Mission completion time, , is an indicator of the performance of the urban airspace within a given period of time, although its relationship with and is not prominent. From the results, the following analysis can be made: (1) For the four operation types, the FCFS algorithm generates more efficient results than the LCFS algorithm for and . This is because sUASs with short flight times complete the flight first, and then the other sUASs can fly in relaxed urban airspace at high speed; (2) for the 1-to- operation type, the LCFS algorithm shows very efficient results for . This indicates that the LCFS algorithm efficiently uses the urban airspace for a given time period; and (3) from the standard deviation of the results except for the 1-to- operation type, the FCFS algorithm is easier to predict each metric as the number of sUASs increases than the LCFS algorithm. The main reason why the standard deviation of the LCFS algorithm results are high is that the variation of each sUAS’ speed profile dependent on the randomly selected starting point and destination point is very large.
5. Conclusions
This work investigated the capacity analysis for the route network-based very low-level urban airspace with regard to the four cases of drone delivery operations. Two different flight planning algorithms were compared for each operation type using the Monte Carlo simulations. From the analysis, the following implications can be made. Firstly, for efficient operation on the same operation type, flight planning should be carefully determined depending on operation factors such as the number of retail points, number of service points, number of sUASs, etc. Secondly, in this study, the FCFS and LCFS flight planning algorithms were used for homogeneous sUASs. For practical operations, however, it is required to consider the airspace users’ priorities, i.e., non-cooperative operation cases with heterogeneous sUASs. Further simulation and verification methodologies will be necessary for future studies because decentralised cases are more complex than the centralised instances studied in this research. Finally, such analyses and results could be used for designing airspace structures depending on urban airspace situations and environments.
We expect that the results could give the following support to policymakers, urban airspace designers, and regulators: (1) When the stakeholders configure a new structure of the urban airspace, they can utilise the metrics to estimate the capacity according to the situation and environment; (2) it is easy to analyse the entry of new stakeholders by increasing the number of retail points; and (3) it is also available as a test-bed for new algorithms.