Motion Control of Autonomous Underwater Helicopter Based on Linear Active Disturbance Rejection Control with Tracking Differentiator
Abstract
:1. Introduction
2. Overview and Modeling of the AUH
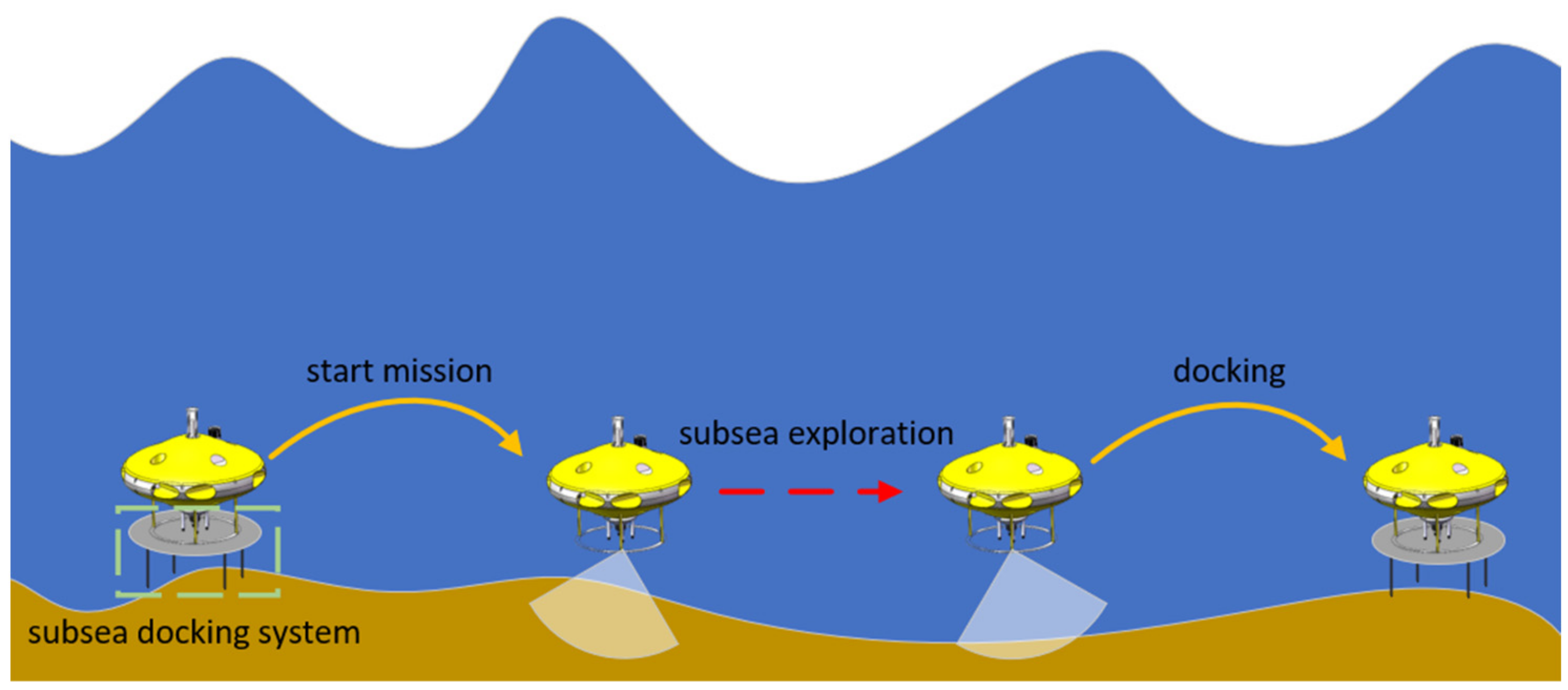
2.1. Overview of the AUH
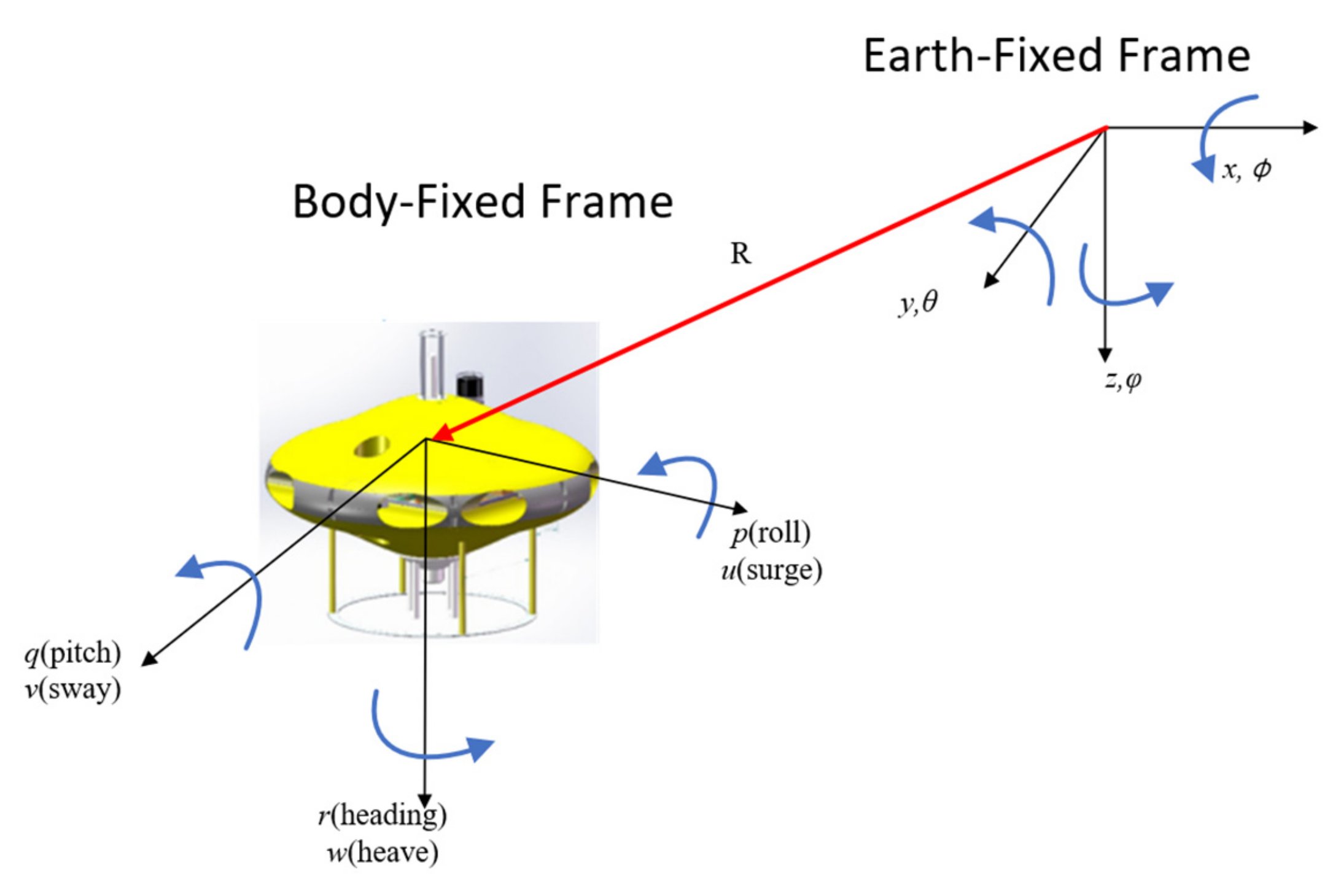
2.2. Modeling of AUH
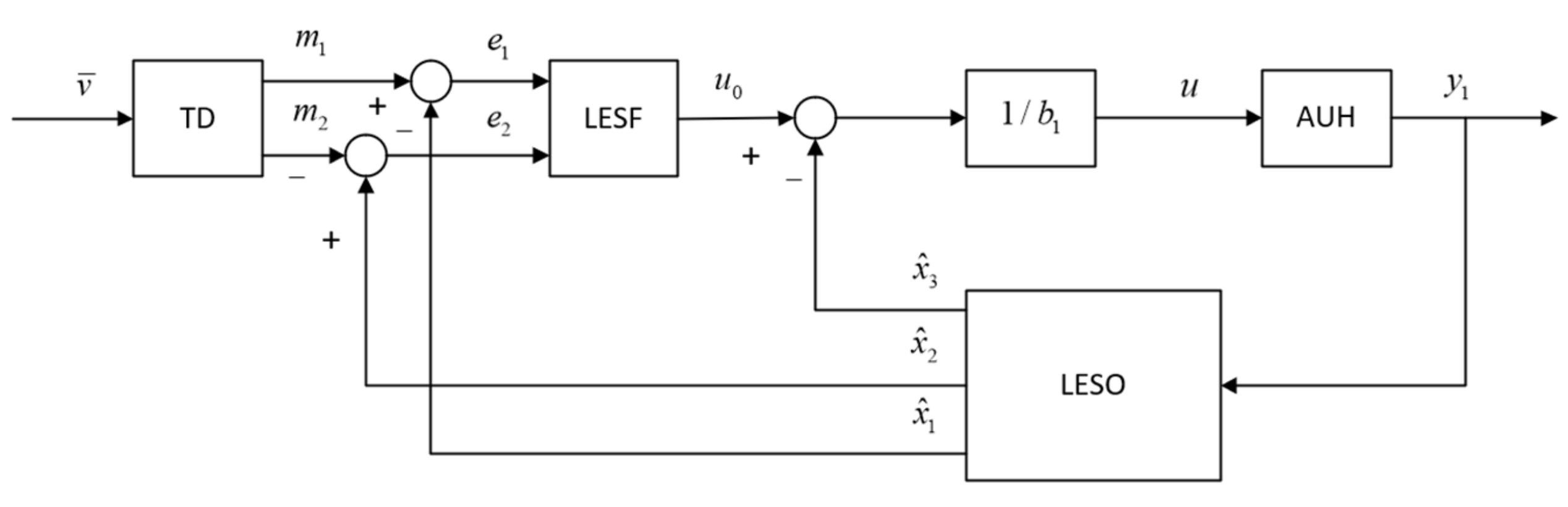
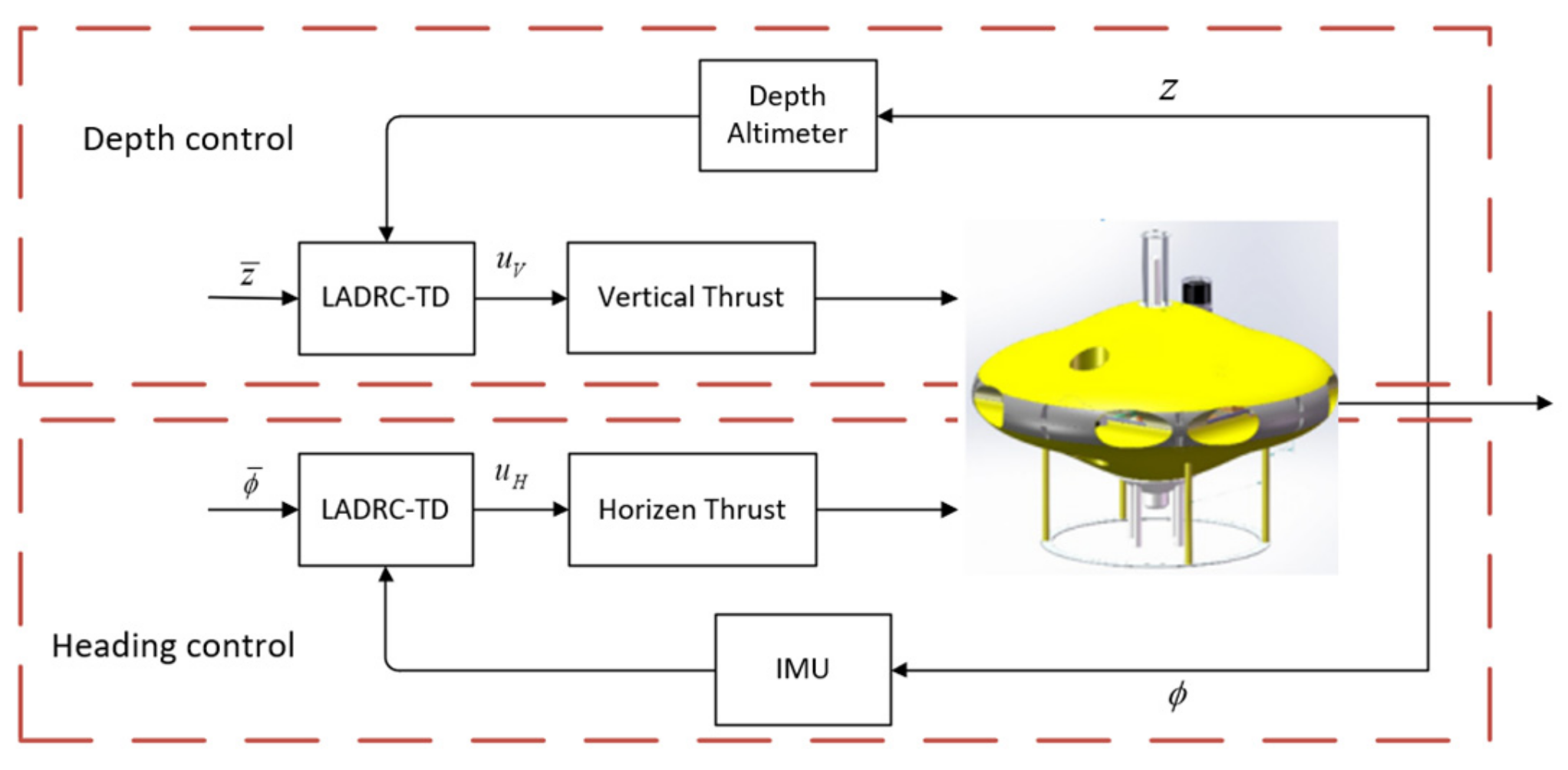
3. Design of AUH Controller
3.1. LESO
3.2. Tracking Differentiator
4. Numerical Simulations
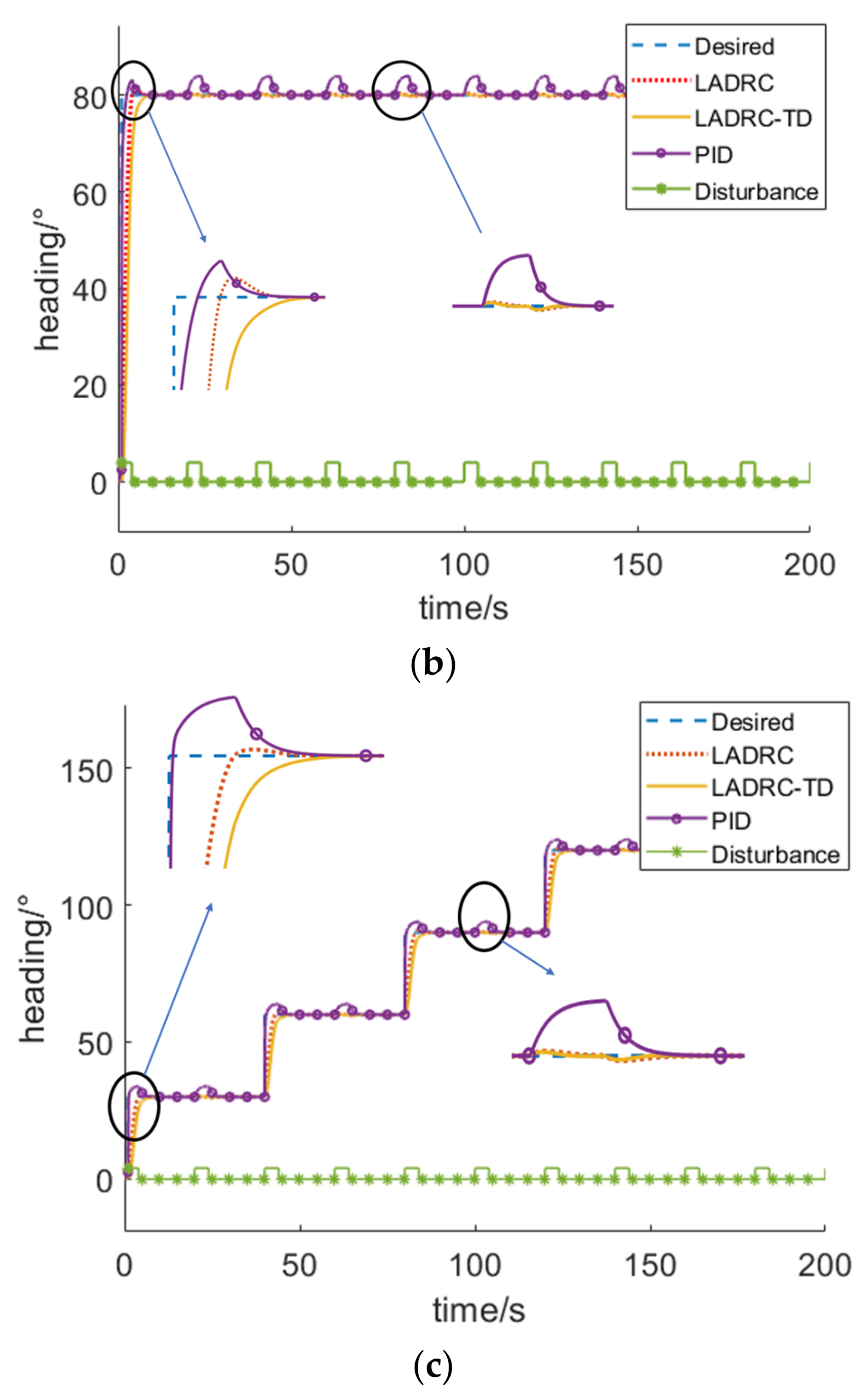
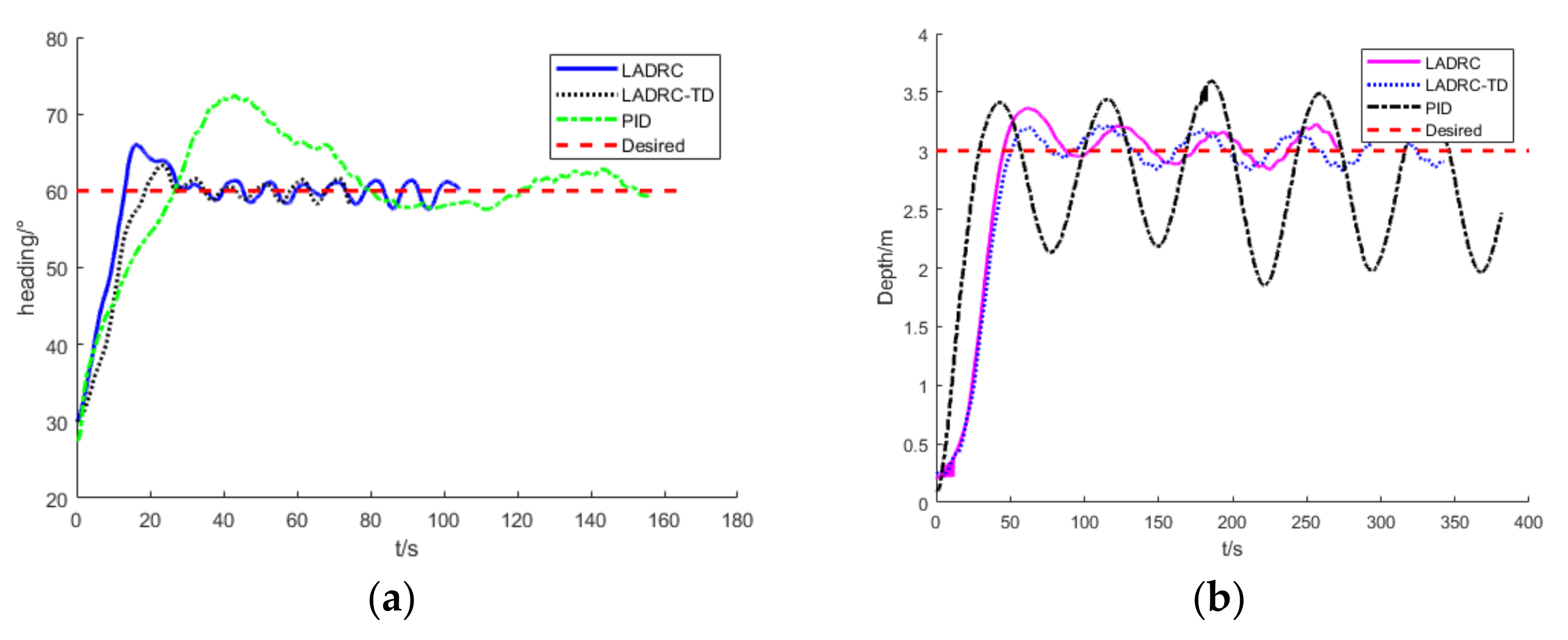
4.1. Heading Control Simulations
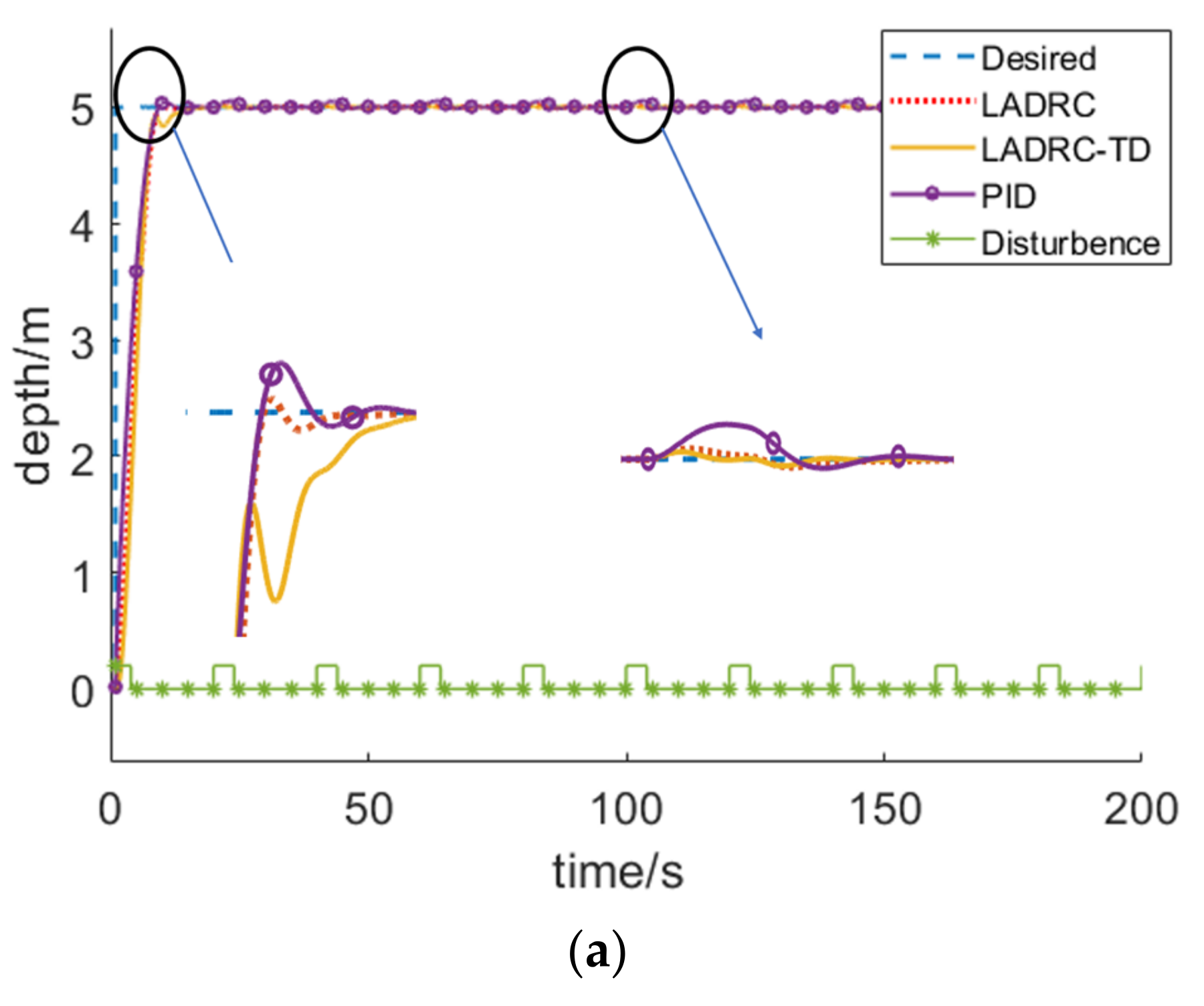
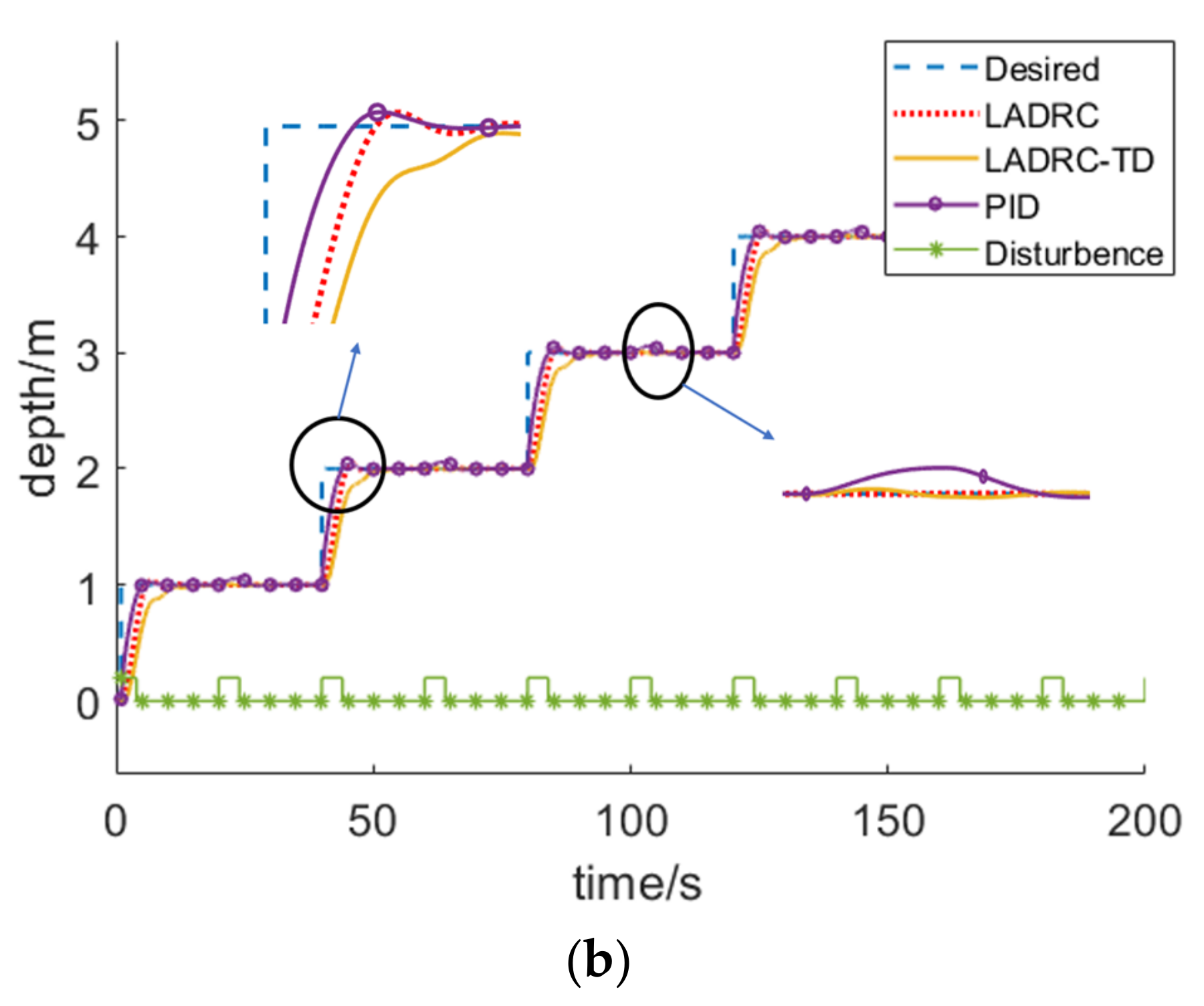
4.2. Depth Control Simulations
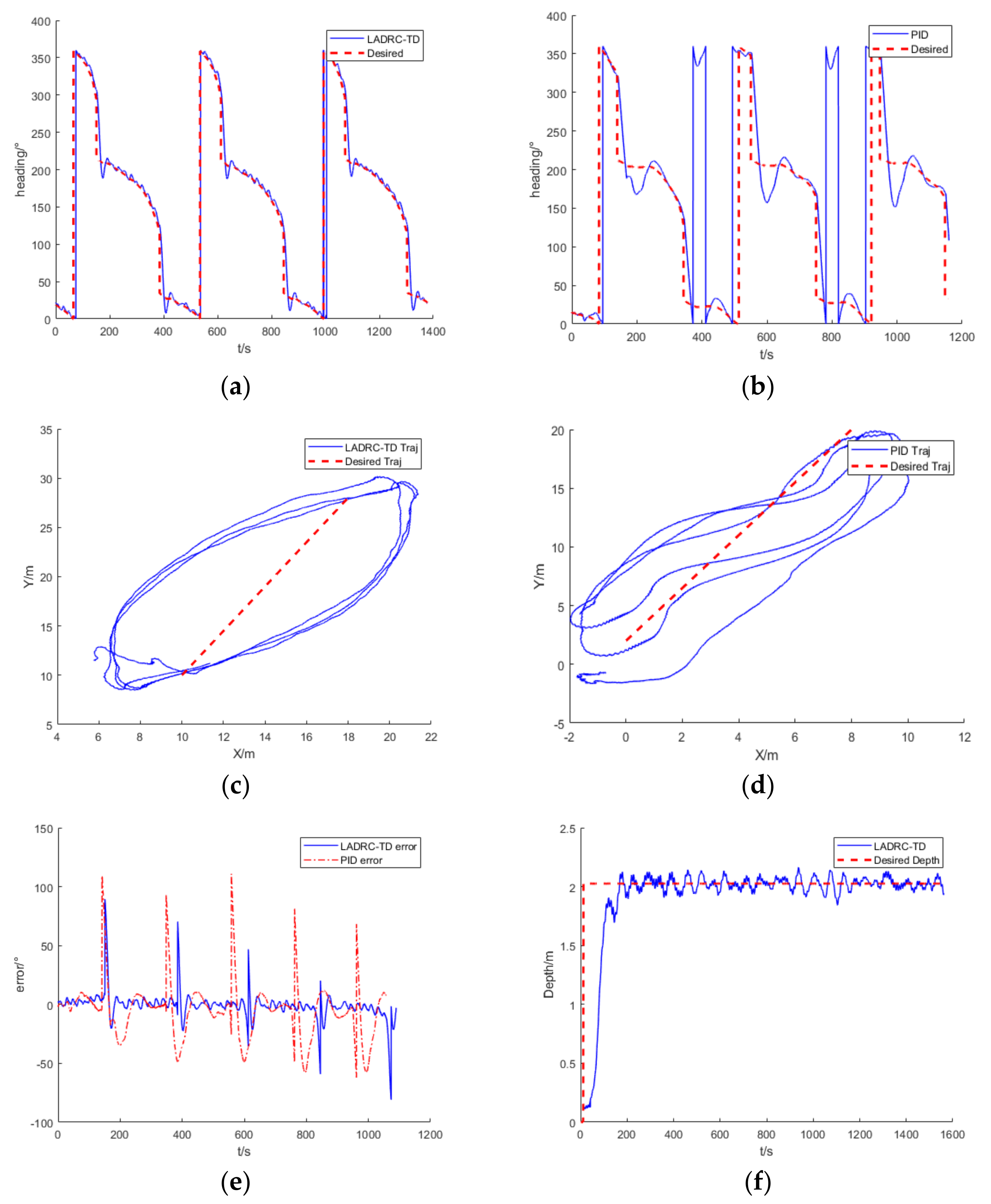
5. Experiments and Results
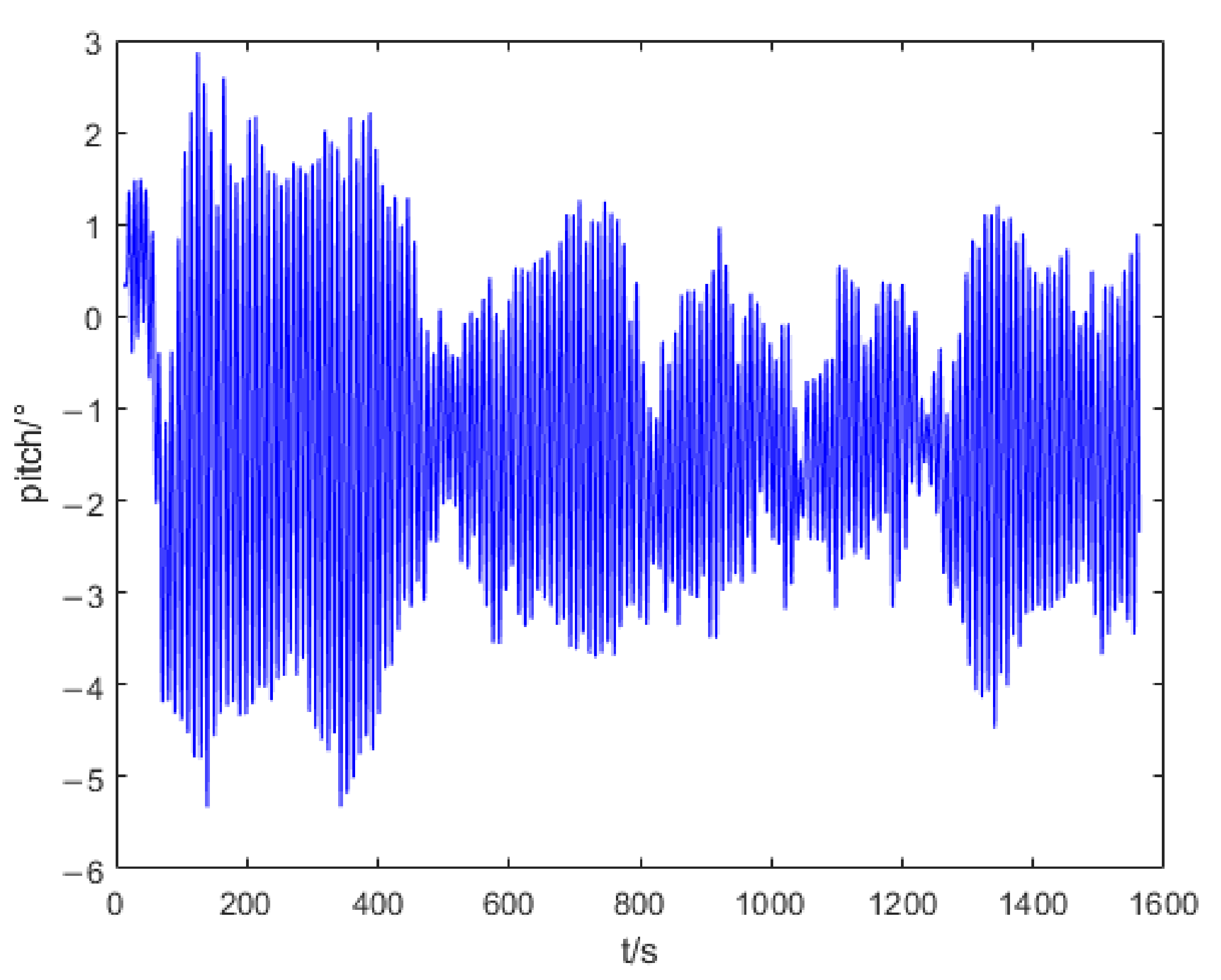
5.1. Pool Experiments
5.2. Results
6. Conclusions
- The LADRC-TD algorithm has the least overshoot, namely 20 cm and 3° in the depth control and heading control, respectively, which is less than PID and LADRC.
- According to the simulations, the anti-interference of LADRC-TD is better than PID and nearly the same as LADRC.
- The steady-state error of LADRC-TD is ±21 cm and ±2.5° in the depth control and heading control, respectively, which is lower than PID and the same as LADRC.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Liu, X.; Huang, H.; Chen, Y. Development of an Autonomous Underwater Helicopter with High Maneuverability. Appl. Sci. 2019, 9, 4072. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Yang, C.; Fan, S.; Zhang, S.; Wang, P.; Xie, Y.; Chen, Y. A Hybrid Underwater Glider for Underwater Docking. In Proceedings of the MTS/IEEE OCEANS 2013, San Diego, CA, USA, 10–13 June 2013; Volume 7. [Google Scholar]
- Cai, C.; Xu, B. Development and Test of a Subsea Docking System Applied to an Autonomous Underwater Helicopter. In Proceedings of the MTS/IEEE OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; Volume 7. [Google Scholar]
- Wang, J.; Wang, C.; Wei, Y.; Zhang, C. Three-Dimensional Path Following of an Underactuated AUV Based on Neuro-Adaptive Command Filtered Backstepping Control. IEEE Access 2018, 6, 74355–74365. [Google Scholar] [CrossRef]
- Gharesi, N.; Ebrahimi, Z.; Forouzandeh, A.; Arefi, M.M. Extended State Observer-Based Backstepping Control for Depth Tracking of the Underactuated AUV. In Proceedings of the 2017 5th International Conference on Control, Instrumentation, and Automation (ICCIA), Shiraz, Iran, 21–23 November 2017; pp. 354–358. [Google Scholar]
- Mat-Noh, M.; Mohd-Mokhtar, R.; Arshad, M.R.; Zain, Z.M.; Khan, Q. Review of Sliding Mode Control Application in Autonomous Underwater Vehicles. Indian J. Geo-Marine Sci. 2019, 48, 973–984. [Google Scholar]
- Du, P.; Yang, W.; Wang, Y.; Hu, R.; Chen, Y.; Huang, S.H. A Novel Adaptive Backstepping Sliding Mode Control for a Lightweight Autonomous Underwater Vehicle with Input Saturation. Ocean Eng. 2022, 263, 112362. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L.; Liu, W.; Li, L. Research on Control Method of AUV Terminal Sliding Mode Variable Structure. In Proceedings of the 2017 International Conference on Robotics and Automation Sciences, Hong Kong, China, 26–29 August 2017; pp. 88–93. [Google Scholar]
- Tanakitkorn, K.; Phillips, A.B.; Wilson, P.A.; Turnock, S.R. Sliding Mode Heading Control of an Overactuated, Hover-Capable Autonomous Underwater Vehicle with Experimental Verification. J. F. Robot. 2018, 35, 396–415. [Google Scholar] [CrossRef]
- Chen, C.W.; Jiang, Y.; Huang, H.C.; Ji, D.X.; Sun, G.Q.; Yu, Z.; Chen, Y. Computational Fluid Dynamics Study of the Motion Stability of an Autonomous Underwater Helicopter. Ocean Eng. 2017, 143, 227–239. [Google Scholar] [CrossRef]
- An, X.; Chen, Y.; Huang, H. Parametric Design and Optimization of the Profile of Autonomous Underwater Helicopter Based on Nurbs. J. Mar. Sci. Eng. 2021, 9, 668. [Google Scholar] [CrossRef]
- Lin, Y.; Lin, Y.; Guo, J.; Li, H.; Wang, Z.; Chen, Y.; Huang, H. Improvement of Hydrodynamic Performance of the Disk-Shaped Autonomous Underwater Helicopter by Local Shape Modification. Ocean Eng. 2022, 260, 112056. [Google Scholar] [CrossRef]
- Du, P.; Huang, S.H.; Yang, W.; Wang, Y.; Wang, Z.; Hu, R.; Chen, Y. Design of a Disc-Shaped Autonomous Underwater Helicopter with Stable Fins. J. Mar. Sci. Eng. 2022, 10, 67. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, J.; Wang, Z.; Zhou, H.; Chen, J.; Hu, X.; Chen, Y. Research on an Autonomous Underwater Helicopter with Less Thrusters. J. Mar. Sci. Eng. 2022, 10, 1444. [Google Scholar] [CrossRef]
- Li, X.; Ren, C.; Ma, S.; Zhu, X. Compensated Model-Free Adaptive Tracking Control Scheme for Autonomous Underwater Vehicles via Extended State Observer. Ocean Eng. 2020, 217, 107976. [Google Scholar] [CrossRef]
- Li, H.; He, B.; Yin, Q. Fuzzy Optimized MFAC Based on ADRC in AUV Heading Control. Electronics 2019, 8, 608. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Zhang, Y.; Sun, Y.; Li, Y. Thruster-AUV’s Motion Adjustment Method Based on Fuzzy Control. In Proceedings of the 2015 International Industrial Informatics and Conputer Engineering Conference, Xi’an, China, 10–11 January 2015; pp. 266–269. [Google Scholar]
- Yang, G.; Yao, J.; Dong, Z. Neuroadaptive Learning Algorithm for Constrained Nonlinear Systems with Disturbance Rejection. Int. J. Robust Nonlinear Control. 2022, 32, 6127–6147. [Google Scholar] [CrossRef]
- Yang, G. Asymptotic Tracking with Novel Integral Robust Schemes for Mismatched Uncertain Nonlinear Systems. Int. J. Robust Nonlinear Control. 2023, 33, 1988–2002. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Estrada, A.; Fridman, L.M. Global and Exact HOSM Differentiator with Dynamic Gains for Output-Feedback Sliding Mode Control. Automatica 2017, 81, 156–163. [Google Scholar] [CrossRef]
- Teixeira, A.; Gouvea, J.A.; Zachi, A.R.L.; Rodrigues, V.H.P.; Oliveira, T.R. Monitoring Function-based Active Disturbance Rejection Control for Uncertain Systems with Unknown Control Directions. Adv. Control Appl. 2021, 3, e66. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, H.; Huang, S.H.; Si, Y.; Shi, K.; Quan, X.; Guo, C.; Chen, C.; Wang, Z.; Wang, Y.; et al. AUH, a New Technology for Ocean Exploration. Engineering 2022. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Active Disturbance Rejection Control: A Paradigm Shift in Feedback Control System Design. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2399–2405. [Google Scholar]
- Gao, Z. Scaling and Bandwidth-Parameterization Based Controller Tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]




| Mass | About 800 kg |
| Diameter | 2 m |
| Net buoyancy | 70 N |
| Propeller layout | Four propellers on the horizon, and two propellers on the vertical, as shown in Figure 3 |
| Maximum Thrust | 200 N per propeller |
| Component | Inertial measurement unit (IMU), depth altimeter, sonar, radio, Iridium, Beidou navigation system, buoyancy adjustment, optical camera, ultra-short baseline (USBL) |
| Depth Control | PID | LADRC | LADRC-TD |
|---|---|---|---|
| Overshoot | 43 cm | 41 cm | 20 cm |
| Anti-interference | worse | baseline | nearly |
| Steady-state error | ±1.1 m | ±21 cm | ±21 cm |
| Heading Control | PID | LADRC | LADRC-TD |
| Overshoot | 12° | 6° | 3° |
| Anti-interference | worse | baseline | nearly |
| Steady-state error | ±3° | ±2.5° | ±2.5° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; An, X.; Feng, R.; Chen, Y. Motion Control of Autonomous Underwater Helicopter Based on Linear Active Disturbance Rejection Control with Tracking Differentiator. Appl. Sci. 2023, 13, 3836. https://doi.org/10.3390/app13063836
Li H, An X, Feng R, Chen Y. Motion Control of Autonomous Underwater Helicopter Based on Linear Active Disturbance Rejection Control with Tracking Differentiator. Applied Sciences. 2023; 13(6):3836. https://doi.org/10.3390/app13063836
Chicago/Turabian StyleLi, Haoda, Xinyu An, Rendong Feng, and Ying Chen. 2023. "Motion Control of Autonomous Underwater Helicopter Based on Linear Active Disturbance Rejection Control with Tracking Differentiator" Applied Sciences 13, no. 6: 3836. https://doi.org/10.3390/app13063836
APA StyleLi, H., An, X., Feng, R., & Chen, Y. (2023). Motion Control of Autonomous Underwater Helicopter Based on Linear Active Disturbance Rejection Control with Tracking Differentiator. Applied Sciences, 13(6), 3836. https://doi.org/10.3390/app13063836









