Sensitivity Improvement of an Optical Fiber Sensor Based on Surface Plasmon Resonance with Pure Higher-Order Modes
Abstract
:Featured Application
Abstract
1. Introduction
2. Sensing Mechanism
3. Theoretical Analysis
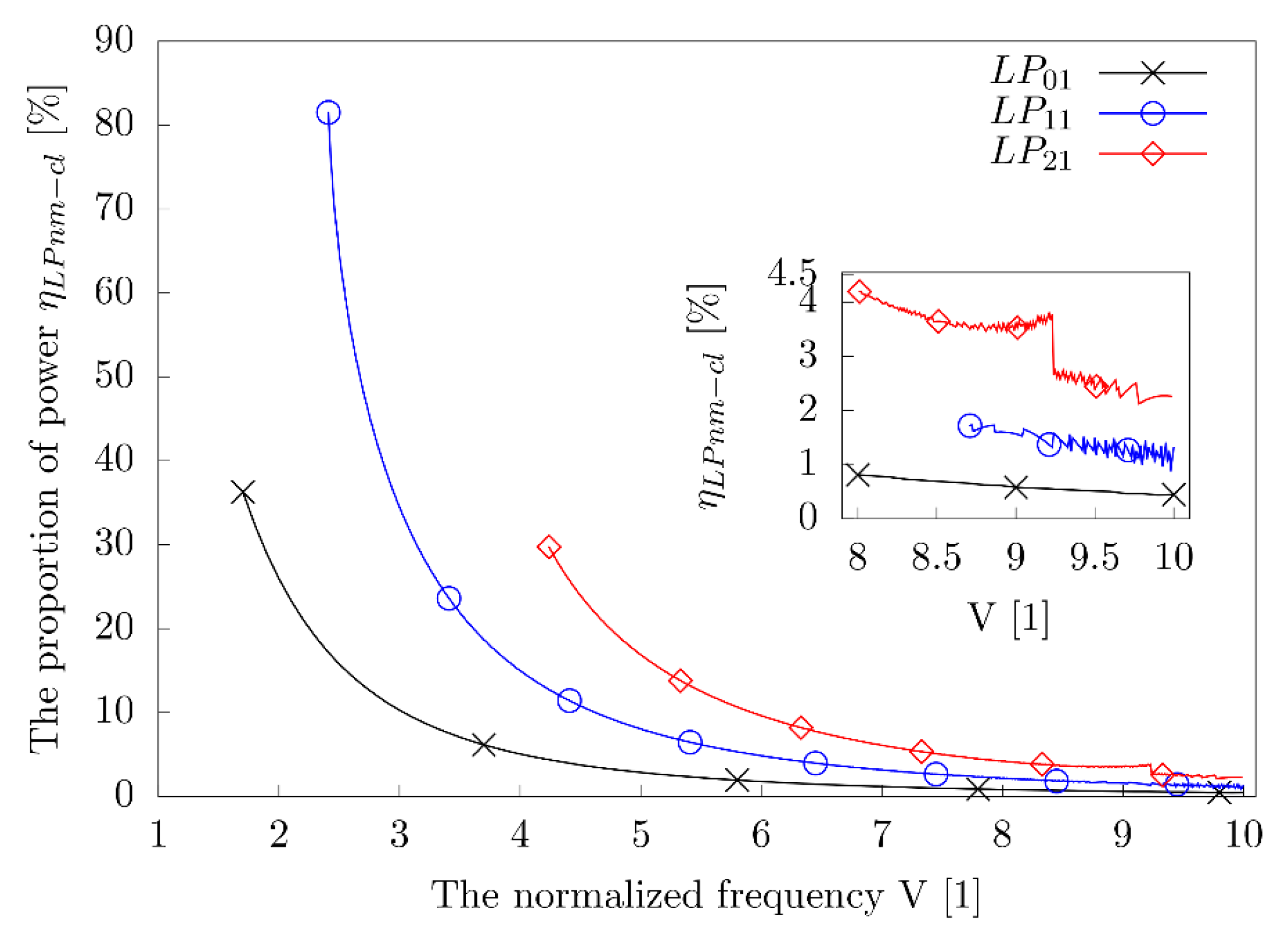
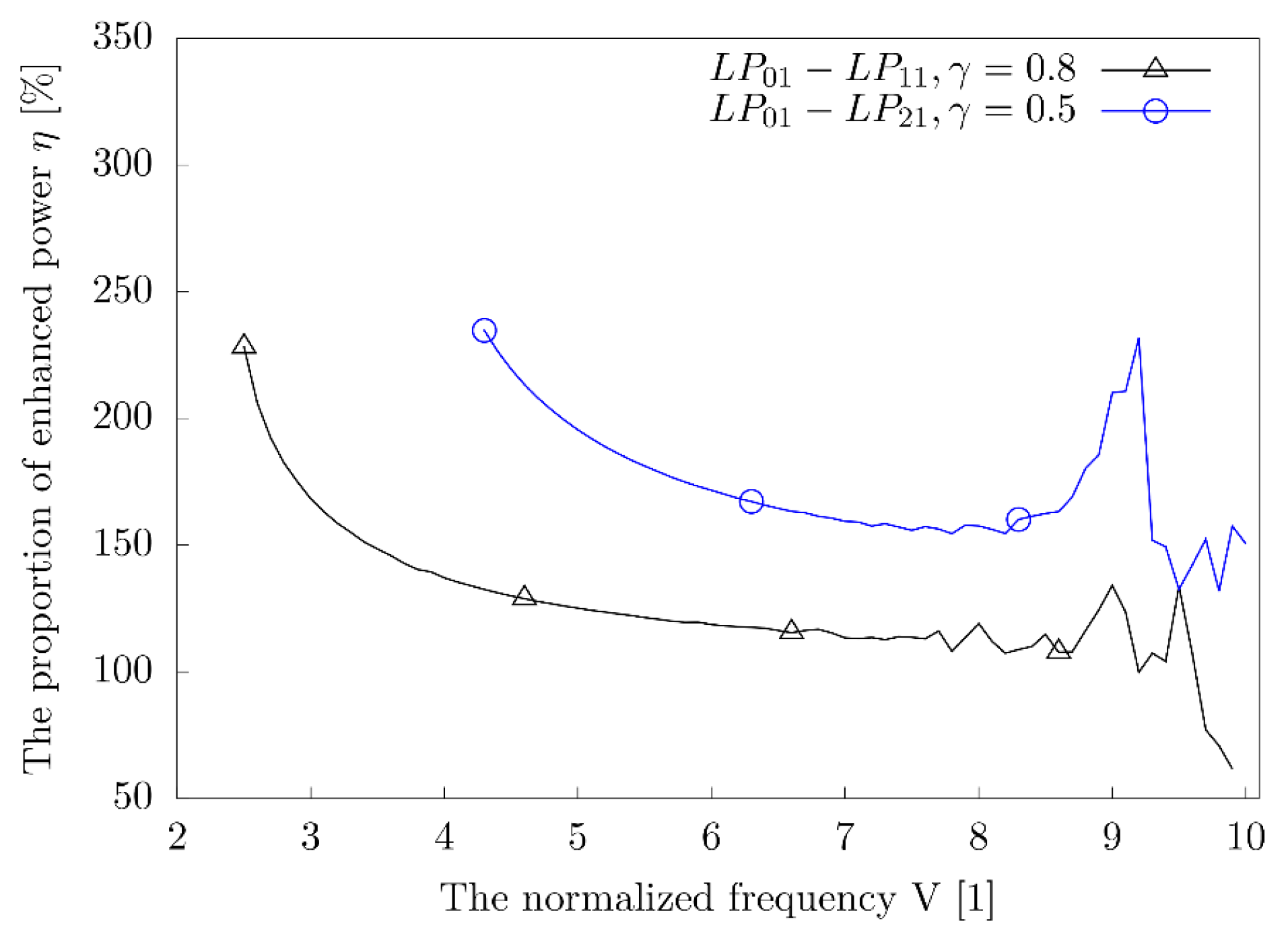
3.1. The Power of Different Modes in the Cladding
3.2. The Principle of an MSC Working in the Visible Band
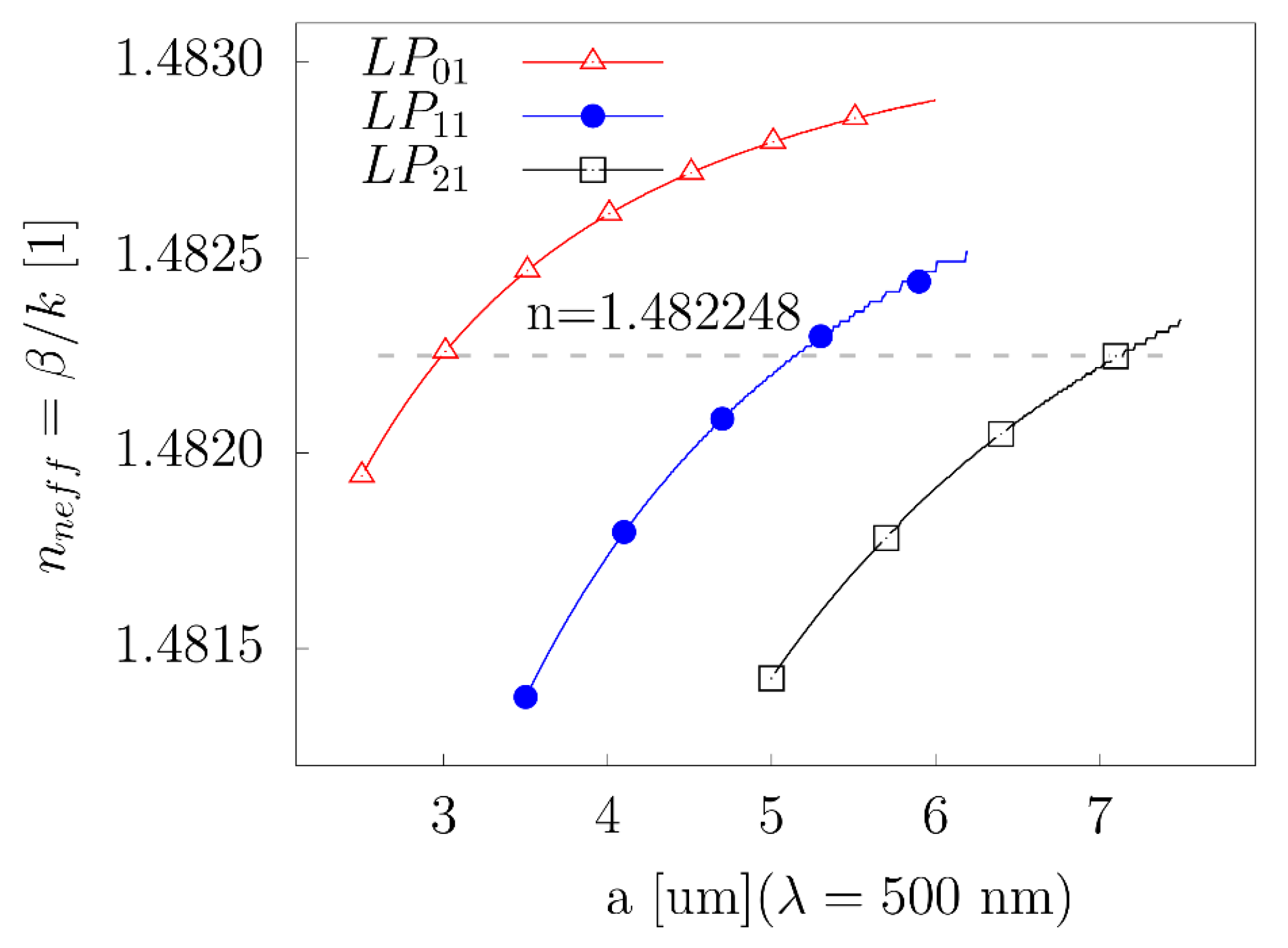
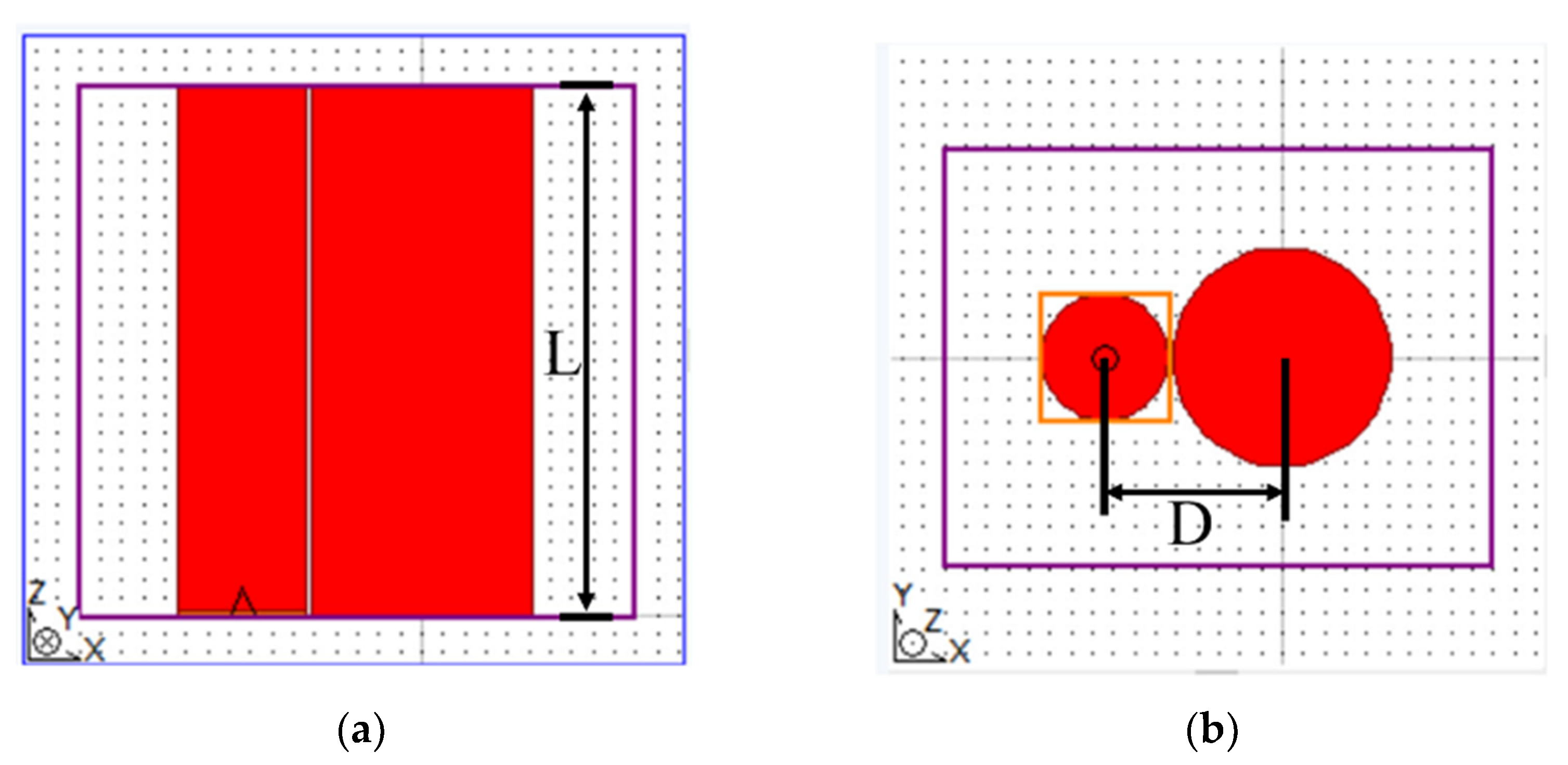
4. Simulations and Discussions
4.1. Simulation of MSC
4.2. Simulation of the Sensing Area for RI Measurement
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Homola, J. Surface Plasmon Resonance Sensors for Detection of Chemical and Biological Species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef]
- Xue, T.; Liang, W.; Li, Y.; Sun, Y.; Xiang, Y.; Zhang, Y.; Dai, Z.; Duo, Y.; Wu, L.; Qi, K.; et al. Ultrasensitive detection of miRNA with an antimonene-based surface plasmon resonance sensor. Nat. Commun. 2019, 10, 28. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Peng, W. Fiber-Optic Surface Plasmon Resonance Sensors and Biochemical Applications: A Review. J. Light. Technol. 2021, 39, 3781–3791. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Springer: New York, NY, USA, 1983; p. 208. [Google Scholar]
- Feng, D.; Liu, G.; Zhang, M.; Jia, D. D-shaped fiber optic SPR biosensors based on a metal-graphene structure. Chin. Opt. Lett. 2013, 11, 110607. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, F.; Qian, S.; Liu, Z.; Wang, Q.; Gu, Y.; Wu, Z.; Jing, Z.; Sun, C.; Peng, W. A Novel Fiber Optic Surface Plasmon Resonance Biosensors with Special Boronic Acid Derivative to Detect Glycoprotein. Sensors 2017, 17, 2259. [Google Scholar] [CrossRef] [Green Version]
- Saha, B.; Goswami, N.; Saha, A. Highly sensitive surface-plasmon-resonance- based fiber optic breast cancer detection by shining a Bessel–Gauss beam: A wave-theory-based approach. Appl. Opt. 2021, 60, 7027–7035. [Google Scholar] [CrossRef]
- Baiad, M.D.; Kashyap, R. Concatenation of surface plasmon resonance sensors in a single optical fiber using tilted fiber Bragg gratings. Opt. Lett. 2015, 40, 115–118. [Google Scholar] [CrossRef]
- Arcas, A.D.S.; Dutra, F.D.S.; Allil, R.C.S.B.; Werneck, M.M. Surface Plasmon Resonance and Bending Loss-Based U-Shaped Plastic Optical Fiber Biosensors. Sensors 2018, 18, 648. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.-H.; Wang, Q.; Zhao, W.-M.; Wang, L.; Jiang, C.-Q.; Cong, X.-W.; Yan, X.; Zhu, A.-S.; Qiu, F.-M.; Chen, B.-H.; et al. A High-FOM surface plasmon resonance sensor based on MMF-TUMMF-MMF structure of optical fiber. Opt. Fiber Technol. 2022, 72, 102970. [Google Scholar] [CrossRef]
- Yao, H.; Shi, F.; Wu, Z.; Xu, X.; Wang, T.; Liu, X.; Xi, P.; Pang, F.; Zeng, X. A mode generator and multiplexer at visible wavelength based on all-fiber mode selective coupler. Nanophotonics 2020, 9, 973–981. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.J.; Jin, J.M. Computation of Special Functions; John Wiley & Sons: New York, NY, USA, 1996; p. 126. [Google Scholar]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Li, S.-G.; Liu, S. Wavelength-selective characteristics of high birefringence photonic crystal fiber with Au nanowires selectively filled in the cladding air holes. Chin. Phys. B 2012, 21, 094219. [Google Scholar] [CrossRef]
- Yuhashi, K.; Ida, J.; Kubodera, S.; Watanabe, K.; Nishiyama, M. A surface plasmon resonance temperature sensor using TiO2 nanoparticles on hetero-core fiber optic structure with Au thin film. Jpn. J. Appl. Phys. 2022, 61, 056501. [Google Scholar] [CrossRef]
- Bremer, K.; Roth, B. Fibre optic surface plasmon resonance sensor system designed for smartphones. Opt. Express 2015, 23, 17179–17184. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Liu, Q.; Masson, J.-F.; Peng, W. Compact multi-channel surface plasmon resonance sensor for real-time multi-analyte biosensing. Opt. Express 2015, 23, 20540–20548. [Google Scholar] [CrossRef]
- Wang, Q.; Jing, J.Y.; Wang, X.Z.; Niu, L.Y.; Zhao, W.M. A D-Shaped Fiber Long-Range Surface Plasmon Resonance Sensor with High Q-Factor and Temperature Self-Compensation. IEEE Trans. Instrum. Meas. 2020, 69, 2218–2224. [Google Scholar] [CrossRef]
- Tang, J.; Zhou, J.; Guan, J.; Long, S.; Yu, J.; Guan, H.; Lu, H.; Luo, Y.; Zhang, J.; Chen, Z. Fabrication of Side-Polished Single Mode-Multimode-Single Mode Fiber and Its Characteristics of Refractive Index Sensing. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 238–245. [Google Scholar] [CrossRef]
- Luo, J.; Liu, G.-S.; Zhou, W.; Hu, S.; Chen, L.; Chen, Y.; Luo, Y.; Chen, Z. A graphene–PDMS hybrid overcoating enhanced fiber plasmonic temperature sensor with high sensitivity and fast response. J. Mater. Chem. C 2020, 8, 12893–12901. [Google Scholar] [CrossRef]
- Ning, W.; Zhang, C.; Tian, Z.; Wu, M.; Luo, Z.; Hu, S.; Pan, H.; Li, Y. Ω-shaped fiber optic LSPR biosensor based on mismatched hybridization chain reaction and gold nanoparticles for detection of circulating cell-free DNA. Biosens. Bioelectron. 2023, 228, 115175. [Google Scholar] [CrossRef]
- Chauhan, M.; Singh, V.K. TiO2 coated tapered optical fiber SPR sensor for alcohol sensing application. J. Opt. 2023, 1–11. [Google Scholar] [CrossRef]
- Li, G.; Singh, R.; Guo, J.; Zhang, B.; Kumar, S. Nb2CTx MXene-assisted double S-tapered fiber-based LSPR sensor with improved features for tyramine detection. Appl. Phys. Lett. 2023, 122, 083701. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Li, C.; Yang, X. Copper-multiwalled carbon nanotubes decorated fiber-optic surface plasmon resonance sensor for detection of trace hydrogen sulfide gas. Opt. Fiber Technol. 2023, 76, 103221. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Q.; Chen, S.; Cheng, F.; Wang, H.; Peng, W. Surface Plasmon Resonance Biosensor Based on Smart Phone Platforms. Sci. Rep. 2015, 5, 12864. [Google Scholar] [CrossRef] [PubMed] [Green Version]


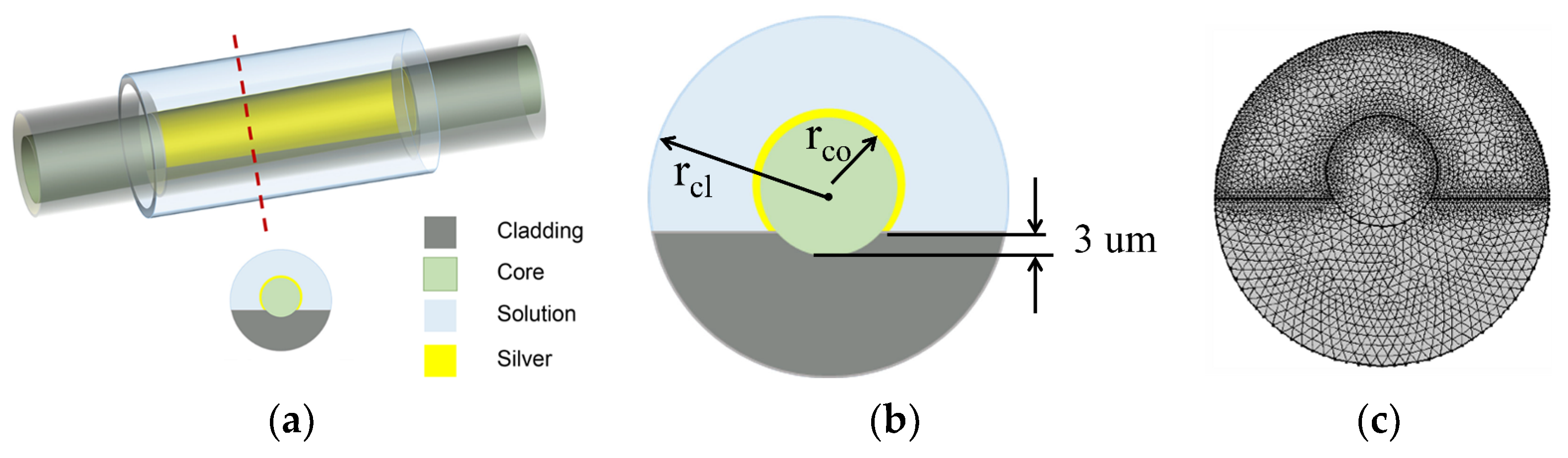
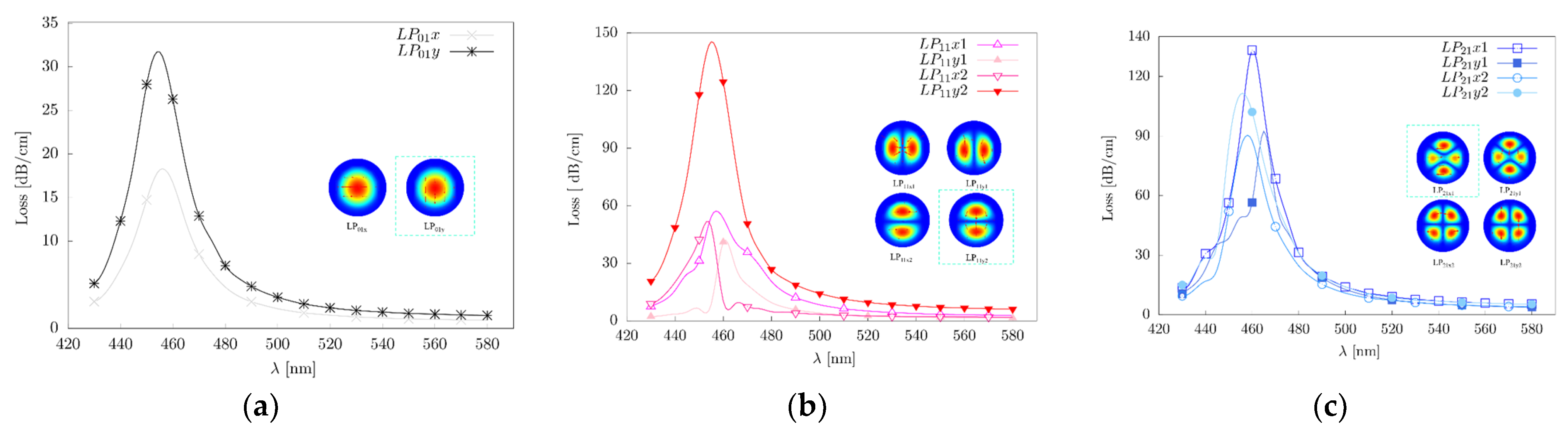
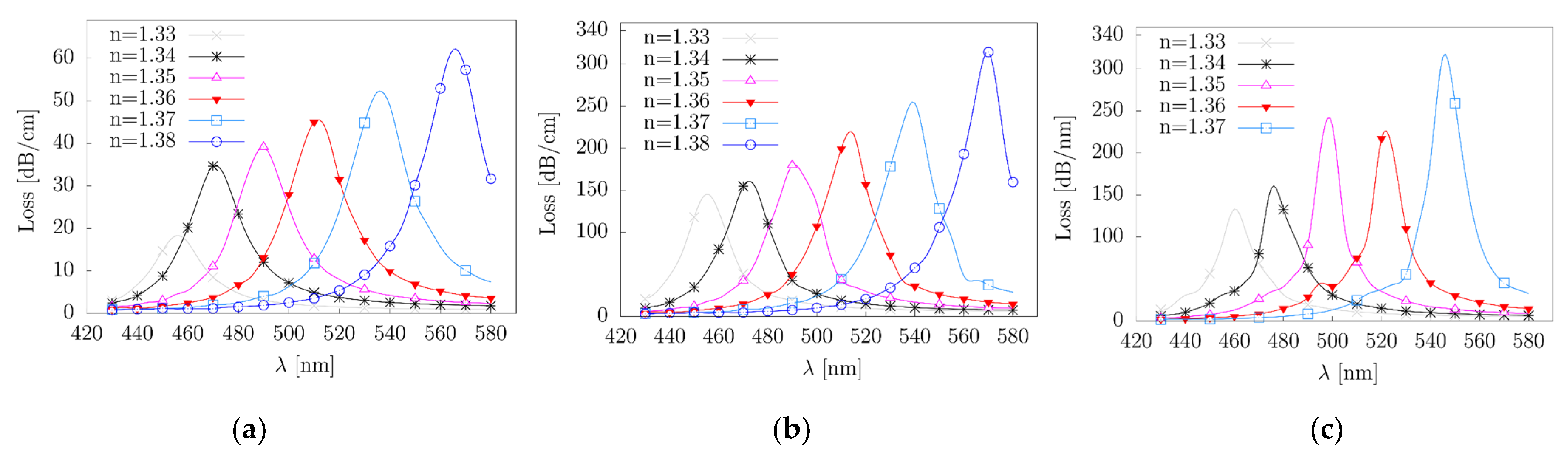
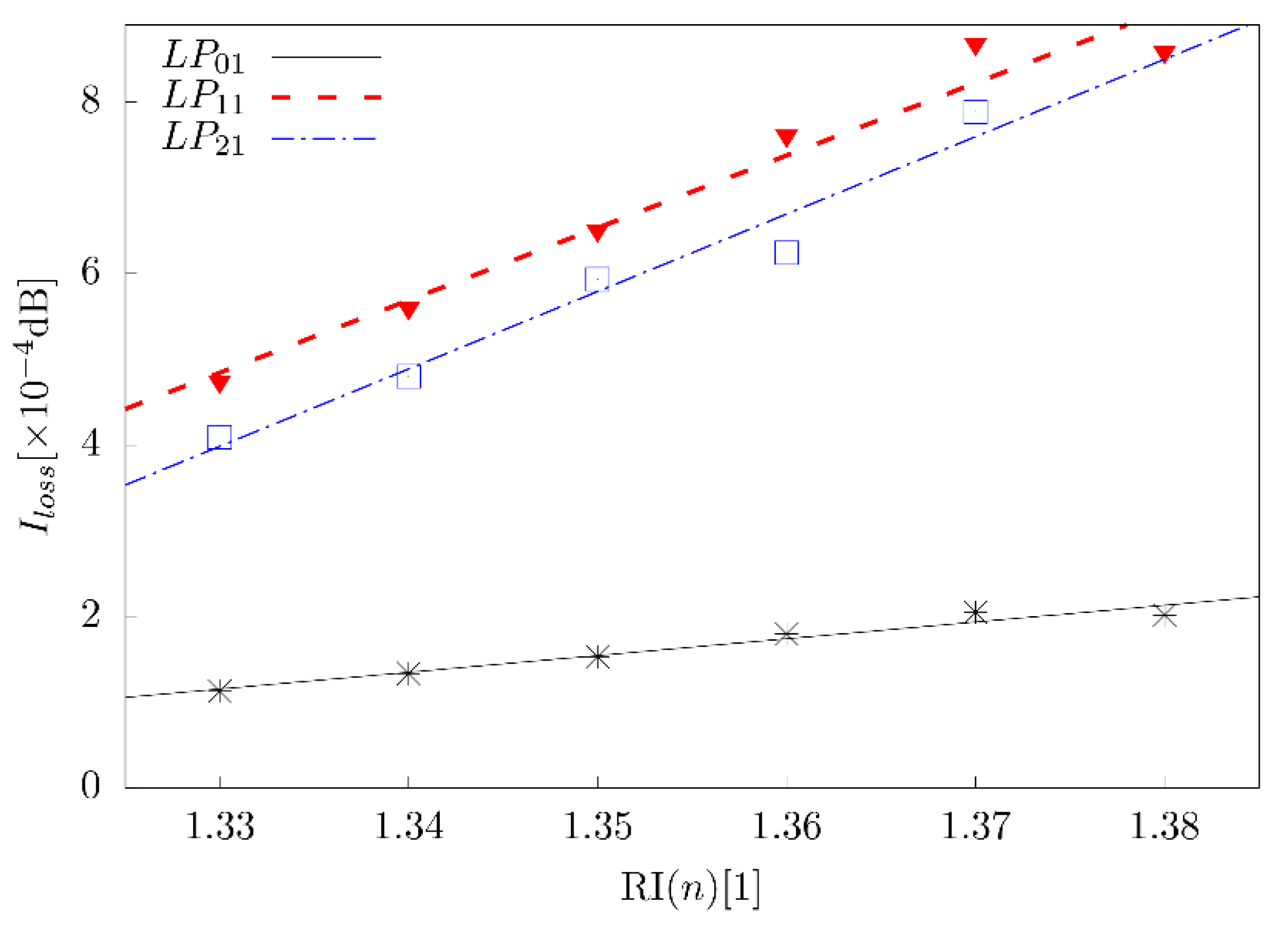
| Index | Parametric Meaning | Index | Parametric Meaning |
|---|---|---|---|
| Fl (R) | The electric field | The efficiency of converting the fundamental mode into a higher order mode of MSC | |
| R | The normalized radius | The wavelength | |
| a | The radius of the fiber | The effective RI of the mode | |
| k | The wavenumber in the vacuum | D | The core distance |
| the propagation constant | L | The fusion length of fiber | |
| the RI of the core | The radius of the core in the simulations | ||
| the RI of the cladding | The radius of the cladding in the simulations | ||
| U | the core parameter | The loss of SPR in the sensing area | |
| W | the cladding parameter | n | The refractive index in the simulations |
| V | The normalized frequency | Iloss | The total loss of the mode, including the , , and mode |
| The efficiency of a light source producing the fundamental mode | The minimum detected loss | ||
| The proportion of the power of the mode in the cladding to the total power | The incident power | ||
| The ratio of the power enhancement of the higher order mode to the fundamental mode | The output power |
| Sensitivity | 1.95 | 8.45 | 9.03 |
| Normalization of Sensitivity | 1.00 | 4.32 | 4.62 |
| Correlation coefficient | 0.98 | 0.98 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Yan, B.; Wang, Q.; Zhao, J.; Zhang, H.; Yu, H.; Fan, H.; Jia, D. Sensitivity Improvement of an Optical Fiber Sensor Based on Surface Plasmon Resonance with Pure Higher-Order Modes. Appl. Sci. 2023, 13, 4020. https://doi.org/10.3390/app13064020
Yang C, Yan B, Wang Q, Zhao J, Zhang H, Yu H, Fan H, Jia D. Sensitivity Improvement of an Optical Fiber Sensor Based on Surface Plasmon Resonance with Pure Higher-Order Modes. Applied Sciences. 2023; 13(6):4020. https://doi.org/10.3390/app13064020
Chicago/Turabian StyleYang, Chuanhao, Bing Yan, Qi Wang, Jing Zhao, Hongxia Zhang, Hui Yu, Haojun Fan, and Dagong Jia. 2023. "Sensitivity Improvement of an Optical Fiber Sensor Based on Surface Plasmon Resonance with Pure Higher-Order Modes" Applied Sciences 13, no. 6: 4020. https://doi.org/10.3390/app13064020
APA StyleYang, C., Yan, B., Wang, Q., Zhao, J., Zhang, H., Yu, H., Fan, H., & Jia, D. (2023). Sensitivity Improvement of an Optical Fiber Sensor Based on Surface Plasmon Resonance with Pure Higher-Order Modes. Applied Sciences, 13(6), 4020. https://doi.org/10.3390/app13064020







