Modelling the Wind Speed Using Exponentiated Weibull Distribution: Case Study of Poprad-Tatry, Slovakia
Abstract
:1. Introduction
2. Description of Studied Area
3. Wind Speed Data Characteristics and Analysis
4. Wind Direction Analysis
5. Methods
5.1. Probability Distributions
5.2. Parameter Estimation
5.3. Goodness-of-Fit and Model Selection Criteria
6. Results and Discussion
- Respective months:
- The entire period and the seasons:
- The datasets in both other papers had high values of kurtosis—in the dataset from [49], the kurtosis was 2.502; in the datasets from [50], the values of kurtosis ranged from 3.877 to 8.806. The datasets here, with the EW distribution as the most suitable one, also possessed high values of the coefficient of kurtosis, ranging from 3.31 to 4.57.
- The datasets in both other papers had positive values of skewness—in the dataset from [49], the skewness was 0.633; in the datasets from [50], the values of skewness ranged from 0.888 to 2.014. The datasets, modelled here, also had values of the coefficient of skewness ranging from 0.95 to 1.31. All of these datasets can be regarded as moderate to highly right skewed.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Safari, B.; Gasore, J. A statistical investigation of wind characteristics and wind energy potential based on the Weibull and Rayleigh models in Rwanda. Renew. Energy 2010, 35, 2874–2880. [Google Scholar] [CrossRef]
- Chen, H.; Birkelund, Y.; Anfinsen, S.N.; Staupe-Delgado, R.; Yuan, F. Assessing probabilistic modelling for wind speed from numerical weather prediction and observation in the Artic. Sci. Rep. 2021, 11, 7613. [Google Scholar] [CrossRef] [PubMed]
- Lun, I.Y.F.; Lam, J.C. A study of Weibull parameters using long-term wind observations. Renew. Energy 2000, 20, 145–153. [Google Scholar] [CrossRef]
- Davenport, A.G. The relationship of wind structure to wind loading. In Proceedings of the Symposium No. 16—Wind Effects on Buildings and Structures, Teddington, UK, 26–28 June 1963; pp. 53–111. [Google Scholar]
- Hemanth Kumar, M.B.; Saravanan, B.; Sanjeevikumar, P.; Holm-Nielsen, J.B. Wind Energy Potential Assessment by Weibull Parameter Estimation Using Multiverse Optimization Method: A Case Study of Tirumala Region in India. Energies 2019, 12, 2158. [Google Scholar] [CrossRef] [Green Version]
- Abbas, G.; Gu, J.; Asad, M.U.; Balas, V.E.; Farooq, U.; Khan, I.A. Estimation of Weibull Distribution Parameters by Analytical Methods for the Wind Speed of Jhimpir, Pakistan—A Comparative Assessment. In Proceedings of the 2022 International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 2–4 December 2022. [Google Scholar]
- Hussain, I.; Haider, A.; Ullah, Z.; Russo, M.; Casolino, G.M.; Azeem, B. Comparative Analysis of Eight Numerical Methods Using Weibull Distribution to Estimate Wind Power Density for Coastal Areas in Pakistan. Energies 2023, 16, 1515. [Google Scholar] [CrossRef]
- Kang, S.; Khanjari, A.; You, S.; Lee, J.-H. Comparison of different statistical methods used to estimate Weibull parameters for wind speed contribution in nearby an offshore site, Republic of Korea. Energy Rep. 2021, 7, 7358–7373. [Google Scholar] [CrossRef]
- Salami, A.A.; Ouedraogo, S.; Kodjo, K.M.; Ajavon, A.S.A. Influence of the random data ampling in estimation of wind speed resource: Case study. Int. J. Renew. Energy Dev. 2022, 11, 133–143. [Google Scholar] [CrossRef]
- Dhakal, R.; Sedai, A.; Pol, S.; Parameswaran, S.; Nejat, A.; Moussa, H. A Novel Hybrid Method for Short-Term Wind Speed Prediction Based on Wind Probability Distribution Function and Machine Learning Models. Appl. Sci. 2022, 12, 9038. [Google Scholar] [CrossRef]
- Singh, K.A.; Khan, M.G.M.; Ahmed, M.R. Wind Energy Resource Assessment for Cook Islands with Accurate Estimation of Weibull Parameters Using Frequentist and Bayesian Methods. IEEE Access 2022, 10, 25935–25953. [Google Scholar] [CrossRef]
- Alsamamra, H.R.; Salah, S.; Shoqeir, J.A.H.; Manasra, A.J. A comparative study of five numerical methods for the estimation of Weibull parameters for wind energy evaluation at Eastern Jerusalem, Palestine. Energy Rep. 2022, 8, 4801–4810. [Google Scholar] [CrossRef]
- Al-Hussieni, A.J.M. A prognosis of wind energy potential as a power generation source in Basra city, Iraq state. Eur. Sci. J. 2014, 10, 163–176. [Google Scholar]
- Okakwu, I.; Akinyele, D.; Olabode, O.; Ajewole, T.; Oluwasogo, E.; Oyedeji, A. Comparative Assessment of Numerical Techniques for Weibull Parameters’ Estimation and the Performance of Wind Energy Conversion Systems in Nigeria. IIUM Eng. J. 2023, 24, 138–157. [Google Scholar] [CrossRef]
- Shu, Z.R.; Jesson, M. Estimation of Weibull parameters for wind energy analysis across the UK. J. Renew. Sustain. Energy 2021, 13, 023303. [Google Scholar] [CrossRef]
- Truhetz, H.; Krenn, A.; Winkelmeier, H.; Müller, S.; Cattin, R.; Eder, T.; Biberacher, M. Austrian Wind Potential Analysis (AuWiPot). In Proceedings of the 12. Symposium Energieinnovation, Graz, Austria, 15–17 February 2012. [Google Scholar]
- Pobočíková, I.; Sedliačková, Z.; Šimon, J.; Jurášová, D. Statistical analysis of the wind speed at mountain site Chopok, Slovakia, using Weibull distribution. IOP Conf. Ser. Mater. Sci. End. 2020, 776, 012114. [Google Scholar] [CrossRef]
- Wais, P. A review of Weibull functions in wind sector. Renew. Sust. Energ. Rev. 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P.; Velázquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sust. Energ. Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Akgül, F.G.; Şenoğlu, B.; Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: Inverse Weibull distribution. Energy Convers. Manag. 2016, 114, 234–240. [Google Scholar] [CrossRef]
- Sukkiramathi, K.; Seshaiah, C. Analysis of wind power potential by the three-parameter Weibull distribution to install a wind turbine. Energy Explor. Exploit. 2020, 38, 158–174. [Google Scholar] [CrossRef] [Green Version]
- Pobočíková, I.; Sedliačková, Z.; Michalková, M. Application of four probability distributions for wind speed modeling. Procedia Eng. 2017, 192, 713–718. [Google Scholar] [CrossRef]
- Sarkar, A.; Singh, S.; Mitra, D. Wind climate modeling using Weibull and extreme value distribution. Int. J. Eng. Sci. Technol. 2011, 3, 100–106. [Google Scholar] [CrossRef]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Kang, D.; Ko, K.; Huh, J. Determination of extreme wind values using the Gumbel distribution. Energy 2015, 86, 51–58. [Google Scholar] [CrossRef]
- Alavi, O.; Mohammadi, K.; Mostafaeipour, A. Evaluating the suitability of wind speed probability distribution models: A case study of east and southeast parts of Iran. Energy Convers. Manag. 2016, 119, 101–108. [Google Scholar] [CrossRef]
- Mohammadi, K.; Alavi, O.; McGowan, J.G. Use of Birnbaum-Saunders distribution for estimating wind speed and wind power probability distributions: A review. Energy Convers. Manag. 2017, 143, 109–122. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Convers. Manag. 2017, 133, 216–234. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Usta, I.; Arik, I.; Yenilmez, I. Wind speed analysis using the Extended Generalized Lindley Distribution. Renew. Energy 2018, 118, 1024–1030. [Google Scholar] [CrossRef]
- Ahmad, Z.; Mahmoudi, E.; Roozegarz, R.; Hamedani, G.G.; Butt, N.S. Contributions towards new families of distributions: An investigation, further developments, characterizations and comparative study. Pak. J. Stat. Oper. Res. 2022, 18, 99–120. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- ul Haq, M.A.; Rao, G.S.; Albassam, M.; Aslam, M. Marshall-Olkin Power Lomax distribution for modeling of wind speed data. Energy Rep. 2020, 6, 1118–1123. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions. Renew. Energy 2007, 32, 518–531. [Google Scholar] [CrossRef]
- Akpinar, S.; Akpinar, E.K. Estimation of wind energy potential using finite mixture distribution models. Energy Convers. Manag. 2009, 50, 877–884. [Google Scholar] [CrossRef]
- Kollu, R.; Rayapudi, S.R.; Narasimham, S.V.L.; Pakkurthi, K.M. Mixture probability distribution functions to model wind speed distributions. Int. J. Energy Environ. Eng. 2012, 3, 27. [Google Scholar] [CrossRef] [Green Version]
- Ouarda, T.B.M.J.; Charron, C. On the mixture of wind speed distribution in a Nordic region. Energy Convers. Manag. 2018, 174, 33–44. [Google Scholar] [CrossRef]
- Mahbudi, S.; Jamalizadeh, A.; Farnoosh, R. Use of finite mixture models skew-t-normal Birnbaum-Saunders components in the analysis of wind speed: Case studies in Ontario, Canada. Renew. Energy 2020, 162, 196–211. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analysing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Hutson, A.D. The exponentiated Weibull family: Some properties and a flood data application. Commun. Stat.-Theory Methods 1996, 25, 3059–3083. [Google Scholar] [CrossRef]
- Nassar, M.M.; Eissa, F.H. On the exponentiated Weibull distribution. Commun. Stat.-Theory Methods 2003, 32, 1317–1336. [Google Scholar] [CrossRef]
- Nassar, M.M.; Eissa, F.H. Bayesian estimation for the exponentiated Weibull model. Commun. Stat.-Theory Methods 2004, 33, 2343–2362. [Google Scholar] [CrossRef]
- Alizadeh, M.; Bagheri, S.F.; Baloui Jamkhaneh, E.; Nadarajah, S. Estimates of the PDF and the CDF of the exponentiated Weibull distribution. Braz. J. Probab. Stat. 2015, 29, 695–716. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. On the moments of the exponentiated Weibull distribution. Commun. Stat.-Theory Methods 2005, 34, 253–256. [Google Scholar] [CrossRef]
- Salem, A.M.; Abo-Kasem, O.E. Estimation for the parameters of the exponentiated Weibull distribution based on progressive hybrid censored samples. Int. J. Contemp. Math. Sci. 2011, 6, 1713–1724. [Google Scholar]
- Pal, M.; Ali, M.M.; Woo, J. Exponentiated Weibull distribution. Statistica 2006, 66, 136–147. [Google Scholar] [CrossRef]
- Barrios, R.; Dios, F. Exponentiated Weibull distribution family under aperture averaging for Gaussian beam waves. Opt. Express 2012, 20, 13055–13064. [Google Scholar] [CrossRef] [Green Version]
- Shittu, O.I.; Adepoju, K.A. On the exponentiated Weibull distribution for modeling wind speed in South Western Nigeria. J. Mod. Appl. Stat. Methods 2014, 13, 431–445. [Google Scholar] [CrossRef] [Green Version]
- Akgül, F.G.; Şenoğlu, B. Comparison of wind speed distributions: A case study for Aegean coast of Turkey. Energy Sources A Recovery Util. Environ. Eff. 2019, 45, 2453–2470. [Google Scholar] [CrossRef]
- Unesco. Tatra Transboundary Biosphere Reserve, Poland/Slovakia. Available online: https://www.unesco.org/en/man-and-biosphere/tatra-transboundary-biosphere-reserve-poland/slovakia-0 (accessed on 11 March 2023).
- Ilčin, J. Problematics of Flight in Mountainous Terrain. Bachelor’s Thesis, Brno University of Technology, Brno, Czech Republic, 2017. [Google Scholar]
- Bochníček, O.; Hrušková, K.; Zvara, I. Climate Atlas of Slovakia, 1st ed.; Slovak Hydrometeorological Institute: Bratislava, Slovakia, 2015; p. 131. [Google Scholar]
- Google Earth. Available online: https://earth.google.com/web/search/Poprad,+Slovakia/@49.05877989,20.29744794,672.117089a,24378.01462403d,35y,0h,0t,0r/data=CnsaURJLCiUweDQ3M2UzYTk0YmNmZGExOTE6MHg5Mzk3NGEwYWVmODZiOTIwGSrNQSuLhkhAIdHHfECgSzRAKhBQb3ByYWQsIFNsb3Zha2lhGAIgASImCiQJI8yHUE9QNUARIcyHUE9QNcAZKLUxbvu7QkAhhILfAjV3UMA (accessed on 8 March 2023).
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; Wiley: Chichester, UK, 2010; p. 704. [Google Scholar]
- Hare, W. Assessment of Knowledge on Impacts of Climate Change—Contribution to the Specification of Art. 2 of the UNFCCC: Impacts on Ecosystems, Food Production, Water and Socio-Economic Systems; External Expertise Report for German Advisory Council on Global Change: Berlin, Germany, 2003; p. 104. [Google Scholar]
- Al Mac. Wind_Rose (Wind_Direction, Wind_Speed). MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/65174-wind_rose-wind_direction-wind_speed (accessed on 13 February 2023).
- Akpinar, E.K.; Akpinar, S. Determination of the wind energy potential for Maden-Elazig, Turkey. Energy Convers. Manag. 2004, 45, 2901–2914. [Google Scholar] [CrossRef]
- Akdag, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]
- Azad, A.K.; Rasul, M.G.; Yusaf, T. Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications. Energies 2014, 7, 3056–3085. [Google Scholar] [CrossRef] [Green Version]
- Shoaib, M.; Siddiqui, I.; Rehman, S.; Khan, S.; Alhems, L.M. Assessment of wind energy potential using wind energy conversion system. J. Clean. Prod. 2019, 216, 346–360. [Google Scholar] [CrossRef]
- Al-Mhairat, B.; Al-Quraaan, A. Assessment of Wind Energy Resources in Jordan Using Different Optimization Techniques. Processes 2022, 10, 105. [Google Scholar] [CrossRef]
- Chang, T.P. Estimation of wind energy potential using different probability density functions. Appl. Energy 2011, 88, 1848–1856. [Google Scholar] [CrossRef]
- Evans, J.W.; Johnson, R.A.; Green, D.W. Two- and Three-Parameter Weibull Goodness-of-Fit Tests; Res. Pap. FPL-RP-493; U.S. Department of Agricultural, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1989; p. 27.
- Krit, M.; Gaudoin, O.; Remy, E. Goodness-of-fit tests for the Weibull and extreme value distributions: A review and comparative study. Commun. Stat.-Simul. Comput. 2021, 50, 1888–1911. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]

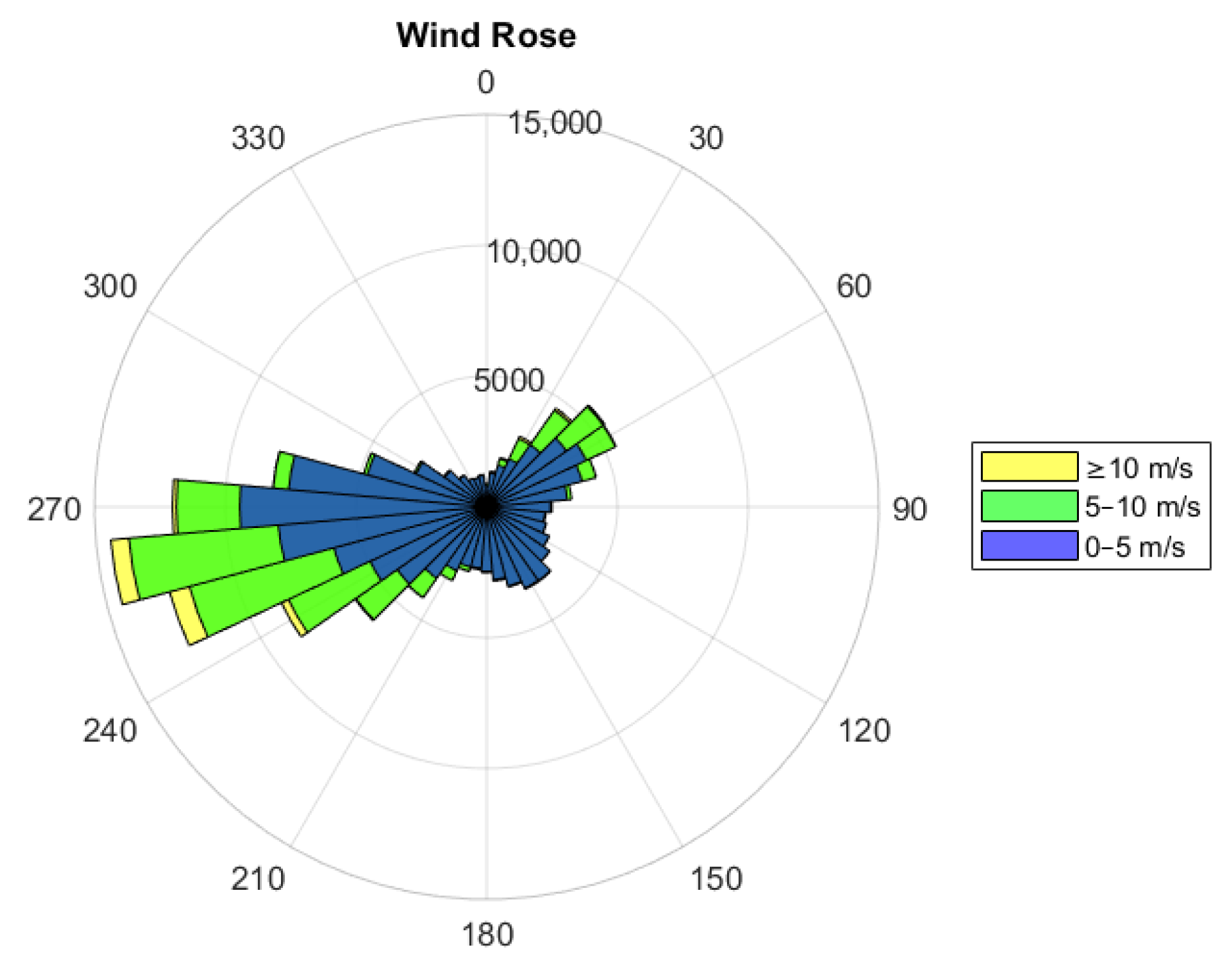
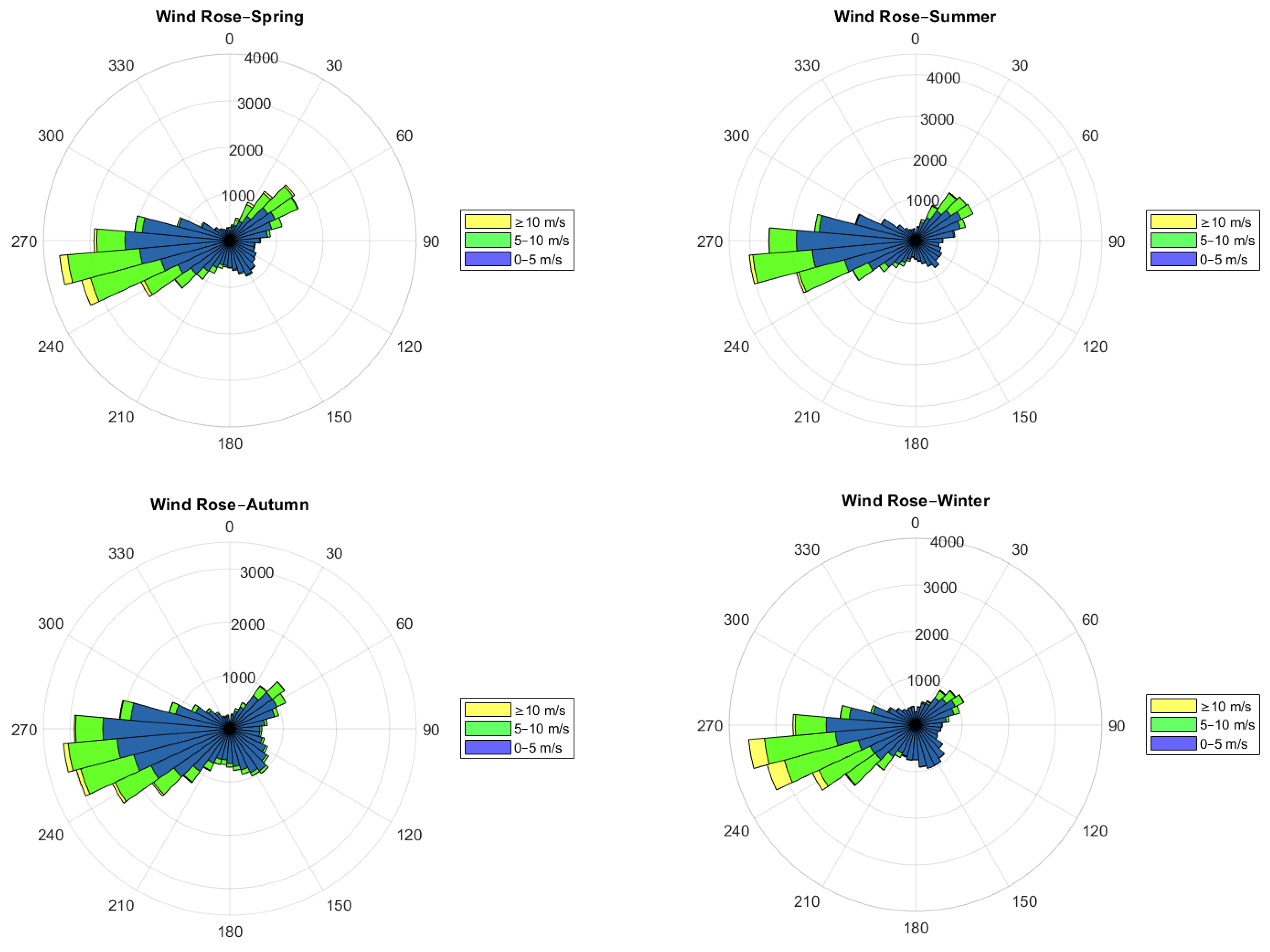
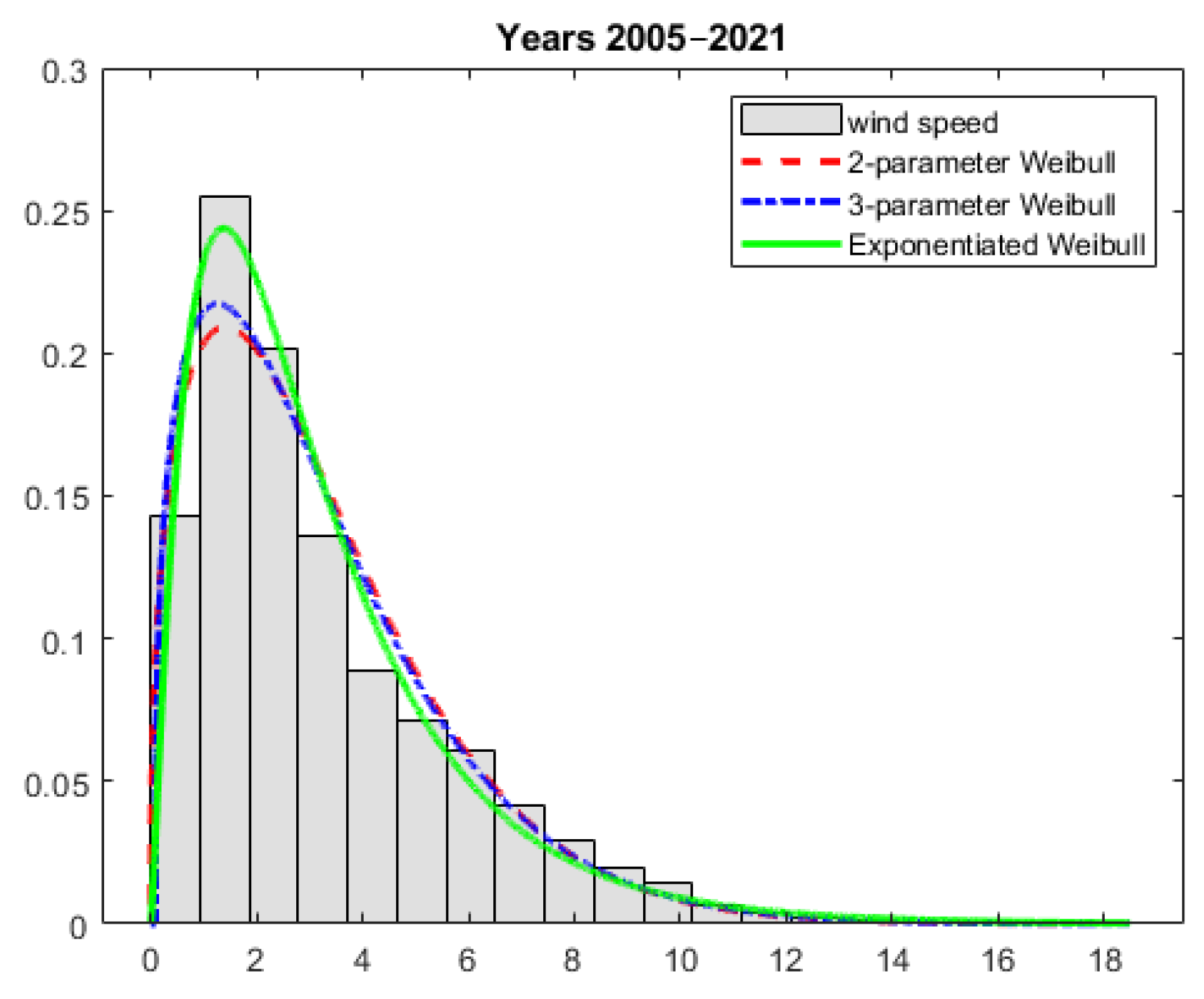
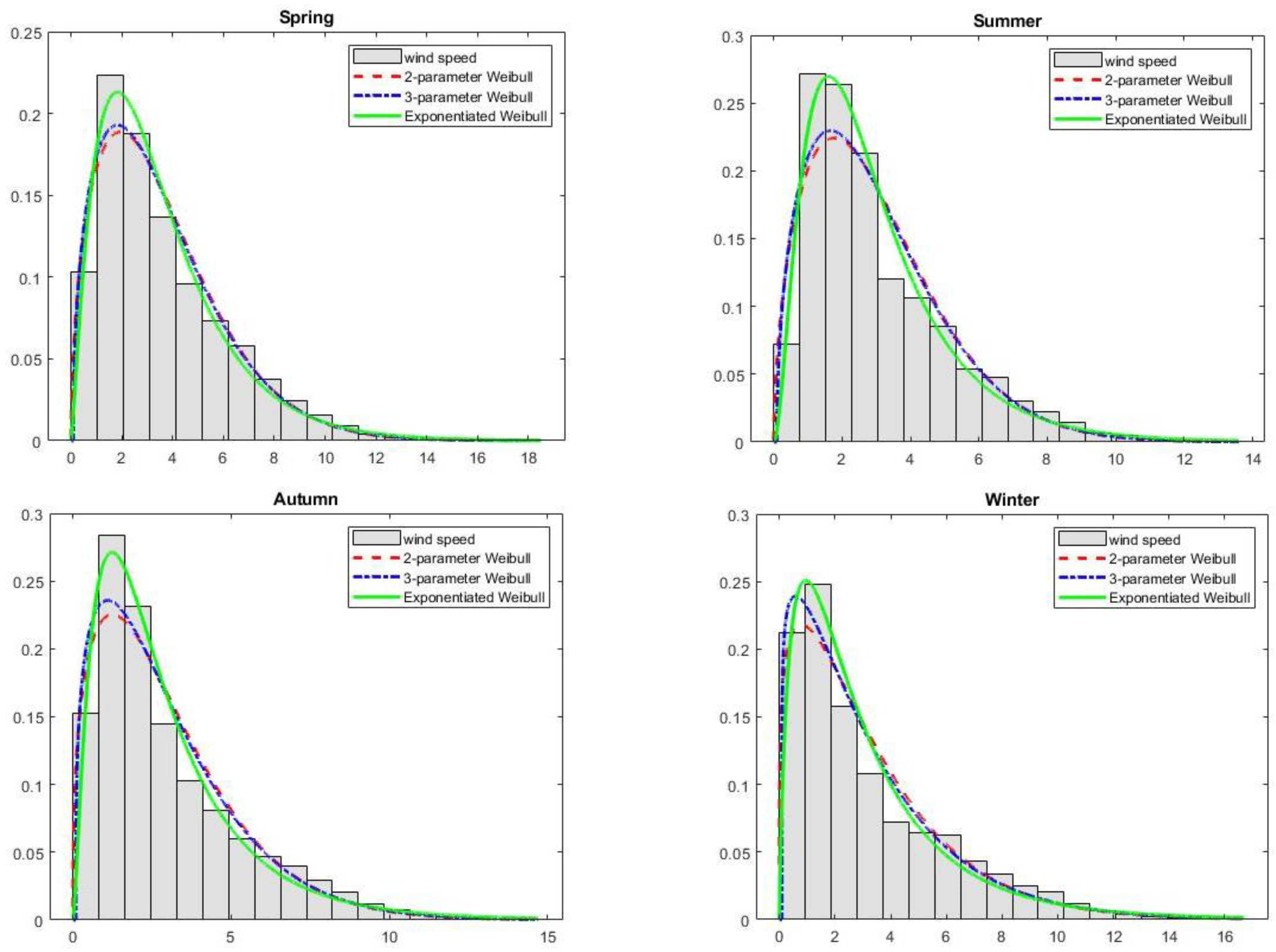
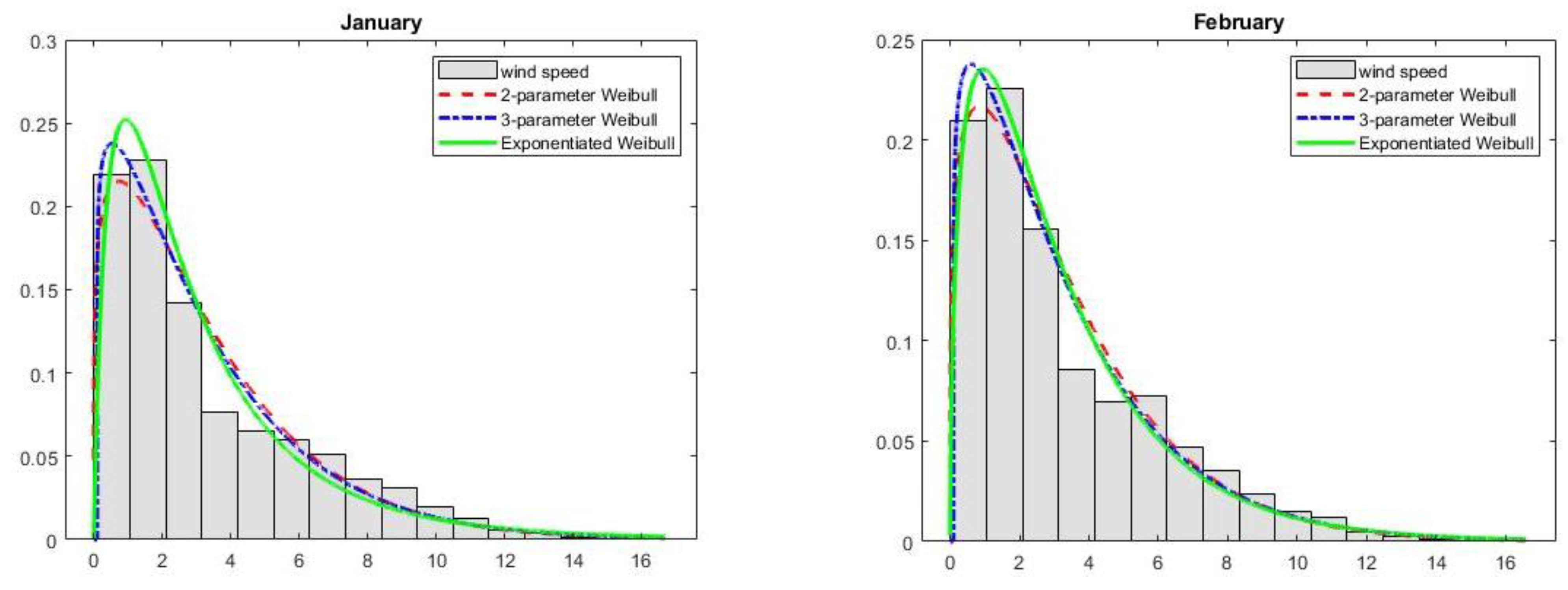
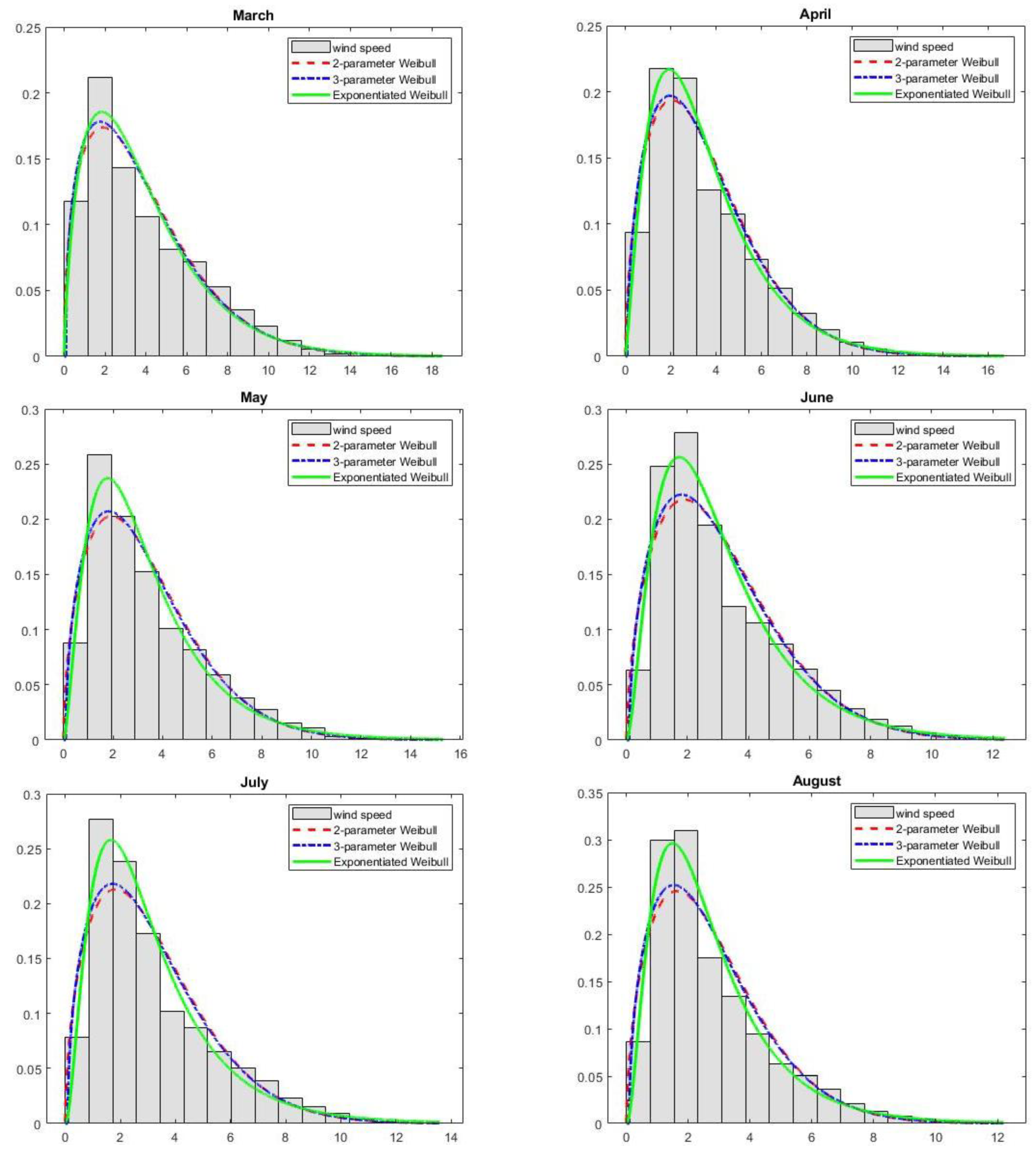

| Period | Mean | Standard Deviation | Min | Max | Lower Quartile | Median | Upper Quartile | Coefficient of Variation (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| January | 3.31 | 2.87 | 0.1 | 16.7 | 1.1 | 2.2 | 5.0 | 86.49 | 1.21 | 3.78 |
| February | 3.23 | 2.70 | 0.1 | 16.6 | 1.2 | 2.3 | 4.7 | 83.69 | 1.23 | 4.13 |
| March | 3.85 | 2.73 | 0.1 | 18.5 | 1.7 | 3.1 | 5.5 | 71.04 | 0.95 | 3.31 |
| April | 3.49 | 2.33 | 0.1 | 16.7 | 1.7 | 2.9 | 4.8 | 66.75 | 1.12 | 4.15 |
| May | 3.33 | 2.26 | 0.1 | 15.3 | 1.6 | 2.7 | 4.5 | 67.77 | 1.17 | 4.21 |
| June | 3.12 | 2.06 | 0.1 | 12.4 | 1.6 | 2.5 | 4.3 | 66.10 | 1.14 | 4.05 |
| July | 3.16 | 2.17 | 0.1 | 13.6 | 1.6 | 2.5 | 4.3 | 68.46 | 1.18 | 3.99 |
| August | 2.75 | 1.86 | 0.1 | 12.2 | 1.4 | 2.2 | 3.7 | 67.62 | 1.28 | 4.57 |
| September | 2.92 | 2.11 | 0.1 | 14.1 | 1.4 | 2.3 | 3.9 | 72.41 | 1.29 | 4.47 |
| October | 2.96 | 2.25 | 0.1 | 14.7 | 1.3 | 2.2 | 4.1 | 75.97 | 1.28 | 4.38 |
| November | 3.03 | 2.52 | 0.1 | 14.3 | 1.1 | 2.1 | 4.2 | 83.15 | 1.31 | 4.23 |
| December | 3.15 | 2.69 | 0.1 | 14.9 | 1.1 | 2.2 | 4.6 | 82.27 | 1.28 | 4.17 |
| Period | Mean | Standard Deviation | Min | Max | Lower Quartile | Median | Upper Quartile | Coefficient of Variation (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| Spring | 3.56 | 2.46 | 0.1 | 18.5 | 1.7 | 2.9 | 4.9 | 69.14 | 1.10 | 3.91 |
| Summer | 3.01 | 2.04 | 0.1 | 13.6 | 1.5 | 2.4 | 4.1 | 67.81 | 1.21 | 4.24 |
| Autumn | 2.97 | 2.30 | 0.1 | 14.7 | 1.3 | 2.2 | 4.1 | 77.44 | 1.32 | 4.44 |
| Winter | 3.23 | 2.76 | 0.1 | 16.7 | 1.1 | 2.2 | 4.8 | 85.27 | 1.24 | 4.02 |
| Period | Mean | Standard Deviation | Min | Max | Lower Quartile | Median | Upper Quartile | Coefficient of Variation (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| Total | 3.19 | 2.41 | 0.1 | 18.5 | 1.4 | 2.4 | 4.5 | 75.56 | 1.25 | 4.32 |
| Distribution | MLM Estimate | |
|---|---|---|
| W2 | Log-likelihood function | |
| Likelihood equations | ||
| W3 | Log-likelihood function | |
| Likelihood equations | ||
| EW | Log-likelihood function | |
| Likelihood equations | ||
| Distribution | Estimated Parameters | Entire Period | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|---|
| W2 | a | 1.3893 | 1.5146 | 1.5680 | 1.3650 | 1.2059 |
| b | 3.5133 | 3.9596 | 3.3696 | 3.2592 | 3.4510 | |
| W3 | a | 1.3263 | 1.4591 | 1.5046 | 1.2978 | 1.1305 |
| b | 3.3802 | 3.8383 | 3.2479 | 3.1216 | 3.2817 | |
| c | 0.0894 | 0.0875 | 0.0914 | 0.0919 | 0.0945 | |
| EW | a | 0.8726 | 1.0340 | 0.8823 | 0.7791 | 0.7642 |
| b | 1.6847 | 2.3591 | 1.3894 | 1.2294 | 1.5294 | |
| γ | 2.5451 | 2.1045 | 3.3732 | 3.2179 | 2.4516 |
| Period | Distribution | KS | AD | ln L | AIC | BIC | R2 | RMSE a |
|---|---|---|---|---|---|---|---|---|
| Entire period | W2 | 0.059 | 662.6 | −308,150.5 | 616,305.0 | 616,324.8 | 0.9909 | 0.028 |
| W3 | 0.050 | 470.5 | −306,925.1 | 613,856.2 | 613,885.9 | 0.9936 | 0.023 | |
| EW | 0.034 | 243.3 | −306,288.0 | 612,582.0 | 612,611.8 | 0.9970 | 0.016 | |
| Spring | W2 | 0.053 | 124.4 | −80,074.0 | 160,152.1 | 160,169.1 | 0.9933 | 0.024 |
| W3 | 0.047 | 92.7 | −79,880.8 | 159,767.6 | 159,793.1 | 0.9950 | 0.021 | |
| EW | 0.035 | 54.6 | −79,757.7 | 159,521.4 | 159,547.0 | 0.9972 | 0.016 | |
| Summer | W2 | 0.067 | 227.4 | −73,395.1 | 146,794.3 | 146,811.4 | 0.9873 | 0.032 |
| W3 | 0.061 | 179.7 | −73,121.5 | 146,248.9 | 146,274.5 | 0.9899 | 0.029 | |
| EW | 0.037 | 54.3 | −72,601.7 | 145,209.5 | 145,235.0 | 0.9972 | 0.015 | |
| Autumn | W2 | 0.066 | 218.7 | −74,507.1 | 149,018.2 | 149,035.2 | 0.9880 | 0.032 |
| W3 | 0.057 | 156.8 | −74,116.8 | 148,239.7 | 148,265.3 | 0.9915 | 0.027 | |
| EW | 0.033 | 64.5 | −73,827.2 | 147,660.4 | 147,685.9 | 0.9970 | 0.016 | |
| Winter | W2 | 0.063 | 215.2 | −78,083.0 | 156,170.0 | 156,187.0 | 0.9884 | 0.032 |
| W3 | 0.049 | 143.7 | −77,557.3 | 155,120.5 | 155,146.0 | 0.9927 | 0.025 | |
| EW | 0.046 | 130.6 | −77,737.6 | 155,481.1 | 155,506.6 | 0.9936 | 0.024 |
| Distribution | Estimated Parameters | Jan. | Feb. | Mar. | Apr. | May | June |
|---|---|---|---|---|---|---|---|
| W2 | a | 1.1862 | 1.2171 | 1.4476 | 1.5725 | 1.5599 | 1.6024 |
| b | 3.5240 | 3.4546 | 4.2539 | 3.9058 | 3.7221 | 3.4978 | |
| W3 | a | 1.1133 | 1.1360 | 1.3928 | 1.5199 | 1.5009 | 1.5403 |
| b | 3.3507 | 3.2860 | 4.1266 | 3.7968 | 3.5984 | 3.3781 | |
| c | 0.0961 | 0.0903 | 0.0875 | 0.0803 | 0.0925 | 0.0910 | |
| EW | a | 0.7044 | 0.9292 | 1.1745 | 1.0970 | 0.9501 | 0.9537 |
| b | 1.3078 | 2.2820 | 3.2900 | 2.4519 | 1.8160 | 1.6601 | |
| γ | 2.8359 | 1.6514 | 1.4615 | 2.0194 | 2.7514 | 2.9133 | |
| Distribution | Estimated Parameters | July | Aug. | Sept. | Oct. | Nov. | Dec. |
| W2 | a | 1.5523 | 1.5765 | 1.4656 | 1.3873 | 1.2650 | 1.2178 |
| b | 3.5363 | 3.0818 | 3.2430 | 3.2543 | 3.2742 | 3.3750 | |
| W3 | a | 1.4918 | 1.5082 | 1.4001 | 1.3198 | 1.1964 | 1.1473 |
| b | 3.4131 | 2.9617 | 3.1175 | 3.1203 | 3.1214 | 3.2118 | |
| c | 0.0922 | 0.0905 | 0.0888 | 0.0902 | 0.0953 | 0.0963 | |
| EW | a | 0.8530 | 0.8841 | 0.8586 | 0.8306 | 0.6598 | 0.6786 |
| b | 1.3725 | 1.2609 | 1.3794 | 1.3990 | 0.8914 | 1.0755 | |
| γ | 3.5642 | 3.4373 | 3.0535 | 2.8575 | 3.9939 | 3.3284 |
| Period | Distribution | KS | AD | ln L | AIC | BIC | R2 | RMSE a |
|---|---|---|---|---|---|---|---|---|
| Jan. | W2 | 0.069 | 93.9 | −27,316.8 | 54,637.6 | 54,652.4 | 0.9855 | 0.036 |
| W3 | 0.056 | 65.3 | −27,117.3 | 54,240.5 | 54,262.8 | 0.9903 | 0.029 | |
| EW | 0.051 | 57.6 | −27,174.5 | 54,355.0 | 54,377.3 | 0.9920 | 0.027 | |
| Feb. | W2 | 0.053 | 42.2 | −24,131.0 | 48,266.0 | 48,280.6 | 0.9924 | 0.026 |
| W3 | 0.038 | 28.8 | −24,000.8 | 48,007.5 | 48,029.5 | 0.9958 | 0.019 | |
| EW | 0.041 | 30.0 | −24,089.7 | 48,185.5 | 48,207.5 | 0.9950 | 0.021 | |
| Mar. | W2 | 0.052 | 39.2 | −27,971.6 | 55,947.1 | 55,962.0 | 0.9938 | 0.023 |
| W3 | 0.045 | 30.0 | −27,911.0 | 55,828.0 | 55,850.3 | 0.9953 | 0.020 | |
| EW | 0.042 | 31.8 | −27,946.2 | 55,898.5 | 55,920.8 | 0.9951 | 0.021 | |
| Apr. | W2 | 0.053 | 35.7 | −25,790.8 | 51,585.7 | 51,600.5 | 0.9939 | 0.023 |
| W3 | 0.048 | 27.3 | −25,743.8 | 51,493.6 | 51,515.8 | 0.9954 | 0.020 | |
| EW | 0.035 | 13.5 | −25,687.6 | 51,381.3 | 51,403.5 | 0.9977 | 0.014 | |
| May | W2 | 0.056 | 53.3 | −26,080.9 | 52,165.7 | 52,180.6 | 0.9916 | 0.026 |
| W3 | 0.050 | 40.5 | −25,999.1 | 52,004.2 | 52,026.5 | 0.9936 | 0.023 | |
| EW | 0.034 | 15.4 | −25,890.7 | 51,787.4 | 51,809.7 | 0.9977 | 0.014 | |
| June | W2 | 0.065 | 59.4 | −24,247.7 | 48,499.4 | 48,514.2 | 0.9900 | 0.029 |
| W3 | 0.059 | 46.4 | −24,170.1 | 48,346.3 | 48,368.5 | 0.9922 | 0.025 | |
| EW | 0.037 | 17.7 | −24,045.0 | 48,095.9 | 48,118.1 | 0.9971 | 0.016 | |
| July | W2 | 0.071 | 89.1 | −25,472.5 | 50,949.1 | 50,964.0 | 0.9853 | 0.035 |
| W3 | 0.065 | 72.4 | −25,380.1 | 50,766.1 | 50,788.5 | 0.9880 | 0.032 | |
| EW | 0.041 | 25.4 | −25,198.1 | 50,402.1 | 50,424.5 | 0.9962 | 0.018 | |
| Aug. | W2 | 0.068 | 77.2 | −23,489.9 | 46,983.8 | 46,998.7 | 0.9871 | 0.032 |
| W3 | 0.062 | 60.0 | −23,391.6 | 46,789.2 | 46,811.5 | 0.9899 | 0.028 | |
| EW | 0.035 | 14.3 | −23,197.7 | 46,401.4 | 46,423.7 | 0.9978 | 0.014 | |
| Sept. | W2 | 0.070 | 77.2 | −23,997.5 | 47,999.1 | 48,013.9 | 0.9864 | 0.033 |
| W3 | 0.063 | 59.7 | −23,899.7 | 47,805.4 | 47,827.6 | 0.9895 | 0.029 | |
| EW | 0.040 | 20.8 | −23,766.2 | 47,538.4 | 47,560.6 | 0.9967 | 0.017 | |
| Oct. | W2 | 0.061 | 66.0 | −25,246.6 | 50,497.2 | 50,512.1 | 0.9894 | 0.030 |
| W3 | 0.052 | 47.0 | −25,127.5 | 50,261.0 | 50,283.3 | 0.9926 | 0.025 | |
| EW | 0.033 | 21.8 | −25,051.8 | 50,109.5 | 50,131.9 | 0.9970 | 0.016 | |
| Nov. | W2 | 0.068 | 89.8 | −25,124.7 | 50,253.4 | 50,268.3 | 0.9858 | 0.035 |
| W3 | 0.057 | 63.5 | −24,947.6 | 49,901.2 | 49,923.4 | 0.9902 | 0.029 | |
| EW | 0.040 | 33.8 | −24,869.7 | 49,745.4 | 49,767.6 | 0.9955 | 0.020 | |
| Dec. | W2 | 0.066 | 85.5 | −26,617.7 | 53,239.3 | 53,254.2 | 0.9871 | 0.034 |
| W3 | 0.055 | 58.5 | −26,418.7 | 52,843.4 | 52,865.8 | 0.9913 | 0.027 | |
| EW | 0.048 | 46.7 | −26,426.6 | 52,859.3 | 52,881.6 | 0.9935 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pobočíková, I.; Michalková, M.; Sedliačková, Z.; Jurášová, D. Modelling the Wind Speed Using Exponentiated Weibull Distribution: Case Study of Poprad-Tatry, Slovakia. Appl. Sci. 2023, 13, 4031. https://doi.org/10.3390/app13064031
Pobočíková I, Michalková M, Sedliačková Z, Jurášová D. Modelling the Wind Speed Using Exponentiated Weibull Distribution: Case Study of Poprad-Tatry, Slovakia. Applied Sciences. 2023; 13(6):4031. https://doi.org/10.3390/app13064031
Chicago/Turabian StylePobočíková, Ivana, Mária Michalková, Zuzana Sedliačková, and Daniela Jurášová. 2023. "Modelling the Wind Speed Using Exponentiated Weibull Distribution: Case Study of Poprad-Tatry, Slovakia" Applied Sciences 13, no. 6: 4031. https://doi.org/10.3390/app13064031





