Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm and Its Engineering Application
Abstract
1. Introduction
- We introduce a GSLEO-AEFA algorithm to improve the performance and balance in between exploitation and exploration phases of the original AEFA.
- We introduce a Gaussian mutation with specular learning strategy to enhance population diversity and as a new strategy for population initialization.
- We introduce a local escaping operator as a method for avoiding stagnation in local optimal.
- We use real world engineering problems to evaluate GSLEO-AEFA.
2. Methodology
2.1. Artificial Electric Field Algorithm (AEFA)
| Algorithm 1 Artificial Electric Field Algorithm (AEFA) |
| Initialize the population of size within search range Set the Initial to 0 Calculate fitness value for all particles Set iteration while stopping requirement is not met do Compute for to do Calculate fitness values Calculate the total force in each direction Equation (5) Calculate acceleration Equation (3) end for end while |
2.2. Proposed GSLEO-AEFA
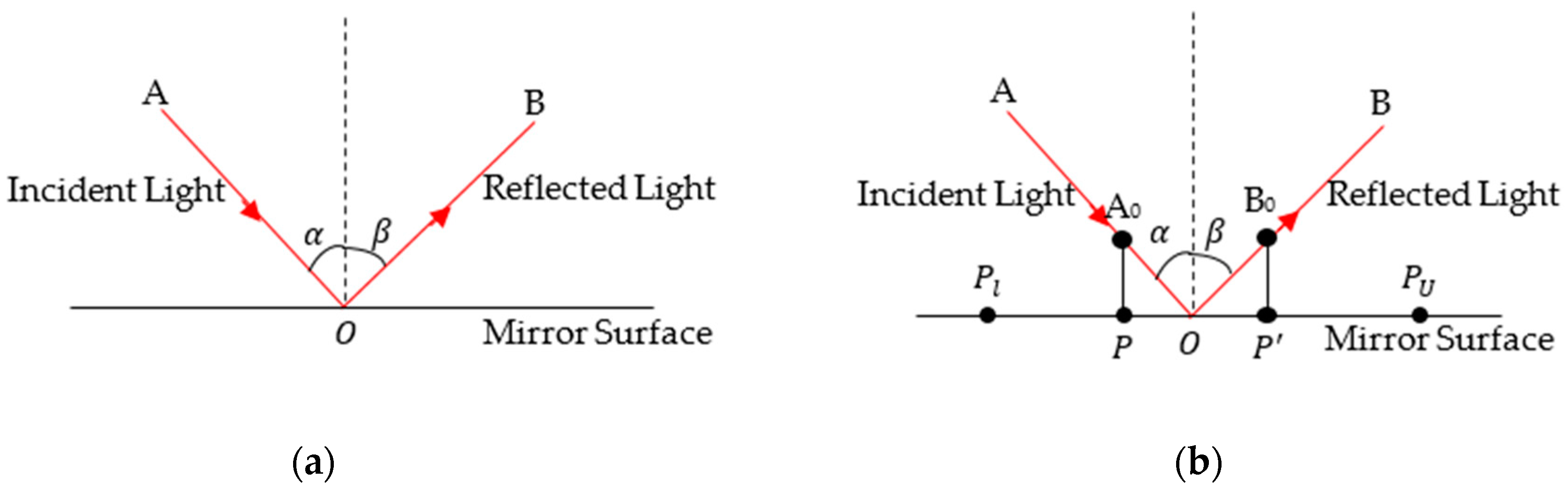
2.2.1. Population Initialization Using Gaussian Mutation Specular Reflection Learning (GS)
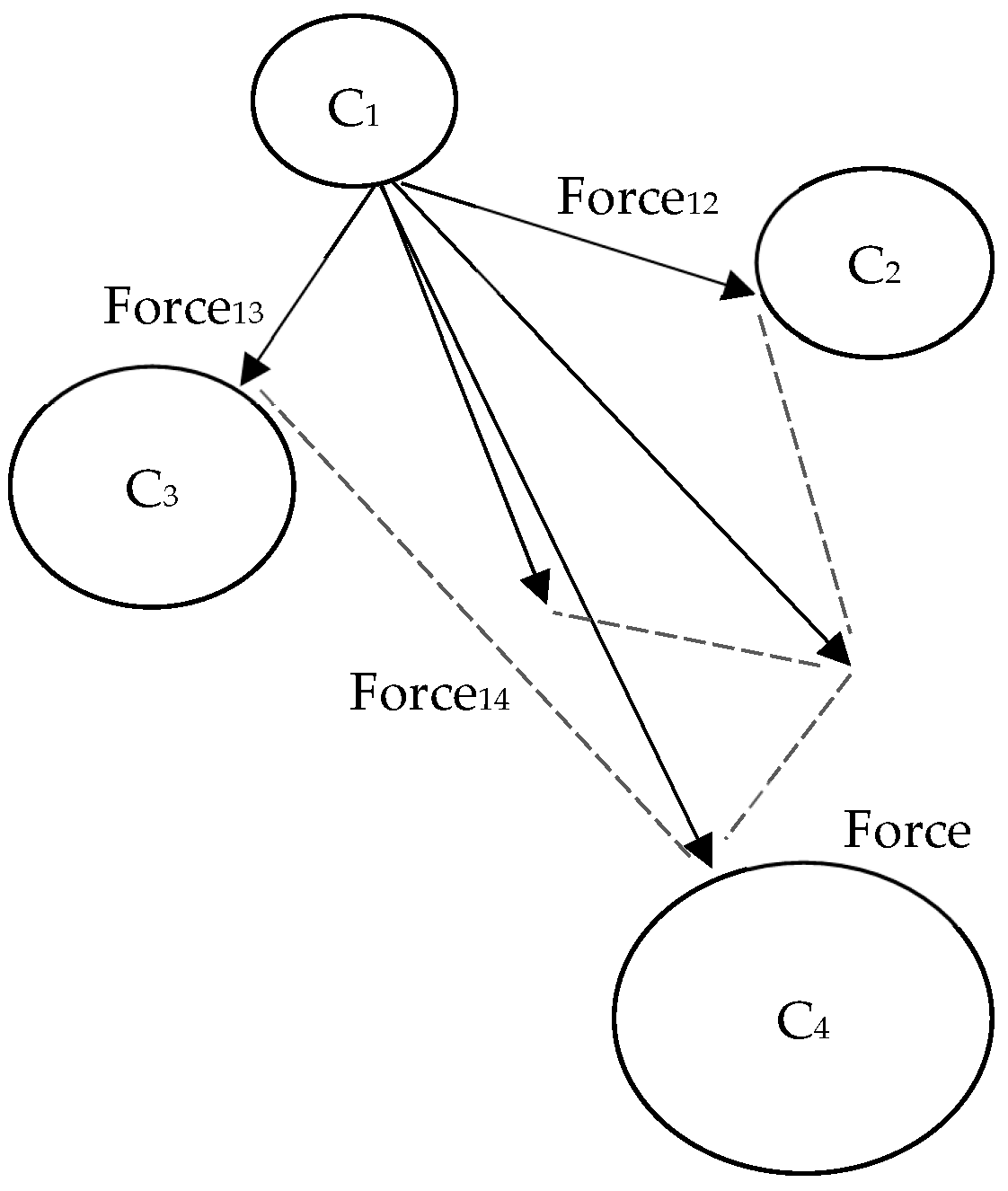
2.2.2. Local Escaping Operator (LEO)
| Algorithm 2 Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm (GSLEO-AEFA) |
| Initialize the population of and using Equations (20) and (21) Calculate the fitness of all particles initialized and select best particles after ranking fitness from best to worst Set the Initial to 0 Calculate fitness value for all particles Set iteration while stopping requirement is not met do Compute for to do Calculate fitness values Calculate the total force in each direction Equation (5) Calculate acceleration Equation (3) if < 0.5 then Update using Equation (22) else Update using Equation (24) end for end while |
3. Experimental Results and Discussion
3.1. Impact of Problem Dimension Analysis
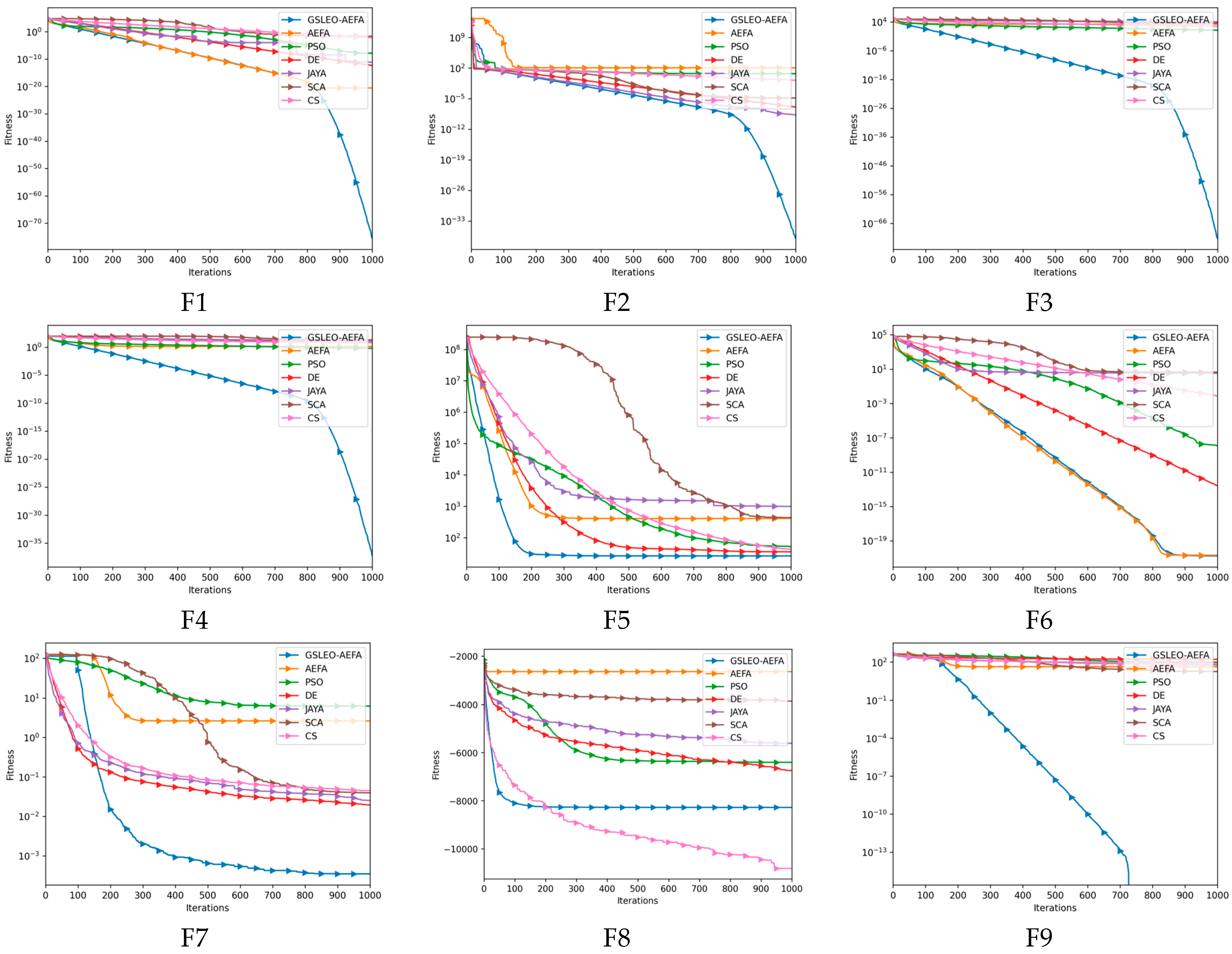
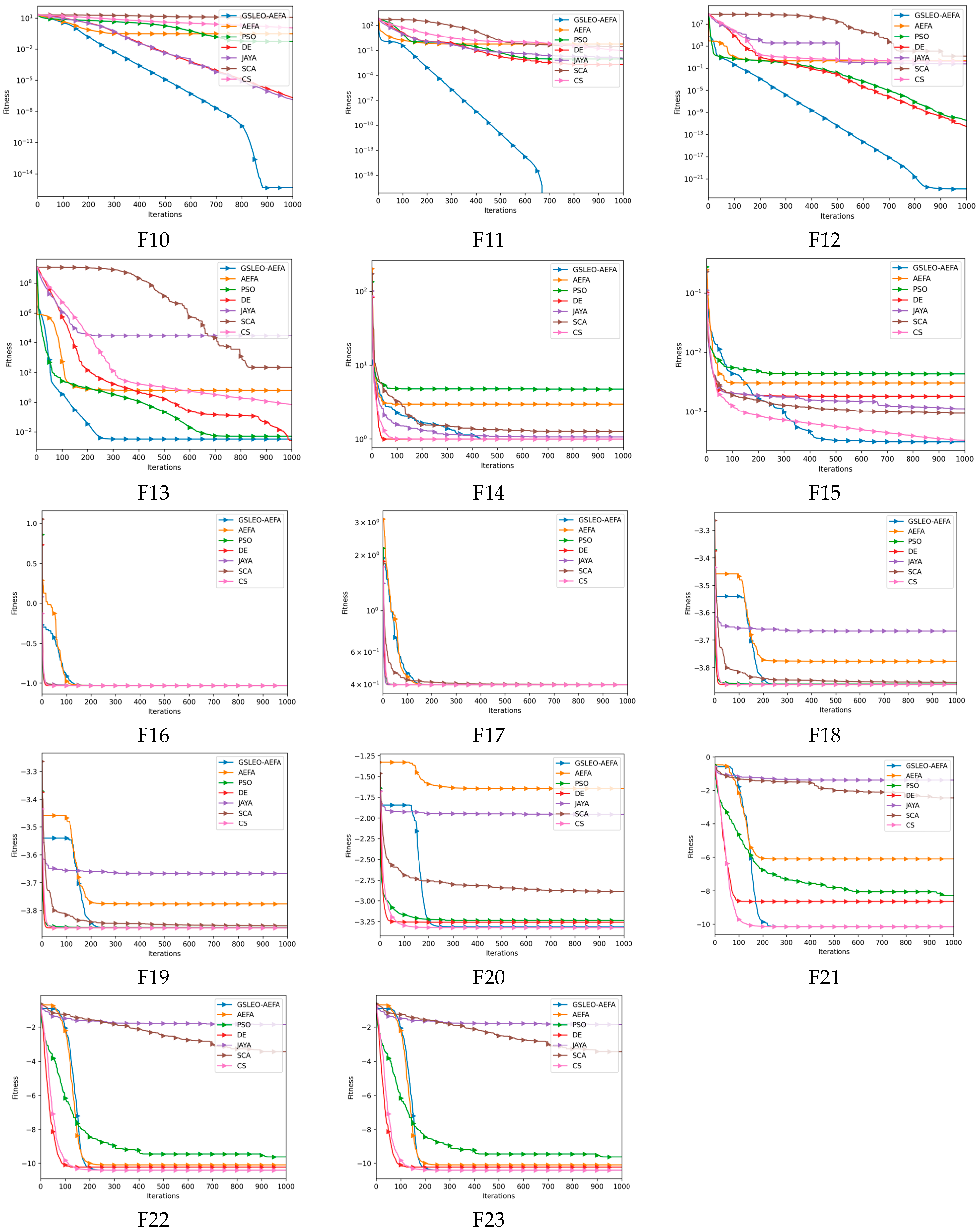
3.2. Convergence Trajectory Analysis
3.3. Statistical Test
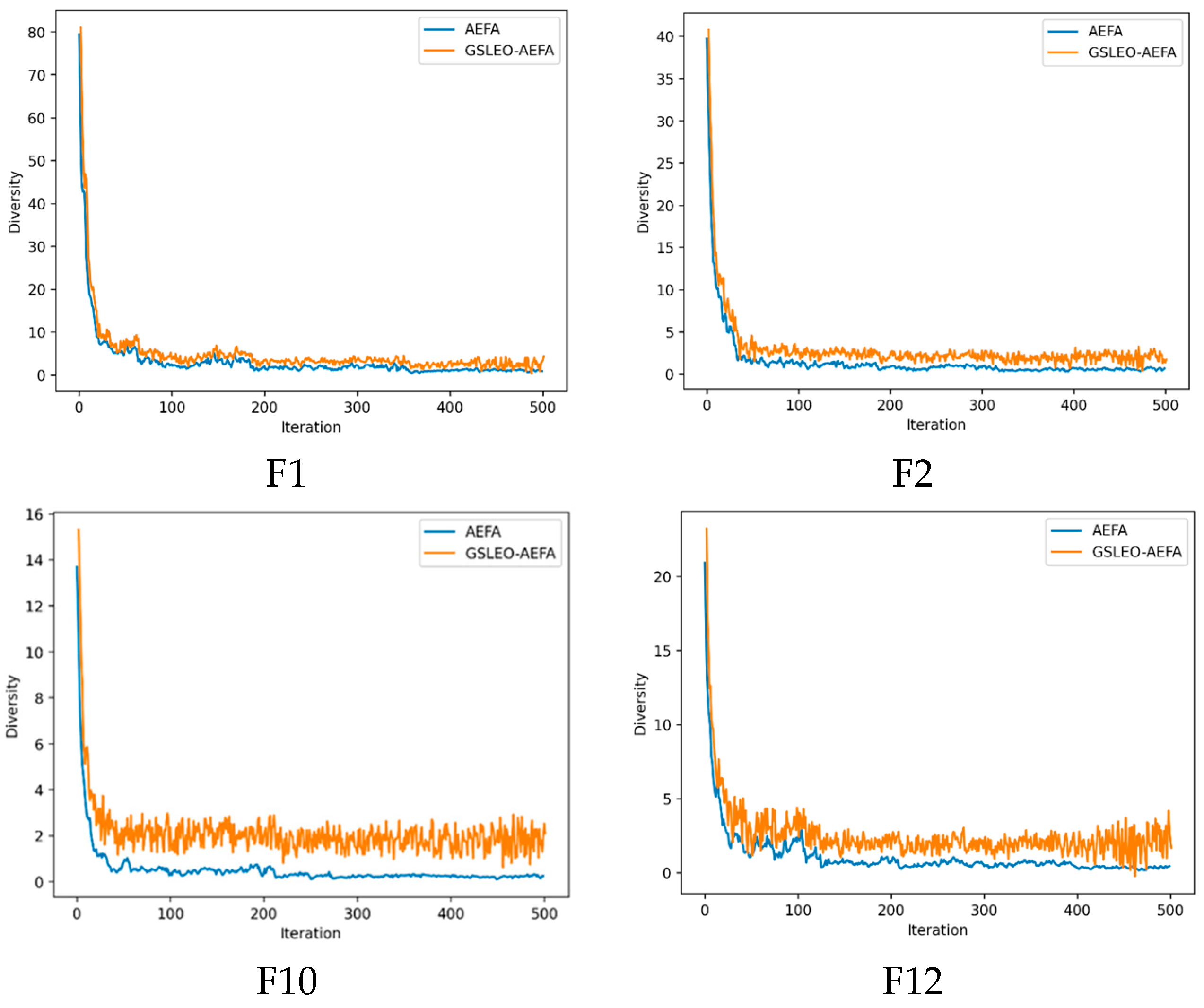
3.4. Diversity Analysis
3.5. Computational Time and Space Complexity Analyses
3.6. Overall Discussion
3.7. Engineering Problems
3.7.1. Parameter Estimation for Frequency-Modulated (FM) Sound Waves
3.7.2. Lennard–Jones Potential Problem (LJ)
3.7.3. Tersoff Potential Function Minimization Problem (TPF)
3.7.4. Antenna Optimization Problem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahariq, I. On the application of the spectral element method in electromagnetic problems involving domain decomposition. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1059–1069. [Google Scholar] [CrossRef]
- Yang, C.X.; Zhang, J.; Tong, M.S. A Hybrid Quantum-Behaved Particle Swarm Optimization Algorithm for Solving Inverse Scattering Problems. IEEE Trans. Antennas Propag. 2021, 69, 5861–5869. [Google Scholar] [CrossRef]
- Donelli, M.; Franceschini, D.; Rocca, P.; Massa, A. Three-Dimensional Microwave Imaging Problems Solved Through an Efficient Multiscaling Particle Swarm Optimization. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1467–1481. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A memory-based Grey Wolf Optimizer for global optimization tasks. Appl. Soft Comput. 2020, 93, 106367. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Abbas, M.; Alshehri, M.A.; Barnawi, A.B. Potential Contribution of the Grey Wolf Optimization Algorithm in Reducing Active Power Losses in Electrical Power Systems. Appl. Sci. 2022, 12, 6177. [Google Scholar] [CrossRef]
- El Gmili, N.; Mjahed, M.; El Kari, A.; Ayad, H. Particle Swarm Optimization and Cuckoo Search-Based Approaches for Quadrotor Control and Trajectory Tracking. Appl. Sci. 2019, 9, 1719. [Google Scholar] [CrossRef]
- Li, Y.; Pei, Y.-H.; Liu, J.-S. Bat optimal algorithm combined uniform mutation with Gaussian mutation. Kongzhi Yu Juece/Control Decis. 2017, 32, 1775–1781. [Google Scholar] [CrossRef]
- Yuan, X.; Miao, Z.; Liu, Z.; Yan, Z.; Zhou, F. Multi-Strategy Ensemble Whale Optimization Algorithm and Its Application to Analog Circuits Intelligent Fault Diagnosis. Appl. Sci. 2020, 10, 3667. [Google Scholar] [CrossRef]
- Ni, J.; Tang, J.; Wang, R. Hybrid Algorithm of Improved Beetle Antenna Search and Artificial Fish Swarm. Appl. Sci. 2022, 12, 13044. [Google Scholar] [CrossRef]
- Sun, L.; Feng, B.; Chen, T.; Zhao, D.; Xin, Y. Equalized Grey Wolf Optimizer with Refraction Opposite Learning. Comput. Intell. Neurosci. 2022, 2022, e2721490. [Google Scholar] [CrossRef]
- David, R.-C.; Precup, R.-E.; Petriu, E.M.; Rădac, M.-B.; Preitl, S. Gravitational search algorithm-based design of fuzzy control systems with a reduced parametric sensitivity. Inf. Sci. 2013, 247, 154–173. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding Bodies Optimization method for optimum discrete design of truss structures. Comput. Struct. 2014, 139, 43–53. [Google Scholar] [CrossRef]
- Zheng, H.; Gao, J.; Xiong, J.; Yao, G.; Cui, H.; Zhang, L. An Enhanced Artificial Electric Field Algorithm with Sine Cosine Mechanism for Logistics Distribution Vehicle Routing. Appl. Sci. 2022, 12, 6240. [Google Scholar] [CrossRef]
- Juárez-Pérez, F.; Cruz-Chávez, M.A.; Rivera-López, R.; Ávila-Melgar, E.Y.; Eraña-Díaz, M.L.; Cruz-Rosales, M.H. Grid-Based Hybrid Genetic Approach to Relaxed Flexible Flow Shop with Sequence-Dependent Setup Times. Appl. Sci. 2022, 12, 607. [Google Scholar] [CrossRef]
- Wang, S.L.; Adnan, S.H.; Ibrahim, H.; Ng, T.F.; Rajendran, P. A Hybrid of Fully Informed Particle Swarm and Self-Adaptive Differential Evolution for Global Optimization. Appl. Sci. 2022, 12, 11367. [Google Scholar] [CrossRef]
- Eltaeib, T.; Mahmood, A. Differential Evolution: A Survey and Analysis. Appl. Sci. 2018, 8, 1945. [Google Scholar] [CrossRef]
- Fogel, G.B. Evolutionary Programming. In Handbook of Natural Computing; Rozenberg, G., Bäck, T., Kok, J.N., Eds.; Springer: Berlin, Heidelberg, 2012; pp. 699–708. ISBN 978-3-540-92910-9. [Google Scholar]
- Liu, X.; Wang, Y.; Zhou, M. Dimensional Learning Strategy-Based Grey Wolf Optimizer for Solving the Global Optimization Problem. Comput. Intell. Neurosci. 2022, 2022, 3603607. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. 2013, 45, 35:1–35:33. [Google Scholar] [CrossRef]
- Anita; Yadav, A. AEFA: Artificial electric field algorithm for global optimization. Swarm Evol. Comput. 2019, 48, 93–108. [Google Scholar] [CrossRef]
- Sinthia, P.; Malathi, M. Cancer detection using convolutional neural network optimized by multistrategy artificial electric field algorithm. Int. J. Imaging Syst. Technol. 2021, 31, 1386–1403. [Google Scholar] [CrossRef]
- Petwal, H.; Rani, R. An Improved Artificial Electric Field Algorithm for Multi-Objective Optimization. Processes 2020, 8, 584. [Google Scholar] [CrossRef]
- Selem, S.I.; El-Fergany, A.A.; Hasanien, H.M. Artificial electric field algorithm to extract nine parameters of triple-diode photovoltaic model. Int. J. Energy Res. 2021, 45, 590–604. [Google Scholar] [CrossRef]
- Niroomand, S. Hybrid artificial electric field algorithm for assembly line balancing problem with equipment model selection possibility. Knowl.-Based Syst. 2021, 219, 106905. [Google Scholar] [CrossRef]
- Das, H.; Naik, B.; Behera, H.S. Optimal Selection of Features Using Artificial Electric Field Algorithm for Classification. Arab. J. Sci. Eng. 2021, 46, 8355–8369. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hashim, F.A.; Ferahtia, S.; Rezk, H. An efficient modified artificial electric field algorithm for solving optimization problems and parameter estimation of fuel cell. Int. J. Energy Res. 2021, 45, 20199–20218. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, Y.; Tang, Z.; Luo, Q. Artificial electric field algorithm with inertia and repulsion for spherical minimum spanning tree. Appl. Intell. 2022, 52, 195–214. [Google Scholar] [CrossRef]
- Alanazi, A.; Alanazi, M. Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied. Energies 2022, 15, 5269. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, P.; Xiong, Y. An improved artificial electric field algorithm and its application in neural network optimization. Comput. Electr. Eng. 2022, 101, 108111. [Google Scholar] [CrossRef]
- Malisetti, N.; Pamula, V.K. Energy efficient cluster based routing for wireless sensor networks using moth levy adopted artificial electric field algorithm and customized grey wolf optimization algorithm. Microprocess. Microsyst. 2022, 93, 104593. [Google Scholar] [CrossRef]
- Nayak, S.C.; Sanjeev Kumar Dash, C.; Behera, A.K.; Dehuri, S. An Elitist Artificial-Electric-Field-Algorithm-Based Artificial Neural Network for Financial Time Series Forecasting. In Biologically Inspired Techniques in Many Criteria Decision Making; Dehuri, S., Prasad Mishra, B.S., Mallick, P.K., Cho, S.-B., Eds.; Springer Nature: Singapore, 2022; pp. 29–38. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Opposition-Based Differential Evolution. IEEE Trans. Evol. Comput. 2008, 12, 64–79. [Google Scholar] [CrossRef]
- Zhang, Y. Backtracking search algorithm with specular reflection learning for global optimization. Knowl.-Based Syst. 2021, 212, 106546. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Shen, L.; Al-hababi, T.; Qian, X.; Cao, M. Inverse Analysis of Structural Damage Based on the Modal Kinetic and Strain Energies with the Novel Oppositional Unified Particle Swarm Gradient-Based Optimizer. Appl. Sci. 2022, 12, 11689. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Shen, L.; Asteris, P.G.; Sokol, M.; Xin, Z.; Cao, M. A new self-adaptive quasi-oppositional stochastic fractal search for the inverse problem of structural damage assessment. Alex. Eng. J. 2022, 61, 1922–1936. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Ülker, E.D. A Quick Performance Assessment for Artificial Electric Field Algorithm. In Proceedings of the 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 9–11 June 2022; pp. 1–5. [Google Scholar]
- Sajwan, A.; Yadav, A. A study of exploratory and stability analysis of artificial electric field algorithm. Appl. Intell. 2022, 52, 10805–10828. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Li, T.; Xie, M.; Zhao, Y. An Improved Transient Search Optimization with Neighborhood Dimensional Learning for Global Optimization Problems. Symmetry 2021, 13, 244. [Google Scholar] [CrossRef]
- Liu, Y.; Heidari, A.A.; Cai, Z.; Liang, G.; Chen, H.; Pan, Z.; Alsufyani, A.; Bourouis, S. Simulated annealing-based dynamic step shuffled frog leaping algorithm: Optimal performance design and feature selection. Neurocomputing 2022, 503, 325–362. [Google Scholar] [CrossRef]
- Dai, M.; Feng, X.; Yu, H.; Guo, W. An opposition-based differential evolution clustering algorithm for emotional preference and migratory behavior optimization. Knowl.-Based Syst. 2023, 259, 110073. [Google Scholar] [CrossRef]
- Nama, S.; Saha, A.K.; Sharma, S. Performance up-gradation of Symbiotic Organisms Search by Backtracking Search Algorithm. J Ambient. Intell Hum. Comput. 2022, 13, 5505–5546. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, C.; Li, S.; Guo, X.; Yang, C. Gaussian Perturbation Specular Reflection Learning and Golden-Sine-Mechanism-Based Elephant Herding Optimization for Global Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, e9922192. [Google Scholar] [CrossRef]
- Emambocus, B.A.S.; Jasser, M.B.; Mustapha, A.; Amphawan, A. Dragonfly Algorithm and Its Hybrids: A Survey on Performance, Objectives and Applications. Sensors 2021, 21, 7542. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Venkata Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Mirjalili, S.; Halima, N.B.; Elhosseini, M.A. Comparing SSALEO as a Scalable Large Scale Global Optimization Algorithm to High-Performance Algorithms for Real-World Constrained Optimization Benchmark. IEEE Access 2022, 10, 95658–95700. [Google Scholar] [CrossRef]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2008, 15, 617. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. CCSA: Conscious Neighborhood-based Crow Search Algorithm for Solving Global Optimization Problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Swagatam, D.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Jadavpur University, Nanyang Technological University: Kolkata, India, 2011. [Google Scholar]
- Zhang, Z.; Chen, H.; Jiang, F.; Yu, Y.; Cheng, Q.S. A Benchmark Test Suite for Antenna S-Parameter Optimization. IEEE Trans. Antennas Propagat. 2021, 69, 6635–6650. [Google Scholar] [CrossRef]

| Algorithms | Parameter Setting |
|---|---|
| GSLEO-AEFA | , |
| AEFA | , |
| PSO | |
| DE | |
| SCA | |
| CS | , |
| Function | Range | Dim | Fmin |
|---|---|---|---|
| [−100, 100] | 30 | 0 | |
| [−10, 10] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−30, 30] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−1.28, 1.28] | 30 | 0 | |
| [−500, 500] | 30 | dim | |
| [−5.12, 5.12] | 30 | 0 | |
| [−32, 32] | 30 | 0 | |
| [−600, 600] | 30 | 0 | |
| [−50, 50] | 30 | 0 | |
| [−50, 50] | 30 | 0 | |
| [−65, 65] | 2 | 1 | |
| [−5, 5] | 4 | 0.0003 | |
| [−5, 5] | 2 | −1.0316 | |
| [−5, 5] | 2 | 0.398 | |
| [−2, 2] | 2 | 3 | |
| [1, 3] | 3 | −3.86 | |
| [0, 1] | 6 | −3.32 | |
| [0, 10] | 4 | −10.1532 | |
| [0, 10] | 4 | −10.4028 | |
| [0, 10] | 4 | −10.5363 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | ||
|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 3.166 × 10−76 | 2.827 × 10−21 | 1.357 × 10−8 | 4.675 × 10−13 | 6.832 × 10−12 | 2.439 × 10−2 | 6.799 × 10−3 |
| STD | 2.431 × 10−77 | 2.779 × 10−21 | 9.256 × 10−10 | 1.958 × 10−14 | 8.728 × 10−15 | 7.300 × 10−3 | 1.435 × 10−3 | |
| F2 | AVG | 1.071 × 10−37 | 1.156 × 102 | 5.334 | 1.194 × 10−7 | 2.093 × 10−9 | 1.408 × 10−5 | 1.631 × 10−1 |
| STD | 3.198 × 10−38 | 4.408 × 101 | 6.310 × 10−5 | 5.981 × 10−8 | 2.115 × 10−10 | 3.339 × 10−6 | 5.914 × 10−2 | |
| F3 | AVG | 6.323 × 10−72 | 1.774 × 103 | 1.414 × 101 | 9.579 × 103 | 1.211 × 104 | 3.726 × 103 | 3.379 × 102 |
| STD | 6.534 × 10−73 | 5.231 × 102 | 4.401 | 4.586 × 102 | 3.148 × 103 | 1.379 × 103 | 5.314 × 101 | |
| F4 | AVG | 5.486 × 10−38 | 1.314 | 6.036 × 10−1 | 1.068 × 101 | 1.041 × 101 | 1.925 × 101 | 5.726 |
| STD | 1.030 × 10−38 | 1.196 | 8.508 × 10−2 | 5.046 | 6.554 | 1.208 × 101 | 3.251 | |
| F5 | AVG | 2.635 × 101 | 4.102 × 102 | 5.220 × 101 | 3.564 × 101 | 9.954 × 102 | 4.391 × 102 | 4.301 × 101 |
| STD | 2.495 × 10−1 | 4.270 × 102 | 7.801 | 1.369 × 10−1 | 1.519 × 10−1 | 5.683 × 10−1 | 3.175 × 101 | |
| F6 | AVG | 1.751 × 10−21 | 2.148 × 10−21 | 1.258 × 10−8 | 2.671 × 10−13 | 3.284 | 4.519 | 7.427 × 10−3 |
| STD | 2.239 × 10−22 | 5.626 × 10−22 | 1.805 × 10−9 | 1.590 × 10−14 | 1.952 × 10−1 | 9.424 × 10−2 | 9.015 × 10−5 | |
| F7 | AVG | 3.495 × 10−4 | 2.632 | 6.237 | 1.958 × 10−2 | 2.528 × 10−2 | 3.961 × 10−2 | 4.488 × 10−2 |
| STD | 4.928 × 10−5 | 1.781 × 10−1 | 4.678 × 10−3 | 1.513 × 10−3 | 8.613 × 10−3 | 3.066 × 10−2 | 1.219 × 10−2 | |
| F8 | AVG | −2.483 × 105 | −7.901 × 104 | −1.922 × 105 | −2.023 × 105 | −1.686 × 105 | −1.158 × 105 | −3.243 × 105 |
| STD | −8.278 × 103 | −2.634 × 103 | −6.406 × 103 | −6.742 × 103 | −5.619 × 103 | −3.859 × 103 | −1.127 × 104 | |
| F9 | AVG | 0 | 4.554 × 101 | 9.836 × 101 | 1.639 × 102 | 6.256 × 101 | 1.884 × 101 | 7.841 × 101 |
| STD | 0 | 9.949 × 101 | 2.097 × 101 | 1.246 × 101 | 2.709 × 101 | 1.204 × 10−1 | 1.165 × 101 | |
| F10 | AVG | 4.441 × 10−16 | 3.164 × 10−1 | 5.499 × 10−2 | 2.089 × 10−7 | 1.407 × 10−7 | 1.165 × 101 | 1.152 |
| STD | 0 | 0 | 8.231 × 10−1 | 6.441 × 10−9 | 2.748 × 10−8 | 1.008 × 101 | 4.479 × 10−1 | |
| F11 | AVG | 0 | 5.602 × 10−1 | 9.275 × 10−3 | 2.053 × 10−3 | 1.157 × 10−2 | 2.772 × 10−1 | 8.599 × 10−2 |
| STD | 0 | 7.477 × 10−2 | 7.390 × 10−3 | 2.460 × 10−4 | 7.472 × 10−14 | 1.884 × 10−1 | 7.931 × 10−2 | |
| F12 | AVG | 1.291 × 10−23 | 2.225 | 3.482 × 10−11 | 2.729 × 10−12 | 6.147 × 10−1 | 1.519 × 101 | 1.652 |
| STD | 6.678 × 10−24 | 2.885 × 10−1 | 2.243 × 10−11 | 1.113 × 10−13 | 1.271 × 10−2 | 1.020 | 7.550 × 10−1 | |
| F13 | AVG | 3.296 × 10−3 | 6.300 | 5.127 × 10−3 | 2.695 × 10−3 | 2.957 × 104 | 2.185 × 102 | 7.119 × 10−1 |
| STD | 0 | 7.164 × 10−1 | 1.099 × 10−3 | 1.084 × 10−3 | 1.166 | 3.592 × 10−1 | 3.981 × 10−1 | |
| F14 | AVG | 9.980 × 10−1 | 2.985 | 4.763 | 9.980 × 10−1 | 1.065 | 1.263 | 9.980 × 10−1 |
| STD | 0 | 1.149 | 2.456 | 0 | 1.062 × 10−3 | 7.200 × 10−4 | 0 | |
| F15 | AVG | 3.109 × 10−4 | 3.054 × 10−3 | 4.344 × 10−3 | 1.826 × 10−3 | 1.119 × 10−3 | 9.437 × 10−4 | 3.289 × 10−4 |
| STD | 1.019 × 10−5 | 6.377 × 10−5 | 1.540 × 10−4 | 2.196 × 10−4 | 2.765 × 10−4 | 3.308 × 10−5 | 6.779 × 10−6 | |
| F16 | AVG | −1.032 | −1.032 | −1.032 | −1.032 | −1.032 | −1.032 | −1.032 |
| STD | 4.441 × 10−16 | 0 | 0 | 0 | 5.000 × 10−7 | 3.000 × 10−6 | 0 | |
| F17 | AVG | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.985 × 10−1 | 3.979 × 10−1 |
| STD | 0 | 0 | 0 | 0 | 0 | 8.784 × 10−4 | 0 | |
| F18 | AVG | 3 | 3 | 3 | 3 | 3.284 | 3 | 3 |
| STD | 0 | 0 | 0 | 0 | 4.250 × 10−4 | 5.500 × 10−6 | 0 | |
| F19 | AVG | −3.863 | −3.777 | −3.861 | −3.863 | −3.667 | −3.855 | −3.863 |
| STD | 0 | 0 | 0 | 0 | 1.088 × 10−1 | 2.215 × 10−3 | 0 | |
| F20 | AVG | −3.314 | −1.646 | −3.237 | −3.259 | −1.957 | −2.886 | −3.322 |
| STD | 0 | 3.028 × 10−1 | 1.527 × 10−1 | 5.945 × 10−2 | 1.353 × 10−1 | 1.960 × 10−1 | 0 | |
| F21 | AVG | −1.015 × 101 | −6.101 | −8.294 | −8.652 | −1.379 | −2.450 | −1.015 × 101 |
| STD | 0 | 3.735 | 3.735 | 0 | 1.265 | 5.761 × 10−1 | 0 | |
| F22 | AVG | −1.040 × 101 | −1.010 × 101 | −9.621 | −1.023 × 101 | −1.854 | −3.455 | −1.040 × 101 |
| STD | 0 | 0 | 0 | 0 | 1.559 | 1.078 | 0 | |
| F23 | AVG | −1.054 × 101 | −1.054 × 101 | −9.862 | −1.031 × 101 | −2.339 | −4.853 | −1.054 × 101 |
| STD | 0 | 0 | 4.057 | 0 | 7.908 × 10−2 | 4.472 × 10−1 | 0 | |
| W/L/T | 12/3/8 | 1/18/4 | 0/19/4 | 1/17/5 | 0/22/1 | 0/23/0 | 1/14/8 | |
| OE | 86.95% | 21.73% | 17.39% | 26.08% | 4.34% | 0% | 39.13% |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | ||
|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 1.312 × 10−75 | 1.311 × 101 | 3.983 × 10−3 | 6.081 × 10−6 | 9.955 × 10−8 | 1.376 × 102 | 2.774 |
| STD | 6.044 × 10−76 | 3.475 × 10−1 | 1.564 × 10−4 | 4.101 × 10−6 | 5.847 × 10−9 | 1.154 × 101 | 1.152 | |
| F2 | AVG | 1.620 × 10−37 | 2.192 × 102 | 2.681 × 101 | 1.064 × 10−3 | 1.191 × 10−6 | 1.124 × 10−2 | 1.990 |
| STD | 2.567 × 10−37 | 6.187 × 101 | 5.091 | 7.480 × 10−4 | 8.203 × 10−7 | 2.452 × 10−3 | 5.229 × 10−1 | |
| F3 | AVG | 1.773 × 10−69 | 5.275 × 103 | 6.116 × 102 | 7.020 × 104 | 6.268 × 104 | 3.841 × 104 | 3.916 × 103 |
| STD | 9.445 × 10−69 | 8.081 × 102 | 1.721 × 102 | 9.668 × 103 | 7.966 × 102 | 7.215 × 103 | 1.412 × 101 | |
| F4 | AVG | 5.798 × 10−38 | 8.926 | 2.353 | 5.746 × 101 | 5.065 × 101 | 5.776 × 101 | 1.445 × 101 |
| STD | 7.141 × 10−38 | 8.845 × 10−1 | 2.473 × 10−1 | 2.310 × 101 | 1.968 | 4.991 | 7.853 × 10−1 | |
| F5 | AVG | 4.698 × 101 | 5.315 × 104 | 1.652 × 102 | 1.685 × 103 | 9.021 × 103 | 1.438 × 106 | 6.367 × 102 |
| STD | 4.170 × 10−1 | 3.820 × 104 | 3.482 × 101 | 2.009 × 101 | 1.645 × 10−1 | 2.404 × 105 | 2.091 × 102 | |
| F6 | AVG | 7.007 × 10−3 | 1.113 × 101 | 2.008 × 10−3 | 6.021 × 10−6 | 7.942 | 1.409 × 102 | 2.841 |
| STD | 1.019 × 10−4 | 5.086 × 10−1 | 7.776 × 10−5 | 2.923 × 10−6 | 8.489 × 10−1 | 3.747 × 101 | 7.485 × 10−1 | |
| F7 | AVG | 2.918 × 10−4 | 4.201 × 102 | 4.192 × 101 | 6.239 × 10−2 | 6.597 × 10−2 | 5.376 × 10−1 | 1.918 × 10−1 |
| STD | 1.265 × 10−4 | 2.671 × 101 | 1.212 × 101 | 1.567 × 10−2 | 1.756 × 10−2 | 3.018 × 10−1 | 6.508 × 10−2 | |
| F8 | AVG | −1.177 × 104 | −3.109 × 103 | −1.020 × 104 | −8.514 × 103 | −6.917 × 103 | −5.053 × 103 | −1.381 × 104 |
| STD | 1.283 × 102 | 2.806 × 102 | 3.958 × 102 | 6.519 × 102 | 1.020 × 102 | 3.026 × 102 | 1.781 × 103 | |
| F9 | AVG | 0 | 1.906 × 102 | 2.523 × 102 | 3.497 × 102 | 1.150 × 102 | 5.247 × 101 | 1.637 × 102 |
| STD | 0 | 2.702 × 101 | 1.893 | 1.600 × 101 | 3.186 × 101 | 3.542 | 1.172 × 101 | |
| F10 | AVG | 4.441 × 10−16 | 3.316 | 6.905 × 10−1 | 6.402 × 10−1 | 4.707 × 10−5 | 1.824 × 101 | 3.490 |
| STD | 0 | 2.252 × 10−1 | 2.308 × 10−1 | 1.130 × 10−3 | 2.021 × 10−5 | 9.498 | 9.095 × 10−2 | |
| F11 | AVG | 0 | 7.215 | 5.453 × 10−3 | 2.384 × 10−3 | 6.795 × 10−3 | 2.092 | 9.397 × 10−1 |
| STD | 0 | 1.062 | 3.695 × 10−3 | 9.500 × 10−7 | 9.182 × 10−4 | 8.224 × 10−1 | 1.529 × 10−1 | |
| F12 | AVG | 2.584 × 10−3 | 7.278 | 2.718 × 10−2 | 6.784 × 10−2 | 1.357 | 2.117 × 106 | 3.802 |
| STD | 1.779 × 10−4 | 1.109 | 2.290 × 10−5 | 5.922 × 10−2 | 6.044 × 10−2 | 4.215 × 105 | 7.237 × 10−1 | |
| F13 | AVG | 6.550 × 10−2 | 1.240 × 102 | 7.207 × 10−3 | 2.900 | 3.611 × 103 | 1.074 × 107 | 3.649 × 101 |
| STD | 1.586 × 10−3 | 1.541 × 102 | 8.781 × 10−4 | 2.738 × 10−4 | 4.381 | 6.499 × 104 | 1.280 × 101 | |
| W/L/T | 11/2/0 | 0/13/0 | 1/12/0 | 1/12/0 | 0/13/0 | 0/13/0 | 0/13/0 | |
| OE | 84.62% | 0% | 7.69% | 7.69% | 0% | 0% | 0% |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | ||
|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 1.825 × 10−73 | 1.091 × 103 | 3.321 | 4.915 | 1.084 × 102 | 5.953 × 103 | 3.227 × 102 |
| STD | 3.217 × 10−74 | 3.016 × 102 | 2.080 | 3.551 | 5.745 × 10−3 | 6.759 × 102 | 5.338 × 101 | |
| F2 | AVG | 2.717 × 10−37 | 4.315 × 102 | 1.135 × 102 | 1.405 | 1.336 × 10−3 | 1.799 | 1.579 × 101 |
| STD | 2.624 × 10−37 | 1.948 × 101 | 8.413 | 6.684 × 10−1 | 3.283 × 10−4 | 6.289 × 10−3 | 5.369 × 10−1 | |
| F3 | AVG | 6.493 × 10−71 | 1.600 × 104 | 1.097 × 104 | 3.346 × 105 | 2.863 × 105 | 1.876 × 105 | 3.266 × 104 |
| STD | 2.866 × 10−72 | 7.989 × 102 | 8.134 × 102 | 3.184 × 104 | 7.466 × 104 | 1.587 × 103 | 2.355 × 103 | |
| F4 | AVG | 3.877 × 10−37 | 1.662 × 101 | 9.432 | 9.636 × 101 | 9.338 × 101 | 8.730 × 101 | 2.282 × 101 |
| STD | 6.640 × 10−38 | 1.495 | 2.698 × 10−1 | 6.600 × 10−1 | 6.479 × 10−1 | 8.400 × 10−1 | 2.082 | |
| F5 | AVG | 9.737 × 101 | 2.570 × 106 | 5.257 × 103 | 1.481 × 104 | 7.654 × 103 | 6.989 × 107 | 7.093 × 104 |
| STD | 4.531 × 10−1 | 2.367 × 103 | 7.594 × 101 | 5.708 × 102 | 3.352 × 103 | 1.956 × 107 | 2.230 × 104 | |
| F6 | AVG | 2.314 | 1.067 × 103 | 2.575 | 3.749 | 2.248 × 101 | 5.981 × 103 | 3.865 × 102 |
| STD | 1.672 × 10−1 | 4.358 × 101 | 1.103 | 1.543 | 6.895 × 10−1 | 1.614 × 103 | 5.581 × 101 | |
| F7 | AVG | 2.347 × 10−4 | 1.842 × 103 | 3.258 × 102 | 5.446 × 10−1 | 4.352 × 10−1 | 4.594 × 101 | 1.285 |
| STD | 6.276 × 10−5 | 7.705 × 101 | 1.977 | 6.282 × 10−2 | 1.667 × 10−1 | 9.523 | 4.334 × 10−1 | |
| F8 | AVG | −2.052 × 104 | −5.031 × 103 | −1.824 × 104 | −1.176 × 104 | −1.053 × 104 | −7.068 × 103 | −1.954 × 104 |
| STD | 2.074 × 102 | 1.335 × 103 | 3.748 × 102 | 6.889 × 102 | 1.966 × 103 | 4.924 × 102 | 1.082 × 103 | |
| F9 | AVG | 0 | 8.151 × 102 | 7.145 × 102 | 8.851 × 102 | 3.946 × 102 | 2.222 × 102 | 4.332 × 102 |
| STD | 0 | 9.659 × 101 | 5.014 × 101 | 1.278 × 101 | 1.397 × 101 | 2.628 × 101 | 1.417 | |
| F10 | AVG | 4.441 × 10−16 | 8.082 | 2.605 | 4.815 | 1.090 × 10−2 | 1.971 × 101 | 6.946 |
| STD | 0 | 8.989 × 10−2 | 2.132 × 10−1 | 2.543 | 2.179 × 10−3 | 5.400 × 10−3 | 6.168 × 10−1 | |
| F11 | AVG | 0 | 4.747 × 101 | 4.632 × 10−2 | 7.983 × 10−1 | 6.488 × 10−2 | 4.328 × 101 | 4.429 |
| STD | 0 | 2.710 | 3.568 × 10−3 | 2.028 × 10−1 | 9.182 × 10−4 | 7.405 | 7.023 × 10−1 | |
| F12 | AVG | 3.018 × 10−2 | 6.694 × 101 | 2.211 | 1.185 × 104 | 5.679 × 104 | 1.592 × 108 | 1.092 × 101 |
| STD | 1.485 × 10−2 | 4.174 × 101 | 1.714 | 2.051 × 103 | 1.489 | 4.429 × 107 | 1.461 | |
| F13 | AVG | 2.857 | 2.595 × 105 | 1.454 × 101 | 8.643 × 104 | 5.953 × 104 | 2.934 × 108 | 5.143 × 103 |
| STD | 3.944 × 10−1 | 1.496 × 105 | 6.216 | 3.281 × 104 | 3.263 × 102 | 2.322 × 108 | 2.547 × 103 | |
| W/L/T | 12/1/0 | 0/13/0 | 0/13/0 | 1/12/0 | 0/13/0 | 0/13/0 | 0/13/0 | |
| OE | 92.31% | 0% | 0% | 7.69% | 0% | 0% | 0% |
| Dimension | Case | − | + | = | R− | R+ | p-Value |
|---|---|---|---|---|---|---|---|
| 30 | GSLEO-AEFA vs. AEFA | 0 | 19 | 4 | 0 | 190 | 1.32 × 10−4 |
| GSLEO-AEFA vs. PSO | 0 | 19 | 4 | 0 | 190 | 1.32 × 10−4 | |
| GSLEO-AEFA vs. DE | 1 | 17 | 5 | 6 | 165 | 5.35 × 10−4 | |
| GSLEO-AEFA vs. JAYA | 0 | 21 | 2 | 0 | 231 | 6.00 × 10−5 | |
| GSLEO-AEFA vs. SCA | 0 | 20 | 3 | 0 | 210 | 8.90 × 10−5 | |
| GSLEO-AEFA vs. CS | 2 | 13 | 8 | 19 | 101 | 1.99 × 10−2 | |
| 50 | GSLEO-AEFA vs. AEFA | 0 | 13 | 0 | 0 | 91 | 1.32 × 10−4 |
| GSLEO-AEFA vs. PSO | 2 | 11 | 0 | 7 | 84 | 1.32 × 10−4 | |
| GSLEO-AEFA vs. DE | 1 | 12 | 0 | 7 | 87 | 5.35 × 10−4 | |
| GSLEO-AEFA vs. JAYA | 0 | 13 | 0 | 0 | 91 | 6.00 × 10−5 | |
| GSLEO-AEFA vs. SCA | 0 | 13 | 0 | 0 | 91 | 8.90 × 10−5 | |
| GSLEO-AEFA vs. CS | 1 | 12 | 0 | 12 | 79 | 1.99 × 10−2 | |
| 100 | GSLEO-AEFA vs. AEFA | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 |
| GSLEO-AEFA vs. PSO | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 | |
| GSLEO-AEFA vs. DE | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 | |
| GSLEO-AEFA vs. JAYA | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 | |
| GSLEO-AEFA vs. SCA | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 | |
| GSLEO-AEFA vs. CS | 0 | 13 | 0 | 0 | 91 | 1.47 × 10−3 |
| Test | Dimension | GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS |
|---|---|---|---|---|---|---|---|---|
| Friedman value | 30 | 1.7 | 4.74 | 4.3 | 3.35 | 5.07 | 5.33 | 3.52 |
| Friedman rank | 1 | 5 | 4 | 2 | 6 | 7 | 3 | |
| Friedman value | 50 | 1.31 | 5.69 | 3.31 | 3.69 | 4 | 5.92 | 4.08 |
| Friedman rank | 1 | 6 | 2 | 3 | 4 | 7 | 5 | |
| Friedman value | 100 | 1 | 5.69 | 3.08 | 4.62 | 3.69 | 5.77 | 4.15 |
| Friedman rank | 1 | 6 | 2 | 5 | 3 | 7 | 4 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | |
|---|---|---|---|---|---|---|---|
| F1 | 23.990 | 23.874 | 40.696 | 1.801 | 10.423 | 10.757 | 9.059 |
| F2 | 23.468 | 23.744 | 37.481 | 1.889 | 10.821 | 11.391 | 9.719 |
| F3 | 30.354 | 26.628 | 14.308 | 4.643 | 7.535 | 14.579 | 15.415 |
| F4 | 25.580 | 23.877 | 11.405 | 1.593 | 2.984 | 10.922 | 9.229 |
| F5 | 25.433 | 24.087 | 11.716 | 1.926 | 3.235 | 11.538 | 9.476 |
| F6 | 32.218 | 23.863 | 11.717 | 1.811 | 3.135 | 11.492 | 9.388 |
| F7 | 26.256 | 24.369 | 12.371 | 2.109 | 3.374 | 11.440 | 9.427 |
| F8 | 25.878 | 24.007 | 12.553 | 1.805 | 3.158 | 11.541 | 9.496 |
| F9 | 25.843 | 24.081 | 11.327 | 1.857 | 3.075 | 10.961 | 9.703 |
| F10 | 54.693 | 24.279 | 12.558 | 2.208 | 3.476 | 11.874 | 33.917 |
| F11 | 92.284 | 24.405 | 12.796 | 2.244 | 3.545 | 21.765 | 36.307 |
| F12 | 90.376 | 25.107 | 13.412 | 3.071 | 4.267 | 12.985 | 37.827 |
| F13 | 28.186 | 25.230 | 13.675 | 3.263 | 4.528 | 12.889 | 11.843 |
| F14 | 27.039 | 15.286 | 12.312 | 12.026 | 10.989 | 12.206 | 21.921 |
| F15 | 8.413 | 6.382 | 2.331 | 1.406 | 0.968 | 2.211 | 2.726 |
| F16 | 6.080 | 4.495 | 0.983 | 0.740 | 0.312 | 0.911 | 1.224 |
| F17 | 6.240 | 4.504 | 1.017 | 0.762 | 0.331 | 0.947 | 1.290 |
| F18 | 6.562 | 4.608 | 1.084 | 0.856 | 0.414 | 1.027 | 1.444 |
| F19 | 9.443 | 6.186 | 2.421 | 1.785 | 1.328 | 2.296 | 3.366 |
| F20 | 11.910 | 8.449 | 3.723 | 1.913 | 1.719 | 3.529 | 4.399 |
| F21 | 17.979 | 10.459 | 6.707 | 5.602 | 5.251 | 6.713 | 10.894 |
| F22 | 21.677 | 12.070 | 8.376 | 7.261 | 6.798 | 8.481 | 16.520 |
| F23 | 27.239 | 14.630 | 24.862 | 9.742 | 9.256 | 11.081 | 21.001 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | |
|---|---|---|---|---|---|---|---|
| x(1) | 1.00 | 0.43 | −1.00 | 1.00 | −0.63 | −1.06 | −1.04 |
| x(2) | 5.00 | 0.15 | −5.00 | 5.00 | 0.00 | 0.00 | −5.02 |
| x(3) | −1.50 | 2.03 | 1.50 | 1.50 | 4.29 | 0.69 | −1.36 |
| x(4) | 4.80 | 4.98 | 4.80 | −4.80 | 4.87 | 0.00 | −4.75 |
| x(5) | 2.00 | 0.83 | −2.00 | −2.00 | 0.18 | −4.45 | 2.01 |
| x(6) | 4.90 | −4.41 | −4.90 | 4.90 | 0.08 | −4.88 | −4.90 |
| f(x) | 0 | 1.963 × 101 | 1.950 × 10−27 | 7.796 × 10−21 | 1.164 × 101 | 1.220 × 101 | 1.888 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | |
|---|---|---|---|---|---|---|---|
| x(1) | 0.673 | 1.338 | 0.000 | 0.319 | 0.551 | 0.000 | 2.140 |
| x(2) | 0.329 | 3.307 | 4.000 | 0.567 | 0.035 | 0.000 | 2.789 |
| x(3) | 0.847 | 2.115 | 3.142 | 1.947 | 0.745 | 0.000 | 1.473 |
| x(4) | 0.316 | 3.639 | −4.000 | −3.980 | −0.237 | 1.184 | 0.508 |
| x(5) | −0.608 | −3.723 | −0.687 | 3.761 | 0.661 | 0.008 | −0.682 |
| x(6) | 0.884 | 0.427 | 4.000 | 3.855 | 0.820 | 0.341 | 0.722 |
| x(7) | −0.292 | 0.706 | −1.507 | −3.970 | −0.992 | 0.337 | 0.393 |
| x(8) | −0.419 | 1.807 | −3.925 | 2.768 | 1.094 | −1.074 | 0.265 |
| x(9) | −0.750 | −3.380 | −0.706 | 4.250 | 0.559 | 0.005 | 0.443 |
| x(10) | −0.533 | −1.841 | −1.260 | −4.250 | −0.219 | −0.909 | −1.221 |
| x(11) | 0.298 | −2.964 | −4.109 | 4.500 | 0.658 | 0.382 | 0.694 |
| x(12) | −0.148 | −3.440 | 0.286 | 4.453 | 1.910 | −4.500 | −1.556 |
| x(13) | 0.359 | 2.205 | −1.105 | 4.500 | 2.766 | 0.220 | 0.327 |
| x(14) | −0.092 | 2.806 | −4.750 | −3.053 | 0.004 | 0.575 | −0.435 |
| x(15) | −0.019 | 1.921 | −1.239 | −1.506 | −4.750 | 0.921 | −0.238 |
| x(16) | −0.390 | 2.510 | −3.925 | −4.357 | −0.384 | 0.172 | −2.438 |
| x(17) | −0.681 | 2.646 | −0.770 | 3.520 | 0.064 | −0.396 | 0.519 |
| x(18) | 0.193 | −2.276 | 5.000 | 5.000 | 0.109 | 0.901 | −2.169 |
| x(19) | 0.601 | 0.835 | −1.502 | −4.099 | 0.002 | 0.314 | 0.090 |
| x(20) | −0.780 | 3.274 | −4.848 | 5.202 | −0.400 | −4.879 | −1.240 |
| x(21) | −0.879 | 1.261 | −0.337 | 5.188 | 1.740 | 0.073 | 1.516 |
| x(22) | 0.596 | −0.687 | −3.449 | −5.197 | 0.242 | −0.085 | 0.888 |
| x(23) | −1.042 | −0.199 | −1.414 | 4.858 | 0.795 | −0.164 | −1.337 |
| x(24) | 0.065 | 3.430 | 4.400 | 4.681 | −0.010 | −0.999 | 0.042 |
| x(25) | −0.130 | 0.348 | −0.642 | −4.883 | 1.285 | −1.179 | −1.877 |
| x(26) | −1.369 | 3.231 | −4.341 | 3.459 | 0.341 | 0.350 | −0.091 |
| x(27) | −0.494 | 2.142 | −0.456 | 4.257 | 0.277 | 0.044 | −1.566 |
| x(28) | −0.289 | 0.692 | −0.814 | −3.372 | −0.743 | −0.659 | 1.224 |
| x(29) | 0.147 | 4.094 | −3.390 | 5.390 | 0.003 | −0.579 | −0.373 |
| x(30) | 0.774 | 1.788 | −0.224 | 4.311 | 1.361 | 0.296 | 0.015 |
| f(x) | −26.027 | −7.072 | −15.126 | −10.615 | −14.233 | −11.513 | −11.646 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | |
|---|---|---|---|---|---|---|---|
| x(1) | 0.000 | 2.497 | 1.984 | 3.427 | 1.135 | 4.000 | 1.613 |
| x(2) | 4.000 | 1.998 | 2.758 | 3.992 | 3.908 | 0.000 | 0.041 |
| x(3) | 3.142 | 2.318 | 2.274 | 0.482 | 0.544 | 0.000 | 1.485 |
| x(4) | −1.000 | 3.773 | −0.367 | −1.000 | −1.000 | −0.643 | 2.922 |
| x(5) | −1.000 | −0.847 | 2.762 | −0.564 | 2.594 | 1.112 | 1.791 |
| x(6) | 3.708 | 2.595 | 2.675 | 1.612 | 1.478 | 0.203 | 3.856 |
| x(7) | 2.029 | 1.302 | 1.293 | −0.282 | 0.650 | −0.004 | 2.913 |
| x(8) | 3.931 | 4.107 | −0.081 | 4.250 | −0.336 | 4.250 | 4.246 |
| x(9) | 4.250 | 1.767 | 3.521 | −1.000 | 1.907 | 0.869 | −0.678 |
| x(10) | 4.250 | 1.168 | 2.749 | 4.250 | 3.417 | 0.378 | 2.498 |
| x(11) | 0.988 | 3.042 | 4.337 | 2.937 | −0.068 | −1.000 | 1.256 |
| x(12) | −1.000 | −0.259 | 0.648 | 4.500 | 0.543 | −0.008 | −0.216 |
| x(13) | −0.252 | 3.947 | 2.291 | 4.500 | 0.733 | 2.123 | 2.467 |
| x(14) | 0.925 | −0.869 | −0.738 | 0.681 | 3.206 | 4.536 | 3.973 |
| x(15) | 4.750 | 0.265 | 1.450 | 3.802 | 2.760 | 0.635 | 3.515 |
| x(16) | 1.140 | 3.452 | 3.454 | 0.258 | 4.672 | 1.995 | 0.205 |
| x(17) | −0.914 | 3.721 | −1.000 | 1.553 | −1.000 | 0.314 | 0.707 |
| x(18) | 4.581 | 1.334 | 3.504 | 2.542 | −1.000 | 1.082 | −0.223 |
| x(19) | 5.000 | 2.934 | 0.756 | 1.062 | −0.443 | 0.957 | 1.043 |
| x(20) | −1.000 | 4.288 | 4.810 | 0.250 | 5.148 | 0.865 | 2.234 |
| x(21) | −0.085 | −0.324 | 1.972 | 1.091 | 2.056 | 4.665 | 1.313 |
| x(22) | 0.438 | 1.828 | 4.238 | −1.000 | 5.167 | 1.721 | 0.115 |
| x(23) | 5.500 | −0.530 | 0.585 | 1.432 | 1.281 | 3.192 | −0.580 |
| x(24) | 4.847 | −0.955 | 1.934 | 0.299 | −0.048 | −0.799 | 4.081 |
| x(25) | 1.548 | 5.123 | 3.034 | 3.795 | −0.393 | −0.054 | 3.977 |
| x(26) | 5.689 | 1.252 | 4.830 | 2.514 | −1.000 | −0.474 | 2.986 |
| x(27) | 2.827 | 2.750 | 2.998 | 2.063 | −0.757 | 2.376 | 1.977 |
| x(28) | −0.686 | 4.798 | 1.078 | 1.325 | 5.491 | −1.000 | 4.752 |
| x(29) | −0.972 | 4.188 | 3.857 | 2.934 | −0.865 | −0.077 | 3.163 |
| x(30) | 6.000 | 4.687 | 4.240 | −1.000 | 1.094 | 4.160 | 4.110 |
| f(x) | −34.108 | −14.888 | −30.559 | −24.606 | −31.065 | −20.620 | −31.737 |
| GSLEO-AEFA | AEFA | PSO | DE | JAYA | SCA | CS | ||
|---|---|---|---|---|---|---|---|---|
| s1 | AVG | 0.000 | 1.351 | 1.083 × 10−2 | 1.603 | 5.448 | 1.370 × 101 | 5.477 |
| STD | 0.000 | 2.469 × 10−1 | 5.946 × 10−4 | 2.752 × 10−1 | 4.379 | 1.915 | 5.862 × 10−1 | |
| s2 | AVG | 8.611 × 10−7 | 6.839 × 101 | 7.255 × 101 | 3.407 × 101 | 9.047 × 101 | 8.684 × 101 | 8.040 × 101 |
| STD | 1.756 × 10−6 | 9.564 | 4.589 | 5.161 | 1.687 × 10+1 | 1.192 × 101 | 3.057 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adegboye, O.R.; Deniz Ülker, E. Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm and Its Engineering Application. Appl. Sci. 2023, 13, 4157. https://doi.org/10.3390/app13074157
Adegboye OR, Deniz Ülker E. Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm and Its Engineering Application. Applied Sciences. 2023; 13(7):4157. https://doi.org/10.3390/app13074157
Chicago/Turabian StyleAdegboye, Oluwatayomi Rereloluwa, and Ezgi Deniz Ülker. 2023. "Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm and Its Engineering Application" Applied Sciences 13, no. 7: 4157. https://doi.org/10.3390/app13074157
APA StyleAdegboye, O. R., & Deniz Ülker, E. (2023). Gaussian Mutation Specular Reflection Learning with Local Escaping Operator Based Artificial Electric Field Algorithm and Its Engineering Application. Applied Sciences, 13(7), 4157. https://doi.org/10.3390/app13074157






