Speed Limit of Linear Induction Motor Subway Trains Running through 65 m Radius Curves on Yard Line
Abstract
:1. Introduction
2. Train-Track Coupling Dynamic Model
2.1. Train System
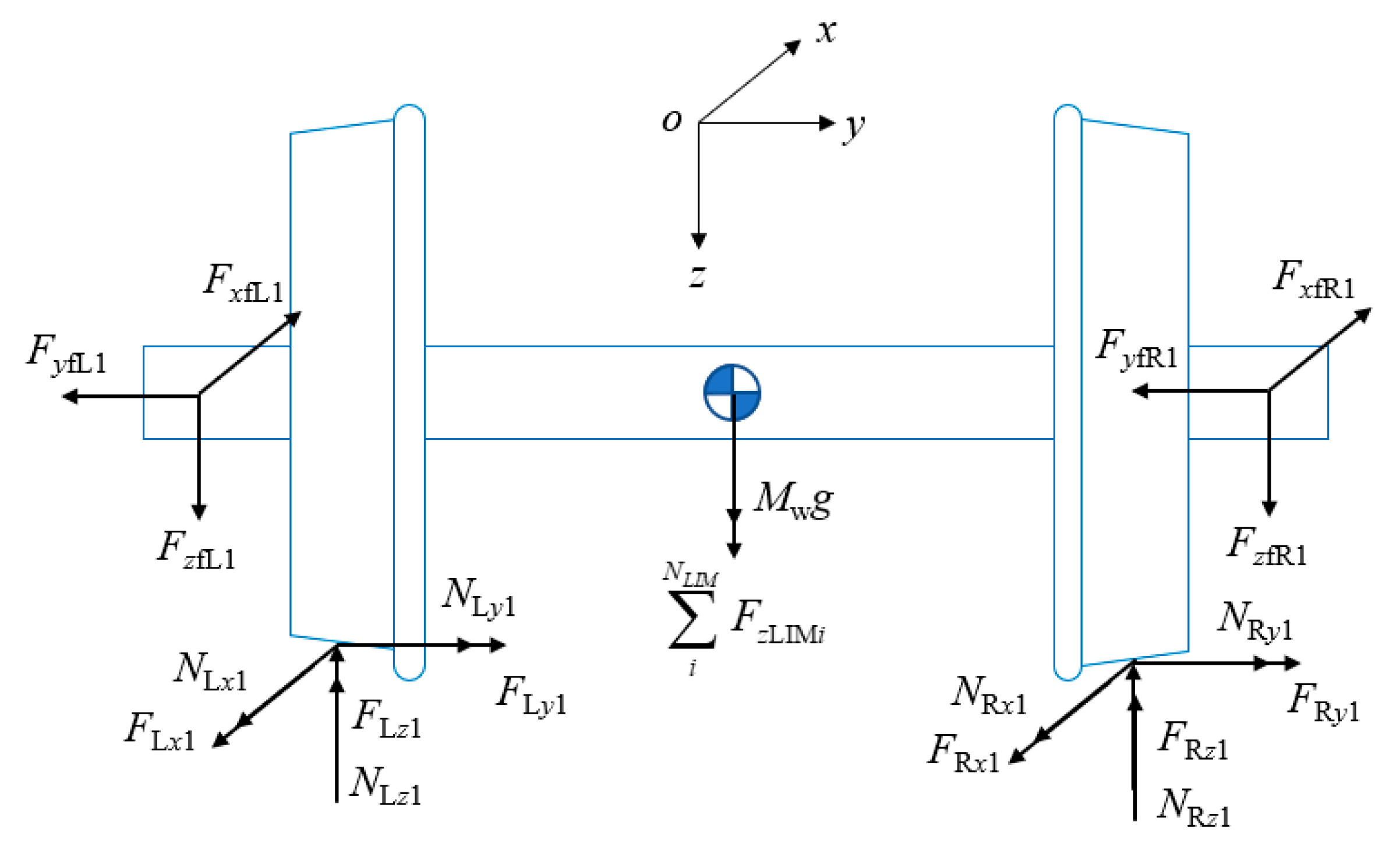
2.1.1. Vehicle System
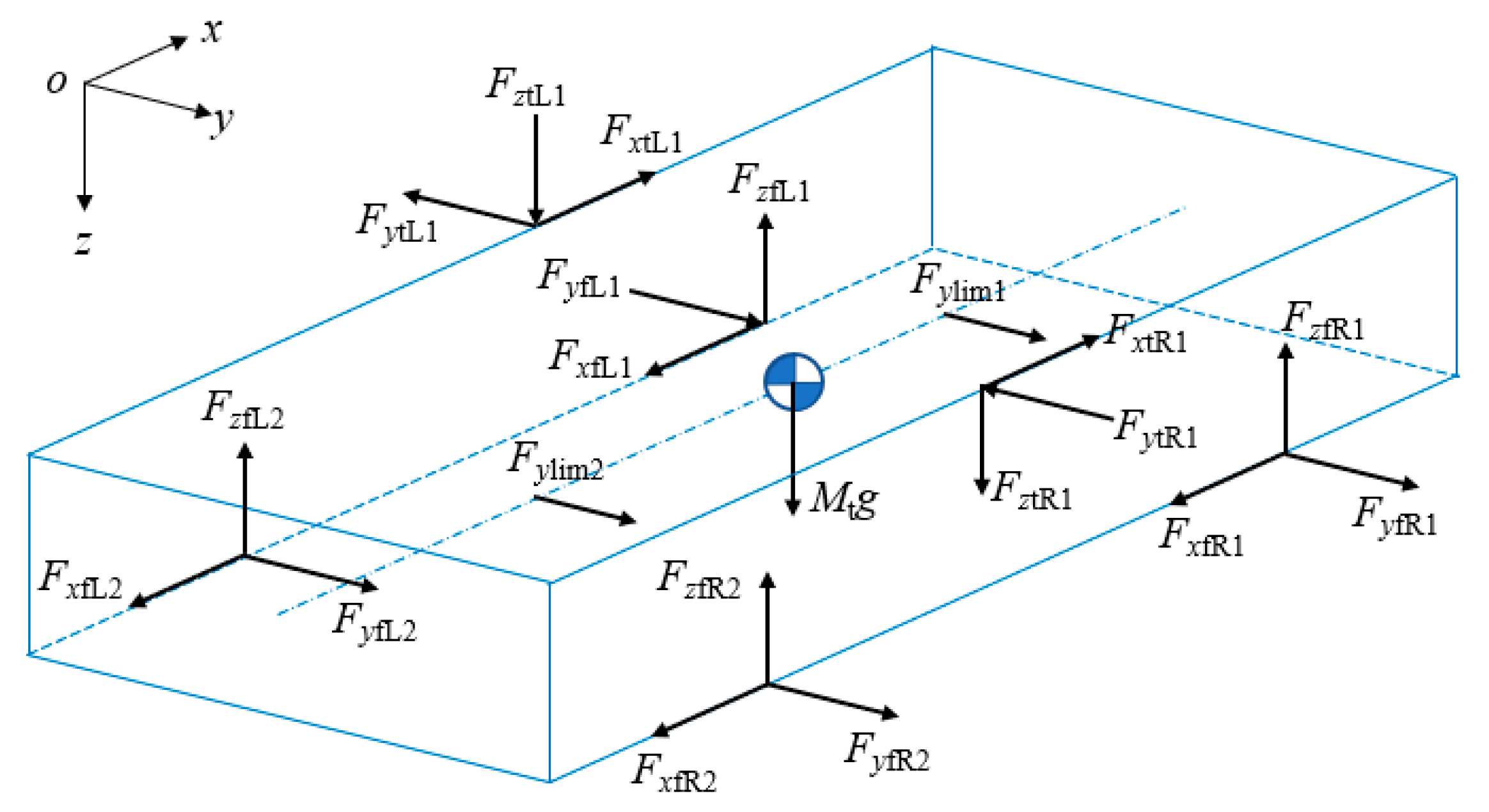
2.1.2. Primary Winding Vibration Differential Equation
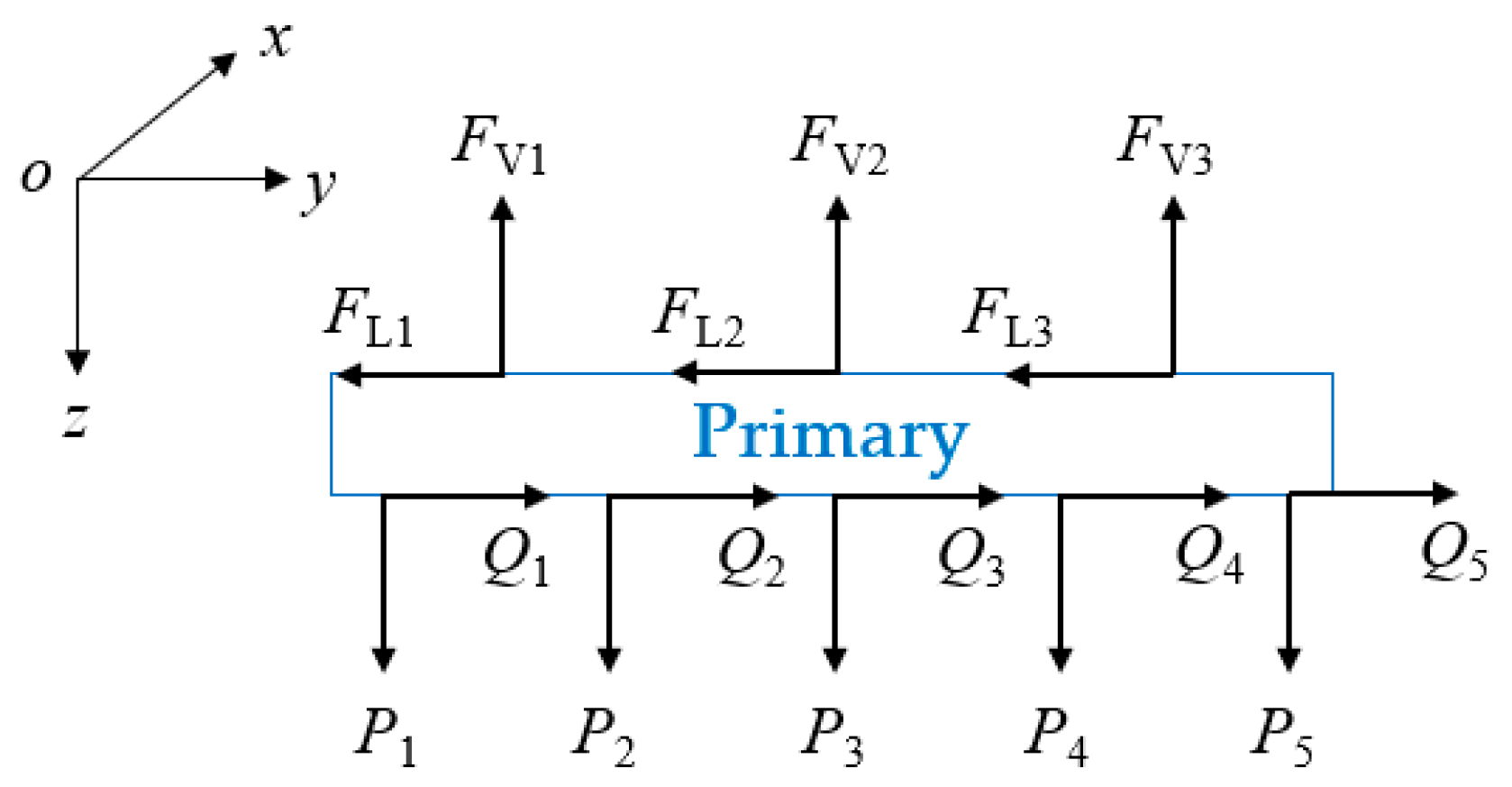
2.1.3. Vehicle End Connection System Model
2.2. Track System
2.2.1. Rail System
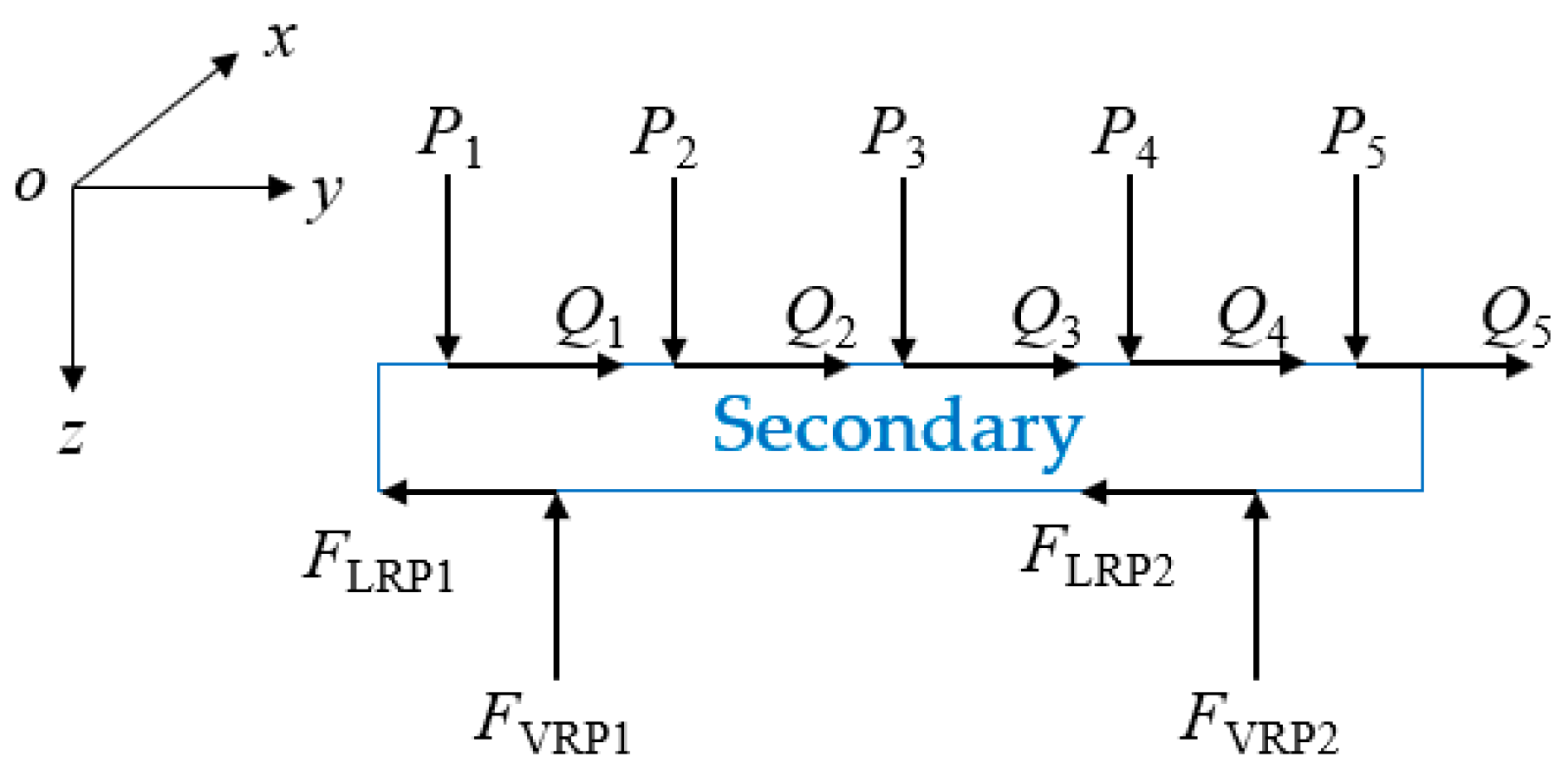
2.2.2. Secondary Conductive Plate Vibration Differential Equation
2.3. Wheel-Rail Interaction System
2.3.1. Wheel-Rail Spatial Contact Geometry Model [17,18]
2.3.2. Normal Force Calculation Model
2.3.3. Creep Force Calculation Model
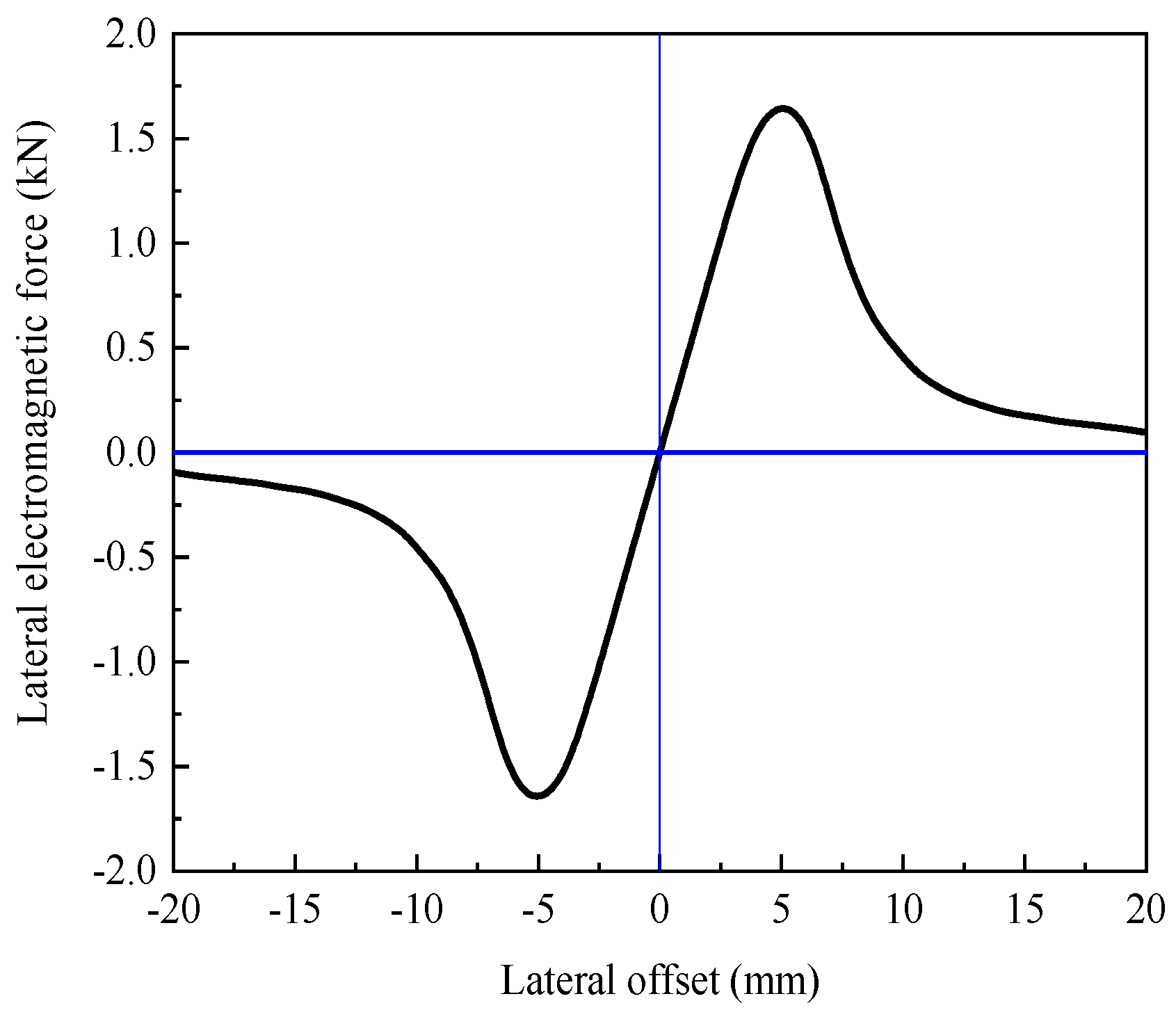
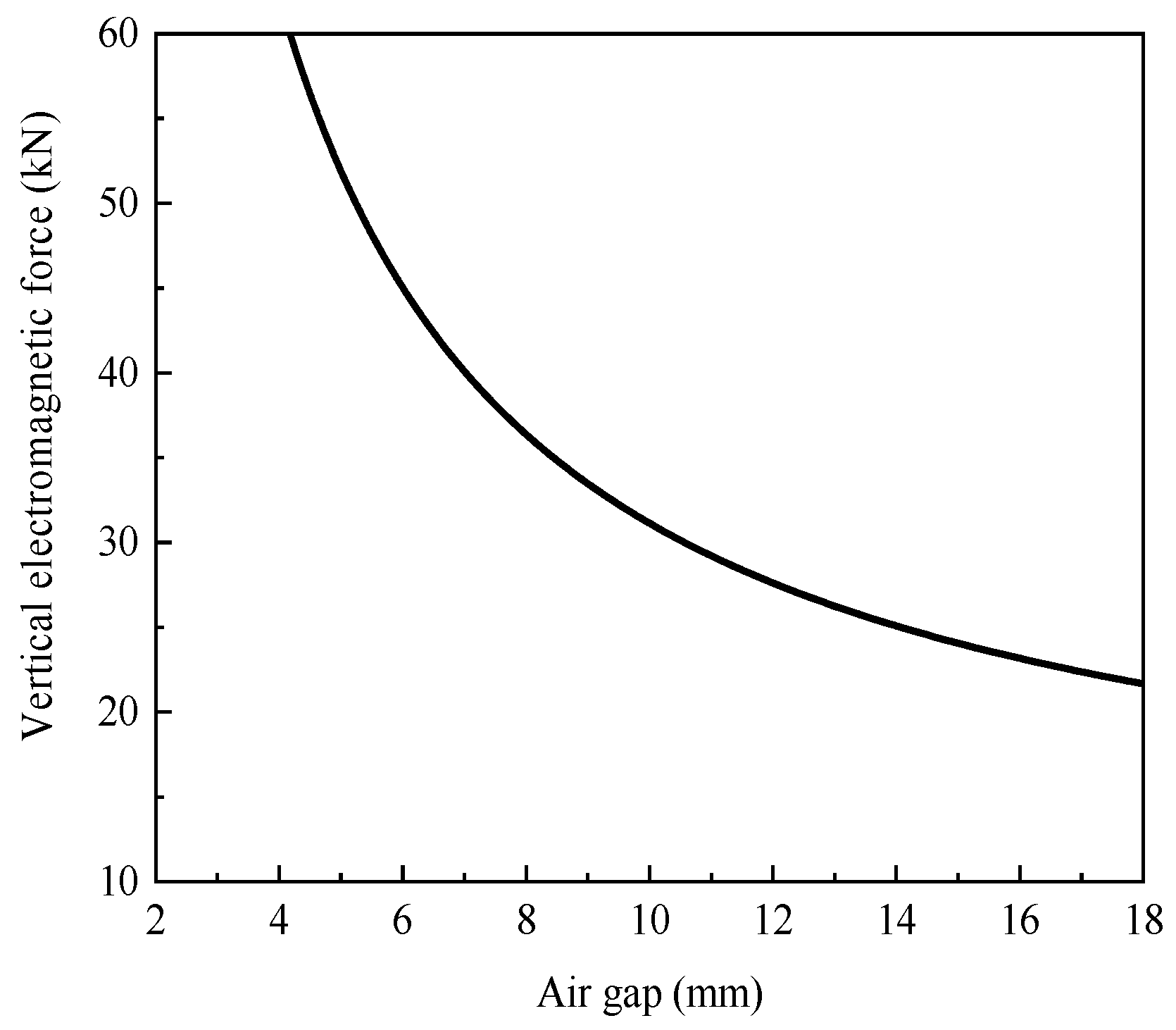
2.4. Electromagnetic Interaction System
3. Operational Safety Evaluation Criteria
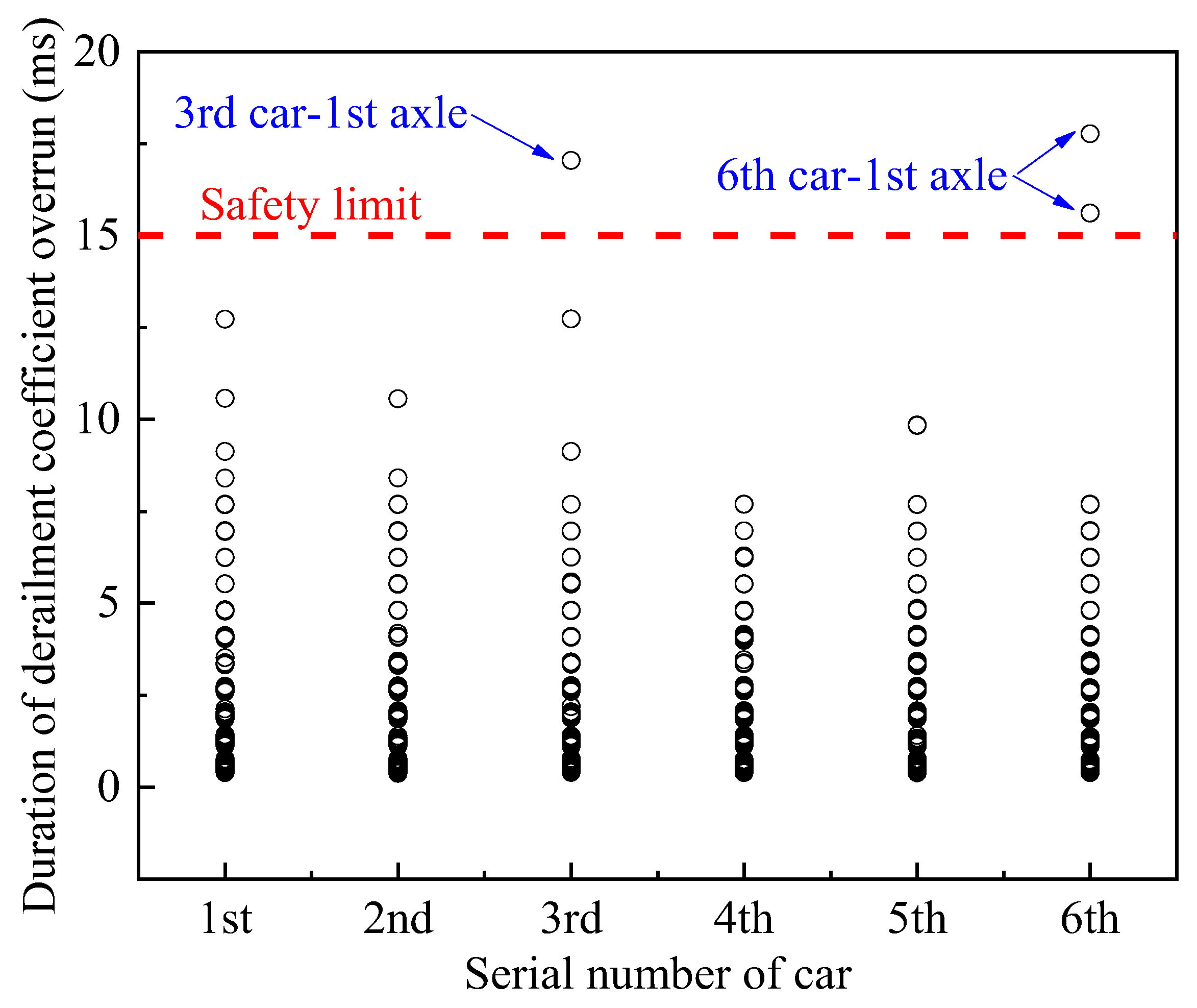
3.1. Derailment Coefficient
3.2. Wheel Unloading Rate
3.3. Axle Lateral Force
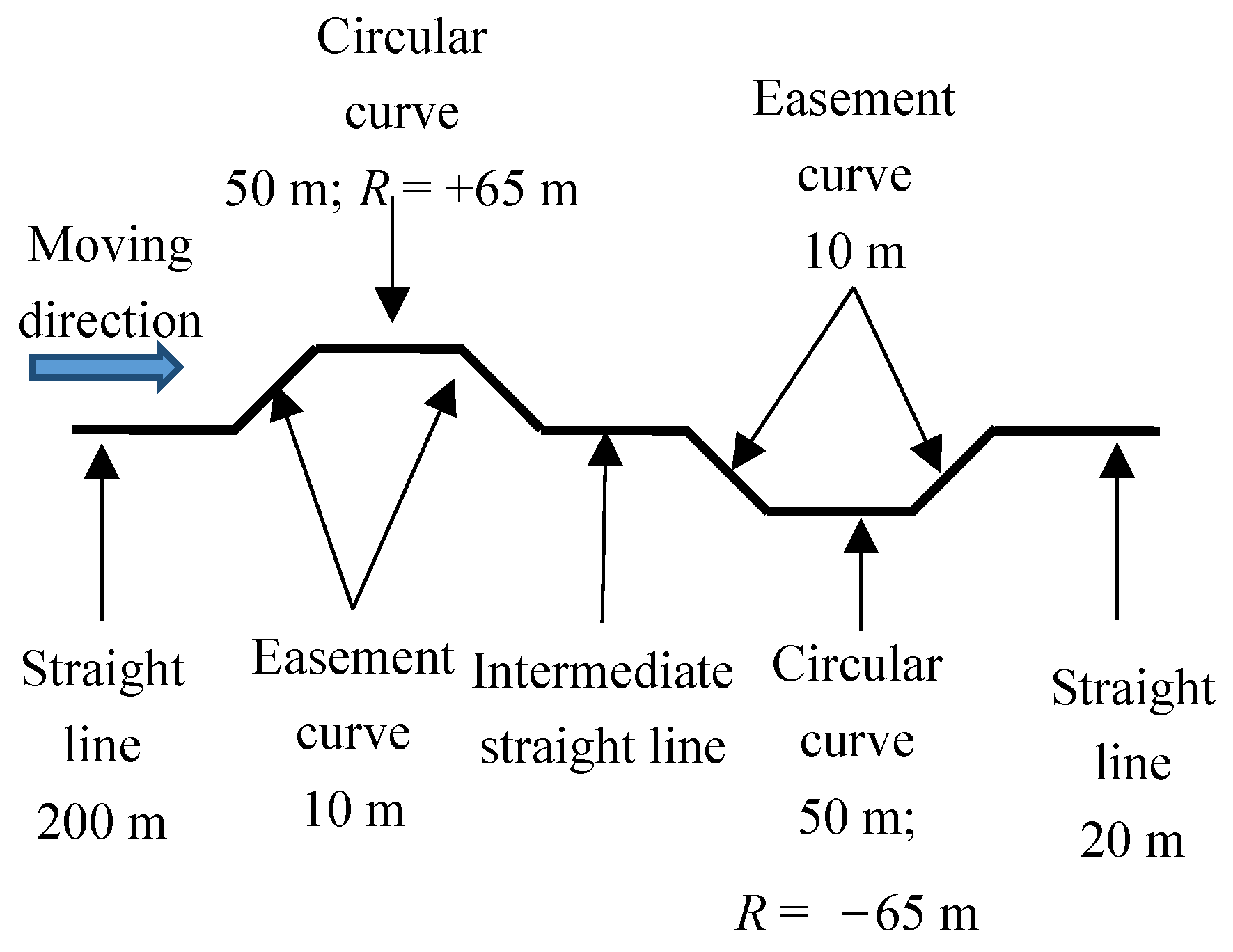
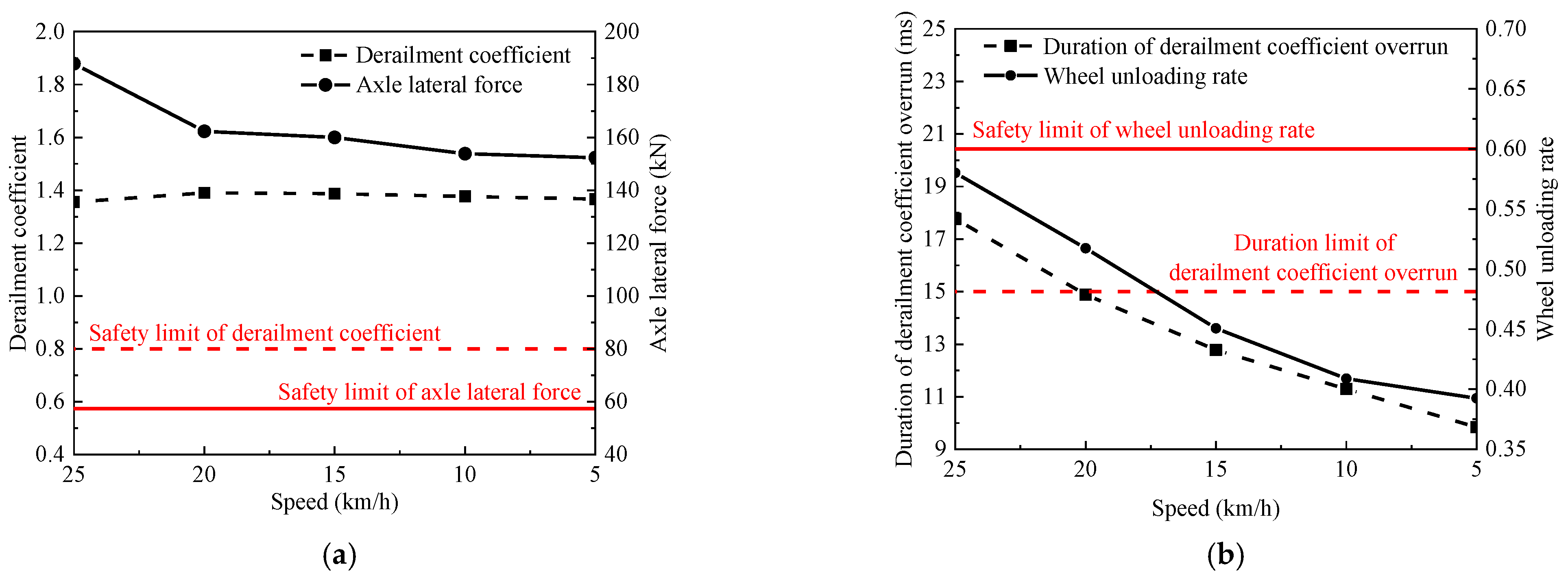
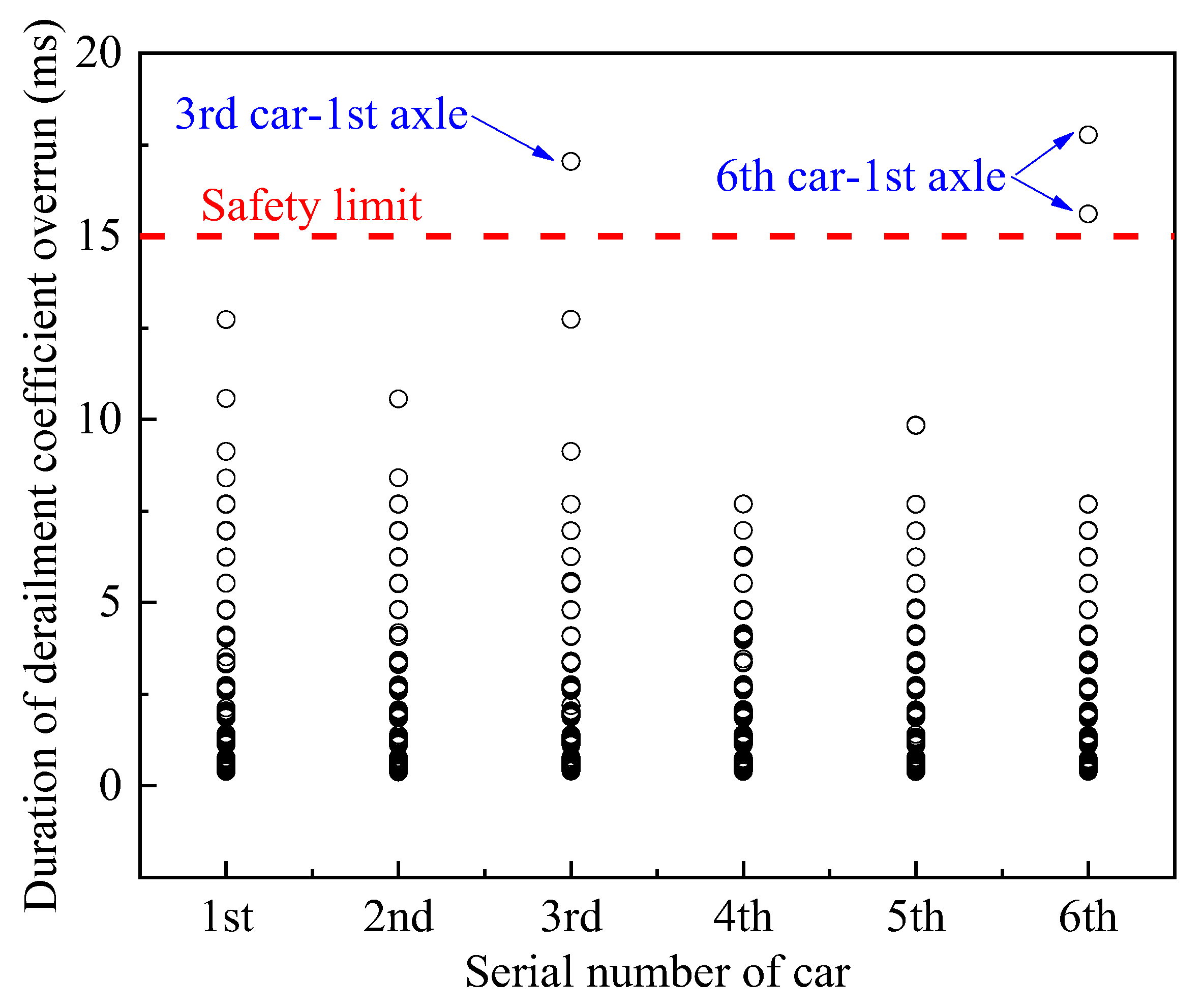
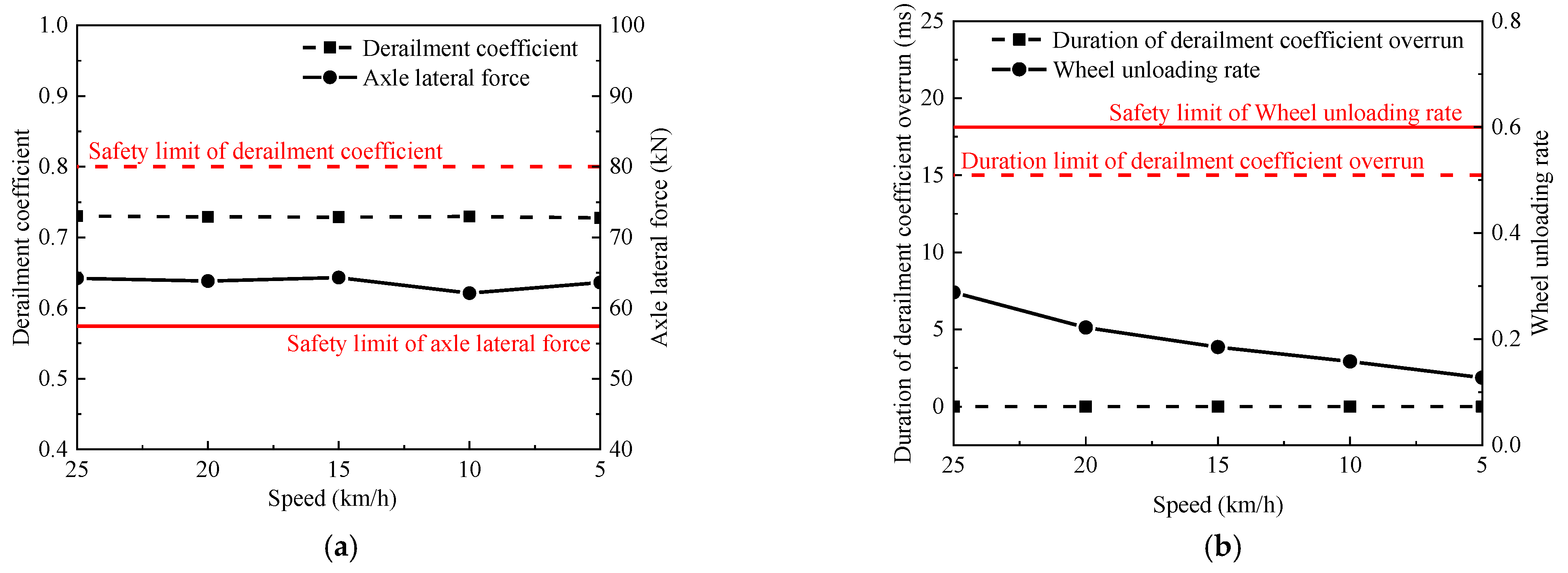
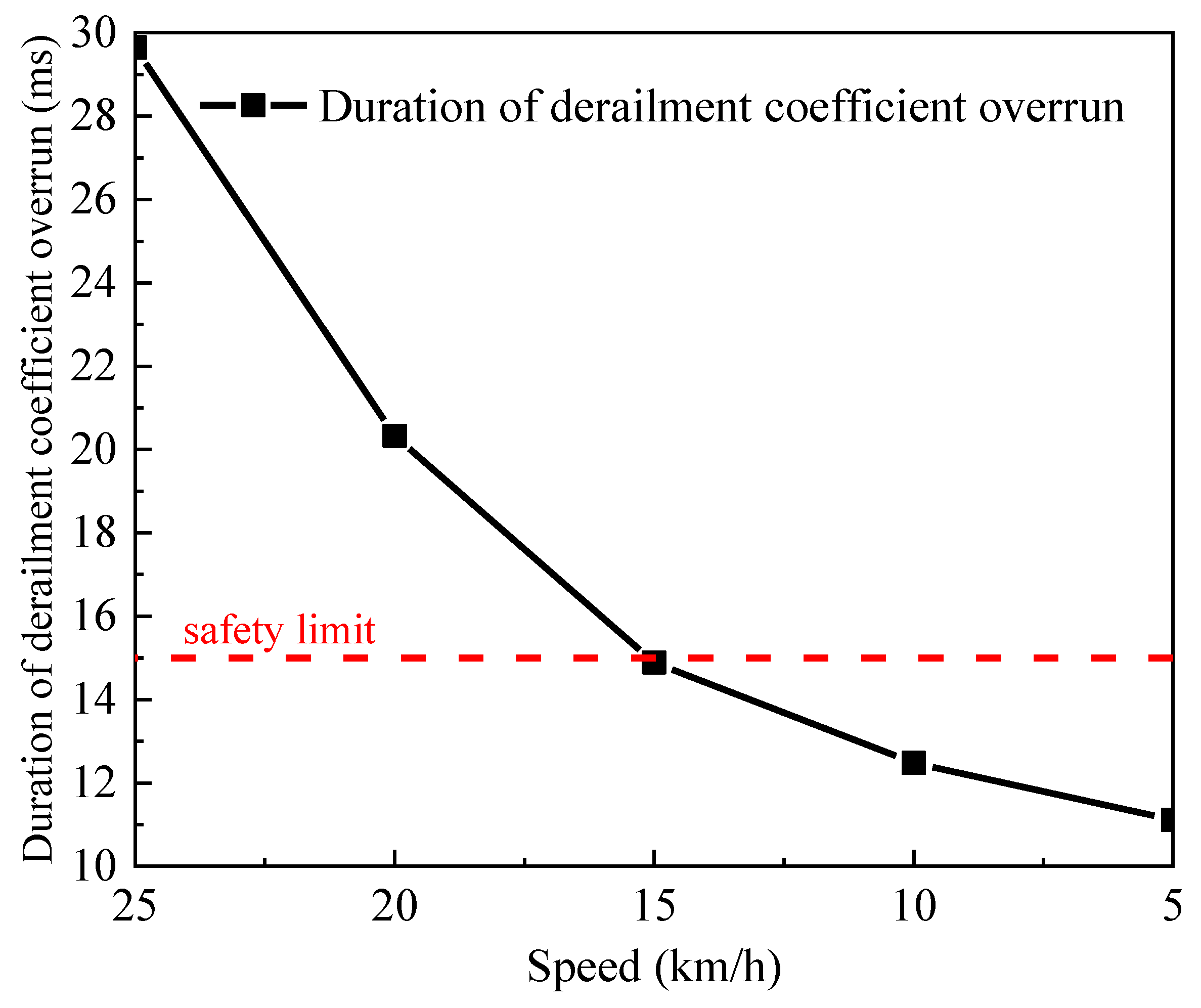
4. Derailment Safety and Speed Limit Analysis
4.1. Conventional Conditions
4.2. Wheel-Rail Extreme Wear Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bollinger, C.R.; Ihlanfeldt, K.R. The Impact of Rapid Rail Transit on Economic Development: The Case of Atlanta’s MARTA. J. Urban Econ. 1997, 42, 179–204. [Google Scholar] [CrossRef]
- Hellinger, R.; Mnich, P. Linear Motor-Powered Transportation: History, Present Status, and Future Outlook. Proc. IEEE 2009, 97, 1892–1900. [Google Scholar] [CrossRef]
- Zeng, H. Advantages and application of linear induction motor in urban transit system. Convert. Technol. Electr. Tract. 2008, 4, 51–53, 59. [Google Scholar]
- Lv, G. Review of the Application and Key Technology in the Linear Motor for the Rail Transit. Proc. CSEE 2020, 40, 5665–5675. [Google Scholar]
- Isobe, E.; Cho, J.; Morihisa, I.; Sekizawa, T.; Tanaka, R. Linear metro transport systems for the 21st century. Hitachi Rev. 1999, 48, 144–148. [Google Scholar]
- Li, N. Characteristics and application of linear motor driven urban mass transit system. Electr. Locomot. Mass Transit Veh. 2005, 28, 3–52. [Google Scholar]
- Hobbs, A.E.W.; Pearce, T.G. The lateral dynamics of the linear induction motor test vehicle. J. Dyn. Syst. J. Dyn. Syst. Meas. Control 1974, 96, 147–157. [Google Scholar] [CrossRef]
- Feng, Y.W.; Wei, Q.C.; Gao, L.; Shi, J. Dynamic simulation of vehicle-track coupling vibrations for linear metro system. In Environmental Vibrations: Prediction, Monitoring, Mitigation and Evaluation (ISEV 2005); CRC Press: Boca Raton, FL, USA, 2021; pp. 131–136. [Google Scholar]
- Li, L. Study on Spatial Coupling Dunamic Characteristics of Vechicle-Turnout in Linear Induction Motor Wheel/Rail Traffic System. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2009. [Google Scholar]
- Li, L.; Xiao, X.B.; Jin, X.S. Interaction of subway LIM vehicle with ballasted track in polygonal wheel wear development. Acta Mech. Sin. 2011, 27, 297–307. [Google Scholar]
- Liu, G. Influence of Electromagnetic Force on the Dynamic Performance of Linear Motor Metro Vehicle. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2015. [Google Scholar]
- Jang, S.M.; Park, Y.S.; Sung, S.Y.; Lee, K.B.; Cho, H.W.; You, D.J. Dynamic characteristics of a linear induction motor for predicting operating performance of magnetic levitation vehicles based on electromagnetic field theory. IEEE Trans. Magn. 2011, 47, 3673–3676. [Google Scholar] [CrossRef]
- Xiong, J.Y. Study on Dynamic Response of Linear Motor Metro Vehicle Coupled with Slab Track. Ph.D. Thesis, South West Jiaotong University, Chengdu, China, 2014. [Google Scholar]
- Liu, B.B.; Zheng, J.; Luo, R.; Wu, P.B. Modeling and dynamics simulation of vehicle with linear induction motor. J. Traffic Transp. Eng. 2009, 9, 37–43. [Google Scholar]
- Yang, Y.F. Study on Dynamic Interactions of Linear Motor Metro Vehicle Coupled with Track. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Zang, C.Z.; Wei, Q.C.; Nie, X.L. Dynamic response of the LIM wheel/rail train in curved section. J. Harbin Inst. Technol. 2019, 51, 110–116. [Google Scholar]
- Chen, G.; Zhai, W.M.; Zuo, H.F. The New Wheel/Rail 3-Dimensionally Dynamically Coupling Model. J. Vib. Eng. 2001, 14, 402–408. [Google Scholar]
- Chen, G.; Zhai, W.M. A New Wheel Rail Spatially Dynamic Coupling Model and its Verification. Veh. Syst. Dyn. 2004, 41, 301–322. [Google Scholar] [CrossRef]
- Jin, X.S.; Liu, Q.Y. Tribology of Wheel and Rail; China Railway Publishing House: Beijing, China, 2004. [Google Scholar]
- Zhai, W.M. Vehicle-Track Coupled Dynamics, 4th ed.; Science Press: Beijing, China, 2015. [Google Scholar]
- Kalker, J.J. On the rolling Contact of Two Elastic Bodies in the Presence of Dry Friction. Ph.D. Thesis, Delft University, Delft, The Netherland, 1967. [Google Scholar]
- Shen, Z.Y.; Hedrick, J.K.; Elkins, J.A. A comparison of alternative creep force models for rail vehicle dynamic analysis. Veh. Syst. Dyn. 1983, 12, 79–83. [Google Scholar] [CrossRef]
- Ishida, H.; Matsuo, M. Safety criteria for evaluation of railway vehicle derailment. Q. Rep. RTRI 1999, 40, 18–25. [Google Scholar] [CrossRef] [Green Version]









| Degree of Freedom | Longitudinal | Lateral | Vertical | Swing | Nodding | Yaw |
|---|---|---|---|---|---|---|
| Car body | Xc | Yc | Zc | Φc | βc | Ψc |
| Bogie frames (i = 1~2) | Xti | Yti | Zti | Φti | βti | Ψti |
| Wheelsets (i = 1~4) | Xwi | Ywi | Zwi | Φwi | βwi | Ψwi |
| Vehicle Components | Value (Unit) |
|---|---|
| Mc | 42.8 (t) |
| Mt | 1.1 (t) |
| Mw | 1.0 (t) |
| Icx, Icy, Icz | 51.0, 986.3, 988.0 (t·m2) |
| Itx, Ity, Itz | 1.1, 0.4, 1.0 (t·m2) |
| Iwx, Iwy, Iwz | 0.6, 0.1, 0.6 (t·m2) |
| Primary suspension stiffness (x, y and z axes) | 5.2, 5.2, 1.2 (kN/mm) |
| Primary suspension damping (x, y and z axes) | 0.0, 0.0, 4.0 (kN·s/m) |
| Secondary suspension stiffness (x, y and z axes) | 0.1, 0.1, 0.4 (kN/mm) |
| Secondary suspension damping (x, y and z axes) | 200, 60, 60 (kN·s/m) |
| dw, ds | 0.6, 0.6 (m) |
| lc, lt | 6.0, 1.0 (m) |
| Htw | 0.4 (m) |
| HcB | 0.7 (m) |
| HBt | 0.3 (m) |
| r0 | 0.365 (m) |
| a0 | 0.7465 (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Wang, J.; Han, J.; Jin, X. Speed Limit of Linear Induction Motor Subway Trains Running through 65 m Radius Curves on Yard Line. Appl. Sci. 2023, 13, 4163. https://doi.org/10.3390/app13074163
Zhou Q, Wang J, Han J, Jin X. Speed Limit of Linear Induction Motor Subway Trains Running through 65 m Radius Curves on Yard Line. Applied Sciences. 2023; 13(7):4163. https://doi.org/10.3390/app13074163
Chicago/Turabian StyleZhou, Qing, Jianuo Wang, Jian Han, and Xuesong Jin. 2023. "Speed Limit of Linear Induction Motor Subway Trains Running through 65 m Radius Curves on Yard Line" Applied Sciences 13, no. 7: 4163. https://doi.org/10.3390/app13074163
APA StyleZhou, Q., Wang, J., Han, J., & Jin, X. (2023). Speed Limit of Linear Induction Motor Subway Trains Running through 65 m Radius Curves on Yard Line. Applied Sciences, 13(7), 4163. https://doi.org/10.3390/app13074163






